运筹学课件第十章排队论
- 格式:ppt
- 大小:351.00 KB
- 文档页数:64






排队论主要公式一、状态平衡方程()()()()⎪⎩⎪⎨⎧=-=-<≤=++---++--12.10,011.10,010.10,1,01111001111k k k k n n n n n n n p p p p k n p p p μλμλμμλλ当系统状态为可数状态时,将上述第一个式子的k 换成∞,而将第三式去掉。
二、的关系为和q s q s W W L L ,,()()()()00;001;10.20210.2113;10.224.10.23s q q s q s q L W L W W W L L Littie λλμλμ===+=+上述四个式子称为公式。
三、标准的M/M/1模型(1)系统在稳定状态下处于状态n 的概率()()13.10,1,1,1,10<≥-=-=ρρρρn p p n n其中μλρ/=,它是系统的平均到达率与平均服务率之比,称为服务强度或称为话务强度。
(2)系统的运行指标10系统中的平均顾客数L S 为()14.10;10,10<<-=-==∑∞=ρλμλρρN n S np L02系统中等待的平均顾客数q L 为()()15.10;1121λμρλρρ-=-=-=∑∞=n n q p n L03 顾客在系统中的逗留时间W 的分布及平均逗留时间S W 为()()()[]()1,0,10.161;10.17s F e W E μλωωωωμλ--=-≥==-04 顾客在系统中的等待时间分布及平均等待时间q W 为()()()()()19.10.118.10,0,1λμρλμμλμωρωωλμ-=-=-=≥-=--s q q W W e F//1N M M 四、系统容量有限制(设为)的模型(1)系统在稳态下处于状态n 的概率01系统空闲的概率为()24.10.1,11;1,1110⎪⎪⎩⎪⎪⎨⎧=+≠--=+ρρρρN p N02 系统中有n 个客户的概率为()()01,1,1,1110.251,1;1nnn n N N p p N ρρρρρρ⎧-≠≤≤⎪⎪-+==⎨⎪=⎪+⎩其中1,/<=p 此处μλρ的条件可以取消。

运筹学100排队论第10章排队论第一节排队服务系统的基本概念一、排队系统的特性排队问题的实例:超市付款,自动取款机取款,医院门诊,乘公交车,设备修理。
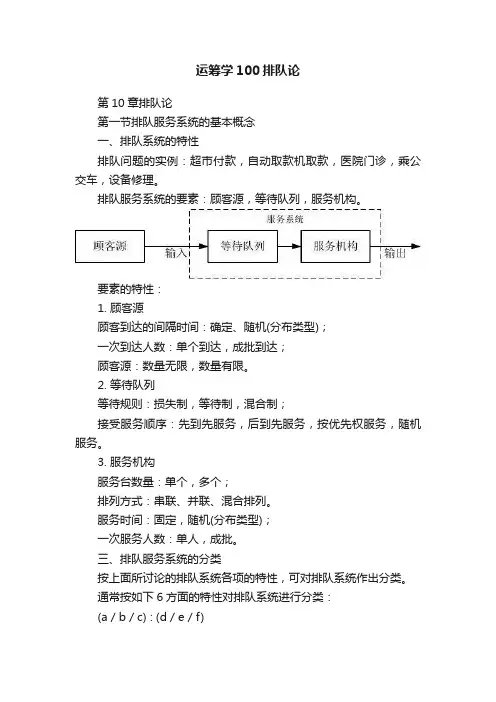
排队服务系统的要素:顾客源,等待队列,服务机构。
要素的特性:1. 顾客源顾客到达的间隔时间:确定、随机(分布类型);一次到达人数:单个到达,成批到达;顾客源:数量无限,数量有限。
2. 等待队列等待规则:损失制,等待制,混合制;接受服务顺序:先到先服务,后到先服务,按优先权服务,随机服务。
3. 服务机构服务台数量:单个,多个;排列方式:串联、并联、混合排列。
服务时间:固定,随机(分布类型);一次服务人数:单人,成批。
三、排队服务系统的分类按上面所讨论的排队系统各项的特性,可对排队系统作出分类。
通常按如下6方面的特性对排队系统进行分类:(a/b/c) : (d/e/f)每个字母代表一个特征,它们分别是:a:顾客到达间隔的分布,有:M──负指数分布;D──确定型;E k ──k 阶爱尔郎分布;GI ──一般相互独立的分布。
b :服务时间的分布有:M 、D 、E k 、Gc :系统中并联的服务台数,记为Sd :系统中最多可容纳的顾客数,∞~1e :顾客源总数,为∞~1f :排队服务规则FCFS ──先到先服务LCFS ──后到先服务用这6个参数我们可以表示出某种类型的排队系统,如:M /M /1/10/∞/FCFS其中后三项可以省略,这时表示的是:a /b /c /∞/∞/FCFS三、排队系统的状态及参数系统状态N (t )——排队系统中的顾客数,包括等待的和正在被服务的。
其与系统运行的时刻t 相关,且是一个随机变量。
稳定状态——当系统状态与时刻t 无关时,称系统处于稳定状态。
在系统开始运行的一段时间内,系统状态随时间而变化,在运行一段时间之后,系统的状态将不随时间变化,此时系统即进入稳定状态。
排队论主要研究系统处于稳定状态的工作情况,以下参数也都针对于稳定状态进行定义。



排队论在日常生活和工作中,人们常常会为了得到某种服务而排队等候。
比如顾客到商店购买东西,病人到医院看病,汽车进加油站加油,轮船进港停靠码头等,都会因为拥挤而发生排队等候的现象。
这时,商店的售货员和顾客,医院的医生和病人,加油站的加油泵和待加油的汽车,码头的泊位和停泊的轮船等,形成了各自的排队服务系统,简称排队系统。
在一个排队系统中,通常包括一个或多个“服务设施”,服务设施可以指人,如售货员,医院大夫等。
也可以是物,如加油泵、码头泊位等。
同时还包括许多进入排队系统要求得到服务的“顾客”。
这里的顾客是指请求服务的人或物。
如到医院看病的病人,或等待加油的汽车等。
作为顾客总希望一到系统马上就能得到服务,但客观情况并非如此。
由于顾客的到达和服务机构对每个顾客的服务时间具有随机性,因此出现排队现象几乎是不可避免的。
当然,为了方便顾客减少排队时间,排队系统可以多开设服务设施。
但那将增加系统的投资和运营成本,还可能发生空闲浪费。
排队论(Queueing Theory)是为解决上述问题而发展起来的一门学科。
排队论起源于上世纪初,当时的美国贝尔(Bell)电话公司发明了自动电话后,满足了日益增长的电话通讯的需要。
但另一方面,也带来了新的问题,即如何合理配置电话线路的数量,以尽可能减少用户的呼叫次数。
如今,通讯系统仍然是排队论应用的主要领域。
同时在运输、港口泊位设计、机器维修、库存控制等领域也获得了广泛的应用。
6. 1 排队系统的基本概念6. 1. 1排队系统的一般表示一个排队系统可以抽象描述为:为了获得服务的顾客到达服务设施前排队,等候接受服务。
服务完毕后就自行离开。
其中把要求得到服务的对象称为顾客,而把服务者统称为服务设施或服务台。
在排队论中,把顾客的到达和离开称为排队系统的输入和输出。
而潜在的顾客总体又称为顾客源或输入源。
因此任何一个排队系统是一种输入-输出系统,其基本结构如图6-1所示。
排队系统图6-16. 1. 2排队系统的特征由排队系统的基本结构可知,任何一个排队系统的特征可以从以下三个方面加以描述。