2020年高中物理竞赛辅导课件★★静电场的环路定理

格式：pdf
大小：759.92 KB
文档页数：16

下载文档原格式

2020年高中物理竞赛辅导课件(电磁学)安培环路定理和应用(共25张PPT)

的平面内半径为 r 的圆为安培环路
B dl
L
2rB oI
I
dB
dS '' dB'
dB ''
dS '
B 0 r R
B oI 2r
rR
B
无限长圆柱面电流外面的磁场与电流
都集中在轴上的直线电流的磁场相同
r
例3 求载流螺绕环内的磁场
设环很细，环的平均半径为R ，总匝数为N，通有电流强度为 I
dI= 2rdr / 2 = rdr
磁场
dB = 0dI/2r =0dr/2
R1
o R2
阴影部分产生的磁场感应强度为
B
R1
0
1 2
0dr
0R1
2
其余部分：
B
R2
R1
1 2
0dr
1 2
0
(
R
2
R1 )
已知：B B则有R2 2R1
R1
o R2
安培环路定理及应用
一.定理表述
表述：在稳恒电流的磁场中，磁感应强度 B 沿任何
分析磁场结构，与长直螺旋管类似，环内磁场只能平行与线圈的轴线
根据对称性可知，在与环共轴的圆周上磁感应强度的大小相等，方向沿圆周的切线方向。磁力线是与环共轴的一系列同心圆。
B
R2
R1
L
p
设螺绕环的半径为R1, R2 ，共有N匝线圈。
以平均半径 R 作圆为安培回路 L,可得：
B dl L
电流密度
IS
(体)电流的(面)密度
如图电流强度为I的电流通过截面S
若均匀通过电流密度为 J I S
(面)电流的(线)密度

2020年高中物理竞赛辅导课件：电磁学(真空中的静电场)04静电场的环路定理(共21张PPT)

xx+dx电荷元产生的电势：
dV
Q L
dx
4 0(L r x)
P点的总电势：
V dV Q L dx
4 0L 0 L r x
Q ln(1 L )
4 0L
r
[讨论] 若 r >> L，结果？
[例1-10]均匀带电(Q)圆环轴线上一点的电势 (V=0)．
dq
R
O
x
X
解：环上dq产生的电势：dV dq
A
B B
VA VB
E dl
A
Edl
A
0
2.电势叠加原理
q1
q2
P
qi
qN
V Vi
[来历] V
E dl
P
P ( Ei ) dl
P Ei dl
Vi
3.电势的计算
[例1-9] 均匀带电(Q)直线段延长线上一点的电势(V=0)．
L O x x+dx
r pX
解：建立坐标轴如图
E dl
P
R 40r 2 dr
40 R
对于球面外一点P,有
V
E dl
P
Q r 40r 2 dr
Q
40r
Q
综之
V
(r
)
4
Q
0
R
4 0 r
(r R) (r R)
Note: 在场强值间断处,电势值不一定间断.
[例1-12] 无限长均匀带电直线周围的电势
P P0 r r0
设线电荷密度,V(r0)=0 轴对称与直线等距的 r 各点,电势相同.
V (r)
P0
E
dl
r0

高二物理竞赛课件：静电场的环路定理、电势

q E 4πε0r 2
(r R)
r1 R
球体内的电场：
r2
ΦE
E 4πr2
1 ε0
4
q πR3
4 3
πr 3
1 ε0
qr 3 R3
3
E
qr 4πε0 R3
ρ 3ε0
r
(r R)
E
q
E连续
q
ρ 4 πR3
为电荷体密度。
oR
r
3
(3) 无限长均匀带电圆柱体的电场
（λ、R）：
电场具有轴对称分布。
➢ 静电场为保守场，静电场力质3
电势能、电势：
静电场为保守场，因而可引入电势能的概念：
静电场力对试探电荷q0所作的功等于q0电势能增量
的负值。
Q
APQ q0 E dl (WQ WP ) ΔW
P
APQ>0时，q0电势能减少； APQ<0时，q0电势能增加。
E
2 0
σ S
E
讨论：两块无限大带等量异号电荷的平行平面间的电场分布。
+σ −σ
+σ −σ
AB
AB
两板外： E0
两板间：
E
0
习题习9-2题9 ：一电荷体密度为ρ的均匀带电球体，r为球心
指向球内一点的位矢，球内挖一球形空腔，求空腔内的场强。
均匀带电球E体内ρ的r 电场分布:（P.159式9.4-7) 3ε0
荷由P移到Q时，电场力所作的功。
将电荷由P点移到Q点时电场力所作的功为： Q
APQ q E dl q( U P UQ )
P
➢ 电场中某点的电势能（电势）的值是相对的，而两点间的电势能差（电势差）是绝对的，与零点的选择无关。电势的零点也可选在其它地方。

高二物理竞赛静电场的环路定理电势能课件

5
A q 0 E B d l E p A E p B ( E p B E p A )
令 EpB 0
EpAAq B0Edl
A E pA
BE pB E源自试验电荷q0在电场中某点的电势能，在数值上等于把它从该点移到零势能处静电场力所作的功.
6
1 真空中一半径为R的半圆细环，均匀带电Q. 设无穷远处为电势零点，求圆心O处的电势U0 . 若将一带电荷量为q的点电荷从无穷远处移到圆心O处，求电场力做的功W.
结论: W仅与q0的始末位置有关，与路径无关.
B
rB
dr
dl
E
r
er
q0
q rA A
2
任意带电体的电场（点电荷的组合）
EEi
i
Wq0
Edl
l
i
q0 lEi dl
结论：静电场力做功，与路径无关.
3
二静电场的环路定理
q Edlq Edl 整个带电球层在球0心处产生的电势为
0
2静电试场用线静不电构场成的闭环合A 路曲定线B 理. 证明C，电场线
解：在球内取半径为r、厚为dr的薄球壳，该壳内所包
含的电荷为 dqdVA4 rr2dr
在半径为r的球面内包含的总电荷为
q dV r4A3d rrA4r
V
0
以该球面为高斯面，由高斯定理得
E 1•d s E 14 r2 A4/r0
s
10
• 所以
E1A2r/40 (r≤R) 方向沿径向，A>0时向外, A<0 时向里在球体外作一半径为r的同心高斯球面，由高斯定理
空腔是等势区，各点电势均为V .
•在球层内取半径为r→r＋dr的薄球层．其电荷为

2023-2024学年高二下学期物理竞赛课件：静电场的环路定理和电势

四、电势差
Q Aab qo
bv v a E dl Wa Wb
电势差：
b
E dl
Wa
Wb
a
qo b qvo v
Uab Va Vb
E dl
a
结论：静电场中a,b两点的电势差，在数值上等于将单位正电荷从a点移至b点电场力所作的功。
Aab W Wa Wb qo (Va Vb )
二、电势能（W）
Wa q0
Wb
保守力作功等于势能的减少 a
b
b
Aab qo a E dl Wa Wb W
Wa,Wb的量值是相对的量；与零势能参考点的选取有关，而势能的增量 W与零势能点选取无关是绝对
的量.
1、对有限的带电体选无限远处作为电势能零点，
Aa
qo
a
E dl
Wa W
1) rib
电场力是保守力
qi ria
qn a
qo
3、若q0在电场中沿L运动一周
A lqo E dl 0
q0
静电场的环路定理：
l
静电场中电场强度 E的环流为零。
l E dl 0
结论：一定量的电荷在静电场中移动时，电场力所作的功只与电荷的起点和终点的位置有关，而与路径无关。即电场力是保守力。静电场是保守场。
致冷系数：
Q2 Q2
A Q1 Q2
K‘系观察者测得相对他静止的棒的长度为：
l0 x2 ' x1 ' l0 称为固有长度
问：在K系中观察者（相对棒运动的观察者）测得
的棒的长度为多少？
他测得棒两端的坐标为x1和x2, t1=t2=t（同时测）
则棒长 l= x2-x1

2020年高中物理竞赛辅导课件★★安培环路定理

而 B dl 所有dl'在垂面上形成L'
即 LB dl LB dl 0I
35
LB dl 0Ii 以无限长载流导线为例
证明：（3）闭合曲线L不包围载流导线
rr
从o点引r 出r的两条射线, 在L上截得 dl、dl
I
电流I
在dBBl 、 d2l2处00IrIr的磁且场B有分 dl别((BB为Bdd： lld))l
第5节安培环路定理
Ampere’s Law
一、安培环路定理
B沿任意闭合曲线L的
LB dl 0Ii
线积分等于穿过闭合曲线
内电流强度代数和的 0倍
电流 I 的正负规定：
（1）I与L的环饶方向成右手关系时, I >0, 反之I <0.
（2）若I不穿过L，则 I =0. 例如：
I3
I1>0 I1
I2 I3
但对回路L上各点的 B 贡献不为0
例如: 图中的I3对r 回路L上各 I3 点产生的 B都不为0。
I1 L
I2
LBdl 0(I1I2) 38
二、安培环路定理的应用
LB dl 0Ii
例6. 求半径为R的无限长载流圆柱面的磁场分布。
解：电流有轴对称性, 则与轴等距离的圆周上B
I
B
相等,方向如图。作以r为半径的同心环路
若 r <R1 若 r >R2
0 Ii 0 B 0
0 Ii 0 NI NI 0
B 0
当 R管截面 <<R 则 r R
B 0nI
n
N
2 R
41
例9. 求无限长直螺线管内的磁场。解：与已管知壁通等有距电离流的I，点单Br位相长等度，上方的向匝与数轴为平n行。,

高二物理竞赛课件：静电场的环路定理和电势

dr
b
rb
dl
dr
E
r
q ra a q0
Aab
dA
rb ra
q0
E
dl
q0q
4 π0
rb dr r ra 2
q0q ( 1 1 )
4 π 0 ra rb
b
rb
dl
dr
E
结论: 当检验电荷 q0 在电场中从 a 移到 b 点时, 电场力做的功 A 只与
r
q0 的始末位置有关, 与路径无关.
原子物理中能量单位 1eV 1.602 1019 J
2、点电荷系的电势
E Ei
i
VP E dl Ei dl
P
iP
q1 q2
r1 r2
q3
r3
E3
E2
P
E1
VP
VPi
i
i
qi （代数和）
4 π 0ri
点电荷系电场中某点的电势，等于各个点电荷单独存在时在该点电势的代数和，此即电势叠加原理。
电势定义：
Va
Wa q0
零点 E dl
a
③电势是相对于电势零点而言的，电势零点选择方法：
有限大小带电体通常以无穷远处为电势零点，实际问题中也常选取大地、电器外壳或某公共点为电势零点.
地球是一个带负电的大导体, 取地球为电势零点与取无穷远处
为电势零点是一致的.
④电势高低的判断:沿着电场线方向,电势降低 (dV E d l )
L
q0
E
dl
0
q0 0,
E dl 0
L
静电场的环路定理：静电场的电场强度沿任意闭合回路
的积分(称为静电场的环流)等于零。

高二物理竞赛课件：静电场的环路定理电势

qr R4
r R, 0
r R
（q为一正常数），计算其内外的场强分布。
解 : (1)球体内
1
S1 E1 ds 0 qi
S1 E1 dS S1 E1dS E14r12
qi
r1 4r 2dr
0
r1 qr 4r 2dr qr14
0 R4
R4
r1 S1 OR
即
q0
b E dl
a
q0 Ua
Ub
U a Ub , Aab 0 q0 0U a Ub , Aab 0
Aab q0 Ua Ub
U a Ub , Aab 0
n
UP
E dl
P
P
Ei dl
n
n
i1 n
UP Ui
P Ei dl Ui
i 1
q1 q2 q3 qi qn
( x d 2) ( | x | d 2) ( x d 2)
点电荷系电场
Aab
b a
q0
E
dl
n
qb
a0
Ei
i 1
dl
n i 1
qi q0
4 0
1 rai
1 rbi
Aab仍与路径无关。
结论静电场力是保守力。
1
B
A
2E
A
L
q0E
dl
q0
E dl
L
0
E dl 0
2、电势能属于电场和试验点电荷所共有。
(1)q0 1C, U P WP AP零电势点
电势反映了电场能（功）方面的性质
（3）电势是相对量，与零电势点选择有关。
实际上：U地球 0
零电势点可任意选择，应使电势表式有意义。

高二物理竞赛课件：静电场的环路定理

E2
q
4 0r 2
E3
qQ
4 0r 2
(R1 r R2 ) (R2 r2 )
所以，在 r 区R1域
V1
R1 r
E dl r E1 dl
R2 R1
E2
dl
R2 E3 dl
0 R2 q dr q Q dr
R1 4 0r 2
R2 4 0r 2
q q qQ
点电荷系
VA
n i 1
qi 4 π ε0ri
电荷连续分布时
dq dV
dV dq 4πε0r
dq
r
A
VA
1 4πε0
dq r
计算电势的方法
（1）利用点电荷电势的叠加原理
V
1 4πε0
dq r
有限大带电体，选无限远处电势为零.
（2）利用
VA
AB
E dl
VB
已知在积分路径上 E的函数表达式
静电场的环路定理
静电场的环路定理
1 静电场的线积分与路径无关
点电荷的电场（库仑定律）
E dl
1 4πε0
q r2
er
dl
er dl dl cos θ dr
r er dl r dr dr
B
rB
dr
dl
E
r
er
q
rA A
E dl 1 q dr 4πε0 r 2
B
q 11
E dl ( )
4 0R1 4 0R2 4 0R2
q
Q
4 0R1 4 0R2
同理，在 R1 r 区 R域2
V2
R2 r
E dl r E2 dl

高二物理竞赛静电场的环路定理电势课件

电偶极子的等势面
等势
面
+
电平行板电容器电场的等势面
++ ++ + + + + +
2.等势面与电场线的关系
q0在等势面上移动, E 与 dl 成 θ 角。
在等势面上移动不作功
dA q0E dl q0E dl cos 0
q0 0， E0，dl 0，
cos 0
S
即 E dl
E
q0 θpd2l
解：设环上电荷线密度为，环上任取一长度为d l
的电荷元，其所带电荷 dq dl qdl
2R
该电荷元在P 点电势为：
dl
dV dq
4π 0 r
1 qdl
4π0 2πRr
r R
O
xP
x
qdl
dl
8π20R R2 x2
R
整个圆环在P点的电势为
O
r
xP
x
V dV
2πR
qdl
0 8π20R R2x2
+ + §7-4 静电场的环路定理电势
结论：电场线与等势面处处正交。
+ + 60×10－19J 电子伏特 + + 60×10－19J 电子伏特
E 0 (r R)
1 q 选N为静电势能的零点，用“0”表示，则
同样也不能直接用公式来计算电势，不然也将得出电场任一点的电势值为无限大的结果。
由环路定理知，静电场是保守场。该定理还可表达为：电场强度的环流等于零。在静电场中，电势相等的点所组成的面称为等势面。
综合静电场高斯定律和环路定理，可知静电场是有源的保守力场，又由于电场线是不闭合的，即不形成旋涡的，所以静电场是无旋场。

高二物理竞赛-环路定理课件

但Uab与零势点选取0无关.
约定: 一般选取无穷远处电势能为零,
Q o R 9 均匀带电球壳的电势.
电势零点的选择是任意的,通常选无限远处的一点为电势零点,电器设备与仪器通常外壳接地,即选地面为电势零点.
4 π r 真空中，有一带电为，半径为的带电球面.
9 均匀带电球壳的电势.
0
4 π 0r
r
电平行板电容器电场的等势面
在静电场中，电势相等的点所组成的面称为等势面。
R 四、电势(Electric Potential)
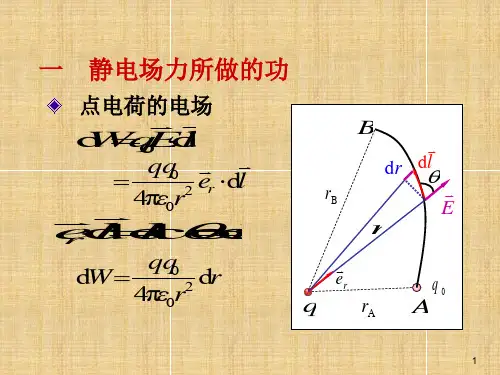
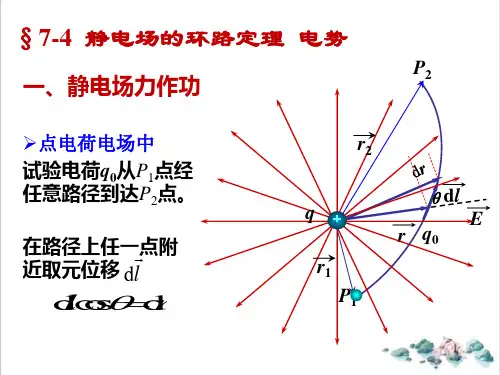
(2) U(r)rEdr Edr 一、静电场力做功的特点内
1
2
R U 具有相对意义, 其值与零势点选取有关, 但Uab与零势点选取无关.
将一个带电量为q的点电荷从电场中的某一点移动到所选定的参考点（假设为O点），电场力对该电荷做的功定义为该电荷在该点的电
x
x
U
E
Y
y
U
E
Z
z
在直角坐标系中梯度算符
i jk x y z
EU
2. 电势差 (voltage)
B
U AB U AU BAEdl
3. 功与电势的关系式
点电荷q在静电场中由A沿任意路径移至B过程中
静电力做的功：
W A BA Bq Edlq (U AU 电B 子)伏特
即
(electron volt)
WAB qUAB 1ev1.061019J
五、电势的计算(Calculating Electric Potential)
结果: 仅与的始末位置有关，与路径无关.
有的电势能, 亦即将单位正电荷由该点移至参考将带电体划分为若干电荷元dq

【高中物理】优质课件：静电场的环路定律

感谢观看
r2 r1 r1r2
r1
(r 2
d2 4
rd
1
cos ) 2
r2
(r 2
d2 4
rd
1
cos ) 2
r1
r
d 2
cos
r2
r
d 2
cos
所以
p
qd cos 4π0r 2
pqd
p
4π
er 0r
2
p＝qd 表示电偶极矩（dipole moment)，方向由
-q 指向 +q。
等位线方程 ( 球坐标系 ) ： r C cos
电位参考点电位参考点可任意选择，但同一问题，一般只能选取一个参考点。
场中任意两点之间的电位差与参考点无关。
选择参考点尽可能使电位表达式比较简单。
工程上一般取大地为参考点，理论上取∞为参考点，点电荷产生的电位：
源点在原点
q
P 4π 0r 2 er
dl
q
4π 0r
源点不在原点
q 4π 0 R
4π 0 V ' r r'
式中dq dV, dS , dl相应的积分原域 V ', S ', l'。
返回上页下页
电力线与等位线（面）曲线上任一点的切线方向是该点电场强度 E 的方向。
E 线微分方程 E dl 0
直角坐标系 Ex Ey Ez dx dy dz
1.1.7 电力线方程
图1.1.10 点电荷与接地导体的电场
E 线愈密处，场强愈大;
E 线与等位线（面）正交；图1.1.11 点电荷与不接地导
体的电场
返回上页下页

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

求：负极上静止电子到正极时的速度？
解：由电势差的定义可得 A q(V V ) (e)(U )
R2 R1
U
1 2
mv2
0
即
eU
1 2
mv2
v
2eU m
Va
Vb
ab
E
dl
47
定义：电场中任意点P
VP
V 0
P
的电势 E dl
Va
Vb
ab
E
dl
单位：伏特或焦耳/库仑, 记为V或J/C, 1V＝1J/C
一、电势差和电势 Electrbic Potential
从L1ab上E一 d节l 讨 L2论ab E可知dl
L2
L1
q0
存在与位置
有关的态函数
a
定义：a、b两点的电势分别为Va、Vb，
则两点间的电势差为 Va Vb ab
E
dl
即：a、b两点的电势差 =
将单位正电荷
从ab电场力作的功 46
例13. 已知真空中两金属圆筒电极间电压为U ，半径分别为 R1、 R2 。
即:静电场中场强沿任意闭合路径的线积分恒等于零
44
注
1º若一矢量场的任意环路积分始终为零，则称该矢量场为无旋场。
静电场两个基本性质：
高斯定理 S E dS
1
0
qi
S内
有源场
环路定理 L E dl 0 无旋场
2º 运动电荷的场不是保守场，而是非保守场，将在磁场部分讨论。
45
第5节电势差和电势 Electric Potential Difference and
结论
每一项都与路径无关
电场力是保守力，静电场是保守力场。
43
二、环路定理
在任意电场中, 将q0 从a 经L1 b 电场力作功：
b L2
L1 q0
a
经L2
ALL11LaabbqL1qqa0bE00qEE0EdldddlllLLL2b22aaabbqqq000EEEdddlll
A
Lq0E
dl
0
LE dl 0 静电场的环路定理
点电荷系场中的电势在点电荷系 q1 , q2 qn 的电场中,
V
q
40r
q1 r1 r2
q2
qi q j
. P
rn
VP
任PPEE意1点ddllP处PP的EE2电1 dl势E2P
En En
dl dl
qn
V1q1
V2
q2
Vk
qn
40r1 40r2
40rn
VP
Vi
i
i
qi
(r2
l2 4
cos2
ql cos
l +q
pe
er
) 40r2
54
例18.长为L 的均匀带电导线, 电荷线密度为+.
求:延长线上任意一点 P 的电势。
解：用迭加法
r
o
x x dx
P
L
l
x
取电荷元 dq dx
dV
dq
40r
dx 40(L l
x)
P 的电势
VP
dV
L
0 4
dx
0(L l
x)
dA F dl Fdl cos =Fdr
则
A
b
Fdr
a
b
q0Edr
a
b
a
q0q
4 0r
2dr
q0q
40
1 ra
1 rb
——点电荷的电场力作功与路径无关
42
2.在点电荷系的电场中(或连续带电体的电场)
qq21Aqai将qqj0电 E荷1qndqql0E0c从qn0a点EbE21移dAl1动EA到2该电bAq点0处场E，EqF的力nFA0在dn场作(l任EEqd0强功1l1E意E为点E2q2c0受E电dElE场nn)力 dl
第4节静电场的环路定理
Circuital Theorem of Electrostatic Fields
一、静电场力的功
1. 在点电荷q的电场中
F
dl dr
b
c
将点电荷q0从a点移动到 b点
在任意点c, q0的位移dl ,
q0 r +dr rb r
受电场力 F q0E
电场力作微功
a ra +q
注意
1o 电场中某点的 “V ” 由场源电荷及场点位置决定，与q0无关。(类似于 E 与q0无关)它描述的是电场“能的性质”。
2o 电势是标量，有正、负。
3o 电势是相对量，相对于 V =0 处而言。原则上可选电场中任意一点的电势为零。
48
注意
4º 电势零点的选取
电荷分布在有限空间，
理论上
取无穷远为 V = 0 点。
电荷分布在无限空间，
取有限远点为V = 0 点。
一般工程上
选大地或设备外壳为V =0点
49
二、电势的计算
1. 用定义法求V
VP
PV
0
E
dl
例14. 求点电荷q电场中任意一点P 的电势V =？
q
P
解:
设r V 0
已知q的电场分布
E
q
4 0r 2
er
根V据P 定P义 E,
P d点l的电P 4势q为0r
40ri
电势叠加原理
任意带电体场中的电势
VP
q
dq
40r
53
例17. 计算电偶极子电场中任意一点P的电势。
解：用迭加法
VP Vi( P)
iq
4 0r
q
4 0r
P r
当 r >> l 可做如下近似
r r+
r
r
l 2
cos
r
r
l 2
cos
VP
q
40
其中 pe
(errrrrq)l
q
40
er
q
l cos
2
er
dlr
rP
q
4 0r
2
dr
q
40rP
q > 0时, VP为正, r V, r处V= 0 min
q < 0时, VP为负, r V, r处V = 0 max
50
例15. 求均匀带电球面电场中任一点P的电势分布。设球面半径为R，总带电量为q。
q
P
r
o
P
Rrຫໍສະໝຸດ V解:r用定义法,
R处 VP
选P EVd=r
E
20r
e无意r
若VP令 VPE=
0 则任意点P的电势为
dr
rP
2 0r
dr
20
ln
义
rP
令某处 r
V
P
P
=Er0d（l 有限PP0值E） dlV0=0，则
P
P
2
0r
dr
2 0
ln
r0 r
rP P'
P0 r0
可见：当电荷分布到无穷远时，
电势零点不能再选在无穷远处。
52
2. 用叠加法求V
4 0
ln
L l
l
55
例19.求一均匀带电圆环轴线上任意点P 的电势. 设圆环半径为R，总带电量为q。
解：根据迭加法，在带电圆环上取电荷元dq
其在P点产生的电势为
dq
dVP
dq
40r
所有电荷在P产生的电势
. R
r
qo x P x
讨论VP12oo|xx4|0d,qR0rV,PV0qP444q00Rq0dR|qx2
|
q
x2 40 R2 x2
x , VP 0
相当于点电荷
56
0,
rP
q
40r2
dr
q
4 0 r
r
R处
VP
E
dr
rR
E1
dr0
R
E2
dr
P
0 Rr
R
q
40r2
dr
q
40
R
与点的位置无关场区是等势区
注意 E =0的区域, “V ”不见得为零 51
例16. 求半径为R, 电荷线密度为的无限长均匀带电
细线的电势分布？解：由例10可知其电场分布