北航最优化方法最新最全答案2015版详解
- 格式:pdf
- 大小:596.00 KB
- 文档页数:44


最优化课后习题答案最优化课后习题答案最优化是一门重要的数学学科,它研究如何在给定的约束条件下,找到一个最优的解决方案。
在学习最优化课程时,我们通常会遇到一些习题,这些习题旨在帮助我们理解和应用最优化的原理和方法。
本文将为大家提供一些最优化课后习题的答案,以帮助大家更好地掌握这门学科。
1. 线性规划问题线性规划是最优化中的一个重要分支,它主要研究线性约束条件下的最优解。
下面是一个线性规划问题的示例:Maximize Z = 3x + 5ySubject to:x + y ≤ 62x + y ≤ 8x, y ≥ 0首先,我们需要将目标函数和约束条件转化为标准形式。
将不等式约束转化为等式约束,引入松弛变量,得到以下标准形式:Maximize Z = 3x + 5ySubject to:x + y + s1 = 62x + y + s2 = 8x, y, s1, s2 ≥ 0接下来,我们可以使用单纯形法求解该线性规划问题。
根据单纯形法的步骤,我们可以得到最优解为 Z = 22,x = 2,y = 4,s1 = 0,s2 = 0。
2. 非线性规划问题除了线性规划,最优化还涉及到非线性规划问题。
非线性规划是指目标函数或约束条件中存在非线性项的最优化问题。
下面是一个非线性规划问题的示例:Minimize f(x) = x^2 + 3x + 5Subject to:x ≥ 0对于这个问题,我们可以使用求导的方法来找到最优解。
首先,求目标函数的导数:f'(x) = 2x + 3将导数等于零,解得 x = -1.5。
由于约束条件x ≥ 0,所以最优解为 x = 0。
3. 整数规划问题整数规划是指在最优化问题中,决策变量必须取整数值的情况。
下面是一个整数规划问题的示例:Maximize Z = 2x + 3ySubject to:x + 2y ≤ 10x, y ≥ 0x, y 为整数对于这个问题,我们可以使用分支定界法来求解。



附录5 《最优化方法》复习题1、设n n A R ⨯∈是对称矩阵,,n b R c R ∈∈,求1()2TT f x x Ax b x c =++在任意点x 处的梯度和Hesse 矩阵.解 2(),()f x Ax b f x A ∇=+∇=.2、设()()t f x td ϕ=+,其中:n f R R →二阶可导,,,n n x R d R t R ∈∈∈,试求()t ϕ''. 解 2()(),()()T T t f x td d t d f x td d ϕϕ'''=∇+=∇+.3、设方向n d R ∈是函数()f x 在点x 处的下降方向,令()()()()()T TT Tdd f x f x H I d f x f x f x ∇∇=--∇∇∇, 其中I 为单位矩阵,证明方向()p H f x =-∇也是函数()f x 在点x 处的下降方向. 证明 由于方向d 是函数()f x 在点x 处的下降方向,因此()0T f x d ∇<,从而()()()T T f x p f x H f x ∇=-∇∇()()()()()()()()T TTT T dd f x f x f x I f x d f x f x f x ∇∇=-∇--∇∇∇∇()()()0T T f x f x f x d =-∇∇+∇<,所以,方向p 是函数()f x 在点x 处的下降方向. 4、n S R ⊆是凸集的充分必要条件是12122,,,,,,,,m m m x x x S x x x ∀≥∀∈的一切凸组合都属于S .证明 充分性显然.下证必要性.设S 是凸集,对m 用归纳法证明.当2m =时,由凸集的定义知结论成立,下面考虑1m k =+时的情形.令11k i i i x x λ+==∑,其中,0,1,2,,1i i x S i k λ∈≥=+,且111k i i λ+==∑.不妨设11k λ+≠(不然1k x x S +=∈,结论成立),记111kii i k y x λλ=+=-∑,有111(1)k k k x y x λλ+++=-+,又1110,1,2,,,111kiii k k i k λλλλ=++≥==--∑,则由归纳假设知,y S ∈,而1k x S +∈,且S 是凸集,故x S ∈.5、设n R S ⊆为非空开凸集,R S f →:在S 上可微,证明:f 为S 上的凸函数的充要条件是2112112()()()(),,T f x f x f x x x x x S ≥+∇-∀∈.证明 必要性.设f 是S 上的凸函数,则12,x x S ∀∈及(0,1)λ∈,有2121((1))()(1)()f x x f x f x λλλλ+-≤+-,于是121121(())()()()f x x x f x f x f x λλ+--≤-,因S 为开集,f 在S 上可微,故令0λ+→,得12121()()()()T f x x x f x f x ∇-≤-,即2112112()()()(),,T f x f x f x x x x x S ≥+∇-∀∈.充分性.若有2112112()()()(),,T f x f x f x x x x x S ≥+∇-∀∈, 则[0,1]λ∀∈,取12(1)x x x S λλ=+-∈,从而11()()()()T f x f x f x x x ≥+∇-,22()()()()T f x f x f x x x ≥+∇-,将上述两式分别乘以λ和1λ-后,相加得1212()(1)()()()((1))T f x f x f x f x x x x λλλλ+-≥+∇+--12()((1))f x f x x λλ==+-,所以f 为凸函数.6、证明:凸规划min ()x Sf x ∈的任意局部最优解必是全局最优解.证明 用反证法.设x S ∈为凸规划问题min ()x Sf x ∈的局部最优解,即存在x 的某个δ邻域()N x δ,使()(),()f x f x x N x S δ≤∀∈.若x 不是全局最优解,则存在x S ∈,使()()f x f x <.由于()f x 为S 上的凸函数,因此(0,1)λ∀∈,有((1))()(1)()()f x x f x f x f x λλλλ+-≤+-<.当λ充分接近1时,可使(1)()x x N x S δλλ+-∈,于是()((1))f x f x x λλ≤+-,矛盾.从而x 是全局最优解.7、设n R S ⊆为非空凸集,R S f →:是具有一阶连续偏导数的凸函数,证明:x 是问题min ()x Sf x ∈的最优解的充要条件是:()()0,T f x x x x S ∇-≥∀∈.证明 必要性.若x 为问题min ()x Sf x ∈的最优解.反设存在x S ∈,使得()()0T f x x x ∇-<,则d x x =-是函数()f x 在点x 处的下降方向,这与x 为问题min ()x Sf x ∈的最优解矛盾.故()()0,T f x x x x S ∇-≥∀∈.充分性.若()()0,T f x x x x S ∇-≥∀∈.反设存在x S ∈,使得()()f x f x <.(())()((1))()f x x x f x f x x f x λλλλλ+--+--=()(1)()()()()0((0,1)f x f x f x f x f x λλλλ+--≤=-<∀,因S 为凸集,f 在S 上可微,故令0λ+→,得()()()()0T f x x x f x f x ∇-≤-<,这与已知条件矛盾,故x 是问题min ()x Sf x ∈的最优解.8、设函数()f x 具有二阶连续偏导数,k x 是()f x 的极小点的第k 次近似,利用()f x 在点k x 处的二阶Taylor 展开式推导Newton 法的迭代公式为 211[()]()k k k k x x f x f x -+=-∇∇.证明 由于()f x 具有二阶连续偏导数,故21()()()()()()()()2T T k k k k k k f x x f x f x x x x x f x x x ϕ≈=+∇-+-∇-.且2()k f x ∇是对称矩阵,因此()x ϕ是二次函数.为求()x ϕ的极小点,可令()0x ϕ∇=,即2()()()0k k k f x f x x x ∇+∇-=,若2()k f x ∇正定,则上式解出的()x ϕ的平稳点就是()x ϕ的极小点,以它作为()f x 的极小点的第1k +次近似,记为1k x +,即211[()]()k k k k x x f x f x -+=-∇∇,这就得到了Newton 法的迭代公式.9、叙述常用优化算法的迭代公式.(1)0.618法的迭代公式:(1)(),().k k k k k k k k a b a a b a λτμτ=+--⎧⎨=+-⎩(2)Fibonacci 法的迭代公式:111(),(1,2,,1)()n k kk k k n k n k k k k k n k F a b a F k n F a b a F λμ---+--+⎧=+-⎪⎪=-⎨⎪=+-⎪⎩.(3)Newton 一维搜索法的迭代公式: 1()()k k k k t t t t ϕϕ+'=-''. (4)最速下降法用于问题1min ()2TT f x x Qx b x c =++的迭代公式: 1()()()()()T k k k k k Tk k f x f x x x f x f x Q f x +∇∇=-∇∇∇ (5)Newton 法的迭代公式:211[()]()k k k k x x f x f x -+=-∇∇. (6)共轭方向法用于问题1min ()2TT f x x Qx b x c =++的迭代公式: 1()T k kk k k Tk kf x d x x d d Qd +∇=-. 10、已知线性规划:123123123123123min ()2;..360,2210,20,,,0.f x x x x s t x x x x x x x x x x x x =-+⎧⎪++≤⎪⎪-+≤⎨⎪+-≤⎪⎪≥⎩(1)用单纯形法求解该线性规划问题的最优解和最优值; (2)写出线性规划的对偶问题; (3)求解对偶问题的最优解和最优值.解 (1)引进变量456,,x x x ,将给定的线性规划问题化为标准形式:123123412351236126min ()2;..360,2210,20,,,,0.f x x x x s t x x x x x x x x x x x x x x x =-+⎧⎪+++=⎪⎪-++=⎨⎪+-+=⎪⎪≥⎩所给问题的最优解为(0,20,0)T x =,最优值为20f =-. (2)所给问题的对偶问题为:123123123123123max ()601020;..32,21,21,,,0.g y y y y s t y y y y y y y y y y y y =---⎧⎪---≤⎪⎪-+-≤-⎨⎪--+≤⎪⎪≥⎩(1) (3)将上述问题化成如下等价问题:123123123123123min ()601020;..32,21,21,,,0.h y y y y s t y y y y y y y y y y y y =++⎧⎪---≤⎪⎪-+-≤-⎨⎪--+≤⎪⎪≥⎩引进变量456,,y y y ,将上述问题化为标准形式:123123412351236126min ()601020;..32,21,21,,,,0.h y y y y s t y y y y y y y y y y y y y y y =++⎧⎪---+=⎪⎪-+-+=-⎨⎪--++=⎪⎪≥⎩ (2)问题(2)的最优解为(0,0,1)T y =,最优值为20h =(最小值). 问题(1)的最优解为(0,0,1)T y =,最优值为20g =-(最大值).11、用0.618法求解 2min ()(3)t t ϕ=-,要求缩短后的区间长度不超过0.2,初始区间取[0,10]. 解 第一次迭代: 取11[,][0,10],0.2a b ε==. 确定最初试探点11,λμ分别为11110.382() 3.82a b a λ=+-=,11110.618() 6.18a b a μ=+-=.求目标函数值:21()(3.823)0.67ϕλ=-=,21()(6.183)10.11ϕμ=-=. 比较目标函数值:11()()ϕλϕμ<. 比较11 6.1800.2a με-=->=. 第二次迭代:212121210, 6.18, 3.82,()()0.67a a b μμλϕμϕλ========.2222220.382()0.382(6.180) 2.36,()(2.363)0.4a b a λϕλ=+-=-==-=.2222()(), 3.82a ϕλϕμμε<-=>.323232320, 3.82, 2.36,()()0.4a a b μμλϕμϕλ========.2333330.382()0.382(3.820) 1.46,()(1.463) 2.37a b a λϕλ=+-=-==-=.3333()(), 3.82 1.46b ϕλϕμλε>-=->. 第四次迭代:434343431.46, 3.82, 2.36,()()0.4a b b λλμϕλϕμ========.444440.618() 1.460.0.618(3.82 1.46) 2.918,()0.0067a b a μϕμ=+-=+-==. 4444()(), 3.82 2.36b ϕλϕμλε>-=->. 第五次迭代:545454542.36, 3.82, 2.918,()()0.0067a b b λλμϕλϕμ========.555550.618() 3.262,()0.0686a b a μϕμ=+-==. 5555()(), 3.262 2.36a ϕλϕμμε<-=->. 第六次迭代:656565652.36, 3.262, 2.918,()()0.0067a a b μμλϕμϕλ========.666660.382() 2.7045,()0.087a b a λϕλ=+-==.6666()(), 3.262 2.7045b ϕλϕμλε>-=->. 第七次迭代:767676762.7045, 3.262, 2.918,()()0.0067a b b λλμϕλϕμ========.777770.618() 3.049,()0.002a b a μϕμ=+-==. 7777()(),b ϕλϕμλε>->. 第八次迭代:878787872.918, 3.262, 3.049,()()0.002a b b λλμϕλϕμ========.888880.618() 3.131,()0.017a b a μϕμ=+-==. 8888()(),a ϕλϕμμε<->.989899982.918, 3.131, 3.049,()()0.002a a b μμλϕμϕλ========.999990.382() 2.999,()0.000001a b a λϕλ=+-==. 9999()(), 3.049 2.918a ϕλϕμμε<-=-<. 故993.0242x λμ+==.12、用最速下降法求解 22112212min ()2243f x x x x x x x =++--,取(0)(1,1)T x =,迭代两次.解 1212()(224,243)T f x x x x x ∇=+-+-, 将()f x 写成1()2TT f x x Qx b x =+的形式,则224,243Q b -⎛⎫⎛⎫== ⎪ ⎪-⎝⎭⎝⎭. 第一次迭代:(0)(0)(1)(0)(0)(0)(0)()()()()()T T f x f x xxf x f x Q f x ∇∇=-∇∇∇ 0(0,3)1013220131/4(0,3)243⎛⎫ ⎪⎛⎫⎛⎫⎛⎫⎝⎭=-= ⎪ ⎪ ⎪⎛⎫⎛⎫⎝⎭⎝⎭⎝⎭⎪⎪⎝⎭⎝⎭. 第二次迭代:(1)(1)(2)(1)(1)(1)(1)()()()()()T T f x f x xx f x f x Q f x ∇∇=-∇∇∇ 3/2(3/2,0)13/27/40223/21/401/4(3/2,0)240-⎛⎫- ⎪-⎛⎫⎛⎫⎛⎫⎝⎭=-= ⎪ ⎪ ⎪-⎛⎫⎛⎫⎝⎭⎝⎭⎝⎭- ⎪⎪⎝⎭⎝⎭. 13、用FR 共轭梯度法求解222123123123min ()()()()f x x x x x x x x x x =-++-++++-,取(0)11(,1,)22T x =,迭代两次.若给定0.01,ε=判定是否还需进行迭代计算. 解 222123121323()3()2()f x x x x x x x x x x =++-++,再写成1()2T f x x Gx =,622262226G --⎛⎫⎪=-- ⎪ ⎪--⎝⎭,()f x Gx ∇=.第一次迭代:(0)()(0,4,0)T f x ∇=,令(0)0()(0,4,0)T d f x =-∇=-,从(0)x 出发,沿0d 进行一维搜索,即求(0)200min ()21648f x d λλλλ≥+=-+的最优解,得(1)(0)0001/6,(1/2,1/3,1/2)T x x d λλ==+=.第一次迭代:(1)()(4/3,0,4/3)T f x ∇=.2(1)02(0)()29()f x f x α∇==∇, (1)100()(4/3,8/9,4/3)T d f x d α=-∇+=---.从(1)x 出发,沿1d 进行一维搜索,即求(1)10142362214181418min ()(,,)262233923392261423f x d λλλλλλλλ≥⎛⎫- ⎪--⎛⎫ ⎪⎪⎪+=------ ⎪ ⎪ ⎪-- ⎪⎝⎭ ⎪- ⎪⎝⎭的最优解,得(2)(1)1111/24/333,1/38/9(0,0,0)881/24/3T x x d λλ-⎛⎫⎛⎫ ⎪ ⎪==+=+-= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭.此时(2)(2)()(0,0,0),()00.01T f x f x ε∇=∇=<=.得问题的最优解为(0,0,0)T x =,无需再进行迭代计算.14、用坐标轮换法求解 2212112min ()242f x x x x x x =+--,取(0)(1,1)T x =,迭代一步.解 从点(0)(1,1)T x =出发,沿1(1,0)T e =进行一维搜索, 即求(0)210min ()43f x e λλλλ≥+=--的最优解,得(1)(0)0012,(3,1)T x x e λλ==+=.再从点(1)x 出发,沿2(0,1)T e =进行一维搜索, 即求(1)220min ()227f x e λλλλ≥+=--的最优解,得(2)(1)1121/2,(3,3/2)T x x e λλ==+=.15、用Powell 法求解2212112min ()3f x x x x x x =+--,取(0)(0,0)T x =,初始搜索方向组01(0,1),(1,0)T T d d ==,给定允许误差0.1ε=(迭代两次). 解 第一次迭代:令(0)(0)(0,0)T y x ==,从点(0)y 出发沿0d 进行一维搜索,易得(1)(0)0000,(0,0)T y y d λλ==+=;接着从点(1)y 出发沿1d 进行一维搜索,得(2)(1)11133,(,0)22T y y d λλ==+=由此有加速方向 (2)(0)23(,0)2T d y y =-=.因为23/2d ε=>,所以要确定调整方向.由于 (0)(1)(2)9()0,()0,()4f y f y f y ===-,按(8.4.17)式有(1)(2)()(1)()()max{()()|0,1}j j f y f y f y f y j +-=-=,因此1m =,并且()(1)(1)(2)9()()()()4m m f y f y f y f y +-=-=. 又因(2)(0)(2)0f y y -=,故(8.4.18)式不成立.于是,不调整搜索方向组,并令(1)(2)3(,0)2T x y ==.第二次迭代:取(0)(1)3(,0)2T y x ==,从点(0)y 出发沿0d 作一维搜索,得(1)(0)000333,(,)424T y y d λλ==+=.接着从点(1)y 出发沿方向1d 作一维搜索,得(2)(1)1113153,(,)884Ty y d λλ==+=. 由此有加速方向(2)(0)233(,)84T d y y =-=.因为2d ε=>,所以要确定调整方向.因(0)(1)(2)945189(),(),()41664f y f y f y =-=-=-, 故按(8.4.17)式易知0m =,并且()(1)(0)(1)9()()()()16m m f y f y f y f y +-=-=. 由于(2)(0)45(2)16f y y -=-, 因此(8.4.18)式成立。

一、 填空题1.若()()⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=212121312112)(x x x x x x x f ,则=∇)(x f ,=∇)(2x f .2.设f 连续可微且0)(≠∇x f ,若向量d 满足 ,则它是f 在x 处的一个下降方向。
3.向量T)3,2,1(关于3阶单位方阵的所有线性无关的共轭向量有 . 4. 设R R f n →:二次可微,则f 在x 处的牛顿方向为 . 5.举出一个具有二次终止性的无约束二次规划算法: .6.以下约束优化问题:)(01)(..)(min 212121≥-==+-==x x x g x x x h t s x x f的K-K-T 条件为:. 7.以下约束优化问题:1..)(min 212221=++=x x t s x x x f的外点罚函数为(取罚参数为μ) .二、证明题(7分+8分)1.设1,2,1,:m i R R g n i =→和m m i R R h ni ,1,:1+=→都是线性函数,证明下面的约束问题:},,1{,0)(},1{,0)(..)(min 1112m m E j x h m I i x g t s x x f j i nk k+=∈==∈≥=∑=是凸规划问题。
2.设R R f →2:连续可微,n i R a ∈,R h i ∈,m i ,2,1=,考察如下的约束条件问题:},1{,0}2,1{,0..)(min 11m m E i b x a m I i b x a t s x f i T i i Ti +=∈=-=∈≥-设d 是问题1||||,0,0..)(min ≤∈=∈≥∇d E i d a Ii d a t s d x f Ti Ti T的解,求证:d 是f 在x 处的一个可行方向。
三、计算题(每小题12分)1.取初始点T x )1,1()0(=.采用精确线性搜索的最速下降法求解下面的无约束优化问题(迭代2步):22212)(m in x x x f +=2.采用精确搜索的BFGS 算法求解下面的无约束问题:21222121)(min x x x x x f -+=3.用有效集法求解下面的二次规划问题:.0,001..42)(min 2121212221≥≥≥+----+=x x x x t s x x x x x f4.用可行方向算法(Zoutendijk 算法或Frank Wolfe 算法)求解下面的问题(初值设为)0,0()0(=x,计算到)2(x 即可):.0,033..221)(min 21211222121≥≥≤+-+-=x x x x t s x x x x x x f参考答案一、填空题 1. ⎪⎪⎭⎫⎝⎛++++3421242121x x x x ⎪⎪⎭⎫⎝⎛4224 2. 0)(<∇d x f T3. T)0,1,2(-,T)1,0,3(-(答案不唯一)。
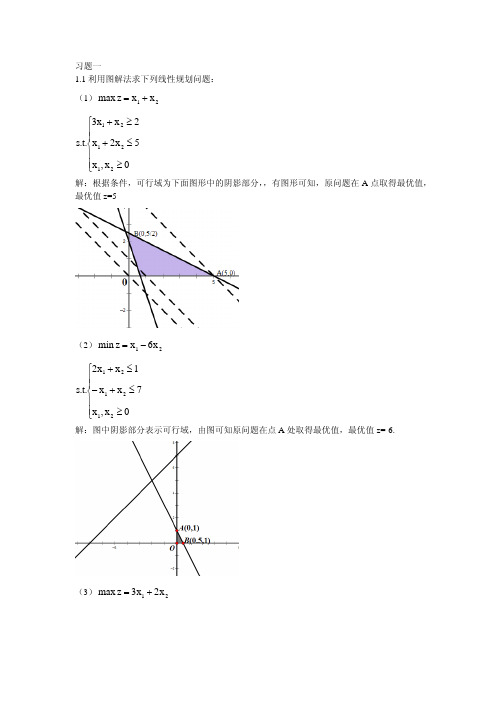
习题一1.1利用图解法求下列线性规划问题: (1)21x x z max +=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 5x 2x 2x x 3.t .s 212121 解:根据条件,可行域为下面图形中的阴影部分,,有图形可知,原问题在A 点取得最优值,最优值z=5(2)21x 6x z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+-≤+0x ,x 7x x 1x x 2.t .s 212121 解:图中阴影部分表示可行域,由图可知原问题在点A 处取得最优值,最优值z=-6.(3)21x 2x 3z max +=⎪⎪⎩⎪⎪⎨⎧≥-≥-≤+-0x ,x 4x 2x 1x x .t .s 212121 解:如图所示,可行域为图中阴影部分,易得原线性规划问题为无界解。
(4)21x 5x 2z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 2x x 6x 2x .t .s 212121 解:由图可知该线性规划可行域为空,则原问题无可行解。
1.2 对下列线性规划问题,找出所有的基解,基可行解,并求出最优解和最优值。
(1)4321x 6x 3x 2x 5z min -+-=⎪⎪⎩⎪⎪⎨⎧≥=+++=+++0x ,x ,x ,x 3x 2x x x 27x 4x 3x 2x .t .s 432143214321 解:易知1x 的系数列向量⎪⎪⎭⎫ ⎝⎛=21p 1,2x 的系数列向量⎪⎪⎭⎫ ⎝⎛=12p 2,3x 的系数列向量⎪⎪⎭⎫⎝⎛=13p 3,4x 的系数列向量⎪⎪⎭⎫⎝⎛=24p 4。
①因为21p ,p 线性无关,故有⎪⎩⎪⎨⎧--=+--=+43214321x 2x 3x x 2x 4x 37x 2x ,令非基变量为0x x 43==,得⎪⎪⎩⎪⎪⎨⎧=-=311x 31x 21,所以得到一个基解)0,0,311,31(x )1(-=是非基可行解; ②因为31p ,p 线性无关,可得基解)0,511,0,52(x)2(=,543z 2=;③因为41p ,p 线性无关,可得基解611,0,0,31(x )3(-=,是非基可行解;④因为32p ,p 线性无关,可得基解)0,1,2,0(x )4(=,1z 4-=;⑤因为42p ,p 线性相关,42x ,x 不能构成基变量; ⑥因为43p ,p 线性无关,可得基解)1,1,0,0(x )6(=,3z 6-=;所以)6()4()2(x ,x ,x是原问题的基可行解,)6(x 是最优解,最优值是3z -=。

最优化基础理论与方法第二版答案
1.什么是最优化?
答:最优化是指从其中一种分析角度,通过确定目标,对已知的约束
条件,有效地分配资源,及早达到最优状态。
2.什么是约束条件?
答:约束条件是指有其中一种特定要求,必须满足一定的范围,方可
实现目标。
3.什么是对偶最佳化?
答:对偶最优化是指通过构建一个对偶函数来求解最优化问题的方法。
4.什么是凸优化?
答:凸优化是指求解连续函数的最优解时,对可行解所表示的约束集
合是一个凸集的一种最优化方法。
5.什么是线性规划?
答:线性规划是指求解一个或多个变量与多个约束条件之间关系的一
种规划方法,其中的目标函数及约束条件均可以用线性表达式表示。
6.什么是随机最优化?
答:随机最优化是指利用随机数学方法求解类优化问题的方法,因为
其优化问题的特殊性,通常不是算法专家所专注的领域。
7.什么是梯度优化?
答:梯度优化是一种利用梯度的方法来最优解的过程。
8.什么是动态规划?
答:动态规划是一种求解最优化问题的一种数学方法,它利用组合优选的思想,把复杂的最优化问题化解为若干子问题,优化问题的一个子问题里面包含优化问题的最优解。
9.什么是最优化算法?。

2015-2016 学年 第一学期期末试卷参考答案学号 姓名 成绩 考试日期: 2016年1月15日考试科目:《数理统计》(B 层)一、填空题(本题共16分,每小题4分)1.设12,,n x x x ,是来自正态总体2(0,)N σ的简单样本,则当c = 时,统计量221()nkk x cxx η==-∑服从F -分布,其中11nk k x x n ==∑。
((1)n n -)2. 设12,,n x x x ,是来自两点分布(1,)B p 的简单样本,其中01p <<,2n ≥,则当c = 时,统计量2ˆ(1)cx x σ=-是参数()(1)q p p p =-的无偏估计,其中11nk k x x n ==∑。
(1n n -)3.设总体X 的密度函数为22,[0,](;)0,[0,]x x p x x θθθθ⎧∈⎪=⎨⎪∉⎩,其中0θ>,12,,,n x x x 是来自总体X 简单样本,则θ的充分统计量是 。
(()n x ) 4.设12,,n x x x ,是来自正态总体2(,)N μσ的简单样本,已知样本均值 4.25x =,μ的置信度为0.95的双侧置信区间下限为3.1,则μ的置信度为0.95的双侧置信区间为(,)。
((3.1,5.4))二、(本题12分)设12,,,n x x x 是来自正态总体2(1,2)N σ的简单样本。
(1)求2σ的极大似然估计2σ;(2)求2σ的一致最小方差无偏估计;(3)问2σ的一致最小方差无偏估计是否为有效估计?证明你的结论。
解(1)似然函数为22211()exp{(1)}4nnii L x σσ==--∑对数似然函数为222211ln ()(ln(4)ln )(1)24n i i n L x σπσσ==-+--∑求导,有222241ln ()1(1)24n i i L n x σσσσ=∂=-+-∂∑ 令22ln ()0L σσ∂=∂,可得θ的极大似然估计为2211ˆ(1)2n i i x n σ==-∑。

《最优化方法》(研究生)期末考试练习题答案二.简答题1.;0, ,843 ,2 2-,3 34 s.t. ,95- min 2121212121≤=--≥+≥++y y y y y y y y y y 2.,065 6143≥+x x (以1x 为源行生成的割平面方程) 注意:在1x 为整数的情况下,因为3x ,04≥x ,该方程自然满足,这是割平面的退化情形,2141 41 43≥+x x (以2x 为源行生成的割平面方程)3.6648.31854.1*2)854.1()(2131.01146.1*2)146.1()(854.13*618.00)(618.0146.13*382.00)(382.03,031311111111111=+-==+-==+=-+==+=-+===μϕλϕμλa b a a b a b a 0.927.21.8540]1.8540[854.1,0)()(,*2211=+===≤x b a 近似的最优解:。
,初始的保留区间为即:。
所以,不经计算也可以看出事实上μϕλϕ4.令1.01.0)(4.04.0)(11)(7.27.2)(222222221)2(*111)1(*111)0(*121)1(*11-=-=-=-=-=-=-=-=-------x x x x x x x e x e x x f ex ex x f x e x x f e x e x x f拟合问题等价于求解下列最小二乘问题:∑=412))((mini ix f三.计算题1.分别用最速下降方法和修正的牛顿法求解无约束问题 22214)(min x x x f +=。
取初始点()()Tx 2,21=,.1.0=ε()().1641642,2821121⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫⎝⎛=∇=⎪⎪⎭⎫⎝⎛=∇d f x x x f T方向为:从而最速下降法的搜索,在初始点,解:()()()()直至满足精度。
继续迭代方向为:从而最速下降法的搜索,,在从而求解得到:其中满足最优步长,.48/6565/19248/65-65/19265/6,65/96)65/6,65/96((-4,-16)*130/172,2 130,/17.)162(4)42()162,42()()(min )(122221)1(1)1(1*)1(*⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛=∇-=-=+==-+-=--=++=+d f x x f d x f d x f d x f TTT Tλλλλλλλλλλ()()2-2- 1648/1002/1 8/1002/1,8002 2,21111⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=∇-=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛==--f G d G G x T索方向为:从而修正的牛顿法的搜,在初始点()()()()即为所求的极小点。

《最优化方法》1一、填空题:1.最优化问题的数学模型一般为:____________________________,其中___________称为目标函数,___________称为约束函数,可行域D 可以表示为_____________________________,若______________________________,称*x 为问题的局部最优解,若_____________________________________,称*x 为问题的全局最优解。
2.设f(x)= 212121522x x x x x +-+,则其梯度为___________,海色矩阵___________,令,)0,1(,)2,1(T T d x ==则f(x)在x 处沿方向d 的一阶方向导数为___________,几何意义为___________________________________,二阶方向导数为___________________,几何意义为____________________________________________________________。
3.设严格凸二次规划形式为:012..222)(min 2121212221≥≥≤+--+=x x x x t s x x x x x f则其对偶规划为___________________________________________。
4.求解无约束最优化问题:n R x x f ∈),(min ,设k x 是不满足最优性条件的第k 步迭代点,则:用最速下降法求解时,搜索方向k d =___________ 用Newton 法求解时,搜索方向k d =___________ 用共轭梯度法求解时,搜索方向k d =___________________________________________________________________________。

最优化⽅法练习题答案精⼼整理练习题⼀1、建⽴优化模型应考虑哪些要素? 答:决策变量、⽬标函数和约束条件。
2、讨论优化模型最优解的存在性、迭代算法的收敛性及停⽌准则。
min ()f x D ∈,对于则有(f ?1例2.1解:*2、研究线性规划的对偶理论和⽅法(包括对偶规划模型形式、对偶理论和对偶单纯形法)。
答:略。
3、⽤单纯形法求解下列线性规划问题:(1)≥≤+-≤++≤-++-=0,,43222..min32131321321321x x x x x x x x x x x t s x x x z ;(2)=≥=++=+-=+-+-=)5,,2,1(052222..4min 53243232132Λi x x x x x x x x x x t s x x z i解:(1)引⼊松弛变量x 4,x 5,x 6因检验数σj >0,表明已求得最优解:*(0,8/3,1/3,0,0,11/3)X =,去除添加的松弛变量,原问题的最优解为:*(0,8/3,1/3)X =。
(2)根据题意选取x 1,x 4,x 5,为基变量:因检验数σ2<0最⼩,故确定x 2为换⼊⾮基变量,以x 2的系数列的正分量对应去除常数列,最⼩⽐值所在⾏对应的基变量x 4作为换出的基变量。
4根据题意约束条件1和2可以合并为1,引⼊松弛变量x 3,x 4,构造新问题。
因检验数σj>0,表明已求得最优解:*(3/5,6/5)X 。
Matlab调⽤代码:Matlab调⽤代码:f=[-10;-15;-12];A=[5,3,1;-5,6,15;-2,-1,-1];b=[9;15;-5];lb=[0;0;0];x=linprog(f,A,b,[],[],lb)输出结果:原题⽆可⾏解。
5、⽤内点法和Matlab软件求解下列线性规划问题:解:⽤内点法的过程⾃⼰书写,参考答案:最优解[4/3 7/3 0] X=;最优值5 Matlab调⽤代码:f=[2;1;1];Aeq=[1,2,2;2,1,0];beq=[6;5]; Array 6解:(x=33y=-39最优解[33];最优值39(2)调⽤matlab编译程序bbmethodf=[-7;-9];G=[-13;71];h=[6;35][x,y]=bbmethod(f,G,h,[],[],[0;0],[],[1;0],1)x=50y=-35最优解[50];最优值357、⽤隐枚举法和Matlab软件求解下列问题:0)(1,2.1,1,输出结果x=1fval=2(2)调⽤代码:f=[-3;-2;5;2;3]; %价值向量fA=[1,1,1,2,1;7,0,3,-4,3;-11,6,0,-3,3]; %不等式约束系数矩阵A,[]中的分号“;”%为⾏分隔符b=[4;8;-1]; %不等式约束右端常数向量b[x,fval]=bintprog(f,A,b,[],[]); %调⽤函数bintprog。
