专题04 数列求和及综合应用(原卷版)

专题04基本不等式及其应用【考点预测】1.基本不等式如果00>>b a ，，那么2b a ab +≤，当且仅当b a =时，等号成立．其中，2ba +叫作b a ，的算术平均数，ab 叫作b a ，的几何平均数．即正数b a ，的算术平均数不小于它们的几何平均数．基本不等式1：若a b ∈，R ，则ab b a 222≥+，当且仅当b a =时取等号；基本不等式2：若a b ∈，+R ，则ab ba ≥+2（或ab b a 2≥+），当且仅当b a =时取等号.注意（1）基本不等式的前提是“一正”“二定”“三相等”；其中“一正”指正数，“二定”指求最值时和或积为定值，“三相等”指满足等号成立的条件.（2）连续使用不等式要注意取得一致.【方法技巧与总结】1.几个重要的不等式（1）()()()2000,0.a a R a a a R ≥∈≥≥≥∈（2）基本不等式：如果,ab R +∈，则2a b+≥(当且仅当“a b =”时取“”).特例：10,2;2a ba a ab a>+≥+≥（,a b 同号）.（3）其他变形：①()2222a b a b ++≥(沟通两和a b +与两平方和22a b +的不等关系式)②222a b ab +≤(沟通两积ab 与两平方和22a b +的不等关系式)③22a b ab +⎛⎫≤ ⎪⎝⎭(沟通两积ab 与两和a b +的不等关系式)④重要不等式串：)2,112a ba b R a b++≤≤≤∈+即调和平均值≤几何平均值≤算数平均值≤平方平均值(注意等号成立的条件).2.均值定理已知,x y R +∈.（1）如果x y S +=(定值),则2224x y S xy +⎛⎫≤=⎪⎝⎭(当且仅当“x y =”时取“=”).即“和为定值，积有最大值”.（2）如果xy P =(定值)，则x y +≥=(当且仅当“x y =”时取“=”).即积为定值，和有最小值”.3.常见求最值模型模型一：)0,0(2>>≥+n m mn xnmx ，当且仅当mnx =时等号成立；模型二：)0,0(2)(>>+≥+-+-=-+n m ma mn ma ax na x m a x n mx ，当且仅当mna x =-时等号成立；模型三：)0,0(2112>>+≤++=++c a bac xc b ax c bx ax x ，当且仅当acx =时等号成立；模型四：0,0,0(421)()(22m n x n m m n mx n mx m m mx n mx mx n x <<>>=-+⋅≤-=-（，当且仅当mnx 2=时等号成立.【典例例题】题型一：基本不等式及其应用例1．下列不等式恒成立的是（）A．12x x+≥B．a b +≥C．22222a b a b ++⎛⎫≥⎪⎝⎭D．222a b ab+≥例2．已知x ，y 都是正数，且x y ≠，则下列选项不恒成立的是（）A．2x y+>B．2x y y x+>C．2xyx y<+D．12xy xy +>例3．《几何原本》卷2的几何代数法（以几何方法研究代数问题）成了后世西方数学家处理问题的重要依据，通过这一原理，很多的代数的公理或定理都能够通过图形实现证明，也称之为无字证明．现有如图所示图形，点F 在半圆O 上，点C 在直径AB 上，且OF AB ⊥，设AC a =，BC b =，则该图形可以完成的无字证明为（）A．0,0)2a ba b +≥>>B．220,0)a b a b +≥>>C．20,0)aba b a b≤>>+D．0,0)2a b a b +≤>>例4．下列不等式中一定成立的是（）A．()2111x x >∈+R B．()12,sin sin xx k x k π+>≠∈Z C．21ln ln (0)4x x x ⎛⎫+>> ⎪⎝⎭D．()212x x x +≥∈R 例5．（多选题）下列函数中最小值为6的是（）A．9ln ln y x x=+B．36sin 2sin y x x=+C．233xxy -=+D．2y例6．（多选题）设0a >，0b >，下列结论中正确的是（）A．()1229a b a b ⎛⎫++≥ ⎪⎝⎭B．()2221a b a b +≥++C．22b a a ba b+≥+D．22a b a b+≥+【方法技巧与总结】熟记基本不等式成立的条件，合理选择基本不等式的形式解题，要注意对不等式等号是否成立进行验证.题型二：直接法求最值例7．若实数a ，b 满足1a b +=，则ab 的最大值为（）A．2B．1C．12D．14例8．若x ，y 为实数，且26x y +=，则39x y +的最小值为（）A．18B．27C．54D．90例9．已知二次函数()22f x ax x c =++（x ∈R ）的值域为[)0,∞+，则14c a+的最小值为（）A．4-B．4C．8D．8-例10．函数()1111642xx x f x -=++的最小值为（）A．4B．C．3D．例11．（多选题）已知a ，b 是两个正数，4是2a 与16b 的等比中项，则下列说法正确的是（）A．ab 的最小值是1B．ab 的最大值是1C．11a b+的最小值是94D．11a b+的最大值是92例12．若,R a b +∈，且11b a +=，则2b a的最大值是_______________.例13．已知正数x 、y 满足124x y +=，则yx的最小值是___________.【方法技巧与总结】直接利用基本不等式求解，注意取等条件.题型三：常规凑配法求最值例14．若11x -<<，则22222x x y x -+=-有（）A．最大值1-B．最小值1-C．最大值1D．最小值1例15．函数131y x x =+-(1)x >的最小值是（）A．4B．3-C．D．3+例16．若0x >，0y >且x y xy +=，则211x y x y +--的最小值为（）A．3B．52C．3D．3+例17．若1x >，则函数211x x y x -+=-的最小值为___________.例18．已知1xy =，且102y <<，则22416x y x y -+最大值为______．例19．（1）求函数()411y x x x =+>-的最小值及此时x 的值；（2）已知函数25102x x y x ++=+，()2,x ∈-+∞，求此函数的最小值及此时x 的值.【方法技巧与总结】1．通过添项、拆项、变系数等方法凑成和为定值或积为定值的形式．2．注意验证取得条件．题型四：消参法求最值例20．若直线30(0,0)ax by a b --=>>过点(1,1)-例21．设正实数x ，y ，z 满足22340x xy y z -+-=，则当xyz取得最大值时，212x y z +-的最大值为（）A．0B．3C．94D．1例22．已知正实数a ，b 满足220ab a +-=，则4a b +的最小值是（）A．2B．2-C．2-D．6例23．若正实数a ，b 满足32+=b a ab ，则2+a bab 的最大值为______．例24．若,x y R +∈，23()()-=x y xy ，则11x y+的最小值为___________.例25．若220,0,422>>+-=a b a b ab ，则12++ab a b的取值范围是_________．【方法技巧与总结】消参法就是对应不等式中的两元问题，用一个参数表示另一个参数，再利用基本不等式进行求解.解题过程中要注意“一正，二定，三相等”这三个条件缺一不可！题型五：双换元求最值例26．设0a >，0b >，若221a b +=2ab -的最大值为（）A．3B．C．1D．2例27．若0a >，0b >，0c >，2a b c ++=，则4a b a b c+++的最小值为______．例28．已知x＋y＝1，y＞0，x＞0，则121x x y ++的最小值为____________．例29．已知0a >，0b >，21a b +=，则11343a b a b+++取到最小值为________．例30．若,x y R +∈，且21x y +=，则22212x y x y +++的最小值为_________例31．若正实数x ，y 满足22x y +=，则224122x y y x +++的最小值是__________．【方法技巧与总结】若题目中含是求两个分式的最值问题，对于这类问题最常用的方法就是双换元，分布运用两个分式的分母为两个参数，转化为这两个参数的不等关系．1．代换变量，统一变量再处理．2．注意验证取得条件．题型六：“1”的代换求最值例32．已知正实数x ，y 满足211x y+=，则436xy x y --的最小值为（）A．2B．4C．8D．12例33．设正项等差数列{}n a 的前n 项和为n S ，若20132013S =，则2201211a a +的最小值为（）A．1B．2C．4D．8例34．若实数a ，b 满足123,12a b a b ⎛⎫+=>> ⎪⎝⎭，则2211a b a b +--的最小值为（）A．6B．4C．3D．2例35．已知20,0,61a b a b >>+=，则162b a+的最小值为（）A．13B．19C．21D．27例36．已知0a >，0b >且1a b +=，则1811a b ⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭的最小值是()A．49B．50C．51D．52例37．已知正数a ，b 满足0ab a b --=，则4a b +的最小值为___________.例38．设0x >，0y >，1x y +=，则212x xy+的最小值为______．例39．函数11x y a -=+图象过定点A ，点A 在直线()31,0mx ny m n +=>>上，则121m n+-最小值为___________.【方法技巧与总结】1的代换就是指凑出1，使不等式通过变形出来后达到运用基本不等式的条件，即积为定值，凑的过程中要特别注意等价变形．1．根据条件，凑出“1”，利用乘“1”法．2．注意验证取得条件．题型七：齐次化求最值例40．已知0,0a b >>，满足222232390,a b a b --+=则32b aa b+的最小值是（）A．B．C．D．例41．已知函数())f x a b =<的定义域为R ，则24b aa b c-++的最大值是___________.例42．若a ，b ，c 均为正实数，则2222ab bca b c +++的最大值为（）A．12B．14C．2D．2例43．已知三次函数32()()f x ax bx cx d a b =+++<在R 上单调递增，则a b cb a ++-最小值为（）例44．已知0a >，0b >，且21a b +=，则12bb a b++的最小值为____________.例45．已知x ，y ，z 为正实数，且240x y z +-=，则2xyz 的最大值为______．例46．若0,0x y >>且224log 3log 9log 81x y+=，则433x y x y++的最小值为___________.【方法技巧与总结】齐次化就是含有多元的问题，通过分子、分母同时除以得到一个整体，然后转化为运用基本不等式进行求解．题型八：利用基本不等式证明不等式例47．已知0a >，0b >．(1)若21a b +=，证明：2233348a b ≤+<；(2)若2a b ab +=，证明：410a b ab ++≥+例48．设函数()124f x x x =+--．(1)求不等式()23f x x ≥-的解集．(2)若()f x 的最大值为222a b c ++，证明：3ab bc ca ++≤．例49．已知正数a ，b ，c 满足3a b c ++=．(1)求abc 的最大值；(2)证明：3333a b b c c a abc ++≥．例50．设a ，b ，c 为正实数，且1a b c ++=.证明：(1)11192a b b c c a ++≥+++；(2)33332ab bc ca abca b c ++-++≥.例51．已知a ，b ，c 都是正数.(1)证明：a b c ++(2)若3a b c ++=，证明：11132a b b c c a ++≥+++.【方法技巧与总结】类似于基本不等式的结构的不等式的证明可以利用基本不等式去组合、分解、运算获得证明.题型九：利用基本不等式解决实际问题例51．设计用232m 的材料制造某种长方体形状的无盖车厢，按交通部门的规定车厢宽度为2m ，则车厢的最大容积是（）A．m3B．16m3m3D．14m3例53．如图，将一矩形花坛ABCD 扩建成一个更大的矩形花坛AMPN ，要求点B 在AM 上，点D 在AN 上，且对角线MN 过点C ，已知4AB =，3AD =，那么当BM =_______时，矩形花坛的AMPN 面积最小，最小面积为______.例54．根据不同的程序，3D 打印既能打印实心的几何体模型，也能打印空心的几何体模型．如图所示的空3cm 的球挖去一个三棱锥P ABC -后得到的几何体，其中PA AB ⊥，BC ⊥平面PAB ，1BC cm =．不考虑打印损耗，求当用料最省时，AC 的长．例55．为响应国家扩大内需的政策，某厂家拟在2019年举行促销活动，经调查测算，该产品的年销量(即该厂的年产量)x 万件与年促销费用t(t≥0)万元满足421kx t =-+(k 为常数)．如果不搞促销活动，则该产品的年销量只能是1万件．已知2019年生产该产品的固定投入为6万元，每生产1万件该产品需要再投入12万元，厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分)．(1)将该厂家2019年该产品的利润y 万元表示为年促销费用t 万元的函数；(2)该厂家2019年的年促销费用投入多少万元时厂家利润最大？【方法技巧与总结】1．理解题意，设出变量，建立函数模型，把实际问题抽象为函数的最值问题．2．注意定义域，验证取得条件．3.注意实际问题隐藏的条件，比如整数，单位换算等．【过关测试】一、单选题1．已知点E 是ABC 的中线BD 上的一点（不包括端点）．若AE xAB y AC =+ ，则21x y+的最小值为（）A．4B．6C．8D．92．已知,a b 为正实数，且196a b a b+=++，则a b +的最小值为（）A．6B．8C．9D．123．若0a >，0b >，()lg lg lg 3a b a b +=+，则a b +的最小值为（）A．B．4+C．6D．3+4．已知1e ，2e 为平面的单位向量，且其夹角为2π3，若)122,xe ye x y +=∈R ，则2x y +的最大值为（）A．B．C．D．-5．设0a >，1b >，若2a b +=，则411a b +-的最小值为（）A．6B．9C．D．186．已知等比数列{}n a 的公比为q ，且51a =，则下列选项不正确的是（）A．372a a +≥B．462a a +≥C．76210a a -+≥D．191911a a a a +=+7．已知a ，R b ∈，满足e e 1a b +=，则下列错误的是（）A．2ln 2a b +≤-B．e <0a b +C．1≥ab D．()222e e 1a b+≥8．已知a ，()0,b ∈+∞，且22347a ab b ++=，则2+a b 的最大值为（）A．2B．3C．D．二、多选题9．已知,x y +∈R ，x y m +=（m 是常数），则下列结论正确的是（）A．若141x y ++的最小值为1m +，则3m =B．若(1)x y +的最大值为4，则3m =的最大值为m ，则2m =D．若4m =，则29y x+的最小值为210．已知220,0,2a b a b >>+=，则以下不等式成立的是（）A．2a b +>B．332a b +≥C．114a b b a ⎛⎫⎛⎫++≥ ⎪⎪⎝⎭⎝⎭D．112a b +≥11．设a ，b 为两个正数，定义a ，b 的算术平均数为()2a bA a b +=,，几何平均数为()G a b ,纪五十年代，美国数学家D．H.Lehmer 提出了“Lehmer 均值”，即()11,p pp p p a b L a b a b --+=+，其中p 为有理数．下列结论正确的是（）A．()()0.51,,L a b L a b ≤B．()()0,,L a b G a b ≤C．()()2,,L a b A a b ≤D．()()1,,n n L a b L a b +≤12．已知函数2()log x f x =，且正实数a ，b 满足()()1f a f b +=，则下列结论可能成立的是（）A．2a b =B．1122a b --+的最大值为32C．2ab =D．2211a b +的最小值为三、填空题13．已知正实数x ，y 满足12e (2)e yxx y -=+，则22y xy x y++的最小值为__________．14．已知2x >，则42x x +-的最小值是______．15．已知0a >，0b >，且2233a b ab a b +=+，则3a b +的最小值为___________.16．已知正实数x ，y 满足：222xx xy y ++=，则232x y y++的最小值为_________．四、解答题17．已知函数()263f x x x =++-．(1)解不等式()10f x ≥的解集；(2)设()()3g x f x x =-+到的最小值为t ，若正数m ，n 满足2m n t +=，求11211m n +++的最小值．18．已知函数()24f x x x =-+-，已知不等式()()0f x kx k ≥>恒成立.(1)求k 的最大值0k ；(2)设0a >，0b >，求证：1223a b a b a b k +≥++.19．设函数()||()f x x a a =-∈R ．(1)若关于x 的不等式()(2)4+-≥f x f x 恒成立，求a 的取值范围；(2)在平面直角坐标系xOy 中，()()1+≤f x f y 所围成的区域面积为S ，若正数b ，c ，d 满足()()++=b d c d S ，求23++b c d 的最小值．20．设函数()142a f x x x x a=-++-()0a >(1)当1a =时，求不等式()52f x ≤的解集；(2)已知不等式()1f x x a ≥+的解集为{}1xx ≤∣，0m >，0n >，m n a +=，求28m n+的最小值.21．设a ，b 为正数，且1a b +=．证明：(1)2≤：(2)()()222a b b a a ++>．22．设a ，b ，c 均为正数，且1a b c ++=．(1)求14a b c++的最小值；。

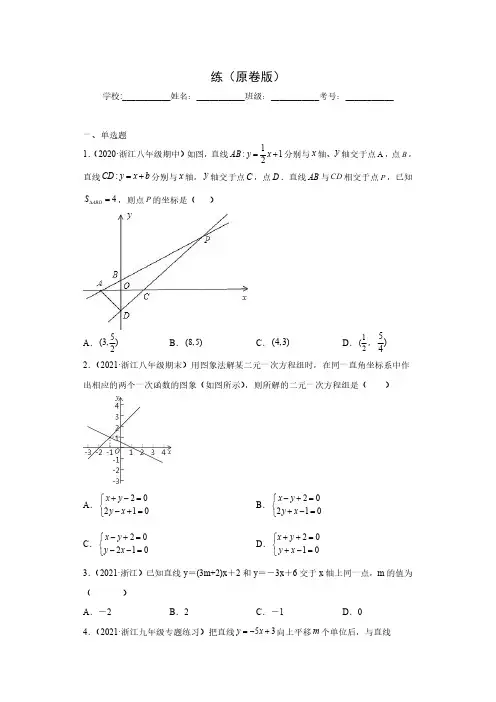
练（原卷版）学校:___________姓名：___________班级：___________考号：___________一、单选题1．（2020·浙江八年级期中）如图，直线1:12AB y x =+分别与x 轴、y 轴交于点A ，点B ，直线:CD y x b =+分别与x 轴，y 轴交于点C ，点D ．直线AB 与CD 相交于点P ，已知4ABD S ∆=，则点P 的坐标是（）A ．5(3,)2B ．(8,5)C ．(4,3)D ．1(2，5)42．（2021·浙江八年级期末）用图象法解某二元一次方程组时，在同一直角坐标系中作出相应的两个一次函数的图象（如图所示），则所解的二元一次方程组是（）A ．20210x y y x +-=⎧⎨-+=⎩B ．20210x y y x -+=⎧⎨+-=⎩C ．20210x y y x -+=⎧⎨--=⎩D ．2010x y y x ++=⎧⎨+-=⎩3．（2021·浙江）已知直线y ＝(3m+2)x ＋2和y ＝－3x ＋6交于x 轴上同一点，m 的值为（）A ．－2B ．2C ．－1D ．04．（2021·浙江九年级专题练习）把直线53y x =-+向上平移m 个单位后，与直线二、填空题5．（2020·浙江）如图，直线1:2l y x =+与直线2:l y kx b =+相交于点(),4P m ，则方程组2y x y kx b=+⎧⎨=+⎩的解是____．6．（2020·浙江八年级期中）已知一次函数y kx b =+与y mx n =+的图象如图所示．（1）写出关于x ，y 的方程组y kx b y mx n=+⎧⎨=+⎩的解为________．（2）若0kx b mx n <+<+，写出x 的取值范围________．7．（2020·浙江）如图，直线1:22l y x =-+交x 轴于点A ，交y 轴于点B ，直线21:12y l x =+交x 轴于点D ，交y 轴于点C ，直线1l 、2l 交于点M ．（1）点M 坐标为________；（2）若点E 在y 轴上，且BME 是以BM 为一腰的等腰三角形，则E 点坐标为________．8．（2021·浙江八年级期末）如图，已知直线1:l y kx b =+与直线21:2l y x m =-+都经过68,55C ⎛⎫- ⎪⎝⎭，直线1l 交y 轴于点()0,4B ，交x 轴于点A ，直线2l 为y 轴交于点D ，P 为y 轴上任意一点，连接PA 、PC ，有以下说法：①方程组12y kx b y x m =+⎧⎪⎨=+⎪⎩的解为6585x y ⎧=-⎪⎪⎨⎪=⎪⎩；②BCD △为直角三角形；③6ABD S = ；④当PA PC +的值最小时，点P 的坐标为()0,1．其中正确的说法是______．9．（第12讲一次函数的应用及综合问题（讲练）-备战2021年中考数学一轮复习讲练测（浙江））对于实数a ，b ，我们定义符号max{a ，b}的意义为：当a≥b 时，max{a ，b}＝a ；当a ＜b 时，max{a ，b]＝b ；如：max{4，﹣2}＝4，max{3，3}＝3，若关于x 的函数为y ＝max{x+3，﹣x+1}，则该函数的最小值是_____．三、解答题10．（2020·浙江八年级期末）如图，在平面直角坐标系中，直线210y x =-+与x 轴交于点B ，与y 轴交于点C ，与直线12y x =交于点A ，点M 是y 轴上的一个动点，设()0,M m .（1）若MA MB +的值最小，求m 的值；（2）若直线AM 将ACO △分割成两个等腰三角形，请求出m 的值，并说明理由.11．（2020·台州市外国语学校九年级月考）如图，直线l 1的解析式为y ＝﹣3x +3，且l 1与x 轴交于点D ，直线l 2经过点A 、B ，直线l 1、l 2交于点C ．（1）求直线l 2的解析表达式；（2）求△ADC 的面积；（3）在直线l 2上存在异于点C 的另一点P ，使得△ADP 与△ADC 的面积相等，请求出点P 的坐标．12．（2019·金华市第五中学八年级期中）如图，点A 、B 的坐标分别为（0，2），（1，0），直线y=12x−3与y 轴交于点C ，与x 轴交于点D ，（1）求直线AB 与CD 交点E 的坐标；（1）若函数y 1的图象经过点(﹣1，5)，求函数y 1的表达式．（2）已知点P(x 1，m )和Q(﹣3，n )在函数y 1的图象上，若m ＞n ，求x 1的取值范围．（3）若一次函数y 2＝ax+b （a≠0）的图象与y 1的图象始终经过同一定点，探究实数a ，b 满足的关系式．14．（2020·浙江翠苑中学八年级月考）已知直线1:l y kx b =+（k ，b 为常数且0k <），经过点()()4,1,B 2,4A -．（1）求直线1l 的函数解析式；（2）若直线2l 是由直线2y x =-向上平移8个单位得到，求直线1l ，直线2l 和x 轴围成图形的面积．15．（2020·浙江）设一次函数()11y m x =-，()21y n x =+（m ，n 是常数，且m≠0，m≠n ，n>0）（1）当m=3，n=2时，①求函数y 1，y 2图象的交点坐标．②若y 1>y 2，求自变量x 的取值范围．（2）在0<x<1的范围内，有且只有部分函数值满足y 1>y 2，求证:m+n<0．16．（2020·浙江八年级期末）平面直角坐标系中，已知直线1l 经过原点与点(),2P m m ，直线2l ：23y mx m =+-(0)m ≠；（1）求证：点(23)--，在直线2l 上；（2）当2m =时，请判断直线1l 与2l 是否相交？17．（2020·浙江八年级期末）已知一次函数1y ax b =+，2y bx a =+（0ab ≠，且a b ¹）（1）若1y 过点(1,2)与点(23)b a --，，求1y 的函数解析式．（2）1y 与2y 的图像交于点(),A m n ，用含a ，b 的式子表示n ．（3）设3y =12y y -，421y y y =-，当34y y >时，求x 的取值范围．18．（2021·浙江九年级专题练习）已知：如图，直线l 1：y 1＝﹣x +n 与y 轴交于A （0，6），直线l 2：y ＝kx +1分别与x 轴交于点B （﹣2，0），与y 轴交于点C ，两条直线相交于点D ，连接AB ．（1）直接写出直线l 1、l 2的函数表达式；19．（2020·浙江）如图，在平面直角坐标系中，一次函数y ＝kx +b 的图象与x 轴交于点A （﹣3，0），与y 轴交于点B ，且与正比例函数y ＝43x 的图象交点为C （m ，4）．（1）求一次函数y ＝kx +b 的解析式；（2）求△BOC 的面积；（3）若点D 在第二象限，△DAB 为等腰直角三角形，则点D 的坐标为．20．（2021·浙江八年级期末）定义：函数()()2424x x m y x x m ⎧-+≥⎪=⎨+<⎪⎩叫做关于m 的对称函数，它与x 轴负半轴交点记为A ，与x 轴正半轴交点记为B ．（1）关于1的对称函数()()241241x x y x x ⎧-+≥⎪=⎨+<⎪⎩与直线1x =交于点C ，如图．①(),0A ，(),0B ，()1,C ．②P 为关于1的对称函数图象上一点（点P 不与点C 重合），当= ABC ABP S S 时，求点P 的坐标；（2）当直线y x =与关于m 的对称函数有两个交点时，求m 的取值范围．。

专题04 数列求和及综合应用【要点提炼】1.常用公式：12＋22＋32＋42＋…＋n 2＝n （n ＋1）（2n ＋1）6.2.(1)数列通项a n 与前n 项和S n 的关系为a n ＝⎩⎨⎧S 1 （n ＝1），S n －S n －1 （n ≥2）.(2)应用a n 与S n 的关系式f (a n ，S n )＝0时，应特别注意n ＝1时的情况，防止产生错误. 3.数列求和(1)分组转化法：一个数列既不是等差数列，也不是等比数列，若将这个数列适当拆开，重新组合，就会变成几个可以求和的部分，分别求和，然后再合并. (2)错位相减法：主要用于求数列{a n ·b n }的前n 项和，其中{a n }，{b n }分别是等差数列和等比数列.(3)裂项相消法：即将数列的通项分成两个式子的代数差的形式，然后通过累加抵消中间若干项的方法，裂项相消法适用于形如⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫c a n a n ＋1(其中{a n }是各项均不为零的等差数列，c 为常数)的数列.温馨提醒 裂项求和时，易把系数写成它的倒数或忘记系数导致错误. 4.数列与函数、不等式的交汇数列与函数的综合问题一般是利用函数作为背景，给出数列所满足的条件，通常利用点在曲线上给出S n 的表达式，还有以曲线上的切点为背景的问题，解决这类问题的关键在于利用数列与函数的对应关系，将条件进行准确的转化.数列与不等式的综合问题一般以数列为载体，考查不等关系或恒成立问题.考点一 数列求和及综合应用考向一 a n 与S n 的关系问题【典例1】 设数列{a n }的前n 项和为S n ，对任意的正整数n ，都有a n ＝5S n ＋1成立，b n ＝－1－log 2|a n |，数列{b n }的前n 项和为T n ，c n ＝b n ＋1T n T n ＋1. (1)求数列{a n }的通项公式；(2)求数列{c n }的前n 项和A n ，并求出A n 的最值.解 (1)因为a n ＝5S n ＋1，n ∈N *， 所以a n ＋1＝5S n ＋1＋1， 两式相减，得a n ＋1＝－14a n ，又当n ＝1时，a 1＝5a 1＋1，知a 1＝－14， 所以数列{a n }是公比、首项均为－14的等比数列. 所以数列{a n }的通项公式a n ＝⎝ ⎛⎭⎪⎫－14n.(2)由(1)知b n ＝－1－log 2|a n |＝2n －1， 数列{b n }的前n 项和T n ＝n 2， c n ＝b n ＋1T n T n ＋1＝2n ＋1n 2（n ＋1）2＝1n 2－1（n ＋1）2， 所以A n ＝1－1（n ＋1）2.因此{A n }是单调递增数列，∴当n ＝1时，A n 有最小值A 1＝1－14＝34；A n 没有最大值.探究提高 1.给出S n 与a n 的递推关系求a n ，常用思路是：一是利用S n －S n －1＝a n (n ≥2)转化为a n 的递推关系，再求其通项公式；二是转化为S n 的递推关系，先求出S n 与n 之间的关系，再求a n .2.由S n 求a n 时，一定注意分n ＝1和n ≥2两种情况，最后验证两者是否能合为一个式子，若不能，则用分段形式来表示.【拓展练习1】 (2020·合肥检测)已知正项数列{a n }的前n 项和为S n ，满足a 2n ＝S n ＋S n －1(n ≥2)，a 1＝1. (1)求数列{a n }的通项公式；(2)设b n ＝(1－a n )2－a (1－a n )，若{b n }是递增数列，求实数a 的取值范围. 解 (1)a 2n ＝S n ＋S n －1(n ≥2)， a 2n －1＝S n －1＋S n －2(n ≥3).相减可得a 2n －a 2n －1＝a n ＋a n －1，∵a n ＞0，a n －1＞0，∴a n －a n －1＝1(n ≥3). 当n ＝2时，a 22＝a 1＋a 2＋a 1，∴a 22＝2＋a 2，a 2＞0，∴a 2＝2. 因此n ＝2时，a n －a n －1＝1成立. ∴数列{a n }是等差数列，公差为1. ∴a n ＝1＋n －1＝n .(2)b n ＝(1－a n )2－a (1－a n )＝(n －1)2＋a (n －1)， ∵{b n }是递增数列，∴b n ＋1－b n ＝n 2＋an －(n －1)2－a (n －1) ＝2n ＋a －1＞0，即a ＞1－2n 恒成立，∴a ＞－1. ∴实数a 的取值范围是(－1，＋∞). 考向二 数列求和 方法1 分组转化求和【典例2】 (2020·山东五地联考)已知等差数列{a n }的前n 项和为S n ，且满足关于x 的不等式a 1x 2－S 2x ＋2＜0的解集为(1，2). (1)求数列{a n }的通项公式；(2)若数列{b n }满足b n ＝a 2n ＋2a n －1，求数列{b n }的前n 项和T n . 解 (1)设等差数列{a n }的公差为d ，因为关于x 的不等式a 1x 2－S 2x ＋2＜0的解集为(1，2)， 所以S 2a 1＝1＋2＝3，得a 1＝d ，又易知2a 1＝2，所以a 1＝1，d ＝1.所以数列{a n }的通项公式为a n ＝n . (2)由(1)可得，a 2n ＝2n ，2a n ＝2n .因为b n ＝a 2n ＋2a n －1，所以b n ＝2n －1＋2n ，所以数列{b n }的前n 项和T n ＝(1＋3＋5＋…＋2n －1)＋(2＋22＋23＋…＋2n ) ＝n （1＋2n －1）2＋2（1－2n ）1－2＝n 2＋2n ＋1－2.探究提高 1.求解本题要过四关：(1)“转化”关，把不等式的解转化为方程根的问题；(2)“方程”关，利用方程思想求出基本量a 1及d ；(3)“分组求和”关，观察数列的通项公式，把数列分成几个可直接求和的数列；(4)“公式”关，会利用等差、等比数列的前n 项和公式求和.2.分组求和的策略：(1)根据等差、等比数列分组；(2)根据正号、负号分组.本题易忽视数列通项的下标如错得a 2n ＝n ，应注意“＝”左右两边保持一致.【拓展练习2】 (2020·潍坊调研)设等差数列{a n }的前n 项和为S n ，且a 2＝8，S 4＝40.数列{b n }的前n 项和为T n ，且T n －2b n ＋3＝0，n ∈N *. (1)求数列{a n }，{b n }的通项公式；(2)设c n ＝⎩⎨⎧a n ，n 为奇数，b n ，n 为偶数，求数列{c n }的前n 项和P n .解 (1)设等差数列{a n }的公差为d ， 由题意，得⎩⎨⎧a 1＋d ＝8，4a 1＋6d ＝40，解得⎩⎨⎧a 1＝4，d ＝4，所以a n ＝4n ， 因为T n －2b n ＋3＝0，所以当n ＝1时，b 1＝3，当n ≥2时，T n －1－2b n －1＋3＝0， 两式相减，得b n ＝2b n －1(n ≥2)，则数列{b n }为首项为3，公比为2的等比数列， 所以b n ＝3·2n －1.(2)c n ＝⎩⎨⎧4n ，n 为奇数，3·2n －1，n 为偶数，当n 为偶数时，P n ＝(a 1＋a 3＋…＋a n －1)＋(b 2＋b 4＋…＋b n ) ＝（4＋4n －4）·n 22＋6（1－4n2）1－4＝2n ＋1＋n 2－2.当n 为奇数时，法一 n －1(n ≥3)为偶数，P n ＝P n －1＋c n ＝2(n －1)＋1＋(n －1)2－2＋4n ＝2n ＋n 2＋2n －1，n ＝1时符合上式.法二 P n ＝(a 1＋a 3＋…＋a n －2＋a n )＋(b 2＋b 4＋…＋b n －1) ＝（4＋4n ）·n ＋122＋6（1－4n －12）1－4＝2n ＋n 2＋2n －1.所以P n ＝⎩⎨⎧2n ＋1＋n 2－2，n 为偶数，2n ＋n 2＋2n －1，n 为奇数.方法2 裂项相消求和【典例3】 (2020·江南六校调研)设数列{a n }的前n 项和为S n ，已知S 1＝2，a n ＋1＝S n ＋2.(1)证明：{a n }为等比数列； (2)记b n ＝log 2a n ，数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫λb n b n ＋1的前n 项和为T n ，若T n ≥10恒成立，求λ的取值范围.(1)证明 由已知，得a 1＝S 1＝2，a 2＝S 1＋2＝4， 当n ≥2时，a n ＝S n －1＋2，所以a n ＋1－a n ＝(S n ＋2)－(S n －1＋2)＝a n ， 所以a n ＋1＝2a n (n ≥2).又a 2＝2a 1，所以a n ＋1a n＝2(n ∈N *)，所以{a n }是首项为2，公比为2的等比数列. (2)解 由(1)可得a n ＝2n ，所以b n ＝n . 则λb n b n ＋1＝λn （n ＋1）＝λ⎝ ⎛⎭⎪⎫1n －1n ＋1， T n ＝λ⎝ ⎛⎭⎪⎫1－12＋12－13＋…＋1n －1n ＋1＝λ⎝ ⎛⎭⎪⎫1－1n ＋1，因为T n ≥10，所以λn n ＋1≥10，从而λ≥10（n ＋1）n ，因为10（n ＋1）n ＝10⎝ ⎛⎭⎪⎫1＋1n ≤20， 所以λ的取值范围为[20，＋∞).探究提高 1.裂项相消求和就是将数列中的每一项裂成两项或多项，使这些裂开的项出现有规律的相互抵消，要注意消去了哪些项，保留了哪些项.2.消项规律：消项后前边剩几项，后边就剩几项，前边剩第几项，后边就剩倒数第几项.【拓展练习3】 设数列{a n }满足a 1＋3a 2＋…＋(2n －1)a n ＝2n . (1)求{a n }的通项公式；(2)求数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n 2n ＋1的前n 项和.解 (1)因为a 1＋3a 2＋…＋(2n －1)a n ＝2n ，① 故当n ≥2时，a 1＋3a 2＋…＋(2n －3)a n －1＝2(n －1)，② ①－②得(2n －1)a n ＝2，所以a n ＝22n －1，又n ＝1时，a 1＝2适合上式，从而{a n }的通项公式为a n ＝22n －1.(2)记⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n 2n ＋1的前n 项和为S n ，由(1)知a n 2n ＋1＝2（2n －1）（2n ＋1）＝12n －1－12n ＋1，则S n ＝⎝ ⎛⎭⎪⎫1－13＋⎝ ⎛⎭⎪⎫13－15＋…＋⎝ ⎛⎭⎪⎫12n －1－12n ＋1＝1－12n ＋1＝2n2n ＋1.方法3 错位相减法求和【典例4】 (2020·济南统测)在①a 3＝5，a 2＋a 5＝6b 2，②b 2＝2，a 3＋a 4＝3b 3，③S 3＝9，a 4＋a 5＝8b 2这三个条件中任选一个，补充至横线上，并解答问题. 已知等差数列{a n }的公差为d (d >1)，前n 项和为S n ，等比数列{b n }的公比为q ，且a 1＝b 1，d ＝q ，________. (1)求数列{a n }，{b n }的通项公式； (2)记c n ＝a nb n，求数列{c n }的前n 项和T n .(注：如果选择多个条件分别解答，按第一个解答计分) 解 选条件①.(1)∵a 3＝5，a 2＋a 5＝6b 2，a 1＝b 1，d ＝q ，d >1， ∴⎩⎨⎧a 1＋2d ＝5，2a 1＋5d ＝6a 1d ，解得⎩⎨⎧a 1＝1，d ＝2或⎩⎪⎨⎪⎧a 1＝256，d ＝512(舍去).∴⎩⎨⎧b 1＝1，q ＝2.∴a n ＝a 1＋(n －1)d ＝2n －1，b n ＝b 1q n －1＝2n －1. (2)∵c n ＝a n b n，∴c n ＝2n －12n －1＝(2n －1)×⎝ ⎛⎭⎪⎫12n －1.∴T n ＝1＋3×12＋5×⎝ ⎛⎭⎪⎫122＋…＋(2n －3)×⎝ ⎛⎭⎪⎫12n －2＋(2n －1)×⎝ ⎛⎭⎪⎫12n －1，12T n ＝12＋3×⎝ ⎛⎭⎪⎫122＋5×⎝ ⎛⎭⎪⎫123＋…＋(2n －3)×⎝ ⎛⎭⎪⎫12n －1＋(2n －1)×⎝ ⎛⎭⎪⎫12n. 上面两式相减，得12T n ＝1＋2⎣⎢⎡⎦⎥⎤12＋⎝ ⎛⎭⎪⎫122＋…＋⎝ ⎛⎭⎪⎫12n －1－(2n －1)×⎝ ⎛⎭⎪⎫12n＝1＋2×12⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫12n －11－12－(2n －1)×⎝ ⎛⎭⎪⎫12n ＝3－(2n ＋3)×⎝ ⎛⎭⎪⎫12n. ∴T n ＝6－(2n ＋3)×⎝ ⎛⎭⎪⎫12n －1.选条件②.(1)∵b 2＝2，a 3＋a 4＝3b 3，a 1＝b 1，d ＝q ，d >1， ∴⎩⎨⎧a 1d ＝2，2a 1＋5d ＝3a 1d 2，即⎩⎨⎧a 1d ＝2，2a 1＋5d ＝6d ， 解得⎩⎨⎧a 1＝1，d ＝2或⎩⎨⎧a 1＝－1，d ＝－2(舍去).∴⎩⎨⎧b 1＝1，q ＝2. ∴a n ＝a 1＋(n －1)d ＝2n －1，b n ＝b 1q n －1＝2n －1. (2)∵c n ＝a n b n，∴c n ＝2n －12n －1＝(2n －1)×⎝ ⎛⎭⎪⎫12n －1.∴T n ＝1＋3×12＋5×⎝ ⎛⎭⎪⎫122＋…＋(2n －3)×⎝ ⎛⎭⎪⎫12n －2＋(2n －1)×⎝ ⎛⎭⎪⎫12n －1，12T n ＝12＋3×⎝ ⎛⎭⎪⎫122＋5×⎝ ⎛⎭⎪⎫123＋…＋(2n －3)×⎝ ⎛⎭⎪⎫12n －1＋(2n －1)×⎝ ⎛⎭⎪⎫12n. 上面两式相减，得12T n ＝1＋2⎣⎢⎡⎦⎥⎤12＋⎝ ⎛⎭⎪⎫122＋…＋⎝ ⎛⎭⎪⎫12n －1－(2n －1)×⎝ ⎛⎭⎪⎫12n＝1＋2×12⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫12n －11－12－(2n －1)×⎝ ⎛⎭⎪⎫12n ＝3－(2n ＋3)×⎝ ⎛⎭⎪⎫12n . ∴T n ＝6－(2n ＋3)×⎝ ⎛⎭⎪⎫12n －1.选条件③.(1)∵S 3＝9，a 4＋a 5＝8b 2，a 1＝b 1，d ＝q ，d >1， ∴⎩⎨⎧a 1＋d ＝3，2a 1＋7d ＝8a 1d ，解得⎩⎨⎧a 1＝1，d ＝2或⎩⎪⎨⎪⎧a 1＝218，d ＝38(舍去)，∴⎩⎨⎧b 1＝1，q ＝2.∴a n ＝a 1＋(n －1)d ＝2n －1，b n ＝b 1q n －1＝2n －1. (2)∵c n ＝a n b n，∴c n ＝2n －12n －1＝(2n －1)×⎝ ⎛⎭⎪⎫12n －1.∴T n ＝1＋3×12＋5×⎝ ⎛⎭⎪⎫122＋…＋(2n －3)×⎝ ⎛⎭⎪⎫12n －2＋(2n －1)×⎝ ⎛⎭⎪⎫12n －1，12T n ＝12＋3×⎝ ⎛⎭⎪⎫122＋5×⎝ ⎛⎭⎪⎫123＋…＋(2n －3)×⎝ ⎛⎭⎪⎫12n －1＋(2n －1)×⎝ ⎛⎭⎪⎫12n. 上面两式相减，得12T n ＝1＋2⎣⎢⎡⎦⎥⎤12＋⎝ ⎛⎭⎪⎫122＋…＋⎝ ⎛⎭⎪⎫12n －1－(2n －1)×⎝ ⎛⎭⎪⎫12n＝1＋2×12⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫12n －11－12－(2n －1)×⎝ ⎛⎭⎪⎫12n ＝3－(2n ＋3)×⎝ ⎛⎭⎪⎫12n . ∴T n ＝6－(2n ＋3)×⎝ ⎛⎭⎪⎫12n －1.探究提高 1.一般地，如果数列{a n }是等差数列，{b n }是等比数列，求数列{a n ·b n }的前n 项和时，可采用错位相减法求和，一般是和式两边同乘以等比数列{b n }的公比，然后作差求解.2.在写“S n ”与“qS n ”的表达式时应特别注意将两式“错项对齐”，以便下一步准确地写出“S n －qS n ”的表达式.【拓展练习4】 (2020·潍坊模拟)在①b 2n ＝2b n ＋1，②a 2＝b 1＋b 2，③b 1，b 2，b 4成等比数列这三个条件中选择符合题意的两个条件，补充在下面的问题中，并求解.已知数列{a n }中，a 1＝1，a n ＋1＝3a n .公差不等于0的等差数列{b n }满足________，求数列⎩⎨⎧⎭⎬⎫b n a n 的前n 项和S n .(注：如果选择多个条件分别解答，按第一个解答计分) 解 因为a 1＝1，a n ＋1＝3a n ，所以{a n }是以1为首项，3为公比的等比数列， 所以a n ＝3n －1.选①②时，设数列{b n }的公差为d 1. 因为a 2＝3，所以b 1＋b 2＝3(ⅰ).因为b 2n ＝2b n ＋1，所以当n ＝1时，b 2＝2b 1＋1(ⅱ). 由(ⅰ)(ⅱ)解得b 1＝23，b 2＝73，所以d 1＝53，所以b n ＝5n －33.所以b n a n＝5n －33n .所以S n ＝b 1a 1＋b 2a 2＋…＋b n a n ＝231＋732＋1233＋…＋5n －33n ，所以13S n ＝232＋733＋1234＋…＋5n －83n ＋5n －33n ＋1.上面两式相减，得23S n ＝23＋5⎝ ⎛⎭⎪⎫132＋133＋…＋13n －5n －33n ＋1 ＝23＋56－152×3n ＋1－5n －33n ＋1＝32－10n ＋92×3n ＋1.所以S n ＝94－10n ＋94×3n .选②③时，设数列{b n }的公差为d 2.因为a 2＝3，所以b 1＋b 2＝3，即2b 1＋d 2＝3.因为b 1，b 2，b 4成等比数列，所以b 22＝b 1b 4，即(b 1＋d 2)2＝b 1(b 1＋3d 2)，化简得d 22＝b 1d 2.因为d 2≠0，所以b 1＝d 2，从而d 2＝b 1＝1，所以b n ＝n . 所以b n a n ＝n 3n －1.所以S n ＝b 1a 1＋b 2a 2＋…＋b n a n ＝130＋231＋332＋…＋n3n －1，所以13S n ＝131＋232＋333＋…＋n －13n －1＋n 3n .上面两式相减，得23S n ＝1＋131＋132＋133＋…＋13n －1－n 3n＝32⎝ ⎛⎭⎪⎫1－13n －n 3n ＝32－2n ＋32×3n . 所以S n ＝94－2n ＋34×3n －1.选①③时，设数列{b n }的公差为d 3.因为b 2n ＝2b n ＋1，所以b 2＝2b 1＋1，所以d 3＝b 1＋1.又因为b 1，b 2，b 4成等比数列，所以b 22＝b 1b 4，即(b 1＋d 3)2＝b 1(b 1＋3d 3)，化简得d 23＝b 1d 3.因为d 3≠0，所以b 1＝d 3，无解，所以等差数列{b n }不存在.故不合题意.考向三 与数列相关的综合问题【典例5】 (2020·杭州滨江区调研)设f (x )＝12x 2＋2x ，f ′(x )是y ＝f (x )的导函数，若数列{a n }满足a n ＋1＝f ′(a n )，且首项a 1＝1. (1)求数列{a n }的通项公式；(2)数列{a n }的前n 项和为S n ，等比数列{b n }中，b 1＝a 1，b 2＝a 2，数列{b n }的前n 项和为T n ，请写出适合条件T n ≤S n 的所有n 的值. 解 (1)由f (x )＝12x 2＋2x ，得f ′(x )＝x ＋2. ∵a n ＋1＝f ′(a n )，且a 1＝1. ∴a n ＋1＝a n ＋2，则a n ＋1－a n ＝2，因此数列{a n }是公差为2，首项为1的等差数列. ∴a n ＝1＋2(n －1)＝2n －1.(2)数列{a n }的前n 项和S n ＝n （1＋2n －1）2＝n 2，等比数列{b n }中，设公比为q ，∵b 1＝a 1＝1，b 2＝a 2＝3， ∴q ＝3.∴b n ＝3n －1，∴数列{b n }的前n 项和T n ＝1－3n 1－3＝3n －12.T n ≤S n 可化为3n －12≤n 2.又n ∈N *，∴n ＝1，或n ＝2.故适合条件T n ≤S n 的所有n 的值为1和2.探究提高 1.求解数列与函数交汇问题要注意两点：(1)数列是一类特殊的函数，其定义域是正整数集(或它的有限子集)，在求数列最值或不等关系时要特别注意；(2)解题时准确构造函数，利用函数性质时注意限制条件.2.数列为背景的不等式恒成立、不等式证明，多与数列的求和相联系，最后利用数列或数列对应函数的单调性处理.【拓展练习5】 已知数列{a n }与{b n }满足：a 1＋a 2＋a 3＋…＋a n ＝2b n (n ∈N *)，若{a n }是各项为正数的等比数列，且a 1＝2，b 3＝b 2＋4. (1)求数列{a n }与{b n }的通项公式； (2)若数列{c n }满足c n ＝a nb n b n ＋1(n ∈N *)，T n 为数列{c n }的前n 项和，证明：T n ＜1. (1)解 由题意知，a 1＋a 2＋a 3＋…＋a n ＝2b n ，① 当n ≥2时，a 1＋a 2＋a 3＋…＋a n －1＝2b n －1，② ①－②可得a n ＝2(b n －b n －1) ⇒a 3＝2(b 3－b 2)＝2×4＝8，∵a 1＝2，a n ＞0，设{a n }的公比为q ， ∴a 1q 2＝8⇒q ＝2，∴a n ＝2×2n －1＝2n (n ∈N *). ∴2b n ＝21＋22＋23＋ (2)＝2（1－2n ）1－2＝2n ＋1－2，∴b n ＝2n －1(n ∈N *).(2)证明 由已知c n ＝a n b n ·b n ＋1＝2n（2n －1）（2n ＋1－1）＝12n －1－12n ＋1－1， ∴T n ＝c 1＋c 2＋…＋c n＝121－1－122－1＋122－1－123－1＋…＋12n －1－12n ＋1－1＝1－12n ＋1－1，当n ∈N *时，2n ＋1＞1，∴12n ＋1－1＞0，∴1－12n ＋1－1＜1，故T n ＜1.【专题拓展练习】一、单选题1．已知数列{}n a 满足()2*11n n n a a a n N+=-+∈，设12111n nS a a a =+++，且10910231a S a -=-，则数列{}n a 的首项1a 的值为（ ）A ．23 B ．1C ．32D ．2【答案】C 【详解】若存在1n a =，由2111n n n a a a --=-+，则可得11n a -=或0n a =，由12111n nS a a a =+++可得0n a ≠，由10910231a S a -=-可得101a ≠所以{}n a 中恒有1n a ≠由211n n n a a a +=-+，可得()111n n n a a a +-=-所以()11111111n n n n n a a a a a +==----，即111111n n n a a a +=---所以1212231111111111111111n n n n S a a a a a a a a a +⎛⎫⎛⎫⎛⎫=+++=-+-++-⎪ ⎪ ⎪------⎝⎭⎝⎭⎝⎭111111n a a +=--- 所以110109*********a S a a a -=---=-，即1010101010123222111111a a a a a a =+--=----= 所以1121a =-，则1112a -=，所以132a = 2．已知在数列{}n a 中，14a =，26a =，且当2n ≥时，149n n a a +=-，若n T 为数列{}nb 的前n 项和，19(3)n n n n a b a a +-=⋅，则当175(3)()8n n a T λ+=-⋅-为整数时，n λ=（ ）A ．6B ．12C ．20D ．24 【答案】D 【详解】当2n ≥时，149n n a a +=-，得134(3)n n a a +-=-，又26a =，∴{3}n a -从第二项开始是首项为3，公比为4的等比数列，∴2334n n a --=⨯(2n ≥)，∴2413432n n n a n -=⎧=⎨⨯+≥⎩，，， 当1n =时，1138T b ==，217155(3)()82a T Z λ=-⋅-=∉，不符合题意， 当2n ≥时，221213411(41)(41)4141n n n n n n b -----⨯==-++++， ∴12221131171()84141841n n n n T b b b ---=++⋅⋅⋅+=+-=-+++， 则111115534154141n n n λ---=⨯⨯⨯=-++，由λ为整数可知141n -+是15的因数， ∴当且仅当2n =时λ可取整数，12λ=，所以24n λ=，3．设n S 为数列{}n a 的前n 项和，*()(11),2n n n n S a n N -+=∈，则数列{}n S 的前7项和为（ ） A ．1256-B ．85256-C ．11024- D ．3411024-【答案】B 【详解】 ∵(1)12nn n n S a -+=， ∴1n =时，1112S a +=-，即1112a a +=-，114a =-，由已知1(1)2nn n n S a =--， 2n ≥时，11111111(1)(1)(1)(1)222n n n nn n n n n n n n n na S S a a a a -----=-=----+=-+-+(*)， (*)式中n 为偶数时，112n n n na a a -=++，112n n a -=-，此时1n -为奇数， ∴n 为奇数时112n n a +=-(*)式中n 为奇数时，112n n n n a a a -=--+，1122n n na a --=-，即1111112222n n n n a -+-⎛⎫=-⨯-+= ⎪⎝⎭，此时1n -为偶数，∴n 为偶数时，12n na =， ∴11,21,2n n nn a n +⎧-⎪⎪=⎨⎪⎪⎩为奇数为偶数，由1(1)2nn n nS a =--，得n 为奇数时，11122n n n S +=-，n 为偶数时，11022nn nS =-=， ∴数列{}n S 的前7项和为11111111421686432256128⎛⎫⎛⎫⎛⎫⎛⎫-+-+-+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭11118541664256256=----=-． 4．若()()*12coscoscoscos 5555n n n S n ππππ-=++++∈N ，则1S 、2S、、2020S 中值为0的共有（ ） A ．202个 B ．404个C ．606个D ．808个【答案】B 【详解】由于4coscos055ππ+=，23cos cos 055ππ+=，5cos 15π=-，69cos cos 055ππ+=，78cos cos 055ππ+=，10cos 15π=，所以234cos coscos cos 05555ππππ+++=， 2310cos cos cos cos 05555ππππ++++=，所以40S =，100S =，()()()101210coscos cos555n n n n n S S πππ++++-=+++()()()()()()1627510cos cos cos cos cos cos 555555n n n n n n ππππππ++++++⎡⎤⎡⎤⎡⎤=++++++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦()()()()()()112255cos cos cos cos cos cos 555555n n n n n n ππππππ++++++⎡⎤⎡⎤⎡⎤=-+-++-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦0=，所以，()10n n S S n N *+=∈，则()44+100n SS n N *==∈，()10100n S S n N *==∈，因此，1S 、2S 、、2020S 中值为0的共有2022404⨯=个.5．已知数列{}n a 为等差数列，首项为2，公差为3，数列{}n b 为等比数列，首项为2，公比为2，设n n b c a =，n T 为数列{}n c 的前n 项和，则当2020n T <时，n 的最大值是（ ） A ．8 B ．9 C ．10 D ．11【答案】A 【详解】解：由题意得：323(1)1n a n n ⨯-=+-=，2nn b =，2321n n n n b c a a ==⨯-=，123n T c c c ∴=+++…n c +123321321321=⨯-+⨯-+⨯-+…321n +⨯-(1233222=⨯+++…)2n n +-()212312n n ⨯-=⨯--1326n n +=⨯--，当8n =时，98326815222020T =⨯--=<； 当9n =时，109326930572020T =⨯--=>，n ∴的最大值为8.6．已知数列{}n a 满足123232n n a a a na ++++=，设1(1)2nn n a b n -=+，n S 为数列{}n b 的前n 项和.若t n S <对任意n *∈N 恒成立，则实数t 的最小值为（ ） A ．1 B ．2C ．32D ．52【答案】C 【详解】1n =时，12a =，因为123232n n a a a na ++++=，所以2n ≥时，1123123(1)2n n a a a n a --++++-=，两式相减得到12n n na -=，故12,n n a n-=1n =时不适合此式，所以11,11,2(1)2(1)nn n n a b n n n n -=⎧⎪==⎨≥+⎪+⎩，当1n =时，111S b ==， 当2n ≥时，111111313123341221n S n n n ⎛⎫=+-+-+-=-< ⎪++⎝⎭， 所以32t ≥；所以t 的最小值32； 7．已知数列{}n a 的前n 项和为n S ，满足2n S an bn =+，（,a b 均为常数），且72a π=.设函数2()sin 22cos 2xf x x =+，记()n n y f a =，则数列{}n y 的前13项和为（ ） A ．132πB ．7πC ．7D ．13【答案】D 【详解】因为2()sin 22cos sin 2cos 12xf x x x x =+=++， 由2n S an bn =+，得()()()2211122n n n S S an bn a n b n an a b n a -=-=+----=-+≥，又11a S a b ==+也满足上式，所以2n a an a b =-+， 则12n n a a a --=为常数，所以数列{}n a 为等差数列； 所以11372a a a π+==，()()111131131313sin 2cos 1sin 2cos 1y f a f a a a a y a =+=++++++()()1111sin 2cos 1sin 22cos 12a a a a ππ=+++-+-+=.则数列{}n y 的前13项和为()()()1213...f a f a f a +++，记()()()1213...M f a f a f a =+++，则()()()13121...M f a f a f a =+++，所以()()11321326M f a f a ⎡⎤=+=⎣⎦，因此13M =.8．公元1202年列昂那多·斐波那契（意大利著名数学家）以兔子繁殖为例，引入“兔子数列”{}n a ：1，1，2，3，5，8，13，21，34，55，……，即11a =，21a =，()*12,2n n n a a a n n --=+∈>N ，此数列在现代物理、化学等学科都有着十分广泛的应用。

1.【2017课标1，理4】记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为A ．1B ．2C ．4D ．82.【2017课标II ，理3】我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（ ）A ．1盏B ．3盏C ．5盏D ．9盏3.【2017课标1，理12】几位大学生响应国家的创业号召，开发了一款应用软件.为激发大家学习数学的兴 趣，他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：已知数列1， 1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下来的两项是20，21，再接下来 的三项是20，21，22，依此类推.求满足如下条件的最小整数N ：N >100且该数列的前N 项和为2的整数幂.那么 该款软件的激活码是A ．440B ．330C ．220D ．1104.【2017浙江，6】已知等差数列{a n }的公差为d ，前n 项和为S n ，则“d >0”是“S 4 + S 6>2S 5”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件5.【2017课标II ，理5】设x ，y 满足约束条件2330233030x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩，则2z x y =+的最小值是（ ）A ．15-B ．9-C ．1D ．96.【2017天津，理2】设变量,x y 满足约束条件20,220,0,3,x y x y x y +≥⎧⎪+-≥⎪⎨≤⎪⎪≤⎩则目标函数z x y =+的最大值为 （A ）23 （B ）1（C ）32（D ）3 7.【2017山东，理4】已知x,y 满足x y 3x y ⎧-+≤⎪+≤⎨⎪+≥⎩30+5030x ，则z=x+2y 的最大值是（A ）0 （B ） 2 （C ） 5 （D ）68.【2017山东，理7】若0a b >>，且1ab =，则下列不等式成立的是（A ）()21log 2a b a a b b +<<+ （B ）()21log 2a b a b a b<+<+ （C ）()21log 2a b a a b b +<+< （D ）()21log 2a b a b a b +<+< 9.【2017课标3，理9】等差数列{}n a 的首项为1，公差不为0．若a 2，a 3，a 6成等比数列，则{}n a 前6项的和为A ．24-B ．3-C ．3D ．810.【2017北京，理4】若x ，y 满足32x x y y x ≤⎧⎪+≥⎨⎪≤⎩，，， 则x + 2y 的最大值为（A ）1 （B ）3（C ）5 （D ）911.【2017浙江，4】若x ，y 满足约束条件03020x x y x y ≥⎧⎪+-≥⎨⎪-≤⎩，则y x z 2+=的取值范围是 A ．[0，6]B ．[0，4]C ．[6，)∞+D ．[4，)∞+12.【2017天津，理8】已知函数23,1,()2, 1.x x x f x x x x ⎧-+≤⎪=⎨+>⎪⎩设a ∈R ，若关于x 的不等式()||2x f x a ≥+在R 上恒成立，则a 的取值范围是（A ）47[,2]16-（B ）4739[,]1616-（C ）[23,2]-（D ）39[23,]16- 13.【2017课标3，理13】若x ，y 满足约束条件y 0200x x y y -≥⎧⎪+-≤⎨⎪≥⎩，则z 34x y =-的最小值为__________.14．【2017课标3，理14】设等比数列{}n a 满足a 1 + a 2 = –1, a 1 – a 3 = –3，则a 4 = ___________.15.【2017课标II ，理15】等差数列{}n a 的前n 项和为n S ，33a =，410S =，则11nk k S ==∑。

专题04 数列【2013高考试题】（2013·新课标Ⅰ文）（6）设首项为1，公比为23的等比数列{}n a 的前n 项和为n S ，则（ ） （A ）21n n S a =- （B ）32n n S a =- （C ）43n n S a =- （D ）32n n S a =-（2013·上海文）2．在等差数列{}n a 中，若123430a a a a +++=，则23a a += ．（2013·辽宁文）（14）已知等比数列{}{}13n n n a S a n a a 是递增数列,是的前项和.若，是方程26540x x S -+==的两个根，则 .（2013·辽宁文）（4）下面是关于公差0d >的等差数列()n a 的四个命题： {}1:n p a 数列是递增数列；{}2:n p na 数列是递增数列； 3:n a p n ⎧⎫⎨⎬⎩⎭数列是递增数列；{}4:3n p a nd +数列是递增数列； 其中的真命题为（A ）12,p p （B ）34,p p （C ）23,p p （D ）14,p p（2013·大纲文）7. 已知数列{}n a 满足130,n n a a ++=24,3a =-则{}n a 的前10项和等于（ ）（A ）()-10-61-3 （B ）()1011-39（C ）()-1031-3 （D ）()-1031+3（2013·北京文）（11）若等比数列{}n a 满足2420a a +=，3540a a +=，则公比q =__________; 前n 项n S =_____.（2013·江西文）12.某住宅小区计划植树不少于100棵，若第一天植2棵，以后每天植树的棵树是前一天的2倍，则需要的最少天数()n n N +∈等于 .（2013·浙江文）19、在公差为d 的等差数列{}n a 中，已知a 1=10，且123,22,5a a a +成等比数列.（Ⅰ）求,n d a ； （Ⅱ) 若0d<，求123||||||||n a a a a ++++ ；（7）设n S 为等差数列{}n a 的前n 项和，8374,2S a a ==-，则9a =（A ）6- （B ）4- （C ）2- （D ）2（2013·安徽文）（19）（本小题满分13分）设数列{}n a 满足12a =，248a a +=,且对任意*n N ∈，函数1212()()cos -sin n n n n n f x a a a x a x a x ++++=-++⋅⋅ ，满足'()02f π=(Ⅰ)求数列{}n a 的通项公式；（Ⅱ）若122nn n a b a =+（），求数列{}n b 的前n 项和n S .（2013·北京文）（20）（本小题共13分）给定数列12,,,n a a a ⋅⋅⋅.对1,2,,1i n =⋅⋅⋅-，该数列前i 项的最大值记为i A ，后n i -项12,,,i i n a a a ++⋅⋅⋅的最小值记为i B ，i i i d A B =-.（Ⅰ）设数列{}n a 为3，4，7，1，写出1d ，2d ，3d 的值；（Ⅱ）设12,,,n a a a ⋅⋅⋅(4)n ≥是公比大于1的等比数列，且10a >.证明：121,,,n d d d -⋅⋅⋅是等比数列. （Ⅲ）设121,,,n d d d -⋅⋅⋅是公差大于0的等差数列，且10d >，证明：121,,,n a a a -⋅⋅⋅是等差数列.（2013·大纲文）17．（本小题满分10分）等差数列{}n a 中，71994,2,a a a == （I ）求{}n a 的通项公式； （II ）设1n nb na =，求数列{}n b 的前n 项和n S .（2013·福建文）17．（本小题满分12分） 已知等差数列}{n a 的公差d =1，前n 项和为n S . (I)若131,,a a 成等比数列，求1a ； (II)若5191S a a a >，求的取值范围。

高中数学《数列求和与综合问题》专项练习题（含答案解析）一、选择题1．数列{a n }的前n 项和为S n ，若a 1＝1，a n ＋1＝3S n (n ≥1)，则a 6＝( ) A ．3×44 B ．3×44＋1 C ．44D ．44＋1A [因为a n ＋1＝3S n ，所以a n ＝3S n －1(n ≥2)， 两式相减得，a n ＋1－a n ＝3a n ，即a n ＋1a n＝4(n ≥2)，所以数列a 2，a 3，a 4，…构成以a 2＝3S 1＝3a 1＝3为首项，公比为4的等比数列，所以a 6＝a 2·44＝3×44.]2．已知数列{a n }是等差数列，其前n 项和为S n ，若a 1a 2a 3＝15，且3S 1S 3＋15S 3S 5＋5S 5S 1＝35，则a 2等于( ) A ．2B ．12C ．3D ．13C [∵在等差数列中，S 2n －1＝(2n －1)a n ，∴S 1＝a 1，S 3＝3a 2，S 5＝5a 3，∴35＝1a 1a 2＋1a 2a 3＋1a 1a 3，∵a 1a 2a 3＝15，∴35＝a 315＋a 115＋a 215＝a 25，即a 2＝3.]3．已知数列{b n }满足b 1＝1，b 2＝4，b n ＋2＝⎝ ⎛⎭⎪⎫1＋sin 2n π2b n ＋cos 2n π2，则该数列的前23项的和为( )A ．4 194B ．4 195C ．2 046D ．2 047A [当n 为偶数时，b n ＋2＝⎝⎛⎭⎪⎫1＋sin 2n π2b n ＋cos 2n π2＝b n ＋1，有b n ＋2－b n ＝1，即偶数项成等差数列，所以b 2＋b 4＋…＋b 22＝11b 2＋11×102×1＝99.当n 为奇数时，b n ＋2＝2b n ，即奇数项成等比数列，所以b 1＋b 3＋…＋b 23＝b 11－2121－2＝212－1＝4 095.所以该数列的前23项的和为99＋4 095＝4 194，故选A ．]4．已知数列{a n }的前n 项和为S n ，且满足a 1＝1，a n ＋a n ＋1＝2n ＋1，则S 2 0192 019＝( )A ．1 010B ．1 009C ．2 020D ．2 019A [S 2 019＝a 1＋(a 2＋a 3)＋(a 4＋a 5)＋…＋(a 2 018＋a 2 019)， ＝(2×0＋1)＋(2×2＋1)＋(2×4＋1)＋…＋(2×2 018＋1)， ＝1＋2×2 018＋11 0102＝2 019×1 010，∴S 2 0192 019＝1 010，故选A ．]5．已知数列{a n }的前n 项和S n ＝2＋λa n ，且a 1＝1，则S 5＝( ) A ．27 B ．5327C ．3116D ．31C [∵S n ＝2＋λa n ，且a 1＝1，∴S 1＝2＋λa 1， 即λ＝－1，∴S n ＝2－a n ，当n ≥2时，S n ＝2－(S n －S n －1)，∴2S n ＝2＋S n －1，即S n ＝12S n －1＋1，∴S n －2＝12(S n －1－2)，∴S n －2＝(－1)×⎝ ⎛⎭⎪⎫12n －1.当n ＝1时也满足．∴S 5＝2－⎝ ⎛⎭⎪⎫124＝3116.故选C ．]6．设曲线y ＝2 018x n ＋1(n ∈N *)在点(1,2 018)处的切线与x 轴的交点的横坐标为x n ，令a n ＝log 2 018x n ，则a 1＋a 2＋…＋a 2 017的值为( )A ．2 018B ．2 017C ．1D ．－1D [因为y ′＝2 018(n ＋1)x n ，所以切线方程是y －2 018＝2 018(n ＋1)(x －1)，所以x n ＝nn ＋1，所以a 1＋a 2＋…＋a 2 017＝log 2 018(x 1·x 2·…·x 2 017)＝log 2 018⎝ ⎛⎭⎪⎫12×23×…×2 0172 018＝log 2 01812 018＝－1.]7．在等比数列{a n }中，公比q ＝2，前87项和S 87＝140，则a 3＋a 6＋a 9＋…＋a 87等于( )A ．1403B ．60C ．80D ．160C [法一：a 3＋a 6＋a 9＋…＋a 87＝a 3(1＋q 3＋q 6＋…＋q 84)＝a1q 2×1q 3291－q 3＝q 21＋q ＋q 2×a 11－q 871－q ＝47×140＝80.故选C ． 法二：设b 1＝a 1＋a 4＋a 7＋…＋a 85，b 2＝a 2＋a 5＋a 8＋…＋a 86，b 3＝a 3＋a 6＋a 9＋…＋a 87，因为b 1q ＝b 2，b 2q ＝b 3，且b 1＋b 2＋b 3＝140，所以b 1(1＋q ＋q 2)＝140，而1＋q ＋q 2＝7，所以b 1＝20，b 3＝q 2b 1＝4×20＝80.故选C ．]8．设等差数列{a n }的前n 项和为S n ，已知a 1＝9，a 2为整数，且S n ≤S 5，则数列⎩⎨⎧⎭⎬⎫1a n ·a n ＋1前n 项和的最大值为( )A ．49B ．1C ．4181D ．151315A [a 1＝9，a 2为整数，可知：等差数列{a n }的公差d 为整数，由S n ≤S 5，∴a 5≥0，a 6≤0，则9＋4d ≥0,9＋5d ≤0，解得－94≤d ≤－95，d 为整数，d ＝－2.∴a n ＝9－2(n －1)＝11－2n . 1a n ·a n ＋1＝111－2n9－2n ＝12⎝⎛⎭⎪⎫19－2n －111－2n ， 数列⎩⎨⎧⎭⎬⎫1a n ·a n ＋1前n 项和为 12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫17－19＋⎝ ⎛⎭⎪⎫15－17＋…＋⎝ ⎛⎭⎪⎫19－2n －111－2n ＝12⎝⎛⎭⎪⎫19－2n －19， 令b n ＝19－2n ，由于函数f (x )＝19－2x 的图象关于点⎝ ⎛⎭⎪⎫92，0对称及其单调性，可知：0＜b 1＜b 2＜b 3＜b 4，b 5＜b 6＜b 7＜…＜0，∴b n ≤b 4＝1.∴最大值为49.故选A ．]二、填空题 9．已知a n ＝2n ，b n ＝3n －1，c n ＝b n a n，则数列{c n }的前n 项和S n 为________．5－3n ＋52n [由题设知，c n ＝3n －12n ，所以S n ＝221＋522＋823＋…＋3n －12n ， ①2S n ＝2＋521＋822＋…＋3n －12n －1，②由②－①得，S n ＝2＋321＋322＋…＋32n －1－3n －12n .故所求S n ＝2＋32⎝ ⎛⎭⎪⎫1－12n －11－12－3n －12n ＝5－3n ＋52n .]10．已知数列{a n }和{b n }满足a 1＝1，a n ＋1a n＝n ＋1n，b n a n＝sin 2n π3－cos 2n π3，n ∈N *，则数列{b n }的前47项和等于________．1 120 [依题意得a n ＋1n ＋1＝a nn ，故数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n n 是常数列，于是有a n n ＝1，a n ＝n 2，b n ＝－n 2cos 2n π3，b 3k －2＋b 3k －1＋b 3k ＝3k －223k －122－(3k )2＝－9k ＋52(k ∈N *)，因此数列{b n }的前47项和为S 47＝S 48－b 48＝－9×161＋162＋52×16＋482＝1 120.]11．设某数列的前n 项和为S n ，若S nS 2n为常数，则称该数列为“和谐数列”．若一个首项为1，公差为d (d ≠0)的等差数列{a n }为“和谐数列”，则该等差数列的公差d ＝________.2 [由S nS 2n ＝k (k 为常数)，且a 1＝1，得n ＋12n (n －1)d ＝k ⎣⎢⎡⎦⎥⎤2n ＋12×2n 2n －1d ，即2＋(n －1)d ＝4k ＋2k (2n －1)d ，整理得，(4k －1)dn ＋(2k －1)(2－d )＝0，∵对任意正整数n ，上式恒成立，∴⎩⎪⎨⎪⎧d 4k －10，2k －12－d0，得⎩⎪⎨⎪⎧d ＝2，k ＝14.∴数列{a n }的公差为2.]12．记S n 为正项等比数列{a n }的前n 项和，若S 4－2S 2＝3，则S 6－S 4的最小值为________．12 [由题可知数列{a n }的公比q ＞0，a n ＞0，则3＝(a 4－a 2)＋(a 3－a 1)＝a 1(q ＋1)·(q 2－1)，则有q ＞1，所以3S 6－S 4＝3a 6＋a 5＝3a 1q ＋1q 4＝a 1q ＋1q 2－1a 1q ＋1q 4＝1q 2－⎝ ⎛⎭⎪⎫1q 22＝14－⎝ ⎛⎭⎪⎫1q 2－122≤14(当且仅当q ＝2时，取等号)，所以S 6－S 4≥12，即S 6－S 4的最小值为12.]三、解答题13．(2018·黔东南州二模)已知数列{a n }的前n 项和为S n ，且满足S n ＝43(a n －1)，n ∈N *.(1)求数列{a n }的通项公式；(2)令b n ＝log 2a n ，记数列⎩⎨⎧⎭⎬⎫1b n －1b n ＋1的前n 项和为T n ，证明：T n ＜12.[解] (1)当n ＝1时，有a 1＝S 1＝43(a 1－1)，解得a 1＝4.当n ≥2时，有S n －1＝43(a n －1－1)，则a n ＝S n －S n －1＝43(a n －1)－43(a n －1－1)，整理得：a na n －1＝4，∴数列{a n }是以q ＝4为公比，以a 1＝4为首项的等比数列．∴a n ＝4×4n －1＝4n (n ∈N *)即数列{a n }的通项公式为：a n ＝4n (n ∈N *)． (2)由(1)有b n ＝log 2a n ＝log 2 4n ＝2n ，则1b n ＋1b n －1＝12n ＋12n －1＝12⎝⎛⎭⎪⎫12n －1－12n ＋1. ∴T n ＝12⎝ ⎛⎭⎪⎫11－13＋⎝ ⎛⎭⎪⎫13－15＋⎝ ⎛⎭⎪⎫15－17＋…＋⎝ ⎛⎭⎪⎫12n －1－12n ＋1 ＝12⎝⎛⎭⎪⎫1－12n ＋1. 易知数列{T n }为递增数列， ∴T 1≤T n ＜12，即13≤T n ＜12.14．(2018·邯郸市一模)已知数列{a n }，{b n }的前n 项和分别为S n ，T n ，b n －a n ＝2n ＋1，且S n ＋T n ＝2n ＋1＋n 2－2.(1)求T n －S n ； (2)求数列⎩⎨⎧⎭⎬⎫b n 2n 的前n 项和R n .[解] (1)依题意可得b 1－a 1＝3，b 2－a 2＝5，…，b n －a n ＝2n ＋1， ∴T n －S n ＝(b 1＋b 2＋…＋b n )－(a 1＋a 2＋…＋a n ) ＝n ＋(2＋22＋…＋2n )＝2n ＋1＋n －2. (2)∵2S n ＝S n ＋T n －(T n －S n )＝n 2－n ， ∴S n ＝n 2－n2，∴a n ＝n －1. 又b n －a n ＝2n ＋1， ∴b n ＝2n ＋n .∴b n2n ＝1＋n2n ， ∴R n ＝n ＋⎝ ⎛⎭⎪⎫12＋222＋…＋n 2n ，则12R n ＝12n ＋⎝ ⎛⎭⎪⎫122＋223＋…＋n 2n ＋1，∴12R n ＝12n ＋⎝ ⎛⎭⎪⎫12＋122＋…＋12n －n2n ＋1， 故R n ＝n ＋2×12－12n ＋11－12－n 2n ＝n ＋2－n ＋22n .。

数列求和及数列的综合应用一、知识梳理 1.特殊数列的求和公式 (1)等差数列的前n 项和公式： S n ＝n （a 1＋a n ）2＝na 1＋n （n －1）2d . (2)等比数列的前n 项和公式： S n ＝⎩⎪⎨⎪⎧na 1，q ＝1，a 1－a n q 1－q ＝a 1（1－q n ）1－q ，q ≠1.2.数列求和的几种常用方法 (1)分组转化法把数列的每一项分成两项或几项，使其转化为几个等差、等比数列，再求解. (2)裂项相消法把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得其和. (3)错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，这个数列的前n 项和可用错位相减法求解.(4)倒序相加法如果一个数列{a n }的前n 项中与首末两端等“距离”的两项的和相等或等于同一个常数，那么求这个数列的前n 项和即可用倒序相加法求解.3.数列应用题常见模型(1)等差模型：如果后一个量比前一个量增加(或减少)的是同一个固定值，该模型是等差模型，增加(或减少)的量就是公差.(2)等比模型：如果后一个量与前一个量的比是同一个固定的非零常数，该模型是等比模型，这个固定的数就是公比.(3)递推数列模型：如果题目中给出的前后两项之间的关系不固定，随项的变化而变化，应考虑a n 与a n ＋1(或者相邻三项等)之间的递推关系，或者S n 与S n ＋1(或者相邻三项等)之间的递推关系. 小结：1.1＋2＋3＋4＋…＋n ＝n （n ＋1）2. 2.12＋22＋…＋n 2＝n （n ＋1）（2n ＋1）6.3.裂项求和常用的三种变形 (1)1n （n ＋1）＝1n －1n ＋1. (2)1（2n －1）（2n ＋1）＝12⎝ ⎛⎭⎪⎫12n －1－12n ＋1.(3)1n ＋n ＋1＝n ＋1－n .二、例题精讲 + 随堂练习1.判断下列结论正误(在括号内打“√”或“×”)(1)若数列{a n }为等比数列，且公比不等于1，则其前n 项和S n ＝a 1－a n ＋11－q.( ) (2)当n ≥2时，1n 2－1＝12(1n －1－1n ＋1).( )(3)求S n ＝a ＋2a 2＋3a 3＋…＋na n 时只要把上式等号两边同时乘以a 即可根据错位相减法求得.( )(4)若数列a 1，a 2－a 1，…，a n －a n －1是首项为1，公比为3的等比数列，则数列{a n }的通项公式是a n ＝3n －12.( ) 解析 (3)要分a ＝0或a ＝1或a ≠0且a ≠1讨论求解. 答案 (1)√ (2)√ (3)× (4)√2.数列{a n }中，a n ＝1n （n ＋1），若{a n }的前n 项和为2 0192 020，则项数n为( ) A.2 018 B.2 019 C.2 020D.2 021解析 a n ＝1n （n ＋1）＝1n －1n ＋1，S n ＝1－12＋12－13＋…＋1n －1n ＋1＝1－1n ＋1＝n n ＋1＝2 0192 020，所以n ＝2019. 答案 B3.等比数列{a n }中，若a 1＝27，a 9＝1243，q >0，S n 是其前n 项和，则S 6＝________.解析 由a 1＝27，a 9＝1243知，1243＝27·q 8， 又由q >0，解得q ＝13，所以S 6＝27⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫1361－13＝3649.答案 36494.(2018·东北三省四校二模)已知数列{a n }满足a n ＋1－a n ＝2，a 1＝－5，则|a 1|＋|a 2|＋…＋|a 6|＝( ) A.9B.15C.18D.30解析 由题意知{a n }是以2为公差的等差数列，又a 1＝－5，所以|a 1|＋|a 2|＋…＋|a 6|＝|－5|＋|－3|＋|－1|＋1＋3＋5＝5＋3＋1＋1＋3＋5＝18. 答案 C5.(2019·北京朝阳区质检)已知数列{a n }，{b n }的前n 项和分别为S n ，T n ，b n －a n ＝2n ＋1，且S n ＋T n ＝2n ＋1＋n 2－2，则2T n ＝________________. 解析 由题意知T n －S n ＝b 1－a 1＋b 2－a 2＋…＋b n －a n ＝n ＋2n ＋1－2， 又S n ＋T n ＝2n ＋1＋n 2－2，所以2T n ＝T n －S n ＋S n ＋T n ＝2n ＋2＋n (n ＋1)－4. 答案 2n ＋2＋n (n ＋1)－46.(2019·河北“五个一”名校质检)若f (x )＋f (1－x )＝4，a n ＝f (0)＋f ⎝ ⎛⎭⎪⎫1n ＋…＋f ⎝⎛⎭⎪⎫n －1n ＋f (1)(n ∈N *)，则数列{a n }的通项公式为________.解析 由f (x )＋f (1－x )＝4，可得f (0)＋f (1)＝4，…，f ⎝ ⎛⎭⎪⎫1n ＋f ⎝⎛⎭⎪⎫n －1n ＝4，所以2a n ＝[f (0)＋f (1)]＋⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫1n ＋f ⎝ ⎛⎭⎪⎫n －1n ＋…＋[f (1)＋f (0)]＝4(n ＋1)，即a n ＝2(n ＋1). 答案 a n ＝2(n ＋1)考点一 分组转化法求和【例1】 (2019·济南质检)已知在等比数列{a n }中，a 1＝1，且a 1，a 2，a 3－1成等差数列.(1)求数列{a n }的通项公式；(2)若数列{b n }满足b n ＝2n －1＋a n (n ∈N *)，数列{b n }的前n 项和为S n ，试比较S n 与n 2＋2n 的大小.解 (1)设等比数列{a n }的公比为q ， ∵a 1，a 2，a 3－1成等差数列， ∴2a 2＝a 1＋(a 3－1)＝a 3，∴q ＝a 3a 2＝2，∴a n ＝a 1q n －1＝2n －1(n ∈N *).(2)由(1)知b n ＝2n －1＋a n ＝2n －1＋2n －1，∴S n ＝(1＋1)＋(3＋2)＋(5＋22)＋…＋(2n －1＋2n －1) ＝[1＋3＋5＋…＋(2n －1)]＋(1＋2＋22＋…＋2n －1) ＝1＋（2n －1）2·n ＋1－2n 1－2＝n 2＋2n－1. ∵S n －(n 2＋2n )＝－1<0，∴S n <n 2＋2n .规律方法 1.若数列{c n }的通项公式为c n ＝a n ±b n ，且{a n }，{b n }为等差或等比数列，可采用分组求和法求数列{c n }的前n 项和.2.若数列{c n }的通项公式为c n ＝⎩⎪⎨⎪⎧a n ，n 为奇数，b n ，n 为偶数，其中数列{a n }，{b n }是等比数列或等差数列，可采用分组求和法求{a n }的前n 项和. 【训练1】 已知等差数列{a n }的前n 项和为S n ，且a 1＝1，S 3＋S 4＝S 5.(1)求数列{a n }的通项公式；(2)令b n ＝(－1)n －1a n ，求数列{b n }的前2n 项和T 2n . 解 (1)设等差数列{a n }的公差为d ，由S 3＋S 4＝S 5可得a 1＋a 2＋a 3＝a 5，即3a 2＝a 5， ∴3(1＋d )＝1＋4d ，解得d ＝2. ∴a n ＝1＋(n －1)×2＝2n －1. (2)由(1)可得b n ＝(－1)n －1·(2n －1).∴T 2n ＝1－3＋5－7＋…＋(2n －3)－(2n －1)＝(－2)×n ＝－2n .考点二 裂项相消法求和【例2】 (2019·郑州模拟)已知数列{a n }的前n 项和为S n ，且a 2＝8，S n ＝a n ＋12－n －1.(1)求数列{a n }的通项公式；(2)求数列⎩⎨⎧⎭⎬⎫2×3n a n a n ＋1的前n 项和T n .解 (1)∵a 2＝8，S n ＝a n ＋12－n －1， ∴a 1＝S 1＝a 22－2＝2，当n ≥2时，a n ＝S n －S n －1＝a n ＋12－n －1－⎝⎛⎭⎪⎫a n 2－n ，即a n ＋1＝3a n ＋2，又a 2＝8＝3a 1＋2， ∴a n ＋1＝3a n ＋2，n ∈N *， ∴a n ＋1＋1＝3(a n ＋1)，∴数列{a n ＋1}是等比数列，且首项为a 1＋1＝3，公比为3， ∴a n ＋1＝3×3n －1＝3n ，∴a n ＝3n －1.(2)∵2×3n a n a n ＋1＝2×3n （3n －1）（3n ＋1－1）＝13n －1－13n ＋1－1.∴数列⎩⎨⎧⎭⎬⎫2×3n a n a n ＋1的前n 项和 T n ＝⎝ ⎛⎭⎪⎫13－1－132－1＋⎝ ⎛⎭⎪⎫132－1－133－1＋…＋⎝ ⎛⎭⎪⎫13n －1－13n ＋1－1＝12－13n ＋1－1.【训练2】 设S n 为等差数列{a n }的前n 项和，已知S 3＝a 7，a 8－2a 3＝3. (1)求a n ；(2)设b n ＝1S n ，求数列{b n }的前n 项和T n .解 (1)设数列{a n }的公差为d ，由题意得⎩⎪⎨⎪⎧3a 1＋3d ＝a 1＋6d ，（a 1＋7d ）－2（a 1＋2d ）＝3，解得a 1＝3，d ＝2， ∴a n ＝a 1＋(n －1)d ＝2n ＋1.(2)由(1)得S n ＝na 1＋n （n －1）2d ＝n (n ＋2)， ∴b n ＝1n （n ＋2）＝12⎝ ⎛⎭⎪⎫1n －1n ＋2.∴T n ＝b 1＋b 2＋…＋b n －1＋b n＝12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1－13＋⎝ ⎛⎭⎪⎫12－14＋…＋⎝ ⎛⎭⎪⎫1n －1－1n ＋1＋⎝ ⎛⎭⎪⎫1n －1n ＋2＝12⎝ ⎛⎭⎪⎫1＋12－1n ＋1－1n ＋2 ＝34－12⎝ ⎛⎭⎪⎫1n ＋1＋1n ＋2.考点三 错位相减法求和【例3】 已知{a n }是各项均为正数的等比数列，且a 1＋a 2＝6，a 1a 2＝a 3.(1)求数列{a n }的通项公式；(2){b n }为各项非零的等差数列，其前n 项和为S n ，已知S 2n ＋1＝b n b n ＋1，求数列⎩⎨⎧⎭⎬⎫b n a n 的前n 项和T n . 解 (1)设{a n }的公比为q ，由题意知⎩⎪⎨⎪⎧a 1（1＋q ）＝6，a 21q ＝a 1q 2，又a n >0，解得⎩⎪⎨⎪⎧a 1＝2，q ＝2，所以a n ＝2n .(2)由题意知：S 2n ＋1＝（2n ＋1）（b 1＋b 2n ＋1）2＝(2n ＋1)b n ＋1， 又S 2n ＋1＝b n b n ＋1，b n ＋1≠0， 所以b n ＝2n ＋1. 令c n ＝b na n ，则c n ＝2n ＋12n ，因此T n ＝c 1＋c 2＋…＋c n＝32＋522＋723＋…＋2n －12n －1＋2n ＋12n ，又12T n ＝322＋523＋724＋…＋2n －12n ＋2n ＋12n ＋1，两式相减得12T n ＝32＋⎝ ⎛⎭⎪⎫12＋122＋…＋12n －1－2n ＋12n ＋1，所以T n ＝5－2n ＋52n .【训练3】 已知等差数列{a n }满足：a n ＋1>a n (n ∈N *)，a 1＝1，该数列的前三项分别加上1，1，3后成等比数列，a n ＋2log 2b n ＝－1. (1)分别求数列{a n }，{b n }的通项公式； (2)求数列{a n ·b n }的前n 项和T n .解 (1)设等差数列{a n }的公差为d ，则d >0，由a 1＝1，a 2＝1＋d ，a 3＝1＋2d 分别加上1，1，3后成等比数列，得(2＋d )2＝2(4＋2d )， 解得d ＝2(舍负)，所以a n ＝1＋(n －1)×2＝2n －1.又因为a n ＋2log 2b n ＝－1，所以log 2b n ＝－n ，则b n ＝12n . (2)由(1)知a n ·b n ＝(2n －1)·12n ， 则T n ＝121＋322＋523＋…＋2n －12n ，①12T n ＝122＋323＋524＋…＋2n －12n ＋1，② 由①－②，得 12T n ＝12＋2×⎝ ⎛⎭⎪⎫122＋123＋124＋…＋12n －2n －12n ＋1. ∴12T n ＝12＋2×14⎝ ⎛⎭⎪⎫1－12n －11－12－2n －12n ＋1，∴T n ＝1＋2－22n －1－2n －12n ＝3－4＋2n －12n ＝3－3＋2n 2n .考点四 数列的综合应用【例4】 某同学利用暑假时间到一家商场勤工俭学.该商场向他提供了三种付酬方案：第一种，每天支付38元；第二种，第一天付4元，第二天付8元，第三天付12元，依此类推；第三种，第一天付0.4元，以后每天比前一天翻一番(即增加1倍).他应该选择哪种方式领取报酬呢？解 设该学生工作n 天，每天领工资a n 元，共领工资S n 元，则第一种方案a n (1)＝38，S n (1)＝38n ；第二种方案a n (2)＝4n ，S n (2)＝4(1＋2＋3＋…＋n )＝2n 2＋2n ；第三种方案a n (3)＝0.4×2n －1，S n (3)＝0.4（1－2n ）1－2＝0.4(2n －1). 令S n (1)≥S n (2)，即38n ≥2n 2＋2n ，解得n ≤18，即小于或等于18天时，第一种方案比第二种方案报酬高(18天时一样高).令S n (1)≥S n (3)，即38n ≥0.4×(2n －1)，利用计算器计算得小于或等于9天时，第一种方案报酬高， 所以少于10天时，选择第一种方案.比较第二、第三种方案，S 10(2)＝220，S 10(3)＝409.2，S 10(3)>S 10(2)，…，S n (3)>S n (2).所以等于或多于10天时，选择第三种方案.【训练4】 已知二次函数y ＝f (x )的图象经过坐标原点，其导函数为f ′(x )＝6x －2，数列{a n }的前n 项和为S n ，点(n ，S n )(n ∈N *)均在函数y ＝f (x )的图象上.(1)求数列{a n }的通项公式；(2)设b n ＝3a n a n ＋1，试求数列{b n }的前n 项和T n . 解 (1)设二次函数f (x )＝ax 2＋bx (a ≠0)，则f ′(x )＝2ax ＋b .由于f ′(x )＝6x －2，得a ＝3，b ＝－2，所以f (x )＝3x 2－2x .又因为点(n ，S n )(n ∈N *)均在函数y ＝f (x )的图象上，所以S n ＝3n 2－2n .当n ≥2时，a n ＝S n －S n －1＝3n 2－2n －[3(n －1)2－2(n －1)]＝6n －5；当n ＝1时，a 1＝S 1＝3×12－2×1＝6×1－5，也适合上式， 所以a n ＝6n －5(n ∈N *).(2)由(1)得b n ＝3a n a n ＋1＝3（6n －5）[6（n ＋1）－5]＝12·⎝ ⎛⎭⎪⎫16n －5－16n ＋1， 故T n ＝12⎣⎢⎢⎡⎦⎥⎥⎤⎝ ⎛⎭⎪⎫1－17＋⎝ ⎛⎭⎪⎫17－113＋…＋⎝ ⎛⎭⎪⎫16n －5－16n ＋1＝12⎝ ⎛⎭⎪⎫1－16n ＋1＝3n 6n ＋1.三、课后练习1.(2019·广州模拟)已知数列{a n }满足a 1＝1，a n ＋1－a n ≥2(n ∈N *)，且S n 为{a n }的前n 项和，则( )A.a n ≥2n ＋1B.S n ≥n 2C.a n ≥2n －1D.S n ≥2n －1解析 由题意得a 2－a 1≥2，a 3－a 2≥2，a 4－a 3≥2，…，a n －a n －1≥2， ∴a 2－a 1＋a 3－a 2＋a 4－a 3＋…＋a n －a n －1≥2(n －1)，∴a n －a 1≥2(n －1)，∴a n ≥2n －1，∴a 1≥1，a 2≥3，a 3≥5，…，a n ≥2n －1，∴a 1＋a 2＋a 3＋…＋a n ≥1＋3＋5＋…＋2n －1，∴S n ≥n （1＋2n －1）2＝n 2. 答案 B2.某厂2019年投资和利润逐月增加，投入资金逐月增长的百分率相同，利润逐月增加值相同.已知1月份的投资额与利润值相等，12月份投资额与利润值相等，则全年的总利润ω与总投资N的大小关系是()A.ω>NB.ω<NC.ω＝ND.不确定解析投入资金逐月值构成等比数列{b n}，利润逐月值构成等差数列{a n}，等比数列{b n}可以看成关于n的指数式函数，它是凹函数，等差数列{a n}可以看成关于n的一次式函数.由于a1＝b1，a12＝b12，相当于图象有两个交点，且两交点间指数式函数图象在一次函数图象下方，所以全年的总利润ω＝a1＋a2＋…＋a12比总投资N＝b1＋b2＋…＋b12大，故选A.答案A3.已知数列{a n}中，a n＝－4n＋5，等比数列{b n}的公比q满足q＝a n－a n－1(n≥2)且b1＝a2，则|b1|＋|b2|＋|b3|＋…＋|b n|＝________.解析由已知得b1＝a2＝－3，q＝－4，∴b n＝(－3)×(－4)n－1，∴|b n|＝3×4n－1，即{|b n|}是以3为首项，4为公比的等比数列，∴|b1|＋|b2|＋…＋|b n|＝3（1－4n）1－4＝4n－1.答案4n－14.(2019·潍坊调研)已知数列{a n}的前n项和为S n，a1＝5，nS n＋1－(n＋1)S n＝n2＋n.(1)求证：数列⎩⎨⎧⎭⎬⎫S n n 为等差数列； (2)令b n ＝2n a n ，求数列{b n }的前n 项和T n .(1)证明 由nS n ＋1－(n ＋1)S n ＝n 2＋n 得S n ＋1n ＋1－S n n ＝1， 又S 11＝5，所以数列⎩⎨⎧⎭⎬⎫S n n 是首项为5，公差为1的等差数列. (2)解 由(1)可知S n n ＝5＋(n －1)＝n ＋4，所以S n ＝n 2＋4n .当n ≥2时，a n ＝S n －S n －1＝n 2＋4n －(n －1)2－4(n －1)＝2n ＋3. 又a 1＝5也符合上式，所以a n ＝2n ＋3(n ∈N *)， 所以b n ＝(2n ＋3)2n ，所以T n ＝5×2＋7×22＋9×23＋…＋(2n ＋3)2n ，① 2T n ＝5×22＋7×23＋9×24＋…＋(2n ＋1)2n ＋(2n ＋3)2n ＋1，② 所以②－①得T n ＝(2n ＋3)2n ＋1－10－(23＋24＋…＋2n ＋1)＝(2n ＋3)2n ＋1－10－23（1－2n －1）1－2＝(2n ＋3)2n ＋1－10－(2n ＋2－8) ＝(2n ＋1)2n ＋1－2.。