随机系统最优控制

最优控制问题综述报告一、最优控制简介最优控制是现代控制理论的重要组成部分，它研究的主要问题是：在满足一定约束条件下，寻求最优控制策略，使得性能指标取极大值或极小值。

最优控制是使控制系统的性能指标实现最优化的基本条件和综合方法。

可概括为：对一个受控的动力学系统或运动过程，从一类允许的控制方案中找出一个最优的控制方案，使系统的运动在由某个初始状态转移到指定的目标状态的同时，其性能指标值为最优。

最优控制是最优化方法的一个应用。

从数学意义上说，最优化方法是一种求极值的方法，即在一组约束为等式或不等式的条件下，使系统的目标函数达到极值，即最大值或最小值。

所谓最优控制问题，就是指在给定条件下，对给定系统确定一种控制规律，使该系统能在规定的性能指标下具有最优值。

也就是说最优控制就是要寻找容许的控制作用（规律）使动态系统（受控系统）从初始状态转移到某种要求的终端状态，且保证所规定的性能指标（目标函数）达到最大（小）值。

其本质是变分学问题。

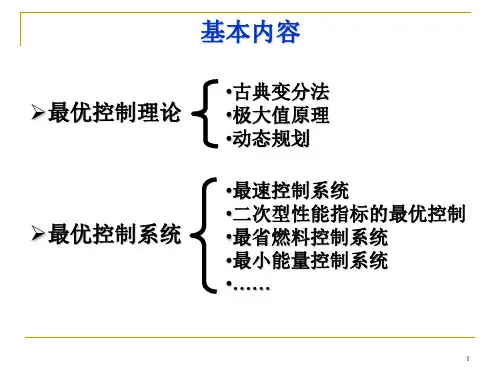
二、产生背景及发展最优控制理论是研究和解决从一切可能的控制方案中寻找最优解的一门学科，基本内容和常用方法包括动态规划、最大值原理和变分法。

这方面的开创性工作主要是由贝尔曼（R.E.Bellman）提出的“动态规划”和庞特里亚金等人提出的“极大值原理”，到了60年代，卡尔曼等人又提出了可控制性及可观测性概念，建立了最优估计理论。

它以20世纪60年代空间飞行器的制导为背景。

它最初的研究对象是由导弹、航天、航海中的制导、导航等自动控制技术、自动控制理论、数字计算技术等领域所总结出来的一类按某个性能指标达到最大或最小的控制问题。

1948年维纳发表了题为《控制论—关于动物和机器中控制与通讯的科学》的论文，第一次科学的提出了信息、反馈和控制的概念，为最优控制理论的诞生和发展奠定了基础。

钱学森1954年所着的《工程控制论》，直接促进了最优控制理论的发展和形成。

1960年，最大值原理、动态规划方法和最优线性调节器的理论被公认为最优控制理论的三大里程碑，标志着最优控制理论的诞生。

随机控制理论的一个主要组成部分是随机最优控制，这类随机控制问题的求解有赖于动态规划的概念和方法。

简介随机控制理论随机控制理论的目标是解决随机控制系统的分析和综合问题。

维纳滤波理论和卡尔曼-布什滤波理论是随机控制理论的基础之一。

内容控制理论中把随机过程理论与最优控制理论结合起来研究随机系统的分支。

随机系统指含有内部随机参数、外部随机干扰和观测噪声等随机变量的系统。

随机变量不能用已知的时间函数描述，而只能了解它的某些统计特性。

自动控制系统分为确定性系统和不确定性系统两类，前者可以通过观测来确定系统的状态，后者则不能。

随机系统是不确定性系统的一种，其不确定性是由随机性引起的。

严格地说，任何实际的系统都含有随机因素，但在很多情况下可以忽略这些因素。

当这些因素不能忽略时，按确定性控制理论设计的控制系统的行为就会偏离预定的设计要求，而产生随机偏差量。

涉及领域飞机或导弹在飞行中遇到的阵风，在空间环境中卫星姿态和轨道测量系统中的测量噪声，各种电子装置中的噪声，生产过程中的种种随机波动等，都是随机干扰和随机变量的典型例子。

随机控制系统的应用很广，涉及航天、航空、航海、军事上的火力控制系统，工业过程控制，经济模型的控制，乃至生物医学等。

研究课题随机控制理论研究的课题包括随机系统的结构特性和运动特性(如动态特性、能控性、能观测性、稳定性)的分析，随机系统状态的估计，以及随机控制系统的综合（即根据期望性能指标设计控制器）。

随机系统中含有随机变量，所以在研究中需要使用随机过程的基本概念和概率统计方法。

严格实现随机最优控制是很困难的。

对于线性二次型高斯(LQG)随机过程控制问题,包括它的特例最小方差控制问题，可以应用分离原理把随机最优控制问题分解成状态估计问题和确定性最优控制问题，最终能得到全局最优的结果。

但对于一般的随机控制问题应用分离原理只能得到次优的结果。

随机状态模型随机系统在连续时间情形下的动态过程，常可用随机微分方程随机微分方程描述,式中x(t)为状态向量，d x(t)为由时刻t至t+d t状态的增量,u(t)为控制输入，θ为随机参数，w(t)为独立增量随机过程,其微分d w(t)可理解为白噪声。

最优控制学院专业班级姓名学号1948年维纳发表了题为《控制论—关于动物和机器中控制与通讯的科学》的论文，第一次科学的提出了信息、反馈和控制的概念，为最优控制理论的诞生和发展奠定了基础。

钱学森1954年所着的《工程控制论》直接促进了最优控制理论的发展和形成。

最优控制理论所研究的问题可以概括为：对一个受控的动力学系统或运动过程，从一类允许的控制方案中找出一个最优的控制方案，使系统的运动在由某个初始状态转移到指定的目标状态的同时，其性能指标值为最优。

这类问题广泛存在于技术领域或社会问题中。

从数学上看，确定最优控制问题可以表述为：在运动方程和允许控制范围的约束下，对以控制函数和运动状态为变量的性能指标函数（称为泛函）求取极值（极大值或极小值）。

解决最优控制问题的主要方法有古典变分法（对泛函求极值的一种数学方法）、极大值原理和动态规划。

最优控制已被应用于综合和设计最速控制系统、最省燃料控制系统、最小能耗控制系统、线性调节器等。

例如，确定一个最优控制方式使空间飞行器由一个轨道转换到另一轨道过程中燃料消耗最少，选择一个温度的调节规律和相应的原料配比使化工反应过程的产量最多，制定一项最合理的人口政策使人口发展过程中老化指数、抚养指数和劳动力指数等为最优等，都是一些典型的最优控制问题。

最优控制理论是50年代中期在空间技术的推动下开始形成和发展起来的。

苏联学者Л.С.庞特里亚金1958年提出的极大值原理和美国学者R.贝尔曼1956年提出的动态规划，对最优控制理论的形成和发展起了重要的作用。

线性系统在二次型性能指标下的最优控制问题则是R.E.卡尔曼在60年代初提出和解决的。

最优控制理论-主要方法解决最优控制问题的主要方法解决最优控制问题，必须建立描述受控运动过程的运动方程为了解决最优控制问题，必须建立描述受控运动过程的运动方程，给出控制变量的允许取值范围，指定运动过程的初始状态和目标状态，并且规定一个评价运动过程品质优劣的性能指标。

随机过程中的最优控制研究一、前言随机过程在当前信息时代中扮演着越来越重要的角色，随机过程模型广泛应用于金融、经济、物理、交通、生物等众多领域中。

而如何在随机过程中实现最优控制问题一直是相关领域中的难点和热点问题，因此对于随机过程中的最优控制问题的研究不仅具有理论意义，更重要的是其在实际应用中的巨大价值。

二、随机过程及其应用随机过程是一个随机变量序列，通常用Xt表示，在数学中，随机过程用于建立描述随机事件变化的数学模型，也称为随机序列，是概率论的基本分支之一。

在金融、经济学、信号处理、交通管理、生物统计学以及物理等领域都有广泛的应用。

在实际应用中，随机过程模型通常是优化问题的基础，比如股票市场、期权定价、货币政策等，他们往往都可以被看作随机过程模型，而最优控制问题则是人们最关心的问题之一。

三、最优控制问题最优控制问题是指如何在已知状态和控制变量的情况下，使某些性能指标取得最优的问题，是控制工程中的基本问题，其目标是在规定条件下使得一个系统的输出信号按照一定要求进行控制，以使效果最符合我们的要求。

最优控制问题的基本假设是被控对象是一个随机过程，在控制变量为随机过程的情况下，能够进行最优控制的研究，进而让控制变量的取值及时进行调整。

最优控制问题的求解通常是基于贝尔曼等人于20世纪初提出的“最优化原理”，也称为“贝尔曼方程”，后者成为现代控制理论与技术的基础。

四、随机过程的最优控制随机系统中的最优控制问题就是要在系统随机变量中寻求最优控制策略，其中包含了模型参数的众多随机性因素。

随机系统中的最优控制问题的一般形式是：在已知初始状态下，以最小化或最优化某种性能指标的标准，设计一个系统补偿器来使输出信号满足性能指标的要求。

随机过程中的最优控制问题涉及到许多领域，其中包括：随机微分方程、随机控制、随机优化等。

在实际应用中，对于不同的应用场景，需要采用不同的随机过程模型和最优控制方法，同时还需要考虑统计随机性对控制效果的影响和应对控制误差及模型参数误差等问题。

带泊松跳跃的正倒向随机最优控制理论及其应用的开题报告一、研究背景及意义随机最优控制理论是博弈、金融、机器人控制等领域研究的重要分支方向之一。

在随机最优控制理论中，常常假设状态空间是连续的、随时间无限延伸的，而且动力学方程满足高斯-马尔可夫假设。

然而，在实际应用中，许多系统的状态变量往往只能在离散时间点上进行观测或者更新，而且状态变量的变化可能包含了突发的跳跃现象，如能源系统、金融市场等领域。

这种具有泊松跳跃的随机过程被称为带泊松跳跃的随机过程。

因此，对于带泊松跳跃的随机过程的研究具有极其重要的理论和实际应用意义。

目前，已有许多学者研究了具有泊松跳跃的随机过程和带泊松跳跃的最优控制问题。

但是，这些研究主要集中在连续时间最优控制领域，带泊松跳跃的离散时间最优控制问题的研究相对较少。

因此，本文拟研究带泊松跳跃的离散时间最优控制问题，为相关领域的研究提供理论参考，并具有重要的实际应用意义。

二、研究内容本文拟研究带泊松跳跃的离散时间最优控制问题。

具体包括以下内容：1. 带泊松跳跃的离散时间随机过程的建模和相关定义。

主要研究带泊松跳跃的离散时间马尔可夫链和带泊松跳跃的离散时间随机过程等。

2. 带泊松跳跃的离散时间最优控制问题的理论分析和求解。

主要研究如何建立带泊松跳跃的离散时间最优控制的数学模型，在此基础上探讨最优解的存在性、唯一性和稳定性。

3. 带泊松跳跃的离散时间最优控制问题的应用研究。

主要研究带泊松跳跃的离散时间最优控制问题在实际应用中的应用，如金融市场中的投资组合问题等。

三、研究方法本文主要采用数学建模和分析的方法进行研究。

具体来说，首先从理论上分析带泊松跳跃的离散时间随机过程的性质，为带泊松跳跃的离散时间最优控制问题的建立提供理论基础。

然后，基于所建立的理论模型，采用动态规划方法或其他最优控制方法求解带泊松跳跃的离散时间最优控制问题。

最后，对所得结果进行数值仿真和对比分析，验证所提出理论的正确性和实用性。

最优控制理论讲义第一章 绪论§1.1最优控制问题静态最优化问题：输入—输出—代数方程 动态最优化问题：输入—输出—微分方程 确定性最优控制：系统参数确定，无随机输入 随机性最优控制：系统参数确定，有随机输入⎩⎨⎧=+=)()()()()(t Cx t Y t Bu t Ax t x⎩⎨⎧+=++=)()()()()()()(t v t Cx t Y t w t Bu t Ax t x例：飞船的月球软着陆问题推力 dtdmkf -= 运动方程 mg dt dmk mg f dtx d m --=-=22)()(][00f t t t m t m dt dtdmJ f-=-=⎰ 初始条件 ⎩⎨⎧======0)(,)(,00f f t x x t t ht x x t t约束条件为 0≤≤-dtdmα 求min J§1.2最优控制的数学模型一 控制系统的数学模型(集中参数系统)直接法建立：动力学、运动学的基本定律，即解析法. 间接法建立：通过“辩识”的途径确定系统的结构与参数.)),(),(()(t t u t x f t x= 其中 T n t x t x t x t x )](,)(),([)(21 =,T r t u t u t u t u )](,)(),([)(21 =,],,[21n f f f f =)(t x 为n 维状态向量,)(t u 为r 维控制向量,f 为n 维函数向量.二 目标集通过)(t u 使)(t x 由)(0t x 到)(f t x ，其中)(0t x 为初始状态，并且通常为已知；)(f t x 为终端状态，即控制所要求达到的目标。

一般来说对终端状态的要求可用如下的约束条件表示：0)),((,0)),((21≤=f f f f t t x g t t x g . 三 容许控制i u 具有不同的物理属性，一般有r 1,2i u i ,,=≤α，即在控制域U 内.凡在闭区间],[0f t t 上有定义，且控制域U 内取值的每一个控制函数)(t u 均称为容许控制。

随机动力学发展史
随机动力学是研究受到随机扰动影响的动力学系统行为的学科，它的发展经历了多个阶段，并广泛应用于工程、自然科学和社会科学等领域。

具体来说：
1. 早期发展：随机过程理论最早源于爱因斯坦对布朗运动的定量研究，这是在1905年。

随后，维纳（Norbert Wiener）在1913年对随机过程进行了进一步的数学研究，奠定了现代随机过程理论的基础。

2. 理论框架的建立：随机动力学的理论框架逐渐建立起来，其中包括对受Gauss白噪声扰动的一维动态系统的研究。

例如，R-S积分就是描述这类系统的一种数学工具，它涉及到随机微分方程和积分方程。

3. 与其他领域的交叉：随机动力学与确定性控制系统最优控制理论相互影响，后者从20世纪50年代开始发展，以庞特利亚金的极大值原理和贝尔曼的动态规划法为标志。

这些理论最初应用于航空航天领域，后来扩展到其他领域，包括随机系统的最优控制。

4. 成熟与应用：经过半个多世纪的发展，随机动力学已成为一个比较成熟的学科。

它在土木工程、机械工程、航空航天、海洋工程等工程领域，以及物理、化学、生物、生态、气象等
自然科学领域，甚至在经济与金融等社会科学领域都得到了广泛的应用。

总的来说，随机动力学的发展史是一个不断深化和拓展的过程，它不仅丰富了我们对自然界和社会现象的理解，也为工程技术的进步提供了重要的理论基础和实用工具。

随机偏微分方程的最优控制随机偏微分方程（StochasticPartialDifferentialEquation,SPDE）是一种解决非线性、随机系统动力学和传播问题的重要方法。

其方法提供了一种高效、灵活的解决方案，可以解决实际的工程和科学问题。

最优控制是 SPDE 重要研究方向之一，它是一种概率和控制的交互作用，为系统的实际应用提供了可行的机会。

本文尝试从理论和应用的角度来讨论随机偏微分方程的最优控制问题。

一、SPDE论SPDE一种用于描述连续空间中随机系统动力学发展的技术。

它包括了一些重要的概念，如概率空间、空间数学和内在噪声。

SPDE主要特点是，其解是由具有不确定性的随机和确定参数组成的概率分布，这意味着 SPDE是将随机概率解决方案和确定控制系统结合起来的一种重要模式。

SPDE究的一个重要目的是研究机会下的最优控制问题。

例如，在给定的控制条件下最大化目标函数，或在给定的频率/时间条件下最小化滤波器系统的期望值，这些都是 SPDE最优控制问题。

二、最优控制最优控制是 SPDE究的一个重要方向，它是一种概率和控制的交互作用，可以用来解决实际的工程和科学问题。

最优控制的主要任务是查找有效的控制策略，以达到指定的目标。

具体地说，它是在给定的控制约束条件下，最优化系统的性能的过程。

最优控制的基本原理是对系统的参数进行优化，以满足给定的目标。

SPDE仿真工具可以帮助研究人员探索参数空间中潜在的最优状态，从而找到最优解。

最优控制问题也可以分为几个类别，如最小化噪声、最大化系统性能、最小化系统响应时间等。

三、应用随机偏微分方程的最优控制是一种极具潜力的技术，在工程和科学中有广泛的应用，如在生物和化学工程中的反应过程优化，在机械工程中的机械结构优化，在控制系统中的参数优化，在信号处理中的滤波器系统优化等。

SPDE最优控制可以帮助研究人员指导设计和优化实际的系统，从而改善系统的性能和结果的准确性。

它还可以帮助研究人员了解系统运行的规律，更好地控制系统，甚至在未来预测系统的行为。