第十五章 透视投影

透视投影矩阵：原理、公式与应用透视投影矩阵是计算机图形学中的核心概念，用于在三维空间中模拟人眼看世界的方式。

本文将详细阐述透视投影矩阵的原理、公式及其在各种应用中的作用。

一、透视投影矩阵的原理透视投影，又称远心投影，是计算机图形学中实现三维场景到二维屏幕映射的重要方法。

透视投影的原理与人眼看世界的方式相似：物体离观察者越远，它们显得越小。

这种投影方式能够产生近大远小的视觉效果，使得生成的图像更加逼真。

在透视投影中，观察者位于一个被称为“投影中心”的点，投影线从这个点出发，穿过三维场景中的物体，相交于一个被称为“投影平面”的二维平面。

投影线与投影平面的交点即为物体在二维屏幕上的像素位置。

通过这种方式，三维空间中的物体被映射到了二维平面上。

二、透视投影矩阵的公式透视投影矩阵的公式如下：M = [ m11 m12 m13 m14m21 m22 m23 m24m31 m32 m33 m34m41 m42 m43 m44 ]其中，mij（i, j = 1, 2, 3, 4）为矩阵的元素。

这个4x4的矩阵包含了透视投影所需的所有参数，如视场角（Field of View, FOV）、宽高比（Aspect Ratio）、近裁剪面距离（Near Clipping Plane Distance）和远裁剪面距离（Far Clipping Plane Distance）等。

通过设定这些参数，我们可以得到一个特定的透视投影矩阵。

这个矩阵随后将应用于三维场景中的每一个顶点，将其从视图空间变换到裁剪空间。

裁剪空间是一个中间坐标系，用于判断哪些顶点位于视锥体内，即哪些顶点最终会被绘制到屏幕上。

三、透视投影矩阵的应用1. 游戏开发：在游戏开发中，透视投影矩阵是实现3D游戏视觉效果的关键。

通过调整透视投影矩阵的参数，游戏开发者可以控制玩家的视野范围、游戏的视角效果等，从而营造出不同的游戏氛围和体验。

2. 电影制作：在电影特效制作中，透视投影矩阵也发挥着重要作用。

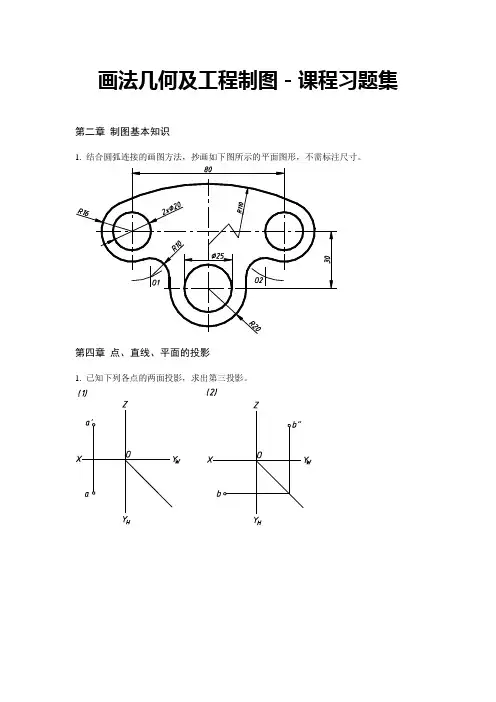
画法几何及工程制图－课程习题集第二章制图基本知识1. 结合圆弧连接的画图方法，抄画如下图所示的平面图形，不需标注尺寸。

第四章点、直线、平面的投影1. 已知下列各点的两面投影，求出第三投影。

2. 已知两点A(10,20,15)、B(15,0,20)，求其三面投影。

3. 画出直线AB的第三投影，并判别它对投影面的相对位置。

4. 已知线段两端点A(25,10,5)、B(5,20,25)，画出其三面投影，并求AB实长及其对水平投影面的倾角。

5. 判别AB和CD两直线的相对位置（必要时由作图结果去判别）。

6. 过A点作直线AB与CD相交，交点B距H面20。

7. ABC上作一点K，使距H面15，距V面18。

8. 已知线段DE ABC，求DE的正面投影。

第五章直线与平面及两平面的相对关系1. 过D 点作平面平行于 ABC 。

2. 过A 点作 ABC 平行于DE 。

3. 求直线与平面的交点，并判别可见性。

4. 求两平面的交线MN，并判别可见性。

5. 求两平面的交线KL，并判别可见性。

6. 已知形体的三个投影，求出其表面上点A、B、C、D的另两面投影。

第七章截交线和相贯线1. 完成带切口形体的三面投影。

(1)(2)（3）(4)2. 完成带切口形体的三面投影。

(1) (2)(3) (4)(5) (6)3. 完成带切口形体的三面投影。

(1) (2)(3) (4)4. 求形体的相贯线。

（1）标出最右、最前点B 。

（2）标出最前点A 、最后点B 、最高点C 、最低点D 。

5. 求形体的相贯线。

（1）（2）第九章轴测投影1. 已知形体的两个投影，画出正等轴测图。

2. 已知形体的两个投影，画出正等轴测图。

3. 已知形体的两个投影，画出斜二测图。

4. 根据形体的投影画正等轴测图。

（1）（2）第十章建筑施工图1. 在首层平面图(1:100)上,完成下列各项内容。

(1) 标出各承重构件的纵向和横向轴线编号;(2) 标出轴线间尺寸和总尺寸,以及室内地面标高(房地面为零点,门厅低20mm);(3) 补画门的图例(外门用双扇平开门,其余用单扇平开门),并标出各门窗编号;(4) 画出楼梯首层图例(梯级宽1500mm,踏步宽250mm,起步线在图中).2. 下图是侧立面图作了1-1剖视图,在图上补画。

透视投影矩阵
第一章什么是透视投影矩阵
透视投影矩阵是一种用于计算三维图形在二维屏幕上的投影的数学工具。

它的目的是模拟
人眼的视觉效果，即把远处的物体变得小一些，近处的物体变得大一些。

这样，我们就可
以在二维屏幕上看到一个有深度的三维图形。

第二章透视投影矩阵的基本概念
透视投影矩阵是一个 4x4 的矩阵，它的前三行用来表示投影的方向，第四行用来表示投
影的位置。

其中，最重要的参数是视点（也称为相机位置）和观察点（也称为目标位置）。

视点表示相机所在的位置，观察点表示相机正在观察的物体的位置。

还有一个重要的参数是上方向，它用来表示相机的方向。

第三章透视投影矩阵的计算
透视投影矩阵的计算涉及到三维向量的运算。

首先，需要计算出视线向量，它是从视点指
向观察点的向量。

然后，需要计算出上方向向量。

最后，需要计算出右方向向量。

这三个
向量是透视投影矩阵的基本元素，我们可以根据这三个向量来构造透视投影矩阵。

第四章透视投影矩阵的应用
透视投影矩阵在计算机图形学中有广泛的应用。

它可以用来实现 3D 游戏中的视角转换、图形变换和光照效果。

此外，透视投影矩阵还可以用来模拟不同的相机焦距效果，例如广角镜头和望远镜。

总的来说，透视投影矩阵是计算机图形学中不可或缺的重要工具。

《建筑制图》第五版名词解释第二章制图基本知识1、比例：图中图形与其实物相应要素的线性尺寸之比。

2、尺寸标注：见P153、作平面图形的步骤：见P20第三章投影的基本知识1、斜投影：投射方向倾斜于投影面时所作出的平行投影。

2、正投影：投射方向垂直于投影面时所作出的平行有影。

见P263、平行投影的特性：度量性、相仿性、集聚性、平行性、定比性4、【例3-1】组合体投影图，见P39第四章点、直线、平面的投影1、点的三面投影，见P422、【例4-1】求一点的第三投影，见P433、【例4-2】根据坐标作三面投影，见P444、【例4-3】点的投影图读法，见P445、【例4-4】投影面上各点的投影，见P45第六章曲线和曲面1、曲线是由点运动而形成的。

曲线可分为平面曲线和空间曲线两大类。

凡曲线上所有点都在同一平面上的，称为平面曲线。

凡曲线上四个连续的点不在同一平面上的，称为空间曲线。

2、与曲线相交于两个点的直线，称为曲线的割线。

见P873、曲面是由直线或曲线在一定约束条件下运动而成的。

这根运动的直线或曲线，称为曲面的母线。

母线运动时所受的约束，称为运动的约束条件。

见P89第七章截交线和相贯线1、假想用来截割形体的平面，称为截平面。

截平面与形体表面的交线称为截交线。

截交线围成的平面图形称为断面。

见P1132、有些建筑形体是有由两个相交的基本形体组成的。

两交线的形体称为相贯体，它们的表面交线称为相贯线。

3、棱柱体截交线画法，见P1154、圆柱上的截交线，见P1185、圆柱上截交线椭圆的作图步骤，见P1196、三棱柱与三棱锥相贯，见P1257、求直立圆柱与直立圆锥的相贯线，见P129第八章建筑形体的表达方法1、标注尺寸的步骤：见P1392、剖面图的产生，见P1413、剖面图的标注，见P1454、把断面投射到与它平行的投影面上，所得的投影，表示出断面的实形，称为断面图。

见P1465、剖面图与断面图的区别，见P146第九章轴侧投影1、根据平行投影的原理，把形体连同确定其空间位置的三根坐标轴一起，沿不平行于任一坐标的方向，投射到新投影面上，所得的投影称为轴测投影。

九年级数学下册《投影与视图》全章教案新人教版第一章：投影的概念与分类教学目标：1. 了解投影的概念，掌握各种投影的分类。

2. 能够运用投影的知识解决实际问题。

教学内容：1. 投影的概念：平行投影、中心投影。

2. 投影的分类：正投影、斜投影。

3. 投影的基本性质。

教学步骤：1. 引入投影的概念，展示各种投影的图片，引导学生观察并思考。

2. 讲解平行投影和中心投影的定义，通过示例让学生理解两种投影的特点。

3. 介绍正投影和斜投影的分类，让学生通过实际例子区分两种投影。

4. 引导学生总结投影的基本性质，如相似性、形状不变等。

5. 布置练习题，让学生巩固所学内容。

教学评价：1. 学生能够准确描述投影的概念和分类。

2. 学生能够运用投影的知识解决实际问题。

第二章：视图的定义与分类教学目标：1. 理解视图的定义，掌握各种视图的分类。

2. 能够运用视图的知识解决实际问题。

教学内容：1. 视图的定义：主视图、左视图、俯视图。

2. 视图的分类：正视图、侧视图、俯视图。

3. 视图的基本性质。

教学步骤：1. 引入视图的概念，展示各种视图的图片，引导学生观察并思考。

2. 讲解主视图、左视图、俯视图的定义，通过示例让学生理解三种视图的特点。

3. 介绍正视图、侧视图、俯视图的分类，让学生通过实际例子区分三种视图。

4. 引导学生总结视图的基本性质，如相互补充、完整性等。

5. 布置练习题，让学生巩固所学内容。

教学评价：1. 学生能够准确描述视图的定义和分类。

2. 学生能够运用视图的知识解决实际问题。

第三章：简单几何体的三视图教学目标：1. 掌握简单几何体的三视图的画法。

2. 能够运用三视图的知识解决实际问题。

教学内容：1. 简单几何体的三视图：正方体、长方体、圆柱体、圆锥体。

2. 三视图的画法与特点。

教学步骤：1. 讲解正方体、长方体、圆柱体、圆锥体的三视图的画法，通过示例让学生理解各种几何体的三视图特点。

2. 引导学生动手画出各种几何体的三视图，并观察其特点。

透视投影详解透视投影透视投影是⽤中⼼投影法将形体投射到投影⾯上，从⽽获得的⼀种较为接近视觉效果的单⾯投影图。

它具消失感、距离感、相同⼤⼩的形体呈现出有规律的变化等⼀系列的透视特性，能逼真地反映形体的空间形象。

透视投影也称为透视图,简称透视。

在建筑设计过程中，透视图常⽤来表达设计对象的外貌，帮助设计构思，研究和⽐较建筑物的空间造型和⽴⾯处理，是建筑设计中重要的辅助图样。

透视投影符合⼈们⼼理习惯，即离视点近的物体⼤，离视点远的物体⼩，远到极点即为消失，成为灭点。

它的视景体类似于⼀个顶部和底部都被切除掉的棱椎，也就是棱台。

这个投影通常⽤于动画、视觉仿真以及其它许多具有真实性反映的⽅⾯。

在平⾏投影中，图形沿平⾏线变换到投影⾯上；对透视投影，图形沿收敛于某⼀点的直线变换到投影⾯上，此点称为投影中⼼，相当于观察点，也称为视点。

平⾏投影和透视投影区别在于透视投影的投影中⼼到投影⾯之间的距离是有限的，⽽平⾏投影的投影中⼼到投影⾯之间的距离是⽆限的。

当投影中⼼在⽆限远时，投影线互相平⾏，所以定义平⾏投影时，给出投影线的⽅向就可以了，⽽定义透视投影时，需要指定投影中⼼的具体位置平⾏投影保持物体的有关⽐例不变，这是三维绘图中产⽣⽐例图画的⽅法。

物体的各个⾯的精确视图可以由平⾏投影得到。

另⼀⽅⾯，透视投影不保持相关⽐例，但能够⽣成真实感视图。

对同样⼤⼩的物体，离投影⾯较远的物体⽐离投影⾯较近物体的投影图象要⼩，产⽣近⼤远⼩的效果.透视投影的原理和实现by Goncely摘要：透视投影是3D渲染的基本概念，也是3D程序设计的基础。

掌握透视投影的原理对于深⼊理解其他3D渲染管线具有重要作⽤。

本⽂详细介绍了透视投影的原理和算法实现，包括透视投影的标准模型、⼀般模型和屏幕坐标变换等，并通过VC实现了⼀个演⽰程序。

1 概述在计算机三维图像中，投影可以看作是⼀种将三维坐标变换为⼆维坐标的⽅法，常⽤到的有正交投影和透视投影。

正交投影多⽤于三维健模，透视投影则由于和⼈的视觉系统相似，多⽤于在⼆维平⾯中对三维世界的呈现。

说明透视投影的含义和种类
透视投影是一种重要的技术，用于将物体在容纳它们的空间中投影到同一维度。

它允许用户从前后，上下和左右的视角来看物体，从而让用户更好地理解几何形状和对象的结构。

透视投影可以用于几乎任何领域，包括图像处理，游戏开发，实时图形，虚拟现实，机器人机器，机械设计和建筑可视化等。

透视投影的主要含义是，当一个物体被投射到一个平面时，它会失去原有的宽度和高度，使物体变得更短，更小，看起来像是伸展到远处。

它在视觉上提供了一种深度感，使用户可以更好地把握距离，把握视觉层次，以及看到物体的立体效果。

透视投影可分为三种：斜交透视投影、正交透视投影和声景图（又称曲线投影）。

斜交透视投影是最常用的投影技术，它可以在多维度投射物体，允许用户从不同的视角来看物体。

它的优势在于容易理解，但缺点是结果的精度较低。

正交透视投影可以使物体更加接近它们的实物，这是由于投影方式的不同而产生的宽度比例差异。

正交透视投影相对来说更贴近实物，所以在图像处理方面使用得更多，但它的缺点是投影结果准确度较低。

最后一种投影是声景图，它在多维度投射物体，但会将画面矫正为椭圆或曲线形状，比如地图上的投影，相当于把球形地球投射到二维平面上，通常用在建筑可视化中。

总而言之，透视投影是一项重要的技术，可以应用于多个领域。

它可以帮助用户更好地理解投影到同一维度的物体，从而更好地把握距离，把握视觉层次，增强视觉效果等。

此外，透视投影可以分为三
种：斜交透视投影、正交透视投影和声景图。