第8章最优消费和投资离散时间

第8章 相关分析2. 离散相关与离散序列的卷积运算一样，离散序列的相关运算也可以分为线性相关和循环相关两种类型。

2.1 基本定义线性相互关的计算对应公式(8-1)的离散化形式，计算离散序列][n x 和][n y 的线性互相关，可得：∑+∞-∞=+⋅=i xy n i y i x n r ][][][ (8-6)对有限长度的离散序列][n x ，1,1,0-=L n 、][n y ，1,1,0-=P n ，且二者的长度分别为L 和P 。

那么，有如下公式成立：∑--=+⋅=nP i xy n i y i x n r 10][][][ (8-7)当P n i ≥+时，0][=+n i y ，所以公式(8-7)中的求和上限为n P --1。

因为序列][n r xy 下标n 的取值范围为：11-≤≤-P n M ，所以与线性卷积的长度一样，序列][n x 和][n y 的线性互相关序列的最大长度也是1-+P L 。

与离散Fourier 变换的相关特性对应的是循环相关(或称圆周相关)，循环互相关的定义已在第二章中出现过，笔者在下面重新书写一遍。

∑-=+⋅=10])[(][][N i N xy n i y i x n r (8-8)其中，N n i )(+表示)(n i +除以N 的余数，][n r xy 下标n 的取值范围为：2/2/N n N <≤-。

可以利用循环相关来计算两个序列的线性相关，只是要对原有序列进行补零处理。

把长度为L 的序列][n x 和长度为P 的序列][n y 补零后拓展序列长度为N 的新序列][n x 和][n y ，只要满足1-+≥P L N ，两个新序列的循环相关就等同于原有两个序列的线性相关。

与连续函数的互相关函数一样，互相关序列][n r xy 既不是偶序列，也不是奇序列，但满足等式：][][n N r n r yx xy -=。

2.2 快速算法计算两个长度相等的序列的循环相关时，如果直接采用公式(8-8)的定义，计算量是非常大的，尤其在N 较大的情况下。

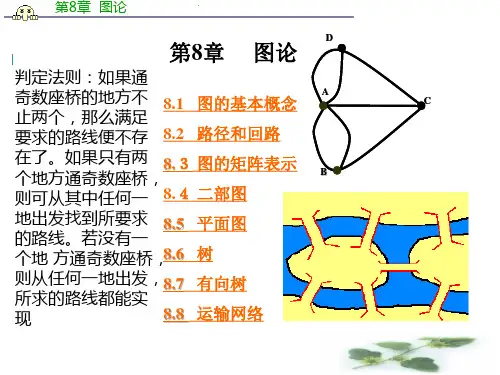
第8章离散时间信号与系统的z域分析8-1 根据定义求以下序列的单边z变换及其收敛域。

解：根据序列单边z变换的定义即可求出上述信号的z变换及收敛域。

8-2 根据单边z变换的位移性质，求以下序列的z变换及其收敛域。

解：单边z变换的位移特性有以下3种形式（8-1）（8-2）（8-3）对于因果序列的位移，利用式（8-1）；非因果序列的位移，利用式（8-2）和（8-3）。

（1）利用因果序列的位移特性，有（2）利用因果序列的位移特性，有（3）利用因果序列的位移特性，有（4）利用因果序列的位移特性，有（5）由于，直接应用指数信号的z变换，可得（6）将改写成，利用因果序列的位移特性，可得8-3 根据z变换的性质，求以下序列的单边z变换及其收敛域。

解：利用z变换的性质求信号z变换的关键是根据待分析信号的构成，确定合适的信号作为基本信号，采用相应的z变换性质。

（1）由，以及z域微分特性，有（2）将改写为利用（1）题结果及因果序列的位移特性，可得（3）将改写为利用的z变换及z域微分特性，有故（4）将改写为利用（3）题结论及因果序列的位移特性，可得（5）将改写为利用卷积特性（6）利用（5）题结果及指数加权特性，有8-4 求以下周期序列的单边z变换。

解：周期为N的单边周期序列可以表示为第一个周期序列及其位移的线性组合，即这样，若计算出的z变换，利用因果序列的位移特性和线性特性，则可求得其单边周期序列的变换为（1）可表示为利用的变换及因果序列的位移特性，可得（2）将改写为利用（1）题的结果及卷积特性，可得8-5 已知，利用z变换的性质，求下列各式的单边z变换及其收敛域。

解：本题的关键是判断各信号是经过什么运算得到的，然后根据其运算，利用相应的z变换性质即可求出它们的z变换。

（1）利用因果序列的位移特性，可得（2）利用指数加权特性，可得（3）利用（1）题结果及指数加权特性，可得（4）利用z域微分特性，可得（5）利用（4）题结果及线性加权特性，可得（6）可以表示为，利用卷积特性可得（7）可以表示为，利用卷积特性可得（8）可以表示为，利用因果序列的位移特性及卷积特性，可得8-6 已知因果序列的z变换式，试求的初值和终值解：利用初值定理和终值定理即可求出的初值和终值。

第八章 离散傅立叶变换8.1 假设()t x c 是一个周期的连续时间信号，其周期为1ms ，它的傅立叶级数为()()∑-=-=9910/23k kt j kc e a t x π. 对于9>k ，傅立叶系数k a 为零，以采样间隔s T 31061-⨯=对()t x c 采样得到[]n x ： []⎪⎪⎭⎫⎝⎛=-6103n x n x c .(a) []n x 是周期的吗？如果是，周期为多少？(b) 采样率是否高于奈奎斯特采样率，也就是说T 是否充分小而且可以避免混叠？ (c) 利用k a 求出[]n x 的离散傅立叶级数系数。

解：（a ）[]∑∑-=-=⎪⎪⎭⎫ ⎝⎛⨯-==⎪⎪⎭⎫ ⎝⎛=--996299610102333610k kn jkk n k j k c ea e a n x n x ππ而() 1,0,62662==+l ee kn jl n k jππ[][]l n x n x 6+=∴∴ []n x 是周期的，周期为6。

（b ）30102-=Ωπ而采样频率为03321012106122Ω>=⨯==Ω--πππT 所以T 足够小，而可以避免混叠。

（c ）[][]()()()∑∑∑∑∑∑-=---==-=--=-=--=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛==99335995062506299621011k k l k l lk n k l n j l n kn j l nl j l N n knNeea e a e e a w n x k X πππππ 8.2 设[]n x ~是一个周期为N 的周期序列，[]n x ~还是一个周期为3N 的周期序列。

令[]k X ~表示作为周期为N 的周期序列的[]n x ~的DFS 系数，[]k X ~3表示作为周期为3N 的周期序列的[]n x ~的DFS 系数。

(a) 用[]k X ~表示出[]k X ~3。

(b) 用公式计算[]k X ~和[]k X ~3，当[]n x ~为图P8.2中给定的序列时，证明你在(a)中得出的结果。