广东省汕头市高考数学四模试卷(理科)

广东省汕头市2020学年度高三数学第四次质量检测卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择）题两部分，满分150分.时间120分钟.第Ⅰ卷（选择题，共40分）一. 选择题：本大题共8小题，每小题5分，共40分.1．已知全集}6,5,4,3,2,1{=U ，集合}4,3,2,1{=P ，}6,5,4,3{=Q ，则=)(Q C P U IA ．}2,1{ B.}4,3{ C. }6,2,1{ D.}4,3,2,1{ 2．下列四个函数中，在区间（0，1）上为增函数的是（ ）A ．x y 2log -=B ．x y sin =C ．x y )21(=D ．21-=xy3．把函数152++=x y 的图像向左平移2个单位，再向下平移1个单位，所得图像的函数解析式为 （A ）72+=x y （B ）92+=x y（C ）12+=x y （D ）12-=x y4．函数)0(,12<+=x y x的反函数是（A ）)2,1(,log 112∈=-x y x（B ）)2,1(,log 112∈-=-x y x （C ）]2,1(,log 112∈=-x y x （D ）]2,1(,log 112∈-=-x y x5．若21:20,:0,|1|xp x x q x +--<>-则p 是q 的A ．充分不必要条件，B ．必要不充分条件，C ．充要条件 ，D 既不充分也不必要条件。

6．函数(),0)(2≠++=a c x b ax x f 其定义域R 分成了四个单调区间，则实数c b a ,,满足（A ）0042>>-a ac b 且 （B ） 02>-a b（C ）042>-ac b （D ）02<-ab7．函数132)(-+=x x x f ，若函数)(x g 的图象与)1(1+=-x f y 的图象关于x y =对称,则)3(g =（A ）3 （B ）5 （C ）29 （D ）27 8．已知),2,2(0)(),,(0)(,)(),(22ba x gb a x f x g x f 的解集为的解集为奇函数>>则不等式的解集是0)()(>x g x f （ ）A ．)2,2(2b aB ．),(22a b --C ．),2()2,(22a b b a --⋃ D ．)2,2(2b a ⋃),(22a b --第Ⅱ卷（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分. 9．在等比数列}{n a 中，36,352=-=a a ，则8a =10．已知2()(2),f x log x =+函数()f x 的图象关于直线y x =对称，则(1)g = .11．f(x)是定义在R 上的增函数，其图象过点A(0,-1)、B (3,1)，则不等式|f(x+1)|<1的解集是 12．若关于x 的不等式a x x >-24的解集为R ，则实数a 的取值范围是 ．13．设=+++++=)1110()119()112()111(,244)(f f f f x f x x Λ则和式14．已知函数2()1log xf x =+ （(14)x ≤≤，则22()()y f x f x =+的最小值是 ；最大值是 ；三、解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.15．（本题满分12分）已知三角函数xxx x x x f 2sin 2cos sin cos sin )(2244-++=（1）求)(x f 最小正周期、最大值和最小值.（2）求)(x f 的对称轴16．（本小题12分）已知数列{}n a 是等差数列，{}n b 是等比数列，且112,a b ==454b =,12323a a a b b ++=+, (I)求数列{}n b 的通项公式； （II ）求数列{}n a 的前10项和10S 。

广东省汕头市2021届新高考数学四模试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．在一个数列中，如果*n N ∀∈，都有12n n n a a a k ++=（k 为常数），那么这个数列叫做等积数列，k 叫做这个数列的公积.已知数列{}n a 是等积数列，且11a =，22a =，公积为8，则122020a a a ++⋅⋅⋅+=（ ）A ．4711B ．4712C ．4713D ．4715【答案】B 【解析】 【分析】计算出3a 的值，推导出()3n n a a n N *+=∈，再由202036731=⨯+，结合数列的周期性可求得数列{}na 的前2020项和. 【详解】由题意可知128n n n a a a ++=，则对任意的n *∈N ，0n a ≠，则1238a a a =，31284a a a ∴==， 由128n n n a a a ++=，得1238n n n a a a +++=，12123n n n n n n a a a a a a +++++∴=，3n n a a +∴=，202036731=⨯+Q ，因此，()1220201231673673714712a a a a a a a ++⋅⋅⋅+=+++=⨯+=.故选：B. 【点睛】本题考查数列求和，考查了数列的新定义，推导出数列的周期性是解答的关键，考查推理能力与计算能力，属于中等题.2．设集合1,2,6,2,2,4,26{}{}{|}A B C x R x ==-=∈-<<，则()A B C =U I ( ) A ．{}2 B ．{1,2,4}C ．{1,2,4,6}D ．{|15}x x ∈-≤≤R【答案】B 【解析】 【分析】直接进行集合的并集、交集的运算即可． 【详解】解：{}2,1,2,4,6A B ⋃=-； ∴(){}1,2,4A B C ⋃⋂=．故选：B ． 【点睛】本题主要考查集合描述法、列举法的定义，以及交集、并集的运算，是基础题.3．已知底面为边长为2的正方形，侧棱长为1的直四棱柱1111ABCD A B C D -中，P 是上底面1111D C B A 上的动点.给出以下四个结论中，正确的个数是（ ）①与点D P 形成一条曲线，则该曲线的长度是2π；②若//DP 面1ACB ，则DP 与面11ACC A 所成角的正切值取值范围是3⎢⎣；③若DP =，则DP 在该四棱柱六个面上的正投影长度之和的最大值为A ．0 B ．1C ．2D ．3【答案】C 【解析】 【分析】①与点D P 形成以1D 的14圆弧MN ，利用弧长公式，可得结论；②当P 在1A （或1)C 时，DP 与面11ACC A 所成角1DA O ∠（或1)DC O ∠当P 在1O 时，DP 与面11ACC A 所成角1DO O ∠最大，可得正切值取值范围是；③设(P x ，y ，1)，则2213x y ++=，即222x y +=，可得DP 在前后、左右、上下面上的正投影长，即可求出六个面上的正投影长度之和． 【详解】 如图：①错误， 因为1D P ===，与点D 的点P 形成以1D 为圆心，的14圆弧MN ，长度为1242⋅=π； ②正确，因为面11//A DC 面1ACB ，所以点P 必须在面对角线11A C 上运动，当P 在1A （或1C ）时，DP与面11ACC A 所成角1DA O ∠（或1DC O ∠最小（O 为下底面面对角线的交点），当P 在1O 时，DP 与面11ACC A 所成角1DO O ∠最大，所以正切值取值范围是⎣；③正确，设(),,1P x y ，则2213x y ++=，即222x y +=，DP 在前后、左右、上下面上的正投影长分别为21y +，21x +，22x y +，所以六个面上的正投影长度之()2222112112222622y x y x ⎛⎫+++++++≤+= ⎪ ⎪⎝⎭，当且仅当P 在1O 时取等号.故选：C .【点睛】本题以命题的真假判断为载体，考查了轨迹问题、线面角、正投影等知识点，综合性强，属于难题．4．已知,a b ∈R ，函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩，若函数()y f x ax b =--恰有三个零点，则（ ） A ．1,0a b <-< B ．1,0a b <-> C ．1,0a b >-< D ．1,0a b >->【答案】C 【解析】 【分析】当0x <时，()(1)y f x ax b x ax b a x b =--=--=--最多一个零点；当0x …时，32321111()(1)(1)3232y f x ax b x a x ax ax b x a x b =--=-++--=-+-，利用导数研究函数的单调性，根据单调性画函数草图，根据草图可得． 【详解】当0x <时，()(1)0y f x ax b x ax b a x b =--=--=--=，得1bx a=-；()y f x ax b =--最多一个零点；当0x …时，32321111()(1)(1)3232y f x ax b x a x ax ax b x a x b =--=-++--=-+-， 2(1)y x a x =+-'，当10a +„，即1a -„时，0y '…，()y f x ax b =--在[0，)+∞上递增，()y f x ax b =--最多一个零点．不合题意；当10a +>，即1a >-时，令0y '>得[1x a ∈+，)+∞，函数递增，令0y '<得[0x ∈，1)a +，函数递减；函数最多有2个零点；根据题意函数()y f x ax b =--恰有3个零点⇔函数()y f x ax b =--在(,0)-∞上有一个零点，在[0，)+∞上有2个零点，如图：∴01ba <-且3211(1)(1)(1)032b a a a b ->⎧⎪⎨+-++-<⎪⎩， 解得0b <，10a ->，310(116,)b a a >>-+∴>-． 故选C ．【点睛】遇到此类问题，不少考生会一筹莫展.由于方程中涉及,a b 两个参数，故按“一元化”想法，逐步分类讨论，这一过程中有可能分类不全面、不彻底. 5．函数1()f x ax x=+在(2,)+∞上单调递增，则实数a 的取值范围是（ ） A ．1,4⎛⎫+∞⎪⎝⎭ B ．1,4⎡⎫+∞⎪⎢⎣⎭C ．[1,)+∞D ．1,4⎛⎤-∞ ⎥⎝⎦【答案】B 【解析】 【分析】对a 分类讨论，当0a ≤，函数()f x 在(0,)+∞单调递减，当0a >，根据对勾函数的性质，求出单调递增区间，即可求解. 【详解】当0a ≤时，函数1()f x ax x=+在(2,)+∞上单调递减， 所以0a >，1()f x ax x =+的递增区间是,a ⎫+∞⎪⎝⎭， 所以2a ≥，即14a ≥. 故选:B. 【点睛】本题考查函数单调性，熟练掌握简单初等函数性质是解题关键，属于基础题.6．设12,F F 分别是双线2221(0)x y a a-=>的左、右焦点，O 为坐标原点，以12F F 为直径的圆与该双曲线的两条渐近线分别交于,A B 两点（,A B 位于y 轴右侧），且四边形2OAF B 为菱形，则该双曲线的渐近线方程为（ ） A ．0x y ±= B ．30x y ±= C ．30x y ±=D ．30x y ±=【答案】B 【解析】 【分析】由于四边形2OAF B 为菱形，且2OF OA =，所以2AOF ∆为等边三角形，从而可得渐近线的倾斜角，求出其斜率. 【详解】如图，因为四边形2OAF B 为菱形，2OF OA OB ==，所以2AOF △为等边三角形，260AOF ︒∠=，两渐近线的斜率分别为3和3-. 故选：B【点睛】此题考查的是求双曲线的渐近线方程，利用了数形结合的思想，属于基础题.7．设命题:p 函数()x x f x e e -=+在R 上递增，命题:q 在ABC ∆中，cos cos A B A B >⇔<，下列为真命题的是（ ） A ．p q ∧ B ．()p q ∨⌝ C ．()p q ⌝∧ D ．()()p q ⌝∧⌝【答案】C 【解析】 【分析】命题p ：函数()xxf x e e-=+在(,0)-∞上单调递减，即可判断出真假．命题q ：在ABC ∆中，利用余弦函数单调性判断出真假． 【详解】解：命题p ：函数()xxf x e e-=+，所以()x x f x e e -=-'，当0x <时，()0f x '<，即函数在(,0)-∞上单调递减，因此是假命题．命题q ：在ABC ∆中，,(0,),cos A B y x π∈=在(0,)π上单调递减，所以cos cos A B A B >⇔<，是真命题．则下列命题为真命题的是()p q ⌝∧． 故选：C ． 【点睛】本题考查了函数的单调性、正弦定理、三角形边角大小关系、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题． 8．双曲线的渐近线与圆(x －3)2＋y 2＝r 2(r ＞0)相切，则r 等于( )A ．B ．2C ．3D ．6【答案】A 【解析】 【分析】由圆心到渐近线的距离等于半径列方程求解即可. 【详解】双曲线的渐近线方程为y ＝±x ，圆心坐标为(3,0)．由题意知，圆心到渐近线的距离等于圆的半径r ，即r＝.答案：A【点睛】本题考查了双曲线的渐近线方程及直线与圆的位置关系，属于基础题. 9．集合*12|x N Z x ⎧⎫∈∈⎨⎬⎩⎭中含有的元素个数为（ ） A ．4 B ．6C ．8D ．12【答案】B 【解析】 解：因为*12|x N Z x ⎧⎫∈∈⎨⎬⎩⎭集合中的元素表示的是被12整除的正整数，那么可得为1，2,3,4，6，,12故选B10．已知集合{2,3,4}A =，集合{},2B m m =+，若{2}A B =I ，则m =（ ） A ．0 B ．1C ．2D ．4【答案】A 【解析】 【分析】根据2m =或22m +=，验证交集后求得m 的值. 【详解】因为{2}A B =I ，所以2m =或22m +=.当2m =时，{2,4}A B =I ，不符合题意，当22m +=时，0m =.故选A.【点睛】本小题主要考查集合的交集概念及运算，属于基础题.11．某校为提高新入聘教师的教学水平，实行“老带新”的师徒结对指导形式，要求每位老教师都有徒弟，每位新教师都有一位老教师指导，现选出3位老教师负责指导5位新入聘教师，则不同的师徒结对方式共有（ ）种. A ．360 B ．240 C ．150 D ．120【答案】C 【解析】 【分析】可分成两类，一类是3个新教师与一个老教师结对，其他一新一老结对，第二类两个老教师各带两个新教师，一个老教师带一个新教师，分别计算后相加即可． 【详解】分成两类，一类是3个新教师与同一个老教师结对，有335360C A =种结对结对方式，第二类两个老教师各带两个新教师，有223533902!C C A =．∴共有结对方式60＋90＝150种． 故选：C ． 【点睛】本题考查排列组合的综合应用．解题关键确定怎样完成新老教师结对这个事情，是先分类还是先分步，确定方法后再计数．本题中有一个平均分组问题．计数时容易出错．两组中每组中人数都是2，因此方法数为22532!C C ．12．若样本1231,1,1,,1n x x x x ++++L 的平均数是10，方差为2，则对于样本12322,22,22,,22n x x x x ++++L ，下列结论正确的是（ ）A ．平均数为20，方差为4B ．平均数为11，方差为4C ．平均数为21，方差为8D ．平均数为20，方差为8【答案】D 【解析】 【分析】由两组数据间的关系,可判断二者平均数的关系,方差的关系,进而可得到答案. 【详解】样本1231,1,1,,1n x x x x ++++L 的平均数是10，方差为2，所以样本12322,22,22,,22n x x x x ++++L 的平均数为21020⨯=,方差为2228⨯=. 故选:D. 【点睛】样本123,,,,n x x x x L 的平均数是x ，方差为2s ，则123,,,,n ax b ax b ax b ax b ++++L 的平均数为ax b +,方差为22a s .二、填空题：本题共4小题，每小题5分，共20分。

汕头四中届高三第四次月考数学理试题本试卷总分值150分. 考试用时120分钟.本卷须知：1、答卷前，考生务必用2B 铅笔在答题卡“考生号〞处填涂考生号，用黑色字迹钢笔或签字笔将自己姓名、考生号、试室号、座位号填写在答题卡上.2、选择题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，答案不能答在试卷上.3、非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上. 如需改动，先划掉原来的答案，然后再写上新的答案. 不准使用铅笔和涂改液. 不按以上要求作答的答案无效.4、考生必须保持答题卡的整洁. 考试结束，将答题卡交回，试卷不用上交.5、不可以使用计算器.参考公式：回归直线ˆybx a =+，其中1122211()(),()nnii i ii i nniii i xx y y x ynx y b a y bx xx xnx====---===---∑∑∑∑.锥体的体积公式：13V Sh =,其中S 表示底面积，h 表示高． 乘法公式：2233()()a b a ab b a b +-+=+．一、选择题：本大题共8小题，每题5分，总分值40分。

在每题给出的四个选项中，只有一项为哪一项符合题目要求的． 1．设集合2{1,2,3,4},{|50}U M x U x x p ==∈-+=，假设U C M ={2，3}，那么实数p 的值为 ( ) A ．—4 B ．4 C ．—6D ．62．1．复数43iz i+=的虚部为 ( ) A ．4- B ． 4 C ．4iD ．i4-3．一个空间几何体的三视图如右图所示，根据图中标出的尺寸(单位：cm)，可得这个几何体的体积是( )A ．4 cm 3B ．5 cm 3C ．6 cm 3D ．7 cm 34．f (x )＝sin(ωx ＋3π) (ω>0)的图象与y ＝－1的图象的相邻两交点间的距离为π，要得到y ＝f (x )的图象，只需把y ＝cos2x 的图象( )A ．向左平移12π个单位 B ．向右平移12π个单位 C ．向左平移125π个单位 D ．向右平移125π个单位5．“不等式20x x m -+>在R 上恒成立〞的一个必要不充分条件是〔 〕 A 、41>m B 、10<<m C 、0>m D 、1>m 6．如图,假设程序框图输出的S 是126,那么判断框①中应为 〔 〕 A ．?5≤nB ．?6≤nC ．?7≤nD ．?8≤n7．正项数列{}n a 中，11=a ，22=a ， 222112(2)n n n a a a n +-=+≥，那么6a 等于〔 〕A ．16B ．8C ．22D ．48、函数()f x 的定义域为D ，假设存在闭区间[,]a b D ⊆，使得函数()f x 满足：①()f x 在[,]a b 内是单调函数；②()f x 在[,]a b 上的值域为[2,2]a b ，那么称区间[,]a b 为()y f x =的“倍值区间〞．以下函数中存在“倍值区间〞的有〔 〕①)0()(2≥=x x x f ； ②()()xf x e x =∈R ；③)0(14)(2≥+=x x xx f ；④)1,0)(81(log )(≠>-=a a a x f xa A.①②③④ B.①②④C.①③④D.①③二、填空题〔本大题共7小题，分为必做题和选做题两局部．每题5分，总分值30分〕 〔一〕必做题9、二项式613x x ⎫⎪⎭展开式的常数项为10. ,a b 均为单位向量，它们的夹角为60︒，那么3a b +=11．设,x y 满足约束条件02323x x y x y ≥⎧⎪+≥⎨⎪+≤⎩,那么z x y =-的最大值是 .12．随机变量2(2,),X N σ-假设()0.26P X a <=，那么(4)P a X a ≤<-=()()()22,20,f x x x g x ax a =-=+>对任意的[]11,2x ∈-都存在[]01,2x ∈-,使得()()10,g x f x =那么实数a 的取值范围是〔二〕选做题：考生只能选做其中一题，两题全答的，只计前一题的得分。

广东省汕头市2024高三冲刺（高考数学）统编版（五四制）模拟(评估卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题若，则的大小关系为（）A．B．C．D．第(2)题已知函数，则曲线在处的切线方程为（）A．B．C．D．第(3)题已知是定义域为的函数，为奇函数，为偶函数，则有①为奇函数，②关于对称，③关于点对称，④，则上述推断正确的是（）A．②③B．①④C．②③④D．①②④第(4)题阅读下图所示的程序框图，运行相应的程序，输出的结果是（）A．B．C．D．第(5)题在边长为1的正方形中，E为线段的中点，F为线段上的一点，若，则（）A．B．C．D．第(6)题已知等差数列的公差为d，其前n项和为，则“”是“”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件第(7)题抛物线上两点（不与重合），满足，则面积的最小值是（）A．4B．8C．16D．18第(8)题已知是椭圆上的动点，若动点到定点的距离的最小值为1，则椭圆的离心率的取值范围是（）A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题若函数的图像的相邻两条对称轴之间的距离为，且该函数图像关于点成中心对称，则下列结论正确的有（）A．是函数的一个周期B．直线是函数图像的一条对称轴C．函数是奇函数D．函数在区间上单调递减第(2)题已知红箱内有6个红球、3个白球，白箱内有3个红球、6个白球，所有小球大小、形状完全相同．第一次从红箱内取出一球后再放回去，第二次从与第一次取出的球颜色相同的箱子内取出一球，然后再放回去，依此类推，第次从与第k次取出的球颜色相同的箱子内取出一球，然后再放回去．记第次取出的球是红球的概率为，则下列说法正确的是（）A．B．C．第5次取出的球是红球的概率为D．前3次取球恰有2次取到红球的概率是第(3)题下列说法正确的是（）A ．若函数（）的最小正周期为，则的值为2B ．函数（）是偶函数C．点是函数图象的一个对称中心D．函数在上的单调递增区间是三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题已知是抛物线上的两个不同的点，且，若点为线段的中点，则到轴的距离的最小值为________．第(2)题第二届消博会（中国国际消费品博览会）于2022年5月在海南国际会展中心举办，甲、乙两人每人从A，B，C，D四个不同的消博会展馆中选2个去参观，则他们参观的展馆不完全相同但都参观A展馆的概率为______．第(3)题某学校有、、、、、6个兴趣小组，其中兴趣小组只剩一个名额，其余名额足够多．现有4位同学选择参加这6个兴趣小组，且每人只选择其中一个，这4位同学恰好参加了其中3个兴趣小组，则他们参加的可能情况有______种．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题已知为的三内角，且其对边分别为若且．（Ⅰ）求角；（Ⅱ）若的面积为求．第(2)题在数列中，，的前项为．(1)求证：为等差数列，并求的通项公式；(2)当时，恒成立，求的取值范围．第(3)题如图，O是圆锥底面圆的圆心，圆锥的轴截面为直角三角形，C是底面圆周上异于A，B的任一点，D是线段的中点，.(1)求证：平面；(2)在母线上是否存在一点，使二面角的余弦值为，若存在，求的值；若不存在，请说明理由.第(4)题已知函数，是自然对数的底数.（1）若函数，讨论在的单调性；（2）若对任意恒成立，求整数的最大值.第(5)题已知数列的前项和为，.（1）若，求证：，，必可以被分为1组或2组，使得每组所有数的和小于1；（2）若，求证：，，…，必可以被分为组（），使得每组所有数的和小于1．。

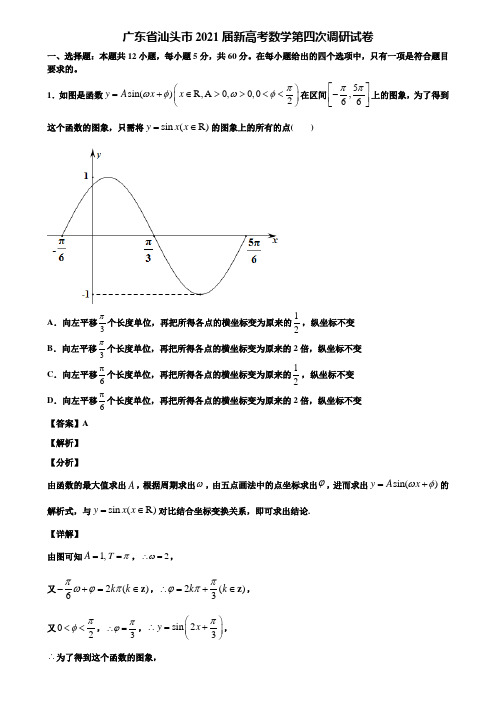
广东省汕头市2021届新高考数学第四次调研试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．如图是函数sin()R,A 0,0,02y A x x πωφωφ⎛⎫=+∈>><<⎪⎝⎭在区间5,66ππ⎡⎤-⎢⎥⎣⎦上的图象，为了得到这个函数的图象，只需将sin (R)y x x =∈的图象上的所有的点( )A ．向左平移3π个长度单位，再把所得各点的横坐标变为原来的12，纵坐标不变 B ．向左平移3π个长度单位，再把所得各点的横坐标变为原来的2倍，纵坐标不变C ．向左平移6π个长度单位，再把所得各点的横坐标变为原来的12，纵坐标不变 D ．向左平移6π个长度单位，再把所得各点的横坐标变为原来的2倍，纵坐标不变 【答案】A 【解析】 【分析】由函数的最大值求出A ，根据周期求出ω，由五点画法中的点坐标求出ϕ，进而求出sin()y A x ωφ=+的解析式，与sin (R)y x x =∈对比结合坐标变换关系，即可求出结论. 【详解】由图可知1,A =T π=，2ω∴=，又2()6k k πωϕπ-+=∈z ，2()3k k πϕπ∴=+∈z ，又02πφ<<，3πϕ∴=，sin 23y x π⎛⎫∴=+ ⎪⎝⎭，∴为了得到这个函数的图象，只需将sin ()y x x R =∈的图象上的所有向左平移3π个长度单位， 得到sin 3y x π⎛⎫=+⎪⎝⎭的图象， 再将sin 3y x π⎛⎫=+ ⎪⎝⎭的图象上各点的横坐标变为原来的12（纵坐标不变）即可.故选:A 【点睛】本题考查函数的图象求解析式，考查函数图象间的变换关系，属于中档题.2．执行下面的程序框图，如果输入1995m =，228n =，则计算机输出的数是（ ）A ．58B ．57C ．56D ．55【答案】B 【解析】 【分析】先明确该程序框图的功能是计算两个数的最大公约数，再利用辗转相除法计算即可. 【详解】本程序框图的功能是计算m ，n 中的最大公约数，所以199********=⨯+，228171157=⨯+，1713570=⨯+，故当输入1995m =，228n =，则计算机输出的数是57. 故选：B. 【点睛】本题考查程序框图的功能，做此类题一定要注意明确程序框图的功能是什么，本题是一道基础题. 3．从装有除颜色外完全相同的3个白球和m 个黑球的布袋中随机摸取一球，有放回的摸取5次，设摸得白球数为X ，已知()3E X =，则()(D X = ) A ．85B ．65C ．45D ．25【答案】B 【解析】由题意知，3~(5,)3X B m +，由3533EX m =⨯=+，知3~(5,)5X B ，由此能求出()D X ． 【详解】由题意知，3~(5,)3X B m +， 3533EX m ∴=⨯=+，解得2m =， 3~(5,)5X B ∴，336()5(1)555D X ∴=⨯⨯-=．故选：B ． 【点睛】本题考查离散型随机变量的方差的求法，解题时要认真审题，仔细解答，注意二项分布的灵活运用．4．已知双曲线C ：22221x y a b-=（0a >，0b >）的右焦点与圆M ：22(2)5x y -+=的圆心重合，且圆M 被双曲线的一条渐近线截得的弦长为 ）A ．2B ．CD ．3【答案】A 【解析】 【分析】由已知，圆心M=222c a b ==+，解方程即可.【详解】由已知，2c =，渐近线方程为0bx ay ±=，因为圆M 被双曲线的一条渐近线截得的弦长为，所以圆心M =2bb c===，故1a =， 所以离心率为2ce a==. 故选：A. 【点睛】本题考查双曲线离心率的问题，涉及到直线与圆的位置关系，考查学生的运算能力，是一道容易题. 5．已知命题p ：若1a >，1b c >>，则log log b c a a <；命题q ：()00,x ∃+∞，使得0302log x x <”，则以下命题为真命题的是（ ） A ．p q ∧B ．()p q ∧⌝C ．()p q ⌝∧D ．()()p q ⌝∧⌝【解析】 【分析】先判断命题,p q 的真假,进而根据复合命题真假的真值表,即可得答案. 【详解】1log logb a a b =，1log log c a a c =，因为1a >，1b c >>，所以0log log a a c b <<，所以11log log a a c b>，即命题p 为真命题；画出函数2xy =和3log y x =图象，知命题q 为假命题,所以()p q ∧⌝为真.故选:B.【点睛】本题考查真假命题的概念,以及真值表的应用,解题的关键是判断出命题,p q 的真假,难度较易.6．五名志愿者到三个不同的单位去进行帮扶，每个单位至少一人，则甲、乙两人不在同一个单位的概率为（ ） A ．25B ．1325C ．35D ．1925【答案】D 【解析】 【分析】三个单位的人数可能为2，2，1或3，1，1，求出甲、乙两人在同一个单位的概率，利用互为对立事件的概率和为1即可解决. 【详解】由题意，三个单位的人数可能为2，2，1或3，1，1；基本事件总数有2231335352332222C C C C A A A A + 150=种，若为第一种情况，且甲、乙两人在同一个单位，共有122332C C A 种情况；若为第二种情况，且甲、乙两人在同一个单位，共有112332C C A 种，故甲、乙两人在同一个单位的概率 为36615025=，故甲、乙两人不在同一个单位的概率为61912525P =-=. 故选：D.本题考查古典概型的概率公式的计算，涉及到排列与组合的应用，在正面情况较多时，可以先求其对立事件，即甲、乙两人在同一个单位的概率，本题有一定难度.7．记M 的最大值和最小值分别为max M 和min M ．若平面向量a r 、b r 、c r，满足()22a b a b c a b c ==⋅=⋅+-=r r r r r r r r，则（ ）A ．max372a c +-=r r B ．max372a c -+=r r C ．min 372a c+-=r r D ．min372a c-+=r r 【答案】A 【解析】 【分析】设θ为a r 、b r 的夹角，根据题意求得3πθ=，然后建立平面直角坐标系，设()2,0a OA ==r u u u r ，()1,3b OB ==r u u u r ，(),c OC x y ==r u u u r，根据平面向量数量积的坐标运算得出点C 的轨迹方程，将a c -r r 和a c +r r转化为圆上的点到定点距离，利用数形结合思想可得出结果.【详解】由已知可得cos 2a b a b θ⋅=⋅=r r r r ，则1cos =2θ，0θπ≤≤Q ，3πθ∴=，建立平面直角坐标系，设()2,0a OA ==r u u u r ，()1,3b OB ==r u u u r ，(),c OC x y ==r u u u r，由()22c a b c ⋅+-=r r r r，可得()(),42322x y x y ⋅-=，即2242322x x y -+-=，化简得点C 的轨迹方程为()223314x y ⎛-+= ⎝⎭，则()222a c x y -=-+r r ，则a c -r r 转化为圆()22314x y ⎛-+-= ⎝⎭上的点与点()2,0的距离，maxa c ==∴-r r，min a c ==-r r ，a c +=r ra c +r r 转化为圆()223124x y ⎛⎫-+-= ⎪ ⎪⎝⎭上的点与点()2,0-的距离，max22a c==∴+r r，m 22im a c ==+r r . 故选：A. 【点睛】本题考查和向量与差向量模最值的求解，将向量坐标化，将问题转化为圆上的点到定点距离的最值问题是解答的关键，考查化归与转化思想与数形结合思想的应用，属于中等题. 8．函数cos 220,2y x x x π⎛⎫⎡⎤=∈ ⎪⎢⎥⎣⎦⎝⎭的单调递增区间是（ ） A ．06,π⎡⎤⎢⎥⎣⎦B ．0,3π⎡⎤⎢⎥⎣⎦ C ．,62ππ⎡⎤⎢⎥⎣⎦D ．,32ππ⎡⎤⎢⎥⎣⎦【答案】D 【解析】 【分析】利用辅助角公式,化简函数的解析式,再根据正弦函数的单调性,并采用整体法,可得结果.【详解】因为cos 22y x x =2sin(2)2sin(2)66x x ππ=-=--，由3222,262k x k k πππππ+-+∈Z ≤≤，解得5,36k x k k Z ππππ+≤≤+∈，即函数的增区间为5[,],36k k k ππππ++∈Z ，所以当0k =时，增区间的一个子集为[,]32ππ. 故选D. 【点睛】本题考查了辅助角公式,考查正弦型函数的单调递增区间,重点在于把握正弦函数的单调性，同时对于整体法的应用,使问题化繁为简,难度较易.9．设x ，y 满足24122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩，则z x y =+的取值范围是（ ）A ．[]5,3-B ．[]2,3C ．[)2,+∞D ．(],3-∞【答案】C 【解析】 【分析】首先绘制出可行域，再绘制出目标函数，根据可行域范围求出目标函数中z 的取值范围. 【详解】由题知x ，y 满足24122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩，可行域如下图所示，可知目标函数在点()2,0A 处取得最小值， 故目标函数的最小值为2z x y =+=， 故z x y =+的取值范围是[)2,+∞. 故选：D. 【点睛】本题主要考查了线性规划中目标函数的取值范围的问题，属于基础题.10．根据最小二乘法由一组样本点(),i i x y （其中1,2,,300i =L ），求得的回归方程是ˆˆˆybx a =+，则下列说法正确的是( )A ．至少有一个样本点落在回归直线ˆˆˆybx a =+上 B ．若所有样本点都在回归直线ˆˆˆybx a =+上，则变量同的相关系数为1 C ．对所有的解释变量i x （1,2,,300i =L ），ˆˆibx a +的值一定与i y 有误差D ．若回归直线ˆˆˆy bx a =+的斜率ˆ0b>，则变量x 与y 正相关 【答案】D 【解析】 【分析】对每一个选项逐一分析判断得解. 【详解】回归直线必过样本数据中心点，但样本点可能全部不在回归直线上﹐故A 错误；所有样本点都在回归直线ˆˆˆybx a =+上，则变量间的相关系数为1±，故B 错误； 若所有的样本点都在回归直线ˆˆˆy bx a =+上，则ˆˆbx a +的值与y i 相等，故C 错误；相关系数r 与ˆb符号相同，若回归直线ˆˆˆy bx a =+的斜率ˆ0b >，则0r >，样本点分布应从左到右是上升的，则变量x 与y 正相关，故D 正确． 故选D ． 【点睛】本题主要考查线性回归方程的性质，意在考查学生对该知识的理解掌握水平和分析推理能力.11．已知(1,2)a =r ，(,3)b m m =+r ，(2,1)c m =--r ，若//a b r r ，则b c ⋅=r r（ ）A ．7-B ．3-C ．3D ．7【答案】B 【解析】 【分析】由平行求出参数m ，再由数量积的坐标运算计算． 【详解】由//a b r r，得2(3)0m m -+=，则3m =，(3,6)b =r ，(1,1)c =-r ，所以363b c ⋅=-=-r r．故选：B ． 【点睛】本题考查向量平行的坐标表示，考查数量积的坐标运算，掌握向量数量积的坐标运算是解题关键．12．在平行六面体1111ABCD A B C D -中，M 为11A C 与11B D 的交点，若,AB a AD b ==u u u r r u u u r r ,1AA c =u u u r r ，则与BM u u u u r相等的向量是（ ）A ．1122a b c ++r r rB ．1122a b c --+r r rC ．1122a b c -+r r rD ．1122-++r r ra b c【答案】D 【解析】 【分析】根据空间向量的线性运算，用,,a b c r r r 作基底表示BM u u u u r即可得解.【详解】根据空间向量的线性运算可知11BM BB B M =+u u u u r u u u r u u u u r11112AA B D =+u u u r u u u u r()1111112AA B A A D =++u u u r u u u u r u u u u r()112AA AB AD =+-+u u u r u u u r u u u r因为,AB a AD b ==u u u r r u u u r r ,1AA c =u u ur r ，则()112AA AB AD +-+u u u r u u u r u u u r1122a b c =-++r r r即1122BM a b c =-++u u u u r r r r ，故选：D. 【点睛】本题考查了空间向量的线性运算，用基底表示向量，属于基础题. 二、填空题：本题共4小题，每小题5分，共20分。

广东省汕头市2019版高考数学四模试卷（理科）（I）卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）复数，则a的取值情况是（）A . a>2或a<-1B . a=3C . a=1或a=3D . -1<a<22. （2分）(2019·随州模拟) 已知全集，集合，，则集合（）A .B .C .D .3. （2分） (2015高一上·腾冲期末) 已知函数f（x）= 则f（f（））=（）A . ﹣2B . -C . 0D .4. （2分）已知某运动员每次投篮命中的概率都为40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器算出0到9之间取整数值的随机数，用1，2，3，4表示命中，用5，6，，7，8，9，0表示不命中；再以每三个随机数为一组，代表三次投篮的结果。

经随机模拟产生了20组随机数：907 966 191 925 271 932 812 458 569 6 83431 257 393 027 556 488 730 113 537 9 89据此估计，该运动员三次投篮恰有两次命中的概率为（）A . 0.35B . 0.30C . 0.25D . 0.205. （2分）执行如图所示的程序框图，如果输入P=153，Q=63，则输出的P的值是（）A . 2B . 3C . 9D . 276. （2分）(2017·大理模拟) 将函数f（x）=sin3x+cos3x的图象沿x轴向左平移∅个单位后，得到一个偶函数的图象，则∅的一个可能取值为（）A .B .C .D . 07. （2分）一个空间几何体的三视图如图所示，则该几何体的的体积为A .B .C .D .8. （2分）(2017·榆林模拟) 若等式x4+4x3+3x2+2x+1=（x+1）4+a（x+1）3+b（x+1）2+c（x+1）+d恒成立，则（a，b，c，d）等于（）A . （1，2，3，﹣1）B . （2，3，4，﹣1）C . （0，﹣1，2，﹣2）D . （0，﹣3，4，﹣1）9. （2分） (2018高二下·黄陵期末) 设两个正态分布N(μ1 ，)(σ1＞0)和N(μ2 ，)(σ2＞0)的密度函数图象如图所示，则有（）A . μ1＜μ2 ，σ1＜σ2B . μ1＜μ2 ，σ1＞σ2C . μ1＞μ2 ，σ1＜σ2D . μ1＞μ2 ，σ1＞σ210. （2分）(2016·兰州模拟) 三棱椎S﹣ABC中，SA⊥面ABC，△ABC为等边三角形，SA=2，AB=3，则三棱锥S﹣ABC的外接球的表面积为（）A . 4πB . 8πC . 16πD . 64π11. （2分）抛物线的准线与双曲线的右准线重合,则m的值是（）A . 16B . 4C . -8D . -1212. （2分）等差数列中的 a1 ， a4027 是函数的极值点，则（）A . 3B . 2C . 4D . 5二、填空题 (共4题；共4分)13. （1分） (2016高一下·苏州期中) 设变量x，y满足约束条件，则z=x﹣3y的最小值是________．14. （1分） (2016高一下·甘谷期中) 若 =（λ，4）， =（﹣3，5），且与的夹角为钝角，则λ的取值范围是________．15. （1分）(2016·天津模拟) 在△ABC中，A=60°，|AB|=2，且△ABC的面积为，则|BC|=________．16. （1分） (2016高二下·清流期中) 在直角坐标系中，定义两点P（x1 ， y1），Q（x2 ， y2）之间的“直角距离”为d（P，Q）=|x1﹣x2|+|y1﹣y2|．现有下列命题：①已知P（1，3），Q（sin2α，cos2α）（α∈R），则d（P，Q）为定值；②原点O到直线x﹣y+1=0上任一点P的直角距离d（O，P）的最小值为；③若|PQ|表示P、Q两点间的距离，那么|PQ|≥ d（P，Q）；④设A（x，y）且x∈Z，y∈Z，若点A是在过P（1，3）与Q（5，7）的直线上，且点A到点P与Q的“直角距离”之和等于8，那么满足条件的点A只有5个．其中的真命题是________．（写出所有真命题的序号）三、解答题 (共7题；共50分)17. （10分） (2016高一下·天津期末) 已知数列{an}的前n项和为Sn ，满足3an﹣2Sn﹣1=0．（1）求数列{an}的通项公式；（2） bn= ，数列{bn}的前n项和为Tn，求f（n）= （n∈N+）的最大值．18. （5分）某个体户计划经销A、B两种商品，据调查统计，当投资额为x（x≥0）万元时，在经销A、B商品中所获得的收益分别为f（x）万元与g（x）万元、其中f（x）=a（x﹣1）+2（a＞0）；g（x）=6ln（x+b），（b ＞0）已知投资额为零时，收益为零．（1）试求出a、b的值；（2）如果该个体户准备投入5万元经营这两种商品，请你帮他制定一个资金投入方案，使他能获得最大收益，并求出其收入的最大值．（精确到0.1，参考数据：ln3≈1.10）．19. （10分）如图所示，凸五面体ABCED中，DA⊥平面ABC，EC⊥平面ABC，AC=AD=AB=1，BC= ，F为BE 的中点．（1）若CE=2，求证：①DF∥平面ABC；②平面BDE⊥平面BCE；（2）若二面角E﹣AB﹣C为45°，求直线AE与平面BCE所成角．20. （10分）(2017·镇江模拟) 在平面直角坐标系xOy中，已知椭圆 =l （a＞b＞0）的焦距为2，离心率为，椭圆的右顶点为A．（1）求该椭圆的方程：（2）过点D（，﹣）作直线PQ交椭圆于两个不同点P，Q，求证：直线AP，AQ的斜率之和为定值．21. （5分） (2016高三上·红桥期中) 已知函数f（x）=lnx﹣a（x﹣1），其中a＞0．（Ⅰ）若函数f（x）在（0，+∞）上有极大值0，求a的值；（提示：当且仅当x=1时，lnx=x﹣1）；（Ⅱ）令F（x）=f（x）+a（x﹣1）+ （0＜x≤3），其图象上任意一点P（x0 ， y0）处切线的斜率k≤恒成立，求实数a的取值范围；（Ⅲ）讨论并求出函数f（x）在区间上的最大值．22. （5分）在直角坐标系xOy中，半圆C的参数方程为（φ为参数，0≤φ≤π），以O为极点，x轴的非负半轴为极轴建立极坐标系．（Ⅰ）求C的极坐标方程；（Ⅱ）直线l的极坐标方程是，射线OM：θ= 与半圆C的交点为O、P，与直线l 的交点为Q，求线段PQ的长．23. （5分） (2016高二下·黄骅期中) 设a，b均大于0，且 + =1．求证：对于每个n∈N* ，都有（a+b）n﹣（an+bn）≥22n﹣2n+1 ．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题；共50分)17-1、17-2、18-1、19-1、19-2、20-1、20-2、21-1、22-1、23-1、。

广东省汕头市高考数学四模试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题；共15分)1. （1分） (2016高二上·上海期中) 已知集合A={﹣1，1，2，4}，B={﹣1，0，2}，则A∪B=________．2. （1分）若复数z满足z2﹣z+1=0，则|z|=________3. （1分） (2016高二下·金堂开学考) 根据如图所示的算法语句，当输入的x为50时，输出的y的值为________．4. （2分）某次歌手大赛中，有10名评委．茎叶图（如图所示）是10名评委给甲、乙两位选手评定的成绩，则选手甲成绩的众数是________ ，选手乙的中位数是________5. （1分）(2014·天津理) 在△ABC中，内角A，B，C所对的边分别是a，b，c，已知b﹣c= a，2sinB=3sinC，则cosA的值为________．6. （1分）菲特台风重创宁波，志愿者纷纷前往灾区救援．现从四男三女共7名志愿者中任选2名（每名志愿者被选中的机会相等），则2名都是女志愿者的概率为________．7. （1分） (2016高二上·桓台期中) 双曲线与椭圆4x2+y2=64有公共焦点，它们的离心率互为倒数，则双曲线方程为________．8. （1分） (2019高一上·三亚期中) 若函数满足，则的解析式是________.9. （1分） (2019高二上·遵义期中) 已知矩形的长，宽，将其沿对角线折起，得到四面体，如图所示：则四面体体积的最大值为________.10. （1分） (2017高三上·荆州期末) 正△ABC中，在方向上的投影为﹣1，且，则=________．11. （1分） (2015高三上·孟津期末) 定义max{a，b}表示实数a，b中的较大的数．已知数列{an}满足a1=a（a＞0），a2=1，an+2= （n∈N*），若a2015=4a，记数列{an}的前n项和为Sn ，则S2016的值为________ ．12. （1分） (2016高一下·随州期末) 若正数x，y满足x+3y=5xy，则3x+4y的最小值是________．13. （1分） (2016高一下·威海期末) 已知点P（﹣1，4）及圆C：（x﹣2）2+（y﹣3）2=1．则下列判断正确的序号为________．①点P在圆C内部；②过点P做直线l，若l将圆C平分，则l的方程为x+3y﹣11=0；③过点P做直线l与圆C相切，则l的方程为y﹣4=0或3x+4y﹣13=0；④一束光线从点P出发，经x轴反射到圆C上的最短路程为．14. （1分） (2017高一上·泰州月考) 已知函数的定义域为，实数的取值范围是________．二、解答题 (共6题；共55分)15. （10分） (2016高三上·新津期中) 已知函数f（x）=sin2xcos2x+sin22x﹣．（1）求函数f（x）的最小正周期及对称中心；（2）在△ABC中，角B为钝角，角A，B，C的对边分别为a、b、c，f（）= ，且sinC= sinA，S△ABC=4，求c的值．16. （15分） (2018高二上·成都月考) 如图，在三棱柱中，底面为正三角形，侧棱底面．已知是的中点，．（1）求证：平面平面；（2）求证：A1C∥平面；（3）求三棱锥的体积．17. （5分） (2016高二下·上饶期中) 在同一平面直角坐标系中，求满足下列图形变换的伸缩变换：曲线4x2+9y2=36变成曲线x′2+y′2=1．18. （10分） (2017高二上·哈尔滨月考) 已知椭圆的离心率为，椭圆短轴的一个端点与两个焦点构成的三角形的面积为 .（1）求椭圆的方程式；（2）已知动直线与椭圆相交于两点.①若线段中点的横坐标为，求斜率的值；②已知点，求证：为定值.19. （10分）(2018·榆林模拟) 已知函数，其中为自然对数底数.（1）求函数的单调区间；（2）已知，若函数对任意都成立，求的最大值.20. （5分） (2016高二上·会宁期中) 已知数列{an}的前n项和为Sn ， a1=1，Sn+1=4an+1，设bn=an+1﹣2an ．证明：数列{bn}是等比数列．参考答案一、填空题 (共14题；共15分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题；共55分)15-1、15-2、16-1、16-2、16-3、17-1、18-1、18-2、19-1、19-2、20-1、。

广东省汕头市棉城中学高三数学理模拟试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 等比数列中，，=4，函数，则（）A．B．C．D．参考答案：C2. 若直角坐标平面内的两点p、Q满足条件：①p、Q都在函数y=f（x）的图象上；②p、Q关于原点对称，则称点对[P，Q]是函数y=f（x）的一对“友好点对”（注：点对[P，Q]与[Q，P]看作同一对“友好点对”）．已知函数，则此函数的“友好点对”有（）对．A．0 B．1 C．2 D．3参考答案：C3. ------------------------------------（）A.0B.1C.2D. 4参考答案：C4. 已知f(x)，g(x)分别是定义在R上的偶函数和奇函数，且f(x)-g(x)=x3+2-x，则f(2)+g(2)=A.4B.-4C.2D.-2参考答案：B5. 若a R，则a=2是（a-1）（a-2）=0的A.充分而不必要条件 B必要而不充分条件C.充要条件 C.既不充分又不必要条件参考答案：A本题主要考查充分条件与必要条件的判断，难度较小。

若a=2时（a－1）(a－2) = 0成立。

充分性成立。

若（a－1）(a－2) = 0 时，a=1或a=2.必要性不成立6. 不等式的解集是（）A、（）B、（）C、（）（）D、（）（）参考答案：C7. 如图所示，两个非共线向量，的夹角为θ，M、N分别为OA与OB的中点，点C在直线MN 上，且=x+y（x，y∈R），则x2+y2的最小值为（）A．B．C．D．参考答案：B【考点】点到直线的距离公式；平面向量坐标表示的应用．【分析】法一：特殊值法，当θ=90°，||=||=1时，建立直角坐标系，得x+y=，所以x2+y2的最小值为原点到直线的距离的平方；解法二：因为点C、M、N共线，所以，有λ+μ=1，由M、N分别为OA与OB的中点，可得x+y=，下同法一【解答】解法一：特殊值法，当θ=90°，||=||=1时，建立直角坐标系，∴=x+y得x+y=，所以x2+y2的最小值为原点到直线的距离的平方；解法二：因为点C、M、N共线，所以，有λ+μ=1，又因为M、N分别为OA与OB的中点，所以=∴x+y=原题转化为：当x时，求x2+y2的最小值问题，∵y=∴x2+y2==结合二次函数的性质可知，当x=时，取得最小值为故选B8. 下列函数中，在（﹣1，1）内有零点且单调递增的是（）A．y=log2x B．y=2x﹣1 C．y=x2﹣2 D．y=﹣x3参考答案：B【考点】函数零点的判定定理；函数单调性的判断与证明．【专题】函数的性质及应用．【分析】根据解析式判断单调性，再根据零点存在性定理判断即可得出答案．【解答】解：y=log x在（﹣1，1）有没有意义的情况，故A不对，y=x2﹣1在（﹣1，0）单调递减，故C不对，y=﹣x3在（﹣1，1）单调递减，故D不对，故A，C，D都不对，∵y=2x﹣1，单调递增，f（﹣1）＜0，f（1）＞0，∴在（﹣1，1）内存在零点故选：B【点评】本特纳考查了函数的单调性，零点的判断，函数解析式较简单，属于容易题．9. 设m,n为非零向量，则“存在负数，使得”是“”的（A）充分而不必要条件（B）必要而不充分条件（C）充分必要条件（D）既不充分也不必要条件参考答案：A若，使，即两向量反向，夹角是180°，那么，反过来，若，那么两向量的夹角为（90°，180°]，并不一定反向，即不一定存在负数，使得，所以是充分不必要条件，故选A.10. 执行如图的程序框图，则输出的值为、、、、参考答案：D由图知本程序的功能是执行此处注意程序结束时，由余弦函数和诱导公式易得：，周期为，，故选二、 填空题:本大题共7小题,每小题4分,共28分11. 设集合，，若，则实数取值范围是.参考答案： 12. 设向量，，若，则参考答案：略13. 在直角△ABC 中，∠C=90°，∠A=30°，BC=1，D 为斜边AB 的中点，则= ．参考答案：﹣1【考点】平面向量数量积的运算． 【专题】计算题．【分析】根据含有30°角的直角三角形的性质，得到AB 与CD 的长度，求出两个向量的夹角是120°，利用向量的数量积公式写出表示式，得到结果． 【解答】解：：∵∠C=90°，∠A=30°，BC=1， ∴AB=2．∵D 为斜边AB 的中点，∴CD=AB=1，∠CDA=180°﹣30°﹣30°=120°． ∴=2×1×cos120°=﹣1，故答案为：﹣1．【点评】本题考查平面向量的数量积的运算，考查含有30°角的直角三角形的性质，是一个基础题．14.在的二项展开式中常数项的值等于 （用数字作答）。

广东省汕头市2024年数学（高考）部编版真题(培优卷)模拟试卷一、单项选择题（本题包含8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题已知集合，，则（）A．B．C．或D．第(2)题设函数的导数为，且，，，则当时，A．有极大值，无极小值B．无极大值，有极小值C．既有极大值又有极小值D．既无极大值又无极小值第(3)题如图，在三棱锥中，，点在平面内，过作于，当与面所成最大角的正弦值是时，与平面所成角的余弦值是（）A．B．C．D．第(4)题下列不等式不正确的是（）A．B．C．D．第(5)题将函数的图像向左平移个单位长度后，得到的图像，若函数在上单调递减，则正数的最大值为A．B．1C．D．第(6)题已知，则（）A．B．C．D．第(7)题在正整数数列中，由1开始依次按如下规则，将某些整数染成红色．先染1；再染3个偶数2，4，6；再染6后面最邻近的5个连续奇数7，9，11，13，15；再染15后面最邻近的7个连续偶数16，18，20，22，24，26，28；再染此后最邻近的9个连续奇数29，31，…，45；按此规则一直染下去，得到一红色子数列：1，2，4，6，7，9，11，13，15，16，……，则在这个红色子数列中，由1开始的第2019个数是（）A．3972B．3974C．3991D．3993第(8)题已知圆与轴相切，则（）A．B．C．2D．3二、多项选择题（本题包含3小题，每小题6分，共18分。

在每小题给出的四个选项中，至少有两个选项正确。

全部选对的得6分，选对但不全的得3分，有选错或不答的得0分） (共3题)第(1)题e是自然对数的底数，，已知，则下列结论一定正确的是（）A．若，则B．若，则C．若，则D．若，则第(2)题已知抛物线的焦点为F，准线与x轴的交点为P，过点F的直线与抛物线交于点M，N，过点P的直线与抛物线交于点A，B，则（）A．B．C．D．第(3)题已知抛物线，F为抛物线C的焦点，下列说法正确的是（）A．若抛物线C上一点P到焦点F的距离是4，则P的坐标为、B．抛物线C在点处的切线方程为C．一个顶点在原点O的正三角形与抛物线相交于A、B两点，的周长为D．点H为抛物线C的上任意一点，点，，当t取最大值时，的面积为2三、填空（本题包含3个小题，每小题5分，共15分。

广东省汕头市2024高三冲刺（高考数学）统编版（五四制）模拟(综合卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题若，则的最小值是（）A．B．2C．D．第(2)题在直角坐标系中，锐角的顶点为坐标原点，始边与轴的非负半轴重合，终边与单位圆交于点.若，则（）A．B．C．D．第(3)题若函数的图象在点处的切线与直线平行，则（）A．B．C．-3D．3第(4)题已知函数则函数的图象大致是（）A．B．C．D．第(5)题函数的图象是A．B．C．D．第(6)题如图框图，当x1=6，x2=9，p=8.5时，x3等于A．7B．8C．10D．11第(7)题在等差数列中，，是方程的两个根，则的前23项的和为（）A．B．C．92D．184第(8)题为落实立德树人的根本任务，践行五育并举，某学校开设三门劳动教育校本课程，现有甲、乙、丙、丁、戊五位同学报名参加该校劳动教育校本课程的学习，每位同学仅报一门，每门至少有一位同学参加，则不同的报名方法有（）A．60种B．150种C．180种D．300种二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题如图，正八面体棱长为2．下列说法正确的是（）A．平面B．当P为棱EC的中点时，正八面体表面从F点到P点的最短距离为C．若点P为棱EB上的动点，则三棱锥的体积为定值D．以正八面体中心为球心，1为半径作球，球被正八面体各个面所截得的交线总长度为第(2)题已知点O为△ABC内的一点，D，E分别是BC，AC的中点，则（）A．若O为AD中点，则B．若O为AD中点，则C．若O为△ABC的重心，则D．若O为△ABC的外心，且BC＝4，则第(3)题在正四棱柱中，已知，，则下列说法正确的有（）A．异面直线与的距离为B．直线与平面所成的角的余弦值为C．若该正四棱柱的各顶点都在球O的表面上，则球O的表面积为D．以A为球心，半径为2的球面与该正四棱柱表面的交线的总长度为三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题已知函数的定义域为，且，，则______．第(2)题已知数列的通项公式为，数列是首项为，公比为的等比数列，若，其中，则公比的取值范围是_________．第(3)题已知为奇函数，当时，，则_________.四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题记的内角的对边分别为，分别以为边长的三个正三角形的面积依次为，已知.(1)求的面积；(2)若，求.第(2)题在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知．(1)求角A 的大小；(2)若，求边上的中线长度的最小值．第(3)题十九大提出：坚决打赢脱贫攻坚战，做到精准扶贫，某帮扶单位为帮助定点扶贫村真正脱贫，坚持扶贫同扶智相结合，帮助贫困村种植脐橙，并利用互联网电商进行销售，为了提高销量，现从该村的脐橙树上随机摘下100个脐橙进行测重，其质量（单位克）分布在区间［200，500内，由统计的质量数据作出频率分布直方图如图所示.（1）按分层抽样的方法从质量在，的脐橙中随机抽取5个，再从这5个脐橙中随机抽取2个，求这2个脐橙质量至少有一个不小于400克的概率；（2）以各组数据的中间数值代替这组数据的平均值，以频率代替概率，已知该村的脐橙种植地上大约还有100000个脐橙待出售，某电商提出两种收购方案：A .所有脐橙均以7元/千克收购；B .低于350克的脐橙以2元/个收购，其余的以3元/个收购.请你通过计算为该村选择收益较好的方案.第(4)题已知函数.(1)求函数的最小值；(2)若为正实数，且，求的最小值.第(5)题已知函数．(1)求的导数；(2)求曲线在点处的切线方程，并求出切线与坐标轴所围三角形的面积．。