解析:过点B作BC⊥AD于C,则△ ABC为 直角三角形,由图能够计算出AC,BC 长度,在直角三角形ABC中,已知AC,BC, 依据勾股定理即可计算AB. 解:如图所表示,过点B作BC⊥AD于C, 由题知AC=4-2+0.5=2.5(m), BC=4.5+1.5=6(m),在直角三角形ABC中,AB为斜边, 则AB= AC 2 BC 2 13 m.
第12页
6.如图所表示,水池中有水,水面是一个边长为10尺 正方形,水池正中央有一根芦苇,它高出水面1尺,假如把 这根芦苇拉向水池一边,那么它顶端恰好抵达池边水面. 水深度和这根芦苇长度分别是多少?
解析:找到题中直角三角形,依据勾股定了解答.
解:设水深为x尺,则芦苇长度为(x+1)尺,
依据勾股定理得x2+
第11页
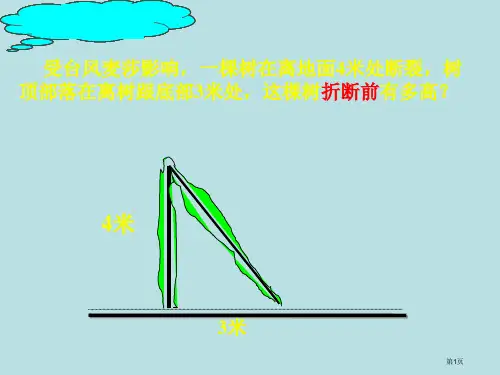
5.如图所表示,有一个儿童拿着一根竹竿要经过一个长 方形门,假如把竹竿竖放就比门高出1尺,斜放就恰好等 于门对角线,已知门宽4尺,求竹竿高与门高.
解析:依据题中所给条件可知竹竿斜放时, 可与门宽和高组成直角三角形,利用勾股
定理可求出门高.
解:设门高为x尺,则竹竿高为(x+1)尺, 依据勾股定理可得x2+42=(x+1)2, 即x2+16=x2+2x+1, 解得x=7.5,7.5+1=8.5(尺). 答:门高为7.5尺,竹竿高为8.5尺.
解:∵ △ ABC是直角三角形, ∴AB2=AC2+BC2. ∵AC=50-15-26=9(mm), BC=40-18-10=12(mm),
AB AC2 BC2 92 122 15mm
答:孔中心A和B间距离是15 mm.
第5页
知识拓展
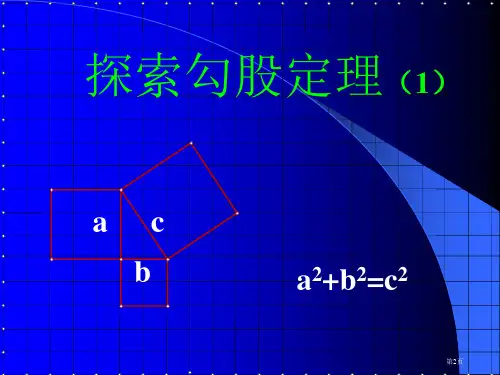
(1)处理两点距离问题:正确画出图形,已知直角 三角形两边长,利用勾股定理求第三边长.