人教版初中数学九年级上册《22.1二次函数的图像和性质》同步练习(含答案解析)

22.1二次函数的图像和性质同步练习(一)一、单项选择题（本大题共有15小题，每小题3分，共45分）1、抛物线的顶点坐标是（）A.B.C.D.2、某广场有一喷水池，水从地面喷出，如图，以水平地面为轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线（单位：米）的一部分，则水喷出的最大高度是（）A.B.C. 2mD. 1m3、已知是的二次函数，与的对应值如下表：其表达式为（）.A.B.C.D.4、抛物线与轴的交点坐标是（）.A.B.C.D.5、在抛物线上的一个点是（）.A.B.C.D.6、一个直角三角形的两条直角边长的和为，其中一直角边长为，面积为，则与的函数的关系式是（）A.B.C.D.7、如图，在矩形中，，，，，则四边形的面积的最大值是（）A.B.C.8、如图，正方形的边长为，以正方形的顶点、、、为圆心画四个全等的圆．若圆的半径为，且，阴影部分的面积为，则能反映与之间函数关系的大致图象是（）A.B.C.D.9、若不等式对恒成立，则的取值范围是（）A.B.C.10、小颖用计算器探索方程的根，作出如图所示的图象，并求得一个近似根，则方程的另一个近似根（精确到）为（）A.B.C.D.11、如图，以为顶点的二次函数的图象与轴负半轴交于点，则一元二次方程的正数解的范围是（）A.B.C.D.12、二次函数的图象如图所示，对称轴是直线，则下列四个结论错误的是（）A.B.C.D.13、二次函数的图象如图所示，则下列说法不正确的是（）A.B.C.D.14、抛物线的顶点坐标是（）A.B.C.D.15、某工厂一种产品的年产量是件，如果每一年都比上一年的产品增加倍，两年后产品与的函数关系是（）A.B.C.D.二、填空题（本大题共有5小题，每小题5分，共25分）16、二次函数的最小值为．17、抛物线的对称轴是直线．18、若抛物线经过点，则．19、若抛物线的顶点在轴的下方，则的取值范围是____________20、抛物线经过点和两点，则．（分数写成a/b形式）三、解答题（本大题共有3小题，每小题10分，共30分）21、求抛物线的顶点和对称轴．22、已知二次函数，当，求函数？；当？时，函数的值为.23、已知二次函数的图象如图所示，请结合图象，判断下列各式的符号．①；②；③；④．22.1二次函数同步练习(一) 答案部分一、单项选择题（本大题共有15小题，每小题3分，共45分）1、抛物线的顶点坐标是（）A.B.C.D.【答案】C【解析】解：，顶点坐标为，故正确答案为：．2、某广场有一喷水池，水从地面喷出，如图，以水平地面为轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线（单位：米）的一部分，则水喷出的最大高度是（）A.B.C. 2mD. 1m【答案】A【解析】解：由题意可得水喷出的最大高度为故正确答案是3、已知是的二次函数，与的对应值如下表：其表达式为（）.A.B.C.D.【答案】C【解析】解：二次函数经过点，抛物线的对称轴为，顶点坐标为，故设解析式为，将点代入解析式，得：，，，故正确答案是.4、抛物线与轴的交点坐标是（）.A.B.C.D.【答案】D【解析】解：令，，即与轴的交点坐标为，故正确答案是：.5、在抛物线上的一个点是（）.A.B.C.D.【答案】C【解析】解：当时，,故点不在抛物线上，当时，,故点不在抛物线上，当时，,故点在抛物线上，当时，,故点不在抛物线上，故正确答案是：.6、一个直角三角形的两条直角边长的和为，其中一直角边长为，面积为，则与的函数的关系式是（）A.B.C.D.【答案】C【解析】解：根据一直角边长为，则另一条直角边为，根据题意得出：．7、如图，在矩形中，，，，，则四边形的面积的最大值是（）A.B.C.D.【答案】B【解析】解：设，则，，设四边形的面积为，依题意，得，即：，，抛物线开口向下，函数有最大值为．8、如图，正方形的边长为，以正方形的顶点、、、为圆心画四个全等的圆．若圆的半径为，且，阴影部分的面积为，则能反映与之间函数关系的大致图象是（）A.B.C.D.【答案】D【解析】解：易得阴影部分的面积为个圆的面积，故由题意得，属于二次函数，根据自变量的取值为，有实际意义的函数在第一象限，故正确的选项应为9、若不等式对恒成立，则的取值范围是（）A.B.C.D.【答案】D【解析】解：由得，，当时，不成立，，关于的一次函数，当时，，当时，，不等式对恒成立，，解得．10、小颖用计算器探索方程的根，作出如图所示的图象，并求得一个近似根，则方程的另一个近似根（精确到）为（）A.B.C.D.【答案】D【解析】解：抛物线与轴的一个交点为，又抛物线的对称轴为：，另一个交点坐标为：，则方程的另一个近似根为．11、如图，以为顶点的二次函数的图象与轴负半轴交于点，则一元二次方程的正数解的范围是（）A.B.C.D.【答案】C【解析】解：二次函数的顶点为，对称轴为，而对称轴左侧图象与轴交点横坐标的取值范围是，右侧交点横坐标的取值范围是．12、二次函数的图象如图所示，对称轴是直线，则下列四个结论错误的是（）A.B.C.D.【答案】B【解析】解：因为二次函数的图象与轴的交点在轴的上方，所以；由已知抛物线对称轴是直线，得；由图知二次函数图象与轴有两个交点，故有；直线与抛物线交于轴的下方，即当时，，即．13、二次函数的图象如图所示，则下列说法不正确的是（）A.B.C.D.【答案】D【解析】解：抛物线与轴有两个交点，；抛物线开口向上，；抛物线与轴的交点在轴的正半轴，；抛物线的对称轴在的正半轴上，．14、抛物线的顶点坐标是（）A.B.C.D.【答案】D【解析】解：顶点式，顶点坐标是，抛物线的顶点坐标为．15、某工厂一种产品的年产量是件，如果每一年都比上一年的产品增加倍，两年后产品与的函数关系是（）A.B.C.D.【答案】C【解析】解：某工厂一种产品的年产量是件，每一年都比上一年的产品增加倍，一年后产品是：，两年后产品y与x的函数关系是：．二、填空题（本大题共有5小题，每小题5分，共25分）16、二次函数的最小值为．【答案】-4【解析】解：二次函数的开口向上，顶点坐标为，所以最小值为．故答案为：．17、抛物线的对称轴是直线．【答案】【解析】解：，其对称轴为．故答案是：．18、若抛物线经过点，则．【答案】-1【解析】解：抛物线经过点，，解得：．故答案为：．19、若抛物线的顶点在轴的下方，则的取值范围是____________【答案】【解析】解：此抛物线的顶点坐标为由题意得即20、抛物线经过点和两点，则．（分数写成a/b形式）【答案】0【解析】解：把点和分别代入得由方程组得，则．三、解答题（本大题共有3小题，每小题10分，共30分）21、求抛物线的顶点和对称轴．【解析】解：，抛物线的顶点坐标为，对称轴是．故答案是：，．22、已知二次函数，当，求函数？；当？时，函数的值为.【解析】解：把代入函数解析式得：；令，则有：，，解得，；综上可知当时，；当，或时，函数的值为.正确答案是：；，.23、已知二次函数的图象如图所示，请结合图象，判断下列各式的符号．①；②；③；④．【解析】解：①抛物线开口向下，则，对称轴在轴的左侧，则，则，抛物线与轴的交点在轴的下方，则，；②抛物线与轴没有交点，所以；③当自变量为时，图象在轴下方，则时，；④当自变量为时，图象在轴下方，则时，．。

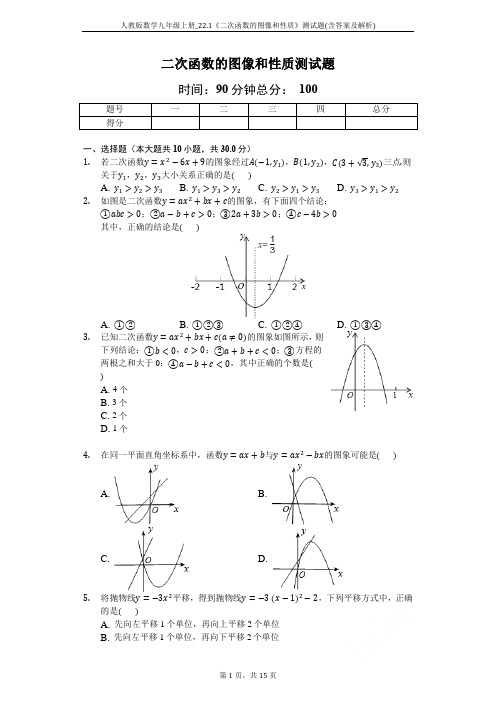
二次函数的图像和性质测试题时间：90分钟总分：100题号一二三四总分得分一、选择题（本大题共10小题，共30.0分）1.若二次函数y=x2−6x+9的图象经过A(−1,y1)，B(1,y2)，C(3+√3,y3)三点.则关于y1，y2，y3大小关系正确的是()A. y1>y2>y3B. y1>y3>y2C. y2>y1>y3D. y3>y1>y22.如图是二次函数y=ax2+bx+c的图象，有下面四个结论：①abc>0；②a−b+c>0；③2a+3b>0；④c−4b>0其中，正确的结论是()A. ①②B. ①②③C. ①②④D. ①③④3.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，则下列结论：①b<0，c>0；②a+b+c<0；③方程的两根之和大于0；④a−b+c<0，其中正确的个数是()A. 4个B. 3个C. 2个D. 1个4.在同一平面直角坐标系中，函数y=ax+b与y=ax2−bx的图象可能是()A. B.C. D.5.将抛物线y=−3x2平移，得到抛物线y=−3(x−1)2−2，下列平移方式中，正确的是()A. 先向左平移1个单位，再向上平移2个单位C. 先向右平移1个单位，再向上平移2个单位D. 先向右平移1个单位，再向下平移2个单位6.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，并且关于x的一元二次方程ax2+bx+c−m=0有两个不相等的实数根，下列结论：①b2−4ac<0；②abc>0；③a−b+c<0；④m>−2，其中，正确的个数有()A. 1B. 2C. 3D. 47.若抛物线y=x2−2x+3不动，将平面直角坐标系xOy先沿水平方向向右平移一个单位，再沿铅直方向向上平移三个单位，则原抛物线图象的解析式应变为()A. y=(x−2)2+3B. y=(x−2)2+5C. y=x2−1D. y=x2+48.二次函数y=2x2−3的图象是一条抛物线，下列关于该抛物线的说法，正确的是()A. 抛物线开口向下B. 抛物线经过点(2,3)C. 抛物线的对称轴是直线x=1D. 抛物线与x轴有两个交点9.在二次函数y=−x2+2x+1的图象中，若y随x的增大而减少，则x的取值范围是()A. x<1B. x>1C. x<−1D. x>−110.直线y=52x−2与抛物线y=x2−12x的交点个数是()A. 0个B. 1个C. 2个D. 互相重合的两个二、填空题（本大题共10小题，共30.0分）11.已知抛物线y=x2−(k+2)x+9的顶点在坐标轴上，则k的值为______．12.二次函数y=−x2+2x+2图象的顶点坐标是______．13.函数y=x2+mx−4，当x<2时，y随x的增大而减小，则m的取值范围是______ ．14.抛物线y=ax2+bx+c经过点A(−5,4)，且对称轴是直线x=−2，则a+b+c=______ ．15.二次函数y=−2(x−1)2+5的图象的对称轴为______ ，顶点坐标为______ ．16.如图，若抛物线y=ax2+bx+c上的P(4,0)，Q两点关于它的对称轴x=1对称，则Q点的坐标为______ ．17.如图，抛物线C1：y=12x2经过平移得到抛物线C2：y=12x2+2x，抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是______ ．18.已知(−3,y1)，(4,y2)，(−1,y3)是二次函数y=x2−4x上的点，则y1，y2，y3从小到大用“<”排列是______．19.如图，二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点，与y轴交于点C，对称轴是直线x=−1，点B的坐标为(1,0).下面的四个结论：①AB=4；②b2−4ac>0；③ab<0；④a−b+c<0，其中正确的结论是______ (填写序号)．20.如图，抛物线y=ax2+bx+c过点(−1,0)，且对称轴为直线x=1，有下列结论：①abc<0；②10a+3b+c>0；③抛物线经过点(4,y1)与点(−3,y2)，则y1>y2；④无论a，b，c取,0)；⑤am2+bm+何值，抛物线都经过同一个点(−caa≥0，其中所有正确的结论是______ ．三、计算题（本大题共4小题，共24.0分）21.已知：二次函数图象的顶点坐标是(3,5)，且抛物线经过点A(1,3)．(1)求此抛物线的表达式；(2)如果点A关于该抛物线对称轴的对称点是B点，且抛物线与y轴的交点是C点，求△ABC的面积．22.已知二次函数y=(m−2)x2+(m+3)x+m+2的图象过点(0,5)．(1)求m的值，并写出二次函数的解析式；(2)求出二次函数图象的顶点坐标和对称轴．23.已知函数y=−x2+(m−1)x+m(m为常数)．(1)该函数的图象与x轴公共点的个数是______．A.0B.1C.2D.1或2(2)求证：不论m为何值，该函数的图象的顶点都在函数y=(x+1)2的图象上．(3)当−2≤m≤3时，求该函数的图象的顶点纵坐标的取值范围．24.如图，已知二次函数y=ax2+bx+c的图象过点A(−1,0)和点C(0,3)，对称轴为直线x=1．(1)求该二次函数的关系式和顶点坐标；(2)结合图象，解答下列问题：①当−1<x<2时，求函数y的取值范围．②当y<3时，求x的取值范围．四、解答题（本大题共2小题，共16.0分）25.如图，已知抛物线y=−x2+bx+c与x轴交于点A(−1,0)和点B(3,0)，与y轴交于点C，连接BC交抛物线的对称轴于点E，D是抛物线的顶点．(1)求此抛物线的解析式；(2)直接写出点C和点D的坐标；(3)若点P在第一象限内的抛物线上，且S△ABP=4S△COE，求P点坐标．注：二次函数y=ax2+bx+c(a≠0)的顶点坐标为(−b2a ,4ac−b24a)(m2+1)=0有实数根．26.已知关于x的一元二次方程x2−(m+1)x+12(1)求m的值；(m2+1)的图象关于x轴的对称图形，然后将所作图(2)先作y=x2−(m+1)x+12形向左平移3个单位长度，再向上平移2个单位长度，写出变化后图象的解析式；(3)在(2)的条件下，当直线y=2x+n(n≥m)与变化后的图象有公共点时，求n2−4n的最大值和最小值．答案和解析【答案】 1. A 2. C 3. B 4. C 5. D6. B7. C8. D 9. B 10. C11. 4，−8，−2 12. (1,3) 13. m ≤−4 14. 415. x =1；(1,5) 16. (−2,0) 17. 418. y 2<y 3<y 1 19. ①②④ 20. ②④⑤21. 解：(1)设抛物线的解析式为y =a(x −3)2+5， 将A(1,3)代入上式得3=a(1−3)2+5，解得a =−12， ∴抛物线的解析式为y =−12(x −3)2+5， (2)∵A(1,3)抛物线对称轴为：直线x =3 ∴B(5,3)，令x =0，y =−12(x −3)2+5=12，则C(0,12)， △ABC 的面积=12×(5−1)×(3−12)=5．22. 解：(1)把(0,5)代入y =(m −2)x 2+(m +3)x +m +2得m +2=5， 解得m =3所以二次函数解析式为y =x 2+6x +5； (2)因为y =x 2+6x +5=(x +3)2−4，所以此二次函数图象的顶点坐标为(−3,−4)，对称轴为直线x =−3． 23. D24. 解：(1)根据题意得{a −b +c =0c =3−b2a =1，解得{a =−1b =2c =3， 所以二次函数关系式为y =−x 2+2x +3，因为y =−(x −1)2+4，所以抛物线的顶点坐标为(1,4)；(2)①当x =−1时，y =0；x =2时，y =3； 而抛物线的顶点坐标为(1,4)，且开口向下， 所以当−1<x <2时，0<y ≤4；②当y =3时，−x 2+2x +3=3，解得x =0或2， 所以当y <3时，x <0或x >2．25. 解：(1)由点A(−1,0)和点B(3,0)得{−9+3b +c =0−1−b+c=0，解得：{b=2，(2)令x =0，则y =3， ∴C(0,3)，∵y =−x 2+2x +3=−(x −1)2+4， ∴D(1,4)；(3)设P(x,y)(x >0,y >0)，S △COE =12×1×3=32，S △ABP =12×4y =2y ，∵S △ABP =4S △COE ，∴2y =4×32， ∴y =3，∴−x 2+2x +3=3，解得：x 1=0(不合题意，舍去)，x 2=2， ∴P(2,3)．26. 解：(1)对于一元二次方程x 2−(m +1)x +12(m 2+1)=0，△=(m +1)2−2(m 2+1)=−m 2+2m −1=−(m −1)2， ∵方程有实数根， ∴−(m −1)2≥0， ∴m =1．(2)由(1)可知y =x 2−2x +1=(x −1)2， 图象如图所示：平移后的解析式为y =−(x +2)2+2=−x 2−4x −2．(3)由{y =2x +n y =−x 2−4x −2消去y 得到x 2+6x +n +2=0， 由题意∆≥0，∴36−4n −8≥0， ∴n ≤7，∵n ≥m ，m =1， ∴1≤n ≤7， 令，∴n =2时，y′的值最小，最小值为−4， n =7时，y′的值最大，最大值为21， ∴n 2−4n 的最大值为21，最小值为−4．1. 解：二次函数对称轴为直线x=−−62×1=3，3−(−1)=4，3−1=2，3+√3−3=√3，∵4>2>√3，∴y1>y2>y3．故选A．先求出二次函数的对称轴，再求出点A、B、C到对称轴的距离，然后根据二次函数增减性判断即可．本题考查了二次函数图象上点的坐标特征，主要利用了二次函数的对称性以及增减性，确定出各点到对称轴的距离的大小是解题的关键．2. 解：∵抛物线开口向上，∴a>0；∵抛物线的对称轴在y轴的右侧，∴x=−b2a>0，∴b<0；∵抛物线与y轴的交点在x轴下方，∴c<0，∴abc>0，所以①正确；∵x=−1时，y>0，∴a−b+c>0，所以②正确；∵x=−b2a =13，∴2a+3b=0，所以③错误；∵x=2时，y>0，∴4a+2b+c>0，把2a=−3b代入得−6b+2b+c>0，∴c−4b>0，所以④正确．故选：C．根据抛物线开口方向得到a>0；根据对称轴得到x=−b2a>0，则b<0；根据抛物线与y轴的交点在x轴下方得到c<0，则abc>0，可判断①正确；当自变量为−1时对应的函数图象在x轴上方，则a−b+c>0，可判断②正确；根据抛物线对称轴方程得到x=−b2a =13，则2a+3b=0，可判断③错误；当自变量为2时对应的函数图象在x轴上方，则4a+2b+c>0，把2a=−3b代入可对④进行判断．本题考查了二次函数的图象与系数的关系：二次函数y=ax2+bx+c(a≠0)的图象为抛物线，当a>0，抛物线开口向上；对称轴为直线x=--b2a；抛物线与y轴的交点坐标为(0,c)．3. 解：∵抛物线开口向下，∴a<0，∵抛物线对称轴x>0，且抛物线与y轴交于正半轴，∴b>0，c>0，故①错误；>0，即x1+x2>0，故③正确；由对称轴x>0，可知x1+x22由可知抛物线与x轴的左侧交点的横坐标的取值范围为：−1<x<0，∴当x=−1时，y=a−b+c<0，故④正确．故选：B．由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．本题主要考查二次函数图象与系数的关系，熟练掌握二次函数y=ax2+bx+c系数符号与抛物线开口方向、对称轴、与x轴、y轴的交点是关键．4. 解：A、对于直线y=ax+b来说，由图象可以判断，a>0，b>0；而对于抛物线>0，应在y轴的右侧，故不合题意，图形错误；y=ax2−bx来说，对称轴x=b2aB、对于直线y=ax+b来说，由图象可以判断，a<0，b>0；而对于抛物线y=ax2−bx<0，应在y轴的左侧，故不合题意，图形错误；来说，对称轴x=b2aC、对于直线y=ax+b来说，由图象可以判断，a>0，b>0；而对于抛物线y=ax2−bx>0，应在y轴的右侧，故符合题意；来说，图象开口向上，对称轴x=b2aD、对于直线y=ax+b来说，由图象可以判断，a>0，b>0；而对于抛物线y=ax2−bx 来说，图象开口向下，a<0，故不合题意，图形错误；故选：C．首先根据图形中给出的一次函数图象确定a、b的符号，进而运用二次函数的性质判断图形中给出的二次函数的图象是否符合题意，根据选项逐一讨论解析，即可解决问题．此主要考查了一次函数、二次函数图象的性质及其应用问题；解题的方法是首先根据其中一次函数图象确定a、b的符号，进而判断另一个函数的图象是否符合题意；解题的关键是灵活运用一次函数、二次函数图象的性质来分析、判断、解答．5. 解：∵y=−3x2的顶点坐标为(0,0)，y=−3(x−1)2−2的顶点坐标为(1,−2)，∴将抛物线y=−3x2向右平移1个单位，再向下平移2个单位，可得到抛物线y=−3(x−1)2−2．故选：D．找到两个抛物线的顶点，根据抛物线的顶点即可判断是如何平移得到．本题考查的是二次函数的图象与几何变换，熟知“上加下减，左加右减”的法则是解答此题的关键．6. 解：如图所示：图象与x轴有两个交点，则b2−4ac>0，故①错误；∵图象开口向上，∴a>0，∵对称轴在y轴右侧，∴a，b异号，∴b<0，∵图象与y轴交于x轴下方，∴c<0，∴abc>0，故②正确；当x=−1时，a−b+c>0，故此选项错误；∵二次函数y=ax2+bx+c的顶点坐标纵坐标为：−2，故二次函数y=ax2+bx+c向上平移小于2个单位，则平移后解析式y=ax2+bx+c−m与x轴有两个交点，此时关于x的一元二次方程ax2+bx+c−m=0有两个不相等的实数根，故④正确．故选：B．直接利用抛物线与x轴交点个数以及抛物线与方程之间的关系、函数图象与各系数之间关系分析得出答案．此题主要考查了二次函数图象与系数的关系，正确把握二次函数与方程之间的关系是解题关键．7. 解：将平面直角坐标系xOy先沿水平方向向右平移一个单位，再沿铅直方向向上平移三个单位，这个相当于把抛物线向左平移有关单位，再向下平移3个单位，∵y=(x−1)2+2，∴原抛物线图象的解析式应变为y=(x−1+1)2+2−3=x2−1，故答案为C．思想判定出抛物线的平移规律，根据左加右减，上加下减的规律即可解决问题．本题考查二次函数图象的平移，解题的关键是理解坐标系的平移和抛物线的平移是反方向的，记住左加右减，上加下减的规律，属于中考常考题型．8. 解：A、a=2，则抛物线y=2x2−3的开口向上，所以A选项错误；B、当x=2时，y=2×4−3=5，则抛物线不经过点(2,3)，所以B选项错误；C、抛物线的对称轴为直线x=0，所以C选项错误；D、当y=0时，2x2−3=0，此方程有两个不相等的实数解，所以D选项正确．故选D．根据二次函数的性质对A、C进行判断；根据二次函数图象上点的坐标特征对B进行判断；利用方程2x2−3=0解的情况对D进行判断．本题考查了二次函数的性质：对于二次函数y=ax2+bx+c(a≠0)，它的顶点坐标是(−b2a ,4ac−b24a)，对称轴为直线x=−b2a，二次函数y=ax2+bx+c(a≠0)的图象具有如下性质：当a>0时，抛物线y=ax2+bx+c(a≠0)的开口向上，x<−b2a时，y随x的增大而减小；x>−b2a时，y随x的增大而增大；当a<0时，抛物线y=ax2+bx+c(a≠0)的开口向下，x<−b2a 时，y随x的增大而增大；x>−b2a时，y随x的增大而减小．9. 解：y=−x2+2x+1=−(x−1)2+2，抛物线的对称轴为直线x=1，∵a=−1<0，∴当x>1时，y随x的增大而减少．故选B．先配方得到抛物线的对称轴为直线x=1，然后根据二次函数的性质求解．本题考查了二次函数的性质：二次函数y=ax2+bx+c(a≠0)的顶点坐标是(−b2a ,4ac−b24a)，对称轴直线x=−b2a，二次函数y=ax2+bx+c(a≠0)的图象具有如下性质：当a>0时，抛物线y=ax2+bx+c(a≠0)的开口向上，x<−b2a时，y随x的增大而减小；x>−b2a 时，y随x的增大而增大；x=−b2a时，y取得最小值4ac−b24a，对称即顶点是抛物线的最低点；当a<0时，抛物线y=ax2+bx+c(a≠0)的开口向下，x<−b2a 时，y随x的增大而增大；x>−b2a时，y随x的增大而减小；x=−b2a时，y取得最大值4ac−b24a，即顶点是抛物线的最高点．10. 解：直线y=52x−2与抛物线y=x2−12x的交点求法是：令52x−2=x2−12x，∴x2−3x+2=0，∴x1=1，x2=2，∴直线y=52x−2与抛物线y=x2−12x的个数是2个．故选C．根据直线与二次函数交点的求法得出一元二次方程的解，即可得出交点个数．此题主要考查了一元二次方程的性质，根据题意得出一元二次方程的解的个数是解决问题的关键．11. 解：当抛物线y=x2−(k+2)x+9的顶点在x轴上时，△=0，即△=(k+2)2−4×9=0，解得k=4或k=−8；当抛物线y=x2−(k+2)x+9的顶点在y轴上时，x=−b2a =k+22=0，解得k=−2．故答案为：4，−8，−2．由于抛物线的顶点在坐标轴上，故应分在x轴上与y轴上两种情况进行讨论．本题考查的是二次函数的性质，解答此题时要注意进行分类讨论，不要漏解．12. 解：∵y=−x2+2x+2=−(x2−2x+1)+3=−(x−1)2+3，故顶点的坐标是(1,3).故填空答案：(1,3)．此题既可以利用y=ax2+bx+c的顶点坐标公式求得顶点坐标，也可以利用配方法求出其顶点的坐标．求抛物线的顶点坐标、对称轴的方法．13. 解：∵x<2时，y随x的增大而减小，∴−m2×1≥2，∴m≤−4．故答案为：m≤−4．根据二次函数的性质，二次函数的顶点的横坐标不小于2列式计算即可得解．本题考查了二次函数的性质，熟记性质，根据顶点的横坐标列出不等式是解题的关键．14. 解：∵对称轴方程为x=−2，∴−b2a=−2，整理可得b=4a，∵抛物线y=ax2+bx+c经过点A(−5,4)，∴4=25a−5b+c，把b=4a代入可得，4=25a−20a+c，解得c=4−5a，∴抛物线解析式为y=ax2+4ax+4−5a，当x=1时，则有a+b+c=a+4a+4−5a=4，故答案为：4．把A点坐标代入抛物线解析式结合对称轴方程可用a分别表示出b和c，则可用a表示出抛物线解析式，再令x=1代入可求得y的值，即a+b+c的值．本题主要考查二次函数的解析式，分别用a表示出b和c，得出抛物线解析式是解题的关键．15. 解：∵y=−2(x−1)2+5，∴抛物线顶点坐标为(1,5)，对称轴为x=1，故答案为：x=1，(1,5)．由抛物线解析式可求得其顶点坐标及对称轴．本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在y=a(x−ℎ)2+k中，对称轴为x=ℎ，顶点坐标为(ℎ,k)．16. 解：∵抛物线y=ax2+bx+c上的P(4,0)，Q两点关于它的对称轴x=1对称，∴P，Q两点到对称轴x=1的距离相等，∴Q点的坐标为：(−2,0)．故答案为：(−2,0)．直接利用二次函数的对称性得出Q点坐标即可．此题主要考查了二次函数的性质，正确利用函数对称性得出答案是解题关键．17. 解：抛物线C1：y=12x2的顶点坐标为(0,0)，∵y=12x2+2x=12(x+2)2−2，∴平移后抛物线的顶点坐标为(−2,2)，对称轴为直线x=−2，当x=−2时，y=12×(−2)2=2，∴平移后阴影部分的面积等于如图三角形的面积为：12×(2+2)×2=4，故答案为：4．确定出抛物线y=12x2+2x的顶点坐标，然后求出抛物线的对称轴与原抛物线的交点坐标，从而判断出阴影部分的面积等于三角形的面积，再根据三角形的面积公式列式计算即可得解．本题考查了二次函数图象与几何变换，确定出与阴影部分面积相等的三角形是解题的关键．18. 解：y1=(−3)2+4×3=21，y2=42−4×4=0，y3=(−1)2+4×1=5，∴y2<y3<y1，故答案为：y2<y3<y1，可分别求出y1、y2、y3的值后，再进行比较大小．本题考查二次函数图象上的点的特征，解题的关键是求出各点的函数值，本题属于基础题型．19. 解：∵抛物线对称轴是直线x=−1，点B的坐标为(1,0)，∴A(−3,0)，∴AB=4，故选项①正确；∵抛物线与x轴有两个交点，∴b2−4ac>0，故选项②正确；∵抛物线开口向上，∴a>0，∵抛物线对称轴在y轴左侧，∴a，b同号，∴ab>0，故选项③错误；当x=−1时，y=a−b+c此时最小，为负数，故选项④正确；故答案为：①②④．利用二次函数对称性以及结合b2−4ac的符号与x轴交点个数关系，再利用数形结合分别分析得出答案．此题主要考查了二次函数图象与系数的关系，正确判断a−b+c的符号是解题关键．20. 解：由图象可知，抛物线开口向上，则a>0，顶点在y轴右侧，则b<0，抛物线与y轴交于负半轴，则c<0，∴abc>0，故①错误；∵抛物线y=ax2+bx+c过点(−1,0)，且对称轴为直线x=1，∴抛物线y=ax2+bx+c过点(3,0)，∴当x=3时，y=9a+3b+c=0，∵a>0，∴10a+3b+c>0，故②正确；∵对称轴为x=1，且开口向上，∴离对称轴水平距离越大，函数值越大，∴y1<y2，故③错误；当x=−ca 时，y=a⋅(−ca)2+b⋅(−ca)+c=c2−bc+aca=c(a−b+c)a，∵当x=−1时，y=a−b+c=0，∴当x=−ca 时，y=a⋅(−ca)2+b⋅(−ca)+c=0，即无论a，b，c取何值，抛物线都经过同一个点(−ca,0)，故④正确；x=m对应的函数值为y=am2+bm+c，x=1对应的函数值为y=a+b+c，又∵x=1时函数取得最小值，∴am2+bm+c≥a+b+c，即am2+bm≥a+b，∵b=−2a，∴am2+bm+a≥0，故⑤正确；故答案为：②④⑤．由开口方向、对称轴及抛物线与y轴交点位置可判断①；由x=3时的函数值及a>0可判断②；由抛物线的增减性可判断③；由当x=−ca 时，y=a⋅(−ca)2+b⋅(−ca)+c=c(a−b+c)a且a−b+c=0可判断④；由x=1时函数y取得最小值及b=−2a可判断⑤．本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c(a≠0)系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．21. (1)设顶点式y=a(x−3)2+5，然后把A点坐标代入求出a即可得到抛物线的解析式；(2)利用抛物线的对称性得到B(5,3)，再确定出C点坐标，然后根据三角形面积公式求解．本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解.一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x 轴有两个交点时，可选择设其解析式为交点式来求解．22. (1)把已知点的坐标代入y =(m −2)x 2+(m +3)x +m +2可求出m 的值，从而得到抛物线解析式；(2)把(1)中的解析式配成顶点式，从而得到二次函数图象的顶点坐标和对称轴．本题考查了在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解.一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x 轴有两个交点时，可选择设其解析式为交点式来求解.也考查了二次函数的性质．23. 解：(1)∵函数y =−x 2+(m −1)x +m(m 为常数)，∴△=(m −1)2+4m =(m +1)2≥0，则该函数图象与x 轴的公共点的个数是1或2，故选D ；(2)y =−x 2+(m −1)x +m =−(x −m−12)2+(m+1)24， 把x =m−12代入y =(x +1)2得：y =(m−12+1)2=(m+1)24， 则不论m 为何值，该函数的图象的顶点都在函数y =(x +1)2的图象上；(3)设函数z =(m+1)24，当m =−1时，z 有最小值为0；当m <−1时，z 随m 的增大而减小；当m >−1时，z 随m 的增大而增大，当m =−2时，z =14；当m =3时，z =4，则当−2≤m ≤3时，该函数图象的顶点坐标的取值范围是0≤z ≤4．(1)表示出根的判别式，判断其正负即可得到结果；(2)将二次函数解析式配方变形后，判断其顶点坐标是否在已知函数图象即可；(3)根据m 的范围确定出顶点纵坐标范围即可．此题考查了抛物线与x 轴的交点，以及二次函数的性质，熟练掌握二次函数的图象与性质是解本题的关键．24. (1)把A 点和C 点坐标代入y =ax 2+bx +c 得到两个方程，再加上对称轴方程即可得到三元方程组，然后解方程组求出a 、b 、c 即可得到抛物线解析式，再把解析式配成顶点式即可得到顶点坐标；(2)①先分别计算出x 为−1和2时的函数值，然后根据二次函数的性质写出对应的函数值的范围；②先计算出函数值为3所对应的自变量的值，然后根据二次函数的性质写出y <3时，x 的取值范围．本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解.一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x 轴有两个交点时，可选择设其解析式为交点式来求解.也考查了二次函数的性质．25. (1)将A 、B 的坐标代入抛物线的解析式中，即可求出待定系数b 、c 的值，进而可得到抛物线的对称轴方程；(2)令x =0，可得C 点坐标，将函数解析式配方即得抛物线的顶点C 的坐标；(3)设P(x,y)(x >0,y >0)，根据题意列出方程即可求得y ，即得D 点坐标．此题主要考查了二次函数解析式的确定、抛物线的顶点坐标求法，图形面积的求法等知识，根据S△ABP=4S△COE列出方程是解决问题的关键．26. (1)由题意△≥0，列出不等式，解不等式即可；(2)画出翻折.平移后的图象，根据顶点坐标即可写出函数的解析式；(3)首先确定n的取值范围，利用二次函数的性质即可解决问题；本题考查抛物线与x轴的交点、待定系数法、翻折变换、平移变换、二次函数的最值问题等知识，解题的关键是理解题意，学会用转化的思想思考问题，属于中考常考题型．。

2020年人教版九年级上册同步练习22.1 二次函数的图象和性质一．选择题（共10小题）1．下列函数属于二次函数的是（）A．y＝x﹣B．y＝（x﹣3）2﹣x2C．y＝﹣x D．y＝2（x+1）2﹣12．当函数y＝（a﹣1）x2+bx+c是二次函数时，a的取值为（）A．a＝1B．a＝﹣1C．a≠﹣1D．a≠13．下列抛物线的图象，开口最大的是（）A．y＝x2B．y＝4x2C．y＝﹣2x2D．无法确定4．抛物线y＝（x﹣3）2﹣5的顶点坐标是（）A．（3，5）B．（﹣3，5）C．（3，﹣5）D．（﹣3，﹣5）5．抛物线y＝x2+4x+7的对称轴是（）A．直线x＝4B．直线x＝﹣4C．直线x＝2D．直线x＝﹣2 6．对于二次函数y＝2（x﹣1）2﹣8，下列说法正确的是（）A．图象开口向下B．当x＞1时，y随x的增大而减小C．当x＜1时，y随x的增大而减小D．图象的对称轴是直线x＝﹣17．下列对二次函数y＝x2﹣2x的图象的描述，正确的是（）A．开口向下B．对称轴是y轴C．经过原点D．对称轴右侧部分下降8．一次函数y＝acx+b与二次函数y＝ax2+bx+c在同一平面直角坐标系中的图象可能是（）A．B．C．D．9．二次函数y＝ax2+bx+c的图象如图所示，则下列结论正确的是（）A．abc＞0B．a+b+c＝0C．4a﹣2b+c＜0D．b2﹣4ac＜0 10．二次函数y＝﹣x2+ax+b的图象如图所示，对称轴为直线x＝2，下列结论不正确的是（）A．a＝4B．当x＞2.5时，y随x的增大而减小C．当x＝﹣1时，b＞5D．当b＝8时，函数最大值为10二．填空题（共8小题）11．若y＝（a+2）x|a|+1是以x为自变量的二次函数，则a＝．12．抛物线y＝3（x﹣1）2+8的顶点坐标为．13．二次函数y＝x2﹣16x﹣8的最小值是．14．当二次函数y＝﹣x2+4x﹣6有最大值时，x＝．15．二次函数y＝x2﹣4x+5﹣m2的图象过点（0，4），则m的值为．16．将抛物线y＝2（x+3）2+4先向右平移1个单位长度，再向下平移5个单位长度，得到的抛物线的解析式为．17．已知点P1（﹣2，y1），P2（2，y2）在二次函数y＝（x+1）2﹣2的图象上，则y1y2．（填“＞”，“＜”或“＝”）18．二次函数y＝ax2+bx+c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线x ＝2，下列结论：①4a+b＝0；②9a+c＞3b；③，3a+c＞0；④当x＞﹣1时，y的值随x 值的增大而增大；⑤4a+2b≥am2﹣bm（m为任意实数）．其中正确的结论有．（填序号）三．解答题（共6小题）19．已知平面直角坐标系xOy中，抛物线y═x2﹣mx+m2+m．（1）若该抛物线经过原点，求m的值；（2）求证该抛物线的顶点在直线y＝x上；（3）若点A（﹣4，0），B（0，2），当该抛物线与线段AB只有一个公共点时，结合函数图象，直接写出m的取值范围．20．在平面直角坐标系xOy中，抛物线y＝﹣x2+2bx+b2+1的对称轴与x轴交于点A，将点A 向左平移b个单位，再向上平移3﹣b2个单位，得到点B．（1）求点B的坐标（用含b的式子表示）；（2）当抛物线经过点（0，2），且b＞0时，求抛物线的表达式；（3）若抛物线与线段AB恰有一个公共点，结合图象，直接写出b的取值范围．21．把抛物线C1：y＝x2+2x+3先向右平移4个单位长度，再向下平移5个单位长度得到抛物线C2．（1）直接写出抛物线C2的函数关系式；（2）动点P（a，﹣6）能否在抛物线C2上？请说明理由；（3）若点A（m，y1），B（n，y2）都在抛物线C2上，且m＜n＜0，比较y1，y2的大小，并说明理由．22．已知抛物线y＝ax2﹣2ax﹣3+2a2（a≠0）．（1）求这条抛物线的对称轴；（2）若该抛物线的顶点在x轴上，求其解析式；（3）设点P（m，y1），Q（3，y2）在抛物线上，若y1＜y2，求m的取值范围．23．已知二次函数y＝﹣x2+bx+c的图象与直线y＝﹣x+3相交于x轴上的点A，y轴上的点B．顶点为P．（1）求这个二次函数的解析式；（2）现将抛物线向左平移m个单位，当抛物线与△PBA有且只有一个公共点时，求m 的值．24．已知：如图，抛物线y＝ax2+4x+c经过原点O（0，0）和点A（3，3），P为抛物线上的一个动点，过点P作x轴的垂线，垂足为B（m，0），并与直线OA交于点C．（1）求抛物线的解析式；（2）当点P在直线OA上方时，求线段PC的最大值．参考答案一．选择题（共10小题）1．解：A．自变量x的次数不是2，故A错误；B．y＝（x﹣3）2﹣x2整理后得到y＝﹣6x+9，是一次函数，故B错误C．由可知，自变量x的次数不是2，故C错误；D．y＝2（x+1）2﹣1是二次函数的顶点式解析式，故D正确．故选：D．2．解：由题意得：a﹣1≠0，解得：a≠1，故选：D．3．解：∵二次函数中|a|的值越小，函数图象的开口越大，又∵||＜|﹣2|＜|4|，∴抛物线y＝x2的图象开口最大，故选：A．4．解：抛物线y＝（x﹣3）2﹣5的顶点坐标是（3，﹣5），故选：C．5．解：因为a＝1，b＝4，c＝7，所以对称轴是直线x＝﹣＝﹣＝﹣2，故选：D．6．解：A、y＝2（x﹣1）2﹣8，∵a＝2＞0，∴图象的开口向上，故本选项错误；B、当x＞1时，y随x的增大而增大；故本选项错误；C、当x＜1时，y随x的增大而减小，故本选项正确；D、图象的对称轴是直线x＝1，故本选项错误．故选：C．7．解：y＝x2﹣2x＝（x﹣1）2﹣1，A．由a＝1＞0知抛物线开口向上，此选项错误；B．此抛物线的对称轴为直线x＝1，此选项错误；C．当x＝0时，y＝0，此抛物线经过原点，此选项正确；D．由a＞0且对称轴为直线x＝1知，当x＞1，即对称轴右侧时，y随x的增大而增大，此选项错误；故选：C．8．解：A、由抛物线可知，a＞0，b＜0，c＞0，则ac＞0，由直线可知，ac＞0，b＞0，故本选项错误；B、由抛物线可知，a＞0，b＞0，c＞0，则ac＞0，由直线可知，ac＞0，b＞0，故本选项正确；C、由抛物线可知，a＜0，b＞0，c＞0，则ac＜0，由直线可知，ac＜0，b＜0，故本选项错误；D、由抛物线可知，a＜0，b＜0，c＞0，则ac＜0，由直线可知，ac＞0，b＞0，故本选项错误．故选：B．9．解：由图象可得，a＞0，b＜0，c＜0，∴abc＞0，故选项A正确；当x＝1时，y＝a+b+c＜0，故选项B错误；当x＝﹣2时，y＝4a﹣2b+c＞0，故选项C错误；该函数图象与x轴两个交点，则b2﹣4ac＞0，故选项D错误；故选：A．10．解：∵二次函数y＝﹣x2+ax+b∴对称轴为直线x＝﹣＝2∴a＝4，故结论A正确；∵对称轴为直线x＝2且图象开口向下，∴当x＞2.5时，y随x的增大而减小，故结论B正确；当x＝﹣1时，由图象知此时y＞0即﹣1﹣4+b＞0∴b＞5，故结论C正确；当b＝8时，y＝﹣x2+4x+8＝﹣（x﹣2）2+12∴函数有最大值12，故结论D不正确；故选：D．二．填空题（共8小题）11．解：由题意得：|a|＝2，且a+2≠0，解得：a＝2，故答案为：2．12．解：∵抛物线y＝3（x﹣1）2+8是顶点式，∴顶点坐标是（1，8）．故答案为：（1，8）．13．解：y＝x2﹣16x﹣8＝（x﹣8）2﹣72，由于函数开口向上，因此函数有最小值，且最小值为﹣72，故答案为：﹣72．14．解：∵y＝﹣x2+4x﹣6，＝﹣（x2﹣4x+4）+4﹣6，＝﹣（x﹣2）2﹣2，∴当x＝2时，二次函数取得最大值．故答案为：2．15．解：∵根二次函数y＝x2﹣4x+5﹣m2的图象过点（0，4），∴5﹣m2＝4，解得m＝±1．故答案为±1．16．解：将抛物线y＝2（x+3）2+4先向右平移1个单位长度，再向下平移5个单位长度可得：y＝2（x+3﹣1）2+4﹣5，即y＝2（x+2）2﹣1，故答案为y＝2（x+2）2﹣1．17．解：当x＝﹣2时，y1＝（﹣2+1）2﹣2＝﹣1；当x＝2时，y2＝（2+1）2﹣2＝7．∵﹣1＜7，∴y1＜y2．故答案为＜．18．解：抛物线过点（﹣1，0），对称轴为直线x＝2，因此可得，抛物线与x轴的另一个交点为（5，0），a﹣b+c＝0，x＝﹣＝2，即4a+b ＝0，因此①正确；当x＝﹣3时，y＝9a﹣3b+c＜0，即9a+c＜3b，因此②不正确；当x＝5时，y＝25a+5b+c＝0，又b＝﹣4a，所以5a+c＝0，而a＜0，因此有3a+c＞0，故③正确；在对称轴的左侧，即当x＜2时，y随x的增大而增大，因此④不正确；当x＝2时，y最大＝4a+2b+c，当x＝m时，y＝am2+bm+c，因此有4a+2b≥am2+bm，故⑤正确；综上所述，正确的结论有：①③⑤，故答案为：①③⑤．三．解答题（共6小题）19．解：（1）∵抛物线经过原点，∴m2+m＝0，解得m1＝0，m2＝﹣2；（2）∵y═x2﹣mx+m2+m＝（x﹣m）2+m，∴该抛物线的顶点坐标为（m，m），∴抛物线的顶点直线直线y＝x上；（3）设直线AB的解析式为y＝kx+b，把点A（﹣4，0），B（0，2）代入得，解得，∴直线AB的解析式为y＝+2，令x+2＝x2﹣mx+m2+m，整理得x2﹣（m+）x+m2+m﹣2＝0，△＝（m+）2﹣4×（m2+m﹣2）＝0，解得m＝，∵此时对称轴为x＝﹣＝＞0，故舍去；把A（﹣4，0）代入y＝x2﹣mx+m2+m得，m2+5m+8＝0，解得m＝﹣2或﹣8；把B（0，2）代入y＝x2﹣mx+m2+m得，m2+m+﹣2＝0，解得m＝﹣1，由图象可知，该抛物线与线段AB只有一个公共点时，﹣8≤m≤﹣1﹣或﹣2≤m≤﹣1+．20．解：（1）由题意得抛物线y＝﹣x2+2bx+b2+1的对称轴为，∴点A坐标为（b，0），∴点B坐标为（0，3﹣b2）（2）把（0，2）代入y＝﹣x2+2bx+b2+1中，解得b＝±1．∵b＞0，∴b＝1．∴抛物线的表达式为y＝﹣x2+2x+2；（3）当抛物线过点B时，抛物线AB有一个公共点，∴b2+1＝3﹣b2∴b＝±1，如图：当b＞1时，抛物线与线段AB无交点；当b＝1时，抛物线与线段AB有一个交点；当﹣1＜b＜1时，抛物线与线段AB有一个交点；当b＝﹣1时，抛物线与线段AB有一个交点；当b＜﹣1时，抛物线与线段AB无交点．∴若抛物线与线段AB恰有一个公共点，则﹣1≤b≤1．21．解：（1）∵y＝x2+2x+3＝（x+1）2+2，∴把抛物线C1：y＝x2+2x+3先向右平移4个单位长度，再向下平移5个单位长度得到抛物线C2：y＝（x+1﹣4）2+2﹣5，即y＝（x﹣3）2﹣3，∴抛物线C2的函数关系式为：y＝（x﹣3）2﹣3．（2）动点P（a，﹣6）不在抛物线C2上，理由如下：∵抛物线C2的函数关系式为：y＝（x﹣3）2﹣3，∴函数的最小值为﹣3，∵﹣6＜﹣3，∴动点P（a，﹣6）不在抛物线C2上；（3）∵抛物线C2的函数关系式为：y＝（x﹣3）2﹣3，∴抛物线的开口向上，对称轴为x＝3，∴当x＜3时，y随x的增大而减小，∵点A（m，y1），B（n，y2）都在抛物线C2上，且m＜n＜0＜3，22．解：（1）∵抛物线y＝ax2﹣2ax﹣3+2a2＝a（x﹣1）2+2a2﹣a﹣3．∴抛物线的对称轴为直线x＝1；（2）∵抛物线的顶点在x轴上，∴2a2﹣a﹣3＝0，解得a＝或a＝﹣1，∴抛物线为y＝x2﹣3x+或y＝﹣x2+2x﹣1；（3）∵抛物线的对称轴为x＝1，则Q（3，y2）关于x＝1对称点的坐标为（﹣1，y2），∴当a＞0，﹣1＜m＜3时，y1＜y2；当a＜0，m＜﹣1或m＞3时，y1＜y2．23．解：（1）∵直线y＝﹣x+3交于x轴上的点A，y轴上的点B，∴A（3，0），B（0，3），把A、B的坐标代入y＝﹣x2+bx+c得，解得，∴二次函数的解析式为y＝﹣x2+2x+3；（2）当抛物线经过点B时，抛物线与△PBA有且只有一个公共点，∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴P（1，4），将抛物线向左平移m个单位，P对应点为（1﹣m，4），∴平移后的抛物线解析式为y＝﹣（x﹣1+m）2+4，把B（0，3）代入得，3═﹣（﹣1+m）2+4，解得m1＝2，m2＝0（舍去），故m的值为2．24．解：（1）把O（0，0），A（3，3）代入得：，解得：，则抛物线解析式为y＝﹣x2+4x；（2）设直线OA解析式为y＝kx，把A（3，3）代入得：k＝1，即直线OA解析式为y＝x，∴P，C，B三点纵坐标相等，∵B（m，0），∴把x＝m代入y＝x中得：y＝m，即C（m，m），把x＝m代入y＝﹣x2+4x中得：y＝﹣m2+4m，即P（m，﹣m2+4m），∵P在直线OA上方，∴PC＝﹣m2+4m﹣m＝﹣m2+3m（0＜m＜3），当m＝﹣＝时，PC取得最大值，最大值为＝．。

九年级上册第二十二章《22.1二次函数的图像和性质》同步练习题一、单选题（每小题只有一个正确答案）1．下列函数中是二次函数的是( )A ． y ＝3x －1B ． y ＝3x 2－1C ． y ＝(x ＋1)2－x 2D ． y ＝ax 2＋2x －32．若y=（a 2+a ） 是二次函数，那么（ ）A ． a=﹣1或a=3B ． a≠﹣1且a ≠0C ． a=﹣1D ． a=33．抛物线y ＝－x 2不具有的性质是( )A ． 开口向下B ． 对称轴是y 轴C ． 与y 轴不相交D ． 最高点是原点4．如图，四个二次函数的图象中，分别对应的是：①2y ax =；②2y bx =；③2y cx =；④2y dx =，则,,,a b c d 的大小关系为( )A ． a b c d >>>B ． a b d c >>>C ． b a c d >>>D ． b a d c >>>5．对于 的图象下列叙述错误的是A ． 顶点坐标为（﹣3，2）B ． 对称轴为x=﹣3C ． 当x ＜﹣3时y 随x 增大而减小D ． 函数有最大值为26．已知二次函数 的图象如图所示，则下列说法正确的是（ ）A ． ＜0B ． ＜0C ． ＜0D ． ＜07．抛物线y=（x ﹣2）2﹣1可以由抛物线y=x 2平移而得到，下列平移正确的是（ ）A ． 先向左平移2个单位长度，然后向上平移1个单位长度B ． 先向左平移2个单位长度，然后向下平移1个单位长度C ． 先向右平移2个单位长度，然后向上平移1个单位长度D ． 先向右平移2个单位长度，然后向下平移1个单位长度8．如图，二次函数 的图象开口向下，且经过第三象限的点 若点P 的横坐标为 ，则一次函数 的图象大致是A．B．C．D．二、填空题9．二次函数y＝kx2－x－2经过点(1，5)，则k＝_________.10．函数y= –的图象是抛物线，则m=__________．11．开口向下的抛物线y＝(m2－2)x2＋2mx＋1的对称轴经过点(－1，3)，则m＝_____．12．如图，这是小明在阅读一本关于函数的课外读物时看到的一段文字，则被墨迹污染的二次项系数是__________．13．抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；③3a+c=0；④当y＞0时，x的取值范围是﹣1≤x＜3；⑤当x＜0时，y随x增大而增大，其中结论正确的是_____（只需填序号）三、解答题14．已知函数y=-(m+2)-(m为常数),求当m为何值时:(1)y是x的一次函数?(2)y是x的二次函数?并求出此时纵坐标为-8的点的坐标.15．某广告公司设计一幅周长为12m的矩形广告牌，广告设计费用为1000元/m2.设矩形的一边长为xm，面积为ym2.(1)求出y与x之间的函数关系式，说明y是不是x的二次函数，并确定x的取值范围；(2)若x＝3时，广告牌的面积最大，求此时的广告费应为多少？16．如图，已知二次函数y=ax2+bx+3的图象交x轴于点A（1，0），B（3，0），交y轴于点C．（1）求这个二次函数的表达式；（2）点P是直线BC下方抛物线上的一动点，求△BCP面积的最大值；（3）直线x=m分别交直线BC和抛物线于点M，N，当△BMN是等腰三角形时，直接写出m的值．参考答案1．B【解析】【分析】根据二次函数的定义:形如,则y是x的二次函数进行判定即可.【详解】A选项,y＝3x－1是一次函数,不符合题意,B选项,y＝3x2－1是二次函数,符合题意,C选项, y＝(x＋1)2－x2整理后y=2x+1是一次函数,不符合题意,D选项, y＝ax2＋2x－3,二次项系数不确定是否等于0,不一定是二次函数,不符合题意,故选B.【点睛】本题主要考查二次函数的定义,解决本题的关键是要熟练掌握二次函数的定义.2．D【解析】【分析】根据二次函数定义，自变量的最高指数是二，且系数不为0，列出方程与不等式即可解答．【详解】根据题意，得：a2﹣2a﹣1=2解得a=3或﹣1又因为a2+a≠0即a≠0或a≠﹣1所以a=3．故选D．【点睛】解题关键是掌握二次函数的定义．3．C【解析】【分析】抛物线y=-x2的二次项系数为-1，故抛物线开口向下，顶点坐标（0，0），最高点为原点，对称轴为y轴，与y轴交于（0，0）．【详解】∵抛物线 y=-x 2的二次项系数为-1，∴抛物线开口向下，顶点坐标（0，0），A 正确；∴最高点为原点，对称轴为y 轴，B 、D 正确；与y 轴交于（0，0），C 错误，故选C ．【点睛】本题考查了基本二次函数y=ax 2的性质：顶点坐标（0，0），对称轴为y 轴，当a ＞0时，开口向上，当a ＜0时，开口向下．4．A【解析】由二次函数中，“当二次项系数为正时，图象开口向上，当二次项系数为负时，图象开口向下”结合“二次项系数的绝对值越大，图象的开口越大”分析可得：a b c d >>>.故选A.点睛：（1）二次函数()20y ax a =≠的图象的开口方向由“a 的符号”确定，当0a >时，图象的开口向上，当0a <时，图象的开口向下；（2）二次函数()20y axa =≠的图象的开口大小由a 的大小确定，当a 越大时，图象的开口越小.5．D 【解析】分析：根据二次函数的性质对照四个选项利用排除法即可得出结论.详解：根据二次函数的性质可知 的顶点坐标为（﹣3，2），故A 正确；对称轴为x =﹣3，故B 正确；开口向上，在对称轴右侧y 随x 增大而减小且函数有最小值2 ，故C 正确D 错误. 点睛：本题考查了二次函数的性质，在解题时可结合函数大致图象来判断.正确理解二次函数的基本性质是解题的关键.6．B【解析】【分析】根据抛物线的开口方向确定a ，根据抛物线与y 轴的交点确定c ，根据对称轴确定b ，根据抛物线与x 轴的交点确定b 2-4ac ，根据x=1时，y ＞0，确定a+b+c 的符号．【详解】∵抛物线开口向上，∴a ＞0，∵抛物线交于y轴的正半轴，∴c＞0，∴ac＞0，A错误；∵-＞0，a＞0，∴b＜0，∴B正确；∵抛物线与x轴有两个交点，∴b2-4ac＞0，C错误；当x=1时，y＞0，∴a+b+c＞0，D错误；故选B．【点睛】本题考查的是二次函数图象与系数的关系，二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y 轴的交点抛物线与x轴交点的个数确定．7．D【解析】分析：抛物线平移问题可以以平移前后两个解析式的顶点坐标为基准研究．详解：抛物线y=x2顶点为（0，0），抛物线y=（x﹣2）2﹣1的顶点为（2，﹣1），则抛物线y=x2向右平移2个单位，向下平移1个单位得到抛物线y=（x﹣2）2﹣1的图象．故选：D．点睛：本题考查二次函数图象平移问题，解答时最简单方法是确定平移前后的抛物线顶点，从而确定平移方向．8．D【解析】【分析】根据二次函数的图象可以判断a、b、的正负情况，从而可以得到一次函数经过哪几个象限，观察各选项即可得答案．【详解】由二次函数的图象可知，，，当时，，的图象经过二、三、四象限，观察可得D选项的图象符合，故选D．【点睛】本题考查二次函数的图象与性质、一次函数的图象与性质，认真识图，会用函数的思想、数形结合思想解答问题是关键.9．8【解析】分析：把（1，5）代入y=kx 2-x-2中，即可得到关于k 的一元一次方程，解这个方程即可求得k 的值． 详解：∵二次函数y=kx 2-x-2经过点（1，5），∴5=k-1-2，解得k=8；故答案为8．点睛：本题考查了二次函数图象上点的坐标特征，抛物线上的点的坐标适合解析式．10．–1【解析】根据抛物线的定义，得 ＝，解得：m=–1． 11．－1【解析】由于抛物线y=（m 2-2）x 2+2mx+1的对称轴经过点（-1，3），∴对称轴为直线x=-1，x=()22222b m a m -=--=-1， 解得m 1=-1，m 2=2．由于抛物线的开口向下，所以当m=2时，m 2-2=2＞0，不合题意，应舍去，∴m=-1．故答案为：-1.12．－2【解析】由题意得,所以a =-2. 13．①②③⑤【解析】【分析】利用抛物线与x 轴的交点个数可对①进行判断;利用抛物线的对称性得到抛物线与x 轴的一个交点坐标为(3,0),则可对②进行判断;由对称轴方程得到b=-2a,然后根据x=-1时函数值为0可得到3a+c=0,则可对③进行判断;根据二次函数的性质对④进行判断.【详解】①∵抛物线与x 轴有两个交点，∴△=b 2﹣4ac ＞0，∴4ac ＜b 2，结论①正确；②∵抛物线y=ax 2+bx+c （a≠0）的对称轴为直线x=1，与x 轴的一个交点坐标为（﹣1，0），∴抛物线与x 轴的另一交点坐标为（3，0），∴方程ax2+bx+c=0的两个根是x1=﹣1，x2=3，结论②正确；③∵抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，∴﹣=1，∴b=﹣2a．∵当x=﹣1时，y=0，∴a﹣b+c=0，即3a+c=0，结论③正确；④∵抛物线与x轴的交点坐标为（﹣1，0）、（3，0），∴当y＞0时，x的取值范围是﹣1＜x＜3，结论④错误；⑤∵抛物线开口向下，对称轴为直线x=1，∴当x＜0时，y随x增大而增大，结论⑤正确．综上所述：正确的结论有①②③⑤．故答案为：①②③⑤．【点睛】二次函数图象与系数的关系：对于二次函数y=ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a 与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右；常数项c决定抛物线与y轴交点位置：抛物线与y轴交于（0，c）；抛物线与x轴交点个数由△决定：△=b2-4ac＞0时，抛物线与x轴有2个交点；△=b2-4ac=0时，抛物线与x轴有1个交点；△=b2-4ac＜0时，抛物线与x轴没有交点．14．(1) m=±;(2) m=2, 纵坐标为-8的点的坐标是(±,-8).【解析】【分析】（1）根据一次函数的定义求m的值即可；（2）根据二次函数的定义求得m的值，从而求得二次函数的解析式，把y=-8代入解析式，求得x的值，即可得纵坐标为-8的点的坐标.【详解】(1)由y=-(m+2)(m为常数),y是x的一次函数,得解得m=±,当m=±时,y是x的一次函数.(2)由y=-(m+2)(m为常数),y是x的二次函数,得解得m=2,m=-2(不符合题意的要舍去),当m=2时,y 是x的二次函数,当y=-8时,-8=-4x2,解得x=±,故纵坐标为-8的点的坐标是(±,-8).【点睛】本题考查了一次函数的定义、二次函数的定义，解题关键是掌握一次函数与二次函数的定义．15．(1)y＝－x2＋6x，是，0＜x＜6 ；（2）9000元【解析】试题分析：（1）矩形的一边长为x m，根据矩形的周长是12m，可得矩形的另一边长为（6－x）m，根据矩形的面积公式即可得出y与x之间的函数表达式；（2）把x＝3代入函数的解析式得出y的值即为广告牌的最大面积，再乘以1000即为此时的广告费．试题解析：解：（1）由题意得出：y＝x(6－x)＝－x2＋6x，是二次函数，0＜x＜6；（2）当x＝3时，y＝－32＋3×6＝9，1000×9＝9000元，即此时的广告费应为9000元．点睛：此题主要考查了根据实际问题抽象出二次函数解析式以及求二次函数值，正确得出二次函数解析式是解题关键．16．（1）这个二次函数的表达式是y=x2﹣4x+3；（2）S△BCP最大=；（3）当△BMN是等腰三角形时，m的值为，﹣，1，2．【解析】分析：（1）根据待定系数法，可得函数解析式；（2）根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得PE的长，根据面积的和差，可得二次函数，根据二次函数的性质，可得答案；（3）根据等腰三角形的定义，可得关于m的方程，根据解方程，可得答案．详解：（1）将A（1，0），B（3，0）代入函数解析式，得＝＝，解得＝＝，这个二次函数的表达式是y=x2-4x+3；（2）当x=0时，y=3，即点C（0，3），设BC的表达式为y=kx+b，将点B（3，0）点C（0，3）代入函数解析式，得＝＝，解这个方程组，得＝＝直线BC的解析是为y=-x+3，过点P作PE∥y轴，交直线BC于点E（t，-t+3），PE=-t+3-（t2-4t+3）=-t2+3t，∴S△BCP=S△BPE+S CPE=（-t2+3t）×3=-（t-）2+，∵-＜0，∴当t=时，S△BCP最大=.（3）M（m，-m+3），N（m，m2-4m+3）MN=m2-3m，BM=|m-3|，当MN=BM时，①m2-3m=（m-3），解得m=，②m2-3m=-（m-3），解得m=-当BN=MN时，∠NBM=∠BMN=45°，m2-4m+3=0，解得m=1或m=3（舍）当BM=BN时，∠BMN=∠BNM=45°，-（m2-4m+3）=-m+3，解得m=2或m=3（舍），当△BMN是等腰三角形时，m的值为，-，1，2．点睛：本题考查了二次函数综合题，解（1）的关键是待定系数法；解（2）的关键是利用面积的和差得出二次函数，又利用了二次函数的性质，解（3）的关键是利用等腰三角形的定义得出关于m的方程，要分类讨论，以防遗漏．。

人教版九年级上册数学22.1二次函数的图像和性质同步训练一、单选题1．抛物线()252y x =--+的顶点坐标是（ ）A ．()5,2-B ．()5,2C ．()5,2--D ．()5,2- 2．当1a x a -≤≤时，二次函数243y x x =-+的最小值为8，则a 的值为（ ） A ．1-或5 B ．0或6 C ．1-或6 D ．0或5 3．将抛物线232y x =+向右平移1个单位，再向上平移3个单位后所得到的抛物线解析式为( ) A ．2)3(15y x =++B ．23(1)5y x =-+C ．23(1)1y x =+-D ．23(1)1y x =--4．如图是一次函数y kx b =+的图象，则二次函数22y kx bx =++的图象可能为（ ）A ．B ．C ．D ．5．若抛物线2y ax bx c =++上的()40P ，，Q 两点关于直线1x =对称，则Q 点的坐标为（ ）A ．()10-，B ．()20-，C ．()30-，D ．()40-，6．已知点()11,A y -，()22,B y -，()32,C y 三点都在二次函数22y x x m =--+的图象上，则1y ，2y ，3y 的大小关系为（ ）A ．123y y y >>B ．132y y y >>C ．312y y y >>D ．213y y y >> 7．如图，抛物线()20y ax bx c a =++≠的对称轴是直线1x =，则下列结论正确的是（ ）A ．0abc >B ．0a b c ++>C ．32b c <D ．b a c >+8．二次函数()20y ax bx c a =++≠的部分图像如图所示，图像过点()10-，对称轴为直线2x =，下列结论：①0abc >；①42a c b +>；①()42a b m am b +≤+（m 为常数）：①320b c ->．其中正确的个数是（ ）A ．1个B ．2个C ．3个D ．4个二、填空题9．若将抛物线22y x =的图象先向右平移5个单位，再向上平移4个单位，得到新抛物线的表达式为______．10．已知抛物线2()y a x h k =-+与x 轴有两个交点()()1,0,3,0A B -，抛物线2()y a x h m k =--+与x 轴的一个交点是()4,0，则m 的值是__________．11．已知二次函数223(0)y ax ax a =-++>，若点(,3)P m 在该函数的图象上，且0m ≠，则m 的值为________．12．请写出一个图像关于1x =对称的二次函数的表达式________．13．请任意写出一个图象开口向上，且顶点坐标为()12-，的二次函数解析式______． 14．函数()=--2y 2x 31的图象可由函数22y x =的图象沿x 轴向_______平移_______个单位，再沿y 轴向_______平移_______个单位得到．15．已知二次函数223y x x =+-，当41x -≤≤时，y 的取值范围为___________． 16．在平面直角坐标系中，若将抛物线2245y x x =-+先向右平移1个单位长度，再向下平移2个单位长度得到抛物线解析式为___________．三、解答题17．已知二次函数y ＝a (x ﹣1)2+4的图象经过点(﹣1，0)．(1)求这个二次函数的解析式；(2)判断这个二次函数的开口方向，对称轴和顶点坐标．18．已知二次函数y =ax 2+bx +3的图象经过点 (－3，0)，(2，－5)．(1)试确定此二次函数的解析式；(2)请你判断点P (－2，3)是否在这个二次函数的图象上？19．已知函数y=（m 2﹣m ）x 2+（m ﹣1）x+m+1．（1）若这个函数是一次函数，求m 的值；（2）若这个函数是二次函数，则m 的值应怎样？20．如图所示，已知抛物线25y ax bx =++（0a <）与x 轴交于点()1,0A -和点()5,0B ，与y 轴交点C ．(1)求抛物线的解折式；(2)点Q 是线段BC 上异于B ，C 的动点，过点Q 作QF x ⊥轴于点F ，交抛物线于点G ．当QCG 为直角三角形时，请直接写出．．．．点G 的坐标．参考答案： 1．B2．C3．B4．C5．B6．A7．A8．A9．()2254y x =-+10．5或111．212．()21y x =-，答案不唯一13．()212y x =--（答案不唯一）14． 右 3 下 115．45y -≤≤/54y ≥≥-16．()2221y x =-+17．(1)y ＝﹣(x ﹣1)2+4；(2)抛物线开口向下，顶点坐标为(1，4)，对称轴为直线x ＝1． 18．（1）y =﹣x 2﹣2x +3；（2）点P （﹣2，3）在这个二次函数的图象上， 19．(1)、m=0；(2)、m≠0且m≠1.20．(1)245y x x =-++(2)()3,8G 或()4,5G ．。

人教版九年级数学上册22.1 二次函数的图象和性质同步训练一、选择题1. 二次函数y＝2x2，y＝－2x2，y＝12x2的共同性质是()A．其图象开口都向上B．其图象的对称轴都是y轴C．其图象都有最高点D．y随x的增大而增大2. 若y＝ax2＋bx＋c，则由表格中的信息可知y与x之间的函数解析式是()A.y＝x2－4x＋3 B．y＝x2－3x＋4C．y＝x2－3x＋3 D．y＝x2－4x＋83. 若二次函数y＝x2＋mx的对称轴是x＝3，则关于x的方程x2＋mx＝7的解为()A. x1＝0，x2＝6B. x1＝1，x2＝7C. x1＝1，x2＝－7D. x1＝－1，x2＝74. 已知二次函数y＝－x2＋2bx＋c，当x＞1时，y的值随x值的增大而减小，则实数b的取值范围是()A．b≥－1 B．b≤－1C．b≥1 D．b≤15. 二次函数y＝2x2－3的图象是一条抛物线，下列关于该抛物线的说法，正确的是()A. 抛物线开口向下B. 抛物线经过点(2，3)C. 抛物线的对称轴是直线x＝1D. 抛物线与x轴有两个交点6. 将函数y＝x2的图象用下列方法平移后，所得的图象不经过点A(1，4)的是() A．向左平移1个单位长度B．向右平移3个单位长度C．向上平移3个单位长度D．向下平移1个单位长度7. 已知抛物线y＝2x2＋bx＋c的顶点坐标是(－1，－2)，则b与c的值分别为() A．－1，－2 B．4，－2C．－4，0 D．4，08. 已知二次函数y＝x2＋bx＋c与x轴只有一个交点，且图象过A(x1，m)、B(x1＋n，m)两点，则m、n的关系为()A. m＝12n B. m＝14n C. m＝12n2 D. m＝14n2二、填空题9. 某抛物线的形状、开口方向与抛物线y＝12x2－4x＋3相同，顶点坐标为(－2，1)，则该抛物线的函数解析式为________________．10. 已知抛物线y＝2(x－1)2上有两点(x1，y1)，(x2，y2)，且1＜x1＜x2，则y1与y2的大小关系是________．11. 抛物线y＝－8x2的开口向________，对称轴是________，顶点坐标是________；当x＞0时，y随x的增大而________，当x＜0时，y随x的增大而________．12. 已知二次函数的图象经过原点及点(－12，－14)，且图象与x轴的另一交点到原点的距离为1，则该二次函数的解析式为________________．13. 如图，抛物线y＝ax2＋bx＋c(a>0)的对称轴是过点(1，0)且平行于y轴的直线，若点P(4，0)在该抛物线上，则4a－2b＋c的值为________．14. 顶点坐标是(2，0)，且与抛物线y＝－3x2的形状、开口方向都相同的抛物线的解析式为________．15. 如图，抛物线y＝ax2＋bx＋c与x轴相交于点A，B(m＋2，0)，与y轴相交于点C，点D在该抛物线上，坐标为(m，c)，则点A的坐标是________．16. 如图，在平面直角坐标系xOy中，已知抛物线y＝ax2＋bx(a＞0)的顶点为C，与x轴的正半轴交于点A，它的对称轴与抛物线y＝ax2(a＞0)交于点B.若四边形ABOC是正方形，则b的值是________．三、解答题17. 已知抛物线y＝ax2经过点A(－2，－8)．(1)求此抛物线的解析式；(2)判断点B(－1，－4)是否在此抛物线上；(3)求出抛物线上纵坐标为－6的点的坐标．18. 在平面直角坐标系xOy中，抛物线y＝ax2＋bx＋2过B(－2，6)，C(2，2)两点．(1)试求抛物线的解析式；(2)记抛物线顶点为D，求△BCD的面积；(3)若直线y＝－12x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点，求b的取值范围．19. 如图，等腰直角三角形ABC的直角边与正方形MNPQ的边长均为10 cm，边CA与边MN在同一直线上，开始时点A与点M重合，△ABC沿MN方向以1 cm/s 的速度匀速运动，当点A与点N重合时，停止运动．设运动的时间为t s，运动过程中△ABC与正方形MNPQ重叠部分的面积为S cm2.(1)试写出S关于t的函数关系式，并指出自变量t的取值范围；(2)当MA＝2 cm时，重叠部分的面积是多少？20. 设函数y＝(x－1)[(k－1)x＋(k－3)](k是常数)．(1)当k取1和2时的函数y1和y2的图象如图所示，请你在同一直角坐标系中画出当k取0时函数的图象；(2)根据图象，写出你发现的一条结论；(3)将函数y2的图象向左平移4个单位，再向下平移2个单位，得到函数y3的图象，求函数y3的最小值．人教版九年级数学上册22.1 二次函数的图象和性质同步训练-答案一、选择题1. 【答案】B2. 【答案】A[解析] ∵x ＝1时，ax 2＝1，∴a ＝1.将(－1，8)，(0，3)分别代入y ＝x 2＋bx ＋c ，得⎩⎨⎧1－b ＋c ＝8，c ＝3，解得⎩⎨⎧b ＝－4，c ＝3.∴y 与x 之间的函数解析式是y ＝x 2－4x ＋3.故选A.3. 【答案】D【解析】∵二次函数y ＝x 2＋mx 的对称轴为x ＝－m2＝3，解得m ＝－6，则关于x 的方程为x 2－6x ＝7，解得，x 1＝－1，x 2＝7.4. 【答案】D [解析] 先根据抛物线的性质得到其对称轴为直线x ＝b ，且当x ＞b 时，y 的值随x 值的增大而减小．因为当x ＞1时，y 的值随x 值的增大而减小，所以b≤1.5. 【答案】D【解析】本题考查了二次函数的性质，由于2>0，所以抛物线的开口向上，所以A 选项错误；由于当x ＝2时，y ＝8－3＝5，所以B 选项错误；由于y ＝2x 2－3的对称轴是y 轴，所以C 选项错误；由2x 2－3＝0得b 2－4ac ＝24>0，则该抛物线与x 轴有两个交点，所以D 选项正确．6. 【答案】D [解析] A ．将函数y ＝x 2的图象向左平移1个单位长度得到函数y ＝(x ＋1)2的图象，它经过点(1，4)；B.将函数y ＝x 2的图象向右平移3个单位长度得到函数y ＝(x －3)2的图象，它经过点(1，4)；C.将函数y ＝x 2的图象向上平移3个单位长度得到函数y ＝x 2＋3的图象，它经过点(1，4)；D.将函数y ＝x 2的图象向下平移1个单位长度得到函数y ＝x 2－1的图象，它不经过点(1，4)．故选D.7. 【答案】D8. 【答案】D【解析】因为二次函数y ＝x 2＋bx ＋c 的图象与x 轴只有一个交点，∴b 2－4c ＝0，即c ＝b 24，由题意知，点A ，B 关于抛物线的对称轴对称，∴12AB＝|n|2＝－b 2－x 1，b ＝－|n|－2x 1, ∴c ＝（－|n|－2x 1）24＝|n|2＋4|n|x 1＋4x 214，∵A(x 1，m)在y ＝x 2＋bx ＋c 上，∴m ＝x 21＋bx 1＋c ，∴ m ＝x 21＋(－|n|－2x 1)· x 1＋|n|2＋4|n|x 1＋4x 214，化简整理得m ＝14n 2，故选D .二、填空题9. 【答案】y ＝12(x ＋2)2＋1 [解析] 已知抛物线的顶点坐标，可以设顶点式y ＝a(x －h)2＋k.又因为该抛物线的形状、开口方向与抛物线y ＝12x 2－4x ＋3相同，所以a ＝12，所以该抛物线的函数解析式是y ＝12(x ＋2)2＋1.10. 【答案】y 1<y 2[解析] ∵抛物线的解析式是y ＝2(x －1)2，∴其对称轴是直线x ＝1，抛物线的开口向上， ∴在对称轴右侧，y 随x 的增大而增大．又∵抛物线y ＝2(x －1)2上有两点(x 1，y 1)，(x 2，y 2)，且1＜x 1＜x 2，∴y 1<y 2.11. 【答案】下y 轴 (0，0) 减小 增大12. 【答案】y ＝x 2＋x 或y ＝－13x 2＋13x 【解析】依题意，所求函数有可能经过(－1，0)，(－12，－14) 或(1，0)，(－12，－14) .设所求函数解析式为y ＝ax 2＋bx ＋c ，图象经过原点，则c ＝0，当图象经过(－1，0)，(－12，－14)时，代入可求得a ＝b ＝1，即所求解析式为y ＝x 2＋x ; 当图象经过(1，0)，(－12，－14)时，代入可求得a ＝－13，b ＝13，即所求解析式为y ＝－13x 2＋13x .综上所述，所求函数的解析式为y＝x 2＋x 或y ＝－13x 2＋13x .13. 【答案】0 【解析】设抛物线与x 轴的另一个交点是Q ，∵抛物线的对称轴是过点(1，0)的直线，与x 轴的一个交点是P(4，0)，∴与x 轴的另一个交点Q(－2，0)，把(－2，0)代入解析式得：0＝4a －2b ＋c ，∴4a －2b ＋c ＝0.14. 【答案】y ＝－3(x －2)215. 【答案】(－2，0)【解析】如解图，过D 作DM ⊥x 轴于点M ，∴M(m ，0)，又B(m ＋2，0)，∴MB ＝2，由C(0，c)，D(m ，c)知：OC ＝DM ，即点C 、D 关于对称轴对称，故点O 、M 也关于对称轴对称，∴OA ＝MB ＝2，∴A(－2，0)．16. 【答案】－2 [解析] 抛物线y ＝ax 2＋bx 的顶点C 的坐标为(－b 2a ，－b 24a)．把x ＝－b 2a 代入y ＝ax 2，得点B 的坐标为(－b 2a ，b 24a )．在y ＝ax 2＋bx 中，令y ＝0，则ax 2＋bx ＝0，解得x 1＝0，x 2＝－b a ，∴A(－ba ，0)．∵四边形ABOC 为正方形，∴BC ＝OA ，∴2·b 24a ＝－b a ，即b 2＋2b ＝0.解得b ＝－2或b ＝0(不符合题意，舍去)．三、解答题17. 【答案】解：(1)∵抛物线y ＝ax 2经过点A(－2，－8)，∴4a ＝－8，解得a ＝－2，∴此抛物线的解析式为y ＝－2x 2.(2)当x ＝－1时，y ＝－2，∴点B(－1，－4)不在此抛物线上．(3)把y ＝－6代入y ＝－2x 2，得－2x 2＝－6，解得x ＝±3，∴抛物线上纵坐标为－6的点的坐标为(3，－6)，(－3，－6)．18. 【答案】解：(1)把B(－2，6)，C(2，2)代入抛物线的解析式得： ⎩⎨⎧6＝a·（－2）2＋b·（－2）＋22＝a·22＋b·2＋2，(1分)解得⎩⎪⎨⎪⎧a ＝12b ＝－1，(2分)∴抛物线的解析式为y ＝12x 2－x ＋2.(3分)(2)抛物线解析式化为顶点式：y ＝12(x －1)2＋32，则抛物线顶点D(1，32)，(4分) 如解图①所示，过点B 、D 、C 分别向x 轴作垂线，垂足分别为点M 、N 、H ，则有：S △BCD ＝S 梯形BMHC －S 梯形BMND －S 梯形DNHC ＝12(6＋2) ×4－12(6＋32)×3－12(32＋2) ×1 ＝3.(6分)解图①解图② (3)如解图②所示，连接BC ，∵直线BC 斜率k BC ＝2－62－（－2）＝－1＜－12，∴过点C 作直线MN 与直线y ＝－12x 平行，设直线MN 的解析式为y ＝－12x ＋b 1，代入C(2，2)， ∴b 1＝3.(7分)作直线EF 与抛物线相切，且与直线y ＝－12x 平行， 设直线EF 的解析式为y ＝－12x ＋b 2，联立抛物线解析式得， ⎩⎪⎨⎪⎧y ＝12x 2－x ＋2y ＝－12x ＋b 2， ∴x 2－x ＋4－2b 2＝ 0， ∵直线EF 与抛物线相切，∴b 2－4ac ＝0，即(－1)2－4(4－2b 2)＝0，(9分)∴b 2＝158，(11分) ∴158＜b ≤3.(12分)注：斜率知识为高中知识，但常渗透于中考压轴题，与二次函数相结合考查，做题时注意其性质的应用．19. 【答案】解：(1)设AB 与MQ 交于点R.∵△ABC 是等腰直角三角形，四边形MNPQ 是正方形， ∴△AMR 是等腰直角三角形． 由题意知，AM ＝MR ＝t ，∴S ＝S △AMR ＝12t·t ＝12t 2(0≤t≤10)．(2)当MA ＝2 cm ，即t ＝2时，重叠部分的面积是12×2×2＝2(cm 2)．20. 【答案】解：(1)当k ＝0时，y ＝－(x －1)(x ＋3)，所画图象如解图所示．(2分)(2)①k 取0和2时的函数图象关于点(0，2)中心对称，②函数y ＝(x －1)[(k －1)x ＋(k －3)](k 是常数)的图象都经过(1，0)和(－1，4)．(5分)(3)由题意可得y 2＝(x －1)[(2－1)x ＋(2－3)]＝(x －1)2，平移后的函数y 3的表达式为y 3＝(x －1＋4)2－2＝(x ＋3)2－2， 所以当x ＝－3时，函数y 3的最小值是－2.(8分)。

人教版九年上册数学22.1：二次函数的图形和性质+同步练习一．选择题（共15小题）1．下列函数中，是二次函数的是（）A．y＝3x﹣1B．y＝3x3﹣x2C．y＝1﹣x﹣x2D．y＝x2+ 2．开口向上，顶点坐标为（﹣9，3）的抛物线为（）A．y＝2（x﹣9）2﹣3B．y＝2（x+9）2+3C．y＝﹣2（x﹣9）2﹣3D．y＝﹣2（x+9）2+33．由二次函数y＝2（x﹣3）2+1，可知正确的结论是（）A．其图象的开口向下B．其图象的对称轴为过点（﹣3，0）且与y轴平行的直线C．其最小值为1D．当x＜3时，y随x的增大而增大4．已知抛物线y＝x2，则以下错误的是（）A．开口向上B．顶点是（0，0）C．对称轴是直线x＝0D．当x＝0时有y最大值为05．若函数y＝x m﹣1+mx+3是二次函数，则m＝（）A．﹣3B．3C．3或﹣3D．26．函数y＝ax2与y＝ax﹣a的图象大致是（）A．B．C．D．7．在二次函数y＝x2﹣3x﹣2的图象上的点是（）A．（1，1）B．（0，2）C．（2，﹣4）D．（﹣1，3）8．抛物线y＝4x2﹣4的顶点坐标是（）A．（0，﹣4）B．（﹣4，0）C．（0，4）D．（4，0）9．二次函数y＝ax2+bx+c的图象如图所示，则点P（a，）所在的象限是（）A．一B．二C．三D．四10．抛物线与x轴交点的横坐标为﹣2和1，且过点（2，8），它的关系式为（）A．y＝2x2﹣2x﹣4B．y＝﹣2x2+2x﹣4C．y＝x2+x﹣2D．y＝2x2+2x﹣411．将抛物线y＝4x2向上平移3个单位，再向左平移2个单位，所得抛物线的表达式为（）A．y＝4（x+2）2+3B．y＝4（x+2）2﹣3C．y＝4（x﹣2）2+3D．y＝4（x﹣2）2﹣312．在函数①y＝3x2；②y＝x2+1；③y＝﹣x2﹣3中，图象开口大小按题号顺序表示为（）A．①＞②＞③B．①＞③＞②C．②＞③＞①D．②＞①＞③13．如图，一次函数y＝ax+b与二次函数y＝ax2+bx+c的大致图象是（）A．B．C．D．14．已知函数y＝ax和y＝a（x+m）2+n，且a＞0，m＜0，n＜0，则这两个函数图象在同一坐标系内的大致图象是（）A．B．C．D．15．已知函数y＝x2﹣2x+k的图象经过点（，y1），（，y2），则y1与y2的大小关系为（）A．y1＞y2B．y1＝y2C．y1＜y2D．不能确定二．填空题（共8小题）16．抛物线上有三点（﹣2，3）、（2，﹣8）、（1，3），此抛物线的解析式为．17．将二次函数y＝5（x+2）2﹣4的图象向左平移3个单位，再向上平移8个单位，所得二次函数图象的表达式为．18．如果函数y＝（k﹣3）+kx+1是二次函数，那么k的值一定是．19．抛物线y＝﹣2x2的开口向，对称轴是，顶点是．20．函数y＝﹣x2+2x的图象是一条，开口向，对称轴是，顶点坐标为．21．二次函数y＝ax2+bx+c的图象如图所示，则a0，b0，c0，b2﹣4ac0，a+b+c0，a﹣b+c0．22．已知（﹣1，y1），（﹣3，y2），（，y3）在函数y＝3x2+6x+12的图象上，则y1，y2和y3的大小关系为．23．二次函数y＝ax2+bx+c的图象如图所示，则点A（a，b）在第象限．三．解答题（共7小题）24．已知二次函数当x＝3时，函数有最大值﹣1，且函数图象与y轴交于（0，﹣4），求该二次函数的关系式．25．已知二次函数的图象如图所示，求它的解析式．26．已知二次函数y＝﹣x2+x+2．（1）求函数图象的开口方向，顶点坐标及对称轴；（2）画出函数的图象；（3）由图象回答：当x为何值时，y＜0；当x为何值时，y＞0．27．已知抛物线经过三个点A（2，6），B（﹣1，0），C（3，0），那么二次函数的解析式是？它的顶点坐标是？28．已知抛物线y＝ax2经过（﹣1，4），且与直线y＝ax+8交于点A，B．（1）求直线和抛物线的解析式；（2）求△AOB的面积．29．填表并解答下列问题：（1）填表后发现：当x从﹣1开始增大时，预测哪一个函数的值先到达16．（2）请你编拟一个二次项系数是1的二次函数，使得当x＝4时，函数值为16．编拟的函数表达式是什么？30．已知函数y＝（k﹣2）是关于x的二次函数，求：（1）满足条件的k的值；（2）当K为何值时，抛物线有最高点？求出这个最高点，这时，x为何值时，y随x的增大而增大？（3）当k为何值时，函数有最小值？最小值是多少？这时，当x为何值时，y与x的增加而减小？人教版九年上册数学22.1：二次函数的图形和性质+同步练习参考答案一．选择题（共15小题）1．下列函数中，是二次函数的是（）A．y＝3x﹣1B．y＝3x3﹣x2C．y＝1﹣x﹣x2D．y＝x2+【解答】解：A、是一次函数，错误；B、最高次是3次，故错误；C、符合二次函数的一般形式y＝ax2+bx+c，正确；D、不是有关自变量的整式，故错误．故选：C．2．开口向上，顶点坐标为（﹣9，3）的抛物线为（）A．y＝2（x﹣9）2﹣3B．y＝2（x+9）2+3C．y＝﹣2（x﹣9）2﹣3D．y＝﹣2（x+9）2+3【解答】解：∵抛物线顶点坐标为（﹣9，3），∴可设抛物线解析式为y＝a（x+9）2+3，∵抛物线开口向上，∴a＞0，故选：B．3．由二次函数y＝2（x﹣3）2+1，可知正确的结论是（）A．其图象的开口向下B．其图象的对称轴为过点（﹣3，0）且与y轴平行的直线C．其最小值为1D．当x＜3时，y随x的增大而增大【解答】解：A、∵二次函数y＝2（x﹣3）2+1中，a＝2＞0，∴其图象的开口向上，故本选项错误；B、∵二次函数的解析式是y＝2（x﹣3）2+1，∴其图象的对称轴是直线x＝3，故本选项错误；C、∵由函数解析式可知其顶点坐标为（3，1），∴其最小值为1，故本选项正确；D、∵二次函数的图象开口向上，对称轴是直线x＝3，∴当x＜3时，y随x的增大而减小，故本选项错误．故选：C．4．已知抛物线y＝x2，则以下错误的是（）A．开口向上B．顶点是（0，0）C．对称轴是直线x＝0D．当x＝0时有y最大值为0【解答】解：由抛物线y＝x2可知，抛物线开口向上，顶点坐标为（0，0），故对称轴为直线x＝0，当x＝0时，y有最小值0，选项D错误，故选D．5．若函数y＝x m﹣1+mx+3是二次函数，则m＝（）A．﹣3B．3C．3或﹣3D．2【解答】解：∵函数y＝x m﹣1+mx+3是二次函数，∴m﹣1＝2，∴m＝3．故选：B．6．函数y＝ax2与y＝ax﹣a的图象大致是（）A．B．C．D．【解答】解：观察抛物线的图象可知a＞0，∴在直线y＝ax﹣a中，a＞0，﹣a＜0，直线经过一、三、四象限，故选B．7．在二次函数y＝x2﹣3x﹣2的图象上的点是（）A．（1，1）B．（0，2）C．（2，﹣4）D．（﹣1，3）【解答】解：A、x＝1时，y＝1﹣3﹣2＝﹣4，不符合；B、x＝0时，y＝﹣2，不符合；C、x＝2时，y＝4﹣6﹣2＝﹣4，满足；D、x＝﹣1时，y＝1+3﹣2＝2，不符合；故选：C．8．抛物线y＝4x2﹣4的顶点坐标是（）A．（0，﹣4）B．（﹣4，0）C．（0，4）D．（4，0）【解答】解：因为y＝4x2﹣4为抛物线解析式的顶点式，所以根据顶点式的坐标特点可知，抛物线的顶点坐标为（0，﹣4）．故选：A．9．二次函数y＝ax2+bx+c的图象如图所示，则点P（a，）所在的象限是（）A．一B．二C．三D．四【解答】解：由函数图象可得各系数的关系：a＞0，b＜0，c＞0，则a＞0，＜0，因此P（a，）位于第四象限．故选：D．10．抛物线与x轴交点的横坐标为﹣2和1，且过点（2，8），它的关系式为（）A．y＝2x2﹣2x﹣4B．y＝﹣2x2+2x﹣4C．y＝x2+x﹣2D．y＝2x2+2x﹣4【解答】解：由题意，设抛物线解析式为y＝a（x﹣1）（x+2），将（2，8）代入，可得8＝a（2﹣1）（2+2），解得a＝2，∴抛物线的解析式为：y＝2（x﹣1）（x+2），化简得，y＝2x2+2x﹣4．故选：D．11．将抛物线y＝4x2向上平移3个单位，再向左平移2个单位，所得抛物线的表达式为（）A．y＝4（x+2）2+3B．y＝4（x+2）2﹣3C．y＝4（x﹣2）2+3D．y＝4（x﹣2）2﹣3【解答】解：原抛物线的顶点为（0，0），向上平移3个单位，再向左平移2个单位，那么新抛物线的顶点为（﹣2，3）．）可设新抛物线的解析式为：y＝4（x﹣h）2+k，代入得：y＝4（x+2）2+3．故选：A．12．在函数①y＝3x2；②y＝x2+1；③y＝﹣x2﹣3中，图象开口大小按题号顺序表示为（）A．①＞②＞③B．①＞③＞②C．②＞③＞①D．②＞①＞③【解答】解：∵抛物线的开口大小是由二次项系数a的绝对值的大小确定，|a|越大则开口越小．∴开口大小按题号顺序表示为②＞③＞①．故选：C．13．如图，一次函数y＝ax+b与二次函数y＝ax2+bx+c的大致图象是（）A．B．C．D．【解答】解：A、由一次函数y＝kx+b的图象可得：a＞0，b＞0，此时二次函数y＝ax2+bx+c 的图象应该开口向上，对称轴x＝﹣＜0，错误；B、由一次函数y＝ax+b的图象可得：a＞0，此时二次函数y＝ax2+bx+c的图象应该开口向上，错误；C、由一次函数y＝ax+b的图象可得：a＞0，b＜0，此时二次函数y＝ax2+bx+c的图象应该开口向上，对称轴x＝﹣＞0，正确．D、由一次函数y＝ax+b的图象可得：a＜0，b＜0，此时二次函数y＝ax2+bx+c的图象应该开口向下，错误；故选：C．14．已知函数y＝ax和y＝a（x+m）2+n，且a＞0，m＜0，n＜0，则这两个函数图象在同一坐标系内的大致图象是（）A．B．C．D．【解答】解：由解析式y＝a（x+m）2+n可知，a＞0，图象开口向上，其顶点坐标为（﹣m，n），又因为m＜0，n＜0；所以顶点坐标在第四象限，排除A、D；C中，由二次函数图象可知a＜0，而由一次函数的图象可知a＞0，两者相矛盾，排除C；选项B正确．故选：B．15．已知函数y＝x2﹣2x+k的图象经过点（，y1），（，y2），则y1与y2的大小关系为（）A．y1＞y2B．y1＝y2C．y1＜y2D．不能确定【解答】解：∵对称轴为x＝﹣＝1，∴点（，y1）的对称点的横坐标为，即称点坐标为（，y2），∴y1＝y2．故选：B．二．填空题（共8小题）16．抛物线上有三点（﹣2，3）、（2，﹣8）、（1，3），此抛物线的解析式为y＝﹣x2﹣x+．【解答】解：设此抛物线的解析式为y＝ax2+bx+c，把点（﹣2，3）、（2，﹣8）、（1，3）代入得，解得．所以此抛物线的解析式为y＝﹣x2﹣x+，故答案为：y＝﹣x2﹣x+．17．将二次函数y＝5（x+2）2﹣4的图象向左平移3个单位，再向上平移8个单位，所得二次函数图象的表达式为y＝5（x+5）2+3．【解答】解：按照“左加右减，上加下减”的规律，y＝5（x+2）2﹣4的图象向左平移3个单位，再向上平移8个单位得到y＝5（x+5）2+3．故答案为：y＝5（x+5）2+3．18．如果函数y＝（k﹣3）+kx+1是二次函数，那么k的值一定是0．【解答】解：∵函数y＝（k﹣3）+kx+1是二次函数，∴k2﹣ak+2＝2，则k2﹣ak＝0，故k的值一定是0．故答案为：0．19．抛物线y＝﹣2x2的开口向向下，对称轴是y轴，顶点是（0，0）．【解答】解：∵抛物线y＝﹣2x2中，a＝﹣2＜0，b＝c＝0，∴抛物线开口向下，对称轴为y轴，顶点为（0，0）．故答案为：向下，y轴，（0，0）．20．函数y＝﹣x2+2x的图象是一条抛物线，开口向下，对称轴是x＝1，顶点坐标为（1，1）．【解答】解：∵a＝﹣1＜0，∴开口向下，对称轴x＝＝1，顶点坐标为（＝1，＝1），即（1，1）．∴函数y＝﹣x2+2x的图象是一条抛物线，开口向下，对称轴是x＝1，顶点坐标为（1，1）．21．二次函数y＝ax2+bx+c的图象如图所示，则a＞0，b＞0，c＜0，b2﹣4ac ＞0，a+b+c＞0，a﹣b+c＜0．【解答】解：（1）∵抛物线开口向上，∴a＞0，∵抛物线对称轴为直线x＝﹣＜0，∴b＞0；∵抛物线与y轴的交点在x轴下方，∴c＜0；（2）∵抛物线与x轴有两个交点∴b2﹣4ac＞0，（3）∵x＝1时，y＞0，∴a+b+c＞0；（4）∵x＝﹣1时，y＜0，∴a﹣b+c＜0；故答案为＞、＞、＜；＞；＞；＜．22．已知（﹣1，y1），（﹣3，y2），（，y3）在函数y＝3x2+6x+12的图象上，则y1，y2和y3的大小关系为y1＜y3＜y2．【解答】解：x＝﹣1时，y1＝3×（﹣1）2+6×（﹣1）+12＝3﹣6+12＝9，x＝﹣3时，y2＝3×（﹣3）2+6×（﹣3）+12＝27﹣18+12＝21，x＝时，y3＝3×（）2+6×+12＝0.75+3+12＝15.75，所以，y1＜y3＜y2．故答案为：y1＜y3＜y2．23．二次函数y＝ax2+bx+c的图象如图所示，则点A（a，b）在第二象限．【解答】解：由图象开口向下，∴a＜0，根据对称轴x＝﹣＞0，∴b＞0，∴点A（a，b）在第二象限，故答案为：二．三．解答题（共7小题）24．已知二次函数当x＝3时，函数有最大值﹣1，且函数图象与y轴交于（0，﹣4），求该二次函数的关系式．【解答】解：根据题意可知顶点坐标为（3，﹣1），设顶点式y＝a（x﹣3）2﹣1，把点（0，﹣4）代入，得﹣4＝a（﹣3）2﹣1，解得a＝﹣，∴y＝﹣（x﹣3）2﹣1．25．已知二次函数的图象如图所示，求它的解析式．【解答】解：∵抛物线顶点坐标为（1，4），代入抛物线顶点式y＝a（x﹣h）2+k（a≠0），得：y＝a（x﹣1）2+4，∵该抛物线又过点（﹣1，0），∴4a+4＝0，解得a＝﹣1，∴y＝﹣（x﹣1）2+4＝﹣x2+2x+3．26．已知二次函数y＝﹣x2+x+2．（1）求函数图象的开口方向，顶点坐标及对称轴；（2）画出函数的图象；（3）由图象回答：当x为何值时，y＜0；当x为何值时，y＞0．【解答】解：（1）y＝﹣x2+x+2＝﹣（x2﹣x）+2＝﹣（x﹣）2+，∴开口向下，顶点坐标为（，），对称轴为直线x＝；（2）图象如图：（3）根据图象可知：x＜﹣1或x＞2时，y＜0；﹣1＜x＜2时，y＞0．27．已知抛物线经过三个点A（2，6），B（﹣1，0），C（3，0），那么二次函数的解析式是？它的顶点坐标是？【解答】解：设二次函数解析式为y＝ax2+bx+c，根据题意得，解得．所以二次函数的解析式为y＝﹣2x2+4x+6，∵y＝﹣2x2+4x+6＝﹣2（x﹣1）2+8，∴抛物线的顶点坐标为（1，8）．28．已知抛物线y＝ax2经过（﹣1，4），且与直线y＝ax+8交于点A，B．（1）求直线和抛物线的解析式；（2）求△AOB的面积．【解答】解：（1）把（﹣1，4）代入y＝ax2得：a＝4，∴直线的解析式为y＝4x+8，抛物线的解析式为y＝4x2；（2）由题意知，联立y＝4x+8及y＝4x2，解得：x1＝2，x2＝﹣1，y1＝16，y2＝4，∴A（2，16），B（﹣1，4），如图所示，作BD垂直于x轴于点D，作AE垂直于x轴于点E，∴S△AOB＝S梯形ABDE﹣S△ODB﹣S△AOE＝×（4+16）×3﹣×1×4﹣×2×16＝12．29．填表并解答下列问题：（1）填表后发现：当x从﹣1开始增大时，预测哪一个函数的值先到达16．（2）请你编拟一个二次项系数是1的二次函数，使得当x＝4时，函数值为16．编拟的函数表达式是什么？【解答】解：填表．故答案为：1，3，5，7；1，0，1，4；（1）由于在第一象限内，两个函数都是y随x的增大而增大，当y＝16时，函数y1＝2x+3中的x＝6.5，函数y2＝x2中的x＝4，故函数y2＝x2值先到达16；（2）如：y3＝（x﹣4）2+16．30．已知函数y＝（k﹣2）是关于x的二次函数，求：（1）满足条件的k的值；（2）当K为何值时，抛物线有最高点？求出这个最高点，这时，x为何值时，y随x的增大而增大？（3）当k为何值时，函数有最小值？最小值是多少？这时，当x为何值时，y与x的增加而减小？【解答】解：（1）∵函数y＝（k﹣2）是关于x的二次函数，∴k满足k2﹣4k+5＝2，且k﹣2≠0，∴解得：k1＝1，k2＝3；（2）∵抛物线有最高点，∴图象开口向下，即k﹣2＜0，∴k＝1，∴最高点为（0，0），当x＜0时，y随x的增大而增大．（3）∵函数有最小值，∴图象开口向上，即k﹣2＞0，∴k＝3，∴最小值为0，当x＜0时，y随x的增大而减小．。

二次函数的图象性质课后练习1.函数()()2213ay a x a x a +=++-+．⑴当a 取什么值时，它为二次函数． ⑵当a 取什么值时，它为一次函数．【解析】考察一次函数和二次函数的概念．⑴二次函数： 2022110a a a a =⎧+=⎧⇒⎨⎨≠-+≠⎩⎩，进而0a =∴当0a =时，上述函数是二次函数．⑵一次函数：① 101303a a a a +==-⎧⎧⇒⎨⎨-≠≠⎩⎩，进而1a =-；②221(1)(3)0a a a ⎧+=⎨++-≠⎩，无解∴当1a =-时，上述函数是一次函数．【答案】⑴0a =；⑵1a =-2. 画出函数23(2)1y x =+-的图象，并指出图象顶点坐标、对称轴及函数最值．【解析】函数23(2)1y x =+-图象开口向上；对称轴为：2x =-；与y 轴的交点()011A ，；点A 关于对称轴对称的点()411B -，， 顶点坐标为()21E --，，最小值为1y =-；与x 轴的交点：令23(2)10x +-=，解得：12x =-，22x =-． 即：与x轴的交点为：20C ⎛⎫-+ ⎪ ⎪⎝⎭，20D ⎛⎫- ⎪ ⎪⎝⎭【答案】如图，顶点坐标为()21E --，，对称轴为：2x =-，最小值为1y =-．3.已知2y ax bx =+的图象如下左图所示，则y ax b =-的图象一定过（ ）A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象限【解析】通过图象可以看出：0a <，02ba->，∴0b >， ∴一次函数 y ax b =-的图象不经过第一象限. 【答案】C4. 在同一坐标系中一次函数y ax b =+和二次函数2y ax bx =+的图象可能为（ ）【解析】考察函数图像与系数的关系．选项A ：一次函数的a ＞0，b ＜0；二次函数的a ＞0，b ＜0． 选项B ：一次函数的a ＜0，b ＞0；二次函数的a ＞0，b ＞0． 选项C ：一次函数的a ＜0，b ＜0；二次函数的a ＜0，b ＞0． 选项D ：一次函数的a ＞0，b ＞0；二次函数的a ＜0，b ＜0．【答案】A5. 已知0a ≠，在同一直角坐标系中，函数y ax =与2y ax =的图象有可能是（ ）【解析】考察系数与函数图像的关系．A 选项：一次函数01a <<，二次函数1a ≥；B 选项：一次函数1a =-， 二次函数1a =；C 选项：一次函数 1a =-， 二次函数1a =；D 选项：一次函数1a =， 二次函数 1a =-．【答案】C 6.若二次函数222y ax bx a =++-（a ，b 为常数）的图象如下图，则a 的值为（ ）BCDACDA. 2-B.C. 1D.【解析】由图象可知220a -=且0a >，∴a =【答案】D7. 已知二次函数2y ax bx c =++的与x 的部分对应值如下表：A. 抛物线开口向上B. 抛物线与y 轴交于负半轴C. 当4x =时，0y >D. 方程20ax bx c ++=的正根在3与4之间【解析】 【答案】D8. 已知二次函数2()0y ax bx c a =++≠的图象如图所示，则下列结论：0ac >①；②方程20ax bx c ++=的两根之和大于0；y ③随x 的增大而增大；④0a b c -+<，其中正确的个数（ ）A ．4个B ．3个C ．2个D ．1个【解析】考察,,a b c 与函数图像之间的关系。

人教版2021年九年级上册22.1《二次函数的图象和性质》同步练习一．选择题1．下列函数中，一定是二次函数是（）A．y＝ax2+bx+c B．y＝x（﹣x+1）C．y＝（x﹣1）2﹣x2D．y＝2．抛物线y＝﹣x2+5x的开口方向是（）A．向左B．向右C．向上D．向下3．抛物线y＝（x﹣5）2的顶点坐标是（）A．（0，﹣5）B．（﹣5，0）C．（0，5）D．（5，0）4．抛物线y＝（x+3）2+2的对称轴是（）A．直线x＝3B．直线x＝﹣3C．直线x＝2D．直线x＝﹣25．对于二次函数y＝﹣2（x+3）2的图象，下列说法正确的是（）A．开口向上B．对称轴是直线x＝﹣3C．当x＞﹣4时，y随x的增大而减小D．顶点坐标为（﹣2，﹣3）6．一次函数y＝ax+b的图象如图所示，则二次函数y＝ax2+bx的图象可能是（）A．B．C．D．7．若点A（﹣1，y1），B（2，y2），C（3，y3）在二次函数y＝（x﹣2）2+3的图象上，则y1、y2、y3的大小关系是（）A．y3＜y2＜y1B．y2＜y3＜y1C．y1＜y3＜y2D．y1＜y2＜y38．已知二次函数y＝（a﹣1）x2，当x＞0时，y随x增大而增大，则实数a的取值范围是（）A．a＞0B．a＞1C．a≠1D．a＜19．关于x的二次函数y＝（x﹣h）2+3，当1≤x≤3时，函数有最小值4，则h的值为（）A．0或2B．2或4C．0或4D．0或2或410．如图是二次函数y＝ax2+bx+c图象的一部分，图象过点A（﹣5，0），对称轴为直线x＝﹣2，给出四个结论：①abc＞0；②4a﹣2b+c＞0；③若B（﹣3，y1）与C（﹣4，y2）是抛物线上两点，则y2＜y1；④5a+c＝0．其中，正确结论的个数是（）A．1B．2C．3D．4二．填空题11．若y＝（2﹣a）x是二次函数，则a＝．12．抛物线y＝3（x﹣1）2+2的对称轴是．13．二次函数y＝（x﹣1）2+2的图象与y轴交点坐标是．14．已知二次函数y＝﹣x2+4x图象的最高点是．15．将抛物线y＝5（x﹣1）2+3向左平移2个单位长度，再向下平移1个单位长度后得到的抛物线解析式为．16．已知A（﹣3，y1）、B（﹣1，y2）是二次函数y＝x2+4x﹣1图象上的两个点，则y1与y2的大小关系为y1y2．17．若二次函数y＝x2﹣2x+m图象的顶点在x轴上方，则实数m的取值范围是．18．如图，二次函数y＝ax2+bx+c（a≠0）的图象与x轴的正半轴交于点A，对称轴为直线x＝1．下面结论：①abc＜0；②2a+b＝0；③3a+c＞0；④方程ax2+bx+c＝0（a≠0）必有一个根大于﹣1且小于0．其中正确的是．（只填序号）三．解答题19．已知二次函数y＝x2+4x﹣6．（1）将二次函数的解析式化为y＝a（x﹣h）2+k的形式；（2）写出二次函数图象的开口方向、对称轴、顶点坐标．20．画出函数y＝x2﹣2x﹣8的图象．（1）先求顶点坐标：（，）；（2）列表x……y……（3）画图．21．已知二次函数y＝ax2+bx+3的图象经过点（﹣3，0），（2，﹣5）．（1）试确定此二次函数的解析式；（2）请你判断点P（﹣2，3）是否在这个二次函数的图象上？22．已知二次函数y＝ax2+bx+c中，函数y与自变量x的部分对应值如下表：x…01234…y…52125…（1）求该二次函数的关系式；（2）当x为何值时，y有最小值，最小值是多少？（3）若A（m，y1），B（c，y2）两点都在该函数的图象上，试比较y1与y2的大小．23．如图，以P为顶点的抛物线y＝（x﹣m）2+k交y轴于点A，经过点P的直线y＝﹣2x+3交y轴于点B．（1）用关于m的代数式表示k．（2）若点A在B的下方，且AB＝2，求该抛物线的函数表达式．24．如图，直线y＝x+n与抛物线y＝ax2+bx+5（a≠0）相交于A（1，2）和B（4，m）两点，点P是线段AB上异于A，B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．（1）求抛物线的解析式．（2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由．参考答案一．选择题1．解：A、当a＝0时，函数不是二次函数，故本选项不符合题意；B、符合二次函数的定义，是二次函数，故本选项符合题意；C、化简后不含二次项，不是二次函数，故本选项不符合题意；D、右边是分式，不是整式，不是二次函数，故本选项不符合题意；故选：B．2．解：∵y＝﹣x2+5x，a＝﹣1＜0，∴抛物线的开口向下．故选：D．3．解：抛物线y＝（x﹣5）2的顶点坐标是（5，0）．故选：D．4．解：由二次函数顶点式y＝a（x﹣h）2+k，可知在y＝（x+3）2+2中，h═﹣3，∴其对称轴为直线x═﹣3．故选：B．5．解：由y＝﹣2（x+3）2得抛物线开口向下，对称轴为直线x＝﹣3，顶点坐标为（﹣3，0），x≤﹣3时y随x增大而增大，x＞﹣3时y随x增大而减小．故选：B．6．解：∵一次函数y＝ax+b的图象经过一、二、四象限，∴a＜0，b＞0，∴二次函数y＝ax2+bx的图象：开口方向向下，对称轴在y轴右侧，故选：D．7．解：y＝（x﹣2）2+3的开口向上，对称轴为直线x＝2，∵A（﹣1，y1），B（2，y2），C（3，y3）在二次函数y＝（x﹣2）2+3的图象上，且B在对称轴上，A到对称轴的距离最远，∴y2＜y3＜y1，故选：B．8．解：∵二次函数y＝（a﹣1）x2，当x＞0时，y随x增大而增大，∴a﹣1＞0，∴a＞1，9．解：∵二次函数的对称轴为：x＝h，∴分为3种情况．①当h＜1时，当1≤x≤3时，y随x的增大而增大，∴当x＝1时取最小值，即：（1﹣h）2+3＝4，解得：h1＝0，h2＝2．由h＜1．得：h＝0；②当1≤h≤3时，y的最小值为顶点值，∵3≠4，∴l≤h≤3时，h无解；③当h＞3时，当1≤x≤3时，y随x的增大而减小，∴当x＝3时取最小值，即：（3﹣h）2+3＝4，解得：h1＝2，h2＝4，∵h＞3，∴h＝4；综上所述，h＝0或4，故选：C．10．解：由图象可知：开口向下，故a＜0，抛物线与y轴交点在x轴上方，故c＞0，∵对称轴x＝﹣＜0，∴b＜0，∴abc＞0，故①正确；由图象可知，x＝﹣2时，y＞0，∴4a﹣2b+c＞0，故②正确；当x＜﹣2时，此时y随x的增大而增大，∵﹣3＞﹣4，∴y2＜y1，故③正确；∵对称轴为x＝﹣2，∴﹣＝﹣2，∵点A（﹣5，0）关于对称轴的对称点是（1，0），∴a+b+c＝0，∴4a+a+c＝0，即5a+c＝0，故④正确；故选：D．二．填空题11．解：由题意得：a2﹣2＝2且2﹣a≠0，解得：a＝﹣2，故答案为：﹣2．12．解：∵抛物线y＝3（x﹣1）2+2，∴该抛物线对称轴是直线x＝1，故答案为：直线x＝1．13．解：∵y＝（x﹣1）2+2，当x＝0时，y＝1+2＝3，∴二次函数y＝（x﹣1）2+2的图象与y轴交点坐标是（0，3）；故答案为：（0，3）．14．解：由题意得，y＝﹣x2+4x＝﹣（x2﹣4x+4）+4＝﹣（x﹣2）2+4，二次函数图象的最高点的坐标为（2，4），故答案为：（2，4）．15．解：将抛物线y＝5（x﹣1）2+3向左平移2个单位长度，再向下平移1个单位长度后得到的抛物线解析式为：y ＝5（x﹣1+2）2+3﹣1，即y＝5（x+1）2+2．故答案为：y＝5（x+1）2+2．16．解：将A，B代入二次函数y＝x2+4x﹣1得：y1＝（﹣3）2+4×（﹣3）﹣1＝9﹣12﹣1＝﹣4，y2＝（﹣1）2+4×（﹣1）﹣1＝1﹣4﹣1＝﹣4，∴y1＝y2，故答案为：＝．17．解：抛物线的对称轴为x＝﹣＝﹣＝1，将x＝1代入y＝x2﹣2x+m，得y＝m﹣1，所以抛物线的顶点为（1，m﹣1），∴m﹣1＞0，∴m＞1，故答案为：m＞1．18．解：由图象可得，a＜0，b＞0，c＞0，则abc＜0，故①正确；∵﹣＝1，∴b＝﹣2a，∴2a+b＝0，故②正确；∵函数图象与x轴的正半轴交点在点（2，0）和（3，0）之间，对称轴是直线x＝1，∴函数图象与x轴的另一个交点在点（0，0）和点（﹣1，0）之间，故④正确；∴当x﹣1时，y＝a﹣b+c＜0，∴y＝a+2a+c＜0，∴3a+c＜0，故③错误；故答案为：①②④．三．解答题19．解：（1）y＝x2+4x+4﹣6﹣4＝（x2+4x+4）﹣10＝（x+2）2﹣10；（2）y＝（x+2）2﹣10，∵a＝1＞0，∴二次函数图象的开口向上．对称轴是直线x＝﹣2，顶点坐标是（﹣2，﹣10）．20．解：（1）y＝x2﹣2x﹣8＝（x﹣1）2﹣9∴其顶点坐标为（1，﹣9）故答案为：1，﹣9（2）列表x…﹣2﹣101234…y…0﹣5﹣8﹣9﹣8﹣50…（3）画图：21．解：（1）由题意得，，解得，，则二次函数的解析式为y＝﹣x2﹣2x+3；（2）当x＝﹣2时，y＝﹣（﹣2）2﹣2×（﹣2）+3＝3，∴点P（﹣2，3）在这个二次函数的图象上．22．解：（1）设抛物线解析式为y＝a（x﹣2）2+1，当x＝0时，y＝5，则4a+1＝5，解得a＝1．所以抛物线解析式为y＝（x﹣2）2+1；（2）当x＝2时，y有最小值，最小值为1；（3）当|m﹣2|＜|c﹣2|时，y1＜y2；当|m﹣2|＝|c﹣2|时，y1＝y2；当|m﹣2|＞|c﹣2|时，y1＞y2．23．解：（1）∵抛物线y＝（x﹣m）2+k，∴P（m，k），∵经过点P的直线y＝﹣2x+3交y轴于点B，∴k＝﹣2m+3．（2）∵y＝﹣2x+3交y轴于点B，∴y＝﹣2×0+3，∴B（0，3），∵AB＝2，∴A（0，1），把（0，1）代入y＝（x﹣m）2+k得，1＝m2+k，∵k＝﹣2m+3，∴1＝m2﹣2m+3，∴m＝2，代入k＝﹣2m+3得，k＝﹣1，∴抛物线的函数表达式为：y＝（x﹣2）2﹣1．24．解：（1）把A（1，2）代入y＝x+n得1+n＝2，解得n＝1，∴一次函数解析式为y＝x+1；把B（4，m）代入y＝x+1得m＝4+1＝5，即B（4，5），把A（1，2），B（4，5）代入y＝ax2+bx+5得，解得，∴抛物线解析式为y＝x2﹣4x+5；（2）存在．设P（t，t+1）（1≤t≤4），∵PC⊥x轴，∴C（t，t2﹣4t+5），∴PC＝t+1﹣（t2﹣4t+5）＝﹣t2+5t﹣4＝﹣（t﹣）2+，当t＝时，PC的长有最大值，最大值为．。