三年高考(2016-2018)数学(理)真题分类解析：专题02-常用逻辑用语

高考全国3卷理科数学真题2016-2018年共3套2018年普通高等学校招生全国统一考试理科数学（全国3卷）注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号，回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答案卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合{}|10A x x =-≥，{}012B =，，，则A B =A ．{}0B ．{}1C ．{}12，D ．{}012，， 2．()()1i 2i +-= A ．3i --B ．3i -+C ．3i -D ．3i +3．中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫棒头，凹进部分叫卯眼，图中木构件右边的小长方体是棒头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是4．若1sin 3α=，则cos 2α=A ．89B ．79C ．79-D ．89-5．522x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为A ．10B ．20C ．40D ．806．直线20x y ++=分别与x 轴，y 轴交于A ，B 两点，点P 在圆()2222x y -+=上，则ABP ∆面积的取值范围是A ．[]26，B ．[]48，C ．D ．⎡⎣7．函数422y x x =-++的图像大致为8．某群体中的每位成品使用移动支付的概率都为p ，各成员的支付方式相互独立，设X 为该群体的10位成员中使用移动支付的人数， 2.4DX =，()()46P X P X =<=，则p =A ．0．7B ．0．6C ．0．4D ．0．39．ABC △的内角A B C ，，的对边分别为a ，b ，c ，若ABC ∆的面积为2224a b c +-，则C =A ．π2B ．π3C ．π4D ．π610．设A B C D ，，，是同一个半径为4的球的球面上四点，ABC ∆为等边三角形且其面积为锥D ABC -体积的最大值为A ．B ．C ．D ．11．设12F F ，是双曲线22221x y C a b-=：（00a b >>，）的左，右焦点，O 是坐标原点．过2F 作C 的一条渐近线的垂线，垂足为P ．若1PF ，则C 的离心率为AB ．2C D12．设0.2log 0.3a =，2log 0.3b =，则A ．0a b ab +<<B ．0ab a b <+<C ．0a b ab +<<D ．0ab a b <<+ 二、填空题：本题共4小题，每小题5分，共20分。

三年高考（2016-2018）数学（理）专题01 集合考纲解读明方向1.掌握集合的表示方法,能判断元素与集合的“属于”关系、集合与集合之间的包含关系.2.深刻理解、掌握集合的元素,子、交、并、补集的概念.熟练掌握集合的交、并、补的运算和性质.能用韦恩(Venn)图表示集合的关系及运算.3.本部分内容在高考试题中多以选择题或填空题的形式出现,以函数、不等式等知识为载体,以集合语言和符号语言表示为表现形式,考查数学思想方法.4.本节内容在高考中分值约为5分,属中低档题.命题探究练扩展2018年高考全景展示1．【2018年理北京卷】已知集合A={x||x|<2}，B={–2，0，1，2}，则A B= A. {0，1} B. {–1，0，1} C. {–2，0，1，2} D. {–1，0，1，2}【答案】A【解析】，因此A B=，选A.点睛：认清元素的属性，解决集合问题时，认清集合中元素的属性(是点集、数集或其他情形)和化简集合是正确求解的两个先决条件.2．【2018年理新课标I卷】已知集合，则A. B.C. D.【答案】B点睛：该题考查的是有关一元二次不等式的解法以及集合的补集的求解问题，在解题的过程中，需要明确一元二次不等式的解集的形式以及补集中元素的特征，从而求得结果.3．【2018年全国卷Ⅲ理】已知集合，，则A. B. C. D.【答案】C【解析】由集合A得,所以，故答案选C.点睛：本题主要考查交集的运算，属于基础题。

4．【2018年理数全国卷II】已知集合，，，，则中元素的个数为A. 9B. 8C. 5D. 4【答案】A【解析】.，当时，；当时，；当时，；所以共有9个，选A.点睛：本题考查集合与元素关系，点与圆位置关系，考查学生对概念理解与识别.5．【2018年理数天津卷】设全集为R，集合，，则A. B. C. D.【答案】B【解析】由题意可得：，结合交集的定义可得：.本题选择B选项.点睛：本题主要考查交集的运算法则，补集的运算法则等知识，意在考查学生的转化能力和计算求解能力.6．【2018年江苏卷】已知集合，，那么________．【答案】{1，8}【解析】由题设和交集的定义可知：.点睛：本题考查交集及其运算，考查基础知识，难度较小.2017年高考全景展示1.【2017课标1，理1】1}，则（）A ．{|0}AB x x =<B ．A B =RC ．{|1}A B x x =>D ．A B =∅【答案】A 【解析】由31x <可得033x <，则0x <，即{|0}B x x =<，所以{|1}{|0}{|0}A B x x x x x x =<<=<，{|1}{|0}{|1}A B x x x x x x =<<=<，故选A.【考点】集合的运算，指数运算性质.【名师点睛】集合的交、并、补运算问题，应先把集合化简再计算，常常借助数轴或韦恩图进行处理.2.【2017课标II ，理】设集合{}1,2,4A =，{}240x x x m B =-+=.若{}1A B =，则B =（ ）A.{}1,3-B.{}1,0C.{}1,3D.{}1,5【答案】C【考点】 交集运算，元素与集合的关系【名师点睛】集合中元素的三个特性中的互异性对解题影响较大，特别是含有字母的集合，在求出字母的值后，要注意检验集合中的元素是否满足互异性.两个防范：一是不要忽视元素的互异性；二是保证运算的准确性.3．【2017课标3，理1】已知集合A ={}22(,)1x y x y +=│，B ={}(,)x y y x =│，则A B 中元素的个数为（ ）A ．3B ．2C ．1D ．0【答案】B【考点】 交集运算；集合中的表示方法.【名师点睛】求集合的基本运算时，要认清集合元素的属性(是点集、数集或其他情形)和化简集合，这是正确求解集合运算的两个先决条件.集合中元素的三个特性中的互异性对解题影响较大，特别是含有字母的集合，在求出字母的值后，要注意检验集合中的元素是否满足互异性.4.【2017北京，理1】若集合A ={x |–2<x <1}，B={x |x <–1或x >3}，则AB =（ ）（A ）{x |–2<x <–1} （B ）{x |–2<x <3}（C ）{x |–1<x <1} （D ）{x |1<x <3}【答案】A 【解析】利用数轴可知{}21A B x x =-<<-，故选A.【考点】集合的运算【名师点睛】集合分为有限集合和无限集合，若集合个数比较少时可以用列举法表示，若集合是无限集合就用描述法表示，注意代表元素是什么，集合的交、并、补运算问题，应先把集合化简再计算，常常借助数轴或韦恩图进行处理.5.【2017浙江，1】已知}11|{<<-=x x P ，}20{<<=x Q ，则=Q P （ ）A ．)2,1(-B ．)1,0(C ．)0,1(-D ．)2,1( 【答案】A【解析】利用数轴，取Q P ,所有元素，得=Q P )2,1(-．【考点】集合运算【名师点睛】对于集合的交、并、补运算问题，应先把集合化简再计算，常常借助数轴或韦恩图处理．6.【2017天津，理1】设集合{1,2,6},{2,4},{|15}A B C x x ===∈-≤≤R ，则()A B C =（ ）（A ）{2} （B ）{1,2,4} （C ）{1,2,4,6} （D ）{|15}x x ∈-≤≤R【答案】B【解析】(){1246}[15]{124}A B C =-=，，，，，， ,选B.【考点】 集合的运算【名师点睛】集合的交、并、补运算问题，应先把集合化简再计算，常常借助数轴或韦恩图进行处理.7.【2017江苏，1】已知集合{1,2}A =，2{,3}B a a =+，若{1}A B =则实数a 的值为 .【答案】1【解析】由题意1B ∈，显然233a +≥，所以1a =，此时234a +=，满足题意，故答案为1．【考点】元素的互异性【名师点睛】(1)认清元素的属性，解决集合问题时，认清集合中元素的属性(是点集、数集或其他情形)和化简集合是正确求解的两个先决条件.(2)注意元素的互异性.在解决含参数的集合问题时，要注意检验集合中元素的互异性，否则很可能会因为不满足“互异性”而导致解题错误.(3)防范空集.在解决有关,A B A B=∅⊆等集合问题时，往往忽略空集的情况，一定先考虑∅是否成立，以防漏解. 2016年高考全景展示1.【2016课标1,理1】设集合2430A x x x =-+< ,{}230x x ->,则A B = （ ） （A ）33,2⎛⎫-- ⎪⎝⎭ （B ）33,2⎛⎫- ⎪⎝⎭ （C ）31,2⎛⎫ ⎪⎝⎭ （D ）3,32⎛⎫ ⎪⎝⎭ 【答案】D考点：集合的交集运算【名师点睛】集合是每年中的必考题,一般以基础题形式出现,属得分题.解决此类问题一般要把参与运算的集合化为最简形式再进行运算,如果是不等式解集、函数定义域及值域有关数集之间的运算,常借助数轴进行运算.2.【2016新课标3理数】设集合{}{}|(2)(3)0,|0S x x x T x x =--≥=> ，则S T =（ ）(A) [2，3] (B)（-∞ ，2]U [3,+∞） (C) [3,+∞） (D)（0，2]U[3,+∞）【答案】D【技巧点拨】研究集合的关系，处理集合的交、并、补的运算问题，常用韦恩图、数轴等几何工具辅助解题．一般地，对离散的数集、抽象的集合间的关系及运算，可借助韦恩图，而对连续的集合间的运算及关系，可借助数轴的直观性，进行合理转化．3.【2016新课标2理数】已知集合{1,}A =2,3，{|(1)(2)0,}B x x x x =+-<∈Z ，则A B =（ ）（A ）{1} （B ）{12}， （C ）{0123}，，， （D ）{10123}-，，，， 【答案】C【解析】试题分析：集合B {x |1x 2,x Z}{0,1}=-<<∈=，而A {1,2,3}=，所以A B {0,1,2,3}=，故选C.考点： 集合的运算.【名师点睛】集合的交、并、补运算问题，应先把集合化简在计算，常常借助数轴或韦恩图处理.4. 【2016山东理数】设集合2{|2,},{|10},x A y y x B x x ==∈=-<R 则A B =（ ）（A ）(1,1)-（B ）(0,1) （C ）(1,)-+∞ （D ）(0,)+∞【答案】C【解析】 试题分析：}0|{>=y y A ，}11|{<<-=x x B ，则A B =∞（-1，+），选C. 考点：1.指数函数的性质；2.解不等式；3.及集合的运算.【名师点睛】本题主要考查集合的并集、补集，是一道基础题目.从历年题目看，集合的基本运算，是必考考点，也是考生必定得分的题目之一.本题与求函数值域、解不等式等相结合，增大了考查的覆盖面.5.【2016浙江理数】已知集合{}{}213,4,P x x Q x x =∈≤≤=∈≥R R 则()P Q ⋃=R ð（ ）A ．[2,3]B ．( -2,3 ]C ．[1,2)D ．(,2][1,)-∞-⋃+∞【答案】B【解析】 试题分析：根据补集的运算得{}[](]24(2,2),()(2,2)1,32,3=<=-∴=-=-R R Q x x P Q 痧．故选B ．考点：1、一元二次不等式；2、集合的并集、补集．【易错点睛】解一元二次不等式时，2x 的系数一定要保证为正数，若2x 的系数是负数，一定要化为正数，否则很容易出错．6.【2016年北京理数】已知集合{|||2}A x x =<，{1,0,1,2,3}B =-，则A B =（ ）A.{0,1}B.{0,1,2}C.{1,0,1}-D.{1,0,1,2}-【答案】C【解析】由}22|{<<-=x x A ，得}1,0,1{-=B A ，故选C.考点：集合交集.【名师点睛】1．首先要弄清构成集合的元素是什么(即元素的意义)，是数集还是点集，如集合)}|)y=，)},(yx=三者是不同的．yf{(xyf{x|(yfx=，)}|{x(2．集合中的元素具有三性——确定性、互异性、无序性，特别是互异性，在判断集合中元素的个数时，以及在含参的集合运算中，常因忽视互异性，疏于检验而出错．3．数形结合常使集合间的运算更简捷、直观．对离散的数集间的运算或抽象集合间的运算，可借助Venn图实施，对连续的数集间的运算，常利用数轴进行，对点集间的运算，则通过坐标平面内的图形求解，这在本质上是数形结合思想的体现和运用．4．空集是不含任何元素的集合，在未明确说明一个集合非空的情况下，要考虑集合为空集的可能．另外，不可忽视空集是任何元素的子集．7.【2016年四川理数】设集合{|22}=-≤≤，Z为整数集，则A ZA x x中元素的个数是（）（A）3 （B）4 （C）5 （D）6【答案】C【解析】由题意，{2,1,0,1,2}A Z=--，故其中的元素个数为5，选C.考点：集合中交集的运算.【名师点睛】集合的概念及运算一直是的热点，几乎是每年必考内容，属于容易题.一般是结合不等式，函数的定义域值域考查，解题的关键是结合韦恩图或数轴解答.8．【2016天津理数】已知集合{1,2,3,4},{|32},，则A B===-∈A B y y x x A=（）（A）{1}（B）{4}（C）{1,3}（D）{1,4}【答案】D【解析】试题分析：{1,4,7,10},A B{1,4}.B==选D.考点：集合运算【名师点睛】本题重点考查集合的运算，容易出错的地方是审错题意，误求并集，属于基本题，难点系数较小.一要注意培养良好的答题习惯，避免出现粗心错误，二是明确集合交集的考查立足于元素互异性，做到不重不漏.9.【2016江苏卷】已知集合则____________.【答案】{}1,2-【解析】试题分析：{1,2,3,6}{|23}{1,2}A B x x =--<<=-考点：集合运算【名师点睛】本题重点考查集合的运算，容易出错的地方是审错题意，属于基本题，难点系数较小.一要注意培养良好的答题习惯，避免出现粗心错误，二是明确江苏对于集合题的考查立足于列举法，强调对集合运算有关概念及法则的理解{1,2,3,6},{|23},A B x x =-=-<<=A B。

专题02 常用逻辑用语考纲解读明方向考点内容解读要求常考题型预测热度1.命题及四种命题间的关系1.理解命题的概念2.了解“若p,则q”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系Ⅱ选择题★★☆2.充分条件与必要条件理解必要条件、充分条件与充要条件的含义Ⅲ选择题★★★3.逻辑联结词“或”“且”“非”了解逻辑联结词“或”“且”“非”的含义Ⅱ选择题★★☆4.全称量词与存在量词1.理解全称量词和存在量词的意义2.能正确地对含有一个量词的命题进行否定Ⅲ选择题★★★分析解读1.本节主要考查充分必要条件的推理判断及四种命题间的相互关系问题.2.本部分内容在高考试题中多以选择题或填空题的形式出现,考查四种命题的真假判断以及充分条件、必要条件的判定和应用,考查学生的逻辑推理能力.3.会判断含有一个量词的全称命题或特称命题的真假,能正确地对含有一个量词的命题进行否定.4.能用逻辑联结词“或”“且”“非”正确地表达相关的数学内容.5.本节内容在高考中约为5分,属中低档题.命题探究练扩展2018年高考全景展示1．2018年浙江卷已知平面α，直线m ，n 满足m α，n α，则“m ∥n ”是“m ∥α”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 2．2018年理数天津卷设，则“”是“”的（ ）A. 充分而不必要条件B. 必要而不重复条件C. 充要条件D. 既不充分也不必要条件 3．2018年理北京卷设a ，b 均为单位向量，则“”是“a ⊥b ”的（ ）A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件2017年高考全景展示1.2017天津，理4设θ∈R ，则“||1212θ-<”是“sin 2θ<”的（ ） （A ）充分而不必要条件 （B ）必要而不充分条件（C ）充要条件（D ）既不充分也不必要条件 2.2017，理3已知命题p:()x x ∀+＞0,ln 1＞0；命题q ：若a ＞b ，则a b 22＞，下列命题为真命题的是（ ）（A ） ∧p q （B ）⌝∧p q （C ） ⌝∧p q （D ）⌝⌝∧p q3.2017北京，理13能够说明“设a ，b ，c 是任意实数．若a ＞b ＞c ，则ab ＞c ”是假命题的一组整数a ， b ，c 的值依次为______________________________．2016年高考全景展示1.2016浙江理数命题“*x n ∀∈∃∈，R N ，使得2n x >”的否定形式是（ ） A ．*x n ∀∈∃∈，R N ，使得2n x < B ．*x n ∀∈∀∈，R N ，使得2n x < C ．*x n ∃∈∃∈，R N ，使得2n x < D ．*x n ∃∈∀∈，R N ，使得2n x <2.2016理数已知直线a ，b 分别在两个不同的平面α，β内.则“直线a 和直线b 相交”是“平面α和平面β相交”的（ ）（A ）充分不必要条件 （B ）必要不充分条件 （C ）充要条件（D ）既不充分也不必要条件3. 2016天津理数设{a n }是首项为正数的等比数列，公比为q ，则“q <0”是“对任意的正整数n ，a 2n −1a 2n <0”的（ ）（A ）充要条件 （B ）充分而不必要条件 （C ）必要而不充分条件 （D ）既不充分也不必要条件。

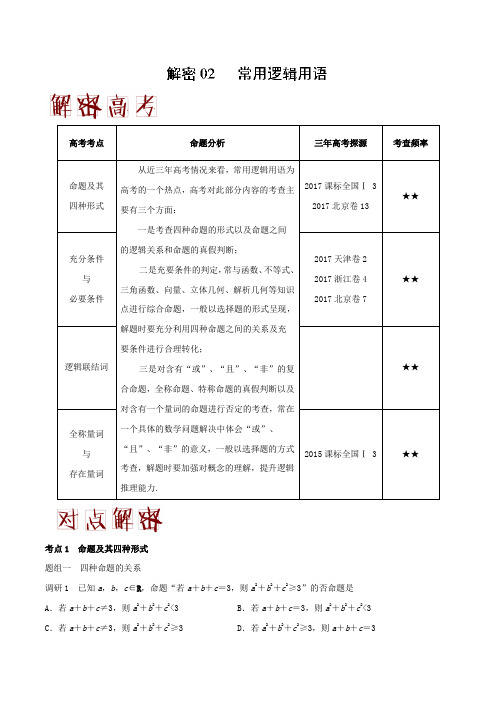
考点1 命题及其四种形式题组一四种命题的关系调研1 已知a，b，c∈R，命题“若a＋b＋c＝3，则a2＋b2＋c2≥3”的否命题是A．若a＋b＋c≠3，则a2＋b2＋c2<3 B．若a＋b＋c＝3，则a2＋b2＋c2<3 C．若a＋b＋c≠3，则a2＋b2＋c2≥3D．若a2＋b2＋c2≥3，则a＋b＋c＝3【解析】否命题是将原命题的条件和结论同时否定，故选A．题组二命题的真假判断调研2 原命题为“若z1，z2互为共轭复数，则|z1|＝|z2|”，关于其逆命题、否命题、逆否命题真假性的判断依次为A．真，假，真B．假，假，真C．真，真，假D．假，假，假【答案】B☆技巧点拨☆四种命题的关系及其真假的判断是高考中的一个热点，多以选择题的形式出现，难度一般不大，往往会结合其他知识点(如函数、不等式、三角、向量、立体几何等)进行综合考查.常见的解法如下：1．判断四种命题间关系的方法①由原命题写出其他三种命题，关键要分清原命题的条件和结论，将条件与结论互换即得逆命题，将条件与结论同时否定即得否命题，将条件与结论互换的同时进行否定即得逆否命题．②原命题和逆否命题、逆命题和否命题有相同的真假性，解题时注意灵活应用.2．命题真假的判断方法①给出一个命题，要判断它是真命题，需经过严格的推理证明；而要说明它是假命题，则只需举一反例即可．②由于原命题与其逆否命题为等价命题，有时可以利用这种等价性间接地证明命题的真假.考点2 充分条件与必要条件题组一直接判断充分、必要条件调研1 已知集合A＝{1，m2＋1}，B＝{2，4}，则“m＝3”是“A∩B＝{4}”的A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【解析】A∩B＝{4}⇒m2＋1＝4⇒m＝±3，故“m＝3”是“A∩B＝{4}”的充分不必要条件．调研2 “x<0”是“ln (x＋1)<0”的A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【答案】B⌝是q的必要而不充分条件，则p是⌝q的调研3 给定两个命题p，q.若pA．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件【答案】A【解析】根据题意可知，q⇒⌝p，但⌝p⇒/q，那么其逆否命题p⇒⌝q，但⌝q⇒/p，所以p是⌝q的充分而不必要条件．☆技巧点拨☆充分条件与必要条件的判断是高考命题的热点，多以选择题形式出现，作为载体，考查知识面广，常与函数、不等式、三角函数、平面向量、立体几何、解析几何等知识综合考查.常见的解法如下：1．命题判断法设“若p，则q”为原命题，那么：①原命题为真，逆命题为假时，则p是q的充分不必要条件；②原命题为假，逆命题为真时，则p是q的必要不充分条件；③当原命题与逆命题都为真时，则p是q的充要条件；④当原命题与逆命题都为假时，则p是q的既不充分也不必要条件．2．集合判断法若p以集合A的形式出现，q以集合B的形式出现，即p：A={x|p(x) }，q：B={x|q(x) }，则⊆，则p是q的充分条件；①若A B②若B A ⊆，则p 是q 的必要条件； ③若A B ⊂≠，则p 是q 的充分不必要条件； ④若B A ⊂≠，则p 是q 的必要不充分条件； ⑤若A B =，则p 是q 的充要条件；⑥若A B ⊂≠且B A ⊂≠，则p 是q 的既不充分也不必要条件. 3．等价转化法①p 是q 的充分不必要条件⇔q ⌝是p ⌝的充分不必要条件； ②p 是q 的必要不充分条件⇔q ⌝是p ⌝的必要不充分条件； ③p 是q 的充要条件⇔q ⌝是p ⌝的充要条件；④p 是q 的既不充分也不必要条件⇔q ⌝是p ⌝的既不充分也不必要条件.题组二 充分、必要条件的应用调研4 “不等式x 2−x ＋m >0在R 上恒成立”的一个必要不充分条件是 A ．m >14B ．0<m <1C ．m >0D ．m >1【答案】C☆技巧点拨☆充分、必要条件的应用主要涉及根据充分、必要条件求解参数的取值范围，具体解法如下：1．解决此类问题一般是把充分条件、必要条件或充要条件转化为集合之间的关系，然后根据集合之间的关系列出关于参数的不等式（组）求解.2．求解参数的取值范围时，一定要注意区间端点值的检验，尤其是利用两个集合之间的关系求解参数的取值范围时，不等式是否能够取等号决定端点值的取舍，处理不当容易出现漏解或增解的现象.考点3 含有逻辑联结词的命题真假的判断调研1 命题p：若sin x>sin y，则x>y；命题q：x2＋y2≥2xy.下列命题为假命题的是A．p∨q B．p∧qC．q D．⌝p【答案】B☆技巧点拨☆1．判断含逻辑联结词命题真假的方法与步骤(1)判断含有逻辑联结词的命题的真假的关键是对逻辑联结词“或”“且”“非”的含义的理解，应根据组成各个命题的语句中所出现的逻辑联结词进行命题结构与真假的判断．(2)判断命题真假的步骤：2．含逻辑联结词命题真假的等价关系(1)p∨q真⇔p，q至少一个真⇔(⌝p)∧(⌝q)假．(2)p∨q假⇔p，q均假⇔(⌝p)∧(⌝q)真．(3)p∧q真⇔p，q均真⇔(⌝p)∨(⌝q)假．(4) p∧q假⇔p，q至少一个假⇔(⌝p)∨(⌝q)真．(5)⌝p真⇔p假；⌝p假⇔p真.考点4 全称量词与存在量词题组一全称命题、特称命题的否定调研1 命题“所有实数的平方都是正数”的否定为A．所有实数的平方都不是正数B．有的实数的平方是正数C．至少有一个实数的平方是正数D．至少有一个实数的平方不是正数【答案】D【解析】该命题是全称命题，其否定是特称命题，即存在实数，它的平方不是正数，结合选项知D正确．☆技巧点拨☆全(特)称命题的否定全称命题与特称命题的否定与命题的否定有一定的区别，否定全称命题和特称命题时，一是要改写量词，全称量词改写为存在量词，存在量词改写为全称量词；二是要否定结论，而一般命题的否定只需直接否定结论即可．题组二全称命题、特称命题的真假判断调研2 命题p：∃x∈N，x3<x2；命题q：∀a∈(0，1)∪(1，＋∞)，函数f(x)＝log a(x−1)的图象过点(2，0)．则A．p假q真B．p真q假C．p假q假D．p真q真【答案】A☆技巧点拨☆全(特)称命题的真假判断①要判断一个全称命题是真命题，必须对限定的集合M中的每个元素x验证p(x)成立，但要判断一个全称命题为假命题，只要能举出集合M中的一个x＝x0，使得p(x0)不成立即可．②要判断一个特称命题为真命题，只要在限定的集合M中，找到一个x＝x0，使p(x0)成立即可，否则这一特称命题就是假命题.题组三由命题真假求参数或参数取值范围调研3 已知命题p：存在x0∈R，mx20＋1<1，q：对任意x∈R，x2＋mx＋1≥0，若p∨( q)为假命题，则实数m 的取值范围是 A ．(−∞，0)∪(2，＋∞) B ．(0，2] C ．[0，2] D ．R【答案】C☆技巧点拨☆根据命题的真假求参数取值范围的求解策略(1)含有逻辑联结词的命题要先确定构成命题的(一个或两个)简单命题的真假，求出此时命题成立的参数的取值范围，再求出含逻辑联结词的命题成立的参数的取值范围． (2)若给出命题为全称命题，则可转化为不等式的恒成立问题.1．（安徽省阜阳市临泉县第一中学2018届高三上学期第二次模拟）命题“若，则a c b c +>+”的逆否命题是 A ．若，则a c b c +≤+B ．若，则C ．若a c b c +>+，则D ．若，则a c b c +≤+【答案】B【解析】由逆否命题的概念可知，命题“若，则”的逆否命题是“若a c b c +≤+，则a b ≤”，故选B ．2．（辽宁省凌源市实验中学、凌源二中2018届高三12月联考）“0x ∀>，2sin x x >”的否定是 A ．0x ∀>，2sin x x <B ．0x ∀>，2sin x x ≤C ．00x ∃≤，002sin x x ≤D ．00x ∃>，002sin x x ≤【答案】D【解析】由全称命题的否定是特称命题，可知“0x ∀>，2sin x x >”的否定是00x ∃>，002sin x x ≤，故选D ．3．（广州市2018届高三第一学期第一次调研测试）设命题p ：1x ∀<，21x <，命题q ：00x ∃>，0012xx >，则下列命题中是真命题的是 A ．p q ∧B ．()p q ⌝∧C ．()p q ∧⌝D ．()()p q ⌝∧⌝【答案】B4．（安徽省淮南市第二中学、宿城第一中学2018届高三第四次考试）已知向量()()1,,,4x x ==a b ，则“2x =-”是“a 与b 反向”的 A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件【答案】C【解析】若a 与b 反向，则存在唯一的实数λ，使得()0λλ=<a b ，即 所以2x =-是“a 与b 反向”的充要条件，故选C ．5．（贵州省遵义航天高级中学2018届高三第一次模拟考试）下列命题中的假命题是A ．2,log 0x x ∃∈=RB ．,cos 1x x ∃∈=RC ．2,0x x ∀∈>RD ．,20x x ∀∈>R【答案】C6．（广东省百校联盟2018届高三第二次联考）已知命题:p “2x >”是“2log 5x >”的必要不充分条件；命题:q 若sin 3x =，则2cos2sin x x =，则下列命题为真命题的是 A ．p q ∧B ．()p q ⌝∧C ．()p q ∧⌝D ．()()p q ⌝∧⌝【答案】A【解析】由对数的性质可知：222log 4log 5=<，则命题p 是真命题；由三角函数的性质可知：若sin x =221sin 33x ⎛⎫== ⎪ ⎪⎝⎭，且211cos212sin 1233x x =-=-⨯=，所以命题q 是真命题.则所给的四个复合命题中，只有p q ∧是真命题. 故本题选择A 选项.7．（全国名校大联考2017−2018年度高三第三次联考）已知数列{}n a ，“{}n a 为等差数列”是“*n ∀∈N ，32n a n =+”的A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B【解析】“{}n a 为等差数列”，公差不一定是3，32n a n =+不一定成立，即充分性不成立； “*n ∀∈N ，32n a n =+”，则13n n a a --=，即{}n a 为等差数列，必要性成立， 所以“{}n a 为等差数列”是“*n ∀∈N ，32n a n =+”的必要而不充分条件，故选B ．8．（湖北省稳派教育2018届高三上学期第二次联考）若0,0x y >>，则“2x y +=不必要条件是 A ．x y =B ．2x y =C ．2x =且1y =D ．x y =或1y =【答案】C9．（辽宁省鞍山市第一中学2018届高三上学期第二次模拟考试（期中））已知命题“x ∃∈R ，使()212102x a x +-+≤”是假命题，则实数a 的取值范围是 A ．(),1-∞- B ．()1,3- C ．()3,-+∞D ．()3,1-【答案】B【解析】由原命题是假命题知其否定“x ∀∈R ，()212102x a x +-+>”是真命题，()2114202a ∴--⨯⨯<，解得13a -<<，故选B ． 10．（山东省淄博市部分学校2018届高三12月摸底考试）下列说法错误的是A ．命题“200020x x x ∃∈--=，R ”的否定是“220x x x ∀∈--≠，R ” B ．在ABC △中，“sin A ＞cos B ”是“ABC △为锐角三角形”的充要条件 C ．命题“若a =0，则ab =0”的否命题是“若0a ≠，则0ab ≠” D ．若p ∨q 为假命题，则p ，q 均为假命题 【答案】B【解析】命题“200020x x x ∃∈--=，R ”的否定是“220x x x ∀∈--≠，R ”，故A 正确； sin 30cos120︒>︒∴，在ABC △中，“sin A ＞cos B ”是“ABC △为锐角三角形”的必要不充分条件，故B 错误；命题“若a =0，则ab =0”的否命题是“若0a ≠，则0ab ≠”，故C 正确；若p ∨q 为假命题，则p ，q 均为假命题，故D 正确.所以错误的是B ．11．（江西省新余市第一中学2018届高三毕业班第四次模拟考试）已知,a b ∈R ，则“1ab =”是“直线10ax y +-=和直线10x by +-=平行”的A ．充分不必要条件B ．充要条件C ．必要不充分条件D ．既不充分又不必要条件【答案】C12．（河南省漯河市高级中学2018届高三上学期第四次模拟考试（12月））已知l ，m 是空间两条不重合的直线，α是一个平面，则“m α⊥，l 与m 无交点”是“l m ∥，l α⊥”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 【答案】B【解析】考虑充分性，若m α⊥，l 与m 无交点，则l m ∥或者l 与m 为异面直线，不一定有l α⊥，即充分性不成立；反之，若l m ∥，l α⊥，则一定有m α⊥，l 与m 无交点，即必要性成立，综上可得，“m α⊥，l 与m 无交点”是“l m ∥，l α⊥”的必要而不充分条件.本题选择B 选项.13．（广东省德庆县香山中学2018届高三第一次模拟试题）已知p ：∃x 0∈R ， 2010mx +≤，q ：∀x ∈R ，x 2＋mx ＋1>0.若p ∧q 为真命题，则实数m 的取值范围是A ．(−∞，−2)B ．[−2，0)C ．(−2，0)D ．[0，2]【答案】C 【解析】∵p ∧q 为真命题，∴p 、q 全为真命题，若p 真，则m <0；若q 真，则m 2−4<0，解得−2<m <2，所以m 的取值范围为(−2，0).本题选择C 选项.14．（江西省2018届高三年级阶段性检测考试（二））命题“24,0x x x ∀∈-≥R ”的否定是__________．【答案】24000,0x x x ∃∈-<R15．（湖北省咸宁市2018届高三重点高中11月联考）若“13x <<不必要条件，则正数a 的取值范围是____________． 【答案】30,5⎛⎤ ⎥⎝⎦【解析】由题意知()13，()21a x a -<， ①当210a -=时，即12a =(0,)+∞，符合题意； ②当210a -<时，即102a <<(0,)+∞，符合题意； ③当210a ->时，即12a >，所以021a x a <<-1325a <≤. 综上所述，正数a 的取值范围是30,5⎛⎤ ⎥⎝⎦.1．（2017新课标全国Ⅰ理科）设有下面四个命题1p ：若复数z 满足1z∈R ，则z ∈R ； 2p ：若复数z 满足2z ∈R ，则z ∈R ；3p ：若复数12,z z 满足12z z ∈R ，则12z z =；4p ：若复数z ∈R ，则z ∈R .其中的真命题为A ．13,p pB ．14,p pC ．23,p pD ．24,p p【答案】B2．（2015新课标全国Ⅰ理科）设命题p ：2,2n n n ∃∈>N ，则p ⌝为A ．2,2n n n ∀∈>NB ．2,2nn n ∃∈≤N C ．2,2n n n ∀∈≤ND ．2,=2n n n ∃∈N 【答案】C【解析】根据命题的否定的概念知，p ⌝:2,2n n n ∀∈≤N ，故选C ．【名师点睛】全称命题的否定与特称命题的否定是高考考查的重点，对特称命题的否定，将存在换成任意，后边变为其否定形式，注意全称命题与特称命题否定的书写，是常规题，很好地考查了学生对双基的掌握程度.3．（2017年高考天津卷）设x ∈R ，则“20x -≥”是“|1|1x -≤”的A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B4．（2017年高考浙江卷）已知等差数列{a n }的公差为d ，前n 项和为S n ，则“d >0”是“4652S S S +>”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 【答案】C【解析】由46511210212(510)S S S a d a d d +-=+-+=，可知当0d >时，有46520S S S +->，即4652S S S +>，反之，若4652S S S +>，则0d >，所以“d >0”是“S 4 + S 6>2S 5”的充要条件，选C ．【名师点睛】本题考查等差数列的前n 项和公式，通过套入公式与简单运算，可知4652S S S d +-=， 结合充分必要性的判断，若p q ⇒，则p 是q 的充分条件，若p q ⇐，则p 是q 的必要条件，该题“0d >”⇔“46520S S S +->”，故互为充要条件．5．（2017年高考北京卷）设m ,n 为非零向量，则“存在负数λ，使得λ=m n ”是“0<⋅m n ”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A【解析】若0λ∃<，使λ=m n ，则两向量,m n 反向，夹角是180︒，那么c o s 1800⋅=︒=-<m n m n m n ； 若0⋅<m n ，那么两向量的夹角为(]90,180︒︒，并不一定反向，即不一定存在负数λ，使得λ=m n ，所以是充分而不必要条件，故选A.6．（2017年高考北京卷）能够说明“设a ，b ，c 是任意实数．若a ＞b ＞c ，则a +b ＞c ”是假命题的一组整数a ，b ，c 的值依次为___________.【答案】−1，−2，−3（答案不唯一）。

中小学教学参考资料教学设计试卷随堂检测近3年（2016——2018）《常用逻辑用语》部分高考真题一．选择题（共22小题）1．（2018•天津）设x∈R，则“x3＞8”是“|x|＞2”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件2．（2018•天津）设x∈R，则“|x ﹣|＜”是“x3＜1”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件3．（2018•上海）已知a∈R，则“a＞1”是“＜1”的（）A．充分非必要条件B．必要非充分条件C．充要条件D．既非充分又非必要条件4．（2018•浙江）已知平面α，直线m，n满足m⊄α，n⊂α，则“m∥n”是“m∥α”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件5．（2018•北京）设a，b，c，d是非零实数，则“ad=bc”是“a，b，c，d成等比数列”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件6．（2018•北京）设，均为单位向量，则“|﹣3|=|3+|”是“⊥”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件7．（2016•四川）设p：实数x，y满足x＞1且y＞1，q：实数x，y满足x+y＞2，则p是q的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件8．（2017•天津）设x∈R，则“2﹣x≥0”是“|x﹣1|≤1”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件9．（2017•天津）设θ∈R，则“|θ﹣|＜”是“sinθ＜”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件10．（2017•北京）设，为非零向量，则“存在负数λ，使得=λ”是“•＜0”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件11．（2017•浙江）已知等差数列{a n}的公差为d，前n项和为S n，则“d＞0”是“S4+S6＞2S5”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件12．（2017•山东）已知命题p：∃x∈R，x2﹣x+1≥0．命题q：若a2＜b2，则a＜b，下列命题为真命题的是（）A．p∧q B．p∧￢q C．￢p∧q D．￢p∧￢q13．（2016•山东）已知直线a，b分别在两个不同的平面α，β内．则“直线a和直线b相交”是“平面α和平面β相交”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件14．（2016•浙江）命题“∀x∈R，∃n∈N*，使得n≥x2”的否定形式是（）A．∀x∈R，∃n∈N*，使得n＜x2B．∀x∈R，∀n∈N*，使得n＜x2C．∃x∈R，∃n∈N*，使得n＜x2D．∃x∈R，∀n∈N*，使得n＜x215．（2016•北京）设，是向量，则“||=||”是“|+|=|﹣|”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件16．（2016•浙江）已知函数f（x）=x2+bx，则“b＜0”是“f（f（x））的最小值与f（x）的最小值相等”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件17．（2016•天津）设x＞0，y∈R，则“x＞y”是“x＞|y|”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件18．（2016•上海）设a∈R，则“a＞1”是“a2＞1”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件19．（2016•天津）设{a n}是首项为正数的等比数列，公比为q，则“q＜0”是“对任意的正整数n，a2n﹣1+a2n＜0”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件20．（2016•上海）设f（x）、g（x）、h（x）是定义域为R的三个函数，对于命题：①f（x）+g（x）、f（x）+h（x）、g（x）+h（x）均为增函数，则f（x）、g（x）、h（x）中至少有一个增函数；②若f（x）+g（x）、f（x）+h（x）、g（x）+h（x）均是以T为周期的函数，则f（x）、g（x）、h （x）均是以T为周期的函数，下列判断正确的是（）A．①和②均为真命题B．①和②均为假命题C．①为真命题，②为假命题D．①为假命题，②为真命题近3年（2016——2018）《常用逻辑用语》部分高考真题参考答案与试题解析一．选择题（共22小题）1．（2018•天津）设x∈R，则“x3＞8”是“|x|＞2”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件【分析】由x3＞8得到|x|＞2，由|x|＞2不一定得到x3＞8，然后结合查充分条件、必要条件的判定方法得答案．【解答】解：由x3＞8，得x＞2，则|x|＞2，反之，由|x|＞2，得x＜﹣2或x＞2，则x3＜﹣8或x3＞8．即“x3＞8”是“|x|＞2”的充分不必要条件．故选：A．【点评】本题考查充分条件、必要条件及其判定方法，是基础题．2．（2018•天津）设x∈R，则“|x﹣|＜”是“x3＜1”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件【分析】先解不等式，再根据充分条件和必要条件的定义即可求出．【解答】解：由|x﹣|＜可得﹣＜x﹣＜，解得0＜x＜1，由x3＜1，解得x＜1，故“|x﹣|＜”是“x3＜1”的充分不必要条件，故选：A．【点评】本题考查了不等式的解法和充分必要条件，属于基础题．3．（2018•上海）已知a∈R，则“a＞1”是“＜1”的（）A．充分非必要条件B．必要非充分条件C．充要条件D．既非充分又非必要条件【分析】“a＞1”⇒“”，“”⇒“a＞1或a＜0”，由此能求出结果．【解答】解：a∈R，则“a＞1”⇒“”，“”⇒“a＞1或a＜0”，∴“a＞1”是“”的充分非必要条件．故选：A．【点评】本题考查充分条件、必要条件的判断，考查不等式的性质等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．4．（2018•浙江）已知平面α，直线m，n满足m⊄α，n⊂α，则“m∥n”是“m∥α”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【分析】根据线面平行的定义和性质以及充分条件和必要条件的定义进行判断即可．【解答】解：∵m⊄α，n⊂α，∴当m∥n时，m∥α成立，即充分性成立，当m∥α时，m∥n不一定成立，即必要性不成立，则“m∥n”是“m∥α”的充分不必要条件．故选：A．【点评】本题主要考查充分条件和必要条件的判断，根据线面平行的定义和性质是解决本题的关键，是基础题．5．（2018•北京）设a，b，c，d是非零实数，则“ad=bc”是“a，b，c，d成等比数列”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【分析】根据充分条件和必要条件的定义结合等比数列的性质进行判断即可．【解答】解：若a，b，c，d成等比数列，则ad=bc，反之数列﹣1，﹣1，1，1．满足﹣1×1=﹣1×1，但数列﹣1，﹣1，1，1不是等比数列，即“ad=bc”是“a，b，c，d成等比数列”的必要不充分条件．故选：B．【点评】本题主要考查充分条件和必要条件的判断，结合等比数列的性质是解决本题的关键．6．（2018•北京）设，均为单位向量，则“|﹣3|=|3+|”是“⊥”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【分析】根据向量数量积的应用，结合充分条件和必要条件的对应进行判断即可．【解答】解：∵“|﹣3|=|3+|”∴平方得||2+9||2﹣6•=9||2+||2+6•，即1+9﹣6•=9+1+6•，即12•=0，则•=0，即⊥，则“|﹣3|=|3+|”是“⊥”的充要条件，故选：C．【点评】本题主要考查充分条件和必要条件的判断，结合向量数量积的公式进行转化是解决本题的关键．7．（2017•上海）已知a、b、c为实常数，数列{x n}的通项x n=an2+bn+c，n∈N*，则“存在k∈N*，使得x100+k、x200+k、x300+k成等差数列”的一个必要条件是（）A．a≥0B．b≤0C．c=0D．a﹣2b+c=0【分析】由x100+k，x200+k，x300+k成等差数列，可得：2x200+k=x100+k x300+k，代入化简即可得出．【解答】解：存在k∈N*，使得x100+k、x200+k、x300+k成等差数列，可得：2[a（200+k）2+b（200+k）+c]=a（100+k）2+b（100+k）+c+a（300+k）2+b（300+k）+c，化为：a=0．∴使得x100+k，x200+k，x300+k成等差数列的必要条件是a≥0．故选：A．【点评】本题考查了等差数列的通项公式、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．8．（2017•天津）设x∈R，则“2﹣x≥0”是“|x﹣1|≤1”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件【分析】求出不等式的等价条件，结合充分条件和必要条件的定义进行判断即可．【解答】解：由2﹣x≥0得x≤2，由|x﹣1|≤1得﹣1≤x﹣1≤1，得0≤x≤2．则“2﹣x≥0”是“|x﹣1|≤1”的必要不充分条件，故选：B．【点评】本题主要考查充分条件和必要条件的判断，结合充分条件和必要条件的定义以及不等式的性质是解决本题的关键．9．（2017•天津）设θ∈R，则“|θ﹣|＜”是“sinθ＜”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件【分析】运用绝对值不等式的解法和正弦函数的图象和性质，化简两已知不等式，结合充分必要条件的定义，即可得到结论．【解答】解：|θ﹣|＜⇔﹣＜θ﹣＜⇔0＜θ＜，sinθ＜⇔﹣+2kπ＜θ＜+2kπ，k∈Z，则（0，）⊊（﹣+2kπ，+2kπ），k∈Z，可得“|θ﹣|＜”是“sinθ＜”的充分不必要条件．故选：A．【点评】本题考查充分必要条件的判断，同时考查正弦函数的图象和性质，运用定义法和正确解不等式是解题的关键，属于基础题．10．（2017•北京）设，为非零向量，则“存在负数λ，使得=λ”是“•＜0”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【分析】，为非零向量，存在负数λ，使得=λ，则向量，共线且方向相反，可得•＜0．反之不成立，非零向量，的夹角为钝角，满足•＜0，而=λ不成立．即可判断出结论．【解答】解：，为非零向量，存在负数λ，使得=λ，则向量，共线且方向相反，可得•＜0．反之不成立，非零向量，的夹角为钝角，满足•＜0，而=λ不成立．∴，为非零向量，则“存在负数λ，使得=λ”是•＜0”的充分不必要条件．故选：A．【点评】本题考查了向量共线定理、向量夹角公式、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．11．（2017•浙江）已知等差数列{a n}的公差为d，前n项和为S n，则“d＞0”是“S4+S6＞2S5”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【分析】根据等差数列的求和公式和S4+S6＞2S5，可以得到d＞0，根据充分必要条件的定义即可判断．【解答】解：∵S4+S6＞2S5，∴4a1+6d+6a1+15d＞2（5a1+10d），∴21d＞20d，∴d＞0，故“d＞0”是“S4+S6＞2S5”充分必要条件，故选：C．【点评】本题借助等差数列的求和公式考查了充分必要条件，属于基础题12．（2017•山东）已知命题p：∃x∈R，x2﹣x+1≥0．命题q：若a2＜b2，则a＜b，下列命题为真命题的是（）A．p∧q B．p∧￢q C．￢p∧q D．￢p∧￢q【分析】先判断命题p，q的真假，进而根据复合命题真假的真值表，可得答案．【解答】解：命题p：∃x=0∈R，使x2﹣x+1≥0成立．故命题p为真命题；当a=1，b=﹣2时，a2＜b2成立，但a＜b不成立，故命题q为假命题，故命题p∧q，￢p∧q，￢p∧￢q均为假命题；命题p∧￢q为真命题，故选：B．【点评】本题以命题的真假判断与应用为载体，考查了复合命题，特称命题，不等式与不等关系，难度中档．13．（2016•山东）已知直线a，b分别在两个不同的平面α，β内．则“直线a和直线b相交”是“平面α和平面β相交”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【分析】直线a，b分别在两个不同的平面α，β内，则“直线a和直线b相交”⇒“平面α和平面β相交”，反之不成立．【解答】解：直线a，b分别在两个不同的平面α，β内，则“直线a和直线b相交”⇒“平面α和平面β相交”，反之不成立．∴“直线a和直线b相交”是“平面α和平面β相交”的充分不必要条件．故选：A．【点评】本题考查了空间位置关系、简易逻辑的判定方法，考查了推理能力，属于基础题．14．（2016•浙江）命题“∀x∈R，∃n∈N*，使得n≥x2”的否定形式是（）A．∀x∈R，∃n∈N*，使得n＜x2B．∀x∈R，∀n∈N*，使得n＜x2C．∃x∈R，∃n∈N*，使得n＜x2D．∃x∈R，∀n∈N*，使得n＜x2【分析】特称命题的否定是全称命题，全称命题的否定是特称命题，依据规则写出结论即可【解答】解：“∀x∈R，∃n∈N*，使得n≥x2”的否定形式是“∃x∈R，∀n∈N*，使得n＜x2“故选：D．【点评】本题考查命题的否定，解本题的关键是掌握住特称命题的否定是全称命题，书写答案是注意量词的变化．15．（2016•浙江）已知实数a，b，c．（）A．若|a2+b+c|+|a+b2+c|≤1，则a2+b2+c2＜100B．若|a2+b+c|+|a2+b﹣c|≤1，则a2+b2+c2＜100C．若|a+b+c2|+|a+b﹣c2|≤1，则a2+b2+c2＜100D．若|a2+b+c|+|a+b2﹣c|≤1，则a2+b2+c2＜100【分析】本题可根据选项特点对a，b，c设定特定值，采用排除法解答．【解答】解：A．设a=b=10，c=﹣110，则|a2+b+c|+|a+b2+c|=0≤1，a2+b2+c2＞100；B．设a=10，b=﹣100，c=0，则|a2+b+c|+|a2+b﹣c|=0≤1，a2+b2+c2＞100；C．设a=100，b=﹣100，c=0，则|a+b+c2|+|a+b﹣c2|=0≤1，a2+b2+c2＞100；故选：D．【点评】本题主要考查命题的真假判断，由于正面证明比较复杂，故利用特殊值法进行排除是解决本题的关键．16．（2016•浙江）已知函数f（x）=x2+bx，则“b＜0”是“f（f（x））的最小值与f （x）的最小值相等”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【分析】求出f（x）的最小值及极小值点，分别把“b＜0”和“f（f（x））的最小值与f（x）的最小值相等”当做条件，看能否推出另一结论即可判断．【解答】解：f（x）的对称轴为x=﹣，f min（x）=﹣．（1）若b＜0，则﹣＞﹣，∴当f（x）=﹣时，f（f（x））取得最小值f（﹣）=﹣，即f（f（x））的最小值与f（x）的最小值相等．∴“b＜0”是“f（f（x））的最小值与f（x）的最小值相等”的充分条件．（2）设f（x）=t，则f（f（x））=f（t），∴f（t）在（﹣，﹣）上单调递减，在（﹣，+∞）上单调递增，若f（f（x））=f（t）的最小值与f（x）的最小值相等，则﹣≤﹣，解得b≤0或b≥2．∴“b＜0”不是“f（f（x））的最小值与f（x）的最小值相等”的必要条件．故选：A．【点评】本题考查了二次函数的性质，简易逻辑关系的推导，属于基础题．17．（2016•天津）设x＞0，y∈R，则“x＞y”是“x＞|y|”的（）A．充要条件B．充分不必要条件C．必要而不充分条件D．既不充分也不必要条件【分析】直接根据必要性和充分判断即可．【解答】解：设x＞0，y∈R，当x＞0，y=﹣1时，满足x＞y但不满足x＞|y|，故由x＞0，y∈R，则“x＞y”推不出“x＞|y|”，而“x＞|y|”⇒“x＞y”，故“x＞y”是“x＞|y|”的必要不充分条件，故选：C．【点评】本题考查了不等式的性质、充要条件的判定，考查了推理能力与计算能力，属于基础题．18．（2016•上海）设a∈R，则“a＞1”是“a2＞1”的（）A．充分非必要条件B．必要非充分条件C．充要条件D．既非充分也非必要条件【分析】根据不等式的关系，结合充分条件和必要条件的定义进行判断即可．【解答】解：由a2＞1得a＞1或a＜﹣1，即“a＞1”是“a2＞1”的充分不必要条件，故选：A．【点评】本题主要考查充分条件和必要条件的判断，利用不等式的关系结合充分条件和必要条件的定义是解决本题的关键，比较基础．19．（2016•四川）设p：实数x，y满足x＞1且y＞1，q：实数x，y满足x+y＞2，则p是q的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【分析】由x＞1且y＞1，可得：x+y＞2，反之不成立，例如取x=3，y=．【解答】解：由x＞1且y＞1，可得：x+y＞2，反之不成立：例如取x=3，y=．∴p是q的充分不必要条件．故选：A．【点评】本题考查了不等式的性质、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．20．（2016•北京）设，是向量，则“||=||”是“|+|=|﹣|”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【分析】根据向量模相等的几何意义，结合充要条件的定义，可得答案．【解答】解：若“||=||”，则以，为邻边的平行四边形是菱形；若“|+|=|﹣|”，则以，为邻边的平行四边形是矩形；故“||=||”是“|+|=|﹣|”的既不充分也不必要条件；故选：D．【点评】本题考查的知识点是充要条件，向量的模，分析出“||=||”与“|+|=|﹣|”表示的几何意义，是解答的关键．21．（2016•天津）设{a n}是首项为正数的等比数列，公比为q，则“q＜0”是“对任意的正整数n，a2n+a2n＜0”的（）﹣1A．充要条件B．充分而不必要条件C．必要而不充分条件D．既不充分也不必要条件【分析】利用必要、充分及充要条件的定义判断即可．【解答】解：{a n}是首项为正数的等比数列，公比为q，+a2n＜0”不一定成立，若“q＜0”是“对任意的正整数n，a2n﹣1例如：当首项为2，q=﹣时，各项为2，﹣1，，﹣，…，此时2+（﹣1）=1＞0，+（﹣）=＞0；+a2n＜0”，前提是“q＜0”，而“对任意的正整数n，a2n﹣1+a2n＜0”的必要而不充分条件，则“q＜0”是“对任意的正整数n，a2n﹣1故选：C．【点评】此题考查了必要条件、充分条件与充要条件的判断，熟练掌握各自的定义是解本题的关键．22．（2016•上海）设f（x）、g（x）、h（x）是定义域为R的三个函数，对于命题：①f（x）+g（x）、f（x）+h（x）、g（x）+h（x）均为增函数，则f（x）、g（x）、h（x）中至少有一个增函数；②若f（x）+g（x）、f（x）+h（x）、g（x）+h （x）均是以T为周期的函数，则f（x）、g（x）、h（x）均是以T为周期的函数，下列判断正确的是（）A．①和②均为真命题B．①和②均为假命题C．①为真命题，②为假命题D．①为假命题，②为真命题【分析】①不成立．可举反例：f（x）=．g（x）=，h（x）=．②由题意可得：f（x）+g（x）=f（x+T）+g（x+T），f（x）+h（x）=f（x+T）+h（x+T），h（x）+g（x）=h（x+T）+g（x+T），可得：g（x）=g（x+T），h （x）=h（x+T），f（x）=f（x+T），即可判断出真假．【解答】解：①不成立．可举反例：f（x）=．g（x）=，h（x）=．②∵f（x）+g（x）=f（x+T）+g（x+T），f（x）+h（x）=f（x+T）+h（x+T），h（x）+g（x）=h（x+T）+g（x+T），前两式作差可得：g（x）﹣h（x）=g（x+T）﹣h（x+T），结合第三式可得：g （x）=g（x+T），h（x）=h（x+T），同理可得：f（x）=f（x+T），因此②正确．故选：D．【点评】本题考查了函数的单调性与周期性、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．二．填空题（共2小题）23．（2018•北京）能说明“若f（x）＞f（0）对任意的x∈（0，2]都成立，则f （x）在[0，2]上是增函数”为假命题的一个函数是f（x）=sinx．【分析】本题答案不唯一，符合要求即可．【解答】解：例如f（x）=sinx，尽管f（x）＞f（0）对任意的x∈（0，2]都成立，当x∈[0，）上为增函数，在（，2]为减函数，故答案为：f（x）=sinx．【点评】本题考查了函数的单调性，属于基础题．24．（2018•北京）能说明“若a＞b，则＜”为假命题的一组a，b的值依次为a=1，b=﹣1．【分析】根据不等式的性质，利用特殊值法进行求解即可．【解答】解：当a＞0，b＜0时，满足a＞b，但＜为假命题，故答案可以是a=1，b=﹣1，故答案为：a=1，b=﹣1．【点评】本题主要考查命题的真假的应用，根据不等式的性质是解决本题的关键．比较基础．。

考纲解读明方向考点内容解读要求常考题型预测热度1.命题及四种命题间的关系1.理解命题的概念2.了解“若p,则q”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系Ⅱ选择题★★☆2.充分条件与必要条件理解必要条件、充分条件与充要条件的含义Ⅲ选择题★★★3.逻辑联结词“或”“且”“非”了解逻辑联结词“或”“且”“非”的含义Ⅱ选择题★★☆4.全称量词与存在量词1.理解全称量词和存在量词的意义2.能正确地对含有一个量词的命题进行否定Ⅲ选择题★★★分析解读1.本节主要考查充分必要条件的推理判断及四种命题间的相互关系问题.2.本部分内容在高考试题中多以选择题或填空题的形式出现,考查四种命题的真假判断以及充分条件、必要条件的判定和应用,考查学生的逻辑推理能力.3.会判断含有一个量词的全称命题或特称命题的真假,能正确地对含有一个量词的命题进行否定.4.能用逻辑联结词“或”“且”“非”正确地表达相关的数学内容.5.本节内容在高考中约为5分,属中低档题.命题探究练扩展2018年高考全景展示 1．2018年浙江卷已知平面α，直线m ，n 满足m α，nα，则“m ∥n ”是“m ∥α”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件2．2018年文北京卷能说明“若a ﹥b ，则”为假命题的一组a ，b 的值依次为_________. 3．2018年天津卷文设，则“”是“” 的（ ） A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件4．2018年北京卷文设a,b,c,d 是非零实数，则“ad=bc ”是“a,b,c,d 成等比数列”的（ ）A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件2017年高考全景展示1.2017天津，文2设x ∈R ，则“20x -≥”是“|1|1x -≤”的（ ）（A ）充分而不必要条件 （B ）必要而不充分条件（C ）充要条件 （D ）既不充分也不必要条件2.2017，文5已知命题p ：,x ∃∈R 210x x -+≥命题q ：若22a b <,则a <b .下列命题为真命题的是（ ）A ．p q ∧ B.p q ∧⌝ C.p q ⌝∧ D.p q ⌝∧⌝3.2017北京，文13能够说明“设a ，b ，c 是任意实数．若a >b >c ，则ab >c ”是假命题的一组整数a ,b ,c 的值依次为______________________________． 2016年高考全景展示1.2016高考四川文科设p:实数x ，y 满足1x >且1y >，q: 实数x ，y 满足2x y +>，则p 是q 的( )(A)充分不必要条件 (B)必要不充分条件(C) 充要条件 (D) 既不充分也不必要条件2.2016高考天津文数设0>x ，R y ∈，则“y x >”是“||y x >”的（ ）（A ）充要条件 （B ）充分而不必要条件（C ）必要而不充分条件 （D ）既不充分也不必要条件3.2016高考上海文科设R a ∈，则“1>a ”是“12>a ”的（ ）（A ）充分非必要条件 （B ）必要非充分条件（C ）充要条件 （D ）既非充分也非必要条件。

专题02常用逻辑用语考纲解读明方向考点内容解读要求 常考题型 预测热度 1.命题及四种命题间的 关系1. 理解命题的概念2. 了解“若p,则q ”形式的命题及其逆 命题、否命题与逆否命题，会分析四种命 题的相互关系n选择题2.充分条件与必要条件 理解必要条件、充分条件与充要条件的 含义出 选择题 ★★★ 3.逻辑联结词“或” “且” “非”了解逻辑联结词“或” “且” “非” 的含义n选择题★★☆4.全称量词与存在量 词 1. 理解全称量词和存在量词的意义2. 能正确地对含有一个量词的命题进 行否定出选择题 ★★★分析解读1. 本节主要考查充分必要条件的推理判断及四种命题间的相互关系问题2. 本部分内容在高考试题中多以选择题或填空题的形式出现 ，考查四种命题的真假判断以及充分条件、必要条件的判定和应用，考查学生的逻辑推理能力•3. 会判断含有一个量词的全称命题或特称命题的真假 ，能正确地对含有一个量词的命题进行否定 •4. 能用逻辑联结词“或” “且”“非”正确地表达相关的数学内容5. 本节内容在高考中约为 5分,属中低档题.命题探究练扩展「0能力要求） -----------------------1.了册叫沖常题的衷示羽式，会分析 UH 种常窗的相耳誥慕.0綁辭充分杀件.临蜜来件忌充此* 杵的盘进行刘斷-再斷充守必竖条件的常用方眶：1盘丈込孑找条怖何阿前遢推式,⑷先对弗題沁 ne 与 雋附 进行真锻刘虬 再下站论.么乘合秋：脊所刿斷的命题与方科的屜■.不難式的綁集 有）t,我所怖述的对餐可议用勒合表示时”可比帯肋更 合IM 的也需关歪J8行充甘乘杵和必更航杵的胃斷.:在月瞬片与©之间的关董时"町由脈命题①英 逆否诒剧的铮桥性转化为判断*¥和円"的艾票”rQ 易第■示〕------------------------------------- ■仁在判聊克林件为型竖条伴时.锲 姜弄淸詞鬆的设闻方式.叮呈尺的克分 不恋要条tr 忖M前兗井不：/要条样 业旷前冲魄法伯牌里足不设碌吊为非零向就 m=Aji ，n 是 “nt ■ w<0 5糾\则二伴去负数儿使得\s r ） 扎充分而不必要条件-屣錘応 B.必要而平充分务件岳匕班忒k 芍歩 G 充分必要条件"的量"JD.既车充分也不必耍条件拾戸片昭亂耳宁纽割曹戸鼻冋 /、箱丸套审■井左臨同丈翎呂人(2017 Jt#I —箋Jfc 帆殺鬲A?量诙月访枪芳向料］K包知识摘备｝ ---------------------1,充分笫杵Q 逊豎牡杵的对称件： MIV UTFP 申0 ・2盘分条件与融要条杵的传遽性: pO 解菩过程〕 ------------------------答秦：A解析；曲祎在员議九可 得曲、帶艾缎H.反向，光角为】EF .SM1K - n=- Iml Ifl ko,tt（ft V. ■ t4i Hl -的夹角为钝州政1卿\故 必戟性不展立.故逛扎声）思路井析〕勺,先理断充分性是否嵐电2.再贰斷心亞杵足苦嵐A 3给出结论，e 解题方法） ---------------- 1------------------------❼关联考点〕-----------------1 一向址共戏的充住条件一2數址和的正伍号史曲的具慕3 一俞題的僮廉判哺一2018年咼考全景展示1. 【2018年浙江卷】已知平面a，直线m n满足m a , n匸a ,则"m// n”是"m// a ”的A.充分不必要条件B. 必要不充分条件C.充分必要条件D. 既不充分也不必要条件【答案】A【解析】试题分折：分析:根据线面平行的判定定理得充分性成立，而必要性显然不成立.详解：因为用E氐总匚所以根据线面平行的判定走理得阳〃$宙阳〃厲不能得出讯与厲內任一直线平行，所^m//n是用"金的充分不必要条件，故选A点睛：充分、必要条件的三种判断方法：(1)定义法：直接判断“若贝A ”、“若-则的真假.并注意和图示相结合，例如为真，贝『'是 -的充分条件.(2)等价法：利用？•与非?非，：？与非？非，? •与非?非的等价关系，对于条件或结论是否定式的命题，一般运用等价法.(3)集合法：若?，则•是的充分条件或是」的必要条件；若•=，则•是的充要条件.2 .【2018年理数天津卷】设XER，则“2 2 ” 是“ JT<1”的A.充分而不必要条件B.必要而.不重复条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】分析：首先求解绝对值不等式，然后求解.三次不等式即可确定两者之间的关系.1 1 1 1 111详解：绝对值不等式22o 2 2 2O D<K U1，由x3<! « x < 1 .据此可知2< -2v 1的充分而不必要条件.本题选择A选项.点睛：本题主要考查绝对值不等式的解法，充分不必要条件的判断等知识，意在考查学生的转化能力和计算求解能力.3.【2018年理北京卷】设a, b均为单位向量y ““闷—I -- - ■'■■I ”是“ a丄b”的A.充分而不必要条件B. 必要而不充分条件C.充分必要条件D. 既不充分也不必要条件【答案】C【解析】分析：先对模平方，将X - 3川=|3垃+旬等价韩化为「b *再根据向量垂直时数量积为零得充真关系.详解:la —3£?| = |3a + &| «la —3b I s= \3a + b\2« a:—6c ■ d + = 9a:+6a - b + b23因为j b均为单位向量，所決亦-6血• b+ 9&2 = ■ i> + d2Q a ■ &=0 0疽丄S 即|a —36| = |3a + b|"是i{a丄泸的充分必要条件选C.点睛：充分、必要条件的三种判断方法.1 •定义法：直接判断“若则：”、“若•则■”的真假•并注意和图示相结合，例如“ ？•”为真，则是的充分条件.2 .等价法：利用？■与非?非’，?与非?非：，?:与非?非■的等价关系，对于条件或结论是否定式的命题，一般运用等价法.3•集合法：若'?，则•是的充分条件或是」的必要条件；若」=，则•是的充要条件.2017年高考全景展示n n 11. 【2017天津，理4】设"R，则| ”是“ sin'—”的（）12 12 2（A）充分而不必要条件（B）必要而不充分条件（C）充要条件（D）既不充分也不必要条件【答案】An n ■ n.1 1 . n n【解析】| | 0 ■—：sin •—,但r - 0,sin ■ —，不满足| | ，所以是12 12 6 2 2 12 12充分不必要条件，选 A.【考点】充要条件【名师点睛】本题考查充要条件的判断，若p= q，则p是q的充分条件，若q= p，则p是q的必要条件，若p= q，则p是q的充要条件；从集合的角度看，若 A B，则A是B的充分条件，若B A ,则A是B的必要条件，若A二B，则A是B的充要条件，若A是B的真子集，则A是B的充分不必要条件，若B 是A的真子集，则A是B的必要不充分条件•2. 【2017山东，理3】已知命题p: _x>0,ln x - 1 >0 ；命题q：若a>b,则a2>b2，下列命题为真命题的是（）（A）p q （B）p q （C p q （D）p q【答案】B【解析】试题分析：由x . 0时x 1 . 1,ln（x・1）有意义，知p是真命题，由2 1,2212; . -2,（-1）2:：: （ -2）2可知q是假命题，即p, q均是真命题，故选 B.【考点】1.简易逻辑联结词.2.全称命题.【名师点睛】解答简易逻辑联结词相关问题，关键是要首先明确各命题的真假，利用或、且、非真值表，进一步作出判断•3. 【2017北京，理13】能够说明“设a, b, c是任意实数•若a>b>c,则a+b>c”是假命题的一组整数a,b, c的值依次为 _________________________________ •【答案】-1 , -2 , -3 （答案不唯一）【解析】试题分析：-1 •-2 •-3,-1 • -2[=-3 •-3相矛盾，所以验证是假命题.【考点】不等式的性质【名师点睛】对于判断不等式恒成立问题，一般采用举反例排除法•解答本题时利用赋值的方式举反例进行验证，答案不唯一2016年高考全景展示1. 【2016浙江理数】命题“ -x R, N ,使得n・x2”的否定形式是（）* 9 * 9A. - x • R, T n •N ，使得n：：：x B .一R，一n・N,使得n ：：：x* 2 * 2C. x ：= R, n•N ,使得n：：：x D . R，一n・N,使得n ：：：x【答案】D【解析】试题分析：-的否定是，的否定是一，n _x2的否定是n ：：：x2.故选D.考点：全称命题与特称命题的否定.【方法点睛】全称命题的否定是特称命题，特称命题的否定是全称命题.对含有存在（全称）量词的命题进行否定需要两步操作：①将存在（全称）量词改成全称（存在）量词；②将结论加以否定.2. [ 2016山东理数】已知直线a, b分别在两个不同的平面 a , B内.则“直线a和直线b相交”是“平面a和平面3相交”的（）（A）充分不必要条件（B）必要不充分条件（C）充要条件（D）既不充分也不必要条件【答案】A【解析】试题分析：“直线a和直线b相交”=“平面:-和平面1相交”，但“平面〉和平面一：相交”=“直线a和直线b相交”，所以“直线a和直线b相交”是“平面:和平面1相交”的充分不必要条件，故选A.考点：1.充要条件；2.直线与平面的位置关系.【名师点睛】充要条件的判定问题，是常考题目之一，其综合性较强，易于和任何知识点结合.本题涉及直线与平面的位置关系，突出体现了试题的基础性，能较好的考查考生分析问题解决问题的能力、空间想象能力等•3. 【20 16天津理数】设｛a n｝是首项为正数的等比数列，公比为q,则“ q<0”是“对任意的正整数n,a2n- l + a2n<0” 的（）（A）充要条件（B）充分而不必要条件（C）必要而不充分条件（D）既不充分也不必要条件【答案】C【解析】试题分析：由题竜得，+吆vOo的（『小乜+ 住（-鸡-1）,故是必要不充分条件，故选U考点：充要关系【名师点睛】充分、必要条件的三种判断方法.1.定义法：直接判断“若p则q”、“若q则p”的真假.并注意和图示相结合，例如“p? q”为真，则p是q的充分条件.2 .等价法：利用p? q与非q?非p, q? p与非p?非q, p? q与非q?非p的等价关系，对于条件或结论是否定式的命题，一般运用等价法.3 .集合法：若A? B,则A是B的充分条件或B是A的必要条件；若A= B,则A是B的充要条件.。

专题30推理与证明考纲解读明方向考纲解读考点 内容解读要求 咼考示例 常考题型 预测热度1.合情推理 与演绎推理(1) 了解合情推理的含义，能利用归纳和类 比等进行简单的推理，了解合情推理在数学 发现中的作用.(2) 了解演绎推理的重要性, 掌握演绎推理的基本模式，并能运用它们进行一些简单推理.(3) 了解合情推理和演绎 推理之间的联系和差异掌握2017 北京,14; 2016课标全国n ,15；2015 福建,15; 2014 课标 I ,14填空题2.直接证明 与间接证明(1) 了解直接证明的两种基本方法一一分析 法和综合法；了解分析法和综合法的思考过 程、特点.(2) 了解间接证明的一种基本方法 ――反证法；了解反证法的思考过程、特点了解2017 江苏,19;2016 江苏,20; 2015 北京,20解答题★★★3.数学归纳了解数学归纳法的原理，能用数学归纳法证掌握 2017 浙江,22 解答题 ★☆☆n 誌題规律:-1,屈考肉容；0悄那期与酗缔懂同 Z 事視羽式：LH 选抒題、填空題为主 3,井值：鮒㊁甘r~O 植心考点'：■Hi思酪分析｝屮不知H 己的成覩一占、丙略为一优1也 「❺能力罢戏) ---------------------- 九了解合悄推理的含罠.龍利用归纳 和娄比零进行简性的推理+ 了琳音情 那即住数学发现中的ft ■:阳zr 堺酬绛椎理的亜資性.韋廉曲舞推理的却本榄式.片掘远用它怕进行 •戟前单摊理彳若为曲优，m 盘知过白己的血细;.若屋酹o(2017课标全回H* 7+ 5令)甲、乙、内、r^WOS) ------------------------------------- 1拾情権理的一般申*:从具休间题T 競疼、骑析*斡纳、类 It •褂出跻论理的左輕形式星三鈕堆,瓦一fit 模式为：(|)乂曲一U 灿的-ftBi 理；｛可小刮握一斷研究的椅珠悄况: (对结论——III 邮一股底理对特殊悄况 .作岀的畀斷打丙的成绩，蜡J 有甲的戒绩串后叩对尢家说: 我述足不如进我的成绩.棍抿且上惜息，则］ 九乙町以知道四人的曲绩附「可以知逬岡人的眦绩 j 匕乙、丁町以知逍对方的處壇 门一乙、丁可以知道白己船成纯 /本題足一逆逻弭桂理蹈*是彈所说 金邮 甲说的话崔解題关能❸轉答过程］ ------------------------- 解析:由題窓可知* “甲看乙、丙苗成绩不 知道自己倘试纯”说圖乙■/內曲人一个忧 養一牛犍奸*而乙看了两的成城.叮以知施 自已的成绩"fZrTT 的旌编也町以知逍 口己的腔妓.故选D拙理与证明~£打到了丙MJ 成绩，町知自己的咸绩一「町曲甲的话却自己与甲也为一优一良,厂看了甲的战绒，战幼削口 J 的成斯)A3題关键；分析解读 1.能利用已知结论类比未知结论或归纳猜想结论并加以证明 2 了解直接证明与间接证明的基本方法，体会数学证明的思想方法3掌握“归纳一猜想一证明”的推理方法及数学归纳法的证明步骤4归纳推理与类比推理是高考的热点•本章在高考中的推理问题一般以填空题形式出现，分值约为5分,属中档题；证明问题一般以解答题形式出现，分值约为12分,属中高档题.2017年高考全景展示1. 【2017课标II，理7】甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩。