高二数学下学期限时训练(6)理(无答案)苏教版

江苏省泰兴中学2016 年春学期高二数学（理）限时训练（2）班级：姓名：学号：得分：541.C9C9=.64C10C92.由数字0， 1，2， 3， 4 能够组成个不高出 30000 的偶数 .3.3 个男生和4个女生排成一排，设“两头不排女生”为事件A，则事件 A 发生的概率为____________.4.四个女生排成一排摄影，今后三个男生参加到队伍中从头排队，如不改变女生原有的相对次序，则现在的排队有种不同样的结果 .5.6 本不同样的书分给甲乙丙三人, 若每人都有书，则有种不同样的分法 .6.C32C42C52K C92__________7.四个不同样的小球放入编号为 1、 2、 3、 4 的四个盒子中，恰有一个空盒的概率为8. 一个容量为n 的样本，分红若干组，已知某组的频数和频次分别为40 和 0.12 5 ，则 n 的值为 ____________9. 已知数据x1 , x2 ,K , x n的平均数x 5 ，方差S2 4 ，则数据3x17,3x27,K ,3x n7 的平均数与标准差的和等于10. 已知 A n556C n7na1x a2 x2Kn ，且（1－2x）＝ a0a n x .(1)求 n 的值；(2) 求a1a2K a n的值.11. 在一次抽查中，要从10 道题中随机抽出 3 道题进行回答，答对了其中 2 道题就获得及格.某考生获得及格的概率高出1，问他最少会几道题？2- 1 -12. 设x R , y、z N , y 2, z 2 ， f x, y, z 1 x y 1 x z（1）当y n, z2n 时,f x, y, z 张开式中 x2的系数是7,求 n 的值；（2）当y z20 时， f x, y, z 张开式中系数最大的项是第几项？并说明原因；证明 : f m, n, n f n, m,m m、n N , 且n m 2- 2 -。

江苏省泰兴中学2016年春学期高二数学（理）限时训练（1）班级： 姓名： 学号： 得分：1.若抛物线y 2＝2px (p >0)的焦点也是双曲线x 2－y 2＝8的一个焦点，则p ＝________.2. 容量为60的样本的频率分布直方图共有n (n >1)个小矩形，若其中一个小矩形的面积等于其余n －1个小矩形面积和的15，则这个小矩形对应的频数是________． 3.按如图所示的流程图运行后，输出的结果是63，则判断框中的整数M 的值是________．4.从{1,2,3,4,5}中随机选取一个数为a ，从{1,2,3}中随机选取一个数为b ，则b >a 的概率是________． 5.在区间和上分别取一个数，记为a ，b ，则方程x 2a 2＋y 2b 2＝1表示焦点在x 轴上且离心率小于32的椭圆的概率为________． 6.曲线C 的方程为x 2m 2＋y 2n2＝1，其中m ，n 是将一枚骰子先后投掷两次所得点数，事件A ：“方程x 2m 2＋y 2n2＝1表示焦点在x 轴上的椭圆”，那么P (A )＝________. 7.点A (2,0)与抛物线y 2＝x 上的动点P 连线的中点M 的轨迹方程为____________．8.身穿红、黄两种颜色衣服的各有两人，身穿蓝色衣服的有一人，现将这五人排成一行，要求穿相同颜色衣服的人不能相邻，则不同的排法种数为________种．9. 某种零件按质量标准分为1,2,3,4,5五个等级．现从一批该零件中随机抽取20个，对其等级进行统计分析，得到频率分布表如下： 0.15 (1)在抽取的20(2)在(1)的条件下，从等级为3和5的所有零件中，任意抽取2个，求抽取的2个零件等级恰好相同的概率．10. 已知函数f (x )＝x 3－3x 及y ＝f (x )上一点P (1，－2)，过点P 作直线l ，根据以下条件求l的方程：(1)直线l和y＝f(x)相切且以P为切点；(2)直线l和y＝f(x)相切且切点异于P.11. 已知函数f(x)＝(x－k)e x.(1)求f(x)的单调区间；(2)求f(x)在区间上的最小值．。

江苏省海头高级中学2014-2015学年第二学期周末训练（6）高二数学试题（选修物理）（考试时间120分钟，总分160分）一、填空题（本大题共14小题，每小题5分，共70分，请将答案填写在答题卷相应的位置上） 1．命题“x ∈N ，x 2≠x ”的否定是 ▲ ．1．x ∈N ，x 2＝x2．在平面直角坐标系xOy 中，焦点为F (5，0)的抛物线的标准方程是 ▲ ．2．y 2＝20x3．设复数z 满足z ·i ＝3＋4i (i 是虚数单位)，则复数z 的模为 ▲ ． 3．54．椭圆x 28＋y 24＝1的右准线方程是 ▲ ．4．x ＝4 5．记函数f (x )＝x ＋1x 的导函数为f (x )，则 f(1)的值为▲ ．5．－16．记命题p 为“若＝，则cos＝cos”，则在命题p 及其逆命题、否命题、逆否命题中，真命题的个数是 ▲ ． 7．27．已知实数x 、y 满足2035000x y x y x y -≤⎧⎪-+≥⎪⎨>⎪⎪>⎩，则y x z )21()41(⋅=的最小值为 .1618．在平面直角坐标系xOy 中，已知焦点在x 轴上的双曲线的渐近线方程为x ±2y ＝0，则该双曲线的离心率为 ▲ ．8．529．在平面直角坐标系xOy 中，抛物线y 2＝4x 的焦点为F ，点P 在抛物线上，若PF ＝2，则点P 到抛物线顶点O 的距离是 ▲． 10．已知函数f (x )＝e x －ax 在区间(0，1)上有极值，则实数a 的取值范围是 ▲ 10．(1，e) 11．“a ＝1”是“函数f (x )＝x ＋a cos x 在区间(0，2)上为增函数”的 ▲ 条件（在“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中，选择适当的一种填空）．11．充分不必要12.对于任意实数x ，不等式()()222240a x a x ----<恒成立，则实数a 的取值范围是▲ 。

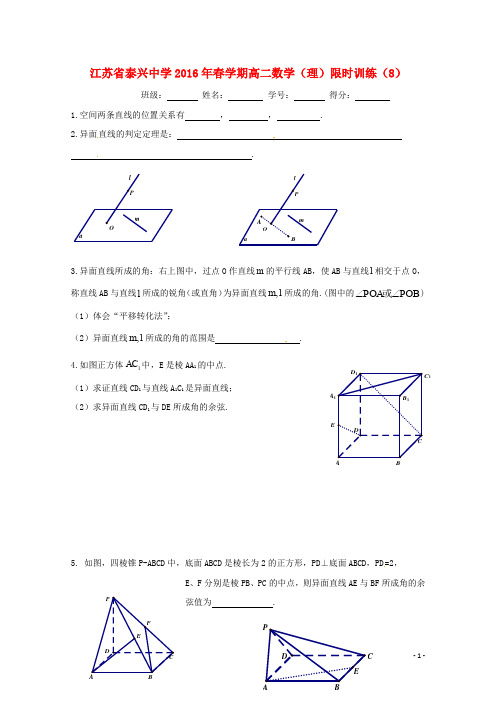
- 1 -江苏省泰兴中学2016年春学期高二数学（理）限时训练（8）班级： 姓名： 学号： 得分：1.空间两条直线的位置关系有 ， ， .2.异面直线的判定定理是： .3.异面直线所成的角：右上图中，过点O 作直线m 的平行线AB ，使AB 与直线l 相交于点O ，称直线AB 与直线l 所成的锐角（或直角）为异面直线,m l 所成的角.(图中的POA POB ∠∠或) （1）体会“平移转化法”；（2）异面直线,m l 所成的角的范围是 . 4.如图正方体1AC 中，E 是棱AA 1的中点. （1）求证直线CD 1与直线A 1C 1是异面直线；（2）求异面直线CD 1与DE 所成角的余弦.5. 如图，四棱锥P-ABCD 中，底面ABCD 是棱长为2的正方形，PD ⊥底面ABCD ，PD =2，E 、F 分别是棱PB 、PC 的中点，则异面直线AE 与BF 所成角的余弦值为 .A 1C 1EC- 2 -6.如图，四棱锥P-ABCD 中，底面ABCD 是棱长为2的正方形，侧面PAD 是正三角形，且侧面PAD ⊥底面ABCD ，E 是棱BC 的中点，则AE 与PC 所成角的余弦值为 .7.在学过空间向量的有关知识后，就可以借助向量工具来解决问题了.“方向向量法”：设异面直线,l m 所成的角为θ，,l m 的方向向量分别为12,e e u r u r，则方向向量的夹角12,e e <>u r u r与异面直线,l m 所成的角θ相等或互补.于是有12cos cos ,e e θ=<>u r u r8.试利用“方向向量法”重新求解5,6两题.9.如图，已知四棱台1111ABCD A B C D -上、下底面分别是边长为3和6的正方形， 16AA =，且1AA ⊥底面ABCD ，点P 、Q 分别在棱1DD 、BC 上.若P 是1DD 的中点，求直线AB 1与PQ 所成的角的大小.。

2019-2020年高二下学期限时训练（二）数学理试题一、 填空题：本大题共14小题，每小题5分，共70分。

请把答案填写在答题卡相应．．．．．的位置上．．．．.1．复数+的虚部是 ▲ .2．一物体的运动方程是，其中的单位是米，的单位是秒，那么物体在时的瞬时速度为____ ▲ ___. 5米/秒3．展开式中的常数项是____ ▲ ___.4．如图所示，用5种不同的颜色涂这些长方形，让每个长方形都涂上一种颜色，且相邻的两个长方形涂不同的颜色，如果颜色可以反复使用，则共有 ▲ ___种不同的涂色方法. 12805．命题“若都是奇数，则是偶数”的逆否命题是____ ▲ ______.“若不是偶数，则不都是奇数”6．设曲线在点（1，）处的切线与直线平行，则 ▲ . 17．方程的解为___ ▲ __.8. 设复数满足的条件是，那么的最大值为_ ▲ __.39．用数字2，3组成四位数，且数字2，3至少都出现一次，这样的四位数共有__ ▲ 个.1410. 被7除时的余数是 ▲ _.411．设直线ｙ＝分别与曲线和交于点M 、N ，则当线段MN 取得最小值时的值为▲ .12.某校高三年级共有六个班,现从外校转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数为______▲_______.（用数字作答）13．观察下列等式：猜想： ▲ （）．14．对于总有成立，则= ▲ . 4二、 解答题：本大题共6小题，共计90分，请在答题卡指定区域内作答，解答时应写出文字说明、证明或演算步骤.15．计算：（1）； （2）答案：（1）；（2）21016．设命题：，命题：；如果“或”为真，“且”为假，求的取值范围.解：若真，则；若真，则；由“或”为真，“且”为假，知、一真一假，得的取值范围.，， ， ……17．某商场销售某种商品的经验表明，该商品每日的销售量y （单位：千克）与销售价格x （单位：元/千克）满足关系式，其中3<x <6，a 为常数，已知销售价格为5元/千克时，每日可售出该商品11千克.（I ）求a 的值，（II ）若该商品的成品为3元/千克，试确定销售价格x 的值，使商场每日销售该商品所获得的利润最大.解：（I ）因为x=5时，y=11，所以（II ）由（I ）可知，该商品每日的销售量所以商场每日销售该商品所获得的利润222()(3)[10(6)]210(3)(6),363f x x x x x x x =-+-=+--<<- 从而，2'()10[(6)2(3)(6)]30(4)(6)f x x x x x x =-+--=-- x所以，当x=4时，函数取得最大值，且最大值等于42.答：当销售价格为4元/千克时，商场每日销售该商品所获得的利润最大.18．从7名男生5名女生中，选出5人，分别求符合下列条件的选法种数有多少种？（1）、必须当选；（2）至少有2名女生当选；（3）选出5名同学，让他们分别担任体育委员、文娱委员等5种不同工作，但体育委员由男生担任，文娱委员由女生担任．解：（1）除、选出外，从其它10个人中再选3人，共有的选法种数为，（种）．（2）方法一：按女同学的选取情况分类：选2名女同学、3名男同学；选3名女同学2名男同学；选4名女同学1名男同学；选5名女同学．所有选法数为：（种）．方法二：从反面考虑，用间接方法，去掉女同学不选或选1人的情况，所有方法总数为：（种）．（3）选出一个男生担任体育班委，再选出1名女生担任文娱班委，剩下的10人中任取3人担任其它3个班委．用分步计数原理可得到所有方法总数为：（种）．19．是否存在a 、b 、c 使得等式1·22+2·32+…+n (n +1)2=(an 2+bn +c ) 对于一切正整数n 都成立？证明你的结论。

⎫ ⎧x∈N8∈ ⎫⎭ ⎩ x+1 ⎭⎩卜人入州八九几市潮王学校平邑县第一二零二零—二零二壹高二数学下学期第六次周末强化限时训练试题〔实验部〕一、单项选择题〔每5分，一共40分〕第I卷〔选择题)1．集合A=⎨x≤0⎬，B=⎨x N⎬，那么A B=〔〕A．{0,1,3}B．{-3,-2,1,3}C．{0,1,3,7}D．{-3,-2,0,1,3}2．以下命题中是真命题的是〔〕①“x>1〞是“x2 1〞的充分不必要条件；②命题“∀x>0，都有sin x 1〞的否认是“∃x0>0，使得sin x0>1〞；③数据x1,x2, ,x8的平均数为6，那么数据2x1-5,2x2-5, ,2x8-5的平均数是6；⎧3x-2y+1=0④当a=-3时，方程组⎨a2x-6y=a有无穷多解.A．①②④B．③④C．②③D．①③④3．某班班会准备从甲、乙等7名学生中选派4名学生发言，要求甲、乙至少有一人参加.当甲乙同时参加时，他们两人的发言不能相邻，那么不同的发言顺序的种数为〔〕A．360 B．520 C．600 D．7204．设(3x+n的展开式的各项系数之和为M，二项式系数之和为N，假设M-17N=480，那么展开式中含x3项的系数为〔〕 A ．40 B ．30C ．20D ．155．一个袋子里装有大小一样的3个红球和2个黄球，从中同时取出2个，那么其中含红球个数的数学期望是〔 〕 A ． B ．1C ．D ．0.66．随机变量X 服从正态分布N (3,σ2),且P (X ≤4)=,那么P (2<X <4)=( )A ．0.84B ．0.68C ．0.32D ．0.167．小明的妈妈为小明煮了5个粽子，其中两个腊肉馅三个豆沙馅，小明随机取出两个，事件A ‘‘取到的两个为同一种馅"，事件B =‘‘取到的两个都是豆沙馅"，那么 P (B ∣A )= 〔 〕1 3 A ．B ．4 413C ．D ．10 108．函数f (x )=-lnx +x +k ，在区间[1,e ]上任取三个实数a ，b ，c 均存在以f (a ),f (b ),f (c )为边长的三e角形，那么实数k 的取值范围是()24A ．(-∞,-1)B ．(-∞,e -3)C ．(-1,+∞)D ．(e -3,+∞)二、多项选择题〔每一小题5分，一共20分〕 9．对于∆ABC ，有如下判断，其中正确的判断是〔 〕A ．假设sin 2A =sin2B ，那么∆ABC 为等腰三角形B ．假设A >B ，那么sin A >sin BC ．假设a =8，c =10，B =60︒，那么符合条件的∆ABC 有两个D ．假设sin 2A +sin 2B <sin 2C ，那么∆ABC 是钝角三角形10．甲、乙、丙三人在政治、历史、地理、物理、化学、生物、技术7门学科中任选3门．假设同学甲必选物理，那么以下说法正确的选项是〔〕A ．甲、乙、丙三人至少一人选化学与全选化学是对立事件B ．甲的不同的选法种数为151C ．乙同学选了物理，乙同学选技术的概率是69D ．乙、丙两名同学都选物理的概率是4911．集合M ={(x ,y )y =f (x )},假设对于∀(x 1,y 1)∈M ,∃(x 2,y 2)∈M ,使得x 1x 2+y 1y 2=0成立,那么称集合M 是“互垂点集〞.给出以下四个集合:M 1={(x ,y )y =x 2+1};M={(x ,y )y =M 3={(x ,y )y =e x };M={(x ,y )y =sin x +1}.其中是“互垂点集〞集合的为( ) A ．M 1 B ．M 2C ．M 3D ．M 412．函数f (x )=e x ⋅x 3，那么以下结论正确的选项是()⎛ A ．f (x )在R 上单调递增B ．f (log 52)<f e-1⎫2⎪<f (ln π) ⎝⎭C ．方程f (x )=-1有实数解D ．存在实数k ，使得方程f (x )=kx 有4个实数解第II 卷〔非选择题)三、填空题〔每一小题5分，一共20分〕213．设函数f (x )=lg( 是 ．x +1-1)的定义域为A ，g (x )=(x -a )2-1的定义域为B ，A ⊆B ，那么a 的取值范围14．给出以下四个命题：⎨⎩①函数y =2sin ⎛2x -π⎫的图像的一条对称轴是直线x =π；6⎪ ⎝⎭3②假设命题p ：“存在x ∈R ,x 2-x -1>0〞，那么p 的否认为：“对任意x ∈R ,x 2-x -1 0〞；③假设x ≠0，那么x +12；x④“a =1〞是“直线x -ay =0与直线x +ay =0互相垂直〞的充要条件．其中正确命题的序号为．15．内某公一共汽车站有7个候车位(成一排),现有甲，乙，丙，丁，戊5名同学随机坐在某个座位上候车,那么甲，乙相邻且丙，丁不相邻的不同的坐法种数为；〔用数字答题〕3位同学相邻，另2位同学也相邻，但5位同学不能坐在一起的不同的坐法种数为 .〔用数字答题〕⎧x 16．函数f (x )=⎪e x+1(x ≥0)，假设函数y =f (f (x )-a )-1有三个零点，那么a 的取值范围是⎪x 2+2x +1(x <0) ．四、解答题〔一共6小题，一共70分〕1x17〔本小题10分〕．函数f 〔x 〕=log 2(x −1)的定义域为A ，函数g 〔x 〕=(2)〔﹣1≤x ≤0〕的值域为B ．〔1〕求A ∩B ；〔2〕假设C ＝{x |a ≤x ≤2a ﹣1}且C ⊆B ，求a 的取值范围．18〔本小题12分〕．p：x2-8x-20≤0；q：1-m2≤x≤1+m2．〔1〕假设p是q的必要条件，求m的取值范围；〔2〕假设⌝p是⌝q的必要不充分条件，求m的取值范围．19〔本小题12分〕．从5名男生和4名女生中选出4人去参加座谈会，问：(1)假设4人中男生和女生各选2人，有多少种选法？(2)假设男生中的甲与女生中的乙至少要有1人在内，有多少种选法？(3)假设4人中必须既有男生又有女生，有多少种选法？⎢⎥ 20〔本小题12分〕．设函数f (x )=ln x -ax 2+bx (a ,b ∈R )，假设曲线y = f (x )在点(1,f (1))处的切线为y =0．〔Ⅰ〕求a ，b 的值；⎡1 〔Ⅱ〕求f (x )在 ⎣e,e ⎤上的极值．⎦21〔本小题12分〕．一个袋中装有大小一样的球10个，其中红球8个，黑球2个，现从袋中有放回地取球，每次随机取1个.求：〔1〕连续取两次都是红球的概率；〔2〕假设取出黑球，那么取球终止，否那么继续取球，直到取出黑球，取球次数最多不超过4次，求取球次数ξ的概率分布列及期望.2a22〔本小题12分〕．函数f(x)=1+2x- -6a ln x存在一个极大值点和一个极小值点.x〔1〕务实数a的取值范围；〔2〕假设函数f(x)的极大值点和极小值点分别为x1和x2，且f(x1)+f(x2)<2-6e，务实数a的取值范围.〔e是自然对数的底数)。

2021年高二下学期限时训练（理科）6含答案班级 姓名 学号 成绩1．已知复数（是虚数单位），则的虚部是 ．2．已知命题“若，则”，则命题及其逆命题、否命题、逆否命题中，正确命题的个数是 ．3．，“”是“”的 条件4．如图，在正四棱锥P －ABCD 中，PA ＝AB ＝2，点M ，N 分别在线段PA 和BD 上，BN ＝13BD ．（1）若PM ＝13PA ，求证：MN ⊥AD ；（2）若二面角M －BD －A 的大小为π4，求线段MN 的长度．5★★．各项均为正数的数列对一切均满足．证明：（1）；（2）．【证明】（1）因为，，所以，所以，且．因为．所以，所以，即．……………………………4分（注：用反证法证明参照给分）（2）下面用数学归纳法证明：．① 当时，由题设可知结论成立；② 假设时，，当时，由（1）得，．由①，②可得，． ……………………………7分下面先证明．假设存在自然数，使得，则一定存在自然数，使得．因为，，，…，，与题设矛盾，所以，．若，则，根据上述证明可知存在矛盾．所以成立． ……………………………10分22．（本小题满分10分）证明：连接AC ，BD 交于点O ，以OA 为x 轴正方向，以OB 为y 轴正方向，OP 为z 轴建立空间直角坐标系．因为PA ＝AB ＝2，则A (1，0，0)，B (0，1，0)，D (0，－1，0)，P (0，0，1)．（1）由BN →＝13BD →，得N (0，13，0)，由PM →＝13PA →，得M (13，0，23)，所以MN →＝(－13，13，－23)，AD →＝(－1，－1，0)．因为MN →·AD →＝0．所以MN ⊥AD ． ………………………………………4分（2）因为M 在PA 上，可设PM →＝λPA →，得M (λ，0，1－λ)．所以BM →＝(λ，－1，1－λ)，BD →＝(0，－2，0)．设平面MBD 的法向量n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧n ·BD →＝0，n ·BM →＝0，得⎩⎨⎧－2y ＝0，λx －y ＋(1－λ)z ＝0， 其中一组解为x ＝λ－1，y ＝0，z ＝λ，所以可取n ＝(λ－1，0，λ)．………………………………8分因为平面ABD 的法向量为OP →＝(0，0，1)，所以cos π4＝|n ·OP →|n ||OP →||，即22＝λ(λ－1)2＋λ2，解得λ＝12， 从而M (12，0，12)，N (0，13，0)，所以MN ＝(12－0)2＋(0－13)2＋(12－0)2＝226． ………………………………………10分Q32519 7F07 缇24397 5F4D 彍28054 6D96 涖 q433412 8284 芄=27885 6CED 泭38770 9772 靲23504 5BD0 寐 ~。

江苏省连云港市赣榆区2016—2017学年高二数学下学期期末复习小题训练6 理（无答案)一、填空题（本大题共10小题,每小题5分，共计50分)1．复数(1)i i -在复平面上对应的点在第 象限；2．将2本不同的数学书和1本语文书在书架上随机排成一行，则2本数学书相邻的概率为 ；3．在某年有奖明信片销售活动中,规定每100万张为1个开奖组，通过随机抽取的方式确定号码的后四位数为2017的为一等奖,这样确定获奖号码的抽样方法是 ；4．在一次教师联欢会上,到会的女教师比男教师多12人,从这些教师中随机挑选一人表演节目,若选到男教师的概率为错误!，则参加联欢会的教师共有 人；5．某同学使用计算器求30个数据的平均数时，错将其中一个数据105输入为15，那么由此求出的平均数与实际平均数的差是 ；6．已知实数x ,y 可以在20<<x ，20<<y 的条件下随机取数，那么取出的数对满足1)1(22<-+y x 的概率是 ；7．设R x ∈，a 为非零常数,且1)(1)()(++-+=a x f a x f x f ，则函数)(x f 的周期是 ； 8．观察下列等式：，，，，1043216321321112222222222-=-+-=+--=-= 根据上述规律，第n 个等式为 ；9．求“方程34()()155x x +=的解”有如下解题思路：设34()()()55x x f x =+，则()f x 在R 上单调递减,且(2)1f =，所以原方程有唯一解2x =．类比上述解题思路，方程623(2)2x x x x +=+++的解为 ；10．数列{}n a 是正项等差数列,若12323123n n a a a na b n++++=++++，则数列{}n b 也为等差数列，类比上述结论，数列{}n c 是正项等比数列,若n d = 则数列{}n d 也为等比数列.二、解答题（本大题共2小题，共计30分．解答时应写出必要的文字说明、证明过程或演算步骤)11．将5个编号为1,2,3，4，5的小球放入5个编号为1,2，3，4,5的盒子中。

（第2题）（第1题）江苏省泰兴中学2016年春学期高二数学（理）限时训练（7）班级： 姓名： 学号： 得分：1.为了解学生课外阅读的情况，随机统计了n 名学生的课外阅读时间，所得数据都在中，其频率分布直方图如图所示．已知在[50 75)，中的频数为100，则n 的值为 ．2．在如图所示的算法流程图中，若输出的y 的值为26，则输入的x 的值为 ． 3．从集合{1，2，3，4，5，6，7，8，9}中任取一个数记为x ，则log 2x 为整数的概率为 ． 4.用0，1，2，3，4，5这六个数字，完成下面问题 (1)可以组成多少个数字不重复的三位数？ (3)可以组成多少个数字不重复的三位奇数？(4)可以组成多少个数字不重复的小于1 000的自然数？（5）若直线0ax by +=中的a b 、可以从已知六个数字中任取2个不同的数字，则方程表示的不同的直线共有多少条？5. 一个袋中装有五个形状大小完全相同的球，球的编号分别为1，2，3，4，5.（1）从袋中随机取两个球，写出所有的基本事件，并求取出的编号之和不大于4的概率; （2）先从袋中随机取一个球，该球的编号为m ，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n ，求2n m -≥的概率6. 设集合{}1,2,3,,(3)M n n =≥L ，记M 的含有三个元素的子集个数为n S ，同时将每一个子集中的三个元素由小到大排列，取出中间的数，所有这些中间的数的和记为n T . （1）求33T S ，44TS ，55T S ，66T S 的值； （2）猜想nnT S 的表达式，并证明之.7. 某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如下表所示.组号分组频数频率第1组[160,165)50.050第2组[165,170)①0.350第3组[170,175)30②第4组[175,180)200.200第5组100.100合计100 1.00(1)(2)为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试，则第3、4、5组每组各抽取多少名学生进入第二轮面试？(3)在(2)的前提下，学校决定在6名学生中随机抽取2名学生接受A考官进行面试，求：第4组至少有一名学生被考官A面试的概率8.9.已知集合A是集合P n＝{1，2，3，…，n} (n≥3，n∈N*)的子集，且A中恰有3个元素，同时这3个元素的和是3的倍数．记符合上述条件的集合A的个数为f(n)．（1）求f(3)，f(4)；（2）求f(n)（用含n的式子表示）．。

江苏省泰兴中学2016年春学期高二数学（理）限时训练（5） 班级： 姓名： 学号： 得分：1.某单位有840名职工, 现采用系统抽样抽取42人做问卷调查, 将840人按1, 2, …, 840随机编号, 则抽取的42人中, 编号落入区间的人数为 ．2.已知集合},4,3,2{},1,0{==B A 若从B A ,中各取一个数，则这两个数之和不小于4的概率为 .3.如图是某市2014年11月份30天的空气污染指数的频率分布直方图.根据国家标准，污染指数在区间)51,0[内，空气质量为优；在区间)101,51[内，空气质量为良；在区间)151,101[内，空气质量为轻微污染；.L 由此可知该市11月份空气质量为优或良的天数有 天.4.根据如图所示的伪代码，则输出的S 的值为 .5.若（1﹣3x ）2015=a 0+a 1x+…a 2015x 2015（x ∈R ），则的值为6.设（1﹣x ）（1+2x ）5=a 0+a 1x+a 2x 2+…+a 6x 6，则a 2= ．7.展开式中的一次项系数为 ． 8. 设函数,．（1）求的展开式中系数最大的项；（2）若（为虚数单位）,求．9.一个摸球游戏，规则如下：在一不透明的纸盒中，装有6个大小相同、颜色各异的玻璃球．参加者交费1元可玩1次游戏，从中有放回地摸球3次．参加者预先指定盒中的某一种颜色的S 0 I 041Pr int While I I I S S I End While S ←←≤←+←+第4题玻璃球，然后摸球．当所指定的玻璃球不出现时，游戏费被没收；当所指定的玻璃球出现1次，2次，3次时，参加者可相应获得游戏费的0倍，1倍，k 倍的奖励（*N k ∈），且游戏费仍退还给参加者．记参加者玩1次游戏的收益为X 元． （1）求概率()0P X =的值； （2）为使收益X 的数学期望不小于0元，求k 的最小值． （注：概率学源于赌博，请自觉远离不正当的游戏！）10.设,,,*N n b a ∈且,b a ≠对于二项式.)(n b a -（1）当4,3=n 时，分别将该二项式表示为),(*N q p q p ∈-的形式；（2）求证：存在,,*N q p ∈使得等式q p b a n -=-)(与q p b a n -=-)(同时成立.。