(101115)第十一讲:PPCF法
- 格式:ppt
- 大小:11.24 MB
- 文档页数:30


生存曲线比较的方法选择及可视化南京医科大学公共卫生学院生物统计学系(211166)㊀魏良敏㊀官锦兴㊀张汝阳㊀陈㊀峰㊀魏永越ә㊀㊀ʌ提㊀要ɔ㊀用Kaplan ̄Meier(KM)方法描述生存曲线ꎬ以及多条KM曲线的比较ꎬ是医学研究尤其是随访研究中常用的方法ꎬ亦是医学统计学教学中的重点和难点ꎮ本文针对生存曲线的不同特征ꎬ从实际应用的角度出发ꎬ介绍多种常用的生存曲线比较的方法㊁应用条件㊁分析案例㊁R程序实现ꎮ以期读者针对生存曲线特征ꎬ选择合适的检验方法ꎬ得出科学的统计学结论ꎮʌ关键词ɔ㊀Kaplan ̄Meier曲线㊀生存曲线㊀比较方法㊀可视化㊀R程序ʌ中图分类号ɔ㊀R181㊀㊀㊀ʌ文献标识码ɔ㊀A㊀㊀㊀㊀DOI㊀10.3969/j.issn.1002-3674.2020.05.035㊀㊀在医学研究中ꎬ往往既关注某一事件(event)是否发生ꎬ同时又关注到事件发生所需的时间(timetoe ̄vent)ꎬ两者结合即统计学中的生存结局(survivalout ̄come)ꎮ但是ꎬ由于研究时长限制ꎬ事件尚未发生而研究即终止(termination)ꎬ或尚未观察到事件发生而研究对象即失访(losttofollowup)ꎬ导致所记录的生存结局有所缺失ꎬ并不完整ꎬ这在统计学中被称为 删失 (censored)ꎮ生存分析(survivalanalysis)方法可同时考虑 事件发生与否 和 至事件发生的时间 ꎬ并充分利用删失数据中的不完全信息ꎬ对生存过程进行描述㊁比较[1]ꎮ因生存结局的重要性和数据的复杂性ꎬ生存数据的分析是医学统计学教学中的重点和难点ꎮ对数据进行合理的可视化ꎬ有利于揭示数据隐藏的信息ꎬ提高结果的展示度和传播力ꎬ近年来ꎬ在统计学教学中愈发受到重视ꎮ美国统计学家EdwardKap ̄lan和PaulMeier于1958年提出乘积极限法(product ̄limitmethodꎬPL)ꎬ基于 不完美 的生存资料ꎬ估计各时间点的生存率ꎬ进而以曲线描述其生存过程(生存曲线)ꎬ故又称为Kaplan ̄Meier(KM)法ꎬ该曲线通常被称为KM曲线ꎮ两条或多条生存曲线的比较ꎬ是生物医学研究中的常见需求ꎬ常用log ̄rank检验[2]ꎮlog ̄rank检验要求生存曲线满足等比例风险假定(propor ̄tionalhazardassumptionꎬPH)ꎬ该条件往往被忽视[3-4]ꎮ国内学者陈征等人对多种KM曲线比较方法进行了较为系统的统计模拟试验评价[5-6]ꎮ然而ꎬ在教学中ꎬ学生对KM曲线比较方法的基本原理理解不足ꎬ各方法的适用条件把握不准ꎬ在实际医学研究中亦是如此ꎮ本文拟简要综述生存曲线比较的各种检验方法ꎬ适用条件ꎬ并展示分析和绘图程序ꎮ三类KM曲线比较方法1.基于加权的log ̄rank检验该类方法的思想是赋予前后时间点不同的权重ꎬ具体的检验方法有:log ̄rank法(LR)㊁Gehan ̄Breslow ̄Wilcoxon法(GW)㊁Tarone ̄Ware法(TW)㊁Peto ̄Peto法(PP)和Harrington ̄Fleming法(HF)ꎮ对于研究中的第i组的tj时刻理论发生事件数为:eij=djnijnjꎬ其中i=1ꎬ ꎬGꎻj=1ꎬ ꎬk(1)其中ꎬG为组数ꎬk为时间点数ꎻnij为第i组tj时间点的可能发生事件的风险人数ꎻdj㊁nj为tj时间点的总发生事件数和总风险人数ꎮ各组实际事件数与理论事件数的(加权)差异为:ui=ðkj=1wj(dij-eij)(2)式中ꎬwj为时刻tj时的权重ꎮ相应的方差为:vig=ðkj=1w2j(nijnj)(δig-nijnj)(nj-djnj-1)dj(3)式中ꎬ如果i=gꎬ则δig=1ꎻ否则为0ꎮ定义:uᶄ=(u1ꎬ ꎬuG)ꎬV={vig}GˑG(4)则检验统计量为:χ2=uᶄV-1u(5)χ2统计量服从自由度为G-1的卡方分布ꎮ若wj=1ꎬ则为log ̄rank检验ꎬ不考虑各时间点风险人数对结果的影响ꎬ即每个时点对KM曲线的比较来说同等重要ꎻ若wj=njꎬ则为Gehan ̄Breslow ̄Wilcoxon法ꎬ以各时点风险人数nj为权重ꎬ较之log ̄rank检验ꎬ该法早期权重较大ꎬ侧重于早期生存曲线差异的比较ꎻ若wj=㊀njꎬ则为Tarone ̄Ware法ꎬ与Wilcoxon法类似ꎬ但权重力度介于log ̄rank和Wilcoxon之间ꎻPeto ̄Peto法以各时点的生存率S(tj)的估计值^S(tj)作为权重:wj=^S(tj)ꎬmodifiedPeto ̄Peto法[7]的权重wj=^S(tj)njnj+1ꎬ两种方法均给予试验早期大一867 ChineseJournalofHealthStatisticsꎬOct.2020ꎬVol.37ꎬNo.5ә通信作者:魏永越ꎬm ̄mail:ywei@njmu.edu.cn些的权重ꎮHarrington ̄Fleming方法更为通用ꎬ设置两个权重(pꎬq)分别对应S(tj)和(1-S(tj)):wj=S(tj)pˑ(1-S(tj))qꎬ可根据需求对权重进行调整ꎬp越大则越侧重早期效应ꎬq越大则越侧重远期效应ꎮ值得注意的是ꎬRenyi于1953年提出基于布朗运动理论改进上述五种假设检验ꎬ以期更适用于曲线交叉的情况ꎬGill于1980年对此进行了详细阐述[8]ꎮ定义统计量:B(t)=Mσ^kkꎬ其中Mi=max(ui)(6)在H0假设前提下B(t)服从布朗运动ꎬ由此得到假设检验P值ꎮ2.基于Omnibus思想现实世界中ꎬKM曲线的分布形式多种多样ꎮ在对实际研究和数据了解不足的情况下ꎬ往往无法准确判断生存曲线的特征ꎬ亦无从选择最合适的检验方法ꎬ导致效能低下ꎮHarrington于1980年将Kolmogorov单样本拟合优度检验和Smirnov两样本拟合优度检验扩展至存在右截尾的生存数据情况ꎬ称为Kolmogorov ̄Smirnov(KS)法ꎮHarrington的模拟试验提示ꎬ该法在特定时点组间存在较大差异的情况下ꎬ优于加权log ̄rank等方法[5]ꎮSchumacher基于KS法进行扩展ꎬ提出Cramér ̄vonMises(CVM)法[9]ꎻStephens于1974年结合Anderson和Darling的理论对KS法进行改进ꎬ给予尾部更高的权重(Anderson ̄DarlingꎬAD法)[10]ꎮKraus于2009年基于Neyman拟合优度(Neymangoodness ̄of ̄fit)思想和Schwarz准则(Schwarzcriteri ̄on)ꎬ提出adaptiveNeymansmooth(NM)检验[11]ꎮ该法的优势在于ꎬ基于数据驱动ꎬ拟合并选择潜在生存函数模式ꎬ基于得分检验构造统计量:Ts=max{VC(τ)TσCC(τ):Cɪζꎬ|C|=d∗}(7)式中ꎬVC(τ)和σCC(τ)分别为V(τ)的子向量和子矩阵ꎬ根据Schwarz准则进行筛选S=argmaxCɪζ{TC-|C|logn}ꎮ另外ꎬ为了避免交叉点前后的组间差异反向对统计量构造的影响ꎬLinꎬWang等基于各时点实际事件数和理论事件数差值的平方(消除差值的方向)构建统计量[12]:Δ=ðkj=1[dij-E(dij)]2ꎬ而LinꎬXu等基于各时点生存函数差值的绝对值构建统计量[13]:Δ=ðkj=1|S1(tj)-S2(tj)|ꎮ两者皆基于中心极限定理构造统计量U=Δ-E(Δ)var(Δ)~N(0ꎬ1)ꎬ但尚未见被实际临床研究所采用ꎮ3.两阶段法Qiu等提出两阶段法[14]ꎬ第一阶段采用传统的log ̄rank检验ꎬ若不拒绝H0(可能是由于KM曲线不满足等比例风险假定或有交叉现象)ꎬ则于第二阶段采用能够考虑不等比例或有交叉的KM曲线比较方法ꎮ原则上来说ꎬ两阶段的方法可以根据需要自由选择ꎬ但由于两阶段统计分析方法不独立ꎬ导致总Ⅰ类错误率的控制存在问题ꎮQiu等从检验水准分配㊁权重构造等角度入手ꎬ使得两阶段的假设检验相独立ꎬ以准确控制Ⅰ类错误率ꎮ设总检验水准为αꎬ和两阶段的检验水准(α1ꎬα2)存在以下关系:α=α1+α2(1-α1)(8)通常情况下ꎬ两个阶段采用相同的检验水准ꎬ可得α1=α2=1-1-αꎮ第二阶段假设检验统计量为:V=supkεɤmɤk-kε(Vm)ꎬ其中Vm与公式(1)~(5)类似:㊀Vm=ðkj=1w(m)j(dij-eij)ðkj=1(w(m)j)2(nijnj)(δig-nijnj)(nj-djnj-1)dj(9)但是交叉点(m)前后赋予不同权重:w(m)j=-1ꎬif㊀j=1ꎬ2ꎬ ꎬmcmꎬotherwise{(10)总的两阶段假设检验P值:P=P1ꎬif㊀P1ɤα1ꎬα1+P2(1-α1)ꎬotherwise{(11)常见KM曲线比较方法及适用条件综述见表1ꎮ分析及可视化程序基于Rsurvminer包的ggsurvplot函数绘制KM曲线:#调用R包library(survminer)#通过survfit指定生存时间(time)ꎬ生存事件(event)和分组变量(by)#其中生存事件event=1为发生目标事件fit<-survfit(Surv(timeꎬevent)~byꎬdata=testset)#通过ggsurvplot绘制KM曲线ꎬ其中加粗的为关键参数967 中国卫生统计2020年10月第37卷第5期表1㊀KM曲线比较方法及其适用条件方法(简称)提出年份适用条件应用案例log ̄rank(LR)[2]1966满足等比例风险假设ꎮNEJMꎬ2017[15]Gehan-Breslow-Wilcoxon(GW)[16]1965侧重于早期差异ꎬ权重力度较大ꎮEBioMedicineꎬ2018[17]Tarone-Ware(TW)[18]1977侧重于早期差异ꎬ权重力度较GW法略小ꎮUrolOncolꎬ2018[19]Peto-Peto(PP)[20]1972侧重于早期差异ꎮmodifiedPeto-Peto[7]1992侧重于早期差异ꎮLancetRespirMedꎬ2019[21]Harrington-Fleming(HF)[22]p=0ꎬq=11982侧重于远期差异ꎮCancerBiolTherꎬ2010[23]p=1ꎬq=1同时兼顾早期或晚期差异ꎮRenyi(RE)[8]1980曲线交叉时效果较原方法好ꎮ仅适用于2组的比较ꎮAsianPacJCancerPrevꎬ2017[24]modifiedKolmogorov-Smirnov(KS)[25]1980特定时点较大组间差异情况ꎮ仅适用于2组的比较ꎮCramér-vonMises(CVM)[26]1984基于KSꎬ给予尾部较高的权重ꎬ基于permutation进行检验ꎮ仅适用于2组的比较ꎮAnderson–Darling(AD)[10]1974基于KSꎬ给予尾部更高的权重ꎬ基于permutation进行检验ꎮ仅适用于2组的比较ꎮLin-Wang(LW)[12]2004KM曲线交叉时适用ꎮ仅适用于2组的比较ꎮLin-Xu(LX)[13]2010KM曲线交叉时适用ꎮ仅适用于2组的比较ꎮadaptiveNeymansmooth(NM)[11]2009适用各种KM曲线分布模式ꎬ结果稳健ꎮ仅适用于2组的比较ꎮtwostage(TS)[14]2008适用各种KM曲线分布模式ꎬ结果稳健ꎮ仅适用于2组的比较ꎮBioDrugsꎬ2019[27]#更详细的参数表ꎬ参见R包帮助km_fig<-ggsurvplot(fitꎬ㊀conf.int=FALSEꎬ㊀㊀㊀㊀#KM曲线区间带㊀risk.table=TRUEꎬ㊀㊀㊀㊀#各时点风险人数㊀xlab= OS(months) ꎬ㊀㊀#x轴标签㊀break.x.by=24ꎬ㊀㊀㊀㊀#x轴标签间隔/步长㊀ggtheme=theme_classic()㊀#图形主题㊀)笔者基于现有R包重构了KM绘图函数km_plot()ꎬ通过预设必要的图形元素和样式参数ꎬ绘制达到发表要求的KM曲线ꎮ另外ꎬR语言中目前尚无一个函数可同时实现以上21种具体KM曲线的比较方法ꎮ因此本文基于survMisc包的comp函数㊁TSHRC包的twostage函数ꎬ编写通用的KM曲线比较函数km_compare()ꎬ并以表格和图形两种形式输出各种方法的假设检验P值ꎮ#通过自定义init函数加载所有程序包ꎬ设置目标期刊图形格式init(journal= nejm )fit=survfit(Surv(timeꎬevent)~byꎬdata=testset)#绘制KM曲线km_fig=km_plot(fitꎬx_step=2ꎬrisk_table=TRUEꎬconf=FALSEꎬxlab= OS(months) ꎬby_labels=c( High ꎬ Low ))#组间比较ꎬ绘制P值排序图km_pval=km_compare(fitꎬtestset)#合并KM曲线及比较结果图km_illustrator(km_figꎬkm_pval)上述R程序可从GitHub网站获取:https://github.com/Wei ̄Lab ̄maker/ꎮ分析案例以癌症基因组图谱(TheCancerGenomeAtlasꎬTCGA)计划中284例宫颈鳞状细胞癌患者组织全基因组表达数据为基础ꎬ展示不同曲线特征情况下的KM曲线比较结果ꎮ1 两条生存曲线满足等比例风险假设以ZNF827基因表达水平(低表达组vs高表达组)和预后关联为例ꎬ两组生存曲线满足等比例风险假定(χ2=0.49ꎬP=0.4850)ꎮKM曲线和组间比较结果如图1所示ꎬ传统log ̄rank法最佳ꎮ此时的twostage法即为第一阶段的log ̄rank法ꎮ多种方法所得结果一致ꎮ2 两条生存曲线前期差异小ꎬ后期差异大以GAB1基因为例ꎬ两组曲线未交叉ꎬ前期几乎无差异ꎬ后期组间差异逐渐变大(图2)ꎮ此时传统log ̄rank检验方法效能较低(P=0.2853)ꎬ而使用Harrington ̄Fleming方法ꎬ采用侧重于晚期组间差异的参数设置(p=0ꎬq=1)ꎬ则两组之间差异有统计学意义(P=0 0364)ꎮ但是ꎬ只有一种方法的P值小于检验水准ꎬ提示该结果尚需进一步验证ꎮ077 ChineseJournalofHealthStatisticsꎬOct.2020ꎬVol.37ꎬNo.5图1㊀不同ZNF827基因表达水平患者的Kaplan ̄Meier生存曲线(∗采用Renyi法构造统计量ꎬ虚线为P=0.05参考线)图2㊀不同GAB1基因表达水平患者的Kaplan ̄Meier生存曲线(∗采用Renyi法构造统计量ꎬ虚线为P=0.05参考线)讨㊀㊀论采用生存曲线来展示生存数据ꎬ选择合适的方法来比较生存曲线ꎬ是医学统计学教学中的重要内容之一ꎬ广泛应用于医学随访研究ꎮ在医学研究中ꎬ因未能准确地评估生存曲线特征[28-29]ꎬ而选用了不恰当的比较方法导致结论存疑的案例并不少见[3]ꎮ因此ꎬ学习并掌握生存曲线比较的各种统计学检验方法及其适用条件ꎬ是对随访资料进行正确分析的前提ꎮ笔者建议在选用比较方法之前ꎬ需绘制生存曲线ꎬ充分了解曲线特征ꎬ同时结合样本量㊁删失率㊁研究目的等具体特征ꎬ而选择合适的方法ꎮ笔者基于各种方法的原理和多个模拟试验研究结论ꎬ简要综述了不同方法的使用条件ꎮ陈征等人认为twostage法和adaptiveNeymansmooth法在不同参数设置情况下ꎬ结果皆较为稳健[5]ꎮ但是模拟试验无法完全覆盖纷繁复杂的曲线特征ꎬ在实际医学研究中由于生存资料的特征千差万别ꎬ根据本文所总结的 应用条件 而选择的方法可能并非最佳选择ꎮ在特定情况下如何优化统计方法选择ꎬ如何综合多种方法的结果ꎬ仍有待探索ꎮ不同方法的结果ꎬ其临床意义解释上亦有所不同ꎮ对于生存曲线存在交叉的情况来说ꎬ虽然某些统计方法提示 组间差异具有统计学意义 ꎬ但仅提示各组生存曲线模式存在差异ꎬ不可直接解释为疗效上的优劣ꎮ各种方法各有特点ꎬ单一的方法可能无法充分反映生存曲线间的差异ꎮ在医学统计学教学过程中ꎬ应以研究目的为导向ꎬ注重各方法的原理和应用条件ꎮ参㊀考㊀文㊀献[1]陈峰ꎬ夏结来.临床试验统计学.北京:人民卫生出版社ꎬ2018.[2]MantelN.Evaluationofsurvivaldataandtwonewrankorderstatis ̄ticsarisinginitsconsideration.Cancerchemotherapyreportsꎬ1966ꎬ50(3):163 ̄170.[3]NagelEꎬGreenwoodJPꎬMcCannGPꎬetal.MagneticResonancePer ̄fusionorFractionalFlowReserveinCoronaryDisease.NEnglJMedꎬ2019ꎬ380(25):2418 ̄2428.[4]CarboneDPꎬReckMꎬPaz ̄AresLꎬetal.First ̄LineNivolumabinStageIVorRecurrentNon ̄Small ̄CellLungCancer.NEnglJMedꎬ2017ꎬ376(25):2415 ̄2426.[5]LiHꎬHanDꎬHouYꎬetal.Statisticalinferencemethodsfortwocrossingsurvivalcurves:acomparisonofmethods.PloSoneꎬ2015ꎬ10(1):e0116774.[6]李慧敏ꎬ韩栋ꎬ陈征ꎬ等.生存曲线交叉时统计推断方法的比较和选择.中国卫生统计ꎬ2013ꎬ30(5):668 ̄672.[7]KleinJ.StatisticalModelsBasedonCountingProcesses.Technomet ̄ricsꎬ1997ꎬ36(1):111 ̄112.[8]GillRD.CensoringandStochasticIntegralsꎬ2010ꎬ34(2):124 ̄.[9]SchumacherMJISR.Two ̄SampleTestsofCramér ̄vonMises ̄andKolmogorov ̄Smirnov ̄TypeforRandomlyCensoredData.Interna ̄tionalStatisticalReviewꎬ1984ꎬ52(3):263 ̄281.[10]StephensMA.EDFStatisticsforGoodnessofFitandSomeCompari ̄sons.JournaloftheAmericanStatisticalAssociationꎬ1974ꎬ69(347):730 ̄737.[11]KrausD.AdaptiveNeyman'ssmoothtestsofhomogeneityoftwosamplesofsurvivaldata.JournalofStatisticalPlanning&Inferenceꎬ2009ꎬ139(10):3559 ̄3569.[12]LinXꎬWangHK.ANewTestingApproachforComparingtheOver ̄allHomogeneityofSurvivalCurves.BiometricalJournalꎬ2010ꎬ46(5):489 ̄496.[13]LinXꎬXuQ.Anewmethodforthecomparisonofsurvivaldistribu ̄tions.Pharmaceuticalstatisticsꎬ2010ꎬ9(1):67 ̄76.[14]QiuPꎬShengJ.ATwo ̄StageProcedureforComparingHazardRateFunctions.JournaloftheRoyalStatisticalSocietyꎬ2010ꎬ70(1):191 ̄208.[15]BinesJEꎬAtTJꎬSatriaCDꎬetal.HumanNeonatalRotavirusVaccine(RV3 ̄BB)toTargetRotavirusfromBirth.JNewEnglandJournalofMedicineꎬ2018ꎬ378(8):719.[16]GehanEA.AGeneralizedWilcoxonTestforComparingArbitrarilySingly ̄CensoredSamples.Biometrikaꎬ1965ꎬ52(1/2):203 ̄223.[17]GuoNLꎬDowlatiAꎬRaeseRAꎬetal.APredictive7 ̄GeneAssayandPrognosticProteinBiomarkersforNon ̄smallCellLungCancer.EBioMedicineꎬ2018ꎬ32:102 ̄110.(下转第775页)景的模拟评价方法ꎮ该方法从整体和个体两个角度对申报试剂进行评价ꎮ首先通过非劣效检验ꎬ使申报试剂与对比试剂在临床试验整体上有较好的临床等效性ꎮ从个体的角度ꎬ当已上市试剂针对某一样本的两次检测结果一致时ꎬ申报试剂的检测结果应与之一致ꎮ如不一致则认为产生了较大的风险ꎬ必须进行细致的分析ꎮ对于已上市试剂两次检测的结果不一致的情况ꎬ则认为该份样本在临床使用时会有不确定的结果ꎬ此时申报试剂的结果与其中一次的不一致的风险是可以接受的ꎮ该方法虽然在一定程度上解决了用药受试者样本稀缺的问题ꎬ但对于阳性样本数量的要求会高于传统的伴随诊断试剂临床试验ꎮ同时由于需要进行3次检测ꎬ纳入样本的组织样本体积也会有硬性的要求ꎬ需要完成3次检测ꎬ这也高于传统的伴随诊断试剂临床试验ꎮFollow ̄on伴随诊断试剂评价方法是一个全新的㊁更多依靠统计学判定的临床评价方法ꎮ由于不依赖于药物治疗效果进行研究ꎬ应在临床评价方法适用性方面有更深入的考虑ꎮ同时ꎬ设定产品的接受标准时也应结合产品的实际情况ꎬ根据患者的风险受益比来评价其临床性能ꎮ参㊀考㊀文㊀献[1]FoodandDrugAdministration.DraftGuidanceforIndustryandFoodandDrugAdministrationStaff ̄InVitroCompanionDiagnosticDevices(releasedJuly14ꎬ2011).http://www.fda.gov/MedicalDevices/De ̄viceRegulationandGuidance/GuidanceDocuments/ucm262292.htm. [2]Li.StatisticalConsiderationandChallengesinBridgingStudyofPer ̄sonalizedMedicine.JournalofBiopharmaceuticalStatisticsꎬ2015ꎬ25(3):397 ̄407.[3]LiM.StatisticalMethodsforClinicalValidationofFollow ̄onCom ̄panionDiagnosticDevicesviaanExternalConcordanceStudy.Statis ̄ticsinBiopharmaceuticalResearchꎬ2016ꎬ8(3):355 ̄363. [4]FDAꎬSummaryofSafetyandEffectivenessDataꎬ2017ꎬhttp://www.accessdata.fda.gov/cdrh_docs/pdf17/P170019B.pdf. [5]NamJM.EstablishingEquivalenceofTwoTreatmentsandSampleSizeRequirementsinMatched ̄PairsDesign.Biometricsꎬ1997ꎬ53(4):1422 ̄1430.[6]EfronB.Missingdataꎬimputationꎬandthebootstrap.JournaloftheAmericanStatisticalAssociationꎬ1994ꎬ89(426):463 ̄475. [7]HeinmöllerPꎬBänferGꎬGrzelinskiMꎬetal.QualityControlofIm ̄munohistochemicalandInSituHybridizationPredictiveBiomarkersforPatientTreatment:ExperiencefromInternationalGuidelinesandInternationalQualityControlSchemes//PredictiveBiomarkersinOn ̄cology.SpringerꎬChamꎬ2019:525 ̄537.(责任编辑:邓㊀妍)(上接第771页)[18]TaroneREꎬWareJ.OnDistribution ̄FreeTestsforEqualityofSur ̄vivalDistributions.Biometrikaꎬ1977ꎬ64(1):156 ̄160.[19]ShumCFꎬBahlerCDꎬSundaramCP.Impactofpositivesurgicalmarginsonoverallsurvivalafterpartialnephrectomy ̄AmatchedcomparisonbasedontheNationalCancerDatabase.UrolOncolꎬ2018ꎬ36(3):90e15 ̄90e21.[20]PetoRꎬPetoJ.AsymptoticallyEfficientRankInvariantTestProce ̄dures.JournaloftheRoyalStatisticalSocietyꎬ1972ꎬ135(2):185 ̄207.[21]vonGroote ̄BidlingmaierFꎬPatientiaRꎬSanchezEꎬetal.Efficacyandsafetyofdelamanidincombinationwithanoptimisedback ̄groundregimenfortreatmentofmultidrug ̄resistanttuberculosis:amulticentreꎬrandomisedꎬdouble ̄blindꎬplacebo ̄controlledꎬparallelgroupphase3trial.TheLancetRespiratoryMedicineꎬ2019ꎬ7(3):249 ̄259.[22]HarringtonDPꎬFlemingTR.Aclassofranktestproceduresforcen ̄soredsurvivaldata.Biometrikaꎬ1982ꎬ69(3):553 ̄566.[23]RodriguezMOꎬRiveroTCꎬdelCastilloBahiRꎬetal.Nimotuzumabplusradiotherapyforunresectablesquamous ̄cellcarcinomaoftheheadandneck.CancerBiolTherꎬ2010ꎬ9(5):343 ̄349.[24]JagathnathKMJꎬMathewAꎬGeorgePS.CancerSurvivalEstimatesDuetoNon ̄UniformLosstoFollow ̄UpandNon ̄ProportionalHaz ̄ards.AsianPacJCancerPrevꎬ2017ꎬ18(6):1493 ̄1497.[25]FlemingTR.ModifiedKolmogorov ̄SmirnovTestProcedureswithApplicationtoArbitrarilyRightCensoredData.Biometricsꎬ1980ꎬ36(4):607 ̄625.[26]KoziolJA.ATwoSampleCRAM&EacuteꎻR‐VONMISESTestforRandomlyCensoredData.BiometricalJournalꎬ1978ꎬ20(6):603 ̄608.[27]BylickiOꎬBarazzuttiHꎬPaleironNꎬetal.First ̄LineTreatmentofNon ̄Small ̄CellLungCancer(NSCLC)withImmuneCheckpointIn ̄hibitors.BioDrugsꎬ2019ꎬ33(2):159 ̄171.[28]YamaueHꎬTsunodaTꎬTaniMꎬetal.RandomizedphaseII/IIIclini ̄caltrialofelpamotideforpatientswithadvancedpancreaticcancer:PEGASUS ̄PCStudy.CancerSciꎬ2015ꎬ106(7):883 ̄890. [29]MatakidouAꎬElGaltaRꎬWebbELꎬetal.Lackofevidencethatp53Arg72Proinfluenceslungcancerprognosis:ananalysisofsurvivalin619femalepatients.LungCancerꎬ2007ꎬ57(2):207 ̄212.(责任编辑:郭海强)。
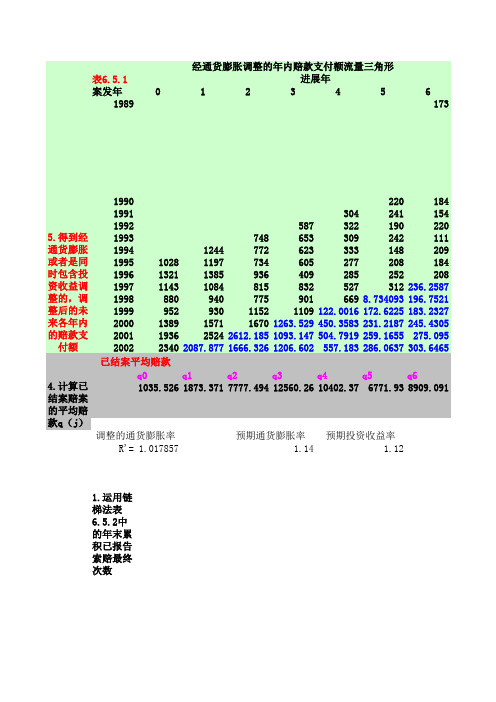
表6.5.1案发年01234561989173199022018419913042411541992587322190220199374865330924211119941244772623333148209199510281197734605277208184199613211385936409285252208199711431084815832527312236.258719988809407759016698.734093196.7521199995293011521109122.0016172.6225183.232720001389157116701263.529450.3583231.2187245.43052001193625242612.1851093.147504.7919259.1655275.095200223402087.8771666.3261206.602557.183286.0637303.6465q0q1q2q3q4q5q61035.5261873.3717777.49412560.2610402.376771.938909.091R'= 1.017857 1.14 1.121.运用链梯法表6.5.2中的年末累积已报告索赔最终次数2.计算累计结案率(注意:年末累积已报告索赔最终次数等于年末累计已结案索赔最终次数3.计算各进展年结案索赔次数f(i,j)4.计算已结案赔案的平均赔款q(j)5.得到经通货膨胀或者是同时包含投资收益调整的,调整后的未来各年内的赔款支付额6.计算未决赔款准备金经通货膨胀调整的年内赔款支付额流量三角形4.计算已结案赔案的平均赔款q(j)5.得到经通货膨胀或者是同时包含投资收益调整的,调整后的未来各年内的赔款支付额调整的通货膨胀率预期通货膨胀率预期投资收益率进展年已结案平均赔款表6.5.27+012345268-6322-5 1.运用链梯法表6.5.2中的年末累积已报告索赔最终次数244-4326-3245-2319-12250187622372269228122932303340346.07141198523272356237923942399 291.8079528.06672191022702307232323362344271.6757477.16193172020842112212921372143.999253.0081730.865416061902193319451955.2461961.649338.8912529.42752113250425412559.5192573.0022581.428379.85195124.2366230827582798.1572818.552833.3972842.677419.27576526.975725142990.8383034.3853056.53072.6013082.663 16262.80~11~22~33~44~5 q7+ 1.189673 1.014561.0072881.0052681.0032758249.769计已结案索赔最终次数),倒退出累积结案率。

第4节 PP 单位根检验法与ADF 单位根检验法DF 检验要求模型的随机扰动项t ε独立同分布。
但在实际应用中这一条件往往不能满足(如上一节中的有关例子)。
一般来说,如果估计模型的DW 值偏离2较大,表明随机扰动项是序列相关的,在这种情况下使用DF 检验可能会导致偏误,需要寻找新的检验方法。
本节我们将介绍在随机扰动项服从一般平稳过程的情况下,检验单位根的PP 检验法和ADF 检验法。
一、 PP (Phillips&Perron )检验首先考虑上一节情形二中扰动项为一平稳过程的单位根检验。
假设数据由(真实过程)φφ∑∞t t -1t t t j t -j j =0y =ρy +u ,u =(B)ε=ε (1) 产生,其中{}t ε独立同分布,∞<==2)(,0)(σεεt t D E 。
∑∞==0)(j j j B B ϕϕ,其中B 为滞后算子,其系数满足条件∞<∑∞=0j j j ϕ。
在回归模型t t t u y y ++=-1ρα中检验假设:0;1:0==αρH与DF 检验(情形二)一样,模型参数的OLS 估计为:⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛∑∑∑∑∑-----t t t t t t y y y y y y N 112111ˆˆρα 在1,0:0==ραH 成立时,上式可改写为:1121111t t t t t t ˆT y u ˆy y y u αρ-----⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭∑∑∑∑∑ 以矩阵()12A diag T ,T =左乘上式两端,得()123122321111121111112211111t t t t t t t t t t t t ˆTyu T A A A ˆy yy u T T y T u T y u T y T y αρ------------------⎧⎫⎧⎫⎛⎫⎛⎫⎛⎫⎪⎪⎪⎪= ⎪ ⎪ ⎪⎨⎬⎨⎬⎪ ⎪ ⎪-⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎩⎭⎩⎭⎛⎫⎛⎫⎪= ⎪ ⎪⎪⎝⎭⎝⎭∑∑∑∑∑∑∑∑∑∑利用有关单位根过程的极限分布(参见第2节),可得()12110221122000111112L W ()W (r )dr ˆT ˆT [W ()]W (r )dr W (r )dr λλαρλγλλ-⎛⎫⎛⎫⎛⎫⎪ ⎪−−→ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰⎰⎰ 其中)1(σϕλ=,∑∞==0220s sϕσγ。


1 试用分数法(Fibonacci法)求f(x)=x2-6x+2在区间[0,10]的极小点,要求缩短后的区间长度不大于原区间的8%?解:F n=1/delta=1/8%=12.5F0=F1=1 F2=2 F3=3 F4=5 F5=8 F6=13所以取n=6第一步:a1=0 b1=10P1=a1+F6-1-1/F6-1+1(b1-a1)=0+5/13*(10-0)=3.846Q1=a1+F6-1/F6-1+1(b1-a1)=0+8/13*(10-0)=6.154F(P1)=F(3.846)=-6.284F(Q1)=F(6.154)=2.948F(P1)< F(Q1) 故x取值区间缩小为[0,6.154]第二步:a2=0 b2=6.154P2=a2+F6-2-1/F6-2+1(b2-a2)=0+3/8*(6.154-0)=2.308Q2=a2+F6-2/F6-2+1(b2-a2)=0+5/8*(6.154-0)=3.846F(P2)=F(2.308)=-6.521F(Q2)=F(3.846)= -6.284F(P2)< F(Q2) 故x取值区间缩小为[0,3.846]第三步:a3=0 b3=3.846P3=a3+F6-3-1/F6-3+1(b3-a3)=0+2/5*(3.846-0)=1.538Q3=a3+F6-3/F6-3+1(b3-a3)=0+3/5*(3.846-0)=2.308F(P3)=F(1.538)=-4.863F(Q3)=F(2.308)= -6.81F(P3)> F(Q3) 故x取值区间缩小为[1.538,3.846]第四步:a4=1.538 b4=3.846P4=a4+F6-4-1/F6-4+1(b4-a4)=1.538+1/3*(3.846-1.538)=2.307Q4=a4+F6-4/F6-4+1(b3-a3)=1.538+2/3*(3.846-1.538)=3.077F(P4)=F(2.307)=-6.520F(Q4)=F(3.077)= -6.994F(P4)> F(Q4) 故x取值区间缩小为[2.307,3.846]第五步:a5=2.307 b5=3.846P5=a5+F6-5-1/F6-5+1(b5-a5)=2.307+1/2*(3.846-2.307)=3.077Q5=a5+F6-5/F6-5+1(b5-a5)= 2.307+1/2*(3.846-2.307)=3.077F(P5)= F(Q5)=F(3.077)=-6.994所以此函数在[0,10]区间内的极小值为-6.994。
【初中数学】初中数学学习方法之超级学习法初中数学
超级学习方法的学习方法。
有兴趣的学生可以学到更多。
超级学习法是由保加利亚的罗扎诺夫博士创造的,它以其高效率和多方面的功用,成为世界十分优秀的学习方法,世界各地都在推行这种学习方法,并将它称为学习的革命。
超级学习法可以用来学习任何学科的知识,尤其是基础课程。
它可以帮助学生轻松记住他们需要记住的一切。
超级学习法大体分为两个部分:一是把精神引导到松驰状态,使学习者在呈α波状态最大限度地提高学习效率的方法;
第二,为了在这种状态下按照一定的节奏学习,尽量将教材编成可操作的模式。
超级学习法要求学生首先有一个学习前的准备工作:
(1)消除身心紧张(有三种方法:呼吸法、身体放松法和心理放松法);
⑵从松驰状态进入α波状态(其方法有感受平静反应,视觉映象α波强化法,靠意念进入α波状态,追忆往日的成功四种)。
上述准备工作完成后,进入学习过程,如记忆定理和公式,可以通过大声朗读和深呼吸交替进行,甚至可以播放特殊的音乐节奏,在愉快的气氛中学习。
初一
,你能灵活地使用它吗。
如果你想知道越来越全面的初中数学学习方法,请注意。