【配套K12】广东省佛山市高明区高中数学 第三章 三角恒等变换 3.1 二倍角的正弦、余弦、正切公式(1)学案

3.1.3 二倍角的正弦、余弦、正切公式2. 3．正弦的二倍角公式的变形(1)sin αcos α＝12sin 2α，cos α＝sin 2α2sin α．(2)1±sin 2α＝(sin α±cos α)2．思考：用tan α能表示sin 2α和cos 2α吗？ [提示] 可以．sin 2α＝2sin αcos α＝2tan α1＋tan 2α. cos 2α＝cos 2α－sin 2α＝1－tan 2α1＋tan 2α. 1.⎝⎛⎭⎪⎫cos π12－sin π12⎝ ⎛⎭⎪⎫cos π12＋sin π12＝()A ．－32B ．－12C ．12D ．32D [原式＝cos 2π12－sin 2π12＝cos π6＝32.]2．sin 15°cos 15°＝ ．14 [sin 15°cos 15°＝12×2sin 15°cos 15°＝12sin 30°＝14.] 3．12－cos 2π8＝ ．－24 [12－cos 2π8＝12⎝ ⎛⎭⎪⎫1－2cos 2π8＝－12cos π4＝－24.]4．若tan θ＝2则tan 2θ＝ ． －43 [tan 2θ＝2tan θ1－tan 2θ＝2×21－22＝－43.]给角求值【例1】 (1)cos 412－sin 412等于( )A ．－12B ．－32C ．12D ．32(2)求下列各式的值．①1－2sin 2750°； ②2tan 150°1－tan 2150°； ③cos π5cos 2π5. (1)D[原式＝⎝⎛⎭⎪⎫cos 2π12－sin 2π12⎝ ⎛⎭⎪⎫cos 2π12＋sin 2π12＝cos 2π12－sin 2π12＝cos π6＝32.](2)[解] ①原式＝cos(2×750°)＝cos 1 500° ＝cos ()4×360°＋60° ＝cos 60°＝12.②原式＝tan(2×150°)＝tan 300°＝tan(360°－60°)＝－tan 60°＝－ 3.③原式＝2sin π5cos π5cos2π52sinπ5＝sin 2π5cos 2π52sin π5＝sin4π54sinπ5＝sinπ54sinπ5＝14.对于给角求值问题，一般有两类：(1)直接正用、逆用二倍角公式，结合诱导公式和同角三角函数的基本关系对已知式子进行转化，一般可以化为特殊角．(2)若形式为几个非特殊角的三角函数式相乘，则一般逆用二倍角的正弦公式，在求解过程中，需利用互余关系配凑出应用二倍角公式的条件，使得问题出现可以连用二倍角的正弦公式的形式．1．求下列各式的值 (1)cos 72°cos 36°； (2)1sin 50°＋3cos 50°.[解] (1)cos 36°cos 72°＝2sin 36°cos 36°cos 72°2sin 36°＝2sin 72°cos 72°4sin 36°＝sin 144°4sin 36°＝14.(2)原式＝cos 50°＋3sin 50°sin 50°cos 50°＝2⎝⎛⎭⎪⎪⎫12cos 50°＋32sin 50°12×2sin 50°cos 50°＝2sin 80°12sin 100°＝2sin 80°12sin 80°＝4.给值求值、求角问题1．公式的变形应用是打开解题突破口的关键，二倍角公式有哪些主要变形？提示：主要变形有：1±sin 2α＝sin 2α＋cos 2α±2sin αcos α＝(sin α±cosα)2，1＋cos 2α＝2cos 2α，cos 2α＝1＋cos 2α2，sin 2α＝1－cos 2α2.2．如何在倍角公式中用2α±π2＝2(α±π4)解题？提示：(1)sin 2α＝cos ⎝ ⎛⎭⎪⎫π2－2α＝cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π4－α＝2cos2⎝ ⎛⎭⎪⎫π4－α－1＝1－2sin 2⎝ ⎛⎭⎪⎫π4－α； (2)cos 2α＝sin ⎝ ⎛⎭⎪⎫π2－2α＝sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π4－α＝2sin ⎝ ⎛⎭⎪⎫π4－αcos ⎝ ⎛⎭⎪⎫π4－α；(3)cos 2α＝sin ⎝ ⎛⎭⎪⎫π2＋2α＝sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π4＋α＝2sin ⎝ ⎛⎭⎪⎫π4＋αcos ⎝ ⎛⎭⎪⎫π4＋α.【例2】 (1)已知α∈⎝ ⎛⎭⎪⎫－π2，π2，且sin 2α＝sin ⎝⎛⎭⎪⎫α－π4，求α.(2)已知sin ⎝ ⎛⎭⎪⎫π4－x ＝513，0＜x ＜π4，求cos 2xcos ⎝ ⎛⎭⎪⎫π4＋x 的值．思路点拨：(1)⎝⎛⎭⎪⎫2α＋π2－2α＝π2，用诱导公式联系求解．(2)用余弦二倍角公式和诱导公式求解． [解](1)∵sin 2α＝－cos ⎝⎛⎭⎪⎫2α＋π2＝－⎣⎢⎡⎦⎥⎤2cos 2⎝⎛⎭⎪⎫α＋π4－1＝1－2cos2⎝⎛⎭⎪⎫α＋π4，sin ⎝ ⎛⎭⎪⎫α－π4＝－sin ⎝ ⎛⎭⎪⎫π4－α＝－cos ⎣⎢⎢⎡⎦⎥⎥⎤π2－⎝ ⎛⎭⎪⎫π4－α＝－cos ⎝ ⎛⎭⎪⎫π4＋α，∴原式可化为1－2cos2⎝⎛⎭⎪⎫α＋π4＝－cos ⎝⎛⎭⎪⎫α＋π4，解得cos ⎝⎛⎭⎪⎫α＋π4＝1或cos ⎝⎛⎭⎪⎫α＋π4＝－12.∵α∈⎝⎛⎭⎪⎫－π2，π2，∴α＋π4∈⎝ ⎛⎭⎪⎫－π4，3π4，故α＋π4＝0或α＋π4＝2π3，即α＝－π4或α＝5π12.(2)∵0＜x ＜π4，sin ⎝ ⎛⎭⎪⎫π4－x ＝513，∴π4－x ∈⎝ ⎛⎭⎪⎫0，π4，cos ⎝ ⎛⎭⎪⎫π4－x ＝1213，cos 2x cos ⎝ ⎛⎭⎪⎫π4＋x ＝cos 2x －sin 2x 22（cos x －sin x ）＝2(cos x ＋sin x )＝2cos ⎝ ⎛⎭⎪⎫π4－x ＝2413.1．若本例(2)中的条件不变，则sin 2xsin ⎝ ⎛⎭⎪⎫π4＋x 的值是什么？[解]sin ⎝ ⎛⎭⎪⎫π4－x ＝22cos x －22sin x ＝513， 平方得sin 2x ＝119169，sin ⎝ ⎛⎭⎪⎫π4＋x ＝cos ⎣⎢⎢⎡⎦⎥⎥⎤π2－⎝ ⎛⎭⎪⎫π4＋x ＝cos ⎝ ⎛⎭⎪⎫π4－x ＝1213，所以sin 2x sin ⎝ ⎛⎭⎪⎫π4＋x ＝119169×1312＝119156.2．若本例(2)中的条件变为tan ⎝ ⎛⎭⎪⎫π4－x ＝512，其他条件不变，结果如何？[解] 因为tan ⎝ ⎛⎭⎪⎫π4－x ＝512，所以sin ⎝ ⎛⎭⎪⎫π4－x ＝512cos ⎝ ⎛⎭⎪⎫π4－x ，又sin2⎝ ⎛⎭⎪⎫π4－x ＋cos 2⎝ ⎛⎭⎪⎫π4－x ＝1， 故可解得cos ⎝ ⎛⎭⎪⎫π4－x ＝1213，原式＝2cos ⎝ ⎛⎭⎪⎫π4－x ＝2413.解决条件求值问题的方法(1)有方向地将已知式或未知式化简，使关系明朗化；寻找角之间的关系，看是否适合相关公式的使用，注意常见角的变换和角之间的二倍关系．(2)当遇到π4±x 这样的角时可利用互余角的关系和诱导公式，将条件与结论沟通．cos 2x ＝sin ⎝ ⎛⎭⎪⎫π2－2x ＝2sin ⎝ ⎛⎭⎪⎫π4－x cos ⎝ ⎛⎭⎪⎫π4－x .类似的变换还有：cos 2x ＝sin ⎝ ⎛⎭⎪⎫π2＋2x ＝2sin ⎝ ⎛⎭⎪⎫π4＋x cos ⎝ ⎛⎭⎪⎫π4＋x ，sin 2x ＝cos ⎝ ⎛⎭⎪⎫π2－2x ＝2cos 2⎝ ⎛⎭⎪⎫π4－x －1，sin 2x ＝－cos ⎝ ⎛⎭⎪⎫π2＋2x ＝1－2cos 2⎝ ⎛⎭⎪⎫π4＋x 等．化简、证明问题【例3】 (1)化简：tan θ＋1＋tan θ－1＝ ．(2)证明：3tan 12°－3sin 12°（4cos 212°－2）＝－4 3. 思路点拨：(1)通分变形．(2)切化弦通分，构造二倍角的余弦→二倍角的正弦→约分求值(1)－tan 2θ [原式＝tan θ－1＋tan θ＋1（tan θ＋1）（tan θ－1）＝2tan θtan 2θ－1＝－2tan θ1－tan 2θ＝－tan 2θ.] (2)证明：左边＝3sin 12°－3cos 12°cos 12°2sin 12°（2cos 212°－1）＝23⎝⎛⎭⎪⎪⎫12sin 12°－32cos 12°2sin 12°cos 12°cos 24°＝23sin （12°－60°）sin 24°cos 24°＝－23sin 48°12sin 48°＝－43＝右边，所以原等式成立．] 证明三角恒等式的原则与步骤(1)观察恒等式两端的结构形式，处理原则是从复杂到简单，高次降低，复角化单角，如果两端都比较复杂，就将两端都化简，即采用“两头凑”的思想．(2)证明恒等式的一般步骤：①先观察，找出角、函数名称、式子结构等方面的差异； ②本着“复角化单角”“异名化同名”“变换式子结构”“变量集中”等原则，设法消除差异，达到证明的目的．2．求证：(1)cos 2(A ＋B )－sin 2(A －B )＝cos 2A cos 2B ； (2)cos 2θ(1－tan 2θ)＝cos 2θ.[证明] (1)左边＝1＋cos （2A ＋2B ）2－1－cos （2A －2B ）2＝cos （2A ＋2B ）＋cos （2A －2B ）2＝12(cos 2A cos 2B －sin 2A sin 2B ＋cos 2A cos 2B ＋sin 2A sin 2B )＝cos 2A cos 2B ＝右边， ∴等式成立．(2)法一：左边＝cos 2θ⎝⎛⎭⎪⎫1－sin 2θcos 2θ＝cos 2θ－sin 2θ＝cos 2θ＝右边． 法二：右边＝cos 2θ＝cos 2θ－sin 2θ＝cos 2θ⎝⎛⎭⎪⎫1－sin 2θcos 2θ＝cos 2θ(1－tan 2θ)＝左边．1．对于“二倍角”应该有广义上的理解，如：8α是4α的二倍；6α是3α的二倍；4α是2α的二倍；3α是32α的二倍；α2是α4的二倍；α3是α6的二倍；α2n 是α2n ＋1的二倍(n ∈N *)．2．二倍角余弦公式的运用在二倍角公式中，二倍角的余弦公式最为灵活多样，应用广泛．常用形式：①1＋cos 2α＝2cos 2α；②cos 2α＝1＋cos 2α2；③1－cos 2α＝2sin 2α；④sin 2α＝1－cos 2α2.1．下列说法错误的是( )A ．6α是3α的倍角，3α是3α2的倍角B ．二倍角的正弦、余弦公式的适用范围是任意角C ．存在角α，使得sin 2α＝2sin α成立D ．对任意角α，总有tan 2α＝2tan α1－tan 2αD [A 正确，β中二倍角的正弦、余弦公式适用任意角，正切公式的适用范围是α，2α≠k π＋π2(k ∈Z )，故B 对，D 错；C 中若α＝k π(k ∈Z )时等式成立．]2．若sin α＝3cos α，则sin 2αcos 2α＝ ． 6 [sin 2αcos 2α＝2sin αcos αcos 2α＝2sin αcos α＝6cos αcos α＝6.] 3．设sin 2α＝－sin α，α∈⎝ ⎛⎭⎪⎫π2，π，则tan 2α的值是 ．3 [∵sin 2α＝－sin α，∴2sin αcos α＝－sin α.由α∈⎝ ⎛⎭⎪⎫π2，π知sin α≠0，∴cos α＝－12，∴α＝2π3， ∴tan 2α＝tan 4π3＝tan π3＝ 3.] 4．已知π2＜α＜π，cos α＝－45. (1)求tan α的值；(2)求sin 2α＋cos 2α的值．[解] (1)因为cos α＝－45，π2＜α＜π， 所以sin α＝35， 所以tan α＝sin αcos α＝－34.(2)因为sin 2α＝2sin αcos α＝－2425， cos 2α＝2cos 2α－1＝725， 所以sin 2α＋cos 2α＝－2425＋725＝－1725.。

3.1 两角和与差的余弦（2）【学习目标】1．进一步熟悉两角和与差的余弦公式．2．培养学生逆用和变用公式的能力.【重点难点】重点：公式的理解与运用．难点：公式的逆用．【学法指导】建议同学们通过例题与练习，多多体会公式是如何使用的？有什么规律吗？【学习过程】一．课前预习１．回顾第一课时的内容，想想公式的推导、公式的特点与运用公式有什么需要注意的地方．２．完成下列的练习：（1）0cos105_____________=（2）33cos cossin sin ________________510510ππππ-= （3）0000cos53cos 67cos37cos157________________+=（4）00cos(30)cos sin(30)sin αααα+++=二．课堂学习与研讨例1．350,,cos ,sin(),cos 22513ππαβπααββ<<<<=+=求的值．练习１．若α是锐角，且31)6sin(=-πα，求cos α的值．例2．已知11sin sin ,cos cos ,22αβαβ-=-+=，求cos()αβ+的值.练习2．()34,sin sin .55αβ=-=,求的值cosα-cosβcos α-β课堂小结：请同学们对例1与例2的方法进行总结．１．２．三．课堂检测1．若5cos(),313παα+=为锐角，则cos ______________α=2．已知0000(cos80,sin80),(cos 20,sin 20),_________A B AB =则四．作业１．（课本137,4P ）已知,αβ都是锐角，111cos ,cos()714ααβ=+=-，求cos β的值．２．（课本137,5P）已知3sin(30),601505αα+=<<，求cosα的值．３．已知3312,(,),sin(),sin()45413ππαβπαββ∈+=--=，求cos()4πα+的值．。

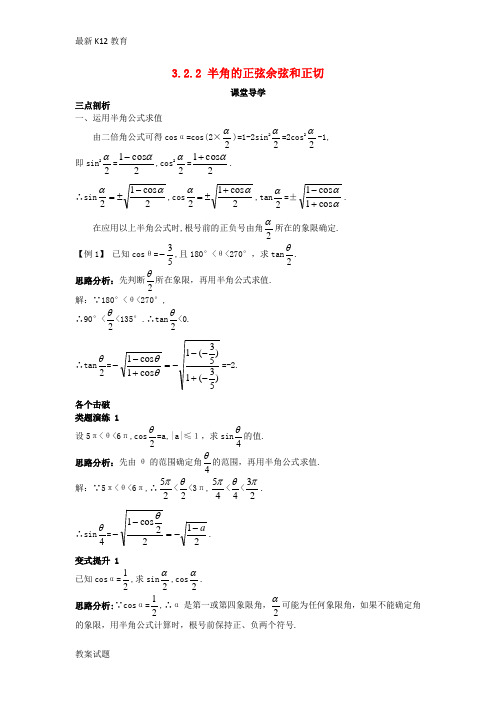
3.2.2 半角的正弦余弦和正切课堂导学三点剖析一、运用半角公式求值由二倍角公式可得cos α=cos(2×2α)=1-2sin 22α=2cos 22α-1, 即sin 22α=2cos 1α-,cos 22α=2cos 1α+. ∴sin 2cos 12αα-±=,cos 2cos 12αα+±=,tan 2α=±ααcos 1cos 1+-. 在应用以上半角公式时,根号前的正负号由角2α所在的象限确定. 【例1】 已知cos θ=53-,且180°<θ<270°，求tan 2θ. 思路分析：先判断2θ所在象限，再用半角公式求值. 解：∵180°<θ<270°, ∴90°<2θ<135°.∴tan 2θ<0. ∴tan 2θ=)53(1)53(1cos 1cos 1-+---=+--θθ=-2. 各个击破类题演练 1设5π<θ<6π,cos2θ=a,|a|≤１，求sin 4θ的值. 思路分析：先由θ的范围确定角4θ的范围，再用半角公式求值. 解：∵5π<θ<6π,∴25π<2θ<3π,45π<4θ<23π. ∴sin 4θ=2122cos 1a --=--θ. 变式提升 1已知cos α=21,求sin 2α,cos 2α. 思路分析:∵cos α=21,∴α是第一或第四象限角，2α可能为任何象限角，如果不能确定角的象限，用半角公式计算时，根号前保持正、负两个符号.解:sin 2α=±22112cos 1-±=-α=±21. cos 2α=±2322112cos 1±=+±=+α. 二、运用公式化简三角函数式在三角恒等变形中,所涉及的三角公式要求做到灵活运用,既要会正用,又要会逆用,更要会变用.特别要注意根号前正负号的选择,要由2α所在的象限来确定. 【例2】 若23π<α<2π,化简:α2cos 21212121++. 思路分析:在逐层去根号时,要根据角的范围确定被开方数的符号. 解：∵23π<α<2π,∴43π<2α<π. ∴原式=αααcos 2121cos 212122cos 121212+=+=++ 2cos )cos 1(212αα=+==-cos 2α. 类题演练 2化简:8cos 228sin 12+=+等于( )A.2sin4B.2sin4-4cos4C.-2sin4-4cos4D.4cos4-2sin4解析:原式=)14cos 2(22)4cos 4(sin 222-+++-2(sin4+cos4)-2cos4=-2sin4-4cos4.答案:C变式提升 2 化简:cos α·cos2α·cos 22α·…·cos 12-n α. 解:原式=1112sin 22sin 22cos 2cos cos ---∙∙∙∙n n n ααααα 12222sin 22sin 2cos 2cos 2cos cos ---∙∙∙∙∙=n n n αααααα=11112322sin 22sin 2sin 2sin cos 2sin 22sin 2cos 2coscos -----=∙∙=∙∙∙∙n n n n n n αααααααααα .。

【创新设计】（浙江专用）2016-2017高中数学 第三章 三角恒等变换 3.1.3 二倍角的正弦、余弦、正切公式课时作业 新人教版必修41.如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x 的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示成x 的函数f (x )，则y ＝f (x )在[0，π]的图象大致为( )解析 如图所示，当x ∈⎝⎛⎭⎪⎫0，π2时，则P (cos x ，sin x )，M (cos x ，0)，作MM ′⊥OP ，M ′为垂足，则|MM ′||OM |＝sin x ，∴f （x ）cos x＝sin x ，∴f (x )＝sin x cos x ＝12sin 2x ，则当x ＝π4时，f (x )max ＝12；当x ∈⎝ ⎛⎭⎪⎫π2，π时，有f （x ）|cos x |＝sin(π－x )，f (x )＝－sin x cos x ＝－12sin 2x ，当x ＝3π4时，f (x )max ＝12.只有B 选项的图象符合. 答案 B 2.3－sin 70°2－cos 210°的值是( ) A.12B.22C.2D.32解析 原式＝3－sin 70°2－12（1＋cos 20°）＝2（3－cos 20°）3－cos 20°＝2.答案 C3.若sin ⎝ ⎛⎭⎪⎫π6－α＝13，则cos ⎝ ⎛⎭⎪⎫2π3＋2α的值为( ) A.－13B.－79C.13D.79解析 cos ⎝⎛⎭⎪⎫2π3＋2α＝－cos ⎝ ⎛⎭⎪⎫π3－2α＝－cos[2⎝ ⎛⎭⎪⎫π6－α]＝－[1－2sin 2⎝ ⎛⎭⎪⎫π6－α]＝2sin 2⎝ ⎛⎭⎪⎫π6－α－1＝－79.答案 B4.设sin 2α＝－sin α，α∈⎝ ⎛⎭⎪⎫π2，π，则tan 2α的值是________.解析 因为sin 2α＝2sin αcos α＝－sin α，α∈⎝ ⎛⎭⎪⎫π2，π，所以cos α＝－12，sin α＝1－cos 2α＝32，所以tan α＝－3，则tan 2α＝2tan α1－tan 2α＝－231－（－3）2＝ 3. 答案35.若α∈⎝⎛⎭⎪⎫0，π2，且sin 2α＋cos 2α＝14，则tan α的值等于________.解析 由sin 2 α＋cos 2α＝14得sin 2 α＋1－2sin 2 α＝1－sin 2 α＝cos 2α＝14.∵α∈⎝⎛⎭⎪⎫0，π2，∴cos α＝12，∴α＝π3，∴tan α＝tan π3＝ 3.答案36.已知函数f (x )＝2cos ⎝ ⎛⎭⎪⎫x －π12，x ∈R .(1)求f ⎝ ⎛⎭⎪⎫－π6的值； (2)若cos θ＝35，θ∈⎝ ⎛⎭⎪⎫3π2，2π，求f ⎝⎛⎭⎪⎫2θ＋π3. 解 (1)f ⎝ ⎛⎭⎪⎫－π6＝2cos ⎝ ⎛⎭⎪⎫－π6－π12＝2cos ⎝ ⎛⎭⎪⎫－π4＝2cos π4＝1； (2)f ⎝ ⎛⎭⎪⎫2θ＋π3＝2cos ⎝ ⎛⎭⎪⎫2θ＋π3－π12＝2cos ⎝⎛⎭⎪⎫2θ＋π4＝cos 2θ－sin 2θ因为cos θ＝35，θ∈⎝ ⎛⎭⎪⎫3π2，2π，所以sin θ＝－45，所以sin 2θ＝2sin θcos θ＝－2425，cos 2θ＝cos 2 θ－sin 2θ＝－725，所以f ⎝ ⎛⎭⎪⎫2θ＋π3＝cos 2θ－sin 2θ＝－725－⎝ ⎛⎭⎪⎫－2425＝1725. 7.求值：(1)sin 6°sin 42°sin 66°sin 78°. (2)sin 50°（1＋3tan 10°）－cos 20°cos 80°1－cos 20°.解 (1)原式＝sin 6°cos 48°cos 24°cos 12° ＝sin 6°cos 6°cos 12°cos 24°cos 48°cos 6°＝sin 96°16cos 6°＝cos 6°16cos 6°＝116. (2)∵sin 50°(1＋3tan 10°) ＝sin 50°·cos 10°＋3sin 10°cos 10°＝sin 50°·2sin 40°cos 10°＝sin 80°cos 10°＝1，cos 80°1－cos 20°＝sin 10°2sin 210°＝2sin 210°， ∴sin 50°（1＋3tan 10°）－cos 20°cos 80°1－cos 20°＝1－cos 20°2sin 210°＝2sin 210°2sin 210°＝ 2. 8.已知cos ⎝ ⎛⎭⎪⎫x －π4＝210，x ∈⎝ ⎛⎭⎪⎫π2，3π4.(1)求sin x 的值. (2)求sin ⎝⎛⎭⎪⎫2x ＋π3的值.解 (1)因为x ∈⎝ ⎛⎭⎪⎫π2，3π4，所以x －π4∈⎝ ⎛⎭⎪⎫π4，π2，于是sin ⎝ ⎛⎭⎪⎫x －π4＝1－cos 2⎝⎛⎭⎪⎫x －π4＝7210，则sin x ＝sin ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫x －π4＋π4＝sin ⎝ ⎛⎭⎪⎫x －π4cos π4＋cos ⎝⎛⎭⎪⎫x －π4sin π4＝7210×22＋210×22＝45.(2)因为x ∈⎝ ⎛⎭⎪⎫π2，3π4，故cos x ＝－1－sin 2x ＝－1－⎝ ⎛⎭⎪⎫452＝－35， sin 2x ＝2sin x cos x ＝－2425，cos 2x ＝2cos 2x －1＝－725，所以sin ⎝⎛⎭⎪⎫2x ＋π3 ＝sin 2x cos π3＋cos 2x sin π3＝－24＋7350.能 力 提 升9.4cos 50°－tan 40°＝( ) A. 2 B.2＋32C. 3D.22－1解析 4cos 50°－tan 40°＝4cos 50°－sin 40°cos 40°＝4cos 50°cos 40°－sin 40°cos 40°＝4sin 40°cos 40°－sin 40°cos 40°＝2sin 80°－sin 40°cos 40°＝2sin （60°＋20°）－sin （60°－20°）cos 40°＝32cos 20°＋32sin 20°cos 40°＝3cos 40°cos 40°＝3，选C.答案 C10.若1－tan θ2＋tan θ＝1，则cos 2θ1＋sin 2θ的值为( )A.3B.－3C.－2D.－12解析 ∵1－tan θ2＋tan θ＝1，∴tan θ＝－12.∴cos 2θ1＋sin 2θ＝cos 2θ－sin 2θ（sin θ＋cos θ）2＝cos θ－sin θcos θ＋sin θ＝1－tan θ1＋tan θ＝1－⎝ ⎛⎭⎪⎫－121＋⎝ ⎛⎭⎪⎫－12＝3. 答案 A11.函数y ＝sin 2x ＋23sin 2x 的最小正周期T 为________. 解析 y ＝sin 2x ＋23sin 2 x ＝sin 2x ＋23×1－cos 2x2＝sin 2x －3cos 2x ＋ 3 ＝2sin ⎝ ⎛⎭⎪⎫2x －π3＋3， 所以周期T ＝2π2＝π.答案 π12.已知tan θ2＝3，则1－cos θ＋sin θ1＋cos θ＋sin θ＝______.解析 1－cos θ＋sin θ1＋cos θ＋sin θ＝2sin 2θ2＋2sin θ2cosθ22cos 2θ2＋2sin θ2cosθ2＝2sin θ2⎝ ⎛⎭⎪⎫sin θ2＋cos θ22cos θ2⎝ ⎛⎭⎪⎫cos θ2＋sin θ2＝tan θ2＝3.答案 313.设f (x )＝sin ⎝⎛⎭⎪⎫2x ＋π6＋2m sin x cos x ，x ∈R .(1)当m ＝0时，求f (x )在⎣⎢⎡⎦⎥⎤0，π3内的最小值及相应的x 的值；(2)若f (x )的最大值为12，求m 的值.解 (1)因为x ∈⎣⎢⎡⎦⎥⎤0，π3，则2x ＋π6∈⎣⎢⎡⎦⎥⎤16π，56π，所以f (x )min＝12，此时x ＝0或π3.(2)令f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π6＋2m sin x cos x ＝⎝⎛⎭⎪⎫m ＋32·sin 2x ＋12cos 2x ＝⎝⎛⎭⎪⎫m ＋322＋14sin(2x ＋φ)，其中tan φ＝12m ＋32，于是f (x )max ＝⎝⎛⎭⎪⎫m ＋322＋14，令⎝⎛⎭⎪⎫m ＋322＋14＝12，得m ＝－32. 探 究 创 新14.已知向量a ＝⎝ ⎛⎭⎪⎫cos x ，－12，b ＝(3sin x ，cos 2x )，x ∈R ，设函数f (x )＝a ·b .(1)求f (x )的最小正周期.(2)求f (x )在⎣⎢⎡⎦⎥⎤0，π2上的最大值和最小值.解 (1)f (x )＝a ·b ＝cos x ·3sin x －12cos 2x＝32sin 2x －12cos 2x ＝sin ⎝⎛⎭⎪⎫2x －π6. 最小正周期T ＝2π2＝π.所以f (x )＝sin ⎝⎛⎭⎪⎫2x －π6的最小正周期为π. (2)当x ∈⎣⎢⎡⎦⎥⎤0，π2时，⎝ ⎛⎭⎪⎫2x －π6∈⎣⎢⎡⎦⎥⎤－π6，5π6，由正弦函数y ＝sin x 在⎣⎢⎡⎦⎥⎤－π6，5π6上的图象知，f (x )＝sin ⎝⎛⎭⎪⎫2x －π6∈⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫－π6，f ⎝ ⎛⎭⎪⎫π2＝⎣⎢⎡⎦⎥⎤－12，1. 所以，f (x )在⎣⎢⎡⎦⎥⎤0，π2上的最大值和最小值分别为1，－12.。

2017-2018学年高中数学第三章三角恒等变换3.1 两角和与差的正弦、余弦和正切公式3.1.1 两角差的余弦公式优化练习新人教A版必修4编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017-2018学年高中数学第三章三角恒等变换3.1 两角和与差的正弦、余弦和正切公式3.1.1 两角差的余弦公式优化练习新人教A版必修4）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017-2018学年高中数学第三章三角恒等变换3.1 两角和与差的正弦、余弦和正切公式3.1.1 两角差的余弦公式优化练习新人教A版必修4的全部内容。

3。

1。

1 两角差的余弦公式［课时作业］［A组基础巩固]1．化简cos(45°－α）cos（α＋15°）－sin（45°－α）sin（α＋15°）的结果是( ）A。

错误!B．－错误!C.错误!D．－错误!解析：原式＝cos(α－45°）cos(α＋15°)＋sin（α－45°）sin（α＋15°)＝cos[（α－45°）－（α＋15°）]＝cos（－60°）＝错误!.答案：A2．已知cos α＝错误!，α∈错误!，则cos错误!的值等于( )A。

错误!B．－错误!C．－错误!D。

错误!解析：∵cos α＝错误!，α∈错误!，∴sin α＝－错误!,∴cos错误!＝cos αcos 错误!＋sin αsin 错误!＝错误!错误!＝－错误!.答案：C3．已知cos错误!＝错误!，0＜θ＜错误!,则cos θ等于( ）A.错误!B。

2017-2018学年高中数学第三章三角恒等变换3.1 两角和与差的正弦、余弦和正切公式3.1.2 两角和与差的正弦、余弦、正切公式优化练习新人教A 版必修4编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017-2018学年高中数学第三章三角恒等变换3.1 两角和与差的正弦、余弦和正切公式3.1.2 两角和与差的正弦、余弦、正切公式优化练习新人教A版必修4）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017-2018学年高中数学第三章三角恒等变换3.1 两角和与差的正弦、余弦和正切公式3.1.2 两角和与差的正弦、余弦、正切公式优化练习新人教A版必修4的全部内容。

3.1.2 两角和与差的正弦、余弦、正切公式[课时作业]［A组基础巩固]1．sin 245°sin 125°＋sin 155°sin 35°的值是( ）A．－错误!B．－错误!C。

12D.错误!解析：原式＝－sin 65°sin 55°＋sin 25°sin 35°＝－cos 25°cos 35°＋sin 25°sin 35°＝－cos（35°＋25°）＝－cos 60°＝－错误!.答案：B2．已知α是锐角，sin α＝错误!，则cos 错误!等于（）A．－错误! B.错误!C．－错误! D.错误!解析：因为α是锐角，sin α＝错误!，所以cos α＝错误!，所以cos 错误!＝错误!×错误!－错误!×错误!＝错误!.答案：B3．设A,B,C为三角形的三个内角，且tan A，tan B是方程3x2－5x＋1＝0的两个实根，则△ABC为( ）A．等边三角形B．等腰直角三角形C．锐角三角形D．钝角三角形解析：因为tan A,tan B是方程3x2－5x＋1＝0的两个实根，所以tan A＋tan B＝错误!,tan A tan B＝错误!，所以tan C＝－tan(A＋B）＝－错误!＝错误!＝－错误!<0，所以错误!<C〈π，故选D。

3.1.3 二倍角的正弦、余弦、正切公式（二）课堂导学三点剖析1.二倍角公式在证明题中的应用【例1】 求证:x x cos 22sin （1+tanx·tan 2x ）=tanx. 思路分析：本题的目标是把等式的左端统一成角x 的正切函数.可能用的公式有sin2x=2sinxcosx ，tan 2x =x x x x x x x sin cos 12cos 2sin 22sin 22cos 2sin2-==. 证法1：左端=x x x cos 2cos sin 2（1+xx x x sin cos 1cos sin -•) =sinx （1+xx cos cos 1-） =xx cos sin =tanx=右端. 证法2：左端=x x x x x x x x x x x x x x x cos sin 2tan 2cos cos 2sin cos 2cos sin 2)2tan(2tan tan cos 22sin =••=--• =x x cos sin =tanx=右端. 温馨提示证明恒等式就是要根据所证等式两端的特征（结构、名称、角度等）来选择最佳方法，本题就是抓住左右两端的次数差异作为突破口，使问题得以解决.2.二倍角公式在化简题中的应用【例2】 已知函数f （x ）=cos 4x-2sinxcosx-sin 4x.（1）求f （x ）的最小正周期；（2）若x∈［0，2π］，求f （x ）的最大值，最小值. 解：（1）因为f （x ）=cos 4x-2sinxcosx-sin 4x=（cos 2x+sin 2x ）（cos 2x-sin 2x ）-sin2x =cos2x-sin2x=2cos （2x+4π），所以f （x ）的最小正周期T=22π=π. （2）因为0≤x≤2π，所以4π≤2x+4π≤π45. 当2x+4π=4π时，cos （2x+4π）取得最大值22； 当2x+4π=π时，cos （2x+4π）取得最小值-1. 所以f （x ）在［0，2π］上的最大值为1， 最小值为2-.温馨提示（1）将cos2x-sin2x 变形为sin （4π-2x ），也会有同样的结果; （2）像这类高次三角函数，首先利用倍角公式通过降幂化为y=Asin （ωx+φ）或y=Acos （ωx+φ）（A ，ω，φ均为常数，A ＞0）的形式，然后再求周期和最值.3.公式的综合、灵活运用【例3】 已知函数f （x ）=3-sin 2x+sinxcosx （1）求f （625π）的值； （2）设α∈（0，π），f （2α）=41-23，求sinα的值 解：（1）∵sin 625π=21，cos 625π=23， ∴f（625π）=-3sin 2625π+sin 625πcos 625π=0 （2）f （x ）=23cos2x-23+21sin2x ∴f（2α）=23cos α+21sin α-23=41-23， 16sin 2α-4sin α-11=0解得sin α=8531±. ∵α∈（0，π），∴sinα＞0故sinα=8531+ 温馨提示要注意公式变形的重要性，不能死记公式，更不能只会正用，同时逆用、变形也要学会只有灵活运用公式，才能灵活解决问题各个击破类题演练1求证：3+cos4α-4cos2α=8sin 4α.证法1：∵左边=2+1+cos4α-4cos2α=2+2cos 22α-4cos2α=2（cos 22α-2cos2α+1）=2（cos2α-1）2=2（-2sin 2α）2=8sin 4α=右边.∴等式成立.证法2：右边=2×4sin 4α=2（1-cos2α）2=2（1-2cos2α+cos 22α）=2-4cos2α+2cos 22α =2-4cos2α+1+cos4α=3+cos4α-4cos2α=左边.∴等式成立.变式提升1 求证:.tan 14cos 4sin 1tan 24cos 4sin 12θθθθθθ-++=-+ 证明：左边=θθθtan 24sin )4cos 1(+- =θθθθθcos sin 22cos 2sin 22sin 22+=θθθθθsin sin cos 2)2cos 2(sin 2+ =2cos 2θ（sin2θ+cos2θ） 右边=θθθ2tan 14sin )4cos 1(-++ =θθθθθθ2222cos sin cos 2cos 2sin 22cos 2•-+ =θθθθθ2cos 2cos )2sin 2(cos 2cos 2•+ =2cos 2θ（sin2θ+cos2θ）∴左边=右边，故等式成立.类题演练2设函数f （x ）=sin 2x+3sinxcosx+α， （1）写出函数f （x ）的单调递增区间;（2）求f （x ）的最小正周期.解：（1）f （x ）=2322cos 1+-x sin2x+a =23sin2x-21cos2x+a+21 =sin （2x-6π）+a+21, 2k π-2π≤2x -6π≤2kπ+2π，k∈Z ， k π-6π≤x≤kπ+3π,k∈Z , ∴f（x ）的单调递增区间是［kπ-6π，kπ+3π］，k∈Z （2）T=222πωπ==π， ∴f（x ）的最小正周期为π.变式提升2已知函数y=sin2x-2（sinx+cosx ）+a 2设t=sinx+cosx ，t 为何值时，函数y 取得最小值；解：∵t=sinx+cosx=2sin （x+4π），-2≤t≤2， ∴t 2=1+2sinxcosx=1+sin2x ，sin2x=t 2-1，∴y=t 2-1-2t+a 2=（t-1）2+a 2-2∵-2≤t≤2，∴当t=1时，函数y 取得最小值a 2-2类题演练3 已知α为第二象限角，且sinα=415，求12cos 2sin )4sin(+++ααπα的值. 解：∵sinα=415，α为第二象限角，∴cosα=-41. ∴sin2α=2sinαcosα=815-. ααπαπαααπα2cos 22sin 4sin cos 4cos sin 12cos 2sin )4sin(++=+++ =151230)41(28152241224152--=-⨯+-⨯-⨯ =.2151)115(2-=--变式提升3函数f （x ）=sin 2（x+4π）-sin 2（x-4π）是（ ） A.周期为π的偶函数 B.周期为π的奇函数C.周期为2π的偶函数D.周期为2π的奇函数解析：f （x ）=2)22cos(12)22cos(1ππ---+-x x =22sin 122sin 1x x --+=sin2x.∴T=22 =π,f（x ）为奇函数. 答案：B。

学习资料3．1.3 二倍角的正弦、余弦、正切公式内容标准学科素养1.会用两角和的正弦、余弦、正切公式推导出二倍角的正弦、余弦、正切公式。

2.能熟练运用二倍角的公式进行简单的恒等变换并能灵活地将公式变形运用. 发展逻辑推理提升数学运算授课提示：对应学生用书第78页［基础认识］知识点二倍角的正弦、余弦、正切公式阅读教材P132～133，思考并完成以下问题能利用S(α±β)，C（α±β），T(α±β）推导出sin 2α，cos 2α，tan 2α的公式吗？（1)在公式Sα＋β中，如果β＝α，有怎样的结果？提示:当β＝α时,sin（α＋β)＝sin 2α＝sin αcos α＋cos αsin α＝2sin αcos α。

（2）在公式Cα＋β中，如果β＝α，有怎样的结果?提示：cos(α＋β)＝cos αcos β－sin αsin β，当β＝α时，cos 2α＝cos2α－sin2α.（3)在Tα＋β中,如果β＝α，有怎样的结果？提示:T（α＋β）＝tan(α＋β)＝错误!，当β＝α时，tan 2α＝错误!.知识梳理三角函数公式简记正弦sin 2α＝2sin__αcos__αS2α余弦cos 2α＝cos2α－sin2αC2α正切tan 2α＝错误!T2α思考在cos 2α＝提示：cos 2α＝2cos2α－1＝1－2sin2α。

［自我检测］1．已知cos x＝错误!,则cos 2x等于()A．－错误! B.错误!C．－错误! D.错误!答案:D2．sin 15°sin 75°的值是()A。

错误!B。

错误! C.错误! D.错误!答案：C授课提示：对应学生用书第79页探究一二倍角公式的正用［教材P133例5、例6]方法步骤：（1)求“单角"的函数值．(2)用“单角”表示“倍角”,代入公式．[例1］化简1＋cos 2α＋错误!（α为第二象限角）．[解析］原式＝1＋2cos2α－1＋错误!＝错误!｜cos α｜＋错误!｜sin α|＝错误!（sin α－cos α)＝2sin错误!.方法技巧直接将S2α、C2α、T2α变为单角“α”的表达形式．跟踪探究已知sin α＝错误!，α∈错误!,求sin 2α，cos 2α，tan 2α的值．解析：∵sin α＝错误!，α∈错误!，∴cos α＝－1－sin2α＝－错误!＝－错误!，∴sin 2α＝2sin αcos α＝2×错误!×错误!＝－错误!，cos 2α＝1－2sin2α＝1－2×错误!错误!＝错误!，tan 2α＝sin 2αcos 2α＝－错误!.探究二二倍角公式的逆用、变形用［教材P135练习5(4）题]求2cos2 22.5°－1. 解析：原式＝cos 45°＝错误!。

3.1.3 二倍角的正弦、余弦、正切公式（1）【学习目标】1．掌握公式α2S 、α2C 、α2T 及其推导过程；2．会应用二倍角公式进行简单的求值、化简．【重点难点】重点：二倍角公式的推导、理解与运用．难点：余弦的二倍角公式．【学法指导】建议同学们重视公式型的特点，特别是二倍角的余弦公式有三种形式，需要在运用的过程加深记忆．另外，仍然需要通过例题与练习，多多体会公式是如何使用的？找出规律性．【学习过程】一．课前预习１．复习公式：=+)sin(βα ；=+)cos(βα ；=+)tan(βα .２．自学教材，P132-P135（1）二倍角公式的推导：当βα=时，由上面的和角公式分别得到公式：=α2sin ；=α2cos ；=α2tan .（2）公式的变形：由公式1cos sin 22=+αα及上面三个公式完成下面填空：①用αsin 表示α2cos 得：α2cos = ；②用αcos 表示α2cos 得 ：α2cos = ；以上（1）、（2）得到的五个公式都叫做什么公式？ .3．快乐体验，求下列各式的值：（1）sin15cos15_________=（2）22cossin ________88ππ-=（3）2tan 22.5__________1tan 22.5=-（4）22cos 22.51_________-=二．课堂学习与研讨例1． 已知),2(,135sin ππ∈α=α，求sin2α，cos2α，tan2α的值.练习1．（1）已知4cos,81285απαπ=-<<，求sin ,cos 44αα的值．（2）已知3sin()5απ-=，求cos2α的值．例２．（1）已知1tan 2,3α=α是第三象限角，求tan α的值．（2）α为第四象限的角，且cossin 222αα-=，求αα2cos 2sin +的值.练习２．（1）已知sin 2sin ,(,)2παααπ=-∈，求tan α的值．（2）已知1tan 23α=，求tan α的值．课堂小结：１．公式α2S 、α2C 、α2T 分别是公式)(βα+S 、)(βα+C 、)(βα+T 的特殊情况； ２．公式的相同特点：从左至右升幂；从右至左降幂；３．应用倍角公式要注意“倍”的关系，即2α是α的两倍，4α是2α的两倍，α是2α的两倍，等等．三．课堂检测1．化简)4(sin )4(cos 22απαπ---得到（ ）A.α2sinB.α2sin -C.α2cosD. α2cos -2．=+-)12sin 12)(cos 12sin 12(cos ππππ（ ） A.21 B.21- C.23 D.23- 3．已知31cos sin =+αα，则=α2sin ( ) A.98- B.98 C.98± D.322四．作业1．教材13815,P A2．函数sin()cos()44y x x ππ=--是（ ） Ａ．周期为2π的奇函数 B ．周期为2π的偶函数C ．周期为π的奇函数D ．周期为π的偶函数3．在△ABC 中，2tan ,54cos ==B A ,求)22tan(B A +的值.。

（全国通用版）2018-2019高中数学第三章三角恒等变换3.1 两角和差的正弦、余弦和正切公式3.1.3 二倍角的正弦、余弦、正切公式检测新人教A 版必修4编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（全国通用版）2018-2019高中数学第三章三角恒等变换3.1 两角和差的正弦、余弦和正切公式3.1.3 二倍角的正弦、余弦、正切公式检测新人教A版必修4）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（全国通用版）2018-2019高中数学第三章三角恒等变换3.1 两角和差的正弦、余弦和正切公式3.1.3 二倍角的正弦、余弦、正切公式检测新人教A版必修4的全部内容。

第三章 3.1 3。

1.3 二倍角的正弦、余弦、正切公式A级基础巩固一、选择题1．对于函数f(x)＝2sin x cos x，下列选项中正确的是（ B ）A．f(x)在（错误!,错误!）上是递增的B．f（x)的图象关于原点对称C．f（x)的最小正周期为2πD．f(x）的最大值为2[解析]因为f（x）＝2sin x cos x＝sin2x，所以f（x)是奇函数,因而f（x)的图象关于原点对称,故选B．2.错误!－sin215°的值是( D )A．错误!B．错误!C．错误!D．错误!［解析］原式＝错误!－错误!＝错误!＝错误!．3。

2－2cos8＋2错误!的化简结果是（ A ）A．2cos4－4sin4 B．2sin4C．2sin4－4cos4 D．－2sin4[解析］原式＝21－cos8＋21－2sin4cos4＝2·错误!＋2错误!＝2｜sin4｜＋2｜sin4－cos4|＝2cos4－4sin4．4．已知sinα＝错误!，则sin4α－cos4α的值为（ A ）A．－错误!B．－错误!C．错误!D．错误!［解析]sin4α－cos4α＝－（sin2α＋cos2α）（cos2α－sin2α）＝－cos2α＝2sin2α－1＝－错误!．5．若α∈错误!,则错误!＋错误!的值为（ D ）A．2cos错误!B．－2cos错误!C．2sin错误!D．－2sin错误!［解析]∵α∈错误!，∴错误!∈错误!，∴原式＝错误!＋错误!＝－sin错误!－cos错误!－sin错误!＋cos错误!＝－2sin错误!．6．已知sin2α＝错误!，则cos2（α＋错误!)＝( A ）A．错误!B．错误!C．错误!D．错误!［解析］本题考查半角公式及诱导公式．由倍角公式可得,cos2（α＋π4)＝错误!＝错误!＝错误!＝错误!，故选A．二、填空题7．(2016·全国卷Ⅲ）若tanθ＝错误!,则cos2θ＝错误!．[解析］cos2θ＝cos2θ－sin2θ＝错误!＝1－tan2θ1＋tan2θ＝1－191＋19＝错误!．8。