第四章 四边形性质探索 复习与小结-
- 格式:ppt
- 大小:724.00 KB
- 文档页数:23

初中数学知识归纳四边形的性质与运算四边形是初中数学中一个重要的图形概念,它具有不同的性质和运算。
本文将对四边形的性质和运算进行归纳总结。
一、四边形的性质四边形是由四条线段相连而成的封闭图形,它具有以下几个基本性质:1. 内角和:四边形的内角和等于360°。
对于任意四边形ABCD,其内角A、B、C、D的和为360°。
2. 对角线性质:四边形的对角线具有一些特殊性质。
例如,平行四边形的对角线相互平分,并且互相垂直。
而矩形的对角线相等。
3. 垂直性质:某些四边形具有垂直性质。
例如,菱形的两条对角线互相垂直。
4. 相等性质:四边形的边和角也具有相等性质。
例如,等边四边形的四条边相等;等角四边形的四个内角相等。
二、四边形的运算四边形的运算主要包括周长和面积的计算。
具体而言,我们可以利用以下公式进行计算:1. 周长的计算:对于任意四边形ABCD,它的周长P等于各边长之和,即P = AB + BC + CD + DA。
2. 面积的计算:四边形的面积S可以根据其不同性质和已知条件利用不同的公式进行计算。
- 矩形的面积可以通过长度和宽度相乘得到,即S = 长 ×宽。
- 平行四边形的面积可以通过底边和高的乘积得到,即S = 底边 ×高。
- 菱形的面积可以通过对角线的乘积再除以2得到,即S = (对角线1 ×对角线2) / 2。
- 任意四边形可以利用海伦公式进行面积的计算,即S = √[p(p - AB)(p - BC)(p - CD)(p - DA)],其中p为四边形的半周长。
三、例题实践现在我们来通过几个例题来实践一下四边形的性质和运算。
例题1:已知一个矩形的长为4 cm,宽为3 cm,求其周长和面积。
解:根据矩形的性质,我们知道该矩形的周长为P = 2 × (4 + 3) = 14 cm,面积为S = 4 × 3 = 12 cm²。


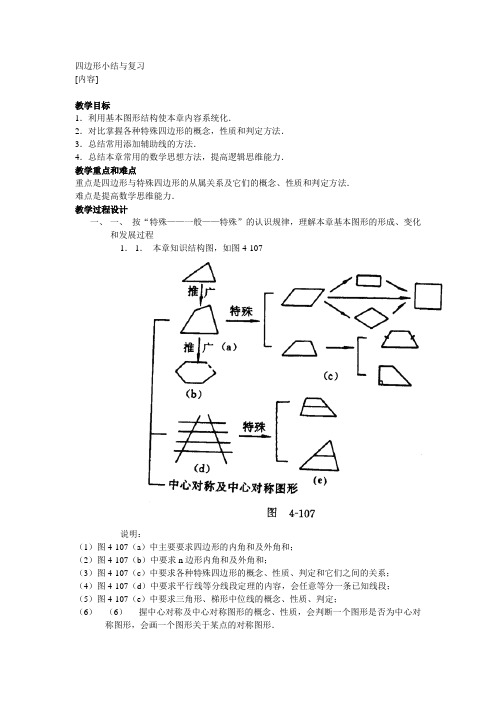
四边形小结与复习[内容]教学目标1.利用基本图形结构使本章内容系统化.2.对比掌握各种特殊四边形的概念,性质和判定方法.3.总结常用添加辅助线的方法.4.总结本章常用的数学思想方法,提高逻辑思维能力.教学重点和难点重点是四边形与特殊四边形的从属关系及它们的概念、性质和判定方法.难点是提高数学思维能力.教学过程设计一、一、按“特殊——一般——特殊”的认识规律,理解本章基本图形的形成、变化和发展过程1.1.本章知识结构图,如图4-107说明:(1)图4-107(a)中主要要求四边形的内角和及外角和;(2)图4-107(b)中要求n边形内角和及外角和;(3)图4-107(c)中要求各种特殊四边形的概念、性质、判定和它们之间的关系;(4)图4-107(d)中要求平行线等分线段定理的内容,会任意等分一条已知线段;(5)图4-107(e)中要求三角形、梯形中位线的概念、性质、判定;(6)(6)握中心对称及中心对称图形的概念、性质,会判断一个图形是否为中心对称图形,会画一个图形关于某点的对称图形.2.常用的例习题所对应的基本图形的性质,有利于探求解题.如:(1)顺次连结四边形各边中点得到的图形,如图4-95.(2)过平行四边形对角线交点的直线交对边或对边的延长线所得对应线段相等(图4-108).典型例题分析,总结解题方法和数学思想方法1.殊四边形的关系的进一步理解,渗透“集合”的思想.例1.填出图4-109中各图形的名称,利用“集合”的思想分清各种四边形之间的关系,并做课本第190页第2题,以巩固各种四边形的判定方法.2.2.四边形性质及中位线知识的应用,总结证明两条线段相等和添加辅助线的方法及分析综合法的使用.例2.例2.如图4-110(a),在梯形ABCD中,AB∥DC,以AD和AC为边作ACED,DC的延长线交EB于F.求证:EF=FB.分析:(1)(1)分解基本图形:“ABCD及对角线”,三个梯形.(2)(2)应用分析综合法探求解题思路,添加辅助线,将EF,FB置于“证明两线段相等”所对应的基本图形中.(3)(3)总结目前证明两条线段相等的方法,添设相应辅助线.在上一章总结方法的基础上,新添的常用方法有:①①特殊四边形的边、对角线的性质;②②平行线间的距离相等;③③过三角形一边中点与第二边平行的直线必平分第三边;④④过梯形一腰中点与底边平行的直线必平分另一腰.说明:本题添加辅助线的方法为四大类.(1)构造三角形中位线或梯形的中位线,如图4-110(b)~(e);(2)构造全等三角形,如图4-110(f)~(h);(3)构造等腰三角形,如图4-110(i);(4)构造以EB为对角线的平行四边形,如图4-110(j).3.总结梯形中常用辅助线,掌握化归思想.梯形中添加辅助线常常可以将梯形化归为三角形、平行四边形、矩形、直角梯形等.同时,还可集中梯形中分散的已知条件,如图4-111(a)中,将梯形的两腰、两底角、两底边之差集中到还可集中梯形中分散的已知条件,如图4-111(a)中,将梯形的两腰、两底角、两底边之差集中到了一个三角形中.另外注意以下两点:(1)从图形变换及化归角度理解梯形中常用辅助线的作法及作用.①平移:图4-111(a),(b)过上底一顶点作腰或一对角线的平行线;②旋转:图4-111(c),(d)以一腰中点为旋转中心旋转△ADE 和△EGC ;③对称:图4-111(e)等腰梯形中作底边高.(2)其他几种作法.①图4-111(e)一般梯形中,过上底两端点作下底的垂线;②在图4-111(f)中,向上延长两腰构成三角形;③在图4-111(g)中,作梯形的中位线.例3已知:如图4-112(a),在梯形ABCD 中,ABDC ,ACDB ,AD=BC=4,ㄥADC=60°,EF 是中位线,交BD 于M ,交AC 于N.(1)求EF ,MN 的长及S 梯形ABCD ;(2)观察MN 与梯形上、下底的关系,并思考结论能否推广到一般梯形?分析?本题可选用图4-112(b),(c)中辅助线的作法,解得EF=32,MN=2,S 梯形ABCD =12,MN=21(DC-AB).此结论对一般梯形同样适用.4.利用变换的思想解题,培养方程、分类讨论的思想,并会用类比联想变更命题. 例4矩形一边长为8,另一边长6,将矩形折叠,使两相对顶点重合.求折痕长.分析:(1)用轴对称的性质理解折叠问题的基本关系.认清对应元素的位置、数量关系,此题中折痕应为矩形ABCD 的对角线AC 的中垂线EF(如图4-113).(2)利用方程的思想解决问题.设CE=x,可证折痕EF 长等于2OE ,先由AE=EC ,及勾股定理求出CE=425,则EF=2OE=215222=-OC CE (3)学完相似形会有更简捷的计算方法.例5已知:点M 为正方形ABCD 的边AB 所在直线上任意一点(点B 除外),MNDM 与ㄥABC 的邻补角的平行线交于N.求证:DM=MN.分析:(1)由于题目中没有明确给出点M 的位置,需对M 点在直线AB 上的位置进行分类讨论. ①点M 在线段AB 内,如图4-114(a);②点M 在线段AB 的延长线上,如图4-114(b);③点M 在线段BA 的延长线上,如图4-114(c);④点M 与A 点重合,如图4-114(d).(2)证明时,结合旋转及对称变换的思想添加辅助线,构造DM ,MN 所在的两个全等三角形.如图4-114(a)中,将△MBN 沿MD 方向平移到M 与D 重合,再将平移后的三角形绕D 点顺时针旋转90°,B点落在边DA上P点处,使DP=MB,因此,如下添加辅助线:在AD上取一点P,使DP=BM,连接PM,证明△DPM MBN.(3)类比联想,此题的结论对等边三角形是否成立?M为等边三角形ABC的边BC所在直线上任意一点(C点除外),作ㄥAMN=60°,射线MN与ㄥACB的邻补角的平分线交于N.求证:AM=MN.(如图4-115)5.利用运动的思维方法将问题推广.例6(1)已知:如图4-116(a),从ABCD的顶点A,B,C,D向形外的任意直线l作垂线AA′,BB′,CC′DD′,垂足分别为A′,B′C′,D′,求证:AA′+CC′=BB′+DD′. (2)将直线l平移运动,会出现几种不同位置?猜想:AA′,BB′CC′,DD′的数量关系会怎样变化?并进行证明.分析:(1)分解基本图形为平行四边形和直角梯形.从结论考虑,从形式上联想到梯形中位线定理,连结AC,BD交于O,并作OO′l′与 O′.(2)总结证明线段和差、倍、分关系的常用方法.(3)直线l向上平移运动,与ABCD的位置关系还会出现两种情况,如图4-116(b),(c).(4)对于推广后的两种情况,可通过添加辅助线化归为利用图4-116(a)中结果,也可类比原题(a)中的方法,再次证明:图4-116(b)中,CC ′-AA ′=BB ′+DD ′;图4-116(c)中,|CC ′-AA ′|=|BB ′-DD ′|.三、师生共同小结1.基本方法.(1)利用基本图形结构使知识系统化;(2)证明两条线段相等及和差关系的方法,也可类比总结证明两角相等,角的和差、倍、分问题,直线垂直、平行关系的方法;(3)利用变换思想添加辅助线的方法;(4)探求解题思路时的分析、综合法.2.基本思想及观点:(1)“特殊——一般——特殊”认识事物的方法;(2)集合、方程、分类讨论及化归的思想;(3)用类比、运动的思维方法推广命题.四、作业从课本第190页复习题四中选取.补充题:1.已知:如图4-117,Rt △ABC 中,ㄥACB 的平分线交对边于E ,交斜边上的高AD 于G ,过G 作FGCB 交AB 于F.求证:AE=BF.2.如图4-118,梯形ABCD 中,ADBC ,AB=CD ,E ,F 和G 分别为OB ,CD ,OA 中点,ㄥAOD=60°.求证:△EFG 是等边三角形.3.已知:如图4-119,梯形ABCD 中,DCAB ,ㄥA+AB=90°,M ,N 分别为CD ,AB 点.求证:MN=12(AB-CD).4.已知:梯形ABCD ,ADBC ,AB=DC ,AD:BC=5:ㄥA ,ㄥD 的平分线都与BC 相交,且两交点把BC 三等分.若梯形周长为57cm.求梯形中位线长.(答:233cm 或10209cm)5.(1)如图4-120,P为正方形,ABCD内一点,PA:PB:PC=1:2:3,求ㄥAPB的度数;(答:135°)(2)2 .求已知:如图4-121正方形ABCD内点E到A,B,C三点的距离之和的最小值为6此正方形的边长;(答:2)(提示:(1)将△APB绕B点顺时针旋转90°,得△CQB,将分散的三条线段PA,PB,PC集中到一起,连结PQ,在△PBQ和△PQC中计算角度.(2)如图4-121,用旋转的方法,把△ABE 绕B点旋转60°,得到△FBG,可证△BEG为等边三角形.并将EA+EB+EC转化为FG+GE+EC,从而找到最小值为FC的长,利用列方程的方法求得边长为2.)6.如图4-122,ABCD是矩形纸片,E为AB上一点,BE:EA=5:3,EC=155,把△BCE沿折痕EC 向上翻折,若点B恰好落在AD边上,设这个点为F.问AB,BC的长各是多少?(答:2430)。

第四章四边形性质探索单元分析关于四边形性质探索单元分析我主要从六个方面进行。
一、明确课标要求1、探索并了解多边形的内角和与外角和公式,了解正多边形的概念。
2、掌握平行四边形、矩形、菱形、正方形、梯形的概念和性质,了解它们之间的关系;了解四边形的不稳定性。
3、探索并掌握平行四边形的有关性质和四边形是平行四边形的条件。
4、探索并掌握矩形、菱形、正方形的有关性质和四边形是矩形、菱形、正方形的条件。
5、探索并了解等腰梯形的有关性质和四边形是等腰梯形的条件。
6、探索并了解线段、矩形、平行四边形、三角形的重心及物理意义(如一根均匀木棒、一块均匀的矩形木板的重心)。
7、通过探索平面图形的镶嵌,知道任意一个三角形、四边形或正六边形可以镶嵌平面,并能运用这几种图形进行简单的镶嵌设计。
二、教材分析1、教材的地位及作用四边形体现着和三角形的紧密联系,突出地显示着图形向三角形转化的意义和作用。
同时,四边形本身还具有美妙而重要的性质,和图形变换中的“平移”“轴对称”“旋转变换”都有广泛的联系,是解决众多数学问题和现实问题的基础,承载着培养和发展学生演绎推理能力的重要作用。
2、教材整体思路首先通过图形的并提引入平行四边形,逐步探索平行四边形的对边、对角、对角线的有关性质以及平行四国形的判别方法。
然后,在直观的、现实的情景和一些探索性活动中分别研究菱形、矩形、正方形、梯形等特殊平行四边形的基本性质和基本制定方法。
最后,通过一个十分有趣的“多边形广场”的连续情景,比较自然地呈现多边形内角和,外角和的探索过程,在平面图形的密铺中进一步强化学生对多边形内的和及其有关几行事实的认识,认识中心对称图形及其基本性质。
与四边形以往的安排方式有所不同,本章特别强调图形性质的探索过程,而不是简单地得到四边形,特殊四边形的有关性质。
3、教学重点与难点教学重点:⑴平行四边形、菱形、矩形、正方形、梯形的概念。
⑵平行四边形、菱形、矩形、正方形、等腰梯形的性质、判别方法及初步应用。

四边形的性质知识点总结四边形是数学中重要的几何图形,具有丰富的性质和特点。
在本文中,将对四边形的性质进行总结和说明,以帮助读者更好地理解和掌握这一概念。
1. 四边形的定义四边形是由四条线段连接而成的闭合图形。
它的特点是具有四条边和四个顶点。
常见的四边形有矩形、正方形、平行四边形、菱形等。
2. 四边形的特征性质2.1 对角线四边形的对角线是连接四边形的两个非相邻顶点的线段。
对角线可以分为两条:一条是连接相邻顶点的线段,另一条是连接非相邻顶点的线段。
对角线有以下性质:- 平行四边形的对角线相等,即两条对角线长度相等。
- 矩形、菱形和正方形的对角线相等。
- 对角线相交于一点的四边形被称为交错四边形,交错四边形的对角线互相平分。
2.2 边与角四边形的边和角也具有一些特征性质:- 矩形和正方形的对边相等,即相对的两边长度相等。
- 平行四边形的对边平行且相等。
- 矩形和平行四边形的内角是180度,即对边的内角和为180度。
- 菱形的内角是120度,即对边的内角和为120度。
2.3 各类四边形的特性不同类型的四边形还有各自独特的特性:- 正方形是一种特殊的矩形,它的四边相等且内角均为90度。
- 矩形的对边相等,内角为90度。
- 平行四边形的对边平行且相等。
- 菱形的对边相等,内角为60度。
- 梯形是具有一对相对平行边的四边形。
梯形中,对边不平行的两个角互补且和为180度。
- 边长相等的四边形被称为等边四边形,如正方形和菱形。
- 具有四个相等内角的四边形被称为等角四边形。
3. 四边形的周长和面积计算在计算四边形的周长和面积时,可以根据不同类型的四边形采用相应的公式。
- 矩形的周长为2倍长加2倍宽,面积为长乘以宽。
- 正方形的周长为4倍边长,面积为边长的平方。
- 平行四边形的周长为2倍长加2倍宽,面积为底边乘以高。
- 菱形的周长为4倍边长,面积为对角线之积的一半。
总结以上,通过对四边形的定义、特征性质以及周长和面积计算公式的总结,我们可以更好地理解四边形的性质和特点。
课题: 四边形小结与复习学习目标:对比掌握各种特殊四边形的概念,性质和判定方法,并能运用这些知识进行有关的证明和计算。
学习重点:平行四边形及特殊的平行四边形、等腰梯形的性质与判定。
学习难点:灵活运用特殊四边形的性质和判定解题。
教学流程:一:课前检测二:自主学习矩形四 边形三:探究展示1、如图,在□ABCD 中,AE⊥BC 于E ,AF⊥CD 于F ,若∠EAF=60°,CF=2cm ,CE=3cm ,求□ABCD 的周长和面积。
F E DCB A2、Rt △ABC 中,∠C=90°,CD 是AB 边上的中线,过A 作CD 的平行线,过C 作AB 的平行线,两线交于点E.求证:四边形ADCE 是菱形。
四:达标检测1、下列命题正确的是( )A.对角线相等且互相平分的四边形是菱形。
B.对角线相等且互相垂直的四边形是菱形。
C.对角线相等且互相平分的四边形是矩形。
D.对角线相等的四边形是等腰梯形。
2、如图,延长正方形ABCD 的一边AB 到点E ,使BE=AC ,则∠E=________.3、顺次连接下列四边形各边的中点所得的四边形是矩形的是( )A.等腰梯形B.矩形C.平行四边形D.菱形4、□ABCD 中,AE 、CF 、BF 、DE 分别为四个内角平分线,求证:EGFH 是矩形。
5、如图,在梯形ABCD 中,AD ∥BC,AB =AD =DC,∠B =60º.(1)求证:AB ⊥AC ;(2)若DC =6,求梯形ABCD的面积 。
D CB A E A BCD H G F ED C B A。
《四边形的性质探索》4.1—4.4知识点精析四边形例1 如图1,矩形ABCD 中,AC 与BD 交于O 点,BE ⊥AC 于E ,CF ⊥BD 于F . 求证:BE = CF . 证明:∵四边形ABCD 是矩形, ∴OB = OC .又∵BE ⊥AC ,CF ⊥BD ,∴∠BEO =∠CFO = 90º. ∵∠BOE =∠COF .∴△BOE ≌△COF . ∴BE = CF .评注:本题主要考查矩形的对角线的性质以及全等三角形的判定. 例2 如图2,点E 、F 分别是菱形ABCD 的边CD 与CB 延长线上的点,且DE = BF ,求证:∠E =∠F .证明:如图2,∵四边形ABCD 是菱形,∴CB = CD ,∠DCA =∠BCA .∵DE = BF ,∴CE = CF .又∵CA = CA ,∴△CEA ≌△CF A .∴∠E =∠F .评注:本题主要考查菱形的性质以及全等三角形的判定. 例3 如图3,已知正方形ABCD ,把一个直角与正方形重合,使直角顶点与A 重合,两边分别与AB 、AD 重合. 将直角绕点A 按顺时针方向旋转,当直角的一边与BC 相交于E 点,另一边与CD 的延长线相交于F 点时,作∠EAF 的平分线相交于G ,连结EG . 求证:(1)BE =DF ;(2)BE +DG = EG .(1)证明:∵四边形ABCD 是正方形,∴AB =AD ,∠BAD =∠B =∠ADF =∠EAF =90°.∴∠BAD -∠EAD =∠EAF -∠EAD ,即∠BAE =∠DAF . ∴△ABE ≌△ADF . ∴BE =DF . (2)∵△ABE ≌△ADF ,∴AE = AF . ∵AG 是∠EAF 的平分线,∴∠EAG =∠F AG . ∵AG = AG ,∴△AEG ≌△AFG . ∴EG = GF . ∵GF = DF +DG ,BE =DF , ∴BE +DG = EG .评注:本题主要考查正方形的性质、同角的余角相等、角平分线的性质以及全等三角形的性质与判定.例4 已知:如图4,在△ABC 中,D 是AB边上的一点,且BD = BC ,BE ⊥CDA BCDM FE 图4A 图2 图3B D图1于E,交AC于点F,请再添加一个条件,使四边形DMCF是菱形,并加以证明.解析:根据菱形的判别方法和已有的已知条件,再添加的条件可为DM∥AC或ME = EF或DM = DF或DM = CF等.证明:如图4,在△ABC中,BD = BC,BE⊥CD,则DE = CE.∵DM∥AC,∴∠MDE =∠FCE.又∵∠DEM =∠CEF,∴△DEM≌△CEF.∴DM = CF.∴四边形DMCF是平行四边形.又∵MF⊥CD,∴平行四边形DMCF是菱形.评注:本题是一道条件开放性问题.判断一个四边形是菱形的基本依据是:菱形的判别方法.首先观察已有的已知条件,再边、角、对角线三方面考虑,探索所添加的条件.。
四边形的分类与性质的总结与分析四边形是几何学中常见的图形,它具有四个边和四个角,形状各异,性质也各不相同。
在这篇文章中,我们将总结和分析四边形的分类与性质,以便更好地理解和应用这一概念。
一、基本分类四边形可以根据其边长和角度的性质进行基本分类。
首先,我们来看边长。
如果四边形的四条边长度均相等,则它是一个等边四边形;如果仅有两条边相等,则它是一个等腰四边形;如果四条边长度都不相等,则它是一个一般四边形。
其次,我们来看角度。
如果四边形的四个角均为直角,则它是一个矩形;如果有两个相邻角为直角,则它是一个平行四边形;如果四个角均不为直角,则它是一个一般四边形。
二、特殊性质除了基本分类外,四边形还具有一些特殊的性质。
1. 矩形矩形是一种特殊的四边形,它的四个角均为直角。
由于直角的性质,矩形的对边相等且平行,对角线相等。
此外,矩形还具有面积和周长的特殊计算公式,分别为面积=长×宽,周长=2×(长+宽)。
2. 平行四边形平行四边形是指具有两个相邻边平行的四边形。
由于平行边的性质,平行四边形的对边相等且平行,对角线互相平分。
平行四边形的面积可以通过底边长度和高的乘积来计算,即面积=底边长度×高。
3. 等腰梯形等腰梯形是一种具有两对边平行且等长的四边形。
由于等腰梯形的特殊性质,它的对角线互相平分,且中线的长度等于两底边长度之和的一半。
等腰梯形的面积可以通过上底和下底的和乘以高再除以2来计算,即面积=(上底+下底)×高/2。
三、应用与拓展四边形的分类和性质不仅仅是几何学的基础知识,它们在实际生活和工作中也有广泛的应用。
1. 建筑设计在建筑设计中,平行四边形的性质常常被用来设计房间的布局和家具的摆放。
通过合理利用平行四边形的对边平行性质,可以使得空间更加充分利用,达到美观和实用的效果。
2. 地理测量在地理测量中,四边形的面积计算是一个重要的环节。
通过测量四边形的边长和角度,可以计算出其面积,从而帮助确定土地的面积和形状。