基坑开挖数值模拟
- 格式:docx
- 大小:724.21 KB
- 文档页数:34






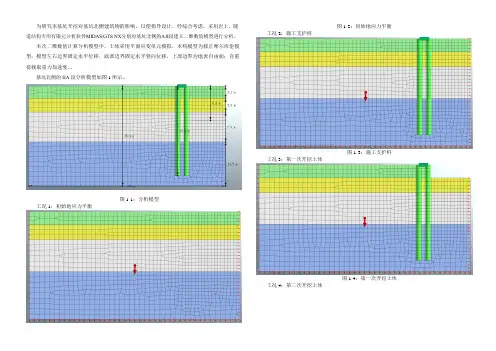
为研究本基坑开挖对基坑北侧建筑物的影响,以便指导设计,经综合考虑,采用岩土、隧道结构专用有限元分析软件MIDAS/GTS NX分别对基坑北侧的AJI段建立二维数值模型进行分析。
本次二维数值计算分析模型中,土体采用平面应变单元模拟,本构模型为修正摩尔库伦模型;模型左右边界固定水平位移,底部边界固定水平竖向位移,上部边界为地表自由面;自重荷载取重力加速度。
基坑北侧的IJA段分析模型如图1所示。
图1-1:分析模型工况1:初始地应力平衡图1-2:初始地应力平衡工况2:施工支护桩图1-3:施工支护桩工况3:第一次开挖土体图1-4:第一次开挖土体工况4:第二次开挖土体图1-5:第二次开挖土体工况5:开挖至坑底图1-6:开挖至坑底模型的横向位移云图详见下列图:图1-7 工况1横向位移云图(初始地应力形成)图1-8 工况2横向位移云图(施工支护桩)图1-9 工况3横向位移云图(第一次开挖土体)图1-10 工况4横向位移云图(第二次开挖土体)图1-11 工况5横向位移云图(开挖至坑底)模型的竖向位移云图详见下列图:图1-12 工况1竖向位移云图(初始地应力形成)图1-13 工况2竖向位移云图(施工支护桩)图1-14 工况3竖向位移云图(第一次开挖土体)图1-15 工况4竖向位移云图(第二次开挖土体)图1-16 工况5竖向位移云图(开挖至坑底)由计算结果可知:当完成基坑开挖至坑底时,基坑附近地面最大水平变形为18.5mm(向基坑方向),最大竖向变形为17.85mm。
基坑北侧地表的水平及竖向位移与基坑侧壁距离的关系如图1-17所示,距基坑北侧6.78m处存在建筑物,由图1-17可知,其竖向位移约为12.54mm 变形均处于基坑开挖允许范围之内,满足要求。
沉降值 (m m )0510********距离 (m)-25-20-15-10-5图1-17开挖至坑底地表水平及竖向位移。

深基坑变形数值模拟结果与监测数据对比分析*戴清宝(浙江恒欣设计集团股份有限公司福建勘察分公司福建泉州362000)摘要笔者以泉州市某基坑支护工程为案例,基坑采用土钉墙的支护型式,设计运用迈达斯计算软件对基坑开挖后的变形情况进行数值模拟计算,结合开挖后的基坑位移监测数据,将基坑变形的数值模拟计算数据与监测数据进行了对比分析㊂关键词深基坑土钉墙迈达斯数值模拟监测中图分类号:T U753.1文献标识码:A 文章编号:1002-2872(2023)11-0173-03随着车库的需求量日渐增长,地下室几乎已成为商品住宅楼及办公楼的标配,地下室的开挖,将影响周边建(构)筑物的安全,基坑支护应运而生㊂土钉墙作为一种最常见的基坑支护型式,有着工艺成熟㊁工期短㊁造价省等优点,成为众多基坑工程的首选方案,在基坑支护工程中应用非常广泛㊂G B55003-2021建筑与市政地基基础通用规范于2022年1月1日起正式实施,该规范第7.1.3条[1]将基坑支护结构及基坑周边土体的变形计算列入强制性条文要求,土钉墙支护体系下的周边土体变形理论计算与工程实际变形量是否存在较大差异?这是一个值得我们考证的内容㊂1工程实例概况工程场地位于泉州市惠安县,场地原为旧民房,场地已整平至ʃ0.000(黄海高程32.60m)㊂场地西侧7 m范围外为民房(1-4F㊁浅基㊁石砌㊁砖混或简易民房㊁持力层为粉质黏土或残积砂质粘性土),北侧民房已拆除,仅存旧围墙㊂南东二侧均为现状水泥路㊂建筑物下设一层整体地下室,基础类型为浅基础,地下室面积约4400m2,支护周长约315m,基坑最大支护深度约6.95m,基坑侧壁安全等级为二级,重要性系数γ0=1.0[2]㊂1.1工程地质概况按地貌类型划分,本场地属冲洪积平原,地势较平缓,据本勘资料,场地内除表层人工填土(Q4m l),第四系土层为冲洪积(Q4a l-p l)及残积(Q4e l)成因,基底为花岗岩类岩石(γ53)㊂工程场地地貌属残积台地地貌单元,场地地层分布情况自上而下分别为:杂填土㊁粉质黏土㊁残积砂质粘性土㊁全风化花岗岩等,物理力学参数见表1,相关地层描述如下:1.1.1杂填土灰黄㊁灰褐等杂色,干,松散,为新近回填(年限<1年),未经专门压实处理,均匀性及密实度差,呈欠固结状态,并具湿陷性,本层以粘性土为主,混含建筑垃圾与少量砂㊁碎石,其中硬质物约占15%~25%;该层场地内均有分布,层厚为0.40~2.40m㊂1.1.2粉质黏土浅黄㊁灰黄色,湿,可塑,主要由粘㊁粉粒组成,土质较均匀,粘性较强,切面稍光滑,无摇振反应,干强度高,韧性中等,含铁锰质氧化物;该层场地内均有分布,层厚为0.90~3.80m,层顶埋深0.40~2.40m㊂1.1.3残积砂质粘性土灰黄色,湿,可塑,捻面稍有光泽,无摇震反应,干强度㊁韧性中等,为花岗岩风化残积形成,成分以粘性土为主,有少量的细粒石英颗粒,粒径>2.0mm的含量范围值为5.9%~14.3%,长石及暗色矿物已全部风化成黏土矿物,具有泡水易软化崩解的特性;该层场地内均有分布,层厚为3.90~9.50m,层顶埋深为1.60~ 4.50m㊂1.1.4全风化花岗岩黄褐色㊁饱和,中粗粒花岗结构,散体状构造,风化显著但不均,标贯击数实测值N>30击/30c m,岩芯呈砂土状,遇水易软化,原生矿物清晰,含多量次生矿物,为极软岩,岩体极破碎,岩石基本质量等级V级,质量指标极差,未发现洞穴㊁临空面㊁风化孤石及 软㊃371㊃(紫砂艺术)2023年11月陶瓷C e r a m i c s *作者简介:戴清宝(1984-),本科,工程师;研究方向为岩土工程㊂弱 夹层;该层场地内均有分布,层厚为0.40~4.30m ,层顶埋深为7.50~12.80m ㊂表1 岩土物理力学参数表地层名称饱和重度γ(k N /m 3)固结快剪С(k P a )固结快剪φ(度)极限粘结强度标准值(f r b K )杂填土18.510.012.015粉质黏土18.622.413.835残积砂质粘性土19.016.223.445全风化花岗岩20.525.025.0601.2 水文地质概况杂填土:透水性强,富水性较弱;粉质黏土㊁残积砂质粘性土㊁全风化花岗岩:含水性与透水性较弱(为弱透水性层)㊂地下水赋存特征为:根据本工程勘察资料,地下水类型为孔隙潜水,赋存于杂填土㊁粉质黏土㊁残积砂质粘性土㊁全风化花岗岩中,主要靠大气降水与地表迳流下渗补给故其富水性受季节性制约㊂工程场地勘察期间测得钻孔孔内初见水位埋深距现地表1.50~2.90m (黄海标高为28.74~30.97m ),稳定水位埋深距现地表2.10~3.60m (黄海标高为28.14~30.27m ),据当地民井调查与建设方提供当地气象部门水文资料,本场地地下水变化幅度1.00~2.00m ,工程场地3~5年最高水位黄海标高为31.00m ;历史最高水位黄海标高为32.30m ㊂图1 支护剖面图1.3 基坑支护方案基坑支护的方式较多,近年来福建沿海一带用的比较多的支护型式有土钉墙㊁拉森钢板桩+预应力锚索㊁S MW 工法桩+预应力锚索㊁S MW 工法桩+钢管内支撑㊁排桩+内支撑等㊂结合本工程周边情况㊁地质条件㊁开挖深度等条件,本基坑工程最终采用土钉墙的支护型式㊂此次对比分析选取本工程案例的其中一个支护剖面进行,选取的支护剖面图见图1㊂2 变形数值模拟分析2.1 模型构成采用M i d a sS o i l w o r k s 计算软件,利用有限元分析法,对经土钉墙加固后的基坑侧壁进行数值模拟变形分析㊂计算模型利用基坑结构的对称性,取典型剖面对基坑侧壁土体进行计算分析,计算范围:基坑坑顶外取基坑开挖深度的2.5倍,基坑坑底以下取基坑开挖深度的1.0倍㊂2.2 数值模拟结果图2 水平位移模拟结果图3 竖向位移模拟结果根据M i d a sS o i l w o r k s 软件计算结果,水平位移最大值约1.8mm ,水平位移模拟结果见图2,竖向位表2 监测点累积位移量统计表监测项目水平位移监测点竖向位移监测点深层水平位移监测点监测点P 6P 7P 8S 6S 7S 8X 3X 4累积位移量(mm )4.5513.516.345.899.547.1310.668.12㊃471㊃ 陶瓷 Ce r a m i c s (紫砂艺术)2023年11月移最大值约14.3mm ,竖向位移模拟结果见图3㊂3 基坑监测实测数据该基坑现地下室外围土方已回填完成,基坑安全隐患已排除,基坑暴露总时长约70天,监测单位共出具52份监测简报,该支护剖面段水平位移监测点编号为P 6㊁P 7㊁P 8,竖向位移监测点编号为S 6㊁S 7㊁S 8,深层水位位移监测点编号为X 3㊁X 4,各监测点最终累积位移量见表2㊂4 对比分析本基坑由建设单位委托具有相应资质的第三方对基坑变形情况进行现场布点㊁监测,监测单位根据施工图及‘建筑基坑工程监测技术规范“[3]的要求实施监测工作,本文假设监测数据为基坑变形情况的真实体现㊂根据监测数据,坡顶水平位移累积位移量最大的点为P 7,累积位移量为13.51mm ,坡顶竖向位累积位移量最大的点为S 7,累积位移量为9.54mm ,深层水平位移累积位移量最大的点为X 3,累积位移量为10.66mm ㊂数值模拟计算该剖面段水平位移最大值1.8mm ,竖向位移最大值14.3mm ,不难发现,数值模拟计算结果与基坑实际位移量存在较大差异,说明数值模拟结果参考价值并不高㊂5 结结基坑变形的数值模拟结果与监测测得的实际变形存在较大差异,即理论与实际存在较大差异,归结为以下几点:(1)数值模拟计算,是将岩土层以参数形式量化后进行的模拟分析,而计算所采用的岩土层物理力学参数,是勘察单位根据现场原位测试或室内试验后所取,其中难免存在差异㊂(2)数值模拟计算是选取剖面段范围最具代表性的地层进行模拟,然而实际上不同位置各地层的埋深㊁层厚等是存在一定差异的㊂(3)理论计算是严格按照设计设定的边界条件进行的,施工现场不大可能和设计设定的边界条件完全一致,包括坡顶荷载㊁支护结构的施工质量等㊂参考文献[1] 中国建筑科学研究院.J G J 120-2012建筑基坑支护技术规程[S ].北京:中华人民共和国住房和城乡建设部,2012.[2] 中华人民共和国住房和城乡建设部.G B55003-2021建筑与市政地基基础通用规范[S ].北京:中华人民共和国住房和城乡建设部,2021.[3] 中华人民共和国住房和城乡建设部.G B50497-2009建筑基坑工程监测技术规范[S ].北京:中华人民共和国住房和城乡建设部,2009.㊃571㊃(紫砂艺术)2023年11月 陶瓷 C e r a m i c s。

基坑开挖数值模拟7数值模拟7.1数值模拟⽅法简介数值模拟技术作为⼀种研究⼿段,已经被⼴泛的应⽤于各⾏各业领域的研究中。
⽬前,数值分析⽅法主要分为⼆⼤类:⼀类是以有限差分法为代表,其特点是直接求解基本⽅程和相应的定解条件的近似解;另⼀类数值分析⽅法是⾸先建⽴和原问题基本⽅程及相应定解条件等效的积分⽅法,然后据之建⽴近似解法。
LS-DYNA作为世界上最著名的通⽤显⽰动⼒分析程序,能够模拟真实世界的各种复杂问题,特别适合求解各种⼆维三维⾮线性结构的⾼速碰撞,爆炸和⾦属成型等⾮线性动⼒冲击问题,同时可以求解传热,流体及流固耦合问题,在⼯程应⽤如汽车安全设计,武器系统设计,⾦属成型,跌落仿真等领域被⼴泛应⽤。
本次采⽤ANSYS/LS-DYNA,进⾏混凝⼟⽀撑梁结构爆破拆除数值模拟研究。
在ANSYS/LS-DYNA环境下,数值模拟的实现总体上分为两个过程:在ANSYS中建⽴结构实体模型,完成有限元⽹格的划分,输出有限元模型信息即输出关键字⽂件;编辑关键字⽂件,在DYNA环境下完成对结构倒塌过程的数值模拟计算。
对结构有限元模型的建⽴过程,数值模拟中采⽤的钢筋和混凝⼟材料模型、接触⽅式等各种计算控制项进⾏了阐述。
LS-DYNA程序中主要提供如下⼏种计算⽅法:(1)Lagrange算法坐标固定在物质上或者说随物质⼀起运动和变形,处理⾃由⾯和物质界⾯⾮常直观,由于⽹格始终对应物质,因此能够精确的跟踪材料边界和描述物质之间的界⾯,这是Lagrange算法的主要优点。
但是,由于⽹格随材料流动⽽变形,⼀旦⽹格变形严重,就会引起数值计算的不稳定,甚⾄使得计算⽆法继续进⾏(如发⽣负体积或复杂声速等问题)。
因此,Lagrange算法在处理⼤变形⼤位移问题时,有其⽆法克服的弊端。
(2)Euler算法⽹格被固定在空间,是不变形的。
物质通过⽹格边界流进流出,物质的⼤变形不直接影响时间步长的计算。
因此,欧拉算法在处理⼤变形问题⽅⾯具有优势。

深基坑开挖数值模拟与实测研究深基坑开挖数值模拟与实测研究1.引言深基坑开挖是城市建设中常见的一项工作。
深基坑的开挖过程受到许多因素的影响,包括地下水位、土壤力学性质、地下管线等。
为了确保基坑开挖的安全和有效性,数值模拟与实测研究成为了解决问题和提供指导的重要手段。
2.数值模拟方法数值模拟方法在深基坑开挖中起着重要的作用。
它通过建立合理的物理模型和计算数学模型,模拟基坑开挖的力学行为和变形规律。
常用的数值模拟方法包括有限元法、有限差分法和边界元法。
2.1 有限元法有限元法是目前应用最广泛的数值模拟方法之一。
它将复杂的物理问题分割为许多小的有限单元,通过连续性原理和平衡原则求解每个单元内的位移、应力和应变等。
有限元法具有模拟问题复杂性较强的优点,可以描述基坑开挖过程中的非线性和变形情况。
2.2 有限差分法有限差分法采用差分近似的方法,将求解区域划分为网格点,通过相邻点的数值关系推导出方程组。
有限差分法是数值模拟方法中应用较多的一种,它具有计算简单、适应性强的特点。
在深基坑开挖中,有限差分法可以模拟地面沉降和基坑变形等问题。
2.3 边界元法边界元法将求解区域分为内部区域和边界区域,通过求解边界上的积分方程来计算内部区域的解。
边界元法适用于模拟基坑开挖中的地下渗流和土体变形等问题。
3.数值模拟与实测研究的应用数值模拟与实测研究在深基坑开挖中发挥了重要的作用。
一方面,数值模拟可以通过预测基坑开挖过程中的变形和应力分布,提供工程施工和监测的依据。
另一方面,实测数据可以用于验证数值模拟结果的准确性。
3.1 数值模拟与施工方案优化在深基坑的实际施工中,精确的数值模拟可以指导施工方案的制定和优化。
通过模拟分析,可以评估不同施工方法对基坑开挖的影响,提前预测可能出现的问题,为施工人员提供合理的建议和措施。
3.2 数值模拟与监测数据分析在基坑开挖过程中,及时监测数据的收集和分析是确保施工安全的重要环节。
数值模拟可以根据监测数据对基坑开挖过程进行反演,验证模拟结果的准确性,并分析实测数据与数值模拟结果之间的差异,为施工人员提供参考和改进方案。
7 数值模拟7.1 数值模拟方法简介数值模拟技术作为一种研究手段,已经被广泛的应用于各行各业领域的研究中。
目前,数值分析方法主要分为二大类:一类是以有限差分法为代表,其特点是直接求解基本方程和相应的定解条件的近似解;另一类数值分析方法是首先建立和原问题基本方程及相应定解条件等效的积分方法,然后据之建立近似解法。
LS-D YNA乍为世界上最著名的通用显示动力分析程序,能够模拟真实世界的各种复杂问题,特别适合求解各种二维三维非线性结构的高速碰撞,爆炸和金属成型等非线性动力冲击问题,同时可以求解传热,流体及流固耦合问题,在工程应用如汽车安全设计,武器系统设计,金属成型,跌落仿真等领域被广泛应用。
本次采用ANSYS/LS-DYN,A 进行混凝土支撑梁结构爆破拆除数值模拟研究。
在ANSYS/LS-DYN环境下,数值模拟的实现总体上分为两个过程:在ANS丫芽建立结构实体模型,完成有限元网格的划分,输出有限元模型信息即输出关键字文件;编辑关键字文件,在DYNA环境下完成对结构倒塌过程的数值模拟计算。
对结构有限元模型的建立过程,数值模拟中采用的钢筋和混凝土材料模型、接触方式等各种计算控制项进行了阐述。
LS-D YNA程序中主要提供如下几种计算方法:(1)Lagrange 算法坐标固定在物质上或者说随物质一起运动和变形,处理自由面和物质界面非常直观,由于网格始终对应物质,因此能够精确的跟踪材料边界和描述物质之间的界面,这是Lagrange 算法的主要优点。
但是,由于网格随材料流动而变形,一旦网格变形严重,就会引起数值计算的不稳定,甚至使得计算无法继续进行(如发生负体积或复杂声速等问题)。
因此,Lagrange 算法在处理大变形大位移问题时,有其无法克服的弊端。
(2)Euler 算法网格被固定在空间,是不变形的。
物质通过网格边界流进流出,物质的大变形不直接影响时间步长的计算。
因此,欧拉算法在处理大变形问题方面具有优势。
欧拉方法通过输运项计算体积、质量、动量和能量的流动。
欧拉计算可以直接通过在离散化格式中包括迁移导数项进行,或通过二步操作完成。
二步法操作的第一步主要是拉格朗日计算,第二步输运阶段是重分计算网格相当于回到它的原来状态。
LS-D YNA程序采用后一种方法。
欧拉算法的缺点是网格中物质边界不清晰,难以捕捉各物质界面。
(3)ALE方法吸取了欧拉法和拉格朗日法两种方法的优点。
ALE算法能够进行自动重分网格操作。
它包括拉格朗日时间步,然后是一个输运步。
输运步可以采用三种方法:1. 发生合理的网格变形时空间网格不再重分(拉格朗日);2. 发生严重的网格变形时重分成原始形状(欧拉);3. 发生严重的网格变形时重分为合理的形状,因此允许网格拓扑(拉格朗日和欧拉)。
混凝土是土木工程结构中应用极为广泛的材料,其最本质的特点是材料组成的不均匀性,并且存在初始微裂缝。
从混凝土受单轴压力时的应力应变关系来看,混凝土卸载时有残余变形,不符合弹性关系;如果对其应用弹塑性本构关系,又很难精确定义屈服条件。
此外,混凝土在到达应力顶峰后,其应力-应变关系曲线有一下降段,即存在应变软化现象,所有这些都给建立混凝土的本构关系带来困难。
多年以来,众多学者进行了大量的试验和理论研究,提出了各种各样的混凝土本构模型。
第一:混凝土本构模型可以分为下面几种:(1)线弹性类本构模型。
线弹性类本构模型是以弹性力学为基础的模型,当混凝土无裂缝时,将混凝土看成线弹性匀质材料而采用线弹性本构模型。
虽然混凝土的变形特性是非线性的,但在一些特定的情况下(比如描述混凝土受拉时的工作性能),采用线弹性类本构模型进行分析还是有足够的精度的,其线弹性本构关系可用广义虎克定律来表示:(1)ij - C ijkl ;kl式中,C ijk 1为材料弹性常数,为四阶张量,共有81个常数。
按照材料假设的不同,又可分为各向异性本构模型、正交各向异性本构模型、各向同性本构模型等,其中C jki根据材料的不同而变换。
(2)塑性理论类本构模型:塑性理论类本构模型是以塑性流动理论为基础,代表性的模型主要有:Mises条件的模型、理想弹塑性脆性断裂模型、应变或工作硬化塑性理论模型等。
模型中考虑了混凝土加载路径和混凝土的硬化,在混凝土的应力- 应变全曲线中,有上升段和下降段。
自从Drucke公设和n yushin公设出现之后,经典塑性力学得到飞速发展,混凝土塑性力学模型也是基于这些公设建立的。
以塑性理论为基础的混凝土本构模型,在对其加载面,包括初始屈服面,后续加载面和破坏包络面等特征面的研究中,这些特征面若以应力空间来表示时,当应力达到屈服后,材料发生应力松弛;若以应变空间表示时,当应变达到松弛面后,材料发生应变松弛。
基于应力状态屈服面或破坏包络面的塑性理论类型的本构模型有弹性- 全塑性模型、线弹性-硬化塑性-断裂模型等;基于松弛面的塑性理论类型的本构模型有塑性模型、塑性断裂模型、硬化断裂模型等。
所有这些模型所做的假设与混凝土的实际性能还存在很大的差别,而且模型的表达式和计算均较复杂,目前还不便于应用。
( 3)其他力学理论类本构模型,许多学者还以新型交叉的力学分支的理论为基础研究混凝土的本构模型。
内时理论模型:内时理论模型最初由Valanis 于1971 年提出,其基本概念为:塑性和粘塑性材料内任一点的现时应力状态是该点整个变形领域内和温度历史的泛函,而特别重要的是该历史是用一个取决于变形中的材料特性和变形程度的内时(Intrinsic Time) 来量度的。
这种模型采用了非弹性应变能逐渐积累的方法而不需考虑塑性理论中的屈服面和流动法则,所以该理论尤其适合没有屈服面的混凝土材料。
由于内时理论能描述混凝土的复杂变形的历史,因而为各国学者所重视。
但由于表达式过多,确定参数又不容易,所以对其推广和应用仍有大量工作要做。
损伤理论模型:针对混凝土材料本身是一种具有固有缺陷-微裂纹的特点,很多学者将损伤力学引用到混凝土本构模型的建立中。
损伤力学研究材料或构件从原生缺陷到形成客观微裂纹直至断裂的过程。
也就是通常指的微裂纹的萌生、扩展或演变、宏观微裂纹的形成、裂纹的稳定扩展和失稳扩展全过程。
损伤力学主要是在连续介质力学和热力学的基础上,用固体力学方法研究材料的宏观力学性能的演变直到破坏的全过程。
20世纪70年代末期,损伤力学局限于研究材料在宏观裂纹出现以前的阶段,当宏观裂纹出现以后,则采用断裂力学的理论和方法进行研究,这是无耦合的分析方法。
实际上,在宏观裂纹出现后,材料的损伤对裂纹尖端附近及其它区域的应力和应变均有影响。
因此,合理的方法应该将损伤耦合到本构方程中进行分析和计算。
这样由于本构方程中将有关的力学参数和损伤进行了耦合,所以分析和计算就变得更为复杂。
非线弹性类本构模型:为了克服线弹性模型的缺点,然后产生了以割线模型形式的非线性弹性类本构模型。
这类模型中,具有代表性的是超弹性模型和亚弹性模型。
除了上述模型外,还有以许多种理论相结合到处的混凝土的本构模型。
第二:LS-D YNA程序中提供的混凝土材料模型:在材料模型方面,LS-DYNA目前拥有近150余种金属和非金属材料模型,涵盖了弹性、弹塑性、超弹、泡沫、玻璃、土壤、混凝土、流体、炸药等材料模型以及多种状态方程,可以考虑材料的失效、损伤、粘性、蠕变、与温度相关、与应变率相关等材料性质。
此外,程序还支持用户自定义材料功能。
LS-D YNA程序中提供的混凝土材料模型主要有以下几种:塑性随动模型*MAT-PLASTIC-KINEMATICH_J_C模型、*MAT_DRUCKER_PRAGER 模型和*MAT_SOIL_AND_FO模型。
本论文有限元模型中的混凝土本构模型选用LS-D YNA中的塑性随动模型*MAT-PLASTIC-KINEMAT Q塑性随动模型(*MAT_PLASTIC_KINEMATIC这是一种各向同性、随动硬化或各向同性和随动硬化混合模型,与应变率相关,可考虑实效,参数简单,较容易确定。
7.2 钢筋混凝土支撑梁结构爆破拆除有限元模型的建立7.2.1 爆破拆除数值模拟基本假设考虑到建立整体钢筋混凝土支撑梁结构模型过程的复杂性,计算结果的可行性及准确性,数值模拟中对模型进行了简化,模型的简化出于以下基本假设:(1)不考虑混凝土支撑梁内的炸药爆炸对整体结构的作用。
如果模拟中按照实际情况建立模型,单元数目巨大,受到当前计算机能力的限制,无法实现数值计算。
由于爆炸对钢筋梁的变形影响较小,所以在模拟中可以直接删除爆破药包附近的混凝土,并没有考虑钢筋梁结构在炸药爆炸下的响应问题(2)钢筋混凝土梁在爆破后,剩余部分的表面是光滑的,由于上面假设是直接删除爆破部分,所以无法模拟混凝土爆破后的形状。
(3)钢筋混凝土的支柱地面没有相对位移,简化为完全固结,即不考虑钢筋梁的坍塌与支撑柱和地面之间的相互作用。
7.2.2钢筋混凝土有限元模型建立过程采用ANSYS建立有限元模型时,采用的数值单位均为国际单位,即长度单位为m时间单位为s,质量的为kg,压力的单位为Pa,速度单位为m/ s 。
为了由实际情况对比实验模拟的准确情况, 我们选用工程实例作为有限元模拟的对象。
综合考虑有限元计算的精确性和时效性, 来确定单元尺寸和单元数量。
7.2.3 钢筋混凝土模型的选取采用数值模拟方法进行钢筋混凝土结构爆破拆除分析前, 首先要就研究的具体问题选择好用于模拟钢筋混凝土材料的物理模型。
当前, 数值计算中, 用于模拟混凝土钢筋材料的有限元模型主要有两类:第一种是把钢筋和混凝土单元各自划分为足够小的单元, 分别考虑钢筋和混凝土的贡献, 称为分离式模型。
第二种也是把钢筋和混凝土单元包含在一个单元之中, 统一考虑钢筋和混凝土的作用, 称为整体式模(1)整体式模型在整体式模型中,将钢筋弥散于整个单元中,并把单元视为连续均匀的材料。
钢筋对整个结构的贡献,可以通过调整单元的材料力学性能参数来体现,例如提高材料的屈服强度、材料的弹性模量等。
其优点是建模方便,分析效率高,但是缺点是不适用于钢筋分布较不均匀的区域,且得到钢筋内力状态比较困难。
主要用于有大量钢筋且钢筋分布较均匀的构件中。
(2)分离式模型,位移协调利用空间梁单元beam161建立钢筋模型,和混凝土单元共用节点。
其优点是建模方便,可以任意布置钢筋并可直观获得钢筋的内力。
缺点是建模比整体式模型要复杂,需要考虑共用节点的位置,且容易出现应力集中问题。
(3)分离式模型,界面单元前两种混凝土和钢筋组合方法假设钢筋和混凝土之间位移完全协调,没有考虑钢筋和混凝土之间的位移,而通过加入界面单元的方法,可以进一步提高分析的精度。
同样利用空间梁单元beam161建立钢筋模型。
不同的是混凝土单元和钢筋单元之间利用弹簧模型来建立连接。