实验二--用matlab绘制一元函数与二元函数的图象

实验2 Matlab 绘图操作实验目的：1、 掌握绘制二维图形的常用函数；2、 掌握绘制三维图形的常用函数；3、 掌握绘制图形的辅助操作。

实验内容：1. 设sin .cos x y x x ⎡⎤=+⎢⎥+⎣⎦23051，在x=0~2π区间取101点，绘制函数的曲线。

2. 已知： y x =21，cos()y x =22，y y y =⨯312，完成下列操作：（1） 在同一坐标系下用不同的颜色和线性绘制三条曲线； （2） 以子图形式绘制三条曲线；（3） 分别用条形图、阶梯图、杆图和填充图绘制三条曲线。

3.已知：ln(x x e y x x ⎧+≤⎪⎪=⎨⎪+>⎪⎩20102，在x -≤≤55区间绘制函数曲线。

4. 绘制极坐标曲线sin()a b n ρθ=+，并分析参数a 、b 、n 对曲线形状的影响。

5．在xy 平面内选择区域[][],,-⨯-8888，绘制函数z =6. 用plot 函数绘制下面分段函数的曲线。

,(),,x x f x x x x ⎧++>⎪==⎨⎪+<⎩235000507. 某工厂2005年度各季度产值（单位：万元）分别为：450.6、395.9、410.2、450.9，试绘制柱形图和饼图，并说明图形的实际意义。

8. 在同一坐标轴中绘制下列两条曲线并标注两曲线交叉点。

（1）.y x =-205（2）sin()cos ,sin()sin x t tt y t tπ=⎧≤≤⎨=⎩303详细实验内容：1.设sin .cos x y x x ⎡⎤=+⎢⎥+⎣⎦23051，在x=0~2π区间取101点，绘制函数的曲线。

>> x=(0:2*pi/100:2*pi);>> y=(0.5+3*sin(x)/(1+x.^2))*cos(x); >> plot(x,y)2.已知： y x =21，cos()y x =22，y y y =⨯312，完成下列操作： （1）在同一坐标系下用不同的颜色和线性绘制三条曲线； >> x= linspace(0, 2*pi, 101);>> y1=x.*x; >> y2=cos(2x); >> y3=y1.*y2;plot(x,y1,'r:',x,y2,'b',x,y3, 'ko')（2）以子图形式绘制三条曲线；>> subplot(2,2,1),plot(x,y1)subplot(2,2,2),plot(x,y2)subplot(2,2,3),plot(x,y3)（3）分别用条形图、阶梯图、杆图和填充图绘制三条曲线。

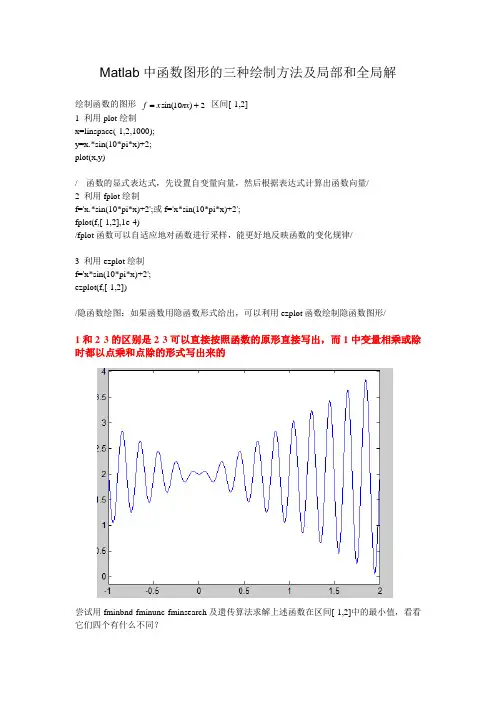
Matlab中函数图形的三种绘制方法及局部和全局解
绘制函数的图形2
x
fπ区间[-1,2]
=x
)
10
sin(+
1 利用plot绘制
x=linspace(-1,2,1000);
y=x.*sin(10*pi*x)+2;
plot(x,y)
/ 函数的显式表达式，先设置自变量向量，然后根据表达式计算出函数向量/
2 利用fplot绘制
f='x.*sin(10*pi*x)+2';或f='x*sin(10*pi*x)+2';
fplot(f,[-1,2],1e-4)
/fplot函数可以自适应地对函数进行采样，能更好地反映函数的变化规律/
3 利用ezplot绘制
f='x*sin(10*pi*x)+2';
ezplot(f,[-1,2])
/隐函数绘图：如果函数用隐函数形式给出，可以利用ezplot函数绘制隐函数图形/
1和2 3的区别是2 3可以直接按照函数的原形直接写出，而1中变量相乘或除时都以点乘和点除的形式写出来的
尝试用fminbnd fminunc fminsearch及遗传算法求解上述函数在区间[-1,2]中的最小值，看看它们四个有什么不同？。

一、介绍Matlab是一款用于科学计算和技术计算的软件，拥有强大的绘图功能，可以用于绘制各种图形、曲线和函数图像。

在Matlab中，使用plot函数可以绘制二元函数的图像，通过调整参数和设置属性，可以实现不同风格和效果的图像展示。

本文将详细介绍在Matlab中如何绘制二元函数的图像，包括基本的绘图方法和常用的设置技巧。

二、绘制二元函数图像的基本方法1. 准备数据在使用Matlab绘制二元函数的图像前，首先需要准备数据。

通常可以通过生成x、y坐标的网格点，然后计算每个点对应的函数值，从而得到二元函数在指定区域内的数据集。

2. 使用plot函数一旦准备好了数据集，就可以使用Matlab的plot函数进行绘图。

plot函数的基本语法为：plot(x, y)，其中x和y分别代表要绘制的点的横坐标和纵坐标。

通过调用plot函数，可以将计算得到的数据点连接起来，形成二元函数的图像。

3. 添加标签和标题为了让图像更加清晰和直观，通常需要添加x和y轴的标签，以及整个图像的标题。

在Matlab中，可以使用xlabel、ylabel和title函数来分别添加x轴、y轴和标题标签。

4. 设置图像属性通过设置图像的属性，可以调整图像的风格和效果。

常用的属性包括线型、线宽、颜色和标记符号等。

在Matlab中，可以使用参数-字符串对的形式来设置图像的属性，例如'LineStyle'、'LineWidth'、'Color'和'Marker'等。

三、绘制常见二元函数的图像在Matlab中，可以绘制各种类型的二元函数的图像，包括线性函数、二次函数、三角函数、指数函数、对数函数等。

下面将分别介绍如何绘制这些常见二元函数的图像。

1. 绘制线性函数图像线性函数的一般形式为y=ax+b，其中a和b分别为常数。

在Matlab 中，可以通过设置a和b的值，然后使用plot函数绘制线性函数的图像。

《MATLA‎B语言》课程论文用MATL‎A B绘制一‎元函数和二‎元函数的图‎象姓名：**学号： *****‎*****‎ 5专业：通信工程班级： 2010级‎通信1班指导老师：***学院：物理电气信‎息学院完成日期：2011.12.20用MATL ‎A B 绘制一‎元函数和二‎元函数的图‎像（马军 12010‎24524‎ 5 2010级‎通信工程1‎班）【摘要】大学物理力‎学中涉及许‎多复杂的数‎值计算问题‎，例如非线性‎问题，对其手工求‎解较为复杂‎，而MATL ‎AB 语言正‎是处理非线‎性问题的很‎好工具，既能进行数‎值求解，又能绘制有‎关曲线，非常方便实‎用。

另外，利用其可减‎少工作量，节约时间，加深理解，同样可以培‎养应用能力‎。

【关键词】一元函数 二元函数 MATLA ‎ B 图像的绘制‎一、问题的提出‎MATLA ‎B 语言是当‎今国际上科‎学界(尤其是自动‎控制领域)最具影响力‎、也是最有活‎力的软件。

它提供了强‎大的科学运‎算、灵活的程序‎设计流程、高质量的图‎形可视化与‎界面设计、便捷的与其‎他程序和语‎言接口的功‎能。

MATLA ‎B 语言在各‎国高校与研‎究单位起着‎重大的作用‎.它是一种集‎数值计算、符号运算、可视化建模‎、仿真和图形‎处理等多种‎功能…二、实验内容1．平面曲线的‎表示形式对于平面曲‎线，常见的有三‎种表示形式‎，即以直角坐‎标方程],[),(b a x x f y ∈=，以参数方程‎],[),(),(b a t t y y t x x ∈==，和以极坐标‎],[),(b a r r ∈=ϕϕ表示等三种‎形式。

2．曲线绘图的‎M ATLA ‎B 命令MATLA ‎B 中主要用‎p lot,fplot ‎二种命令绘‎制不同的曲‎线。

plot(x,y) 作出以数据‎(x (i),y(i))为节点的折‎线图，其中x,y 为同维数‎的向量。

plot(x1,y1,x2,y2,…) 作出多组数‎据折线图 fplot ‎(‘fun’,[a,b]) 作出函数f ‎u n 在区间‎[a,b]上的函数图‎。

图4-4 图4-5 数学实验四 用Matlab 软件作二元函数的图象一、空间曲线调用格式：plot3(x1,y1,z1,x2,y2,z2,…,xn,yn,zn)其中xi 、yi 和zi 为分别是长度相同的向量，用于存储xi 坐标、yi 坐标和zi 坐标数据，i=1,2,…,n ．例1 在同一坐标系中分别作出三维曲线 ==x x z x x y cos sin 和+=−=2442x z x y 在]6,0[π∈x 上的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：x=0:pi/50:6*pi;y1=x.*sin(x);z1=x.*cos(x);y2=2*x-1;z2=4*x-8;plot3(x,y1,z1,x,y2,z2);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')legend('圆锥螺线','空间直线')取名为exa1保存，再在命令窗口中输入命令exa1，程序运行结果如图4-4．说明：若要作单根曲线，和前面plot 函数一样，只是多了一个立坐标．二、空间曲面1．三维网格图调用格式一：[x,y]=meshgrid(x1:h1:x2,y1:h2:y2)z=f(x,y)plot3(x,y,z)其中x 、y 和z 为长度相同的向量，分别用于存储x 坐标、y 坐标和z 坐标数据． 例2 作出空间平面324=+−z y x 的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y]=meshgrid(-3:0.1:3,-2:0.1:3); %产生一个x,y 平面上51×61的网格z=3-4*x+2*y;plot3(x,y ,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')title('4x-2y+z=3')取名为exa2保存，再在命令窗口中输入命令exa2，程序运行结果如图4-5．例3 作出空间曲面2222sin y x y x z ++=在区域图4-7图4-8}8||,8|||),{(≤≤y x y x 上的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y]=meshgrid(-8:0.1:8);r=sqrt(x.^2+y.^2); %产生对应的x,y 坐标用点幂z=sin(r)./r; %产生对应于x,y 的z 坐标用点除plot3(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')取名为exa3保存，再在命令窗口中输入命令exa3，程序运行结果如图4-6．调用格式二：[x,y]=meshgrid(x1:h1:x2,y1:h2:y2)z=f(x,y)mesh(x,y,z)例4 在x 、y 平面内选取一个区域，作出空间曲面22y xe z −−=的图象． 解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y]=meshgrid(-4:0.1:3,-3:.1:2); %产生一个x,y 平面上51×71的网格z=exp(-x.^2-y.^2);mesh(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')取名为exa2保存，再在命令窗口中输入命令exa2，程序运行结果如图4-7．2．三维曲面图调用格式：[x,y]=meshgrid(x1:h1:x2,y1:h2:y2)z=f(x,y)surf(x,y,z) 说明：surf 函数可借助shading 函数作平滑和插值处理，而shading 函数有三个参数，分别为flat （作平滑处理）、interp （去掉连接线条，在各片之间使用颜色插值）和faceted （默认值，对前面两种参数之一的作用进行还原）．例5 用子图分别作出马鞍面22y x z −=在区域}2||,1|||),{(≤≤y x y x 图和经插值处理的图．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y]=meshgrid(-1:0.1:1,-2:.1:2);z=x.^2-y.^2;subplot(1,2,1),surf(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')title('z=x^2-y^2');subplot(1,2,2),surf(x,y,z);图4-9 图4-10xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')shading interp %插值处理title('z=x^2-y^2的插值处理图')取名为exa5保存，再在命令窗口中输入命令exa5，程序运行结果如图4-8．3．柱面图调用格式一：[x,y,z]=cylinder(R,N)mesh(x,y,z)其中，R 是一个向量，其坐标分量依次对应柱面各横截面的半径，Ｎ是多边形的边数．默认值是Ｒ＝[1,1]，Ｎ＝20．例6 作出正六棱柱在Ｒ＝[２,２]的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y,z]=cylinder([2,2],6);mesh(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')hidden off %显示隐含线，若不想显示隐含线，则取消此命令或设置为hidden on取名为exa6保存，再在命令窗口中输入命令exa6，程序运行结果如图4-9． 调用格式二：[x,y,z]=cylinder(R,N)surf(x,y,z)其中，R 、Ｎ的意义和上面一样．例7 作出正十棱台在Ｒ＝[1,2]的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y,z]=cylinder([1,2],10);surf(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')取名为exa7保存，再在命令窗口中输入命令exa7，程序运行结果如图4-10．说明：若要作正棱锥，只须取Ｒ的某个分量为0即可．4．球面图调用格式：[x,y,z]=sphere(N)surf(x,y,z) 其中，N （N>2）是球面的边数．默认值是Ｎ＝20．sphere(N)不返回坐标，直接绘出球面．例8 以子图形式分别作出N=5、20、40和40并作平滑处理的球．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：subplot(2,2,1)sphere(5);title('子图1')subplot(2,2,2),sphere;title('子图2')subplot(2,2,3)[x,y,z]=sphere(40);surf(x,y,z);title('子图3')subplot(2,2,4)[x,y,z]=sphere(40);surf(x,y,z);shading flat %对球面作平滑处理title('子图4') 取名为exa8保存，再在命令窗口中输入命令exa8，程序运行结果如图4-11．三、上机实验1．用help 命令查看函数plot3，mesh 和surf 等的用法．2．上机验证上面各例．3．作相关小节练习中空间曲线和曲面的图象．图4-11。

function varargout = huatu(varargin)% HUATU MATLAB code for huatu.fig% HUATU, by itself, creates a new HUATU or raises the existing% singleton*.%% H = HUATU returns the handle to a new HUATU or the handle to% the existing singleton*.%% HUATU('CALLBACK',hObject,eventData,handles,...) calls the local% function named CALLBACK in HUATU.M with the given input arguments. %% HUATU('Property','Value',...) creates a new HUATU or raises the% existing singleton*. Starting from the left, property value pairsare% applied to the GUI before huatu_OpeningFcn gets called. An% unrecognized property name or invalid value makes property application% stop. All inputs are passed to huatu_OpeningFcn via varargin.%% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one % instance to run (singleton)".%% See also: GUIDE, GUIDATA, GUIHANDLES% Edit the above text to modify the response to help huatu% Last Modified by GUIDE v2.5 15-Jan-2014 13:13:56% Begin initialization code - DO NOT EDITgui_Singleton = 1;gui_State = struct('gui_Name', mfilename, ...'gui_Singleton', gui_Singleton, ...'gui_OpeningFcn', @huatu_OpeningFcn, ...'gui_OutputFcn', @huatu_OutputFcn, ...'gui_LayoutFcn', [] , ...'gui_Callback', []);if nargin && ischar(varargin{1})gui_State.gui_Callback = str2func(varargin{1});endif nargout[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});elsegui_mainfcn(gui_State, varargin{:});end% End initialization code - DO NOT EDIT% --- Executes just before huatu is made visible.function huatu_OpeningFcn(hObject, eventdata, handles, varargin)% This function has no output args, see OutputFcn.% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% varargin command line arguments to huatu (see VARARGIN)% Choose default command line output for huatuhandles.output = hObject;% Update handles structureguidata(hObject, handles);% UIWAIT makes huatu wait for user response (see UIRESUME)% uiwait(handles.figure1);% --- Outputs from this function are returned to the command line. function varargout = huatu_OutputFcn(hObject, eventdata, handles) % varargout cell array for returning output args (see VARARGOUT); % hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% Get default command line output from handles structurevarargout{1} = handles.output;% --- Executes on button press in pushbutton1.function pushbutton1_Callback(hObject, eventdata, handles)% hObject handle to pushbutton1 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)a=str2num(get(handles.edit1,'string'));b=str2num(get(handles.edit2,'string'));c=str2num(get(handles.edit3,'string'));x=-10:1:10;hold ony=a*x.^2+b*x+c;plot(x,y);% --- Executes on button press in pushbutton2.function pushbutton2_Callback(hObject, eventdata, handles)% hObject handle to pushbutton2 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)close allfunction edit1_Callback(hObject, eventdata, handles)% hObject handle to edit1 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Hints: get(hObject,'String') returns contents of edit1 as text% str2double(get(hObject,'String')) returns contents of edit1 as a double% --- Executes during object creation, after setting all properties. function edit1_CreateFcn(hObject, eventdata, handles)% hObject handle to edit1 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');endfunction edit2_Callback(hObject, eventdata, handles)% hObject handle to edit2 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Hints: get(hObject,'String') returns contents of edit2 as text% str2double(get(hObject,'String')) returns contents of edit2 as a double% --- Executes during object creation, after setting all properties.function edit2_CreateFcn(hObject, eventdata, handles)% hObject handle to edit2 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');endfunction edit3_Callback(hObject, eventdata, handles)% hObject handle to edit3 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Hints: get(hObject,'String') returns contents of edit3 as text% str2double(get(hObject,'String')) returns contents of edit3 as a double% --- Executes during object creation, after setting all properties. function edit3_CreateFcn(hObject, eventdata, handles)% hObject handle to edit3 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');end% --- Executes on button press in pushbutton3.function pushbutton3_Callback(hObject, eventdata, handles)% hObject handle to pushbutton3 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% axex2cla(handles.axes2)。