下学期第三章考点练习
- 格式:pdf
- 大小:1.78 MB
- 文档页数:8

浙教版七年级下第三章3.3-3.5节练习以及答案解析一、单选题1.小刚同学用力踢一下草坪上静止的足球,足球滚动起来,滚动一段距离后会停下来.关于这个过程,下列描述中正确的是()A. 以足球为参照物,草坪和它是同向运动的B. 踢一下静止的足球,足球滚动起来,说明力是使物体运动的原因C. 足球最终会停下来,说明力可以改变物体的运动状态D. 足球最终会停下来,是因为足球具有惯性2.今年五一假期,小江一家开车到开化钱江源游玩。
下列是小江对游玩场景的描写,其中符合科学道理的是( )A. 早上冲出家门,由于受到惯性的作用,跑到车边很难停下B. 上车后系上安全带可以减小行车时的惯性,从而减少意外伤害C. 上山过程中惯性越来越大,导致爬山越来越慢D. 爬上山顶抛出太阳帽,太阳帽离手前后惯性不变3.如图所示,质量相同的甲、乙两人所用绳子相同,甲拉住绳子悬在空中处于静止状态;乙拉住绷紧绳子的中点把绳子拉断了.则()A. 绳子对甲的拉力小于甲受到的重力B. 绳子对甲的拉力大于甲对绳子的拉力C. 乙拉断绳子前瞬间,绳受到的拉力一定小于乙受到的重力D. 乙拉断绳子前瞬间,绳受到的拉力一定大于乙受到的重力4.静止在水平桌面的科学书,与科学书受到的重力相互平衡的力是( )A. 桌面对书的支持力B. 书对桌面的压力C. 桌子的重力D. 地面对桌子的支持力5.用测力计两次拉着重为G的物体竖直向上运动,两次运动的s-t图象,如图所示,其对应的测力计示数分别为F1,F2,则F1和F2的关系是()A. F1>F2B. F1=F2C. F1<F2D. 以上三种情况都有可能6.在科学活动课中,同学们以“假如没有……”为主题展开讨论。
以下是由四位同学提出的具有代表性的观点,你认为正确的是()A. 假如物体没有受到力的作用,物体就不会运动B. 假如没有了空气,光将无法传播C. 假如没有了惯性,离开喷泉口的水就不会继续向上运动D. 假如没有了重力,弹簧测力计就不能再用来测量物体受到的力7.如图,在一辆放在水平地面上的表面光滑的小车上,静止放置质量为m1、m2的两个小球(m2>m1).当车从静止状态突然水平向右启动时,则两个小球()A. 一起向左运动,且m2的速度大于m1的速度B. 一起向右运动,且m2的速度大于m1的速度C. 一起向左运动,且m2的速度等于m1的速度D. 对地面仍保持静止8.运输机参加抗震救灾,在沿水平向右作匀速直线运动过程中,间隔相同时间从飞机上静止释放四个相同的物资.如图能正确表示物资着地位置的是(地面水平,空气阻力不计)()A. B.C. D.9.关于惯性,下列说法正确的是()A. 物体在阻力相同的情况下,速度大的不容易停下来,所以速度大的物体惯性大B. 推动地面上静止的物体比维持这个物体做匀速运动所需的力大,所以静止的物体惯性大C. 在月球上举重比在地球上容易,所以同一个物体在月球上比在地球上惯性小D. 物体的惯性与物体运动速度的大小、物体运动状态的改变、物体所处的位置无关10.李明同学在学习运动和力的知识后,对下列问题认识正确的是()A. 两个力方向相同,大小相等则作用效果一定相同B. 两个力大小相同,方向相反则一定是一对平衡力C. 运动物体突然不受力则它将永远运动下去D. 物体受力越大则惯性也越大11.下列说法正确的是()A. 作用在物体上的几个力一定是同时产生、同时存在、同时消失B. 两个不接触的物体之间一定没有力的作用C. 足球离脚后还能继续向前运动是由于受到惯性的作用D. 竖直向上抛出的石子上升到最高点时处于非平衡状态(不计空气阻力)12.如图所示,吊在天花板下面的电灯处于静止状态,如果某一天,吊线突然间断开的同时,所受外力全部消失,则电灯将( )A. 保持原来的静止状态B. 竖直向下加速运动C. 竖直向下匀速运动D. 竖直向上匀速运动13.关于“运动和力”的关系,下列说法中正确的是()A. 力是使物体产生运动的原因B. 力是维持物体运动的原因C. 力是改变物体运动状态的原因D. 物体受到力的作用,运动状态一定改变14.关于牛顿第一定律,下列说法正确的是( )A. 该定律是通过斜面小车实验直接得到的B. 该定律不能用实验证明,只是一种猜想C. 该定律可以用实验证明,因为它是力学的一个基本定律D. 该定律是在可靠的事实基础上,通过科学推理概括出来的,虽然不能用实验证明,但能经受住实践的检验15.对于汤姆如图所示的多项活动解释合理的是()A. 快速拉出桌布茶具在惯性力作用下留在桌面B. 图中人受到的重力和地面对人的支持力是一对平衡力C. 经过努力没提起杠铃说明杠铃所受拉力小于等于重力D. 划船时船桨对水的作用力大于水对船桨的作用力16.探究“推断物体不受力时运动”(如图)时,同学们得到如下结论,错误的是()A. 控制小车从斜面同一高度滑下是为了让小车滑到水平面时的初速度相同B. 通过(a)(b)(c)三次实验,可直接验证牛顿第一定律C. 由于惯性,小车到达水平面后继续向前运动D. 实验中主要运用了控制变量和理想实验法17.如图,在车厢中的a是用绳拴在底部上的氢气球,b是用绳挂在车厢顶的金属球,开始时它们和车一起向右作匀速直线运动,若忽然刹车使车厢作匀减速运动,则下列几个图能正确表示刹车期间车内的情况是()A. B. C. D.18.关于重力,下列说法中错误的是()A. 重力是由于地球对物体吸引而产生的B. 重力是物体本身的固有属性C. 重力的大小跟物体的质量成正比D. 重力的方向总是竖直向下19.静止在水平桌面上的文具盒,受到的平衡力是()A. 文具盒受到的重力和文具盒对桌面的压力B. 文具盒受到的重力和桌面对文具盒的支持力C. 文具盒对桌面的压力和桌面对文具盒的支持力D. 文具盒对桌面的压力和文具盒对地球的吸引力TV科教频道曾报道:有一辆小车载人后停在水平放置的地磅上时,左前轮、右前轮、左后轮、右后轮对地磅的压力分别为4750N、4980N、4040N、3960N。

(附答案)人教版初中物理第三章物态变化考点专题训练单选题1、下列物体中属于晶体的是()A.橡胶B.沥青C.冰块D.石蜡2、日光灯用久后,灯管两端会出现黑斑,这些黑斑是灯丝中的钨()A.汽化而成B.升华而成C.先汽化后液化而成D.先升华后凝华而成3、盛夏,打开冰箱门、会看到“白气”冒出;寒冷的冬天,户外的人也会不断呼出“白气”、对这两种“白气”的分析正确是()A.前者是汽化现象,是冰箱内的水蒸气汽化形成的B.前者是液化现象,是冰箱外的水蒸气液化形成的C.后者是汽化现象,是口腔内的水蒸气汽化形成的D.后者是液化现象,是口腔外的水蒸气液化形成的4、口罩成为常态防疫“神器”,戴眼镜的人们常因口罩佩戴出现镜片模糊的情况,这是液化现象。
下列实例中与它物态变化相同的是()A.初春,冰雪消融B.夏天,清晨草叶或树叶上形成露珠C.深秋,屋顶的瓦上结了一层霜D.冬天,室外冰冻的衣服变干了5、下列物体中属于晶体的是()A.橡胶B.沥青C.冰块D.石蜡6、下列措施中,能使蒸发变快的是()A.给盛有水的杯子盖好杯盖B.用电热吹风机吹湿头发C.把蔬菜放入塑料袋内保存D.把水果放入冰箱冷藏室内保存7、关于物态变化,下列说法正确的是()A.灯泡里的灯丝用钨制成是因为钨的沸点高B.盛夏,剥开包装纸后冰棒会冒“白气”是汽化现象C.水在凝固过程中不断放出热量,温度保持不变D.深秋的早晨,地面上经常会出现白色的霜,这是液化现象8、如图所示是粤北某天天气预报的信息图片,关于图片中信息的解释正确的是()A.雪的形成过程中放出热量B.雨的形成是汽化现象C.雨夹雪时气温一定是0℃以下D.当天夜里的温度最高可达5℃9、如图所示是粤北某天天气预报的信息图片,关于图片中信息的解释正确的是()A.雪的形成过程中放出热量B.雨的形成是汽化现象C.雨夹雪时气温一定是0℃以下D.当天夜里的温度最高可达5℃10、在“探究蜡烛的熔化特点”和“观察碘锤中的物态变化”两个活动中,采用水浴法加热的主要目的是()A.都是为了受热均匀B.都是为了控制温度C.前者是为了受热均匀,后者是为了控制温度D.前者是为了控制温度,后者是为了受热均匀11、下图中,正确描述巴中铁路铁轨的铸造过程中凝固阶段温度变化的是()A.B.C.D.12、冷链储运中常用一种装有制冷装置的冷藏车,用于运输冷冻食品和疫苗药品等,制冷装置通过液态制冷剂汽化将车的“热”搬运到外面,实现制冷。

北师大版七年级下册数学第三章知识点详细归纳附第三章测试卷及参考答案第三章变量之间的关系@考点归纳1.自变量一、变量的概念2.因变量变量之间的关系 1. 表格法2. 关系式法二、变量的表达方法(1).速度时间图象3. 图象法(2).路程时间图象一、变量、自变量、因变量1、在某一变化过程中,不断变化的量叫做变量。
2、如果一个变量y随另一个变量x的变化而变化,则把x叫做自变量,y叫做因变量。
3、自变量与因变量的确定:(1)自变量是先发生变化的量;因变量是后发生变化的量。
(2)自变量是主动发生变化的量,因变量是随着自变量的变化而发生变化的量。
(3)利用具体情境来体会两者的依存关系。
二、表格1、表格是表达、反映数据的一种重要形式,从中获取信息、研究不同量之间的关系。
(1)首先要明确表格中所列的是哪两个量;(2)分清哪一个量为自变量,哪一个量为因变量;(3)结合实际情境理解它们之间的关系。
2、绘制表格表示两个变量之间关系(1)列表时首先要确定各行、各列的栏目;(2)一般有两行,一行表示自变量,第二行表示因变量;(3)写出栏目名称,有时还根据问题内容写上单位;(4)在一行列出自变量的各个变化取值;第二行对应列出因变量的各个变化取值。
(5)一般情况下,自变量的取值从左到右应按由小到大的顺序排列,这样便于反映因变量与自变量之间的关系。
三、关系式1、用关系式表示因变量与自变量之间的关系时,通常是用含有自变量(用字母表示)的代数式表示因变量(也用字母表示),这样的数学式子(等式)叫做关系式。
2、关系式的写法不同于方程,必须将因变量单独写在等号的左边。
3、求两个变量之间关系式的途径:(1)将自变量和因变量看作两个未知数,根据题意列出关于未知数的方程,并写成关系式的形式。
(2)根据表格中所列的数据写出变量之间的关系式;(3)根据实际问题中的基本数量关系写出变量之间的关系式;(4)根据图象写出与之对应的变量之间的关系式。
4、关系式的应用:(1)利用关系式能根据任何一个自变量的值求出相应的因变量的值;(2)同样也可以根据任何一个因变量的值求出相应的自变量的值;(3)根据关系式求值的实质就是解一元一次方程(求自变量的值)或求代数式的值(求因变量的值)。


第三章整式及其加减B卷压轴题考点训练一、填空题=,=1212240a a an a=++-()216na a =-元,∴当20n >时,该户应缴纳的水费为()216na a -元;故答案为:()216na a -;(3)解:∵12224´=,∴12x >,当1220x <£时,甲用水量超过312m 但不超过320m ,乙用水量超过320m ,∴()()()12212 1.5212220122 1.5402022x x ´+-´´+´+-´´+--´´243362424804x x =+-+++-()116x =-元;当2028x <<时,甲的用水量超过320m ,乙的用水量超过312m 但不超过320m ,∴()()()1222012 1.522022122401223x x ´+-´´+-´´+´+--´´242448024843x x=++-++-()76x =+元,当2840x ££时,甲的用水量超过320m ,乙的用水量不超过312m ,∴()()()1222012 1.522022402x x ´+-´´+-´´+-´2424480802x x=++-+-()248x =+元;综上所述,当1220x <£时,甲,乙两户一个月共缴纳的水费()116x -元;当2028x <<时,甲,乙两户一个月共缴纳的水费()76x +元;当2840x ££时,甲,乙两户一个月共缴纳的水费()248x +元.【点睛】本题主要考查了有理数的四则混合计算的实际应用,整式加减计算的实际应用,正确理解题意利用分类讨论的思想求解是解题的关键.。

1.平移定义:在平面内,将一个图形沿____________移动一定的______,这样的图形移动称为平移.性质:平移不改变图形的大小和形状.图形平移后,对应线段________,对应角_________;对应点连线__________________________.作图:先确定图形的关键点平移后的位置,再按原来的方式连接,即可得到平移后的图形.2.旋转定义:在平面内,将一个图形绕一个_________沿某个方向转动一个_______,这样的图形运动称为旋转.性质:旋转不改变图形的大小和形状.图形旋转后对应线段_________,对应角________,对应点到旋转中心的距离_____________.任意一对对应点与旋转中心的连线所成的角都是_________.作图:(1)先找出图形中的关键点;(2)分别作出这几个点旋转后的对应点;(3)按原来位置依次连接各点即可得到旋转后的图形.3.中心对称(1)中心对称定义:如果把一个图形绕着某一点旋转180°,能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心.(2)中心对称图形把一个图形绕某个点旋转180°,如果旋转后的图形与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.性质:成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.►考点一平移和平移作图[方法技巧]平移要注意起点和终点,平移的方向和距离►考点二旋转和旋转作图例2在Rt△ABC中,∠C=90°,AC=1,BC=3,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(点A,O的对应点分别为点A′,O′,且A′,O′,O,C恰好在一条直线上),求:∠ABC, ∠A′BC的度数及OA+OB+OC的和.►考点三平移和旋转的应用2.在图3-8的四个三角形中,不能由3-7中的△ABC经过旋转或平移得到的是( )3.如图3-9,△ABC和△ADE都是等腰直角三角形,∠ACB和∠ADE都是直角,点C在AE 上,△ABC绕着A点经过逆时针旋转后与△ADE重合得到图(1),再将图(1)作为“基本图形”绕着A点经过逆时针连续旋转得到图(2).图(1),图(2)中旋转的角度分别为( ) A.45°,90° B.90°,45°C.60°,30° D.30°,60°4.下列图案都是由字母“m”经过变形、组合而成的,其中不是中心对称图形的是( )5..如图3-14(1)所示,在长为a,宽为b的一块草坪上修了一条宽为1的笔直小路,则余下草坪的面积可表示为________;如图(2),现为了增加美感,把这条小路改为宽恒为1的弯曲小路,则此时余下草坪的面积为________.6.如图3-16所示,一个矩形场地ABCD,长=102 m,宽AD=51 m,A,B两处入口的小路宽均为1 m,两条小路汇合处路宽为2 m,其余部分种植草坪,则草坪的面积为________.7.如图3-18,花边中的图案以正方形为基础,由圆弧或圆构成,仿照例图,请你为班级黑板报设计一条花边,要求:(1)只需画出组成花边的一个图案,不写画法,不需配文字;(2)以所给的正方形为基础,用圆弧或圆画出;(3)图案应有美感;(4)与例图不同.8.答案1-4 CBAB5 .ab-a ab-a6.5000m27.45。

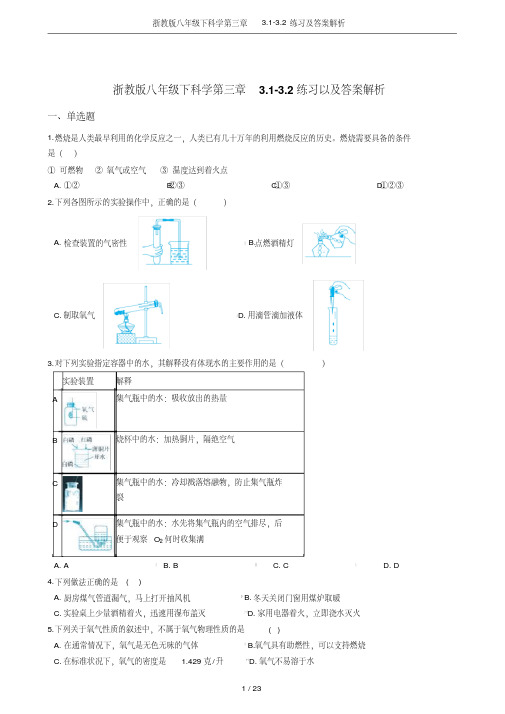
浙教版八年级下科学第三章 3.1-3.2练习以及答案解析一、单选题1.燃烧是人类最早利用的化学反应之一,人类已有几十万年的利用燃烧反应的历史。
燃烧需要具备的条件是()①可燃物②氧气或空气③温度达到着火点A. ①②B. ②③C. ①③D. ①②③2.下列各图所示的实验操作中,正确的是()A. 检查装置的气密性B. 点燃酒精灯C. 制取氧气D. 用滴管滴加液体3.对下列实验指定容器中的水,其解释没有体现水的主要作用的是()实验装置解释A 集气瓶中的水:吸收放出的热量B 烧杯中的水:加热铜片,隔绝空气C 集气瓶中的水:冷却溅落熔融物,防止集气瓶炸裂D 集气瓶中的水:水先将集气瓶内的空气排尽,后便于观察O2何时收集满A. AB. BC. CD. D4.下列做法正确的是( )A. 厨房煤气管道漏气,马上打开抽风机B. 冬天关闭门窗用煤炉取暖C. 实验桌上少量酒精着火,迅速用湿布盖灭D. 家用电器着火,立即浇水灭火5.下列关于氧气性质的叙述中,不属于氧气物理性质的是( )A. 在通常情况下,氧气是无色无味的气体B. 氧气具有助燃性,可以支持燃烧C. 在标准状况下,氧气的密度是 1.429克/升D. 氧气不易溶于水6.下列实验操作中,“先”与“后”的顺序正确的是()A. 制取气体时,先装药品,后检查装置的气密性B. 做氧气的助燃性实验时,先检查氧气的纯度,后点火C. 用排水法收集氧气结束时,先把导管移离水面,后停止加热D. 给试管里的液体加热时先加热,后预热7.实验室用如图所示装置制取氧气,下列有关说法不正确的是()A. 试管中加入的药品是二氧化锰和过氧化氢B. 实验前应检查装置的气密性C. 待导管口产生连续均匀的气泡时才开始收集氧气D. 实验结束时应先从水槽中取出导管,再停止加热8.“防火胜于救火”,科学认识燃烧,增强安全防范意识是每个公民应具备的安全素养之一。
下列说法错误的是()A. 身上着火不可乱跑,要就地打滚使火熄灭B. 水能灭火,是因为水能使可燃物的温度降低到着火点以下C. 对于不明原因引起的失火,我们宁可让其自生自灭,也不能贸然采取灭火措施D. 油库、面粉厂、纺织厂、轮穀厂、橡胶厂和煤矿的坑道内等场所要严禁烟火,以避免爆炸的发生9.下列说法中,正确的是()①需要加热才能发生的反应一定是吸热反应;②化学能可转化为光能,光能不能转化为化学能;③镁与盐酸的反应中,参加反应的镁、盐酸的能量和大于氯化镁溶液、氢气的能量和;④化学反应一定伴随能量变化,有能量变化一定发生化学反应A. ①②③B. ③④C. ②③④D. 只有③10.下列有关燃烧、灭火的分析正确的是()A. 火上浇油:增大可燃物与氧气的接触面积B. 钻木取火:提高可燃物的温度达到着火点C. 吹灭烛火:降低着火点D. 电器着火:用水浇灭11.运用如图所示装置探究可燃物的燃烧条件,下列说法错误的是()A. ①②现象对比,说明温度达到可燃物的着火点是燃烧条件之一B. ①③现象对比,说明有氧气参与是燃烧条件之一C. 白磷的着火点低于80 ℃D. 热水只起到加热作用12.下列说法:①呼吸作用、食物腐烂、铁生锈都是缓慢氧化;②燃烧是可燃物与氧气发生的剧烈的化合反应;③急速的燃烧一定会爆炸;④自燃是缓慢氧化引起的;⑤白磷在空气中和氧气中的着火点不同;⑥燃烧、自燃、缓慢氧化的共同点都是氧化反应并都有热量产生。

第三章 位置与坐标B 卷压轴题考点训练1.如图,在△ACB 中,∠ACB =90°,AC =BC ,点C 的坐标为(﹣2,0),点A 的坐标为(﹣8,3),点B 的坐标是_____.【答案】(1,6)【详解】解:如图所示,过A 和B 分别作AD OC^于D ,BE OC ^于E ,即12390Ð=Ð=Ð=°,∴∠DAC +∠ACD =∠ACD +∠ECB=90°,∴DAC ECB Ð=Ð,∴ACD CBE Ð=Ð,在Rt ACD △,Rt CEB △中,∵DAC ECB AC CB ACD CBE Ð=Ðìï=íïÐ=Ðî,∴(ASA)ADC CEB @V V ,∴DC BE =,AD CE =,∵点C 的坐标为(2,0)-,点A 的坐标为(8,3)-,∴2OC =,3AD CE ==,8OD =,∴6CD OD OC =-=,1OE CE OC =-=,∴6BE =,∴则B 点的坐标是(1,6).故答案是:(1,6).2.如图,P 为MON Ð内部的已知点,连接OP ,A 为OM 上的点,B 为ON 上的点,当PAB ∆周长的最小值与OP 的长度相等,MON Ð的度数为___°.【答案】30【详解】解:作点P 关于OM 的对称点C ,关于ON 的对称点D ,连接CD ,交OM 于A ,交ON 于B .此时,△PAB 的周长最小. 连接OC ,OD ,PA ,PB .∵点P 与点C 关于OM 对称∴OM 垂直平分PC∴∠COM=∠MOP ,PA=CA ,OC=OP同理,可得∠DON=∠NOP ,PB=DB ,OD=OP∴∠COA+∠DOB=∠AOP+∠BOP=∠MON∴∠COD=2∠MON又∵△PAB 的周长=PA+AB+BP=CA+AB+BD=CD=OP∴OC=OD=CD∴△COD 是等边三角形∴∠MON 30=°故答案为:30.3.已知点A ,B 的坐标分别为(2,0),(2,4),以A ,B ,P 为顶点的三角形与ABO V 全等,点P 与点O 不重合,写出符合条件的点P 的坐标:___________.【答案】(4,4)或(0,4)或(4,0)4.如图,点A 的坐标为()4,0,点B 的坐标为()0,1-,分别以OB ,AB 为直角边在第三、第四象限作等腰Rt OBF △,等腰Rt ABE △,连接EF 交y 轴于P 点,点P 的坐标是______.【答案】()0,3-【详解】解:如图,作EN y ^轴于N ,5.如图,Rt△ABC≌Rt△FDE,∠ABC=∠FDE=90°,∠BAC=30°,AC=4,将Rt△FDE沿直线l向右平移,连接BD、BE,则BD+BE的最小值为___.别找一点E、F,使得BEFV周长的最小值为__________.V的周长最小,则BEF7.如图,在平面直角坐标系中,等腰直角三角形1OAA 的直角边OA 在x 轴上,点1A 在第一象限,且1OA =,以点1A 为直角顶点,1OA 为一直角边作等腰直角三角形12OA A ,再以点2A 为直角顶点,2OA 为直角边作等腰直角三角形23OA A ……依此规律,则点2022A 的坐标是________.8.如图,在平面直角坐标系中,点A (0,4)在y 轴正半轴上,点B (-3,0)在x 轴负半轴上,且AB =5,点M 坐标为(3,0),N 点为线段OA 上一动点,P 为线段AB 上的一动点,则MN +NP 的最小值为___________.9.如图,在平面直角坐标系中,点A 从()14,0A -依次跳动到()241A -,,()33,1A -,()430A -,,()520A -,,()623A -,,()713A -,,()810A -,,()913A --,,()1003A -,,()1100A ,,…,按此规律,则点2022A 的坐标是______________【答案】(804,1)【详解】解:观察图形可知,n为正整数时,n A 的纵坐标为0,1,3,﹣3纵坐标为0的点:14581114,,,A A A A A A LL纵坐标为1的点:2312132223,,,A A A A A A LL纵坐标为3的点:6716172627,,,A A A A A A LL纵坐标为﹣3的点:91019202930,,,A A A A A A LL可以看出纵坐标为1,3,﹣3时,n取连续的两个数为一组,则10个10个的增加,∵2021=10×202+1,纵坐标为1的规律()()()210121011n n A A +-+-+,∴2022A 的纵坐标为1,由()21012022n +-=,解得n =203,∵2022A 正好是2A 往右循环203次,∴2022A 横坐标为﹣4+(203-1)×4=804,∴点2022A 的坐标是(804,1),故答案为:(804,1)10.如图,四边形OABC 是正方形,点M ,N 都在OA 的延长线上,且OM =MN =2,则BM+BN 的最小值为______.则MN′=BM+BN 的值最小,由对称性可知,ON ON ¢=,11.如图,在平面直角坐标系上有点A (1,0),第一次点A 跳动至点A 1(﹣1,1),第二次点A 1跳动至点A 2(2,1),第三次点A 2跳动至点A 3(﹣2,2),第四次点A 3跳动至点A 4(3,2),依此规律跳动下去,则点A 2017与点A 2018之间的距离是__________.【答案】2019【详解】由跳动规律可归纳类推出以下3条规律:(其中n 为正整数)(1)点51213,,,,n A A A A -L 的横坐标依次为1,2,3,,n----L (2)点2462,,,,n A A A A L 的横坐标依次为2,3,4,,1n +L (3)点1A 与点2A ,点3A 与点4A ,点5A 与点6A ,L ,点21n A -与2n A 的纵坐标分别相等2017210091=´-Q ,201821009=´\点2017A 的横坐标为1009-,点2018A 的横坐标为100911010+=,且点2017A 与点2018A 的纵坐标相等则点2017A 与点2018A 之间的距离是10101009)0(219--=故答案为:2019.12.对于平面直角坐标系xOy 中的图形G 和点P ,给出如下定义:将图形G 沿上、下、左、右四个方向中的任意一个方向平移一次,平移距离小于或者等于1个单位长度,平移后的图形记为G ¢,若点P 在图形G ¢上,则称点P 为图形G 的稳定点,例如,当图形G 为点(2,3)-时,点(1,3),(2,3.5)M N --都是图形G 的稳定点.(1)已知点(1,0),(2,0)A B -.①在点1234133(2,0),(4,0),1,,,222P P P P æöæö--ç÷ç÷èøèø中,线段AB 的稳定点是___________.②若将线段AB 向上平移t 个单位长度,使得点(0,1)E 或者点(0,5)F 为线段AB 的稳定点,写出t 的取值范围___________.(2)边长为a 的正方形,一个顶点是原点O ,相邻两边分别在x 轴、y 轴的正半轴上,这个正方形及其内部记为图形G .若以(0,2),(4,0)为端点的线段上的所有点都是这个图形G 的稳定点,直接写出a 的最小值___________.【答案】(1)①1P ,3P ;②0≤t ≤2或4≤t ≤6;(2)3【解析】(1)解:①如图1中,观察图象,根据图形G 的稳定点的定义可知:1P ,3P 是线段AB 的稳定点.故答案为:1P ,3P ;②如图2中,观察图象可知当0≤t ≤2或4≤t ≤6时,点E (0,1)或者点F (0,5)为线段AB 的稳定点.故答案为:0≤t ≤2或4≤t ≤6;(2)解:如图3中,正方形OABC 的边长为a ,P (0,2),Q (4,0),观察图象可知当3≤a 时,线段PQ 上的点都是图形G 的稳定点.∴a 的最小值为3,故答案为:3.13.在平面直角坐标系中,(6,),(,0),(0,)A a B b M c ,且2(2)|6|0b a -+-=,P 点为y 轴上一动点.(1)求点B 、M 的坐标;(2)当P 点在线段OM 上运动时,试问是否存在一个点P 使13PAB S =V ,若存在,请求出P 点的坐标;若不存在,请说明理由.(3)不论点P 点运动到直线OM 上的任何位置(不包括点O ,M ),PAM Ð、APB Ð、PBO Ð三者之间是否都存在某种固定的数量关系,如果有,请写出来并请选择其中一种结论进行证明;如果没有,请说明理由.于B.(1)求△ABC的面积;(2)如图2,过点B作BD CA∥交y轴于D,且AE,DE分别平分∠CAB与∠BDO,求∠AED的度数;(3)如图1,在y轴上是否存在点P,使得△ACP和△ABC的面积相等?若存在,求出点P坐标;若不存在,请说明理由.15.如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2 +2b-=0,过C作CB⊥x轴于B.(1)直接写出三角形ABC的面积;(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.。
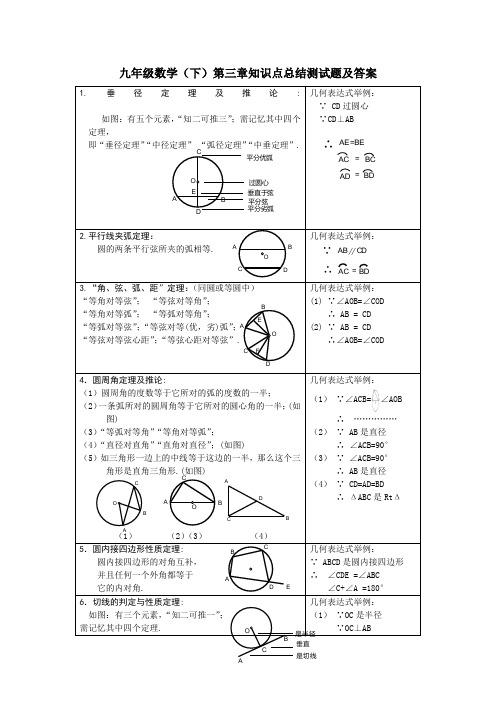
九年级数学(下)第三章知识点总结测试题及答案1.垂径定理及推论: 如图:有五个元素,“知二可推三”;需记忆其中四个定理,即“垂径定理”“中径定理” “弧径定理”“中垂定理”.几何表达式举例: ∵ CD 过圆心 ∵CD ⊥AB 2.平行线夹弧定理:圆的两条平行弦所夹的弧相等.几何表达式举例: 3.“角、弦、弧、距”定理:(同圆或等圆中)“等角对等弦”; “等弦对等角”;“等角对等弧”; “等弧对等角”;“等弧对等弦”;“等弦对等(优,劣)弧”;“等弦对等弦心距”;“等弦心距对等弦”.几何表达式举例: (1) ∵∠AOB=∠COD∴ AB = CD (2) ∵ AB = CD∴∠AOB=∠COD4.圆周角定理及推论:(1)圆周角的度数等于它所对的弧的度数的一半; (2)一条弧所对的圆周角等于它所对的圆心角的一半;(如图) (3)“等弧对等角”“等角对等弧”; (4)“直径对直角”“直角对直径”;(如图)(5)如三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(如图)(1) (2)(3) (4) 几何表达式举例: (1) ∵∠ACB=∠AOB∴ …………… (2) ∵ AB 是直径∴ ∠ACB=90° (3) ∵ ∠ACB=90°∴ AB 是直径 (4) ∵ CD=AD=BD∴ ΔABC 是Rt Δ5.圆内接四边形性质定理:圆内接四边形的对角互补, 并且任何一个外角都等于 它的内对角.几何表达式举例:∵ ABCD 是圆内接四边形 ∴ ∠CDE =∠ABC∠C+∠A =180° 6.切线的判定与性质定理: 如图:有三个元素,“知二可推一”; 需记忆其中四个定理.几何表达式举例: (1) ∵OC 是半径∵OC ⊥ABABCD OA B CDE O 平分优弧过圆心垂直于弦平分弦平分劣弧∴ AC BCAD BD ==AE=BEA BC DEFOA B COABCDEABC OA B CD∵ ∴ ∥=AB CD ACBDABCO是半径垂直是切线(1)经过半径的外端并且垂直于这条半径的直线是圆的切线;(2)圆的切线垂直于经过切点的半径;‴(3)经过圆心且垂直于切线的直线必经过切点; ‴(4)经过切点且垂直于切线的直线必经过圆心.∴AB 是切线 (2) ∵OC 是半径∵AB 是切线 ∴OC ⊥AB (3) ……………7.切线长定理:从圆外一点引圆的两条切线, 它们的切线长相等;圆心和这一 点的连线平分两条切线的夹角.几何表达式举例:∵ PA 、PB 是切线 ∴ PA=PB ∵PO 过圆心 ∴∠APO =∠BPO 8.弦切角定理及其推论:(1)弦切角等于它所夹的弧对的圆周角;(2)如果两个弦切角所夹的弧相等,那么这两个弦切角也相等;(3)弦切角的度数等于它所夹的弧的度数的一半.(如图)几何表达式举例:(1)∵BD 是切线,BC 是弦∴∠CBD =∠CAB(2)∵ ED ,BC 是切线 ∴ ∠CBA =∠DEF9.相交弦定理及其推论: (1)圆内的两条相交弦,被交点分成的两条线段长的乘积相等;(2)如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段长的比例中项.几何表达式举例:(1) ∵PA ²PB=PC ²PD∴……… (2) ∵AB 是直径∵PC ⊥AB∴PC 2=PA ²PB10.切割线定理及其推论:(1)从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项;(2)从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.几何表达式举例:(1) ∵PC 是切线,PB 是割线 ∴PC 2=PA ²PB (2) ∵PB 、PD 是割线∴PA²PB=PC ²PD11.关于两圆的性质定理:(1)相交两圆的连心线垂直平分两圆的公共弦; (2)如果两圆相切,那么切点一定在连心线上.几何表达式举例: (1) ∵O 1,O 2是圆心∴O 1O 2垂直平分AB (2) ∵⊙1 、⊙2相切∴O 1 、A 、O 2三点一线AB CD ABC DEF P ABO AB CPA BC D P AB O1O2A O1O2AB C D P A B CPO ∵ EF AB =A B O (1) (2)12.正多边形的有关计算:(1)中心角αn ,半径R N , 边心距r n ,边长a n ,内角βn , 边数n ;(2)有关计算在Rt ΔAOC 中进行.公式举例:(1) αn =; (2)几何B 级概念:(要求理解、会讲、会用,主要用于填空和选择题)一 基本概念:圆的几何定义和集合定义、 弦、 弦心距、 弧、 等弧、 弓形、弓形高三角形的外接圆、三角形的外心、三角形的内切圆、 三角形的内心、 圆心角、圆周角、 弦 切角、 圆的切线、 圆的割线、 两圆的内公切线、 两圆的外公切线、 两圆的内(外) 公切线长、 正多边形、 正多边形的中心、 正多边形的半径、 正多边形的边心距、 正多边形的中心角. 二 定理:1.不在一直线上的三个点确定一个圆.2.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆.3.正n 边形的半径和边心距把正n 边形分为2n 个全等的直角三角形. 三 公式:1.有关的计算:(1)圆的周长C=2πR ;(2)弧长L=;(3)圆的面积S=πR 2.(4)扇形面积S 扇形 =;(5)弓形面积S 弓形 =扇形面积S AOB ±ΔAOB 的面积.(如图)2.圆柱与圆锥的侧面展开图:(1)圆柱的侧面积:S 圆柱侧 =2πrh ; (r:底面半径;h:圆柱高)(2)圆锥的侧面积:S 圆锥侧 =. (L=2πr ,R 是圆锥母线长;r 是底面半径)四 常识:1. 圆是轴对称和中心对称图形.2. 圆心角的度数等于它所对弧的度数.3. 三角形的外心 ⇔ 两边中垂线的交点 ⇔ 三角形的外接圆的圆心;三角形的内心 ⇔ 两内角平分线的交点 ⇔ 三角形的内切圆的圆心. 4. 直线与圆的位置关系:(其中d 表示圆心到直线的距离;其中r 表示圆的半径)直线与圆相交 ⇔ d <r ; 直线与圆相切 ⇔ d=r ; 直线与圆相离 ⇔ d >r. 5. 圆与圆的位置关系:(其中d 表示圆心到圆心的距离,其中R 、r 表示两个圆的半径且R ≥r )两圆外离 ⇔ d >R+r ; 两圆外切 ⇔ d=R+r ; 两圆相交 ⇔ R-r <d <R+r ;αnβnABCDEOa r n nnR两圆内切 ⇔ d=R-r ; 两圆内含 ⇔ d <R-r. 6.证直线与圆相切,常利用:“已知交点连半径证垂直”和“不知交点作垂直证半径” 的方法加辅助线.7.关于圆的常见辅助线:O CAB已知弦构造弦心距.OA BC已知弦构造Rt Δ.OABC已知直径构造直角.OAB已知切线连半径,出垂直.O BC AD P圆外角转化为圆周角.OACD BP圆内角转化为圆周角.ODC PAB构造垂径定理.OACDPB构造相似形.M01ANO2两圆内切,构造外公切线与垂直.01CNO2DEABM两圆内切,构造外公切线与平行. NAM02O1两圆外切,构造内公切线与垂直.CBMNADEO 102两圆外切,构造内公切线与平行.CE A DB O两圆同心,作弦心距,可证得AC=DB.A CBO102两圆相交构造公共弦,连结圆心构造中垂线. BAC OPPA 、PB 是切线,构造双垂图形和全等.OABCDE相交弦出相似.OP ABC一切一割出相似, 并且构造弦切角.OBCEADP两割出相似,并且构造圆周角. OABCP双垂出相似,并且构造直角.BACD EF规则图形折叠出一对全等,一对相似.FED BAC O GH圆的外切四边形对边和相等.ABOCD若AD ∥BC 都是切线,连结OA 、OB 可证∠AOB=180°,即A 、O 、B 三点一线.EACBOD等腰三角形底边上的的高必过内切圆的圆心 和切点,并构造相似形.EFCDBAORt ΔABC 的内切圆半径:r=.O补全半圆.ABCo1o2AB=.CABo1o2AB=.AC D PO BPC 过圆心,PA 是切线,构造 双垂、Rt Δ. BCD OAPO 是圆心,等弧出平行和相似.DE MABCFN G作AN ⊥BC ,可证出:.九年级数学(下)第三章测试题(答题时间:120分钟 总分:120分)一、选择题:(每题3分,共36分) 1. 下列五个命题:(1)两个端点能够重合的弧是等弧;(2)圆的任意一条弧必定把圆分成劣弧和优弧两部分;⑶经过平面上任意三点可作一个圆;⑷任意一个圆有且只有一个内接三角形;⑸三角形的外心到各顶点距离相等.其中真命题有( ) A. 1个 B. 2个 C. 3个 D. 4个2. AB 是⊙O 的弦,∠AOB=88°,则弦AB 所对的圆周角等于( ) A. 44° B. 22° C. 44°或136° D. 22°或68°3. O 是△ABC 的外心,且∠ABC+∠ACB=100°,则∠BOC=( ) A. 100° B. 120° C. 130° D. 160°4. 一个点到圆的最大距离为9cm ,最小距离为4cm ,则圆的半径是( ) A. 5cm 或13cm B. 2.5cm C. 6.5cm D. 2.5cm 或6.5cm5. 如图1,⊙O 外接于△ABC ,AD 为⊙O 的直径,∠ABC=30°,则∠CAD=( ) A. 30° B. 40° C. 50° D. 60°6. 如图2,△ABC 的三边分别切⊙O 于D ,E ,F ,若∠A=50°,则∠DEF=( ) A. 65° B. 50° C. 130° D. 80°BDCA OBEDCA FO图1 图2 图3 7.在Rt △ABC 中,∠C=90°,AB=5,内切圆半径为1,则三角形的周长为( ) A. 15 B. 12 C. 13 D. 148. 在Rt △ABC 中,∠C=90°,AB=5cm ,BC=3cm ,以A 为圆心,以4cm 为半径作圆,•则直线BC 与⊙A 的位置关系是( )A. 相交B. 相切C. 相离D. 无法确定9. 已知两圆的圆心距为3,两圆的半径分别是方程x 2-4x+3=0的两根,•那么这两个圆的位置关系是( )A. 外离B. 外切C. 相交D. 内切10. ⊙O 的半径为3cm ,点M 是⊙O 外一点,OM=4cm ,则以M 为圆心且与⊙O •相切的圆的半径一定是( )A. 1cm 或7cmB. 1cmC. 7cmD. 不确定11. 一个扇形半径30cm ,圆心角120°,用它作一个圆锥的侧面,则圆锥底面半径为( ) A. 5cm B. 10cm C. 20cm D. 30cm12. 如图3所示,在△ABC 中,AB=AC ,以AB 为直径的⊙O 交BC 于点D ,交AC 于点E ,•连结OD 、AD ,则以下结论:①D 是BC 的中点;②AD ⊥BC ;③AD 是∠BAC 的平分线;④OD ∥AC .其中正确结论的个数为( )A. 1个B. 2个C. 3个D. 4个二、填空题. (每题3分,共30分)13. ⊙O 中,弦MN 把⊙O 分成两条弧,它们的度数比为4:5,如果T 为MN 中点,则∠TMO=_________,则弦MN 所对的圆周角为_______.14. ⊙O 到直线L 的距离为d ,⊙O 的半径为R ,当d 、R 是方程x 2-4x+m=0的根,且L •与⊙O 相切时,m 的值为_________.15. ⊙O 中,若弦AB 、BC 所对的圆心角分别为120°、80°,则弦AC •所对的圆心角为_____;16. 如图4所示,AB 为⊙O 的直径,C 、D 是⊙O 上的两点,∠BAC=20°,⋂⋂=CD AD ,•则∠DAC 的度数是_______.17. 在△ABC 中,AB=5cm ,BC=3cm ,AC=4cm ,则△ABC 的内切圆的半径为_________.18. △ABC 三边与⊙O 分别切于D ,E ,F ,已知AB=7cm ,AC=5cm ,AD=2cm ,则BC=________. 图419. 如图5所示,P 为⊙O 外一点,PA 、PB 、AB 都与⊙O 相切,∠P=40°,则∠AOB 的度数为_________.20. 两圆相切,圆心距等于2cm ,其中一个圆的半径等于3cm ,•则另一个圆的半径等于_________.21. 已知两圆外离,圆心距d=12,大圆半径R=7,则小圆半径r •的所有可能的正整数值为_________.22. 圆心角为120°的扇形的弧长是2πcm ,则此扇形的面积为___________. 图5三、解答题. (第23、24、25题各6分、第26题各7分,第27题8分,共34分) 23. 如图6,从点P 向⊙O 引两条切线PA ,PB ,切点为A ,B ,AC 为弦,BC 为⊙O •的直径,若∠P=60°,PB=2cm ,求AC 的长.24. 如图,已知扇形AOB 的半径为12,OA ⊥OB ,C 为OB 上一点,以OA 为直径的半圆O 1与以BC 为直径的半圆O 2相切于点D .求图中阴影部分面积.BCAPO图625. 如图所示,⊙I 是△ABC 的内切圆,AB=9,BC=8,CA=10,点D 、E 分别为AB 、AC 上的点,且DE 是⊙I 的切线,求△ADE 的周长.26. 如图,C 是⊙O 的直径AB 延长线上一点,过点C 作⊙O •的切线CD ,D 为切点,连结AD ,OD ,BD .请根据图中给出的已知条件(不再标注字母,不再添加辅助线)写出两个你认为正确的结论.27. 如图,已知弦AB 与半径相等,连结OB ,并延长使BC=OB . (1)问AC 与⊙O 有什么关系.(2)请你在⊙O 上找出一点D ,使AD=AC (自己完成作图,并证明你的结论).mBDCAOB CAO【试题答案】 一、选择题:1. A .2. D .3. C .4. D5. D6. A .7. B .8. B .9. C . 10. A . 11. B . 12. D . 二、填空题:13. 10°,80°或100° 14. 4. 15. 40°或160°.16. 35°17. 1cm . 18. 8cm .19. 70°.20. 1cm 或5cm .21. 1,2,3,4.22. 3πcm 2 三、解答题:23. 解:连结AB .∵∠P=60°,AP=BP , ∴△APB 为等边三角形.AB=PB=2cm ,PB 是⊙O 的切线,PB ⊥BC , ∴∠ABC=30°, ∴AC=AB ²tan30°=2²33=233.24. 解:扇形的半径为12,则1O ⊙r =6,设⊙O 2的半径为R . 连结O 1O 2,O 1O 2=R+6,OO 2=12-R .∴Rt △O 1OO 2中,36+(12-R )2=(R+6)2, ∴R=4. S 扇形=14π·122=36π,S ′=12π·62=18π,S ″=12π²42=8π. ∴S 阴=S 扇形-S ′-S ″=36π-18π-8π=10π.25. 11.26. 答案:CD 2=CB ²CA 或∠CDB=∠A . 27. 解:(1)证明:如图,∵AB 与半径相等,∴∠OAB=60°,∠OBA=60°.∵BC=OB=AB ,∴∠BAC=30°, ∴∠OAC=90°,∴AC 与⊙O 相切.(2)①延长BO 交⊙O 于D ,则必有AD=AC . 证明:∵∠BOA=60°,OA=OD , ∴∠D=30°.又∵∠C=30°,∴∠C=∠D ,∴AD=AC .②作∠OAB 的角平分线交⊙O 于D ,则AD=AC证明略。

浙教版七年级下册第三章事件的可能性练习及答案班级学号姓名一、细心选一选(每小题3分,共36分)1.数学老师抽一名同学回答问题,,抽到女同学是………………………………( )A.必定事件B.不确定事件C.不可能事件D.无法判定2.在一个装有黑色围棋的盒子中摸出一颗棋子,摸到一颗白棋是………………( )A.必定事件B.不确定事件C.不可能事件D.无法判定3.从一副扑克牌中任意抽出一张,可能性相同的的是……………………………( )A.大王与黑桃B.大王与10C.10与红桃D.红桃与梅花4.一个袋中装有8只红球,每个求出颜色外都相同,人一摸一个球,则…… ( )A.专门可能摸到红球B. 可能摸到红球C. 一定摸到红球D.不大可能摸到红球5.从一副扑克牌(除去大王)中任取一张,抽到的可能性较小的是………………( )A.红桃5B.5C.黑桃D.梅花5或86. 下列事件中,不确定事件是……………………………………………………( )A.在空气中,汽油遇上火就燃烧B.向上用力抛石头,石头落地C.下星期六是晴天D.任何数和零相乘,积仍为零7.甲袋中装着2只红球、8只白球,乙袋中装着8只红球、2只白球。
假如你想从两个口袋中取出一只白球,成功机会较大的是………………………………………( )A.甲袋B.乙袋C.甲、乙两个口袋一样D.无法确定8.如图是一个能够自由转动的转盘,转动那个转盘,当它停止转动时,指针最可能停留的区域是………………………………………( )A.1B. 2C. 3D. 49.掷一枚平均的骰子,骰子停止转动后朝上一面的点数显现以下情形的概率最小的是…………………………………………………………………………………( )A.偶数B.奇数C.比5小的数D.数610.从1到9这9个自然数中任取一个,是2的倍数的概率是………………( )A.39B.49C.59D.111. 从1到9这9个自然数中任取一个,是2的倍数或是3的倍数的概率是……( )A. 19B.29C.23D.5912.一个盒子里装有若干个红球和白球,每个球除颜色以外都相同.5位同学进行摸球游戏,每位同学摸10次(摸出1球后放回,摇匀后再连续摸),其中摸到红球数依次为8,5,9,7,6,则估量盒中红球和白球的个数是……………………………( )A.红球比白球多B.白球比红球多C.红球、白球一样多D.无法估量二、用心填一填:(每小题3分,共18分)13.围棋有黑、白两种棋子,混合在一起后,随意从中摸出3个棋子,正好颜色相同,这是事件(填“必定”、“不可能”或“不确定”)14.从装有8个红球、2个白球的袋子中随意摸出一个球,摸到可能性较小的是球.15.袋中装有10个小球,颜色为红、白、黑三种,除颜色外其他均相同。




浙教版九年级下科学第三章3.1-3.3练习以及答案解析一、单选题1.饮食安全与人体健康息息相关,下列事例不属于非细菌性食物中毒的是()A.食用残留农药的蔬菜引起中毒B.食用含亚硝酸盐的腌制品引起中毒C.食用毒蘑菇引起中毒D.食用超过保质期的月饼引起中毒2.健康是人生最宝贵的财富之一。
下列关于现代生活与人类健康的叙述,正确的是()A.感冒药是家庭常备药物,过期一两周仍可服用B.香烟中的尼古丁、焦油等会损坏人体的呼吸系统C.吸毒能使人在短时间内极度兴奋,可以少量使用毒品D.遇到好玩的网络游戏,可以废寝忘食地连续数日去攻关3.食品卫生与身体健康密切相关。
下列做法会导致食品对人体健康有害的是()A.用石灰水保存鸡蛋B.蒸馒头加适量纯碱C.在食品中添加防腐D.在食盐中添加适量碘元素4.酒后驾车明显表现为反应慢、动作不协调,容易导致交通事故。
这主要是因为酒精影响驾驶员的()A.脊髓、肝脏B.眼睛、心脏C.脑干、肺D.大脑、小脑5.体育课后口渴难耐,如果四位同学回到教室发现每个人只有半杯水,从各位的对话中,你认为需要加强心理健康教育的同学应该是( )A.“哈,还有半杯水,真不错!”B.“太渴了,有水喝真好!”C.“OK!半杯水也能解决问题.”D.“哎,真倒霉!怎么只有半杯水”6.在德州市春季中小学运动会上,多项记录被“尘封”,难以打破,学生身体素质总体下滑。
关于此现象的观点叙述,正确的是( )A.只要吃的好,身体素质就好B.科学文化素质比身体素质更重要C.实施健康计划,坚持阳光体育活动D.体育竞技是运动员的职责,与我们无关7.下列各项中,哪一个的健康状况最理想?( )A.对人生悲观失望,不存在任何幻想的小毕B.无病,精神萎靡不振的阿菊C.虽然没钱,但乐于助人的小红D.为了达到目的不择手段的小明8.人的身体、心理和社会适应性等方面都应该保持健康良好的状态。
下列做法中,不利于健康的是( )A.进行体育锻炼,增强身体体质B.遇到烦心事,就抽烟、喝酒解闷C.学习与他人相处、合作和交流D.发现食品过了保质期就不食用9.在日常生活中,下列行为习惯不利于健康的是( )①常换毛巾和牙刷②常到街边小摊吃零食③蒙着被子睡大觉④借酒解愁A.①②③B.①②④C.①③④D.②③④10.小青同学得了流感,他自己到药店里买了一些头孢类抗生素,可是吃了几天后并没有减轻鼻塞、头痛等症状,其原因可能是()A.这种抗生素药力不够B.抗生素失效了C.流感病毒有很强的抗药性D.抗生素不能抑制病毒的生长和繁殖11.在公共场合咳嗽或打喷嚏时,口腔或鼻腔液滴喷出2米以外,对他人带来最大危害是()A.在公共场合咳嗽或打喷嚏不礼貌,影响他人B.在公共场合咳嗽或打喷嚏,液滴容易溅到别人衣服上,不文明C.在公共场合咳嗽或打喷嚏,液滴中细菌等会四处散布,危害他人健康D.以上说法都正确12.青霉素为20世纪医学上的重大发现,小明列出了以下几项有关青霉素的知识,其中有错误的是()A.青霉素是青霉分泌的一种抗生素B.青霉素能使细菌的细胞壁变薄C.青霉素是由多种成分组成的混合物,其中一些对细菌是致命的D.青霉素是治疗细菌性疾病的特效药,目前青霉素类抗生素还在使用13.幽门螺旋杆菌能损伤胃黏膜造成胃炎和胃溃疡,可通过饮食等途径传播给健康人,对此正确的认识是()A.幽门螺旋杆菌与酵母菌都属于细菌B.幽门螺旋杆菌引起的胃炎不是传染病C.聚餐使用“公筷”可以防止传染幽门螺旋杆菌D.抗生素对抑制幽门螺旋杆菌没有效果14.手足口病是一种常见的儿童传染性疾病,CA16病毒感染是主要致病原因。

高中物理第三章相互作用-力必考考点训练单选题1、躺椅在生活中用途广泛,图甲中人双脚离地而坐,图乙中人双脚着地而坐。
两图中位于水平地面上的人和椅子都保持静止状态,下列说法正确的是()A.甲中人对躺椅的压力是由椅子发生形变产生的B.甲中人不同的躺姿会改变躺椅对人的合力C.乙中人脚用力蹬地时,躺椅对人背部摩擦力一定沿椅面向上D.乙中人脚用力蹬地时,脚对地的摩擦力大小与躺椅对地的摩擦力大小相等答案:DA.甲中人对躺椅的压力是由人发生形变产生的,A错误;B.甲中人不同的躺姿,躺椅对人的作用力均与人的重力大小相等,方向相反,B错误;C.乙中人脚用力蹬地时,如果人的背部相对于躺椅有向上运动的趋势时,人背部所受摩擦力一定沿椅面向下,C错误;D.以人和躺椅整体为研究对象.乙中人脚用力蹬地时,地对脚的摩擦力和地对躺椅的摩擦力等大反向,由牛顿第三定律知:脚对地的摩擦力大小和地对脚的摩擦力大小相等,可得脚对地的摩擦力大小与躺椅对地的摩擦力大小相等,D正确。
故选D。
2、图甲是我国自主研发的世界第一台高温超导高速磁悬浮列车,这台车的设计速度高达每小时620公里,被称赞为“世界上跑得最快的列车”。
图乙是某磁悬浮列车的原理图。
轨道P的磁场与车体Q的磁场之间产生排斥力使车体悬浮。
已知P对Q的排斥力为F1,Q对P的排斥力为F2,则()A.F1大于F2B.F1小于F2C.F1和F2是一对平衡力D.F1和F2是一对作用力与反作用力答案:DF1和F2是车体与轨道之间的相互作用力,大小相等、方向相反,作用在不同的物体上。
故选D。
3、如图所示,俄国寓言故事《天鹅、大虾和梭鱼》中说:“有一次,天鹅、大虾和梭鱼,想把一辆大车拖着跑,他们都给自己上了套,拼命地拉呀拉呀,大车却一动也不动了。
”下列对这段话理解正确的是()A.因为大车太重了,所以不动B.因为天鹅、大虾和梭鱼的力气太小了,所以拉不动大车C.大车其实运动了,只是因为移动距离太小,看不出来D.因为大车所受的合力为零答案:D大车处于静止状态,故大车所受合力为零。