当前位置：文档之家 › 自动控制原理-相位超前校正

自动控制原理-相位超前校正

  • 格式：ppt
  • 大小：5.87 MB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

自动控制原理7-2频率域中的无源串联超前校正

自动控制原理7-2频率域中的无源串联超前校正

可能引入噪声
由于无源元件的局限性， 无源串联超前校正器可能 会引入额外的噪声，影响 系统性能。
未来研究方向与展望
新型无源元件研究
随着科技的发展，新型的无源元件不断涌现，如薄膜电阻、 高温超导材料等，为无源串联超前校正器的设计提供了新 的可能性。
集成化与微型化研究
随着微电子技术的发展，无源串联超前校正器的集成化与 微型化成为可能，这将有助于减小系统体积和重量，提高 系统的便携性和可靠性。
提高系统性能的实例
温度控制系统
在温度控制系统中，通过串联超 前校正器，可以减小系统的调节 时间和超调量，提高温度控制的 稳定性和准确性。
伺服控制系统
在伺服控制系统中，串联超前校 正器能够提高系统的跟踪性能和 抗干扰能力，减小误差并提高控 制精度。
串联超前校正器的比较与选择
参数选择
串联超前校正器的参数选择需要根据具体的应用场景和控制要求进 行优化，以达到最佳的系统性能。
03
无源串联超前校正器具有结构简单、易于实现的特点，适用于各种线 性控制系统。
ቤተ መጻሕፍቲ ባይዱ04
频率域中的无源串联超前校正方法可以与其他控制策略相结合，进一 步优化系统的性能。
对实际应用的指导意义
在实际应用中，可以根据系统的具体需求，选择合适 的无源串联超前校正器参数，以获得更好的系统性能。
输标02入题
对于一些具有特定要求的控制系统，如快速响应、高 精度和高稳定性的系统，可以采用频率域中的无源串 联超前校正方法来改善其动态性能。
04 无源串联超前校正器的应 用实例
在控制系统中的应用
控制系统稳定性增强
抑制高频噪声
通过串联超前校正器，可以改善控制 系统的相位裕度，提高系统稳定性。

自动控制原理3(超前校正网络).

自动控制原理3(超前校正网络).

-60
b
例6-5图2
180(s+1) G(s) = s(s/6+1)(50s+1)(0.01s+1)
√
42.8o h =27.7dB
3.29 c
ts=1.65s
零阶保持器
T=0.2
T=0.4
T=0.8
T=3
Z域等效变换
[1(t)+t]*=[1(t)]*+[t]*
*
闭环实极点分布与相应的动态响应形式
Im
Z平面
0
1
Re
闭环复极点分布与相应的动态响应形式 Im
–1
1
Re
o
设计校正网络使图示系统
o
k v = 30, ≥40 , hdB ≥10dB, c ≥2.3
ω= 2.7时 φo(2.7)= –133o
3 .7 s + 1 G c (s ) 41s + 1
OK
45.1
2.39 c
o
h 14.2dB
迟后-超前校正网络
G*(s)=G*(s+jnωs)
[E*(s)G1(s) G2(s)]*=E*(s)[G1(s) G2(s)]*
1 * 设G1(s)G (s)=G (s) ， 则有： 2 G (s ) G (s + jn s ) n 1 T * [E (s + jns )G(s + jns )] [E*(s)G(s)]*= T n
* s
1 1 G (s + jks ) 1 G[s + j(n + k )s ] *G[s + jms ] [E (s )G (s + jn )] T∵ n m E (s)与∑无关， TT

自动控制原理(6-2)

自动控制原理(6-2)

④ 令超前校正装置的最大超前角φm=φ0，并按下式 令超前校正装置的最大超前角φ 计算校正网络的系数a 计算校正网络的系数a值：
1+sinϕm a= 1−sinϕm
如φm>60°，则应考虑采用有源校正装置或两级 60° 超前网络串联； ⑤ 将校正网络在ωm处的增益定为 10lga， 同时确定未 将校正网络在ω 处的增益定为10lga 校正系统Bode 曲线上增益为－10lga 校正系统 Bode曲线上增益为－ 10lga 处的频率即为 校正后系统的剪切频率 ωc =ωm。
Rf R 1
R + R2 a= 1 >1 R2
=−
Rf [1+(R + R2 )Cs] 1
式中 K =
T = R2C
注意： 注意：负号是因为采用了负反馈的运放，如果再串联 一只反相放大器即可消除负号。
超前网络的频率特性为： Gc ( jω) = 1+ jωaT
1+ jωT
20 lg Gc / dB
0 − 20lg12 = −40 lgω 1 −lg1 c
即得
ωc1 = 12 = 3.46s−1
L(ω )(dB)
40 30 20 10 0 -10 -20 -30 0.1 0.2 0.5 1 10 -20dB/dec Go 20lg12 -40dB/dec 20dB/dec Gc
ω
G
ω1 ωc1 ωc 2
三、相位超前校正
1.相位超前校正装置的传递函数和Bode图 1.相位超前校正装置的传递函数和 相位超前校正装置的传递函数和Bode图 相位超前校正装置可用如图6 相位超前校正装置可用如图6-9所示的电气网络实现。
图6-9 相位超前校正装置

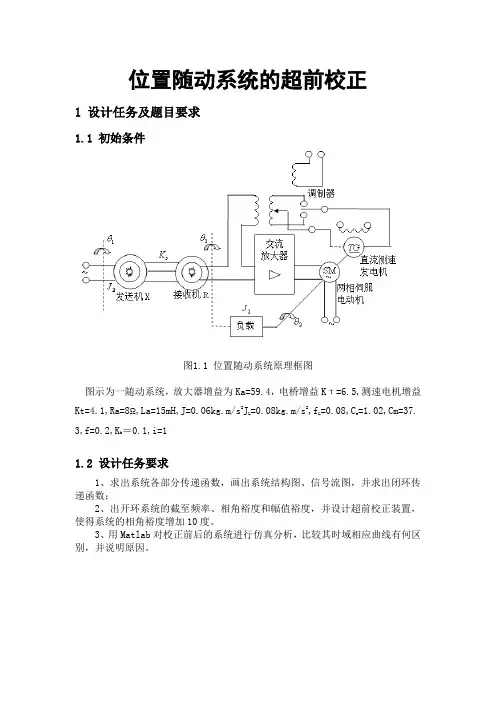
《自动控制原理》课程设计位置随动系统的超前校正

《自动控制原理》课程设计位置随动系统的超前校正

位置随动系统的超前校正1 设计任务及题目要求1.1 初始条件图1.1 位置随动系统原理框图图示为一随动系统，放大器增益为Ka=59.4，电桥增益Kτ=6.5,测速电机增益Kt=4.1,Ra=8Ω,La=15mH,J=0.06kg.m/s2JL =0.08kg.m/s2,fL=0.08,Ce=1.02,Cm=37.3,f=0.2,Kb＝0.1,i=11.2 设计任务要求1、求出系统各部分传递函数，画出系统结构图、信号流图，并求出闭环传递函数；2、出开环系统的截至频率、相角裕度和幅值裕度，并设计超前校正装置，使得系统的相角裕度增加10度。

3、用Matlab对校正前后的系统进行仿真分析，比较其时域相应曲线有何区别，并说明原因。

2 位置随动系统原理2.1 位置随动系统工作原理工作原理：该系统为一自整角机位置随动系统，用一对自整角机作为位置检测元件，并形成比较电路。

发送自整角机的转自与给定轴相连；接收自整角机的转子与负载轴（从动轴）相连。

TX 与TR 组成角差测量线路。

若发送自整角机的转子离开平衡位置转过一个角度1θ，则在接收自整角机转子的单相绕组上将感应出一个偏差电压e u ，它是一个振幅为em u 、频率与发送自整角机激励频率相同的交流调制电压，即sin e em u u t ω=⋅在一定范围内，em u 正比于12θθ-，即12[]em e u k θθ=-，所以可得12[]sin e e u k t θθω=-这就是随动系统中接收自整角机所产生的偏差电压的表达式，它是一个振幅随偏差（12θθ-）的改变而变化的交流电压。

因此，e u 经过交流放大器放大，放大后的交流信号作用在两相伺服电动机两端。

电动机带动负载和接收自整角机的转子旋转，实现12θθ=，以达到跟随的目的。

为了使电动机转速恒定、平稳，引入了测速负反馈。

系统的被控对象是负载轴，被控量是负载轴转角2θ，电动机施执行机构，功率放大器起信号放大作用，调制器负责将交流电调制为直流电供给直流测速发电机工作电压，测速发电机是检测反馈元件。

自动控制原理--滞后超前校正与PID校正

自动控制原理--滞后超前校正与PID校正

G s 1 T1s 1 aT2s
1 T1s 1 T2s
°
其中：
E1
1,a 1且.a 1 °
C1
R1
°
R2
E2
C2
°
Phase (deg); Magnitude (dB)
To: Y(1)
Bode Diagrams
From: U(1) 0
-5
-10
-15
-20 50
0
-50
ቤተ መጻሕፍቲ ባይዱ
10-4
10-3
10-2
应 50o 处的g 0.082 rad s，相应幅频特性为Lg 45.5db
据此，由20log KP Lg 45db 求得：KP 0.0053 。
为减少对相角裕量校正效果影响，PI控制器转折 频率 1 KI KP 选择远离g 处，取1 g 10 0.0082 rad s 求得：KI 0.000044 。于是，PI控制器传递函数
• PID调节器是一种有源校正网络，它获得了 广泛的应用，其整定方法要有所了解。
系统校正的设计方法
分析法
综合法
分析法：
选择一种校正装置
设计装置的参数
校验
综合法： 设计希望特性曲线 校验
确定校正装置的参数
期望特性综合设计方法：
1、先满足精度要求，并画出原系统Bode图； 2、根据Bode定理，系统有较大的相位裕量，幅频特性在剪切频
G( j)
1
j2T( jT 1)
63.5
0.707
二阶最佳指标:
L() -20dB/dB
1/2T
()
p % 4.3%
180°
ts (6 ~ 8)T
1/T

自动控制理论课程设计——超前校正环节的设计

自动控制理论课程设计——超前校正环节的设计

超前校正环节的设计一、课设的课题已知单位反馈系统开环传递函数如下：()()()10.110.3O kG s s s s =++试设计超前校正环节，使其校正后系统的静态速度误差系数6v K ≤，相角裕度为45度，并绘制校正前后系统的单位阶跃响应曲线，开环Bode 图和闭环Nyquist 图。

二、课程设计目的1. 通过课程设计使学生更进一步掌握自动控制原理课程的有关知识，加深对内涵的理解，提高解决实际问题的能力。

2. 理解自动控制原理中的关于开环传递函数，闭环传递函数的概念以及二者之间的区别和联系。

3. 理解在自动控制系统中对不同的系统选用不同的校正方式，以保证得到最佳的系统。

4. 理解在校正过程中的静态速度误差系数，相角裕度，截止频率，超前(滞后)角频率，分度系数，时间常数等参数。

5. 学习MATLAB 在自动控制中的应用，会利用MA TLAB 提供的函数求出所需要得到的实验结果。

6. 从总体上把握对系统进行校正的思路，能够将理论操作联系实际、运用于实际。

三、课程设计思想我选择的题目是超前校正环节的设计，通过参考课本和课外书，我大体按以下思路进行设计。

首先通过编写程序显示校正前的开环Bode 图，单位阶跃响应曲线和闭环Nyquist 图。

在Bode 图上找出剪切频率，算出相角裕量。

然后根据设计要求求出使相角裕量等于45度的新的剪切频率和分度系数a 。

最后通过程序显示校正后的Bode 图，阶跃响应曲线和Nyquist 图，并验证其是否符合要求。

四、课程设计的步骤及结果 1、因为()()()10.110.3O k G s s s s =++是Ⅰ型系统，其静态速度误差系数Kv=K,因为题目要求校正后系统的静态速度误差系数6v K ≤，所以取K=6。

通过以下程序画出未校正系统的开环Bode 图，单位阶跃响应曲线和闭环Nyquist 图： k=6;n1=1;d1=conv(conv([1 0],[0.1 1]),[0.3 1]); [mag,phase,w]=bode(k*n1,d1); figure(1);margin(mag,phase,w); hold on;figure(2)s1=tf(k*n1,d1); sys=feedback(s1,1); step(sys); figure(3);sys1=s1/(1+s1) nyquist(sys1); grid on; 结果如下：M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramFrequency (rad/sec)图1--校正前开环BODE 图由校正前Bode 图可以得出其剪切频率为 3.74，可以求出其相角裕量0γ=1800-900-arctan0.10c ω-arctan0.30c ω=21.20370。

自控原理第六章

自控原理第六章

ui（t）
R2 C
－
Ts 1 Gc ( s) Ts 1
2013-8-1 《自动控制原理》第六章
无源滞后网络
ቤተ መጻሕፍቲ ባይዱ
22
极点分布如图所示，极点总位于零点的右边，具体位置与 β有关。若T值够大，则构成一对开环偶极子，提高了系统 的稳态性能。
1 1 滞后网络的零点 zc ，极点 pc ，零、 T T
2013-8-1 《自动控制原理》第六章 15
第二节 常用校正装置及其特性
一、超前校正装置 C
又称微分校正，分为无源超 前网络和有源超前网络
+
R1 R2
+
U 0 ( s) R2 Gc ( s ) U i ( s) R1 R2
R2 R1 R2
(a 1) T R1C
R1Cs 1 ui(t) R2 R1Cs 1 R1 R2 -
2013-8-1 《自动控制原理》第六章 17
另外从校正装置的表达式来看，采用无源超前校正 装置进行串联校正时，系统的开环增益要下降倍，为了 补偿超前网络带来的幅值衰减，通常在采用无源RC超前 校正装置的同时串入一个放大倍数Kc=1/ 的放大器。超 前校正网络加放大器后，校正装置的传递函数
Ts 1 Gc ( s) Ts 1
2013-8-1
《自动控制原理》第六章
1
第一节
控制系统校正的基本概念
一、校正的一般概念
自动控制系统工程研究 分析：建立系统的数学模型并计算其性能指标 设计：根据各项性能指标来合理的选择控制方案 和结构形式 系统的校正 用添加新的环节去改善系统性能的过程称为系统的 校正，所添加的环节称为校正装置。

6-2 超前-滞后校正

6-2 超前-滞后校正
16
1
2.65
引入超前校正网络的传递函数：
1 α Ts 1 1 0.378s 1 G c (s) α Ts 1 3 0.126s 1
（4）引入 倍的放大器。为了补偿超前网络造成的衰减，引 入倍的放大器， 3 。得到超前校正装置的传递函数
1 0.378s 1 0.378s 1 α G 0 (s) 3 3 0.126s 1 0.126s 1
《自动控制原理》
—— 频率特性法（6－2）
（超前校正）
1
6.3 频率域中的无源串联超前校正 三个频段的概念
L() dB
15

c

15
低频段
中频段
高频段
2
校正方法通常有两种： 1. 分析法。实际上是一种试探的方法，可归结为： 原系统频率特性+校正装置频率特性=希望频率特性 G0(jω) + Gc(jω) = G(jω) 从原有的系统频率特性出发，根据分析和经验，选 取合适的校正装置，使校正后的系统满足性能要求。 2. 综合法。这种方法的基本可归结为： 希望频率特性原系统频率特性=校正装置频率特性 G(j) G0(j) = Gc(j) 根据系统品质指标的要求，求出满足性能的系统开 环频率特性，即希望频率特性。再将希望频率特性与 原系统频率特性相比较，确定校正装置的频率特性。
17
通过超前校正分析可知： （1）提高了控制系统的相对稳定性——使系统的稳定 裕量增加，超调量下降。 工业上常取α=10，此时校正装置可提供约550的超前 相角。为了保证系统具有300600的相角裕量，要求校 正后系统ωc处的幅频斜率应为－20dB/dec，并占有一定 的带宽。 (2) 加快了控制系统的反应速度——过渡过程时间减 小。由于串联超前校正的存在，使校正后系统的c、r 及b均变大了。带宽的增加，会使系统响应速度变快。 （3）系统的抗干扰能力下降了—— 高频段抬高了。 （4）控制系统的稳态性能是通过步骤一中选择校正后 系统的开环增益来保证的。

自动控制原理6.3 串联校正

自动控制原理6.3 串联校正


10lg
1

，所对应的

就是

' c
，且 m


'。
c
§6—3 串联校正
4） 1

1 T
，m

1
T
，2

1
T
,
1
m
c' ,
2

m

c'
s
1
Gc s
1
s
1

Ts 1
Ts 1
2
5）画 Lc、L'、c、 ' 曲线。


1 sin 350 1 sin 350

1 0.57 1 0.57
0.27
则10lg 1


5.6db ，在L 上量
5.6db
所对
L
0
( )
db
-20 -20
1 c
1
'
2
c
+20
-40
-40
m
0
90
0
m '

校正装置

校正后系统

Gk s

100.45s 1 ss 10.12s 1
§6—3 串联校正
' 1800 c1 1800 900 tg10.45 4.3 tg14.3
tg1 0.12 4.3 900 62.70 76.90 27.30 48.50 450
3、步骤：
1）根据ess确定K；
2）根据K、υ绘制原系统的 L、，确定未校正

自动控制原理--基于频率特性法的串联超前校正

自动控制原理--基于频率特性法的串联超前校正
超前校正会使系统瞬态响应的速度变快。校正后系统的截 止频率增大。这表明校正后，系统的频带变宽，瞬态响应 速度变快；但系统抗高频噪声的能力变差。对此，在校正 装置设计时必须注意。
超前校正一般虽能较有效地改善动态性能，但未校正系统 的相频特性在截止频率附近急剧下降时，若用单级超前校 正网络去校正，收效不大。因为校正后系统的截止频率向 高频段移动。在新的截止频率处，由于未校正系统的相角 滞后量过大，因而用单级的超前校正网络难于获得较大的 相位裕量。
前 180 90 tan1(0.8 3.54) 19.4
计算超前网络参数α和T：方法一 选取校正后系统的开环截止频率
G(s) K s(0.8s 1)
m c 5rad / s
在校正后系统的开环截止频率处原系统的幅值与校正 装置的幅值大小相等、符号相反
Lo (c)
20
lg
10
c 0.8c
开环对数渐进幅频特性如伯特图中红线所示。校正后系 统的相位裕量为
" 180 90 tan1 4 tan1 2 tan1 0.5 50.9
满足系统的性能指标要求。
基于上述分析，可知串联超前校正有如下特点：
这种校正主要对未校正系统中频段进行校正，使校正后中 频段幅值的斜率为-20dB/dec，且有足够大的相位裕量。
根据对截止频率 c的要求，计算超前网络参数α和T；
关键是选择最大超前角频率等于要求的系统截止频率，即
m c 以保证系统的响应速度，并充分利用相角超前特性。显然，
m c成立的条件是 Lo (c) 10 lg
而
m
T
1
求出T
求出α
画出校正后系统的波特图并验证已校正系统的相角裕度。
用频率法对系统进行串联超前校正的一般步骤可归纳为：

自动控制原理 相位超前校正

自动控制原理 相位超前校正

用频率法设计超前网络的步骤：
（1）根据稳态误差要求，确定开环增益K。 （2）根据已确定的开环增益K，绘制原系统的对数频率特性曲 线 L0 (),0 () ，计算其稳定裕度 0 , Lg 0 。
（3）确定校正后系统的截止频率 c 和网络的 值。 ① 若事先已对校正后系统的截止频率 c 提出要求，则可按要 求值选定 c 。然后在Bode图上查得原系统的 L0 (c ) 值。 取 m c ，使超前网络的对数幅频值 Lc (m（正值）与 ) （负值）之和为0，即令 L0 (c )
1 d ( ) 由 0 可求得最大超前角频率为 m T d
由于 1 1 T , 2 1 (T ) ，故可表示为 m 12 网络的最大超前角正好出现在两个转折频率 1和 2 的几何中 心，网络的最大超前角为
1 1 m arctan arcsin 1 2
Gc (s) Ts 1 Ts 1
T
1
m
N
满足性能指标要求？
Y
结束
例：设控制系统如图所示。若要求系统在单位斜坡输入信号作 用时， ① 稳态误差 ess 0.1， ② 相角裕度 45， ③ 幅值裕度 Lg 10dB ，试设计串联无源超前网络。
R (s )

K s ( s 1)
相频特性表明：在 0 的所有频率下，均有 ( ) 0，即网 络的输出信号在相位上总是超前于输入信号。
在转折频率 1 1 T 和 2 1 (T )之间存在着最大值 m ，根据超 前网络的相频特性表达式，即
( ) arctanT arctanT
L0 (c ) 10lg
进而求出超前网络的 值。
1

自动控制原理 第五章第十二节频率法串联校正——超前校正

自动控制原理 第五章第十二节频率法串联校正——超前校正

① 由 e*ss
K
② 由 G0 (s) L0 (w ) wc0 g 0 wc0 , g 0 均不足
③ 确定 m = g * − g 0 + (5 ~ 10)
a = 1 + sinm , 10lg a 1 − sinm
④ 作图设计 A − B − C − D Gc (s)
⑤ G(s) = Gc (s) G0 (s) 验算是否满足要求
g = 180 + (wc1 )
= 180 + arctan 5.16 − 90 − arctan 5.16 − arctan 5.16
1.94
13.73
= 180 + 69.4 − 90 − 79 − 20.6 = 58.8 ( 60)
5.12 频率法串联校正——超前校正
例1
G(s) = K s(s + 1)
− +
1 1
a = 1 + sinm 1 − sinm
● 超前网络特点：相角超前，幅值增加
● 最有效的 a (4, 10)
● 一级超前网络最大超前角为60º
5.12 频率法串联校正——超前校正
2. 串联超前校正 实质 — 利用超前网络相角超前特性提高系统的相角裕度
超前校正步骤 (设给定指标 e*ss , wc* , g *)
= 1 aTs + 1 a Ts + 1
a = R1 + R2 1 R2
T = R1R2C R1 + R2
a Gc(s)
=
aTs + 1 Ts + 1
=
Gc (s)
5.12 频率法串联校正——超前校正
1. 超前网络特性

自动控制原理7-2频率域中的无源串联超前校正..

自动控制原理7-2频率域中的无源串联超前校正..
1
3. 最大负相移发生在转折 1 频率 T 与 β1T 的几何中点。
m arc sin
β 1 β 1 arc sin 1 β 1β
0
T

m
1
T
20

20 lg
( )
0
β
1 sin (- m ) 1 - sin (- m )


m
90
9
例1 若单位反馈系统开环传递函数为
1
α 1 2 α
1 sin m 1 - sin m
α 1
α
12
10lg
50
10
8 6 10lg(dB)
m
40
30
20
10
4
2
0
1 3 5 7 9
0

11 13 15 17
19
当α大于15以后， m的变化很小，α一般取115之间。
6
例1 若单位反馈系统开环传递函数为

0
90
180
0 20
12
(2) 确定校正后系统的增益剪切频率c。 在此频率上，系统要求的相位裕量应等于要求的相 位裕量再加上(50120)---补偿迟后校正网络本身在c 处的相位迟后。 确定c。 原系统在 c0 处的相角衰减得很快，采用超前校正作 用不明显，故考虑采用迟后校正。现要求校正后系统 的 γ 40 0 ，为了补偿迟后校正网络本身的相位迟后， 需再加上50120的补偿角，所以取 Δγ=400+(50—120)=520 (补偿角取120) 在伯德图上可找得，在=0.5s-1附近的相位角等于 -128 0 ( 即相位裕量为 52 0 ) ，故取此频率为校正后系统 的增益剪切频率。即： ωc=0.5s-1

自动控制原理第六章第三讲超前网络及其串联校正

自动控制原理第六章第三讲超前网络及其串联校正
由上式可求出a ，再由
根据截止频率
的要求，计算超前网络参数a和T；
求出Ｔ；
即可得超前网络的传递函数：
则已校正系统的传递函数为：
绘出校正后的对数幅频特性：
验证已校系统的相角裕度 ，若不满足 要求，应重选 ,一般使其增大。
步骤：
确定开环增益K（根据稳态误差的要求）；
(
s
E
)
(
1
s
G
)
(
s
G
)
(
2
s
G
)
(
s
C
)
(
s
G
r
+
系统输出：
系统误差：
当：
时，
对输入的 误差全补偿条件
说明： 以上结论仅在理想条件下成立：
无论是输出响应完全复现输入或是完全不受扰动影响, 都是在传递函数零、极点对消能够完全实现的基础上得到的。
由于控制器和对象都是惯性的装置, 故G1(s)和G2(s)的分母多项式的s阶数比分子多项式的s阶数高。 据补偿式可见, 要求选择前馈装置的传递函数是它们的倒数, 即Gr(s)或Gn(s)的分子多项式的s阶数应高于其分母多项式的s阶数, 这就要求前馈装置是一个理想的(甚至是高阶的)微分环节。
滞后-超前网络贡献的幅值衰减的最大值
由相角裕度要求，估算网络滞后部分的交接频率 ， 得：
01
结束
02
绘制已校正系统Bode图，校验性能指标
03
反馈校正
开环传函为：
工作原理 设图中局部反馈回路为G2c(s)， 其频率特性为 ：
反馈校正、复合校正基本原理
整个反馈回路的 传递函数等效为：
理想的微分环节实际不存在, 所以完全实现传递函数的零、极点对消在实际上也是做不到的。

自动控制原理实验系统超前校正实验报告

自动控制原理实验系统超前校正实验报告

实验五系统超前校正（4学时）本实验为设计性实验一、实验目的1．了解和观测校正装置对系统稳定性及动态特性的影响。

2．学习校正装置的设计和实现方法。

二、实验原理工程上常用的校正方法通常是把一个高阶系统近似地简化成低阶系统，并从中找出少数典型系统作为工程设计的基础，通常选用二阶、三阶典型系统作为预期典型系统。

只要掌握典型系统与性能之间的关系，根据设计要求，就可以设计系统参数，进而把工程实践确认的参数推荐为“工程最佳参数”，相应的性能确定为典型系统的性能指标。

根据典型系统选择控制器形式和工程最佳参数，据此进行系统电路参数计算。

在工程设计中，经常采用二阶典型系统来代替高阶系统（如采用主导极点、偶极子等概念分析问题）其动态结构图如图7-1所示。

同时还经常采用“最优”的综合校正方法。

图7-1二阶典型系统动态结构图二阶典型系统的开环传递函数为)2()1()(2nnssTssKsGξωω+=+=闭环传递函数2222)(nnnsssωξωω++=Φ式中KTTKn21,==ξω，或者nn TKξωξω21,2==二阶系统的最优模型（1）最优模型的条件 根据控制理论，当22707.0==ξ时，其闭环频带最宽，动态品质最好。

把22=ξ代入KT21=ξ得到，KT T K 21,21==或，这就是进行校正的条件。

（2）最优模型的动态指标为%3.4%100%21/=⨯=--ξξπσe ，T t ns 3.43≈=ω三、实验仪器及耗材1．EL —AT3自动控制原理实验箱一台； 2．PC 机一台； 3．数字万用表一块 4．配套实验软件一套。

四、实验容及要求未校正系统的方框图如图7-2所示，图7-3是它的模拟电路。

图7-2未校正系统的方框图矫正后未调整电路图图7-3未校正系统的模拟电路设计串联校正装置使系统满足下述性能指标（1） 超调量%σ≤5% （2） 调节时间t s ≤1秒（3） 静态速度误差系数v K ≥20 1/秒 1．测量未校正系统的性能指标 （1）按图7-3接线；（2）加入单位阶跃电压，观察阶跃响应曲线，并测出超调量%σ和调节时间t s 。

自动控制原理自动控制系统的校正

自动控制原理自动控制系统的校正

2021/8/5
3
举一个例子说明校正的作用。 上一章的例５-７：系统的开环传递函数为
G (s)H (s)
10
s(10.0s2 )1(0.2s)
首先分析一下，未校正系统的性能
稳态误差：有一个积分环节，是I型系统．
开环增益
，稳态速度误差系数
K10 而 Kp,Ka0
Kv10
2021/8/5
4
L()
40 20dB / dec
2021/8/5
1
概述
前面介绍了分析控制系统的三种基本方法： 时域分析法、根轨迹法和频域分析法。利用这些 方法能够在系统结构和参数已经确定的情况下， 计算或估算系统的性能指标：稳态性能指标和暂 态性能指标 。这类问题是系统的分析问题。
系统分析：已知结构、参数→数学模型→动、 静态性能分析→性能指标与参数的关系
1、稳态性能指标
系统的稳态性能与开环系统的型别v与开环传递系数K有关，常用静态误差系 数衡量，误差系数越大（等效于K越大），稳态误差ess就越小。
2021/8/5
8
2、动态性能指标
1）时域指标：最大超调量Mp（反映平稳性）、调节时间ts（反映快速性）。 2）频域指标：
（1）开环频域指标： 稳定性指标：相位裕量、幅值裕量GM、中频段宽度； 快速性指标：幅值穿越频率c。 （2）闭环频域指标：Mr、ωr、ωb 3）复域指标：
2021/8/5
10
二、校正的基本方式
1. 串联校正
R(s)
-
校正装置 Gc(s)
控制器
被控对象 C(s) Go(s)
校正装置和未校正系统的前向通道的环节相串联，这
种方式叫做串联校正。
优点：结构较简单，通常将串联校正装置安置在前向通

自动控制原理超前校正课程设计

自动控制原理超前校正课程设计

目录一．设计题目二. 设计报告正文2.1 设计思路 (2)2.2根据稳态误差要求，确定K的值 (2)2.3系统的开环传递函数的结构图 (3)2.4计算待校正系统的相角裕度 (3)2.5校正后的系统传递函数 (3)2.6验证已校正系统的相角裕度 (4)三. 实现与验证编程 (4)3.1制出待校正系统的bode图和单位阶跃响应 (4)3.2算未校正系统的幅值裕量和相位裕....................... 错误!未定义书签。

3.3前校正网络的传递函数................................. 错误!未定义书签。

3.4系统的开环传递函数及伯德图........................... 错误!未定义书签。

3.5算校正后系统的幅值裕量和相位裕量..................... 错误!未定义书签。

3.5校正前后的Bode图 (10)四. 设计总结参考文献 (10)自动控制原理课程设计一．设计题目设单位负反馈系统的开环传递函数为)1()(+=s s K s G用相应的频率域校正方法对系统进行校正设计，使系统满足如下动态和静态性能：(1) 相角裕度045≥γ；(2) (2) 在单位斜坡输入下的稳态误差为1.0=sse ； (3) 系统的剪切频率小于7.5rad/s 。

要求：（1） 分析设计要求，说明校正的设计思路（超前校正，滞后校正或滞后－超前校正）；（2） 详细设计（包括的图形有：校正结构图，校正前系统的Bode 图，校正装置的Bode 图，校正后系统的Bode 图）；（3） 用MATLAB 编程代码及运行结果（包括图形、运算结果）；（4） 校正前后系统的单位阶跃响应图。

二、设计报告正文2.1设计思路超前校正装置具有相位超前作用,它可以补偿原系统过大的滞后相角，从而增加系统的相角裕度和带宽，提高系统的相对稳定性和响应速度。

超前校正通常用来改善系统的动态性能，在系统的稳态性能较好而动态性能较差时，采用超前校正可以得到较好的效果。

自动控制原理6 第一节超前校正

自动控制原理6 第一节超前校正

Gc (s)
1 Ts，
1 Ts
1
L() 20lg
1 (T)2
20lg 1 (T)2
() tg1T tg1T
m
1
T
频率特性的主要特点是：
所有频率下相频特
性为正值，且在频率
m处相频特性()存 在最大相位超前量m。
m发生在对数刻度的
坐标中1/T与1/( T )
的几何中点。
① 求m
令 d() 0，可得 d
20 lg 1 2T 2 20 lg 1 T 2
T 2
T 2
20 lg (1 ) 1
20 lg 10 lg
-90
1
m
1
T
T
19
三、基于伯德图的相位超前校正
R - Gc
C
G
图中，Gc为校正装置，G为 对象。
基于伯德图设计超前校正装置的步骤如下：
① 求出满足稳态性能指标的开环增益K值；
1
二、校正方式
按照校正装置在系统中的连接方式，控制系统校正方式可 分为串联校正、并联校正、前馈校正和复合校正四种。
⒈串联校正装置一般串联于系统前向通道之中系统误差检 测点之后和放大器之前。
R(s) E(s) Gc (s)
-
GP (s) C(s)
B(s)
H (s)
2
⒉并联校正装置接在系统局部反馈通道之中，并联校正也 称为反馈校正。
这里主要介绍基于伯德图的单输入-单输出的线性 定常控制系统的设计和校正的方法和步骤。
6
第一节 用频率法设计串联校 正器的基本概念
9
Im
-1
Re
K2
K1
10
第二节 相位超前校正

自动控制原理与系统第6章 自动控制系统的校正

自动控制原理与系统第6章 自动控制系统的校正
③ 在信号输入处由电容器 构成C0的微分环节很小。 高频很容易进入，而很多干扰信号都是高频信号，因 此比例微分校正容易引入高频干扰，这是它的缺点。
④ 比例微分校正对系统的稳态误差不产生直接的
结论：
比例微分校正将使系统的稳定性和快 速性改善，但抗高频干扰能力明显下降。
由于PD校正使系统的相位前移，所 以又称它为相位超前校正。
Integral Derivative Compensation ) (相位滞后-超前校正)
Tm 为伺服电动机的机电时间常数，设 Tm 0.2s ；Tx 为检测滤波时间常数，设 Tx 10ms 0.01s ；k1 为系
统的总增益，设 K1 35
随动系统固有部分的传递函数为：
G1
s
降低增益，将使系统的稳定性改善，但使系统的稳
态精度变差。若增加增益，系统性能变化与上述相反。
•应用:
调节系统的增益，在系统的相对稳定性和稳态精度
之间作某种折衷的选择，以满足(或兼顾)实际系统的要
求，是最常用的调整方法之一。
3、比例-微分(PD)校正(Proportional-Derivative） (相位超前校正)
串联校正是将校正装置串联在系统的前向通路中，来
改变系统结构，以达到改善系统性能的方法。
2、比例（P）校正（Proportion Compensation） 举例分析:
图6-1为一随动系统框图，图中G1 s 为随动系统的固
有部分的传递函数。
若G1 s 中，K1=100，T1=0.2s，T2=0.01s；则系统固
s T1s 1 s 0.1s 1 s 0.1s 1
图6-6 比例积分校正对系统性能的影响
增设PI ① 系统由0型系统变为Ⅰ型系统，从而实现了无
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 1
校正后系统的开环传递函数为
10(0.45s 1) Gk (s) s(s 1)(0.12s 1)
（5）根据求得的校 正网络传递函数和 校正后系统的开环 传递函数，绘制校 正网络和校正后系 统的对数频率特性 曲线。
（6）校验校正后系统是否满足给定指标的要求。
① 系统的截止频率 3.16rad/s 4.3rad/s
第二节 串联校正
一、超前校正装置
超前校正又称为微分校正。超前校正装置既可由无源网络 组成，也可由运算放大器加入适当电路的有源网络组成。前者 称为无源超前网络，后者称为有源超前网络。
C
设 ui ,uo分别为网络的输入、输出 电
R1
R2
uo (t)
Gc (s)
采用超前网络对系统作 串联校正时，校正后系统的 开环放大倍数要下降 倍， 这就导致稳态误差的增加， 可能满足不了对系统稳态性 能的要求。
为使系统在校正前后的开环放大倍数保持不变，需由提 高放大器的放大倍数来补偿。校正后网络放大倍数衰减 倍， 放大器的放大倍数就得增大 倍1。
补偿后相当于在系统中串入
L0
(c
)
10
lg
1
0
进而求出超前网络的 值。
② 若事先未提出对校正后系统截止频率 c 的要求，可从给出
的相角裕度 要求出发，通过以下的经验公式求得超前网络
的最大超前角m ；
1 sin m 1 sin m
m 0
给定的
校正前
5º~10º
：校正网络引入后截止频率右移（增大）而导致相角裕度减小的补偿量。
用频率法设计超前网络的步骤：
（1）根据稳态误差要求，确定开环增益K。
（2）根据已确定的开环增益K，绘制原系统的对数频率特性曲
线 L0 (), 0 () ，计算其稳定裕度 0 , Lg0 。
（3）确定校正后系统的截止频率c 和网络的 值。
① 若事先已对校正后系统的截止频率c 提出要求，则可按要
求值选定 c 。然后在Bode图上查得原系统的L0 (c ) 值。 取 m c ，使超前网络的对数幅频值 Lc (m（) 正值）与 L0 (c )（负值）之和为0，即令
心，网络的最大超前角为
m
arctan 1 2
arcsin 1 1
( m )
1 sin m 1 sin m
当
m时，网络的对数幅值为
Lc
(m
)
10
lg
1
二、串联超前校正
超前网络进行串联校正的基本原理：利用超前网络的相角超前 特性。只要正确地将超前网络地转折频率1 T 和1 (T )选在待校 正系统截止频率的两旁，并适当选择参数 和 T，就可以使已 校正系统的截止频率和相角裕度满足性能指标的要求，从而改 善闭环系统的动态性能。闭环系统的稳态性能要求可通过选择 已校正系统的开环增益来保证。
② 系统的相角裕度
180 (c )
180 90 arctan0.45 4.3 arctan4.3 arctan0.12 4.3 48.5 45 ③ 幅值裕度 Lg
校正后的系统性能指标达到规定的要求。
（7）校正网络的实现。
R2 0.27
R1 R2
T R1C 0.45s
稳态误差的要求
画出未补偿系统的Bode图，并求 0 , Lg0
m 0
5～10
1 sin m 1 sin m
求未补偿系统幅值为 10 lg(1 ) 处的频率，m c
初步确定超前补偿网络参数 ,T
T 1
m
Gc
(
s)
Ts 1
Ts 1
满足性能指标要求？
结束
N
Y
例：设控制系统如图所示。若要求系统在单位斜坡输入信号作 用时，
1
Gc (s)
，即
1
Gc
(s)
Ts 1
Ts 1
补偿后的Bode图为
幅频特性表明：频率 在 1 T 至1 (T ) 之间时，L() 的曲线的斜率为20，与纯微 分环节的对数幅频特性的斜 率完全相同，这意味着在 [1 T ～1 (T )]斜率范围内对 输入信号有微分作用。
相频特性表明：在 0 的所有频率下，均有() 0，即网 络的输出信号在相位上总是超前于输入信号。
① 稳态误差 ess 0.1，
② 相角裕度 45，
③ 幅值裕度 Lg 10dB，试设计串联无源超前网络。
R(s)
K
C(s)
s(s 1)
解：（1）因为系统为Ι型系统
Kv
K, ess
1 K
0.1 K 10
取 K 10 ，则待校
正系统的开环传递 函数为
G0 (s)
10 s(s 1)
相应的Bode图为
（4）确定校正网络的传递函数
T 1 1 0.45s
m 4.3 0.27
（取 1
1 T
2.2rad/s ）
T 0.270.45 0.12s
（取2
1
T
8.3rad/s）
采用无源超前校正网络时，需考虑补偿校正损失：K 1 3.7
则校正网络的传递函数为
Gc
(s)
Ts 1
Ts 1
0.45s 0.12s
（2）原系统的截止频率c 3.16rad/s，相角裕度 0 17.6，
幅值裕度 Lg 。
0 17.6 与题目要求的 45相差甚远。为了在不减小K值的
前提下，获得45º的相角裕度，必须在系统中串入超前校正网 络。
（3）确定校正后系统的截止频率c 和网络的 值。
m 0 45 17.6 7.6 35
R2 R1 R2
.
R1Cs 1
R2 R1 R2
R1Cs
1
设
T
R1C
及
R2 R1 R2
( 1)
，则有
Gc
(s)
Ts 1
Ts 1
超前网络的频率特性为
Gc ( j)
jT 1 jT 1
1 2T 2 1 22T
2
(arctanT
arc tan T
)
其Bode图为
www.hzdiy www.sy /dx / www.hzdiy www.sy /dx / http://sj .39.ne t/dx/150504/4618687.htm l http://sj .39.ne t/dx/150504/4618686.htm l http://sj .39.ne t/dx/150504/4618685.htm l http://sj .39.ne t/dx/150504/4618684.htm l http://sj .39.ne t/dx/150504/4618682.htm l http://sj .39.ne t/dx/150504/4618680.htm l http://sj .39.ne t/dx/150504/4618678.htm l http://sj .39.ne t/dx/150504/4618676.htm l http://sj .39.ne t/dx/150504/4618673.htm l http://sj .39.ne t/dx/150504/4618671.htm l http://sj .39.ne t/dx/150427/4615726.htm l http://sj .39.ne t/dx/150427/4615724.htm l http://sj .39.ne t/dx/150427/4615723.htm l http://sj .39.ne t/dx/150427/4615718.htm l http://sj .39.ne t/dx/150427/4615717.htm l http://sj .39.ne t/dx/150427/4615716.htm l http://sj .39.ne t/dx/150427/4615715.htm l http://sj .39.ne t/dx/150427/4615714.htm l http://sj .39.ne t/dx/150427/4615711.htm l http://sj .39.ne t/dx/150427/4615710.htm l
在转折频率 1 1 T 和2 1 (T )之间存在着最大值m ，根据超 前网络的相频特性表达式，即
() arctanT arctanT
由
d ( ) d
0 可求得最大超前角频率为
m
1
T
由于 1 1 T ,2 1 (T )，故可表示为 m 12
网络的最大超前角正好出现在两个转折频率 1和2 的几何中
计算出值 ，然后在未校正系统的L0 () 特性曲线上查出其幅值 等于 10 lg(1 ) 所对应的频率，这就是校正后系统的截止频
率c，且m c 。
（4）确定校正网络的传递函数。根据所求得的m 和 两值，
求出时间常数为
T 1
m
m
1
T
即可写出校正网络的传递函数为
Gc
(
s)
Ts 1
Ts 1
（5）绘制校正网络和校正后系统的对数频率特性曲线。
1 sin m 1 sin 35 0.27 1 sin m 1 sin 35
10lg 1 10lg 1 5.6dB
0.27
在原系统 L0 () 曲线上查得幅值为－5.6dB时所对应的频率为 4.3rad/s，故选校正后系统的截止频率 c 4.3rad/s ，且有
m c 4.3rad/s
（6）校验校正后系统是否满足给定指标的要求。若校验结果 证实系统校正后已全部满足性能指标的要求，则设计工作结束。 反之，若校验结果发现系统校正后仍不满足要求，则需重选一 次 和m ，重c 新计算，直至完全满足给定的指标要求为止。