常微分方程第4章习题答案

第四章 高阶微分方程§4.1 线性微分方程的一般理论习题4．11．设)(t x 和)(t y 是区间[]b a ,上的连续函数，证明：若在区间[]b a ,上有≠)()(t y t x 常数或≠)()(t x t y 常数，则)(t x 和)(t y 在区间[]b a ,上线性无关．（提示：用反证法） 证明 )(t x 和)(t y 是区间[]b a ,上线性相关，则存在不全为0的常数21,c c 使得0)()(21≡+t y c t x c ，[]b a t ,∈，若)0(,021≠≠c c 或得12)()(c c t y t x -≡（或21)()(c c t x t y -≡）[]b a t ,∈∀成立。

与假设矛盾，故)(t x 和)(t y 在区间[]b a ,上线性无关．2．证明非齐次线性方程的叠加原理：设)(1t x ，)(2t x 分别是非齐次线性方程)()()(1111t f x t a dt xd t a dt x d n n n n n =+++-- （1） )()()(2111t f x t a dtxd t a dt x d n n n nn =+++-- （2） 的解，则)()(21t x t x +是方程)()()()(21111t f t f x t a dtxd t a dt x d n n n n n +=+++-- （3） 的解．证明 因为)(1t x ，)(2t x 分别是方程（1）、（2）的解，所以)()()(1111111t f x t a dt x d t a dt x d n n n n n =+++-- ， )()()(2212112t f x t a dtx d t a dt x d n n n nn =+++-- ， 二式相加得，)()())(()()()(21211211121t f t f x x t a dt x x d t a dt x x d n n n n n +=++++++-- ，即)()(21t x t x +是方程（3）的解．3.（1）．试验证022=-x dt x d 的基本解组为tt e e -,，并求方程t x dtx d cos 22=-的通解。

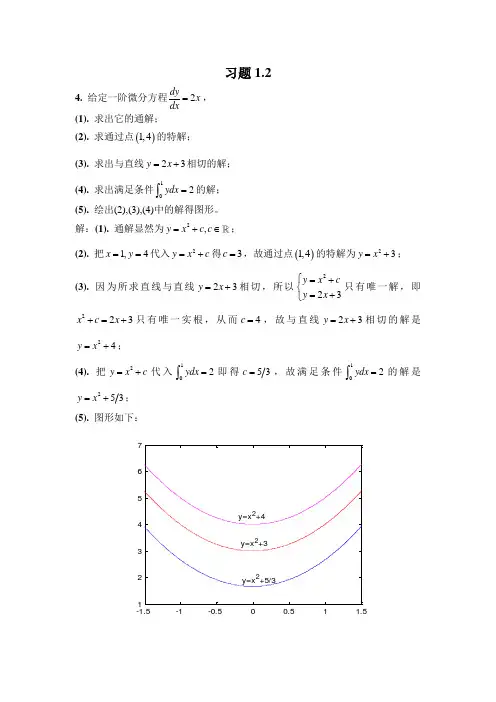
习题1.24. 给定一阶微分方程2dyx dx=， (1). 求出它的通解； (2). 求通过点()1,4的特解； (3). 求出与直线23y x =+相切的解； (4). 求出满足条件102ydx =⎰的解；(5). 绘出(2),(3),(4)中的解得图形。

解：(1). 通解显然为2,y x c c =+∈；(2). 把1,4x y ==代入2y x c =+得3c =，故通过点()1,4的特解为23y x =+；(3). 因为所求直线与直线23y x =+相切，所以223y x cy x ⎧=+⎨=+⎩只有唯一解，即223x c x +=+只有唯一实根，从而4c =，故与直线23y x =+相切的解是24y x =+；(4). 把2y x c =+代入12ydx =⎰即得5c =，故满足条件12ydx =⎰的解是253y x =+；(5). 图形如下：-1.5-1-0.500.51 1.512345675. 求下列两个微分方程的公共解：242422,2y y x x y x x x y y ''=+-=++--解：由2424222y x x x x x y y +-=++--可得()()222210y x xy -++=所以2y x =或212y x =--，2y x =代入原微分方程满足，而212y x =--代入原微分方程不满足，故所求公共解是代入原微分方程不满足。

6. 求微分方程20y xy y ''+-=的直线积分曲线。

解：设所求直线积分曲线是y kx b =+，则将其代入原微分方程可得2200010k b k xk kx b k b k b k k -=⎧+--=⇒⇒====⎨-=⎩或所以所求直线积分曲线是0y =或1y x =+。

8. 试建立分别具有下列性质的曲线所满足的微分方程：(2). 曲线上任一点的切线介于两坐标轴之间的部分等于定长l ； (5). 曲线上任一点的切线的纵截距等于切点横坐标的平方。

国家开放大学电大本科《常微分方程》网络课形考任务1-6试题及答案国家开放大学电大本科《常微分方程》网络课形考任务1-6试题及答案100%通过考试说明：2020年秋期电大把该网络课纳入到“国开平台”进行考核，该课程共有6个形考任务，针对该门课程，本人汇总了该科所有的题，形成一个完整的标准题库，并且以后会不断更新，对考生的复习、作业和考试起着非常重要的作用，会给您节省大量的时间。

做考题时，利用本文档中的查找工具，把考题中的关键字输到查找工具的查找内容框内，就可迅速查找到该题答案。

本文库还有其他网核及教学考一体化答案，敬请查看。

课程总成绩=形成性考核×50%+终结性考试×50%形考任务1题目1本课程的教学内容共有五章，其中第三章的名称是（）．选择一项：A.一阶线性微分方程组B.定性和稳定性理论简介C.初等积分法D.基本定理题目2本课程安排了6次形成性考核任务，第2次形成性考核作业的名称是（）．选择一项：A.第一章至第四章的单项选择题B.第二章基本定理的形成性考核书面作业C.初等积分法中的方程可积类型的判断D.第一章初等积分法的形成性考核书面作业题目3网络课程主页的左侧第3个栏目名称是：（）．选择一项：A.课程公告B.自主学习C.课程信息D.系统学习题目4网络课程的“系统学习”栏目中第一章初等积分法的第4个知识点的名称是（）．选择一项：A.一阶隐式微分方程B.分离变量法C.全微分方程与积分因子D.常数变易法题目5网络课程的“视频课堂”栏目中老师讲课的电视课共有（）讲．选择一项：A.18B.20C.19D.17题目6网络课程主页的左侧“考试复习”版块中第二个栏目名称是：（）．选择一项：A.考核说明B.复习指导C.模拟测试D.各章练习汇总题目7请您按照课程的学习目标、学习要求和学习方法设计自己的学习计划，并在下列文本框中提交，字数要求在100—1000字．答：常微分方程是研究自然现象，物理工程和工程技术的强有力工具，熟练掌握常微分方程的一些基本解法是学习常微分方程的主要任务，凡包含自变量，未知函数和未知函数的导数的方程叫做微分方程。

国家开放大学电大本科《常微分方程》网络课形考任务6试题及答案形考任务6常微分方程学习活动6第三章一阶线性方程组、第四章n 阶线性方程的综合练习本课程形成性考核综合练习共3次，内容主要分别是第一章初等积分法的综合练习、第二章基本定理的综合练习、第三章和第四章的综合练习，目的是通过综合性练习作业，同学们可以检验自己的学习成果，找出掌握的薄弱知识点，重点复习，争取尽快掌握．要求：首先请同学们下载作业附件文档并进行填写，文档填写完成后请在本次作业页面中点击“去完成”按钮进入相应网页界面完成任务，然后请将所做完的作业文档以附件的形式上传到课程上，随后老师会在课程中进行评分。

一、填空题1．若A (x )在(-∞,+∞)上连续，那么线性齐次方程组Y A Y )(d d x x =，n R Y ∈的任一非零解在1+n R 空间 不能 与x 轴相交．2．方程组n x x xR Y R Y F Y ∈∈=,),,(d d 的任何一个解的图象是n + 1维空间中的一条积分曲线． 3．向量函数组Y 1(x ), Y 2(x ),…,Y n (x )线性相关的 必要 条件是它们的朗斯期行列式W (x )=0． 4．线性齐次微分方程组n x x x R Y R Y A Y ∈∈=,,)(d d ，的一个基本解组的个数不能多于n + 1 个． 5．若函数组)()(21x x ϕϕ，在区间),(b a 上线性相关，则它们的朗斯基行列式)(x W 在区间),(b a 上恒等于零 ．6．函数组⎩⎨⎧==x y x y cos sin 21的朗斯基行列式)(x W 是 x x x x x W sin cos cos sin )(-=． 7．二阶方程02=+'+''y x y x y 的等价方程组是⎪⎩⎪⎨⎧--='='y x xy y y y 2111． 8．若)(1x y ϕ=和)(2x y ϕ=是二阶线性齐次方程的基本解组，则它们 没有 共同零点．9．二阶线性齐次微分方程的两个解)(1x y ϕ=,)(2x y ϕ=成为其基本解组的充要条件是 线性无关（或：它们的朗斯基行列式不等于零） ．10．n 阶线性齐次微分方程线性无关解的个数最多为N 个．11．在方程y″+ p (x )y′+q (x )y = 0中，p (x ), q (x )在(-∞,+∞)上连续，则它的任一非零解在xOy 平面上可以与x 轴横截相交．12．二阶线性方程20y y y '''++=的基本解组是e ,e x x x --．13．线性方程0y y ''+=的基本解组是 cos ,sin x x ．14．方程02=+'+''y x y x y 的所有解构成一个 2 维线性空间．15．n 阶线性齐次微分方程的所有解构成一个 n 维线性空间．二、计算题1．将下列方程式化为一阶方程组（1）0)()(=++x g x x f x &&&（2）0)()()(321=+'+''+'''y x a y x a y x a y。

常微分方程习题4.2 2、解下列方程 （1）045)4(=+''-x x x解：特征方程1122045432124-==-===+-λλλλλλ，，，有根故通解为x=t t t te c e c e c e c --+++432221(2)03332=-'+''-'''x a x a x a x解：特征方程0333223=-+-a a a λλλ有三重根a =λ故通解为x=at at at e t c te c e c 2321++ （3）04)5(=''-x x解：特征方程0435=-λλ有三重根0=λ，=4λ2，=5λ-2故通解为54232221c t c t c e c e c x t t ++++=-(4)0=+'+''x x x解：特征方程012=++λλ有复数根=1λ,231i +-=2λ,231i-- 故通解为t e c t ec xt t 23sin 23cos 212211--+=(5) 12+=-''t s a s解：特征方程022=-a λ有根=1λa,=2λ-a当0≠a 时，齐线性方程的通解为s=atat e c e c -+21Bt A s +=~代入原方程解得21aB A -== 故通解为s=atat e c e c -+21-)1(12-t a当a=0时,)(~212γγ+=t t s 代入原方程解得21,6121==γγ故通解为s=t c c 21+-)3(612+t t (6) 32254+=-'+''-'''t x x x x解：特征方程025423=-+-λλλ有根=1λ2,两重根=λ 1 齐线性方程的通解为x=t t t te c e c e c 3221++又因为=λ0不是特征根，故可以取特解形如Bt A x +=~代入原方程解得A=-4，B=-1 故通解为x=t t t te c e c e c 3221++-4-t (7) 322)4(-=+''-t x x x解：特征方程121201224-===+-λλλλ重根，重根有 故齐线性方程的通解为x=t t t t te c e c te c e c --+++4321 取特解形如c Bt At x ++=2~代入原方程解得A=1，B=0,C=1 故通解为x=t t t t te c e c te c e c --+++4321+12+t (8)t x x cos =-'''解：特征方程013=-λ有复数根=1λ,231i +-=2λ,231i--13=λ 故齐线性方程的通解为t t t e c t e c t ec x 321221123sin 23cos ++=--取特解形如t B t A x sin cos ~+=代入原方程解得A=21,21-=B 故通解为t t t e c t e c t ec x 321221123sin 23cos ++=--)sin (cos 21t t +-(9) t x x x 2sin 82=-'+''解：特征方程022=-+λλ有根=1λ-2,=2λ 1 故齐线性方程的通解为x=tte c e c 221-+因为+-2i 不是特征根取特解形如t B t A x 2sin 2cos ~+=代入原方程解得A=56,52-=-B 故通解为x=tte c e c 221-+t t 2sin 562cos 52--（10）t e x x =-'''解：特征方程013=-λ有复数根=1λ,231i +-=2λ,231i--13=λ 故齐线性方程的通解为t t t e c t e c t ec x 321221123sin 23cos ++=-- =λ1是特征方程的根，故t Ate x =~代入原方程解得A=31 故通解为t t t e c t e c t ec x 321221123sin 23cos ++=--+t te 31（11）t e s a s a s =+'+''22解：特征方程0222=++a a λλ有2重根=λ-a 当a=-1时，齐线性方程的通解为s=t t te c e c 21+,=λ1是特征方程的2重根，故t e At x 2~=代入原方程解得A=21通解为s=22121t te c e c t t ++, 当a ≠-1时，齐线性方程的通解为s=at at te c e c --+21,=λ1不是特征方程的根，故t Ae x =~代入原方程解得A=2)1(1+a故通解为s=at at te c e c --+21+te a 2)1(1+ （12）t e x x x 256=+'+''解：特征方程0562=++λλ有根=1λ-1,=2λ-5 故齐线性方程的通解为x=tte c ec 521--+=λ2不是特征方程的根，故t Ae x 2~=代入原方程解得A=211故通解为x=t te c ec 521--++te 2211 （13）t e x x x t cos 32-=+'-''解：特征方程0322=+-λλ有根=1λ-1+2i,=2λ-1-2i 故齐线性方程的通解为t e c t e c x t t 2sin 2cos 21+=i ±-1 不是特征方程的根, 取特解行如t e t B t A x -+=)sin cos (~代入原方程解得A=414,415-=B 故通解为t e c t e c x t t 2sin 2cos 21+=+t e t t --)sin 414cos 415( (14) t t x x 2cos sin -=+''解：特征方程012=+λ有根=1λi,=2λ- i 故齐线性方程的通解为t c t c x sin cos 21+= 对于t x x sin =+'',=1λi,是方程的解， 设)sin cos (~t B t A t x +=代入原方程解得A=21-B=0 故t t x cos 21~-=对于t x x 2cos -=+'' ，设t B t A x 2sin 2cos ~+=代入原方程解得A=31 B=0 故t x 2cos 31~= 故通解为t c t c x sin cos 21+=t t cos 21-t 2cos 31+ 15）1442++=+'-''ttee x x x解：0442=+-λλ，22,1=λ，齐次方程的通解为)()(212t C C e t x t +=。

马知恩周义仓编常微分⽅程定性与稳定性⽅法部分习题参考解答第⼀章 基本定理1设有 $$\bex \frac{\rd \bbx}{\rd t}=\bbf(t,\bbx),\quad \bbx(t_0)=\bbx^0,\quad (t_0,\bbx^0)\in \bbR\times \bbR^n. \eex$$试证: 若 $\bbf\in C^1(G)$, 则在 $(t_0,\bbx^0)$ 的领域内, 此 Cauchy 问题的解存在惟⼀.证明: 由 $f\in C^1(G)$ 蕴含 $f\in C(G)$ 且在 $G$ 内适合 Lipschitz 条件知有结论.2试讨论下列⽅程解的存在区间:(1) $\dps{\frac{\rd y}{\rd x}=\frac{1}{x^2+y^2}}$;(2) $\dps{\frac{\rd y}{\rd x}=y(y-1)}$.解答:(1) 由 $\dps{\frac{\rd x}{\rd y}=x^2+y^2}$ 的解的存在区间有限知 $y$ 有界, ⽽由解的延拓定理, 原⽅程解的存在区间为 $\bbR$.(2) 直接求解有 $\dps{y=\frac{1}{1-\frac{y_0-1}{y_0}e^x}}$, ⽽a.当 $0\leq y_0\leq 1$ 时, 原⽅程解的存在区间为 $\bbR$;b.当 $y_0<0$ 时, 原⽅程解的存在区间为 $\dps{\sex{\ln\frac{y_0}{y_0-1},\infty}}$;c.当 $y_0>1$ 时, 原⽅程解的存在区间为 $\dps{\sex{-\infty,\ln\frac{y_0}{y_0-1}}}$.3 设有⼀阶微分⽅程式 $$\bex \frac{\rd x}{\rd t}=(t-x)e^{tx^2}. \eex$$ 试证: 过任⼀点 $(t_0,x_0)\in\bbR^2$ 的右⾏解的存在区间均为 $[t_0,+\infty)$.证明: 由 $$\bex \frac{\rd x}{\rd t}=(t-x)e^{tx^2}=\left\{\ba{ll} <0,&x>t,\\ >0,&x<t \ea\right. \eex$$ 知解在 $\sed{x>t}$ 内递减,在 $\sed{x<t}$ 内递增. 当 $x_0>t_0$ 时, 在 $$\bex \sed{(t,x);t\in\bbR, t_0<x<x_0} \eex$$ 内应⽤解的延伸定理知解定与$\sed{x=t}$ 相交, 之后解递增, 在 $$\bex \sed{(t,x);t\in\bbR,x<t} \eex$$ 内应⽤延伸定理及⽐较定理即知结论.4设有⼀阶⽅程 $\dps{\frac{\rd x}{\rd t}=f(x)}$, 若 $f\in C(-\infty,+\infty)$, 且当 $x\neq 0$ 时有 $xf(x)<0$. 求证过 $\forall\(t_0,x_0)\in\bbR^2$, Cauchy 问题的右⾏解均在 $[t_0,+\infty)$ 上存在, 且 $\dps{\lim_{t\to+\infty}x(t)=0}$.证明: 由题意, $$\bex f(x)\left\{\ba{ll} >0,&x<0,\\ <0,&x>0. \ea\right. \eex$$ ⽽由 $f$ 的连续性, $f(0)=0$. 于是当 $x_0=0$ 时,由解的唯⼀性知 $x=0$. 当 $x_0>0$ 时, 在 $$\bex \sed{(t,x);t\in\bbR,0<x<x_0} \eex$$ 内应⽤延伸定理及惟⼀性定理知 $x(t)$ 递减趋于 $0$. 当 $x_0<0$ 时, 在 $$\bex \sed{(t,x);t\in\bbR,x_0<x<0} \eex$$ 内应⽤延伸定理及惟⼀性定理知 $x(t)$ 递增趋于 $0$.5若 $\bbf(t,\bbx)$ 在全空间 $\bbR\times\bbR^n$ 上连续且对 $\bbx$ 满⾜局部 Lipschitz 条件且 $$\bex \sen{\bbf(t,\bbx)}\leq L(r),\quad r=\sqrt{\sum_{i=1}^n x_i^2},\quad \bbx=(x_1,\cdots,x_n)^T, \eex$$ 其中 $L(r)>0, r>0$, 且 $$\bee\label{1.5:1}\int_a^{+\infty}\frac{\rd r}{L(r)}=+\infty,\quad a>0. \eee$$ 试证: 对 $\forall\ (t_0,\bbx^0)\in\bbR\times\bbR^n$, Cauchy 问题的解均可对 $t$ ⽆限延拓.证明: 由解的延伸定理, 仅须证明在任何有限区间 $-\infty<\alpha<t<\beta<+\infty$ 上, $\bbx(t)$ 有界. 为此, 令 $y(t)=\sen{\bbx(t)}$,则 $$\beex \bea \frac{\rd y(t)}{\rd t}&=2\bbx(t)\cdot\frac{\rd \bbx(t)}{\rd t} =2\bbx(t)\cdot \bbf(t,\bbx(t)),\\\sev{\frac{\rd y(t)}{\rd t}} &\leq 2\sqrt{y(t)}\cdot L\sex{\sqrt{y(t)}},\\ \frac{\rd \sqrt{y(t)}}{L\sex{\sqrt{y(t)}}}&\leq \rd t,\\ \int_\alpha^\beta \frac{\rd \sqrt{y(t)}}{L\sex{\sqrt{y(t)}}} &\leq \int_\alpha^\beta \rd t=\beta-\alpha. \eea \eeex$$ 这与\eqref{1.5:1} ⽭盾 (事实上, 当 $\alpha,\beta\gg 1$, $|\alpha-\beta|\ll 1$ 时, 不等式右端可任意⼩, ⽽不等式左端有积分发散知可⼤于某⼀正常数).6设有微分⽅程 $$\bex \frac{\rd \bbx}{\rd t}=\bbf(t,\bbx), \eex$$ $\bbf\in C(G\subset \bbR\times\bbR^n)$, 试证: 若对$\forall\ (t_0,\bbx^0)\in G$, Cauchy 问题的解都存在唯⼀, 则解必对初值连续依赖.证明: 参考[家⾥蹲⼤学数学杂志第134期, 常微分⽅程习题集, 第1600页].7 试在定理 1.1 的假设下, 利⽤ Gronwall 引理直接证明解对初始时刻 $t_0$ 的连续依赖性.证明: 参考定理 1.7 的证明.8 设有⼀阶 Cauchy 问题 $$\bex \frac{\rd y}{\rd x}=x^2+(y+1)^2,\quad y(0)=0. \eex$$ 试利⽤⽐较定理证明, 若设解的右⾏饱和区间为 $[0,\beta)$, 则 $\dps{\frac{\pi}{4}\leq \beta\leq 1}$.证明: 仅须注意到当 $0\leq x\leq 1$ 时, $$\bex (y+1)^2\leq x^2+(y+1)^2\leq 1+(y+1)^2. \eex$$ 再利⽤⽐较定理即知结论.第⼆章 动⼒系统的基本知识1试证明: $\Omega_P=\vno$ 的充要条件是 $L_P^+$ 趋于⽆穷.证明: $\ra$ ⽤反证法. 若 $L_P^+$ 不趋于⽆穷, 则 $$\bex \exists\ M>0, t_n\nearrow +\infty,\st \sen{\mbox{ $\varphi$}(P,t_n)}\leq M. \eex$$ 由 Weierstrass 定理, $$\bex \exists\ \sed{t_n'}\subset \sed{t_n},\st \mbox{ $\varphi$}(P,t_n)\to Q,\eex$$ ⽽ $Q\in \Omega_P$, 这是⼀个⽭盾. $\la$ 亦⽤反证法. 若 $\Omega_P\neq \vno$, ⽽设 $Q\in \Omega_P$, 则 $$\bex\exists\ t_n\nearrow+\infty,\st \mbox{ $\varphi$}(P,t_n)\to Q. \eex$$ 这与 $L_P^+$ 趋于⽆穷⽭盾.2试证明: 若 $\Omega_P$ 仅含惟⼀奇点 $P^*$, 则当 $t\to+\infty$ 时必有 $L_P^+$ 趋向于 $P^*$.证明: ⽤反证法. 设 $$\bee\label{2.2:1} \exists\ \ve_0>0,\ t_n\nearrow+\infty, \st \sen{\mbox{ $\varphi$}(P,t_n)-P^*}\geq\ve_0. \eee$$ 则(1)若 $\sed{t_n}$ 有有界的⼦列, 则适当抽取⼦列 $\sed{t_n'}$ 后有 $$\bex \mbox{ $\varphi$}(P,t_n')\to Q. \eex$$ 于是 $Q\in\Omega_P=\sed{P^*}$. 这与 \eqref{2.2:1} ⽭盾.(2)若 $\sed{t_n}$ ⽆有界的⼦列, 则 $\dps{\lim_{n\to\infty}\mbox{ $\varphi$}(P,t_n)=\infty}$, ⽽ $\infty\in\Omega_P=\sed{P^*}$, ⼜是⼀个⽭盾.3试证明: 若 $\Omega_P$ 有界且 $\Omega_P$ ⾮闭轨, 则 $\forall\ R\in \Omega_P$, $\Omega_R$ 与 $A_R$ 必均为奇点.证明: ⽤反证法证明 $\Omega_R$ 为奇点集, $A_R$ 为奇点集类似可证. 设 $\Omega_R$ 含有常点. 由 $R\in \Omega_P$ 及$\Omega_P$ 为不变集知 $L_R\subset \Omega_Q$. 于是按引理 2.3, $L_R$ 为闭轨线, $L_R=\Omega_R\subset \Omega_P$. 这与 $\Omega_P$ ⾮闭轨⽭盾.4试证明: ⼀系统的圈闭奇点的集合是⼀闭集.证明: 全体奇点的集合为 $$\bex \sed{\bbx^*\in G; \bbf(\bbx^*)=\mbox{ $0$}}. \eex$$ 由 $\bbf$ 的连续性即知结论.5 若 $L_P^+$ 有界且 $\Omega_P$ 仅由奇点构成, 能否断定 $\Omega_P$ 仅含⼀个奇点?解答: 不能断定. 仅能说 $\Omega_P$ 为由奇点构成的连通闭集或闭轨线.6 设 $O(0,0)$ 是⼀平⾯⾃治系统的惟⼀奇点, 且是稳定的, 全平⾯没有闭轨线. 试证: (1) 此系统的任⼀轨线必负向⽆界; (2) 任⼀有界的正半轨闭进⼊奇点 $O$.证明:(1) ⽤反证法. 若有⼀轨线负向有界, 则在定理 2.8 中, 由全平⾯没有闭轨线知 (3),(4) 不成⽴; 由 $O$ 为惟⼀奇点知 (1),(2),(5) 不成⽴. 这是⼀个⽭盾.(2) 对有界正半轨⽽⾔, 定理 2.8 中仅有 (1),(2),(5) 可能成⽴. 若 (1),(2) 成⽴, 则结论已证; ⽽由全平⾯没有闭轨线知 (5) 不成⽴.第三章 稳定性理论1 讨论⽅程 $$\bee\label{3.1:1} \sedd{\ba{ll}\frac{\rd x_1}{\rd t}=x_2,\\ \frac{\rd x_2}{\rd t}=-a^2\sin x_1\ea} \eee$$ 零解的稳定性.解答: 选取 $$\bex V(\bbx)=\frac{x_2^2}{2}+a^2(1-\cos x_1), \eex$$ 则 $V$ 在原点的⼀邻域内是正定的, 且沿 \eqref{3.1:1} 的轨线有 $$\bex \dot V(\bbx)=V_{x_1}x_1'+V_{x_2}x_2'=0. \eex$$ 由此, 零解是稳定的, 但不是渐近稳定的.2 证明⽅程 $\dps{\frac{\rd x}{\rd t}=-x+x^2}$ 的零解是指数渐近稳定的, 但不是全局渐近稳定的.证明: 解该微分⽅程有: $$\bex \ba{ccc} -\frac{1}{x^2}\frac{\rd x}{\rd t}=\frac{1}{x}-1,&\frac{\rd y}{\rd t}=y-1\\sex{y=\frac{1}{x}},&\frac{\rd z}{\rd t}=-e^{-t}\ \sex{z=e^{-t}y},\\ z=e^{-t}+C,&y=Ce^t+1,&x=\frac{1}{1+Ce^t}. \ea \eex$$由此, 原微分⽅程的解为 $$\bex x=0,\mbox{ 或 }x(t)=\frac{1}{1+Ce^t}. \eex$$ 取初值 $(t_0,x_0),\ x_0\neq 0$, 有 $$\bexx(t,t_0,x_0)=\frac{x_0}{1+e^{t-t_0}(1-x_0)}. \eex$$ 故当 $|x_0|<1$ 时, $$\bex |x(t,t_0,x_0)|\leq \sev{\frac{1}{x_0}-1}e^{-(t-t_0)}. \eex$$ 这说明零解是指数渐近稳定的. 但由于从 $(t_0,1)$ 出发的解 $x(t,t_0,1)=1$ 不趋于零解, ⽽零解不是全局渐近稳定的.3 在相空间 $\bbR^n$ 中给出 $\dps{\frac{\rd \bbx}{\rd t}=\bbf(t,\bbx),\ \bbf(t,0)=0}$ 的零解稳定、渐近稳定、不稳定的⼏何解释.解答: 零解是稳定的 $\lra\ \forall\ \ve>0,\ \exists\ \delta>0,\ \forall\ P\in B_\delta,\ L_P^+\subset B_\ve$; 零解是渐进稳定的$\lra\ \exists\ U\ni O,\ \forall\ P\in U,\ L_P^+\to 0$; 零解是不稳定的 $\lra\ \exists\ \ve_0>0,\ \exists\ P_n\to0, \stL_{P_n}^+\bs B_\ve\neq \vno$.4判断下列系统零解的稳定性:(1) $\dps{\sedd{\ba{ll} \frac{\rd x_1}{\rd t}=mx_2+\alpha x_1(x_1^2+x_2^2),\\ \frac{\rd x_2}{\rd t}=-mx_1+\alphax_2(x_1^2+x_2^2); \ea}}$;(2) $\dps{\frac{\rd^2x}{\rd t^2}+\sex{\frac{\rd x}{\rd t}}^3+f(x)=0,}$ 其中 $xf(x)>0\ (x\neq 0), f(0)=0$;(3) $\dps{\frac{\rd^2x}{\rd t^2}-\sex{\frac{\rd x}{\rd t}}^2sgn\sex{\frac{\rd x}{\rd t}}+x=0}$.解答:(1) 取 $$\bex V=x_1^2+x_2^2, \eex$$ 则 $V$ 正定, 且沿微分⽅程的轨线有 $$\bex \dot V=2\alpha(x_1^2+x_2^2)\sedd{\ba{lll} \mbox{正定},&\alpha>0,\\ 0,&\alpha=0,\\ \mbox{负定},&\alpha<0. \ea} \eex$$ 于是当 $\alpha>0$ 时, 由定理 3.3, 零解是不稳定的; 当 $\alpha=0$ 时, 由定理 3.1, 定理是稳定的; 当 $\alpha<0$ 时, 由定理 3.1, 零解是渐近稳定的.(2) 令 $\dps{x_1=x,x_2=\frac{\rd x}{\rd t}}$, 则 $$\bex \frac{\rd x_1}{\rd t}=x_2,\quad \frac{\rd x_2}{\rd t}=-x_2^3-f(x_1). \eex$$ 取 $$\bex V=\frac{x_2^2}{2}+\int_0^{x_1}f(t)\rd t, \eex$$ 则 $V$ 正定, 且沿微分⽅程的轨线有 $\dot V=-x_2^4\leq 0.$再 $$\bex \sed{\bbx;\dot V(\bbx)=0}=\sed{0}, \eex$$ 我们据定理 3.2 知零解是渐近稳定的.(3) 令 $\dps{x_1=x,x_2=\frac{\rd x}{\rd t}}$, 则 $$\bex \frac{\rd x_1}{\rd t}=x_2,\quad \frac{\rd x_2}{\rd t}=x_2^2sgn(x_2)-x_1. \eex$$ 取 $$\bex V=\frac{x_1^2+x_2^2}{2}, \eex$$ 则 $V$ 正定, 且沿微分⽅程的轨线有 $\dot V=x_2^2|x_2|$是正定的. 我们据定理 3.3 知零解是不稳定的.5 若存在有⽆穷⼩上界的正定函数 $V(t,\bbx)$, 它沿着 $$\bex (3.3.1)\quad \frac{\rd\bbx}{\rd t}=\bbf(t,\bbx),\quad \bbf(t,0)=0 \eex$$ 解曲线的全导数 $\dot V(t,\bbx)$ 负定, 证明 (3.3.1) 的零解是渐近稳定的.证明: 仅须注意到存在正定函数 $W(x)$, $W_1(x)$ 使得 $$\bex W(\bbx)\leq V(t,\bbx)\leq W_1(\bbx). \eex$$ ⽽可仿照定理 3.1 的证明.6 讨论 $\dps{\frac{\rd x}{\rd t}=\frac{g'(t)}{g(t)}x}$ 零解的稳定性, 其中 $\dps{g(t)=\sum_{n=1}^\infty \frac{1}{1+n^4(t-n)^2}}$. 能否得到零解渐近稳定的结果? 为什么?解答: 直接求解有 $$\bex x(t)=\frac{x_0}{g(t_0)}{g(t)}, \eex$$ ⽽由 $$\bex |x(t)|\leq\frac{|x_0|}{g(t_0)}\sez{2+\sum_{n\neq [t],[t]+1}\frac{1}{1+n^4(t-n)^2}} \leq \frac{|x_0|}{g(t_0)}\sez{2+\sum_{n=1}^\infty\frac{1}{n^4}} \eex$$ 知零解是稳定的; 由$$\bex |x(k)|=\frac{|x_0|}{g(t_0)}\sez{1+\sum_{n\neq k}\frac{1}{n^4(k-n)^2}}\geq \frac{|x_0|}{g(t_0)} \eex$$ 知零解不是渐近稳定的.7证明 $\dps{\frac{\rd x}{\rd t}=-\frac{x}{t+1}}$ 的零解是渐近稳定的, 但不存在有⽆穷⼩上界的正定函数 $V(t,x)$, 使得 $\dotV(t,x)$ 负定 (该习题表明习题 5 中渐近稳定性定理中的条件不是必要的).证明: 直接求解有 $$\bex x(t)=\frac{x_0}{1+t}. \eex$$ ⽽零解是渐近稳定的.。

爱启航在线考研第四章常微分方程4.1答案：应选（C ）解析：原方程写成23e 0+'+=yxyy ，分离变量有23e d =e d y x y y x --，积分得232e 3e --=x y C ，其中C 为任意常数.4.2答案：应填sin e=C xy ，其中C 为任意常数.解析：原方程分离变量，有d cos d ln sin =y xx y y x，积分得1ln |ln |ln |sin |ln =+y x C ，通解为ln sin =y C x 或sin e=C x y ，其中C 为任意常数.4.3答案：应填()2112e-=x y x 解析：原方程化为d 1d ⎛⎫=- ⎪⎝⎭y x x y x .积分得通解211ln ||ln ||2y C x x =-，即122ex y Cx -=.由初值(1)1=y 解出12e C =得特解.故答案为：()2112e-=x y x .4.4答案：应选（B ）解析：原方程求导得()2()'=f x f x ，即()2()'=f x f x ，积分得2()e =x f x C ，又(0)ln 2=f ，故ln 2=C ，从而2()e ln 2=x f x .故应选（B ）.4.5解：曲线()=y f x 在点(,)x y 处的切线方程为()'-=-Y y y X x ，令0=X ，得到切线在y 轴截距为'=-xy y xy ，即(1)'=-xy y x .此为一阶可分离变量的方程，于是d 11d ⎛⎫=- ⎪⎝⎭y x y x ，两边积分有1ln ||ln =-y C x x ，得爱启航线考研到e =x Cx y .又()11e y -=，故1=C ，于是曲线方程为e =xx y .4.6解：22d d 11+y y y x x x x =∆=+，得2d d 1=+y y x x ，变量分离2d 1d 1=+y x y x.两边积分得1ln arctan y x C =+.可得arctan exy C =又()0y =π，则C =π.所以arctan πexy =，()πarctan141πeπe y ==.4.7解：令=yu x，即=y ux ，则y u x u ''=+，又由题给表达式可得2y u u '=，即有u x u '+2u u =-d 1d 22=-x xu u ，两边积分得1ln 1ln ln u x C -=+，即ln(1ln ln 1=-+⇒-=⇒-=y Cu x C x xy C x x.4.8答案：应填2(ln ||)=+x y y C 解析：将x 看成未知函数，原方程改写为2d 1d 222+==+x x y x y xy y x这是一个伯努利方程，令2=z x ，有d 1d -=z z y y ，得11d d 2e ed (ln ||)-⎛⎫⎰⎰==+=+ ⎪ ⎪⎝⎭⎰y y y y x z y C y y C .故答案为：2(ln ||)=+x y y C ，其中C 为任意常数.4.9答案：应填()cos +x C x解析：属于一阶非齐次线性方程，直接根据一阶非齐次线性微分方程的通解公式即可得出答案.故答案为：()cos +x C x ，其中C 为任意常数.4.10答案：应填1爱启航在线考研解析：()2d 2d 22e 4e d e4ed x x xxy x x C x x C--⎛⎫⎰⎰=+=+ ⎪⎝⎭⎰⎰222e (21)e (21)e x x xx C x C --⎡⎤=-+=-+⎣⎦.当0=x 时，1=-y ，则0=C .可得21=-y x ，则()11=y .故答案为1.4.11答案：应填1解析：由11()()'+=y P x y Q x 及22()()'+=y P x y Q x 得()()1212()()()αββαβ'+++=+y y P x ay y Q x .又因12αβ+y y 满足原方程，故应有()()()β+=a Q x Q x ，即1αβ+=.故答案为1.4.12解：()sin d sin d e cos e d -⎛⎫⎰⎰=+ ⎪⎝⎭⎰x xx x gx x x C ()cos cos e cos ed -=+⎰xxx x C又()00g =，故()()cos cos cos 0e cos ed cos ed limlime lim xxxx x x x x Cx x Cg x xxx--→→→++==⋅=⎰⎰cos 0e lim cos e 1x x x -→⋅=.4.13解：2d 1d 2y x x y =-，则2d 2d x x y y =-，即2d 2d x x yy-=-()()2d 2d 222222111e e d e e d e 224yy y y y x y y C y y C y y C --⎛⎫⎰⎰⎡⎤=-+=-+=+++ ⎪⎣⎦⎝⎭⎰⎰.4.14解：令=tx u ，则u t x d d =，则代入到题给表达式101()d ()d xf tx t f u u x =⎰⎰，可得20()d 2()xf u u xf x x =+⎰.两边求导得()2()2()2f x f x xf x x '=++，则()2()2f x xf x x '+=-.从而11131d d 2222222()e (1)ed 33x x x x f x x C x x C x Cx ---⎛⎫⎛⎫⎰⎰=-+-+=-+ ⎪⎝ ⎝⎭=⎪⎭⎰.爱启航在线考研4.15解：将原方程改写成211cos sin y x x yy '+=-，并令1z y =，则21z y y ''=-，且原方程化为sin cos z z x x '-=-.d de (sin cos )e d x x z x x x C -⎡⎤⎰⎰=-+⎢⎥⎣⎦⎰e (sin cos )e d x x x x x C -⎡⎤=-+⎣⎦⎰()e sin ed cose d xxx x x x x C --=-+⎰⎰，其中()sin e d sin d e sin e e cos d x x x x x x x x x x ----=-=-+⎰⎰⎰，故()e sin e e sin x x x z x C C x -=-+=-，即1e sin x C x y=-为所求通解.4.16答案：应选（C ）解析：因原方程阶数为2，通解中应包含两个任意常数（可求出通解为3126++x C C x ）；特解中不含有任意常数（3*6=x y 为特解）；36+x Cx 满足原方程，为原方程的解，故选项（A ），（B ），（C ）都不对，应选（C ）.4.17解：（1）令y p '=，则d d p y x ''=，从而2d 1d pp x=+，则2d d 1p x p =+积分得p arctan 1arctan p x C =+，故()1d tan d yp x C x=+=，则两边对x 积分1d tan()d y x C x =+⎰⎰，得()1121sin()d ln cos cos()x C y x x C C x C +==-+++⎰.（2）()10xy xy C '''=⇒=，即1y xC '=，故12ln y C x C =+.4.18解：由21e x y =，得212e x y x '=，()22124e x y x ''=+；由22e x y x =，得222(12)e x y x '=+，()22364e x y x x ''=+.因爱启航在线考研()()()22222211144224e 42e 42e 0x x x y xy x y x x x x '''-+-=+-⋅+-=.()()()()222232222244264e 412e 42e 0x x x y xy x y x x x x x x '''-+-=+-++-=.故1y 与2y 都是方程的解.又因21y x y =不等于常数，故1y 与2y 线性无关.于是方程的通解为()2112212e x y C y C y C C x =+=+.4.19答案：应选（A ）解析：根据高阶线性微分方程根的形式可知，选（A ）.4.20答案：应选（B ）解析：由题意可知，-1是特征方程二重特征根，1是特征方程的特征根，故特征方程为()()2110+-=r r ，即3210+--=r r r .故三阶常系数齐次线性方程为0y y y y ''''''+--=.故选（B ）.4.21答案：应选（C ）解析：：特征方程为2220++=r r 即2(1)1+=-r ，解得特征根为1,21i r =-±.而()e sin x f x x -=，i 1i w ±=-±λ是特征根，故特解的形式为*e (cos sin )x y x a x b x -=+.4.22答案：应填()*22e xy x ax bx c dx =+++解析：特征方程为220-=r r ，特征根10r =,22r =.对21()1=+f x x ，10λ=是特征根，所以()*21y x ax bx c =++.对22()exf x =，22λ=也是特征根，故有*22e =x y dx .从而***12=+y y y 就是特解.故答案为()*22e x y x ax bx c dx =+++.4.23解：所给微分方程的特征方程为256(2)(3)0++=++=r r r r ，特征根为12=-r ,23=-r .于是，对应齐次微分方程的通解为2312)e e xx y x C C --=+.爱启航在线考研设所给非齐次方程的特解为*e xy A -=.将*()y x 代入原方程，可得1A =.由此得所给非齐次方程得特解*e xy -=.从而，所给微分方程得通解为2312()e e e xx x y x C C ---=++，其中1C ,2C 为任意常数.4.24答案：应选（C ）解析：将()()000y y '==代入3e xy py qy '''++=，得()01''=y .()()()()()22000ln 122limlimlimlim 2x x x x x x x y x y x y x y x →→→→+===='''.故选C.4.25答案：应填12e(cos sin )e xxC x C x ++解析：所给微分方程的特征方程为22201i -+=⇒=±r r r ，从而齐次通解为12e (cos sin )x C x C x +，设特解为e x A ，代入方程得e 2e 2e e 1x x x x A A A A -+=⇒=，即得特解为e x .非齐次通解为12e(cos sin )e xx C x C x ++.。