晶体结构的分析与计算

课时跟踪检测（三十二） 晶胞结构的分析与计算1.如图所示是某原子晶体A 空间结构中的一个单元，A 与某物质B反应生成C ，其实质是每个A —A 键中插入一个B 原子，则C 物质的化学式为( )A ．ABB ．A 5B 4C ．AB 2D ．A 2B 5解析：选C 根据结构可知，在晶体C 中，每个A 连有4个B ，每个B 连有2个A ，故C 中A ∶B ＝1∶2，故C 的化学式为AB 2。

2.石墨晶体是层状结构，在每一层内，每个碳原子都跟其他3个碳原子相结合。

据图分析，石墨晶体中碳原子数与共价键数之比为( )A ．2∶3B ．2∶1C ．1∶3D ．3∶2解析：选A 每个碳原子被3个六边形共用，每个共价键被2个六边形共用，则石墨晶体中碳原子数与共价键数之比为⎝⎛⎭⎫6×13∶⎝⎛⎭⎫6×12＝2∶3。

3.食盐晶体的结构示意图如图所示。

已知食盐的密度为ρ g·cm －3，摩尔质量为M g·mol －1，阿伏加德罗常数为N A ，则在食盐晶体中Na ＋和Cl －的间距大约是( )A. 32M ρN Acm B. 3M 2ρN A cm C. 32N A ρM cm D. 3M 8ρN A cm 解析：选B 食盐晶胞中含有4个Na ＋和4个Cl －，每个晶胞的体积为4M ρN Acm 3，设食盐晶体里Na ＋和Cl －的间距为x cm ，所以可得(2x )3＝4M ρN A ，解得x ＝ 3M 2ρN A ，即在食盐晶体中Na ＋和Cl －的间距大约是3M 2ρN A cm 。

4.(2020·济宁模拟)萤石(CaF 2)的晶胞如图所示(1)白球代表的粒子为________。

(2)Ca 2＋和F －的配位数分别为______、________。

(3)晶体中F －配位的Ca 2＋形成的空间结构为________形；Ca 2＋配位的F －形成的空间结构为________形。

晶体结构计算范文一、晶体结构计算的原理和方法晶体结构是由一个个原子或离子组成的有序排列，这种有序排列在结晶体中呈现出周期性的空间分布。

晶体结构计算的主要目标是确定晶体中原子的准确位置和其之间的相互作用，以及晶格参数等信息。

晶体结构计算的方法主要有实验方法、理论计算方法和模拟方法等。

实验方法包括X射线衍射、电子衍射、中子衍射等，通过分析衍射的图样可以确定晶体的结构。

理论计算方法主要是基于量子力学原理，包括密度泛函理论、分子力学等，通过计算得到晶体的能量、晶格参数和原子位置等信息。

模拟方法主要有分子动力学模拟、蒙特卡洛模拟等，模拟系统的原子运动和相互作用，从而得到晶体的结构和性质。

二、晶体结构计算的应用晶体结构计算在材料科学、物理化学等领域具有广泛的应用。

首先，晶体结构计算可以用于研究材料的物理和化学性质。

通过计算分析可以预测材料的电子能带结构、光学性质、磁性等，为材料的设计和应用提供理论基础。

其次，晶体结构计算可以用于材料的合成和工艺优化。

通过计算和模拟可以预测材料的晶体生长行为，优化合成工艺，提高材料的质量和性能。

此外，晶体结构计算还可以用于研究材料的相变过程、相图和微观性质变化等，对材料的相变机制和性质变化规律进行深入研究。

三、晶体结构计算的实际案例展示为了更好地展示晶体结构计算的应用，我们以典型的半导体材料硅Sio2为例进行分析。

硅是一种广泛应用于电子器件中的材料，其结构具有平面型和空间型两种。

通过晶体结构计算可以得到硅的结构参数、晶体中原子的位置等信息。

首先，通过X射线衍射实验可以得到硅的晶胞结构和晶格参数。

然后，利用密度泛函理论和分子动力学模拟等方法进行计算分析，得到硅晶体中原子的位置以及相互作用等信息。

通过计算和模拟可以发现硅晶体中的晶格缺陷、晶界和表面等问题，并对其进行优化和修复，得到具有优异性能的硅晶体材料。

在实际应用中，硅晶体的结构计算可以用于电子器件的设计和性能优化。

通过模拟和计算可以预测材料的电子能带结构，优化器件的导电性能和光学特性，提高器件的效率和可靠性。

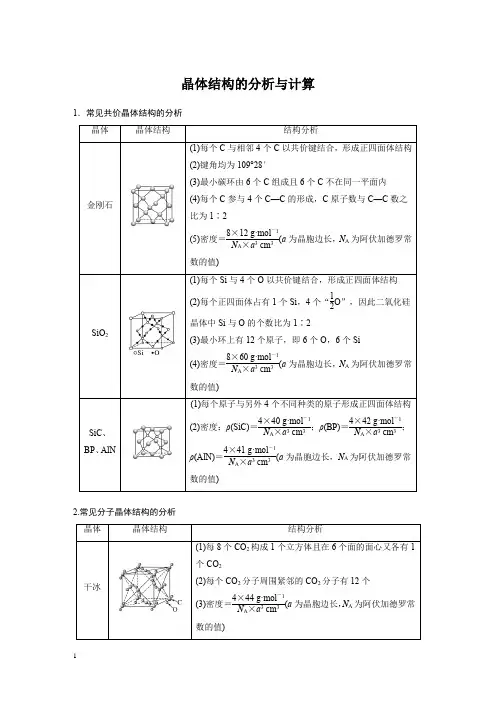
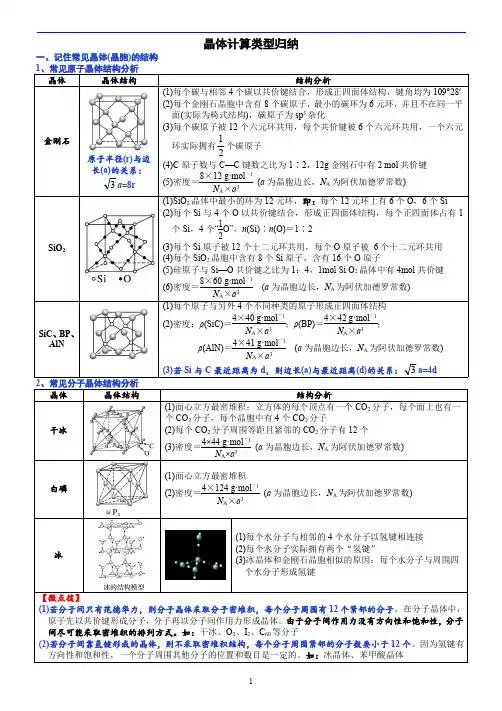
晶体结构的分析与计算1．常见共价晶体结构的分析2.常见分子晶体结构的分析3.常见离子晶体结构的分析684F－：8；Ca2＋：41．AB型化合物形成的晶体结构多种多样。

下图所示的几种结构所表示的物质最有可能是分子晶体的是()A．①③B．②⑤C．⑤⑥D．③④⑤⑥2．如图为几种晶体或晶胞的示意图：请回答下列问题：(1)上述晶体中，微粒之间以共价键结合形成的晶体是________。

(2)冰、金刚石、MgO、CaCl2、干冰5种晶体的熔点由高到低的顺序为______________________。

(3)NaCl晶胞与MgO晶胞相同，NaCl晶体的离子键________(填“大于”或“小于”)MgO 晶体的离子键，原因是___________________________________________________________。

(4)CaCl2晶体中Ca2＋的配位数________。

(5)冰的熔点远高于干冰，除H2O是极性分子、CO2是非极性分子外，还有一个重要的原因是_______________________________________________________________________________。

3．[2017·全国卷Ⅲ，35(5)]MgO具有NaCl型结构(如图)，其中阴离子采用面心立方最密堆积方式，X­射线衍射实验测得MgO的晶胞参数为a＝0.420 nm，则r(O2－)为________nm。

MnO 也属于NaCl型结构，晶胞参数为a′＝0.448 nm，则r(Mn2＋)为________nm。

4．Li2O具有反萤石结构，晶胞如图所示。

已知晶胞参数为0.466 5 nm，阿伏加德罗常数的值为N A，则Li2O的密度为________________________________________g·cm－3(列出计算式)。

5．[2018·全国卷Ⅱ，35(5)]FeS2晶体的晶胞如图所示。

晶体结构是近几年来高考考查的重点和热点，特别是晶体结构的计算更是其 中的重中之重，它体现了高考考试说明中提出的“将化学问题抽象为数学问题， 利用数学工具，通过计算推理解决化学问题的能力”的要求 ，是高考向“ 3+X ”综 合发展的趋势。

在高考的第二轮复习中有必要加以归纳整理。

晶体结构的计算通 常有以下类型:例1：在氯化钠晶体（图1）中，与氯离子距离最近的钠离子有 ____ 个；与氯离子距离最近的氯离子有_________ 个。

解析：我们可以选定中心的氯离子作为基准，设立方体的边长为 a ，则 氯离子与钠离子之间的最近距离为 2，此钠离子位于立方体六个面的面心上， 即有六个钠离子；氯离子间的最近距离为，共有12个。

（如图标号1-12 所示）。

例2： 二氧化碳晶体中，与二氧化碳分子距离最近的二氧化碳分子有 __________ 个。

解析：在图2的二氧化碳分子晶体结构中，8个二 氧化碳分子处于正方体的8个顶点上，还有6个处于正 方体的六个面的面心上。

此时可选定面心的二氧化碳分 子为基准，设正方体的边长为 a,则二氧化碳分子间的最近距离为 子a ，从图中看有8个，它们分别位于该侧面的四个顶点及与之相连的四个面的面心上。

此时 晶体中距离最近的微粒数的计算:• Na + OCl^应注意，图中所给出的结构仅是晶胞。

所谓晶胞，是晶体中最小的重复结构单元, 就是说晶体是以晶胞为核心向空间延伸而得到的，单个的晶胞不能表示整个晶体它能全面正确地表示晶体中各微粒的空间关系。

也的结构。

所以在我们观察晶体结构时应充分发挥空间想象的能力，要将晶胞向各个方向（上，下，左，右，前，后）扩展。

图2向右扩展得图3（为容易观察, 用？表示二氧化碳分子），从中可以看出与二氧化碳分子距离最近的二氧化碳分子有12 个。

从以上的分析可以看出，要正确确定晶体中距离最近的微粒的数目，首先要对晶体结构熟悉，其次要有良好的空间想象能力，要有以晶胞为核心向空间扩展的意识。

XRD晶体结构分析X射线衍射（XRD）是一种常用的晶体结构分析技术，通过测量固体样品对入射X射线的散射模式，可以获得样品的晶体结构信息。

本文将详细介绍XRD晶体结构分析的原理、仪器以及应用。

首先，我们来看一下XRD晶体结构分析的原理。

当入射X射线遇到晶体样品时，它们会与晶体中的原子发生相互作用，散射出来。

这个散射过程可以分为布拉格衍射和多普勒散射两个部分。

布拉格衍射是由于入射X射线与晶体中的原子发生相互作用后，形成反射或折射。

根据布拉格衍射定律，n\lambda=2dsinθ，其中n是整数，λ是入射X射线的波长，d是晶体的晶面间距，θ是衍射角。

通过测量衍射角，我们可以计算出晶面间距，从而了解晶体的结构。

多普勒散射是由于入射X射线与晶体中电子的相互作用而发生的。

相比于布拉格衍射，多普勒散射更加复杂，并且难以精确计算。

因此，在XRD晶体结构分析中，我们通常只考虑布拉格衍射。

为了实现XRD晶体结构分析，我们需要使用X射线衍射仪器。

X射线衍射仪器主要包括X射线发生器、样品支撑装置、X射线探测器以及数据处理系统。

X射线发生器是产生入射X射线的设备。

常见的X射线发生器包括X 射线管和同步辐射装置。

X射线管通过加热阴极来产生电子，这些电子在阳极上产生高速冲击，从而产生X射线。

同步辐射装置则利用高能电子加速器，使电子在加速过程中释放出X射线。

样品支撑装置用于将晶体样品放置在入射X射线路径上。

在XRD晶体结构分析中，我们通常使用平行面支撑法来固定样品，以确保样品的位置稳定和精确。

X射线探测器用于测量样品对入射X射线的散射情况。

常用的X射线探测器有点式探测器和面阵探测器。

点式探测器将散射X射线聚焦到一个小面积上，以获得高空间分辨率的数据。

而面阵探测器则可以同时收集多个数据点，加快数据采集速度。

数据处理系统是将X射线衍射的散射数据转换为晶体结构信息的关键部分。

一般来说，我们会使用计算机软件对数据进行处理和分析。

常见的软件包括XDS、CCP4、PHENIX等。

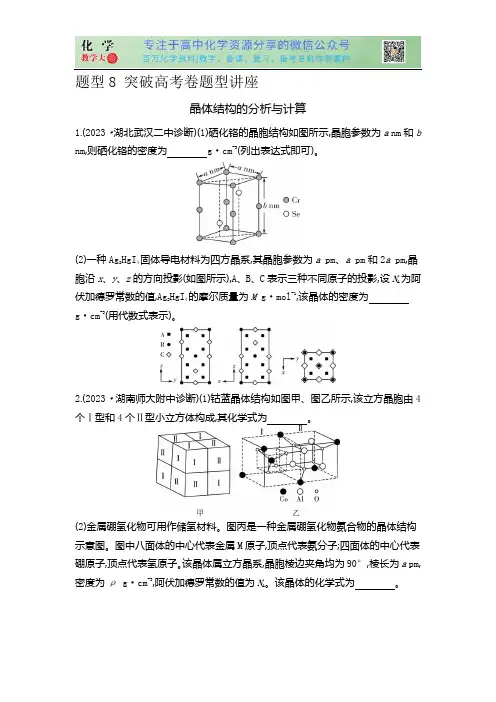
题型8 突破高考卷题型讲座晶体结构的分析与计算1.(2023·湖北武汉二中诊断)(1)硒化铬的晶胞结构如图所示,晶胞参数为a nm和b nm,则硒化铬的密度为g·cm-3(列出表达式即可)。

(2)一种Ag2HgI4固体导电材料为四方晶系,其晶胞参数为a pm、a pm和2a pm,晶胞沿x、y、z的方向投影(如图所示),A、B、C表示三种不同原子的投影,设N A为阿伏加德罗常数的值,Ag2HgI4的摩尔质量为M g·mol-1,该晶体的密度为g·cm-3(用代数式表示)。

2.(2023·湖南师大附中诊断)(1)钴蓝晶体结构如图甲、图乙所示,该立方晶胞由4个Ⅰ型和4个Ⅱ型小立方体构成,其化学式为。

(2)金属硼氢化物可用作储氢材料。

图丙是一种金属硼氢化物氨合物的晶体结构示意图。

图中八面体的中心代表金属M原子,顶点代表氨分子;四面体的中心代表硼原子,顶点代表氢原子。

该晶体属立方晶系,晶胞棱边夹角均为90°,棱长为a pm,密度为ρ g·cm-3,阿伏加德罗常数的值为N A。

该晶体的化学式为。

3.[2021·全国乙卷·35(4)]在金属材料中添加AlCr2颗粒,可以增强材料的耐腐蚀性、硬度和机械性能。

AlCr2具有体心四方结构,如图所示。

处于顶角位置的是原子。

设Cr和Al原子半径分别为r Cr和r Al,则金属原子空间占有率为%(列出计算表达式)。

4.(2021·湖北卷·10)某立方晶系的锑钾(Sb-K)合金可作为钾离子电池的电极材料,图a为该合金的晶胞结构图,图b表示晶胞的一部分。

下列说法正确的是( )。

A.该晶胞的体积为a3×10-36 cm3B.K和Sb原子数之比为3∶1C.与Sb最邻近的K原子数为4a pmD.K和Sb之间的最短距离为125.(2021·重庆卷·18节选)研究发现纳米CeO2可催化O2-分解。

实验一、晶体结构分析一一、实验目的掌握14种空间格子的几何特征与球体密堆积理论，了解配位多面体的配置。

二、实验仪器十四种空间点阵结构模型，球形模型三、实验内容1．了解14种空间格子的几何形态，分析空间格子类型；2．熟悉密堆积理论，注意观察球体堆积时，周围空隙的类型、位置与数量情况；3．了解几种配位多面体的配置情况。

四、实验方法1．观察14种空间格子模型表征14种空间格子，用晶格常数α、β、γ和a、b、c；并判断其所属晶系。

2．观察球体密堆积模型用球体模型进行面心立方紧密堆积、六方紧密堆积和体心立方近似密堆积，分析球体周围空隙的类型、数目和位置分布。

观察分析面心立方紧密堆积、六方紧密堆积和体心立方近似密堆积的单位晶胞，注意其四、八面体空隙分布，判断其数量。

3．观察配位多面体模型模型五、实验报告1．绘制14种空间格子的几何形态，并用注明晶格常数的形式表示出所有14种空间格子；2．分析三种常见的球体堆积情况，绘制出其单位晶胞，画出其（111）、（110）（100）晶面原子排布图[ 密排六方需画出（0001）晶面 ]；3．分析体心立方与面心立方单位晶胞中四、八面体空隙的位置分布与数量，并绘图；4．对不同配位多面体绘图，讨论其临界半径比。

（注：在预习报告中要将14种空间格子的几何图形画好）六、思考题面心立方结构中四面体空隙的数目有几个？他们都是如何分布的？八面体空隙有几个？如何分布？实验二、典型晶体结构分析一、实验目的掌握几种典型矿物的结构，了解晶胞的几何特征。

二、实验仪器晶体结构模型，球和短棒三、实验内容1．对照实际具体结构模型，熟悉金刚石、石墨、氯化钠、氯化铯、闪锌矿、纤锌矿、金红石、碘化镉、萤石、钙钛矿、尖晶石的晶体结构特征；2．观察层状和架状硅酸盐矿物的晶体结构模型的特点，注意观察高岭土、方石英的结构；3．标定萤石模型中所有质点的几何位置；4．组装一个晶体结构模型。

四、实验方法1．分析晶胞模型金刚石、石墨、氯化钠、氯化铯、闪锌矿、纤锌矿、金红石、碘化镉、萤石、钙钛矿、尖晶石均为一个单位晶胞，通过一个单位晶胞，分析晶胞所属空间格子类型及正负离子或原子所处的空间位置，对照模型，分析正负离子的配位数。

体心立方晶格晶胞原子数体心立方晶格晶胞是晶体结构中的一种重要类型，它具有特殊的对称性和特性，是晶体学教学和研究中的重要内容之一。

本文将从晶胞构造、对称性分析、原子数计算等方面详细介绍体心立方晶格晶胞的特点和原子数。

一、晶胞构造体心立方晶格是一种立方晶体结构，其晶胞构造可以用如下方法描述：先由10个球形原子在体心布满的方式构成一个简单立方，再在每个立方体的每个面心位点上加一个原子。

这样，每个晶胞中包含1/8个原子位于立方体的8个角上，以及1个原子位于立方体的中央，共计9个原子。

晶胞的边长是a，中心原子对角距是a*（√3）。

二、对称性分析体心立方晶格具有多种对称性，包括平移对称性、旋转对称性和反射对称性等。

平移对称性表现为晶体无论按任意方向平移都具有相同的结构，旋转对称性表现为晶体在某些方向和角度上具有相同的结构，反射对称性表现为晶体通过某些面的镜像对称具有相同的结构。

这些对称性使得晶体结构具有特殊的性质和规律，方便研究和应用。

三、原子数计算对于体心立方晶格，每个晶胞中含有9个原子，其中8个原子位于8个角上，一个原子位于晶胞中央。

为了计算更大尺寸的晶体中的原子数，我们可以按照以下公式进行计算：N = (1/8 * n_1 + 1/2 * n_2)（1）其中N是晶体中的原子数，n_1是立方体角上的原子数，n_2是立方体面心位点上的原子数。

根据晶胞构造所述，n_1=8, n_2=1，代入公式（1）可得：N = (1/8 * 8 + 1/2 * 1) = 1 + 1/2 = 3/2因此，体心立方晶格的每个晶胞中含有3/2个原子。

这个结论不符合实际情况，所以我们需要对公式（1）进行修正：N = 2 * (1/8 * n_1 + 1/2 * n_2)（2）根据晶胞构造所述，n_1=8, n_2=1，代入公式（2）可得：N = 2 * (1/8 * 8 + 1/2 * 1) = 2 * (1 + 1/2) = 2 * 3/2 = 3 修正后的公式（2）计算结果表明，体心立方晶格的每个晶胞中含有3个原子，符合实际情况。

晶胞结构的分析与计算——晶体结构与性质章温习〔第2课时〕【学习目的】1.能依据分摊法确定晶体的组成；提高笼统思想才干，提升微观辨识与微观探析的开展水平。

〔重难点〕2.经过典型晶胞再看法，学会应用晶胞的基本特点剖析晶体中微粒配位数。

3.树立解晶胞的普通观念、思想模型，能类比迁移相关知识处置新情境新效果；提升处置复杂效果的才干。

〔重难点〕主题学习内容与要求概括归理前置作业金属晶面子心立方最密堆积所得晶胞如下图〔1〕晶胞中的原子有几种位置？列式计算一个晶胞中有几个原子？〔2〕计算晶胞中微粒数目的方法是什么？〔写右侧栏中〕〔3〕假定晶胞边长为a，那么晶胞中最临近两个金属原子间的距离为？〔4〕该堆积方式中金属原子配位数是多少？确定配位数的依据是什么？〔写右侧栏中〕解晶胞的思想模型学晶胞结构的观念主题一确定晶体的组成主效果1-1. A、B构成化合物的晶胞如以下图所示，那么其化学式为？效果1-2.最近发现一种由钛原子和碳原子构成的气态团簇分子，如上图，顶角和面心的原子是钛原子，棱的中心和体心的原子是碳原子，它的化学式是？效果1-3.〔1〕石墨的片层结构中，平均每个六元环含几个碳原子？〔2〕12g金刚石中含有C-C键的个数是多少？题一确定晶体的组成效果1-4.分摊法能处置哪些效果？运用分摊法时应留意什么效果？〔写右侧栏中〕【协作探求】石英晶体的晶胞如图，确定其化学式的方法有哪些？〔请结合必要的算式作答〕主题二剖析晶体中微粒的配位数【温习回忆】CsCl、NaCl、CaF2晶胞中，配位状况对比CsCl晶胞数目NaCl晶胞数目CaF2晶胞数目Cs+配位数Na+配位数Ca2+配位数Cl-配位数Cl-配位数F-配位数Cs+→Cs+Na+→Na+Ca2+→Ca2+Cl-→Cl-Cl-→Cl-F-→F-【协作探求】〔1〕CsCl晶胞中Cs+、Cl-的位置各有几种？CsCl晶胞配位状况剖析对NaCl晶胞配位状况剖析有何协助？〔2〕阴阳离子的电荷比是如何影响离子晶体结构的？〔3〕请给出你以为合理的剖析配位数的普通步骤〔写右侧栏中〕主题效果3-1.金属晶体体心立方最密堆积所得晶胞如下图，假定金属原子的半径为r，那么该堆积的空间应用率是多少？〔列式计算〕三晶胞中微粒数目间距综算计算假定某种金属的摩尔质量为M，用N A表示阿伏加德罗常数，那么该晶体的密度是多少？〔列式计算〕效果3-2.晶体空间应用率、密度计算的关键区分是什么？如何处置？〔写右侧栏中〕【协作探求】在一定温度下NiO晶体可以自发地分散并构成〝单分子层〞〔如图〕，可以以为氧离子作密置单层陈列，镍离子填充其中，计算每平方米面积上分散的该晶体的质量〔氧离子的半径为r m，用含有r的代数式表达结果，写出计算进程〔相对原子质量O 16，Ni59〕整合提升【随堂练习】1.有以下某晶体的空间结构表示图。

晶体结构的计算方法晶体结构的计算方法是通过计算机模拟和各种实验技术来确定晶体的原子排列方式和结构特征。

通过计算方法可以预测晶体的力学性质、电学性质、光学性质和热学性质等。

这些预测以及对晶体结构的理解有助于设计新材料、优化材料性能和解释实验结果。

下面将介绍常见的晶体结构计算方法。

1. 密度泛函理论（Density Functional Theory，DFT）密度泛函理论是现代材料计算中最常用的方法之一、该理论基于电子结构的泛函理论，通过求解系统的电子密度函数来计算晶体的能量、结构和性质。

DFT的基本思想是将体系的总能量表示为电子的密度的函数。

通过求解Kohn-Sham方程，可以得到体系中的电荷密度分布和电子能级结构。

DFT方法可以模拟大多数晶体和材料的结构和性质，并且具有较高的计算效率。

2. 分子动力学模拟（Molecular Dynamics，MD）分子动力学模拟是一种基于牛顿运动定律的方法，它模拟原子或分子在经典力场作用下的运动轨迹，从而获得晶体的结构和动力学性质。

通过冷却、加热、压缩、拉伸等操作，可以模拟实验中无法实现的条件，并研究晶体的变形、相变、热膨胀和热导等特性。

MD方法可以提供分子尺度上晶体的变形和热运动信息，并揭示材料的物理机制。

3. 第一性原理计算方法（First-Principles Calculation）4. 蒙特卡罗模拟（Monte Carlo Simulation）蒙特卡罗模拟是一种统计模拟方法，通过随机抽样和概率统计的方法模拟系统的行为。

在晶体结构计算中，蒙特卡罗模拟可以模拟晶体的随机行为、相变和热力学等过程。

通过引入不同的物理模型和相互作用势能，可以模拟不同条件下的晶体结构和性质。

蒙特卡罗模拟方法可以有效地研究相变、精细结构和相互作用动力学等问题。

除了这些方法，还有许多其他的计算方法被应用于晶体结构计算，例如微扰理论、格林函数方法、电子迁移路径分析等。

不同的计算方法具有不同的适用范围和计算复杂度，根据具体问题的需求选择不同的方法进行晶体结构的计算和模拟。

晶体结构的分析与计算
晶体结构是研究物质结构的重要工具，且晶体结构的理解和计算是研究晶体物理性质的重要环节。

一般情况下，研究晶体结构可以采用实验测量，或者从理论角度进行计算和分析。

本文将主要介绍晶体结构的理论计算和分析方法。

晶体结构计算主要是通过对原子数据或经典力场模型的理论模拟进行计算，给出单位晶体的几何结构，从而得出晶体结构的基本描述。

其中，原子数据计算是指以原子原子半径和原子间相对位置及其他参数为基本参数，使用编程计算机模拟晶体结构的方法。

其中，一般而言，原子间之间的位置及其数量以初始结构尔定义，根据这些原子的位置和量，求出晶体的空间坐标和原子的位错等参数，从而构建晶体的格子，以确定晶体的空间结构。

而经典力场模型计算虽然也可以得出晶体结构，但与原子数据计算相比，其精度和准确性就会受到极大程度的影响。

因此，经典力场模型计算的主要应用，主要是用于拟合实验数据，以获取晶体结构参数，改善晶体结构的准确性。

晶体结构分析主要是通过晶体拓扑结构、晶体相位结构、晶体近似和位错结构等方法进行的。