第6章 多相聚合物体系的流变行为
- 格式:ppt
- 大小:11.82 MB
- 文档页数:27

第六章 聚合物的流变性能一、概念:牛顿流体与非牛顿流体、假塑性流体、宾汉流体、表观粘度、粘流活化能、韦森堡效应(包轴效应)、巴拉斯效应(挤出物胀大现象)、不稳定流动、第一法向应力差二、知识点:聚合物流变学:为高分子成型加工奠定理论基础,绝大数高分子成型加工都是熔融态加工的,如挤出,注射,吹塑等。
高分子熔融时;外力作用发生粘性流动,形变随时间发展,不可塑的粘性流动。
同时表现出可逆的弹性形变。
弹性形变及其后的松驰影响制品的外观,尺寸稳定性。
聚合物的流动并不是高分子链之间的简单滑移,而是运动单元依次跃迁的结果。
6.1牛顿流体和非牛顿流体1、牛顿流体: 剪切形变dy dx =γ,剪切应力F =τ,切变速率)s ( )()(1-dydv dt dx dy d dy dx dt d dt dr ====∙γ速度精度牛顿流动定律: ∙=γητ 牛顿流体:水、甘油、高分子稀溶液。
粘度η:反映液体流动阻力,单位Pa·S2、非牛顿流体:①宾汉流体:需要最小切应力。
如油漆、沥青。
②假塑性流体:切力变稀,大多数聚合物熔体。
③膨胀性流体:切力变稠,胶乳、悬浮体系等。
非牛顿流体定义表现粘度ηa表现粘度随时间变化:①触变体:η随t 而增加而减小;内部物理结构的破坏;胶冻,油漆、有炭黑的橡胶。
②触凝体:η随t 而增加而增大;某种结构的形成。
(饱和聚酯少见)3、聚合物的粘性流动:幂律方程:τ=K γn n=1牛顿流体流体 n<1假塑性流体 n>1 膨胀性流体普适流动曲线(图9-7)①实际聚合物熔体分三个区域:第一牛顿区:零切粘度;假塑性区:随γ增大而减小;第二牛顿区:极限粘度。
缠结理论解释:缠结破坏、形成的过程。
塑料工业上:熔解指数:标准化熔解指数代中测定,一定温度,一定负荷(2160g ),从标准毛细管中流出,单位时间(10min),流出的聚合物质量(克数);PE :190℃,2160g 的熔解指数MI190/2160。

多相/多组分聚合物体系流变学研究郑强*浙江大学高分子系,杭州,310027*Email: zhengqiang@由于具有重大的学术价值和应用价值,对于非均相高分子复杂体系的流变行为和形态结构的研究已经引起了广泛关注[1, 2]。
多相/多组分聚合物的流变性质与其组分间相互作用、相形态密切相关,而且与均相高聚合物相比较,其行为要复杂得多。
近年来,随着大量新型功能高分子材料的不断出现,对于材料流变性质与功能特性(例如,凝胶和聚电解质的特殊结构以及热和导电等功能特性)的相关研究,无论是其重要的理论价值还是其重要的工程指导意义,均为人们所共知。
近年来,浙江大学流变学课题组利用流变学方法对多相/多组分聚合物体系的形态结构展开了多方面的研究,其中包括:(1) 填充体系的结构与流变行为[3-7],(2) 导电高分子复合材料的流变响应[8-12],(3) 聚电解质溶液的流变特性[13, 14],(4) 生物食品材料的流变行为[15, 16]等。
上述研究的开展,不仅丰富了流变学研究体系,也为应用流变学方法研究和表征多相/多组分聚合物体系的结构-性能关系提供了大量有价值的依据。
参考文献1.Ferry J D. Viscoelastic Properties of Polymers. New York: Wiley, 19802.Zheng Q, Zuo M, Chin. J. Polym. Sci., 2005, 4: 341~3543.Hu HG, Zheng Q, J. Mater. Sci., 2005, 40: 49~2514.Dong Q Q, Zheng Q, Du M, Song Y H, J. Soc. Rheo. Japan, 2004, 32: 271~2765.Zhang X W, Pan Y, Zheng Q, Yi X S, J. Polym. Sci. Polym. Phys., 2000, 38, 27396.Xu X M, Tao X L, Gao CH, Zheng Q, J. Appl. Polym. Sci., 2008, 107: 1590~15977.Shangguan Y G, Zhang C H, Xie Y L, Zheng Q, Polymer, 2010, 51: 500~5068.Zhou J F, Song YH, Zheng Q*, Wu Q, Zhang M Q, Carbon, 2008, 46: 679~691.9.Zhou J F, Song Y H, Shangguan Y G, Zheng Q, J Appl. Polym. Sci., 2008, 110:2001~2008.10.Liu Z H, Song Y H, Zhou J F, Zheng Q, J Mater Sci., 2008, 43: 4823 ~ 483311.Cao Q, Song Y H, Tan Y Q, Zheng Q. Polymer, 2009, 50(26): 6350~635612.Cao Q, Song Y H, Tan Y Q, Zheng Q. Carbon, 2010, 48(15): 4268~4275.13.Wu Q, Du M, Ye T, Shangguan Y G, Zhou J P, Zheng Q, Coll. & Polym. Sci., 2009, 287:911~91814.Wu Q, Shangguan YG, Du M, Zhou J P, Song Y H, Zheng Q, J. Coll. Interface Sci. 2009,339: 236~24215.Sun SM, Song YH, Zheng Q, Food Hydrocolloids, 2008, 22: 1090~109616.Sun SM, Song YH, Zheng Q, J. Cereal Sci., 2008, 48: 613~618.。

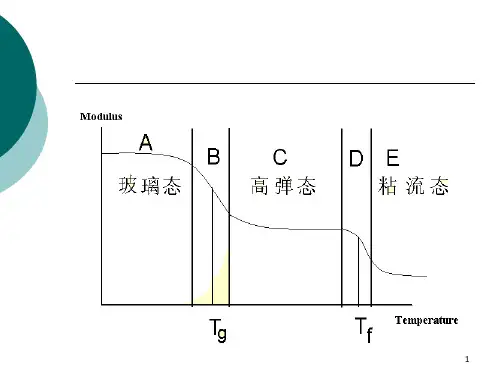
第六章聚合物的粘性流动概述在流动温度(T f)~分解温度(T d)之间,高聚物处于粘性流动状态。
通过分子热运动,高分子链发生质心相对位移,就表现出宏观的流动(不可回复的形变)。
流动温度(T f):非晶态高聚物整链开始运动的温度。
由于高聚物分子量的多分散性,一般高聚物没有明确的流动温度,而只有一个较宽的软化温度范围(一般几十度)。
粘流态主要特征,从宏观看是在外力场作用下,熔体产生不可逆永久变形(塑性形变和流动);从微观看,处于粘流态的大分子链能产生重心相对位移的整链运动。
值得注意的是在粘流态下,材料的形变除有不可逆的流动成份外,还有部分可逆的弹性形变成份,因此这种流动称为“弹性流动”或“类橡胶液体流动”。
绝大多数线型高分子材料具有粘流态。
对无定型聚合物而言,温度高于流动温度即进入粘流态。
对结晶型聚合物而言,分子量低T)即进入粘流态;时,温度高于熔点(m分子量高时,熔融后可能存在高弹态,需继续升温,高于流动温度才进入粘流态。
交联和体型高分子材料不具有粘流态,如硫化橡胶及酚醛树脂,环氧树脂,聚酯等热固性树脂,分子链间有化学键联系,不破坏这些联系,分子链就无法相对移动。
某些刚性分子链和分子链间有强相互作用的聚合物,如纤维素酯类,聚四氟乙烯、聚丙烯腈、聚乙烯醇等,其分解温度(T)低于流动温度(f T),d因而也不存在粘流态。
表6-1给出一些聚合物的流动温度参考值。
表6-1 部分聚合物的流动温度●研究的意义高聚物的成型加工大都在粘性流动状态下进行,而且在成型过程中所形成的聚集态结构对所得到产品的性能表现有至关重要的、决定性的影响。
因此,研究高聚物在流动状态的性质,以及高聚物的结构和外界条件(如温度、受力等)的影响就非常重要。
●两种基本流动方式(非湍流)——剪切流动versus拉伸流动第一种:剪切流动产生横向速度梯度场的流动称为“剪切流动”(速度梯度场与流动方向相垂直)。
剪切流动也称为层流。
例如:河水的流动;管道中的流动。


第六章微相分离多组分聚合物体系Scott扩展到聚合物共混体系均聚物共混时,混合的自由能变化为Flory-Huggins 的高分子溶液统计热力学理论溶剂A和高分子B混合时的自由能变化:v 为体积分数,n 为摩尔分数,χ1为HUggis 参数Φ为体积分数, V R 为摩尔链节体积,V 为总体积。
N:聚合度¾高分子体系中微相形态的演化非常缓慢,在样品制备过程中如果体系偶然陷落到某些非稳定状态,就比较难以转变到热力学稳定态¾实验观测与理论计算¾自洽场理论(self-consistent field theory, SCFT):平均场理论,忽略热涨落¾决定嵌段共聚物微相分离的结构参数:嵌段共聚物微相分离时的嵌段混合焓正比于嵌段间的相互作用参数;微相分离的熵变与嵌段共聚物的聚合度(N)相关;嵌段共聚物组成也是影响相分离时的混合焓和混合熵的重要因素。
嵌段共聚物的组成(体积分数)f和组合参数反映了嵌段共聚物微相分离趋势的强弱对称嵌段共聚物¾自洽场理论的核心思想:对高分子链进行“粗粒化”(coarse-graining)处理¾把一个高分子看成是在空间中运动的“粒子”所走过的一条“路径”。
对含大量高分子的体系,把各个高分子之间的复杂的多体相互作用简化为一个共同的外加势场的作用。
¾1965年Edwards 自回避行走的高分子的线团尺寸(自回避行走的高分子在空间中的形状可以由一个在外场中进行扩散运动的粒子所走过的路径来表示,并且这个粒子的运动方程正好是薛定谔方程。
(高分子形态问题与量子力学之间的深刻联系)R∝N3/5g自洽场理论计算得到的两嵌段高分子本体的热力学相图(谱方法在Fourier空间严格求解)强分离限区域χN>100, S(立方体心相)、C(六方堆积柱分散相)和L(交替分层相)弱分离限区域CPS、S、C、G(双连续立方螺旋相)和L均相区χN<10.5M. W. Matsen, M. Schick. Phys. Rev. Lett., 1994, 72, 2660三嵌段(ABC )聚合物f A 、f B 、NCore-shell sphere/cylinderSpheres in lamellae Rings on cylinderABC线性嵌段高分子在两维空间中的微相形态(a)层状相;(b)柱状相;(c)核-壳结构的柱状相;(d)四方相;(e)和(f)两种含球状相的层状相;(g)含球状相的柱状相Qiu F, et. al., Phys. Rev. E, 2004, 69, 1803动态密度泛函理论(自组装演化动态过程)稀溶液的组装由于嵌段弹性体中聚苯乙烯(PS )内聚能密度较大,两端的PS 嵌段分别与其它链上的PS 嵌段聚集在一起,形成相畴为10~30nm 的球状物(称为微区),作为物理交联点分散在聚丁二烯(PB)的连续相中。



聚合物的流变性流变学是研究材料流动和变形规律的一门科学.聚合物液体流动时,以粘性形变为主,兼有弹性形变,故称之为粘弹体,它的流变行为强烈地依赖于聚合物本身的结构,分子量及其分布,温度,压力,时间,作用力的性质和大小等外界条件的影响.9.1牛顿流体与非牛顿流体9.1.1 非牛顿流体描述液体层流行为最简单的定律是牛顿流动定律.凡流动行为符合牛顿流动定律的流体,称为牛顿流体.牛顿流体的粘度仅与流体分子的结构和温度有关,与切应力和切变速率无关.式中:——剪切应力,单位:牛顿/米2(N/㎡);——剪切速率,单位:s-1;——剪切粘度,单位:牛顿秒/米2(Ns/㎡),即帕斯卡秒(Pas).非牛顿流体:不符合牛顿定律的液体,即η是或时间t的函数. 包括:1,假塑性流体(切力变稀体)η随的↗而↙例:大多数聚合物熔体2,膨胀性流体(切力变稠体)η随的↗而↗例:泥浆,悬浮体系,聚合物胶乳等. 3,宾汉流体. ττy,发生流动.按η与时间的关系,非牛顿流体还可分为:(1)触变体:维持恒定应变速率所需的应力随时间延长而减小. (2)流凝体:维持恒定应变速率所需的应力随时间延长而增加.牛顿流体,假塑性流体与膨胀性流体的应力-应变速率关系可用幂律方程来描述:式中:K为稠度系数n:流动指数或非牛顿指数n=1时,牛顿流体 k=η; n>1 时,假塑性流体; n<1时,膨胀性流体. 定义表观粘度9.2 聚合物的粘性流动9.2.1 聚合物流动曲线聚合物的流动曲线可分为三个主要区域:图9-1 聚合物流动曲线1,第一牛顿区低切变速率,曲线的斜率n=1,符合牛顿流动定律.该区的粘度通常称为零切粘度,即的粘度.2,假塑性区(非牛顿区)流动曲线的斜率n<1,该区的粘度为表观粘度ηa,随着切变速率的增加,ηa值变小. 通常聚合物流体加工成型时所经受的切变速率正在这一范围内.3,第二牛顿区在高切变速率区,流动曲线的斜率n=1,符合牛顿流动定律.该区的粘度称为无穷切粘度或极限粘度η∞.从聚合物流动曲线,可求得ηo,η∞和ηa. 聚合物流体假塑性行为通常可作下列解释:1,从大分子构象发生变化解释;2,从柔性长链分子之间的缠结解释;9.2.2聚合物流体流变性质的测定方法测定粘度主要方法:落球粘度计法,毛细管粘度计法,同轴圆筒转动粘度计法和锥板转动粘度计法.(一)落球粘度计落球粘度计可以测定极低剪切速率(γ)下的切粘度.它既可测定高粘度牛顿液体的切粘度,也可测定聚合物流体的零切粘度.(二)毛细管粘度计毛细管粘度计使用最为广泛,它可以在较宽的范围调节剪切速率和温度,最接近加工条件.常用的剪切速率范围为101~106s-1,切应力为104~106Pa.除了测定粘度外,还可以观察挤出物的直径和外形或改变毛细管的长径比来研究聚合物流体的弹性和不稳定流动(包括熔体破裂)现象.(三)同轴圆筒粘度计有两种形式:一种是外筒转动内筒不动;另一种是内筒转动,外筒固定,被测液体装入两个圆筒间.下面介绍内筒转动的粘度计.同轴圆筒粘度计因内筒间隙较小,主要适用于聚合物浓溶液,溶胶或胶乳的粘度测定. (四)锥板粘度计锥板粘度计是用于测定聚合物熔体粘度的常用仪器.1,熔融指数(MI) 单位时间(一般 10min)流出的聚合体熔体的质量(克).MI↗,流动性↗(常用于塑料) 2,门尼粘度在一定温度和一定转子转速下,测定未硫化胶时转子转动的阻力. 门尼粘度↗,流动性↙(常用于橡胶)9.2.3 熔体粘度的影响因素1,分子量的影响分子量M大,分子链越长,链段数越多,要这么多的链段协同起来朝一个方向运动相对来说要难些.此外,分子链越长,分子间发生缠结作用的几率大,从而流动阻力增大,粘度增加.当MMc 是因为超过临界分子量以后,分子链之间的缠结更为厉害.在高剪切速率下,粘度对分子量的影响减小,是因为在高剪切速率下,更容易发生解缠.图9-3分子量对聚合物粘度的影响图9-3 分子量对聚合物粘度的影响可以发现,分子量大的聚合物的粘度对剪切速率的依赖更大.原因:分子量大则易缠结,剪切速率小时粘度较大;剪切速率增加后,由于解缠粘度下降很快.2,分子量分布分子量相同,分子量分布宽的含长链多,缠结严重,故粘度高.随着剪切速率的增加,解缠严重,长链对粘度的贡献降低,所以粘度下降严重.图9-4分子量分布对聚合物粘度的影响3,分子链支化的影响短支化时,相当于自由体积增大,流动空间增大,从而粘度减小.长支化时,相当长链分子增多,易缠结,从而粘度增加.4,温度一般温度升高,粘度下降.各种聚合物的粘度对温度的敏感性有所不同.粘度与温度的关系可用A rrhen ius方程来描述.DEh -粘流活化能,与分子结构有关系,一般分子链越刚硬,或分子间作用力越大,则流动活化能高,这类聚合物的粘度对温度敏感.图9-5温度对熔融黏度的影响图9-6剪切力(或速率)对熔融黏度的影响5,剪切速率大多数聚合物熔体为假塑性流体,其粘度随剪切速率的增加而下降.柔性链容易缠结,剪切速率对其影响更大,如图9-6所示.9.3聚合物熔体的弹性表现聚合物熔体在流动过程中,不仅产生不可逆的塑性形变,同时伴有可逆的高弹形变,并同样具有松弛特性,这是聚合物熔体区别于小分子流体的重要特点之一.当聚合物的相对摩尔质量很大,外力对其作用的时间很短或速度很快,温度稍高于熔点或粘流时,产生的弹性形变特别显著.几种典型的熔体弹性现象:1,爬杆效应(韦森堡效应)爬杆效应:当聚合物熔体或浓溶液在容器中进行搅拌时,因受到旋转剪切的作用,流体会沿内筒壁或轴上升,发生包轴或爬杆现象.爬杆现象产生的原因:法向应力差.2,挤出胀大现象挤出胀大现象:当聚合物熔体从喷丝板小孔,毛细管或狭缝中挤出时,挤出物的直径或厚度会明显地大于模口尺寸,有时会胀大两倍以上,这种现象称作挤出物胀大现象,或称巴拉斯(B arus)效应.3,不稳定流动-熔体破裂现象聚合物熔体在挤出时,当剪切速率过大超过某临界值时,随剪切速率的继续增大,挤出物的外观将依次出现表面粗糙,不光滑,粗细不均,周期性起伏,直至破裂成碎块这些现象统称为不稳定流动或弹性湍流,其中最严重的为熔体破裂.。

