放大器极零点与频率响应

运算放大器零极点补偿
运算放大器的零极点补偿是通过调整电路中的零点和极点位置来优化放大器的稳定性和频率响应。

零极点补偿通常包括以下几个方面：
1. 主极点补偿：这种补偿的主要目的是降低控制带宽，确保在功率部分或其他已加补偿部分的相位达到180度之前，增益降至0dB。

这有助于防止运算放大器产生振荡。

2. 双极点、单零点补偿：适用于功率部分只有一个极点的补偿场景，例如所有电流型控制和非连续方式电压型控制。

3. 三极点、双零点补偿：适用于输出带LC谐振的拓扑结构，如所有没有使用电流型控制的电感电流连续方式拓扑。

4. 零点和极点的作用：零点和极点分别表示增益曲线上的不同界限。

零点表现为高通特性，即经过零点后，增益以+20dB/dec增加；而极点表现为低通特性，即经过极点后，增益以-20dB/dec降低。

5. 电容的作用：在补偿网络中，电容C1主要用于与电阻R2一起提升相位，同时也提高了低频增益。

电容C2增加了一个高频极点，有助于降低开关噪声干扰。

6. 稳定性考虑：在设计补偿网络时，需要确保系统的稳定性。

这意味着在保证稳定的前提下，补偿元件的值应尽可能小，以减少对电路性能的影响。

总的来说，零极点补偿是运算放大器设计中的一个重要环节，它直接影响到放大器的性能和稳定性。

通过合理地设置零点和极点，可以使放大器在不同的工作频率下保持良好的性能，同时避免不稳定现象的发生。

放大电路频率响应放大电路频率响应是指放大电路对输入信号频率的响应程度。

在实际应用中，我们通常会使用放大电路来放大特定频率范围内的信号。

因此，了解和研究放大电路的频率响应对于电子工程师来说至关重要。

1. 频率响应的定义放大电路的频率响应是指输出信号的幅度和相位与输入信号幅度和相位之间的关系。

频率响应通常以幅频特性和相频特性来描述。

幅频特性表示了放大电路在不同频率下的增益变化情况，而相频特性则表示了输出信号与输入信号之间的相位差随频率变化的情况。

2. 低频放大电路的频率响应低频放大电路通常是指对低频信号进行放大的电路，如音频放大器。

在低频范围内，放大电路的增益通常是比较高的，且相位差变化较小，可以近似认为是线性的。

因此，在低频范围内，放大电路的频率响应一般是比较平坦的。

这也是为什么音频放大器可以将输入信号的音频频率范围放大到可听的范围。

3. 高频放大电路的频率响应高频放大电路通常用于对高频信号进行放大，如射频放大器。

在高频范围内，放大电路的增益会随着频率的增加而下降，并且相位差也会随之变化。

这是因为高频信号的传输特性会受到电感、电容和电阻等因素的影响。

因此，在设计和应用高频放大电路时，需要考虑这些因素，以获得所需的频率响应。

4. 频率响应测量与分析为了准确测量和分析放大电路的频率响应，常用的方法包括频率响应曲线测量和Bode图分析。

在频率响应曲线测量中，会对放大电路输入不同频率的测试信号，然后测量输出信号的幅度和相位差。

通过将这些数据绘制成曲线，可以得到放大电路在不同频率下的频率响应特性。

而Bode图则将频率响应的幅度和相位差以对数坐标的形式绘制出来，更直观地反映了放大电路的频率响应情况。

总结：放大电路的频率响应对于实际应用具有重要意义。

了解放大电路的频率响应可以帮助我们选择适合的放大电路来满足特定的需求。

通过频率响应测量和分析，我们可以更好地研究和设计放大电路，以实现所需的频率响应特性。

放大电路中的频率响应分析频率响应是指电路对不同频率信号的响应程度，它描述了一个电路在不同频率下的增益和相位关系。

在放大电路中，频率响应分析十分重要，可以帮助我们了解电路的放大特性及其在不同频率下的表现。

本文将对放大电路中的频率响应进行详细的分析和探讨。

1. 引言在电子电路设计中，信号的放大是一项基本且必要的技术。

而放大电路的频率响应对信号的增益和相位有着重要的影响。

了解和分析放大电路的频率响应可以帮助我们优化电路设计，达到更好的信号放大效果。

2. 频率响应的定义与意义频率响应是指电路对不同频率信号的放大或衰减程度。

可以用增益-频率特性曲线来描述。

频率响应分析有助于我们了解电路的放大范围和频率范围内的增益情况。

3. 放大电路中的频率响应特性不同类型的放大电路，其频率响应特性存在差异。

接下来我们将讨论常见的放大电路的频率响应特性。

3.1 集成放大器的频率响应集成放大器是一种常见的放大电路。

在低频范围内，集成放大器的增益较高，但在高频范围内会出现增益下降的情况。

这是因为集成放大器的极点和零点的存在。

3.2 增强型共射放大器的频率响应增强型共射放大器的频率响应特性会受到电容的影响。

输入和输出的电容以及内部电容会对频率响应产生影响，因此在高频范围内，增强型共射放大器的增益会下降。

4. 频率响应分析方法在分析放大电路的频率响应时，我们可以使用频谱分析或者特定频率点响应分析的方法。

频谱分析可以得到整个频率范围内的响应情况，而特定频率点响应分析则可以更详细地了解某个特定频率下的放大情况。

5. 频率响应优化策略为了优化放大电路的频率响应，我们可以采取一些策略。

比如使用补偿电容来提高高频增益，调整电容和电感的数值以改变频率响应特性等。

6. 实例分析在这一节中，我们将以具体的实例来分析和展示频率响应的影响。

通过实际的测量数据，我们可以更直观地观察到频率响应曲线的变化。

7. 结论频率响应是放大电路分析中的重要内容。

通过频率响应分析，可以帮助我们深入了解电路的放大特性和响应情况。

滤波器设计中的极点与零点的选择与布局在滤波器设计中，极点与零点的选择与布局起着至关重要的作用。

极点和零点是滤波器频率响应的关键元素，它们决定了滤波器的特性和性能。

本文将探讨极点和零点的选择与布局对滤波器设计的影响，以及在不同应用中如何合理选择和布置它们。

一、极点与零点的含义及作用极点和零点都是滤波器系统转移函数的特征根，它们描述了该系统的频率响应。

极点是滤波器传递函数的分母等于零的点，它决定了滤波器的衰减特性和稳定性。

零点是滤波器传递函数的分子等于零的点，它能够提高滤波器的选择性和频率响应。

极点和零点的选择与布局与滤波器的频率响应特性密切相关。

通过合理选择和布置极点和零点，可以实现所需的滤波器特性，如通带和阻带的增益、截止频率等。

二、极点与零点的选择原则1. 极点的选择原则（1）稳定性：极点位置应该在左半平面，这样才能保证滤波器的稳定性。

如果极点位置在右半平面，滤波器会产生震荡或不稳定的响应。

（2）滤波器特性：极点的数量和位置决定了滤波器的特性。

例如，二阶低通滤波器通常具有两个实根或共轭复根，决定了滤波器的截止频率和衰减。

2. 零点的选择原则（1）选择性：零点的位置和数量决定了滤波器的选择性能。

合理选择和布置零点可以提高滤波器对特定频率的抑制能力。

（2）增益：零点对滤波器的增益也有影响。

在某些应用中，零点的位置可以用来提高或降低滤波器的增益。

三、极点与零点的布局方法1. 极点的布局方法（1）Bessel滤波器：Bessel滤波器通过在$s$平面上均匀分布极点来实现平坦的群延迟特性。

这种布局方法适用于需要保持信号波形的应用，例如音频信号处理。

（2）Butterworth滤波器：Butterworth滤波器的极点在单位圆上均匀分布，能够实现最大斜率的通带过渡带抑制特性。

这种布局方法适用于需要在通带和阻带之间平衡性能的应用。

（3）Chebyshev滤波器：Chebyshev滤波器的极点主要分布在椭圆轨迹上，能够实现更陡的过渡带和更高的选择性。

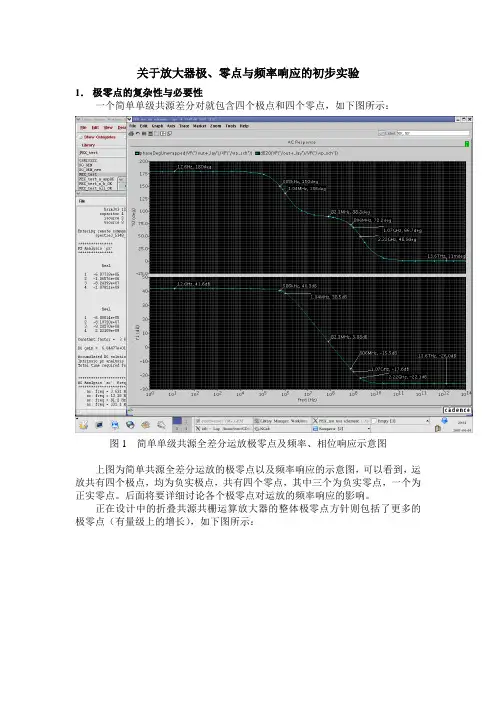
关于放大器极、零点与频率响应的初步实验1．极零点的复杂性与必要性一个简单单级共源差分对就包含四个极点和四个零点，如下图所示：图1 简单单级共源全差分运放极零点及频率、相位响应示意图上图为简单共源全差分运放的极零点以及频率响应的示意图，可以看到，运放共有四个极点，均为负实极点，共有四个零点，其中三个为负实零点，一个为正实零点。

后面将要详细讨论各个极零点对运放的频率响应的影响。

正在设计中的折叠共源共栅运算放大器的整体极零点方针则包括了更多的极零点（有量级上的增长），如下图所示：图2 folded-cascode with gain-boosting and bandgap all-poles details图3 folded-cascode with gain-boosting and bandgap all-zeros details从上述两张图可以看到，面对这样数量的极零点数量（各有46个），精确的计算是不可能的，只能依靠计算机仿真。

但是手算可以估计几个主要极零点的大致位置，从而预期放大器的频率特性。

同时从以上图中也可以看到，详细分析极零点情况也是很有必要的。

可以看到46个极点中基本都为左半平面极点（负极点）而仿真器特别标出有一个正极点（RHP ）。

由于一般放大器的极点均应为LHP ，于是可以预期这个右半平面极点可能是一个设计上的缺陷所在。

（具体原因现在还不明，可能存在问题的方面：1。

推测是主放大器的CMFB 的补偿或者频率响应不合适。

2。

推测是两个辅助放大器的带宽或频率响应或补偿电容值不合适）其次可以从极零点的对应中看到存在众多的极零点对（一般是由电流镜产生），这些极零点对产生极零相消效应，减少了所需要考虑的极零点的个数。

另外可以看到46个零点中45个为负零点，一个为正零点，这个正零点即是需要考虑的对放大器稳定性产生直接影响的零点。

以上只是根据仿真结果进行的一些粗略的分析，进一步的学习和研究还需要进行一系列实验。

共源级放大器的频率响应一、引言共源级放大器（Common Source Amplifier）是一种常用的放大电路，广泛应用于各种电子设备和系统中。

了解其频率响应特性对于分析和优化电路性能具有重要意义。

本文将详细讨论共源级放大器的频率响应，分析影响频率响应的各种因素，并探讨如何在实际应用中改善频率响应。

二、共源级放大器的频率响应特性1.低频响应共源级放大器的低频响应主要受到晶体管输入电容和输出电容的影响。

当输入信号频率较低时，输入电容对信号的衰减较小，使得放大器具有良好的低频响应。

然而，随着频率的增加，输入电容的阻抗逐渐降低，导致信号衰减加剧，低频响应变差。

2.高频响应共源级放大器的高频响应受到晶体管特性、负载电阻和输入输出电容等因素的影响。

在高频段，晶体管的输入和输出电容对信号的衰减较大，同时负载电阻也会对高频信号产生阻抗，从而导致高频响应恶化。

3.带宽和滚降带宽是衡量放大器频率响应宽度的指标，滚降则反映了信号在频率响应中的衰减程度。

为了获得较好的带宽和滚降特性，需要优化电路设计和选用合适的晶体管。

三、影响频率响应的因素1.晶体管的特性晶体管的输入和输出电容、电流放大系数等特性参数对频率响应具有重要影响。

选用低输入输出电容、高电流放大系数的晶体管可以提高放大器的频率响应。

2.负载电阻负载电阻的选取也会影响共源级放大器的频率响应。

负载电阻越小，高频响应越好；但过大则会使低频响应变差。

因此，在设计电路时需要权衡负载电阻的大小。

3.输入和输出电容输入和输出电容对频率响应的影响已在前文提及。

减小输入和输出电容可以提高放大器的频率响应，但同时也会增加电路的复杂性和成本。

四、改善频率响应的方法1.选用合适的晶体管选用低输入输出电容、高电流放大系数的晶体管可以有效提高共源级放大器的频率响应。

此外，采用宽带晶体管技术也可以拓宽放大器的带宽。

2.优化电路设计通过调整电路参数，如负载电阻、输入输出电容等，可以优化共源级放大器的频率响应。

放大器的频率响应(1)放大电路中存在电抗元件耦合电容1C ，2C 和射极旁路电容Ce ，以及电路的分布电容0C 。

和管子的极间电容。

因此对不同频率它呈现的阻抗不同，放大电路对不同频率成分的放大倍数和相位移不同。

放大倍数与频率的关系，称为幅频特性，相位与频率的关系称为相频特性。

放大器对不同频率放大倍数的不同将引起幅频失真；放大器对不同频率的相位移不同，将引起相频失真。

上述失真统称为频率失真，由于它们是曲线性元件引起的，故又常称为线性失真。

(2)影响低频段的频率响应主要受耦合电容1C ，2C 和旁路电路Ce 的影响。

影响高频段的频率响应，主要受三极管的极间电容和电路分布电容0C 的影响。

在等效放大电路的频率响应电路中要根据高、低频时不同电容的影响取舍。

如高频等效电路主要考虑极间电容和分布电容的影响，忽略其他电容的影响；低频等效电路主要考虑耦合电容和旁路电容Ce 的影响，忽略其他电容的影响。

(3)上限频率H f 和下限频率L f ，。

截止频率：定义放大倍数下降到中频区放大倍数的21时所对应的频率。

用分贝表示是比中频区放大增益的分贝数下降3 dB 。

下限频率L f ：低频段的截止频率。

上限频率H f ：高频段的截止频率。

频带宽度：L H BW f f f -=。

如果输入信号的频率在频率宽度范围内，放大器的放大倍数和相位移为常数；如果超出了频带宽度，则产生线性失真。

(4)多级放大器频率特性分析。

多级放大器总的上限频率^比其中任何一段的上限频率都要低；下限频率L f 。

比其中任何一级的下限频率都要高。

即多级放大器的级数增加了，总的放大倍数增大了，但总的频带宽度变窄了。

(5)组合电路频率响应的定性分析。

共射一共基组合放大电路：它的上限频率主要决定于共射电路，而共射电路的上限频率又随其负载电阻减小而提高。

共射电路的负载电阻正是共基放大电路的输入电阻，其值很小，所以这种电路组合以后，它的上限频率比负载直接接于共射放大电路的输出端时要高得多，这样的组合可以提高GBW 值，一般用在负载电阻较大的场合。

共源级放大器的频率响应
共源极放大器（Cascode Amplifier）的频率响应特点如下：
1.频率特性：共源极放大器的频率响应具有负相频和极点的固有特性。

这意味着放大器对于低频信号是低通滤波器，对于高频信号是高通滤波器。

其带宽受制于电路参数。

2.增益和带宽：共源极放大器的增益大小取决于输入阻抗和输出阻抗的比值，并且随频率增加而减小。

因为频率越高，阻抗越小，所以低频段的增益大于高频段的增益。

高频段（如RF电路）的设计目标通常为-3dB带宽是截止频率的2~3倍，在1GHz时，应至少保证300MHz的带宽。

3.输入阻抗和输出阻抗：共源极放大器的输入阻抗非常高，可以近似为无穷大。

但是，输出阻抗非常低，甚至在电阻几欧姆级别下仍具有相当高的功率容量。

因此，共源极放大器具有很高的输入阻抗和非常低的输出阻抗。

综上，共源极放大器在电路设计中可以作为放大器、滤波器和衰减器使用，根据其特点可以进行不同的应用场景选择。

什么是放大器的频率响应放大器的频率响应是指放大器对不同频率输入信号的增益变化情况。

频率响应是评估放大器性能的重要指标之一，它描述了放大器在不同频率下是否能够保持稳定的增益，并在一定范围内传递输入信号的频率特性。

频率响应通常表示为放大器的增益与频率之间的关系。

在理想情况下，放大器应该使得所有频率的输入信号都能够得到相同的增益。

然而，实际情况中放大器的频率响应可能会受到一些限制和非线性因素的影响。

因此，了解和分析放大器的频率响应对于正确选择和设计放大器至关重要。

放大器的频率响应可以通过绘制Bode图来表示。

Bode图是一种将放大器的幅频特性和相频特性绘制在一张图上的图示方法。

通过Bode 图，我们可以清晰地观察到放大器在不同频率下的增益变化情况。

通常，放大器在低频时会有较高的增益，随着频率的增加，其增益值会逐渐下降。

这种现象被称为低频截止。

此外，放大器在高频时也会出现增益下降的情况，这是由于放大器的内部元件（如晶体管）的衰减效应和频率响应限制所导致。

高频截止频率是指放大器增益下降到其最大增益的3dB处的频率。

放大器的频率响应还可以受到输入和输出耦合电容的影响。

这些耦合电容会限制低频信号的传输，从而导致低频增益下降。

为了改善放大器的频率响应，可以采取一些措施。

例如，可以使用负反馈电路来提高放大器的稳定性和频率响应。

负反馈电路通过将放大器的输出与输入之间进行比较，并校正其增益特性，从而改善了放大器的频率响应。

总之，放大器的频率响应是指放大器对不同频率信号的增益变化情况。

了解和分析放大器的频率响应对于正确选择和设计放大器至关重要。

通过采取一些措施，如负反馈电路，可以改善放大器的频率响应，使其能够更好地满足实际应用的需求。

电路中的放大器的增益与频率响应在现代电子科技的应用中，放大器是起到非常重要作用的一个电路元件。

放大器能够将电信号的幅度进行放大，以增强信号的强度和质量。

然而，在放大器的设计和应用过程中，我们需要考虑的因素不仅仅是增益，还要关注频率响应。

放大器的增益是指输入信号与输出信号之间的增加倍数。

在常见的放大器电路中，如共射放大器、共基放大器和共集合放大器等，都具有不同的增益特点。

在这些放大器中，增益的大小与直流偏置、电容电阻等元件的选择有关。

我们可以根据需求来选择不同的放大器电路来实现不同的放大倍数。

然而，放大器的增益并不是越大越好。

放大器的增益过大会导致信号失真和噪声增加。

因此，在实际应用中，我们需要根据具体需求，选择合适的增益范围。

另一个需要关注的是放大器的频率响应。

频率响应是指放大器在不同频率下对信号的放大程度。

我们知道，信号是由不同频率的分量组成的，需要放大器在不同频率下都能够正确地放大信号。

在放大器的设计中，频率响应往往会随着频率的增加而发生变化。

这是由放大器的电路特性决定的。

例如，晶体管的频率特性受到晶体管内部电容和电感等因素的影响。

因此，在使用放大器时，我们需要对其频率响应进行评估和优化。

为了解决频率响应的问题，我们通常会采用一些补偿措施。

例如，引入负反馈电路或者使用滤波电路等来限制放大器的频率响应。

这样可以使放大器在特定的频率范围内具有较好的放大效果，避免信号失真和波形变形等问题。

除了增益和频率响应，放大器的线性度、失真度、输入输出阻抗等也是需要考虑的因素。

这些因素都会对放大器的性能产生影响。

因此，在放大器的设计和应用中，我们需要全面考虑这些因素，并进行合理的折衷和选择。

总之，电路中的放大器不仅仅是简单的放大信号的功能，还需要关注增益和频率响应等因素。

增益决定了信号放大的倍数，而频率响应则关系到放大器在不同频率下的放大能力。

要设计出性能良好的放大器，需要综合考虑各种因素，并进行合理的设计和优化。

放大器主极点和次极点放大器主极点和次极点是放大器设计和调试中非常重要的参数和指标。

主极点和次极点的选择和设置直接影响着放大器的性能和稳定性。

本文将对放大器主极点和次极点进行详细的介绍和分析。

放大器的主极点是指放大器开环传递函数的极点中最远离原点的极点。

主极点的位置决定了放大倍数和频率响应的上限。

主极点越远离原点，放大倍数就越高，频率响应的上限也就越高。

主极点的位置还决定了放大器的带宽。

主极点越远离原点，放大器的带宽也就越宽。

因此，主极点的选择非常重要，可以通过改变主极点的位置来调节放大器的放大倍数和频率响应。

主极点的选择是一个权衡的过程。

一方面，为了实现较大的放大倍数和较宽的带宽，应选择较远离原点的主极点。

另一方面，主极点离原点越远，放大器的稳定性就越差。

因此，主极点的选择还需要考虑放大器的稳定性。

在实际设计中，一般会根据需要平衡放大倍数、带宽和稳定性的要求来选择主极点的位置。

放大器的次极点是指放大器开环传递函数的极点中离原点最近的极点。

次极点的位置决定了放大器的带宽和稳定性。

次极点越接近原点，放大器的带宽就越窄。

如果次极点太接近原点，放大器的带宽可能会非常窄，导致高频信号无法放大。

因此，次极点的位置对放大器的带宽有很大的影响。

次极点的选择也需要权衡不同的因素。

一方面，为了实现较宽的带宽，应选择次极点较远离原点的位置。

另一方面，次极点离原点越远，放大器的稳定性就越好。

因此，次极点的选择还需要综合考虑带宽和稳定性的要求。

在放大器设计中，主极点和次极点的选择是互相关联的。

主极点和次极点的位置决定了放大器的放大倍数、频率响应和稳定性。

在实际设计中，需要针对不同的应用需求和工作条件来选择主极点和次极点的位置。

一般来说，放大器的主极点和次极点应该选择在工作频率的一定范围内，同时满足放大倍数的要求和稳定性的要求。

总之，放大器的主极点和次极点是放大器设计和调试中非常重要的参数和指标。

主极点和次极点的选择直接影响着放大器的性能和稳定性。

运算放大器极点频率
运算放大器是一种重要的电子元件，它在电路中扮演着放大信号、滤波、积分、微分等重要角色。

在运算放大器的设计中，极点频率是一个非常重要的参数，它决定了运算放大器的性能和稳定性。

极点频率是指运算放大器的放大倍数随着频率的变化而发生变化的频率点。

在运算放大器的频率响应曲线中，极点频率是一个重要的参考点。

当频率超过极点频率时，运算放大器的放大倍数开始下降，这意味着它的放大能力受到了限制。

因此，极点频率是运算放大器的一个重要性能指标。

在运算放大器的设计中，极点频率的选择非常重要。

如果极点频率过低，运算放大器的放大能力会受到限制，无法满足高频信号的放大需求。

如果极点频率过高，运算放大器的稳定性会受到影响，容易出现振荡等问题。

因此，极点频率的选择需要综合考虑电路的实际需求和运算放大器的性能参数。

在实际应用中，我们可以通过改变运算放大器的反馈电阻和电容来调整极点频率。

当反馈电阻增大或电容减小时，极点频率会升高，运算放大器的放大能力会增强。

反之，当反馈电阻减小或电容增大时，极点频率会降低，运算放大器的稳定性会增强。

极点频率是运算放大器的一个重要性能指标，它决定了运算放大器的放大能力和稳定性。

在运算放大器的设计和应用中，我们需要综
合考虑电路的实际需求和运算放大器的性能参数，选择合适的极点频率，以保证电路的正常工作。