二次函数特点及应用

二次函数特点及应用论文二次函数是一种重要的数学函数，由于其特殊的数学性质和广泛的应用领域，被广泛应用于各种实际问题中。

本文将介绍二次函数的一些基本特点和常见应用领域。

二次函数的基本特点二次函数是一种具有以下一般形式的函数：y = ax²+ bx + c其中，a、b、c 为常数，且a 不等于0。

二次函数的图像是一个开口向上或向下的抛物线，其重要的特点如下：1. 顶点二次函数的图像上有一个特殊的点，称为顶点。

顶点是抛物线的最高点（当抛物线开口向下时）或最低点（当抛物线开口向上时）。

顶点的横坐标为-b/2a，纵坐标为f(-b/2a) = a(-b/2a)²+ b(-b/2a) + c。

2. 对称轴对称轴是垂直于抛物线的一条直线，它将抛物线分成两个对称的部分。

对称轴的方程为x = -b/2a。

3. 零点二次函数的零点是指函数图像与x 轴相交的点。

零点的个数和位置取决于二次函数的系数所确定的方程的根的数目和位置。

4. 函数值域二次函数的函数值域是由其顶点的纵坐标和开口方向来决定的。

当抛物线开口向上时，函数值域是y 大于等于顶点的纵坐标。

当抛物线开口向下时，函数值域是y 小于等于顶点的纵坐标。

二次函数的常见应用二次函数在各种领域中都有广泛的应用，如物理、经济学和工程学等。

以下是其中的一些常见应用领域：1. 品牌销售二次函数可被应用于拟合销售量与时间的变化趋势。

如此可以预测销售量的未来趋势并相应地安排市场策略。

2. 物理学二次函数可被应用于模拟物理系统的运动，如自由落体运动和弹性碰撞等。

3. 经济学二次函数在经济学中有着广泛的应用，如在市场需求分析，消费者对复杂商品的需求，和成本分析等方面。

4. 工程学二次函数在工程学领域中还可用于求解物体运动的轨迹和分析系统的稳定性等方面。

结论二次函数是一种重要的数学函数，其具有一些基本特点和广泛的应用领域。

通过理解二次函数的特点和应用，可以帮助我们更好地理解各种实际问题的本质和求解方法，从而更好地解决实际问题。

二次函数的应用与实际问题解决二次函数是高中数学中一个非常重要的概念，它在现实生活中有广泛的应用。

本文将介绍二次函数的基本概念和特点，并以几个实际问题为例，阐述二次函数在实际问题解决中的应用。

一、二次函数的基本概念和特点二次函数是代数学中的一种函数类型，其数学表达式为：\[y = ax^2 + bx + c\]其中，a、b、c为常数，且a≠0。

在二次函数中，x为自变量，y为因变量，它们之间存在一种二次关系。

二次函数的图像是一个抛物线，具有一些特点：1. 对称轴二次函数的对称轴是一个垂直于x轴的直线，它将图像分为两个对称的部分。

对称轴的方程为\(x = -\frac{b}{2a}\)。

2. 零点二次函数的零点是函数图像与x轴相交的点，也就是满足方程\(ax^2 + bx + c = 0\)的x的值。

如果方程有实根，则函数图像与x轴有两个交点，如果方程无实根，则函数图像与x轴没有交点。

3. 极值点二次函数的极值点是函数图像上离对称轴最近（或最远）的点，其y坐标称为极值。

如果a>0，则函数的图像开口向上，极值点是最低点；如果a<0，则函数的图像开口向下，极值点是最高点。

4. 函数增减性二次函数的增减性取决于a的正负性。

当a>0时，函数在对称轴左侧递减，在对称轴右侧递增；当a<0时，函数在对称轴左侧递增，在对称轴右侧递减。

以上是二次函数的基本概念和特点，下面我们将介绍几个实际问题，并运用二次函数解决这些问题。

二、实际问题的应用1. 弹体运动问题假设一个弹体从地面上射出，其轨迹可以用二次函数描述。

我们已知弹体离地面的高度与时间的关系为$h = -5t^2 + 20t$，其中h表示高度（米），t表示时间（秒）。

现在要求解这个问题的几个具体情况：（1）弹体达到最大高度时的时间和高度是多少？（2）弹体什么时间落地？（3）弹体射出后的高度变化过程。

对于（1），我们可以通过求解二次函数的极值点来得到。

二次函数图像特点应用
二次函数应用⎧
⎪
⎨
⎪
⎩
刹车距离最值问题
一、刹车距离问题
第一步：让学生观察影响汽车刹车距离的主要因素，找出这些因素是：
1.汽车行驶的速度
2.路面的摩擦系数
第二步：建立适当的函数模型
第三部：根据函数模型来解决实际生活中刹车距离问题
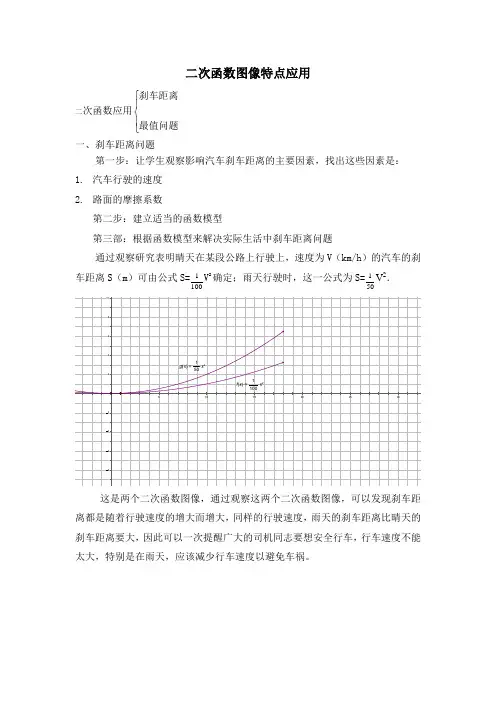
通过观察研究表明晴天在某段公路上行驶上，速度为V（km/h）的汽车的刹
车距离S（m）可由公式S=1
100V2确定；雨天行驶时，这一公式为S=1
50
V2．
这是两个二次函数图像，通过观察这两个二次函数图像，可以发现刹车距离都是随着行驶速度的增大而增大，同样的行驶速度，雨天的刹车距离比晴天的刹车距离要大，因此可以一次提醒广大的司机同志要想安全行车，行车速度不能太大，特别是在雨天，应该减少行车速度以避免车祸。

二、最值问题
在某一指定的高度让学生以一定的初速度向上抛出一物体，忽略空气阻力的情况下抛出时间和上升高度之间的关系。

这是一个和物理知识，因此大家很快就能找出其中的关系，从而建立了恰当的数学模型。

设在距离地面2m高的某处把一物体以初速度V
（m/s）竖直向上抛出，•在不计空气阻力的情况下，其上升高度s（m）与抛出时间t（s）满足：
S=V
0t-
1
2
gt2（其中g是常数，通常取10m/s2），
为研究问题的方便可设V0=10m/s。

度，在0到一秒内，物体上升的高度随时间t的增大而增大，而在1秒到2秒之间物体上升的高度随着t的增大而减小，到2秒的时候物体就落地了。

通过这个实例，我们不仅可以研究到二次函数的最值，还可以通过图像观察它的单调性及其图像的开口方向。

二次函数的特点和应用——研究性学习二次函数是高中数学的一个重要内容，其在数学和实际生活中具有广泛的应用。

本文将通过研究性学习的方式，探讨二次函数的特点和应用。

一、二次函数的定义及特点1. 定义：二次函数是指形如y = ax^2 + bx + c的函数，其中a、b、c是不全为零的常数，a称为二次函数的系数，b、c为一次项和常数项。

2.特点：（1）顶点：二次函数的顶点是函数图像的最高点或最低点，其坐标为（-b/2a,f(-b/2a)）。

（2）开口方向：二次函数的开口方向可由a的正负确定。

当a>0时，二次函数开口向上；当a<0时，二次函数开口向下。

（3）对称轴：二次函数的对称轴是通过顶点且垂直于x轴的直线，其方程为x=-b/2a。

（4）零点：二次函数的零点就是方程y = ax^2 + bx + c = 0的解，有时也称为根。

二次函数可能有0、1或者2个零点。

（5）平移变换：对二次函数进行平移变换可以通过改变函数的系数实现。

平移可以使二次函数的顶点、对称轴位置发生变化。

二、二次函数的应用1.物理学中的应用（1）自由落体问题：当物体自由下落时，它的高度与时间之间的关系可以用二次函数表示。

（2）抛物线轨迹：抛体运动的轨迹是一个抛物线，可以用二次函数描述。

2.经济学中的应用（1）成本函数和利润函数：企业的成本和利润函数往往是二次函数，通过对函数进行分析可以最优化企业的经营策略。

（2）供需曲线：市场的供需关系可以通过二次函数来表示，通过解方程可以求得市场的均衡价格和数量。

3.工程学中的应用（1）弹簧的伸长：弹簧的伸长与所加力的关系可以用二次函数表示。

（2）飞行器轨迹：飞行器的轨迹通常是一个抛物线，可以用二次函数描述。

4.生物学中的应用（1）物种数量的变化：一些物种数量的变化可以用二次函数来描述，通过分析可以预测物种的生态变化趋势。

（2）生物发育曲线：生物的发育过程往往可以用二次函数来表示，如种子发芽过程、昆虫蛹化过程等。

中考二次函数知识点汇总二次函数是一种常见的数学函数，它的形式为f(x) = ax^2 + bx + c，其中a、b、c为常数，且a≠0。

在中考中，掌握二次函数的相关知识点及其应用是非常重要的。

下面是关于中考二次函数的知识点的详细汇总。

一、二次函数的图像特点1.开口方向：当a>0时，二次函数的图像开口向上；当a<0时，二次函数的图像开口向下。

2.对称轴：二次函数的对称轴为直线x=-b/2a。

3.最值：当a>0时，二次函数的最小值为y=f(-b/2a)；当a<0时，二次函数的最大值为y=f(-b/2a)。

4. 零点：二次函数的零点是使f(x) = 0的x值，可通过求解二次方程ax^2 + bx + c = 0来得到。

二、二次函数的性质1.单调性：当a>0时，二次函数是开口向上的，即可知函数在开区间(-∞,-b/2a)上是递增的，在开区间(-b/2a,+∞)上是递减的；当a<0时，二次函数是开口向下的，即可知函数在开区间(-∞,-b/2a)上是递减的，在开区间(-b/2a,+∞)上是递增的。

2. 零点：根据二次函数的定义，可求出二次函数的零点为x = (-b± √(b^2-4ac))/2a。

当判别式（即b^2-4ac）大于零时，二次函数有两个不相等的实根；当判别式等于零时，二次函数有两个相等的实根；当判别式小于零时，二次函数没有实根。

3.达到最值的条件：当a>0时，二次函数取得最小值的横坐标是x=-b/2a；当a<0时，二次函数取得最大值的横坐标是x=-b/2a。

三、二次函数与一次函数的关系1. 平移：二次函数f(x) = ax^2 + bx + c可以通过平移来得到一次函数g(x) = mx + n。

二次函数f(x)与一次函数g(x)的图像关系为：将二次函数的图像向上平移c个单位，然后将平移后的图像沿y轴方向压缩或拉伸，直到到达一次函数g(x)的图像。

二次函数数学知识点高一二次函数是高中数学中的一个重要知识点，它是一种常见的函数类型，在现实生活和各个学科中都有广泛的应用。

本文将从二次函数的定义、特点、图像、性质等多个方面进行论述，帮助读者更好地理解和掌握二次函数的相关知识。

一、二次函数的定义与特点二次函数是形如$f(x) = ax^2 + bx + c$的函数，其中$a, b, c$都是实数且$a\neq 0$。

其中，$a$决定了二次函数的开口方向（正负号），$b$决定了二次函数的对称轴位置，$c$决定了二次函数与纵轴的交点。

二次函数的图像通常为抛物线，它有以下几个特点：1. 开口方向：若$a > 0$，则抛物线开口向上；若$a < 0$，则抛物线开口向下。

2. 对称轴：对称轴是一条垂直于横轴的直线，其方程为$x = \frac{-b}{2a}$。

3. 最值：当$a > 0$时，二次函数的最小值为$c - \frac{b^2}{4a}$；当$a < 0$时，二次函数的最大值为$c - \frac{b^2}{4a}$。

4. 零点：二次函数与$x$轴的交点称为零点。

二次函数有可能有1个、2个或0个零点，这取决于判别式$D = b^2 - 4ac$的值。

二、二次函数的图像与性质1. 完整图像：为了绘制二次函数的图像，我们可以找到对称轴上的一个点，然后根据对称性质绘制其他部分。

还可以根据开口方向、最值等信息来确定图像的大致形状。

2. 平移与伸缩：对于一般的二次函数，平移与伸缩可以通过改变对称轴和系数来完成。

平移可以通过将对称轴上的点坐标改变相应量来实现，而伸缩可以通过改变系数$a$来实现。

3. 零点与轨迹：对于二次函数中的零点，可以通过求解方程$f(x) = 0$来求得。

如果将二次函数平移或伸缩，零点的位置会相应地改变。

当二次函数开口向上时，轨迹低于抛物线；当二次函数开口向下时，轨迹高于抛物线。

三、二次函数的应用二次函数是应用数学中的一个重要工具，被广泛运用于各个领域。

二次函数的性质及图像分析引言：二次函数是高中数学中一个重要的概念，它在数学和实际问题中都有广泛的应用。

本文将介绍二次函数的性质及图像分析，帮助读者更好地理解和应用二次函数。

一、二次函数的定义与一般形式二次函数是指形如y=ax^2+bx+c的函数，其中a、b、c为实数且a≠0。

其中，a决定了二次函数的开口方向和开口的大小，b决定了二次函数的对称轴位置，c决定了二次函数的纵轴截距。

二、二次函数的图像特点1. 开口方向：当a>0时，二次函数开口向上；当a<0时，二次函数开口向下。

2. 对称轴：二次函数的对称轴是一个垂直于x轴的直线，其方程为x=-b/2a。

3. 零点：二次函数与x轴的交点称为零点，即使y=0的解，可以通过求解二次方程ax^2+bx+c=0得到。

4. 极值点：当二次函数开口向上时，函数的最小值称为极值点；当二次函数开口向下时，函数的最大值称为极值点。

5. 函数增减性：二次函数的增减性与a的正负有关，当a>0时，二次函数在对称轴两侧递增；当a<0时，二次函数在对称轴两侧递减。

三、二次函数图像的分析与应用1. 开口方向的影响：二次函数的开口方向决定了函数的增减性和极值点的位置。

在实际问题中，可以通过二次函数的开口方向来判断某一现象的趋势，例如物体的抛射运动中，开口向上的二次函数可以表示物体上升的高度，开口向下的二次函数可以表示物体下降的高度。

2. 对称轴的作用：二次函数的对称轴决定了函数图像的对称性。

在实际问题中，对称轴可以帮助我们找到函数图像的关键点，例如求解二次函数的最值、求解二次函数与其他图像的交点等。

3. 零点的意义：二次函数的零点表示函数与x轴的交点，即函数的解。

在实际问题中，零点可以帮助我们求解方程，解决实际问题，例如求解二次方程来确定某一物体的位置、时间等。

4. 极值点的应用：二次函数的极值点表示函数的最值，可以帮助我们求解最优解问题。

在实际问题中，可以通过求解二次函数的极值点来确定某一问题的最优解，例如求解最短路径、最大利润等。

二次函数知识归纳与总结二次函数是数学中的重要内容，具有广泛的运用。

下面对二次函数的知识进行归纳与总结。

一、定义与特点二次函数是形如y=ax²+bx+c（a≠0）的函数，其中a、b、c为常数。

二次函数的图像呈现抛物线状，开口方向由a的正负决定。

二次函数有以下特点：1.抛物线的开口方向：当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

2.抛物线的对称轴：对称轴的方程为x=-b/2a，对称轴平分抛物线，并且抛物线上的任意点关于对称轴对称。

3.抛物线的顶点：顶点坐标为(-b/2a,f(-b/2a))，其中f(-b/2a)是抛物线上的最值（最大值或最小值）。

4.解析式中的系数：a决定了抛物线的开口方向和抛物线的坡度；b决定了对称轴的位置；c决定了抛物线与y轴的交点。

二、图像与性质1.抛物线的图像：当a>0时，抛物线的图像开口向上，顶点位于y轴上方；当a<0时，抛物线的图像开口向下，顶点位于y轴下方。

2.抛物线的最值：当a>0时，抛物线的最小值为f(-b/2a)；当a<0时，抛物线的最大值为f(-b/2a)。

3. 零点与交点：抛物线与x轴的交点称为零点，即解方程ax²+bx+c=0的解；抛物线与y轴的交点坐标为(0,c)。

4.纵轴交点：设抛物线与y轴交于点A，若点A的纵坐标为c>0，则a>0；若点A的纵坐标为c<0，则a<0。

三、解析式的变形与性质1.完全平方：二次函数的解析式中，可通过完全平方的方法将二次项变形为平方项。

例如，x²+4x=0可变形为(x+2)²-4=0。

2. 方程与不等式的解：二次方程ax²+bx+c=0的解可通过因式分解、配方法、求根公式等方法求得。

二次不等式ax²+bx+c>0或ax²+bx+c<0的解可通过图像法分析得到。

3. 判别式：二次函数的判别式Δ=b²-4ac可以判断二次方程的根的情况。

九年级二次函数所有知识点九年级二次函数是数学课程中的重要内容，掌握好二次函数的知识，对于解决实际问题和进一步学习高中数学都具有重要意义。

接下来，我们将逐一介绍九年级二次函数的所有知识点。

一、二次函数的定义二次函数是形如y = ax²+ bx + c的函数，其中a、b、c为常数，a ≠ 0。

其中，a为二次函数的二次项系数，b为一次项系数，c为常数项。

二、二次函数的图像特点1. 凹凸性：当a>0时，二次函数的图像开口朝上，凹；当a<0时，二次函数的图像开口朝下，凸。

2. 对称轴：二次函数的图像关于直线x = -b/2a 对称。

3. 最值点：当a>0时，二次函数的最值点为最低点，最小值为c-b²/4a；当a<0时，二次函数的最值点为最高点，最大值为c-b²/4a。

三、二次函数的零点1. 零点定义：二次函数的零点是函数曲线与x轴的交点，即求解方程ax² + bx + c = 0。

2. 判别式：二次函数零点的判别式Δ = b²-4ac，当Δ>0时，有两个不同的实根；当Δ=0时，有两个相等的实根；当Δ<0时，无实数根。

3. 求根公式：根据判别式Δ的值，可以使用求根公式x = (-b±√Δ)/2a 求得二次函数的零点。

四、二次函数的图像与系数的关系1. a的取值：当a>0时，二次函数图像开口朝上，a的绝对值越大，图像越扁平；当a<0时，二次函数图像开口朝下，a的绝对值越大，图像越陡峭。

2. b的取值：b的正负决定了二次函数对称轴与y轴的位置关系，当b>0时，对称轴在y轴右侧；当b<0时，对称轴在y轴左侧。

3. c的取值：c的值决定了二次函数图像与y轴的位置关系，当c>0时，图像在y轴上方；当c<0时，图像在y轴下方。

五、二次函数的应用1. 最值问题：通过求二次函数的最值点，可以解决最值问题，如最大值、最小值的求解。

二次函数像特点二次函数（quadratic function）是一种数学函数，其定义域为实数集，且函数的表达式为f(x) = ax² + bx + c，其中a、b、c为实数且a ≠ 0。

二次函数是函数中最简单且常见的一种类型，其在数学、物理、工程和经济等领域中都有广泛的应用。

本文将讨论二次函数的特点及其在实际中的应用。

首先，二次函数的图像是一个拱形，称为抛物线（parabola）。

抛物线可以向上开口（a > 0），也可以向下开口（a < 0）。

此外，二次函数的图像对称于抛物线的顶点。

顶点坐标为(-b/2a, f(-b/2a))，其中x值是通过f(x) = ax² + bx + c 中的-x/2a计算得出的。

其次，二次函数的图像是连续的，并且没有间断点。

因为二次函数是一个多项式函数，多项式函数在实数轴上是处处可导的，也就是说在每个点的导数都存在。

另外，二次函数的性质还包括：1. 范围（range）：对于向上开口的二次函数（a > 0），其范围为f(x) ≥ y_min，其中y_min是抛物线的最小值；对于向下开口的二次函数（a < 0），其范围为f(x) ≤ y_max，其中y_max是抛物线的最大值。

2. 零点（zero）：即函数值等于零的点，用来求解方程f(x) = 0。

对于二次函数，可以使用求根公式x = (-b ± √(b²-4ac))/(2a)来找到其零点。

3. 函数的增减性：对于向上开口的二次函数，当x增加时，函数的值也随之增加；对于向下开口的二次函数，当x增加时，函数的值减少。

4. 函数的凹凸性：凹（concave up）表示抛物线向上开口，凸（concave down）表示抛物线向下开口。

5. 对称轴（axis of symmetry）：函数图像关于对称轴对称。

对称轴的方程为x = -b/2a。

除了以上基本特点外，二次函数还能通过平移、伸缩和翻转等变换来改变其图像。

二次函数的实际应用总结二次函数是高中数学中重要的一类函数。

它具有形如y=ax^2+bx+c的特点，其中a、b、c是实数且a不等于0。

二次函数有许多实际应用，涉及到物理、经济和生活中的各种问题。

本文将总结几个二次函数的实际应用。

一、物体自由落体物体自由落体是一个常见的物理问题，可以用二次函数来描述。

当一物体从高处自由落下时，它的高度与时间之间的关系可以由二次函数表示。

设物体自由落下的高度为H（米），时间为t（秒），重力加速度为g（9.8米/秒²），则有公式H = -gt²/2。

其中负号表示高度的减小，因为物体向下运动。

通过这个二次函数，我们可以计算物体在不同时间下的高度，进而研究物体的运动规律。

例如，我们可以计算物体自由落地所需的时间，或者计算物体在某个时间点的高度。

这在工程设计和物理实验中具有重要意义，帮助我们预测和控制物体的运动。

二、开口向上/向下的抛物线二次函数的图像通常是一个抛物线，其开口的方向由二次项系数a的正负决定。

当a大于0时，抛物线开口向上；当a小于0时，抛物线开口向下。

对于开口向上的抛物线，我们可以将其应用到生活中的一些情景。

比如，一个喷泉的水柱，水流高度与时间之间的变化可以用开口向上的二次函数来描述。

同样，开口向下的抛物线也有实际应用。

例如，一个弹簧的变形量与受力之间的关系常常是开口向下的二次函数。

通过了解抛物线的性质和方程，我们可以更好地理解和解决与之相关的问题。

三、经济学中的应用二次函数在经济学中也有广泛的应用。

例如，成本函数和收入函数常常是二次函数。

企业的成本与产量之间的关系可以用二次函数来刻画。

同样，市场需求和供给也可以用二次函数来表达。

在经济学中，研究成本、收入、需求和供给的函数对于决策和市场分析至关重要。

通过对二次函数的运用，我们可以计算某一产量下的成本和收入，并了解市场价格的影响因素。

这有助于企业决策和经济政策的制定。

四、其他实际应用除了以上提到的应用，二次函数还可以用于建模和预测其他实际问题。

二次函数的特性二次函数是一种形式为y=ax^2+bx+c的函数，其中a、b、c为常数，且a不等于0。

二次函数在数学中具有一些独特的特性，本文将介绍二次函数的性质和特点。

一、图像特性1. 平移：二次函数的图像可以通过平移来改变其位置。

对于函数y=ax^2+bx+c，当向右平移h个单位时，函数变为y=a(x-h)^2+b(x-h)+c；当向上或向下平移k个单位时，函数变为y=a(x-h)^2+b(x-h)+c+k。

2. 对称轴：二次函数的图像关于一条直线对称，这条直线称为对称轴。

对于函数y=ax^2+bx+c，对称轴的公式为x=-b/2a。

3. 开口方向：二次函数的图像的开口方向取决于系数a的正负。

若a>0，则开口向上；若a<0，则开口向下。

4. 顶点：二次函数的图像的顶点是函数的极值点，对于函数y=ax^2+bx+c，顶点的坐标为(-b/2a, f(-b/2a))。

二、性质特征1. 零点：二次函数的零点是函数与x轴的交点，即函数取值为0的点。

对于函数y=ax^2+bx+c，零点的求解可使用二次方程的求根公式，即x=(-b±√(b^2-4ac))/(2a)。

2. 判别式：二次函数的判别式可以判断二次方程的根的情况。

判别式的计算公式为Δ=b^2-4ac，当Δ>0时，函数有两个不相等的实根；当Δ=0时，函数有两个相等的实根；当Δ<0时，函数无实根。

3. 极值点：二次函数的顶点是函数的极值点。

当a>0时，顶点为函数的最小值点；当a<0时，顶点为函数的最大值点。

4. 单调性：二次函数在对称轴两侧具有不同的单调性。

当a>0时，函数在对称轴左侧递减，在右侧递增；当a<0时，函数在对称轴左侧递增，在右侧递减。

5. 奇偶性：二次函数的奇偶性与系数b相关。

当b为偶数时，函数为偶函数，对称轴为y轴；当b为奇数时，函数为奇函数，对称轴为原点。

三、应用领域1. 物理学：二次函数常被应用于描述自由落体运动、抛物线的轨迹以及弹性系数等物理现象。

二次函数重点难点总结二次函数是高中数学的一个重要章节，也是数学中最基础、最直观的一类函数之一、在学习二次函数的过程中，可能会遇到一些难点和重点。

下面我将从定义、图像、性质及应用等方面总结二次函数的难点和重点。

一、定义1. 二次函数的定义：二次函数是一种形如y = ax² + bx + c 的函数，其中 a、b、c 是常数，且a ≠ 0。

难点在于理解二次函数的定义及其与一次函数之间的区别。

二、图像1. 二次函数的图像特点：二次函数的图像是抛物线。

方程y = ax² + bx + c 描述了抛物线在坐标平面上的图像。

难点在于理解二次函数图像的基本形状，包括开口方向、顶点位置和对称轴等。

2.顶点、对称轴和焦点：顶点是二次函数图像的最高点或最低点。

对称轴是通过顶点并且垂直于x轴的直线。

焦点是指离顶点最近的点。

难点在于求解顶点、对称轴和焦点的具体方法。

3.平移、缩放和翻转：二次函数图像可以通过改变a、b、c来进行平移、缩放和翻转。

平移是指将图像在坐标平面上移动。

缩放是指将图像在坐标平面上拉伸或收缩。

翻转是指将图像在坐标平面上关于一些轴翻转。

难点在于理解平移、缩放和翻转对二次函数图像的影响。

三、性质1.零点和判别式：二次函数的零点是指使函数取值为0的x坐标。

判别式可以用来判断二次函数的根的情况。

难点在于求解二次函数的零点和判别式。

3.最大值和最小值：二次函数图像的最大值和最小值分别是顶点的y 坐标。

难点在于求解二次函数图像的最大值和最小值。

四、应用1.最优化问题：二次函数常常用于解决最优化问题，如求解最大值和最小值。

这类问题涉及到对二次函数图像进行分析和优化。

难点在于将最优化问题转化为二次函数，以及求解最优解的方法。

2.抛射问题：二次函数也可以用于解决抛射问题。

这类问题涉及到对二次函数图像的判读和应用。

难点在于将抛射问题转化为二次函数，并求解相关信息。

五、推广综上所述，二次函数的难点和重点主要包括定义、图像、性质及应用等方面。

二次函数的实际应用场景引导学生思考二次函数的特点二次函数是数学中的重要概念之一，它在现实生活中有许多实际应用场景。

通过展示这些场景，可以引导学生思考二次函数的特点。

在本文中，我将介绍几个二次函数的实际应用，并说明这些应用中二次函数的一些特点。

第一个应用场景是物体的自由落体。

当一个物体自由下落时，它的高度与时间之间的关系可以用二次函数来描述。

具体来说，如果我们以物体开始下落的时刻为起点，以物体位置与地面之间的距离为纵轴，以时间为横轴，那么得到的图像就是一个抛物线。

这个抛物线的开口方向取决于物体的运动方向，抛物线的顶点表示物体的最高点。

第二个应用场景是弹簧振子。

当一个质点通过弹簧与支持物相连并受到重力作用时，弹簧的伸缩长度与时间之间的关系可以用二次函数来描述。

具体来说，如果我们以弹簧处于平衡位置时的长度为起点，以弹簧长度为纵轴，以时间为横轴，那么得到的图像也是一个抛物线。

这个抛物线的开口方向取决于质点的运动方向，抛物线的顶点表示弹簧的最大伸长或最大缩短位置。

第三个应用场景是抛体运动。

当一个物体以一定的初速度和角度抛出时，它的水平位移与时间之间的关系可以用二次函数来描述。

具体来说，如果我们以物体抛出时的水平位置为起点，以物体的水平位移为纵轴，以时间为横轴，那么得到的图像仍然是一个抛物线。

这个抛物线的开口方向取决于物体的抛出角度，抛物线的顶点表示物体的最远水平位移。

通过以上三个实际应用场景，我们可以总结出二次函数的一些特点。

首先，二次函数的图像总是一个抛物线，它具有对称轴和顶点。

对称轴可以通过函数的零点来确定，顶点则是抛物线的最高点或最低点。

其次，二次函数的开口方向和顶点的位置取决于函数的系数。

正系数导致抛物线开口向上，负系数导致抛物线开口向下。

最后，二次函数的图像可以用来描述各种物理运动过程，例如自由落体、弹簧振子和抛体运动。

通过引入这些实际应用场景，我们可以引导学生思考二次函数的特点，并更好地理解这一概念。

高中教材知识点：二次函数的图像与性质一、知识点介绍二次函数是高中阶段数学学习的重要内容之一，它是一种关于自变量的二次多项式函数。

了解二次函数的图像与性质对于理解函数的变化规律和应用具有重要意义。

本文将详细介绍高中教材中二次函数的图像与性质，包括基本定义、图像特点、性质及常见的例题解析。

二、基本定义1. 二次函数：二次函数是一个关于自变量x 的函数，一般可以表示为f(x) = ax^2 + bx + c，其中a、b、c 是实数且 a ≠0。

2. 二次函数的图像：二次函数的图像是平面直角坐标系中的一条曲线，通常是开口向上或向下的抛物线。

三、图像特点1. 抛物线的开口方向：二次函数中的系数a 决定了抛物线的开口方向。

当 a > 0 时，抛物线开口向上；当 a < 0 时，抛物线开口向下。

2. 邻域与单调性：二次函数的图像在抛物线的开口处有一个顶点，抛物线在这个顶点的邻域内是单调递增或单调递减的。

四、性质1. 零点与因式分解：二次函数的零点是方程f(x) = 0 的解，可以通过因式分解或求根公式来得到。

2. 对称性：二次函数的图像关于顶点对称。

即，若(h, k) 是抛物线的顶点，则点(2h, k) 也在抛物线上。

3. 最值：当抛物线开口向上时，最小值为顶点的纵坐标；当抛物线开口向下时，最大值为顶点的纵坐标。

五、例题解析1. 图像特点例题：题目：根据二次函数的表达式f(x) = 2x^2 - 3x + 1，确定该二次函数的开口方向和顶点。

解析：根据系数 a 的值，可以确定开口方向。

由题目中的系数可知 a = 2，因此抛物线开口向上。

顶点可以通过求解抛物线的顶点坐标得到。

根据顶点公式，顶点的横坐标为x = -b/2a，纵坐标为f(x) = f(-b/2a)。

代入系数的值，得到顶点的坐标为(-(-3)/2(2), f(-(-3)/2(2))) = (3/4, 13/8)。

2. 性质应用例题：题目：已知二次函数f(x) = ax^2 + bx + c，其图像与x 轴交于两点，且顶点的纵坐标为4。

二次函数与反比例函数初步总结二次函数和反比例函数是高中数学中重要的内容，而且在实际生活中也有广泛的应用。

本文将对二次函数和反比例函数进行初步总结，主要包括定义、特点、图像、性质等方面的内容。

一、二次函数1. 定义：二次函数是形如y = ax² + bx + c（a ≠ 0）的函数，其中a、b、c是已知的实数，a表示二次项的系数，b表示一次项的系数，c 表示常数项。

2.特点：(1)曲线的形状：二次函数的图像是一条平滑的曲线，且开口方向由二次项系数a的正负决定。

-当a>0时，开口向上，形如"U"形；-当a<0时，开口向下，形如"倒U"形。

(2) 零点：二次函数的零点是函数图像与x轴的交点，即满足y = 0的x值。

二次函数的零点个数与判别式Δ（即b²-4ac）有关：-当Δ>0时，二次函数有两个不同的零点；-当Δ=0时，二次函数有两个相等的零点；-当Δ<0时，二次函数没有实数解，无零点。

(3)对称轴：二次函数的对称轴是函数图像的中心线，也是二次函数图像的对称轴。

对称轴的方程为x=-b/2a。

(4)极值点：二次函数的极值点是函数图像的最高点或最低点，也是对称轴上的点。

极值点的纵坐标为y轴上的最小值或最大值。

3.图像：通过画出对称轴、极值点、零点等关键点，可以得到二次函数的图像。

通过连接关键点，就能画出完整的二次函数曲线。

二、反比例函数1.定义：反比例函数是形如y=k/x的函数，其中k是常数，x≠0。

2.特点：(1)曲线的形状：反比例函数的图像是一条拱形曲线，且通过原点(0,0)。

当x趋近于正无穷或负无穷时，函数值趋于0。

(2)反比例关系：反比例函数表达了两个变量之间的反比关系，即一个变量的增大导致另一个变量的减小，反之亦然。

(3)单调性：反比例函数在定义域内是单调的，即x增大导致y减小，x减小导致y增大。

(4)随x趋于0的变化：当x趋近于0时，y的绝对值趋近于无穷大，即y趋于正无穷或负无穷。

二次函数知识点总结二次函数是高中数学中的一个重要内容，其知识点涉及函数的定义、性质、图象、解析式、应用等。

下面是对二次函数知识点的总结。

一、函数的定义和基本性质：二次函数是形如y=ax^2+bx+c（a≠0）的函数，其中a、b、c 为实数，a称为二次函数的系数。

①定义域：二次函数的定义域是任意实数集R。

②值域：对于二次函数y=ax^2+bx+c，当a>0时，函数的值域是[0,+∞)，当a<0时，函数的值域是(-∞，0]，当a=0时，函数的值域是{c}。

③对称轴：二次函数的对称轴是垂直于x轴的直线x=-b/2a。

④顶点：二次函数的顶点是对称轴上的点(-b/2a, f(-b/2a))，其中f(x)=ax^2+bx+c。

⑤开口方向：当a>0时，二次函数开口向上；当a<0时，二次函数开口向下。

二、图象和性质：①图象特点：二次函数在平面直角坐标系内的图象是一个抛物线。

②定点：二次函数开口向上时，顶点是最小点；二次函数开口向下时，顶点是最大点。

③与坐标轴的交点：二次函数与x轴的交点叫做零点，是方程ax^2+bx+c=0的解；与y轴的交点是函数的常数项c。

④单调性：二次函数的单调性受其系数a的符号影响。

当a>0时，二次函数在对称轴两侧递增；当a<0时，二次函数在对称轴两侧递减。

⑤零点与解析式：对于二次函数y=ax^2+bx+c，其零点可以通过求解方程ax^2+bx+c=0得到，其中的判别式Δ=b^2-4ac可以判断二次方程的解的情况。

三、解析式和变形：①标准形式：二次函数的标准形式是y=ax^2+bx+c。

②顶点式：二次函数的顶点式是y=a(x-h)^2+k，其中(h,k)为顶点坐标。

③因式分解式：当二次函数可因式分解时，可以表示成y=a(x-p)(x-q)的形式。

四、一些常见问题和解法：①如何确定二次函数的开口方向和顶点：若a>0，则开口向上，顶点为抛物线的最小值；若a<0，则开口向下，顶点为抛物线的最大值。

二次函数像的变化规律与特点总结二次函数是高中数学学习中的一个重要内容，它具有特殊的形式和性质。

本文将总结二次函数像的变化规律与特点，并探讨其在实际问题中的应用。

一、二次函数的标准形式二次函数的标准形式为：y = ax² + bx + c，其中a、b、c为常数，a ≠ 0。

该函数通常在坐标系中呈现抛物线的形状，开口方向由a的正负决定。

若a>0，则抛物线开口向上；若a<0，则抛物线开口向下。

二、二次函数的基本性质1. 零点：即二次函数与x轴相交的点。

二次函数的零点可以通过解一元二次方程求得，一般有两个实根、一个实根或两个虚根。

2. 顶点：即二次函数抛物线的最高点（开口向下时）或最低点（开口向上时）。

顶点的横坐标为x = -b/2a，纵坐标为y = f(x)。

3. 对称轴：二次函数的抛物线是关于x = -b/2a这条直线对称的。

4. 单调性：当a>0时，二次函数在对称轴左侧单调递增，在对称轴右侧单调递减；当a<0时，二次函数在对称轴左侧单调递减，在对称轴右侧单调递增。

5. 零点的个数与判别式：一元二次方程的判别式Δ = b² - 4ac可以判断二次函数与x轴相交的情况。

当Δ>0时，有两个不同的实根；当Δ=0时，有两个相同的实根；当Δ<0时，没有实根。

6. 函数的最值：当a>0时，二次函数的最小值为顶点的纵坐标；当a<0时，二次函数的最大值为顶点的纵坐标。

三、二次函数的变化规律二次函数的另一个重要特点是图像的变化规律。

根据二次函数的标准形式，可以得出以下结论：1. 当a>0时，随着x的增大，函数值逐渐增大；随着x的减小，函数值逐渐减小。

函数图像向上开口，呈现“U”字型。

2. 当a<0时，随着x的增大，函数值逐渐减小；随着x的减小，函数值逐渐增大。

函数图像向下开口，呈现“倒U”字型。

3. 当a的绝对值增大时，抛物线的开口越来越窄；当a的绝对值减小时，抛物线的开口越来越宽。