第一章 机械振动学基础

旋转机械的振动与处理主讲人:晋风华第一章机械振动基础一、振动的定义二、振动具有两重性三、振动研究目标（目的）四、振动的分类五、振动问题的研究方法六、振动分析的力学模型七、振动分析的数学模型七、振动研究的分析工具一、振动的定义机械振动是指物体在平衡位置附近所作的往复运动。

例如：钟摆的振动琴弦的振动车船的振动机床的振动桥梁的振动旋转机械振动等二、振动具有两重性有害的一面：降低机械加工的精度和光洁度，危害结构的强度，发生大变形导致机器或结构的破坏甚至酿成灾难性的事故。

有利的一面：振动给料机、振动筛选机、振动破碎机、振动球磨机、振动打桩、振动测桩、振动抛光、结构的减振、抗震等都是利用振动的特性进行工作的。

汽轮机组振动的危害机组振动是评价汽轮发电机组运行状况优劣的重要标志之一，亦是机组设计、制造、安装、检修质量的综合反映。

在汽轮发电机组运行过程中，往往只要机组发生故障，一般均会伴随着出现异常振动。

异常振动可以认为是发生故障的前兆，同时振动又会使故障扩大和形成新的故障。

主要危害：（1）零部件承受很大应力，促使材料疲劳或损坏；（2）紧固件松弛，造成汽缸中分面等处的蒸汽泄漏；（3）动静部分摩擦，加剧轴承磨损；（4）主轴弯曲；（5）基础振动；（6）引起其它机组振动等。

振动过大造成机组损坏的实例1953年，美国Tanner Screek电站一台125MW机组低压转子断裂。

1972年，德国某电站一台500MW机组低压转子、发电机、主励磁机与辅助励磁机之间的联轴器螺栓被扭断，低压转子在装叶轮处断裂。

1972年，日本海南电厂一台600MW机组在超速试验过程中，低压转子、发电机和励磁机断裂，整个轴系断为17段。

我国一台50MW机组因汽轮机进入低温蒸汽，汽缸急剧收缩，动静间隙减小引起动静碰磨，解列甩负荷时，主汽门、调节汽门关闭迟缓，机组超速至3600r/min左右，造成轴系断裂成12段，汽轮机缸体爆炸。

1988年，秦岭发电厂200MW汽轮发电机组，在升速过程中，因故障导致转速飞升到3400r/min以上，引发机组共振和油膜振荡，造成轴系断裂的特大事故，在10～11s内使整个30m长的轴系断为13段，主机基本毁坏。

机械振动学总结 第一章 机械振动学基础第二节 机械振动的运动学概念第三节机械振动是种特殊形式的运动。

在这运动过程中，机械振动系统将围绕其平衡位置作往复运动。

从运动学的观点看，机械振动式研究机械系统的某些物理量在某一数值近旁随时间t 变化的规律。

用函数关系式来描述其运动。

如果运动的函数值，对于相差常数T 的不同时间有相同的数值，亦即可以用周期函数来表示，则这一个运动时周期运动。

其中T 的最小值叫做振动的周期，Tf 1=定义为振动的频率。

简谐振动式最简单的振动，也是最简单的周期运动。

一、简谐振动物体作简谐振动时，位移x 和时间t 的关系可用三角函数的表示为式中：A 为振幅，T 为周期，ϕ和ψ称为初相角。

如图所示的正弦波形表示了上式所描述的运动，角速度ω称为简谐振动的角频率简谐振动的速度和加速度就是位移表达式关于时间t 的一阶和二阶导数，即可见，若位移为简谐函数，其速度和加速度也是简谐函数，且具有相同的频率。

因此在物体运动前加速度是最早出现的量。

可以看出，简谐振动的加速度，其大小与位移成正比，而方向与位移相反，始终指向平衡位置。

这是简谐振动的重要特征。

在振动分析中，有时我们用旋转矢量来表示简谐振动。

图P6旋转矢量的模为振幅A ，角速度为角频率ω若用复数来表示，则有)sin()cos()(ψωψωψω+++==+t jA t A z Ae z t j用复指数形式描述简谐振动，给计算带来了很多方便。

因为复指数t j e ω对时间求导一次相当于在其前乘以ωj ，而每乘一次j ，相当于有初相角2π。

二．周期振动满足以下条件：1)函数在一个周期内连续或只有有限个间断点，且间断点上函数左右极限存在；2)在一个周期内，只有有限个极大和极小值。

则都可展成Fourier 级数的形式，若周期为T 的周期振动函数，则有式中22n n n b a A += nn n b a =ψt a n 三、简谐振动的合成一、同方向振动的合成1.俩个同频率的简谐振动)sin(222ψω+=t A x ，)sin(2222ψω+=t A x它们的合成运动也是该频率的简谐振动2.俩个不同频率振动的合成若21ωω≤，则合成运动为若21ωω≥ ，对于A A A ==21 ,则有上式可表示为二、两垂直方向振动的合成1.同频率振动的合成如果沿x 方向的运动为沿y 方向的运动为2不同频率振动的合成对于俩个不等的简谐运动它们的合成运动也能在矩形中画出各种曲线。

《机械振动学讲义》§1 绪论所谓振动，广义地讲，指一个物理量在它的平均值附近不停地经过极大值和极小值而往复变化。

机械振动指机械或结构在它的静平衡位置附近的往复弹性运动。

本书涉及的振动如果没有特别说明，均指机械振动。

机械振动所研究的对象是机械或结构，在理论分析中要将实际的机械或结构抽象为力学模型，即形成一个力学系统。

可以产生机械振动的力学系统，称为振动系统，简称系统。

一般来说，任何具有弹性和惯性的力学系统均可能产生机械振动。

振动系统发生振动的原因是由于外界对系统运动状态的影响，即外界对系统的激励或作用。

如果外界对某一个系统的作用使得该系统处于静止状态，此时系统的几何位置称为系统的静平衡位置。

依据系统势能在静平衡位置附近的性质，系统的静平衡位置可以分为稳定平衡，不稳定平衡和随遇平衡等几种情况。

机械振动中的平衡位置是系统的稳定平街位置。

系统在振动时的位移通常是比较小的，因为实际结构的变形一船是比较小的。

在上程和日常生活中有大量的，丰富多彩的振动现象。

例如，车辆行驶时的振动，发功机运转时的振动，演奏乐器时乐器的振动。

在很多情况下机械振动是有害的，比如，车辆行驶时的振动会使乘员感到不适，在用车床加工零件时车刀的振动会使零件的加工精度下降。

而在某些情况下，人们又利用振动进行工作。

比如，建筑1：利用捣固棒的振动使水泥沙浆混合均匀。

对于工程实际中的结构振动问题，人们关心振动会不会使结构的位移、速度、加速度等物理量过大。

因为位移过大可能引起结构各个部件之间的相互干涉。

比如汽车的轮铀与大梁会因为剧烈振动而频繁碰撞，造成大梁过早损坏，并危及行车安全。

又如，汽车行驶中如果垂直振动加速度过大，将会影响汽车的平顺性，给乘员带来不适或危及所载货物的安全。

振动过大也造成结构的应力过大，即产生过大的动应力，有时这种动应力比静应力大的多，容易使结构早期损坏。

另外，振动过大会引起其他的副作用，如剧烈的振动会使结构产生强烈的噪声，等等。

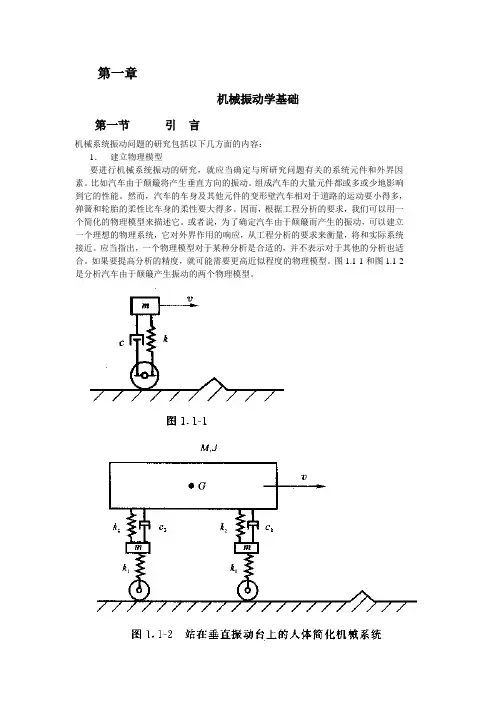
第一章机械振动学基础第一节引言机械系统振动问题的研究包括以下几方面的内容：1．建立物理模型要进行机械系统振动的研究，就应当确定与所研究问题有关的系统元件和外界因素。

比如汽车由于颠簸将产生垂直方向的振动。

组成汽车的大量元件都或多或少地影响到它的性能。

然而，汽车的车身及其他元件的变形壁汽车相对于道路的运动要小得多，弹簧和轮胎的柔性比车身的柔性要大得多。

因而，根据工程分析的要求，我们可以用一个简化的物理模型来描述它。

或者说，为了确定汽车由于颠簸而产生的振动，可以建立一个理想的物理系统，它对外界作用的响应，从工程分析的要求来衡量，将和实际系统接近。

应当指出，一个物理模型对于某种分析是合适的，并不表示对于其他的分析也适合。

如果要提高分析的精度，就可能需要更高近似程度的物理模型。

图1.1-1和图1.1-2是分析汽车由于颠簸产生振动的两个物理模型。

在低颠和低振级的情况下，若把人体看做一个机械系统，就可以用图1.1-3所示形式的线性集总参量系统来粗略近似。

不幸的是，怎样才能得到一个确切描述实际系统的物理模型还没有一般的规则。

这通常取决于研究者的经验和才智。

2．建立数学模型有了所研究系统的物理模型，就可以应用某些物理定律对物理模型进行分析，以导出一个或几个描述系统他特征的方程。

通常，振动问题的数学模型表现为微分方程的形式。

3.方程的求解要了解系统所发生运动的特点和规律，就要对数学模型进行求解，以得到描述系统运动的数学表达式，通常，这种数学表达式是位移表达式，表示为时间的函数。

表达式表明了系统运动与系统性质和外界作用的关系。

4.结果的阐述根据方程解提供的规律和系统的工作要求及结构特点，我们就可以作出设计或改进的决断，以获得问题的最佳解决方案。

本教程的重点是论述机械振动系统的数学模型的建立和方程的求解这两个问题。

第二节机械振动的运动学概念机械振动是一种特殊形式的运动。

在这种运动过程中，机械运动系统将围绕其平衡位置作往复运动。

振动基础知识一、振动的种类及其特点各种机器设备在运行中，都不同程度地存在振动，这是运行机械的共性。

然而，不同的机器，或同一台机器的不同部位，以及机器在不同的时刻或不同的状态下，其产生的振动形式又往往是有差别的，这又体现了设备振动的特殊性。

我们可以从不同的角度来考察振动问题，常把机械振动分成以下几种类型。

1.按振动规律分类按振动的规律，一般将机械振动分为如图2-2几种类型这种分类，主要是根据振动在时间历程内的变化特征来划分的。

大多数机械设备的振动类型是周期振动，准周期振动，窄带随机振动和宽带随机振动，以及某几种振动类型的组合。

一般在起动或停车过程中的振动信号是非平稳的。

设备在实际运行中，其表现的周期信号往往淹没在随机振动信号之中。

若设备故障程度加剧，则随机振动中的周期成分加强，从而整台设备振动增大。

因此，从某种意义上讲，设备振动诊断的过程，就是从随机信号中提取周期成分的过程。

2.按产生振动的原因分类机器产生振动的根本原因，在于存在一个或几个力的激励。

不同性质的力激起不同的振动类型。

据此，可将机械振动分为三种类型：（1）自由振动给系统一定的能量后，系统所产生的振动。

若系统无阻尼，则系统维持等幅振动；若系统有阻尼，则系统为衰减振动。

（2）受迫振动元件或系统的振动是由周期变化的外力作用所引起的，如不平衡、不对中所引起的振动。

（3）自激振动在没有外力作用下，只是由于系统自身的原因所产生的激励而引起的振动，如油膜振荡、喘振等。

因机械故障而产生的振动，多属于受迫振动和自激振动。

3.按振动频率分类机械振动频率是设备振动诊断中一个十分重要的概念。

在各种振动诊断中常常要分析频率与故障的关系，要分析不同频段振动的特点，因此了解振动频段的划分与振动诊断的关系很有实用意义。

按着振动频率的高低，通常把振动分为3种类型：图2-2 振动按规律分类这里应当指出，目前对划分频段的界限，尚无严格的规定和统一的标准。

不同的行业，或同一行业中对不同的诊断对象，其划分频段的标准都不尽一致，我们在各类文献中可见到多种不同的划分方法。