高考试题分类汇编数学必修2部分试题

最新北师⼤版⾼中数学必修⼆测试题全套含答案解析最新北师⼤版⾼中数学必修⼆测试题全套含答案解析章末综合测评(⼀)⽴体⼏何初步(时间120分钟，满分150分)⼀、选择题(本⼤题共12⼩题，每⼩题5分，共60分.在每⼩题给出的四个选项中，只有⼀项是符合题⽬要求的)1.下列推理错误的是()A.A∈l，A∈α，B∈l，B∈α?lαB.A∈α，A∈β，B∈α，B∈β?α∩β＝ABC.l?/α，A∈l?A?αD.A∈l，lα?A∈α【解析】若直线l∩α＝A，显然有l?/α，A∈l，但A∈α，故C错.【答案】 C2.下列说法中，正确的是()A.经过不同的三点有且只有⼀个平⾯B.分别在两个平⾯内的两条直线⼀定是异⾯直线C.垂直于同⼀个平⾯的两条直线是平⾏直线D.垂直于同⼀个平⾯的两个平⾯平⾏【解析】A中，可能有⽆数个平⾯；B中，两条直线还可能平⾏、相交；D中，两个平⾯可能相交.【答案】 C3.已知⽔平放置的△ABC是按“斜⼆测画法”得到如图1所⽰的直观图，其中B′O′＝C′O′＝1，A′O′＝32，那么原△ABC的⾯积是()图1 A. 3 B.2 2C.32 D.34【解析】由题图可知，原△ABC的⾼为AO＝3，∴S△ABC ＝12×BC×OA＝12×2×3＝3，故选A.【答案】 A4.下列四个命题判断正确的是()A.若a∥b，a∥α，则b∥αB.若a∥α，bα，则a∥bC.若a∥α，则a平⾏于α内所有的直线D.若a∥α，a∥b，b?/α，则b∥α【解析】A中b可能在α内；B中a与b可能异⾯；C中a可能与α内的直线异⾯；D 正确.【答案】 D5.已知⼀个圆锥的展开图如图2所⽰，其中扇形的圆⼼⾓为120°，底⾯圆的半径为1，则该圆锥的体积为()图2A.22π3 B.2π3C.2π3 D.3π【解析】因为扇形弧长为2π，所以圆锥母线长为3，⾼为22，所求体积V＝1 3×π×12×22＝22π3.【答案】 A6.如图3所⽰，在正⽅体ABCD-A1B1C1D1中，若E是A1C1的中点，则直线CE垂直于()图3A.ACB.BDC.A1DD.A1D1【解析】CE平⾯ACC1A1，⽽BD⊥AC，BD⊥AA1，所以BD⊥平⾯ACC1A1，所以BD⊥CE.【答案】 B7.正⽅体AC1中，E，F分别是DD1，BD的中点，则直线AD1与EF所成⾓的余弦值是()A.12 B.33 D.62【解析】连接BD1，则BD1∥EF，∠BD1A是异⾯直线AD1与EF所成的⾓.∵AB⊥AD1，∴cos∠BD1A＝AD1BD1＝63.【答案】 C8.如图4所⽰，则这个⼏何体的体积等于()图4 A.4 B.6C.8D.12【解析】由三视图得⼏何体为四棱锥，如图记作S -ABCD ，其中SA ⊥平⾯ABCD ， SA ＝2，AB ＝2，AD ＝2，CD ＝4，且ABCD 为直⾓梯形，∠DAB ＝90°，∴V ＝13SA ×12(AB ＋CD )×AD ＝13×2×12×(2＋4)×2＝4，故选A. 【答案】 A9.如图5，ABCD -A 1B 1C 1D 1为正⽅体，下⾯结论错误的是( )图5A.BD ∥平⾯CB 1D 1B.AC 1⊥BDC.AC 1⊥平⾯CB 1D 1D.异⾯直线AD 与CB 1所成的⾓为60°【解析】由于BD ∥B 1D 1，易知BD ∥平⾯CB 1D 1；连接AC ，易证BD ⊥平⾯ACC 1，所以AC 1⊥BD ；同理可证AC 1⊥B 1C ，因BD ∥B 1D 1，所以AC 1⊥B 1D 1，所以AC 1⊥平⾯CB 1D 1；对于选项D ，∵BC ∥AD ，∴∠B 1CB 即为AD 与CB 1所成的⾓，此⾓为45°，故D 错.【答案】 D10.圆柱被⼀个平⾯截去⼀部分后与半球(半径为r )组成⼀个⼏何体，该⼏何体三视图中的主视图和俯视图如图6所⽰.若该⼏何体的表⾯积为16＋20π，则r ＝( )图6D.8【解析】如图，该⼏何体是⼀个半球与⼀个半圆柱的组合体，球的半径为r，圆柱的底⾯半径为r，⾼为2r，则表⾯积S＝12＋2×4πrπr2＋4r2＋πr·2r＝(5π＋4)r2.⼜S＝16＋20π，∴(5π＋4)r2＝16＋20π，∴r2＝4，r＝2，故选B.【答案】 B11.如图7，以等腰直⾓三⾓形ABC的斜边BC上的⾼AD为折痕，把△ABD和△ACD折成互相垂直的两个平⾯后，某学⽣得出下列四个结论：图7①BD⊥AC；②△BCA是等边三⾓形；③三棱锥D-ABC是正三棱锥；④平⾯ADC⊥平⾯ABC.其中正确的是()A.①②④B.①②③C.②③④D.①③④【解析】由题意知，BD⊥平⾯ADC，故BD⊥AC，①正确；AD为等腰直⾓三⾓形斜边BC上的⾼，平⾯ABD⊥平⾯ACD，所以AB＝AC＝BC，△BAC是等边三⾓形，②正确；易知DA ＝DB ＝DC ，⼜由②知③正确；由①知④错.故选B.【答案】 B12.已知三棱锥S -ABC 的所有顶点都在球O 的球⾯上，△ABC 是边长为1的正三⾓形，SC 为球O 的直径，且SC ＝2，则此棱锥的体积为( )A.26B.36C.23D.22【解析】由于三棱锥S -ABC 与三棱锥O -ABC 底⾯都是△ABC ，O 是SC 的中点，因此三棱锥S -ABC 的⾼是三棱锥O -ABC ⾼的2倍，所以三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍.在三棱锥O -ABC 中，其棱长都是1，如图所⽰， S △ABC ＝34×AB 2＝34，⾼OD ＝12－? ??332＝63，∴V S -ABC ＝2V O -ABC ＝2×13×34×63＝26. 【答案】 A⼆、填空题(本⼤题共4⼩题，每⼩题5分，共20分，将答案填在题中的横线上) 13.设平⾯α∥平⾯β，A ，C ∈α，B ，D ∈β，直线AB 与CD 交于点S ，且点S 位于平⾯α，β之间，AS ＝8，BS ＝6，CS ＝12，则SD ＝________.【解析】由⾯⾯平⾏的性质得AC ∥BD ，AS BS ＝CSSD ，解得SD ＝9. 【答案】 914.如图8所⽰，将等腰直⾓△ABC 沿斜边BC 上的⾼AD 折成⼀个⼆⾯⾓，此时∠B ′AC ＝60°，那么这个⼆⾯⾓⼤⼩是________.图8【解析】连接B ′C ，则△AB ′C 为等边三⾓形，设AD ＝a ，则B ′D ＝DC ＝a ，B ′C ＝AC ＝2a ，所以∠B ′DC ＝90°.【答案】 90°15.若⼀个底⾯边长为62，侧棱长为6的正六棱柱的所有顶点都在⼀个球⾯上，则此球的体积为________.【解析】球的直径等于正六棱柱的体对⾓线的长.设球的半径为R ，由已知，可得2R ＝62×22＋(6)2＝23，R ＝ 3. 所以球的体积为43πR 3＝4π3×(3)3＝43π. 【答案】 43π16.将正⽅形ABCD 沿对⾓线BD 折成直⼆⾯⾓A -BD -C ，则异⾯直线AB 与CD 所成的⾓等于________.【解析】如图所⽰，分别取BC ，AC 的中点G 、F ，连接EG ，GF ，EF ，则EG ∥CD ，GF ∥AB ，∴∠EGF 就是AB 与CD 所成的⾓. 由题意EG ＝GF ＝EF ＝a2，∴△EFG 是等边三⾓形，∴∠EGF ＝60°. 【答案】 60°三、解答题(本⼤题共6⼩题，共70分.解答应写出⽂字说明，证明过程或演算步骤) 17.(本⼩题满分10分)如图9所⽰，四棱锥V -ABCD 的底⾯为边长等于2 cm 的正⽅形，顶点V 与底⾯正⽅形中⼼的连线为棱锥的⾼，侧棱长VC ＝4 cm ，求这个正四棱锥的体积.图9 【解】连接AC，BD相交于点O，连接VO，∵AB＝BC＝2 cm，在正⽅形ABCD中，求得CO＝ 2 cm，⼜在直⾓三⾓形VOC中，求得VO＝14 cm，∴V V－ABCD＝13S ABCD·VO＝13×4×14＝4314(cm3).故这个正四棱锥的体积为4314cm3.18.(本⼩题满分12分)如图10所⽰，P是?ABCD所在平⾯外⼀点，E，F分别在P A，BD 上，且PE∶EA＝BF∶FD.求证：EF∥平⾯PBC.图10【证明】连接AF延长交BC于G，连接PG.在?ABCD中，易证△BFG∽△DF A，∴GFF A＝BFFD＝PEEA，∴EF∥PG.⽽EF?/平⾯PBC，PG平⾯PBC，∴EF ∥平⾯PBC .19.(本⼩题满分12分)如图11，长⽅体ABCD -A 1B 1C 1D 1中，AB ＝16，BC ＝10，AA 1＝8，点E ，F 分别在A 1B 1，D1C 1上，A 1E ＝D 1F ＝4.过点E ，F 的平⾯α与此长⽅体的⾯相交，交线围成⼀个正⽅形.图11(1)在图中画出这个正⽅形(不必说明画法和理由)； (2)求平⾯α把该长⽅体分成的两部分体积的⽐值. 【解】 (1)交线围成的正⽅形EHGF ，如图：(2)作EM ⊥AB ，垂⾜为M ，则AM ＝A 1E ＝4，EB 1＝12，EM ＝AA 1＝8. 因为四边形EHGF 为正⽅形，所以EH ＝EF ＝BC ＝10. 于是MH ＝EH 2－EM 2＝6，AH ＝10，HB ＝6.故S 四边形A 1EHA ＝12×(4＋10)×8＝56， S 四边形EB 1BH ＝12×(12＋6)×8＝72.因为长⽅体被平⾯α分成两个⾼为10的直棱柱，所以其体积的⽐值为97? ????79也正确.20.(本⼩题满分12分)如图12所⽰，在长⽅体ABCD -A 1B 1C 1D 1中，AB ＝AD ＝1，AA 1＝2，M 是棱CC 1的中点.证明：平⾯ABM ⊥平⾯A 1B 1M .图12【证明】由长⽅体的性质可知A1B1⊥平⾯BCC1B1，⼜BM平⾯BCC 1B1，所以A1B1⊥BM.⼜CC1＝2，M为CC1的中点，所以C1M＝CM＝1.在Rt△B1C1M中，B1M＝B1C21＋MC21＝2，同理BM＝BC2＋CM2＝2，⼜B1B＝2，所以B1M2＋BM2＝B1B2，从⽽BM⊥B1M.⼜A1B1∩B1M＝B1，所以BM⊥平⾯A1B1M，因为BM平⾯ABM，所以平⾯ABM⊥平⾯A 1B1M.21.(本⼩题满分12分)如图13，在四棱锥P-ABCD中，P A⊥底⾯ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，P A＝AB＝BC，E是PC的中点.图13(1)求证：AE⊥平⾯PCD；(2)求⼆⾯⾓A-PD-C的正弦值.【解】(1)证明：在四棱锥P-ABCD中，因P A⊥底⾯ABCD，CD平⾯ABCD，故CD⊥P A.由条件CD⊥AC，P A∩AC＝A，∴CD⊥平⾯P AC，⼜AE平⾯P AC，∴AE⊥CD.由P A＝AB＝BC，∠ABC＝60°，可得AC＝P A.∵E是PC的中点，∴AE⊥PC.⼜PC∩CD＝C，∴AE⊥平⾯PCD.(2)过点E作EM⊥PD，垂⾜为M，连接AM，如图所⽰.由(1)知，AE⊥平⾯PCD，AM在平⾯PCD内的射影是EM，则AM⊥PD.因此∠AME是⼆⾯⾓A-PD-C的平⾯⾓.由已知，可得∠CAD＝30°.22.(本⼩题满分12分)⼀个空间⼏何体的三视图及部分数据如图14所⽰.图14(1)请画出该⼏何体的直观图，并求它的体积；(2)证明：A1C⊥平⾯AB1C1；(3)若D是棱CC1的中点，在棱AB上取中点E，判断DE是否平⾏于平⾯AB1C1，并证明你的结论.【解】(1)⼏何体的直观图如图.四边形BB1C1C是矩形，BB1＝CC1＝3，BC＝1，四边形AA1C1C是边长为3的正⽅形，且垂直于底⾯BB1C1C，∴其体积V＝12×1×3×3＝32.(2)证明：∵∠ACB＝90°，∴BC⊥AC.∵三棱柱ABC-A1B1C1为直三棱柱，∴BC⊥CC1.∵AC∩CC1＝C，∴BC⊥平⾯ACC1A1，∴BC⊥A1C.∵B1C1∥BC，∴B1C1⊥A1C.∵四边形ACC1A1为正⽅形，∴A1C⊥AC1.∵B1C1∩AC1＝C1，∴A1C⊥平⾯AB1C1.(3)当E为棱AB的中点时，DE∥平⾯AB1C1.证明：如图，取BB1的中点F，连接EF，FD，DE，∵D，E，F分别为CC1，AB，BB1的中点，∴EF∥AB1.∵AB1平⾯AB1C1，EF?/平⾯AB1C1，∴EF∥平⾯AB1C1.∵FD∥B1C1，∴FD∥平⾯AB1C1，⼜EF∩FD＝F，∴平⾯DEF∥平⾯AB1C1.⽽DE平⾯DEF，∴DE∥平⾯AB1C1.章末综合测评(⼆)解析⼏何初步(时间120分钟，满分150分)⼀、选择题(本⼤题共12⼩题，每⼩题5分，共60分.在每⼩题给出的四个选项中，只有⼀项是符合题⽬要求的)1.空间两点A(3，－2,5)，B(6,0，－1)之间的距离为()A.6B.7C.8D.9【解析】|AB|＝(3－6)2＋(－2－0)2＋(5＋1)2＝7，故选B.【答案】 B2.过两点A (－2，m )，B (m,4)的直线倾斜⾓是45°，则m 的值是( ) A.－1 B.3 C.1D.－3【解析】由k AB ＝m －4－2－m＝tan 45°＝1，解得m ＝1.【答案】 C3.过点(－1,3)且平⾏于直线x －2y ＋3＝0的直线⽅程为( ) A.x －2y ＋7＝0 B.2x ＋y －1＝0 C.x －2y －5＝0D.2x ＋y －5＝0【解析】∵直线x －2y ＋3＝0的斜率为12，∴所求直线的⽅程为y －3＝12(x ＋1)，即x －2y ＋7＝0.【答案】 A4.已知直线l 1：ax －y －2＝0和直线l 2：(a ＋2)x －y ＋1＝0互相垂直，则实数a 的值为( ) A.－1 B.0 C.1D.2【解析】 l 1的斜率为a ，l 2的斜率为a ＋2，∵l 1⊥l 2，∴a (a ＋2)＝－1，∴a 2＋2a ＋1＝0即a ＝－1. 【答案】 A 5.如图1，在正⽅体OABC -O 1A 1B 1C 1中，棱长为2，E 是B 1B 上的点，且|EB |＝2|EB 1|，则点E 的坐标为( )图1A.(2,2,1)B.? ?2，2，23 C.? ?2，2，13 D.? ?2，2，43【解析】∵|EB |＝2|EB 1|，∴|EB |＝23|BB 1|＝43. ⼜E 在B 1B 上，∴E 的坐标为? ?2，2，43.【答案】 D6.若以点C (－1,2)为圆⼼的圆与直线x －2y ＋3＝0没有公共点，则圆的半径r 的取值范围为( )A.? ????0，255 B.? ????0，355 C.(0，5)D.(0,25)【解析】设圆⼼到直线的距离为d ，则d ＝|－1－4＋3|12＋(－2)2＝255.若直线与圆没有公共点，则05，故选A.【答案】 A7.已知直线l 1的⽅程为x ＋Ay ＋C ＝0，直线l 2的⽅程为2x －3y ＋4＝0，若l 1，l 2的交点在x 轴上，则C 的值为( )A.2B.－2C.±2D.与A 有关【解析】在2x －3y ＋4＝0中，令y ＝0，得x ＝－2，即直线2x －3y ＋4＝0与x 轴的交点为(－2,0).∵点(－2,0)在直线x ＋Ay ＋C ＝0上，∴－2＋A ×0＋C ＝0，∴C ＝2.【答案】 A8.若a ，b 满⾜a ＋2b ＝1，则直线ax ＋3y ＋b ＝0必过定点( ) A.? ????－12，－16 B.? ????12，－16 C.? ??12，16 D.? ??－12，16 【解析】令a ＝－1，b ＝1或a ＝1，b ＝0，得直线⽅程分别为－x ＋3y ＋1＝0，x ＋3y ＝0，其交点为? ??12，－16，此即为直线所过的定点.故选B.【答案】 B9.已知平⾯内两点A (1,2)，B (3,1)到直线l 的距离分别是2， 5－2，则满⾜条件的直线l的条数为()A.1B.2C.3D.4【解析】由题知满⾜题意的直线l在线段AB两侧各有1条，⼜因为|AB|＝5，所以还有1条为过线段AB上的⼀点且与AB垂直的直线，故共3条.【答案】 C10.若圆⼼在x轴上，半径为5的圆O位于y轴左侧，且与直线x＋2y＝0相切，则圆O 的⽅程是()A.(x－5)2＋y2＝5B.(x＋5)2＋y2＝5C.(x－5)2＋y2＝5D.(x＋5)2＋y2＝5【解析】设圆⼼O(a,0)，(a<0)，则5＝|a|1＋22，∴|a|＝5，∴a＝－5，∴圆O的⽅程为(x＋5)2＋y2＝5.【答案】 D11.直线y＝kx被圆x2＋y2＝2截得的弦长为()A.2 2B.2C. 2D.与k的取值有关【解析】由于圆x2＋y2＝2的圆⼼在直线y＝kx上，所以截得弦为圆x2＋y2＝2的直径，⼜其半径为2，故截得的弦长为2 2.【答案】 A12.已知点P(x，y)是直线y＝22x－4上⼀动点，PM与PN是圆C：x2＋(y－1)2＝1的两条切线，M，N为切点，则四边形PMCN 的最⼩⾯积为()A.43 B.23。

必修二第一章立体几何一、选择题2．（2011 全国课标I 理 6）在一个几何体的三视图中，正视图和俯视图以下图，则相应的侧视图能够为【答案】 D【分析】此题观察三视图．3 条切割圆锥后剩下的由三视图可知，此几何体是由一个圆锥沿四条均分圆锥侧面的母线中的部分，所以 A 、 B 均错， C 明显是错的．3．（ 2011 山东理 11）以下图是长和宽分别相等的两个矩形．给定以下三个命题：①存在三棱柱，其正（主）视图、俯视图以以下图；②存在四棱柱，其正（主）视图、俯视图以以下图；③存在圆柱，其正（主）视图、俯视图以以下图．此中真命题的个数是A ．3B．2C．1D．0【答案】 A【分析】假如把直三棱柱和圆柱放倒，则可获得如图的正视图和俯视图，①③正确；简单判断②正确所以 3 个命题都正确，选 A ．4．（2011 广东理 7）如图 1－ 3，某几何体的正视图（主视图）是平行四边形，侧视图（左视图）和俯视图都是矩形，则该几何体的体积为A．6 3B．9 3C．12 3D．18 3【答案】 B【分析】由该几何体的三视图可各该几何体是一个平行六面体，底面是以 3 为边长的正方形，该六面体的高221 3. ，所以该几何体的体积为32 3 93．5．（2011 安徽理6）一个空间几何体得三视图以下图，则该几何体的表面积为A ．48B ． 32+8C． 48+8D． 80【答案】 C【分析】6．（2011 浙江理 3）若某几何体的三视图以下图，则这个几何体的直观图能够是【答案】 D【分析】7．（2011 北京理 7）某四周体的三视图以下图，该四周体四个面的面积中最大的是A．8B．62C．10D．82【答案】C【分析】此题观察了三视图的有关知识．由三视图可知，该四周体能够描绘为：SA面 ABC ，ABC90，且SAAB4, BC3，从而能够计算并比较得面SAC 的面积最大，为 10，故应选 C ．【技巧点拨】依据所给的三视图，将其“复原 ”是解题的重点，自然，同时也要注意所给的数据，为了保证解题的正确性，能够将 “体”再复原成三视图，这样做一个查验，能够提升解题的正确率．8．（2011 湖南理 3）某几何体的三视图如图，则该几何体的体积为A ．912B ．918C ．942D ． 361822【答案】 B【分析】有三视图可知该几何体是一个长方体和球构成的组合体，其体积4 333 2=9V（ ）+318 ．3229．（ 2011 辽宁理 8）如图，四棱锥 S ABCD 的底面为正方形， SD底面 ABCD ，则以下结论中不正确 的是 ．．．A ． ACSB SBDB ． AB/ / 平面 SCDSBDSA所成的角等于SC与平面 所成的角C ．与平面D ． AB 与 SC 所成的角等于 DC 与 SA 所成的角【答案】 D【分析】本小题以四棱锥为载体，观察空间中点、线、面的地点关系．选项 A 正确 因为 SD 垂直于平面 ABCD ，而 AC 在平面 ABCD 中，所以 AC 垂直于 SD ；再由 ABCD 为正方形， 所以 AC 垂直于 BD ；而 BD 与 SD 又是两条订交直线，所以，AC 垂直于平面 SBD ，从而垂直于 SB ；选项B 正确因为AB 平行于 CD ，而 CD 在平面 SCD 内， AB 不在平面 SCD 内，所以 AB 平行于平面 SCD．选项 C 正确，SASBD所成的角就是角SAC， SC与平面 SBD所成的角就是与平面角 SCASAC又是等腰三角形，所以这两个角相等．选项D 错误AB与 SC所成的角等，而三角形于角 SCD，而 DC与 SASAB，这两个角是互补的．所成的角是角【技巧点拨】解决此类问题第一要从理论上娴熟的掌握有关的性质定理和判断定理，其次是正确的应用图象，使之问题详细化，此外，必需时也能够应用空间向量的知识来求解有关的角、线面关系问题．10．（ 2011 辽宁理 12）已知球的直径SC 4 ， A 、 B 是该球球面上的两点，AB 3 ，ASCBSC 30 ，则棱锥 SABC 的体积为A ．33B ．23C ． 3D ．1【答案】 C【分析】此题主要观察三棱锥的构造特点和体积公式、球的构造特点，观察学生的空间想象能力和 把立体几何问题转变为平面几何问题的能力．由题可知AB 必定在与直径 SC 垂直的小圆面上，做过 AB 交直径 SC 于 D ，以下图，设 SDx ，则 DC 4 x ，此时所求棱锥即切割成两个棱锥S ABD 和 CABD ，在 SAD 和SBD 中，因为 SC 为直径，所以SBCSAC 90 0 所以 DBCDAC 600 ，在 SBD 中，BD3x ，在 BDC 中， BD 3(4 x) ，所以 3x = 3 (4x) ，得 x3 ，所以 ABD33V1 3 ．为正三角形，体积 S ABD 43【技巧点拨】球的作用只限于载体，利用球研究有关几何体的体积或其余的问题，在应用中对于球可用的就是他的半径、大圆性质和其余线面关系问题．一些问题中要能够透过球的表面体，看到研究问题的本质．11．（ 2011 浙江理 4）以下命题中错误 的是．．A ．假如平面平面 ，那么平面内必定存在直线平行于平面B ．假如平面不垂直于平面 ，那么平面内必定不存在直线垂直于平面C ．假如平面D ．假如平面【答案】 D【分析】平面平面，平面 平面 ， I =l ，那么 l 平面，那么平面 内全部直线都垂直于平面12．（2011 全国11）已知平面截一球面得圆M，过圆心M且与成 60二面角的平面截该球面得圆N ．若该球面的半径为4，圆M的面积为4，则圆N 的面积为A ．7B ．9C．11D．13【答案】D【分析】本小题主要观察了球及球的截面的有关知识．如图：因为 OM 面e M ，由 e M的面积为4，故AM 2 ．在 Rt OAM 中， OA4， AM2，OAM60， OM23．又因为ON面e N ，在 Rt OMN 中，OMN30，ON OM gsin 303，NB OB2ON 213 ，所以 e N 的面积为( 13)213．13．（ 2011 四川 3）l1，l2，l3是空间三条不一样的直线，则以下命题正确的选项是A ．l1l2， l2l 3 l1 Pl3B．l1l 2， l 2 Pl 3l1l3C．l2Pl3Pl3l1， l2， l3共面 D ．l1，l2，l3共点l1， l2， l3共面【答案】 B【分析】若 l1l 2， l2l3则 l1， l 3有三种地点关系，可能平行、订交或异面，故 A 不对．固然l1∥ l 2∥ l3，或 l1， l2， l3共点，可是 l1， l2， l3可能共面，也可能不共面，故C、 D 也不正确．14．（ 2011 重庆 9）高为2的四棱锥 S ABCD 的底面是边长为1的正方形，点 S、 A、 B、C、4D 均在半径为 1 的同一球面上，则底面ABCD 的中心与极点 S 之间的距离为A ．22C．1 D ．2B ．42【答案】 C【分析】设底面中心为G ，球心为 O ，则易得AG22，于是 OG，用一个与 ABCD 所在22平面距离等于2的平面去截球， S便为此中一个交点，此平面的中心设为 H ，则42722OH222，故 SH21227，故 SG SH 2HG 21．2444884二、填空题15．（ 2011 全国课标I理15）已知矩形ABCD 的极点都在半径为 4 的球O的球面上，且AB 6, BC 2 3 ，则棱锥O ABCD 的体积为______________．【答案】 8 3【分析】此题观察球的截面、四棱锥的体积计算．波及空间想象能力、逻辑思想能力和简单计算．∵ AB6,BC 23，∴AC AB2BC 2 4 3 ，其为球的截面圆的直径，设棱锥 O ABCD 的高为 h，则h42(2 3)2 2 ，∴棱锥 O ABCD 的体积为1 h AB BC 83．3【技巧点拨】球的全部截面都是圆，而矩形的对角线恰巧是其外接圆的直径．16．（ 2011 福建理12）三棱锥P ABC 中， PA底面 ABC ， PA3，底面 ABC 是边长为 2 的正三角形，则三棱锥P ABC 的体积等于___________．【答案】3【分析】观察椎体的体积公式，属于简单题．V 1 31 2 2sin 600332【技巧点拨】求几何体体积的重点是找好底和高．17．（ 2011高考天津理10）一个几何体的三视图以下图（单位：m ），则这个几何体的体积为__________ m3【答案】 6【分析】18．（ 2011 辽宁理 15）一个正三棱柱的侧棱长和底面边长相等，体积为 2 3 ，它的三视图中的俯视图以下图，左视图是一个矩形，则这个矩形的面积是____________．【答案】 2 3【分析】本小题主要观察了正三棱柱的三视图有关知识，观察空间想象能力．设正三棱柱底面边长为 a ，利用体积为 2 3 ，很简单求出这个正三棱柱的底面边长和侧棱长都是2，所以底面正三角形的高为√3，故所求矩形的面积为 2 3 ．【技巧点拨】求解三视图问题要注意知足三个视图在长、宽、高之间的关系．利用这类关系常常能够更简捷求解有关问题．19．（ 2011 全国16）已知E、F分别在正方体ABCD A1B1C1 D1棱 BB1、 CC1上，且 B1E 2EB ，CF 2FC1，则面AEF与面ABC所成的二面角的正切值等于_____________．【答案】23【分析】本小题主要观察了无棱二面角的作法及求法．如图：连 FE 并延伸交 CB 的延伸线于 G ，连 AG ，过 B 作 BH AG ，连 EH为面 AEF 与面ABC所成的二面角的平面角．易求得tan2EHB3，则由三垂线定理知EHB．20．（ 2011 四川 15）如图，半径为R 的球 O 中有一内接圆柱．当圆柱的侧面积最大时，球的表面积与该圆柱的侧面积之差是．【答案】 2R2【分析】 S侧 2 r 2 R2r 2 4 r 2 (R2r 2 ) 时，S 侧 取最大值时， r2R 2 r 2r 2R2r2R ，22则S 球 S 侧 4R 2 2R 2 2R 2．21．（ 2011 上海春天13）有一种多面体的饰品，其表面由6 个正方形和8 个正三角形构成（如图），AB 与 CD 所成角的大小是______________．【答案】3【分析】 AB 与 CD 是正方形的边，则 AB // EF ， CD // FG ，因为 EF 和 FG 是正三角形 EFG 的两边，则 AB 与 CD 所成的角为 ．322．（ 2011 上海 7）若圆锥的侧面积为 2 ，底面积为，则该圆锥的体积为 __________ ．【答案】33【分析】此题观察（立体几何中）圆锥的有关量（侧面积、体积）的计算公式，观察计算能力． 依 题 意 ， 底 面 半 径 为 r 1 ， 侧 面 积 21(2r ) l l 2 ， 故 圆 锥 的 体 积 为 ：21 l2 r 23 ． 33三、解答题23．（ 2011 山东理 19）在以下图的几何体中， 四边形 ABCD 为平行四边形， ACB 90 ，EA平面 ABCD ， EF //AB ， FG / /BC ， EG//AC ， AB2EF ．（Ⅰ）若 M 是线段（Ⅱ）若 AC BC 【分析】（Ⅰ）连结AD 上的中点，求证：2 AE ，求平面角AAF ，GM / / 平面 ABFEBF C 的大小．；因为 EF//AB， FG//BC ，EFI FG F，所以平面 EFG// 平面 ABCD，又易证EFG∽FG EF111ABC ，所以AB，即 FG BC ，即 FG AD ，又M为AD的中点，BC222所以 AM 1AD ，又因为FG / / BC / / AD，所以FG / / AM，所以四边形AMGF是平行四边形，2故 GM / /FA ，又因为 GM平面 ABFE ， FA平面 ABFE ，所以 GM / / 平面 ABFE ．（Ⅱ）取 AB 的中点 O ，连结 CO ，因为 AC BC ，所以 CO AB ，又因为 EA平面 ABCD ， CO平面 ABCD ，所以 CO EA ，又 EAI AB A ，所以 CO平面 ABFE ，在平面 ABFE 内，过点 O 作 OH BF于H，连结CH ，由三垂线定理知：CH BF ，所以CHO 为二面角 A BF C 的平面角．设 AB2EF2a ，因为ACB90 ，AC BC2a ，CO a ，AE 2a ，连结FO，2简单证得FO/ /EA且FO26a ，所以OH 2 a23a ，所以在a ，所以 BF22263Rt COH 中， tan CHO CO3 ，故 CHO60 ，所以二面角 A BF C 的大小为 60 ．OH24．（ 2011 广东理 18）如图，在椎体P ABCD 中， ABCD 是边长为 1 的棱形，且DAB 60 ，PA PD 2， PB 2， E ，F 分别是 BC ，PC 的中点．（1） 证明： AD 平面 DEF ；（2） 求二面角 PAD B 的余弦值．【分析】（ 1） 取 AD 的中点 G ，又 PA PD ，所以 PG AD ，由题意知ABC 是等边三角形，所以 BGAD ，又 PG ，BG 是平面 PGB 的两条订交直线，∴ AD 平面 PGB ，∵ EF //PB ， DE / /GB ∴ 平面 DEF // 平面 PGB ， ∴AD 平面 DEF（ 2）由（ 1）知PGB 为二面角 P ADB 的平面角，由已知可得AC3 ，由 AD 平面 PGB ， AD/ /BC ，可知 PB BC ，所以 PC5 ，又 PA2 ，所以 △ PAC 是直角三角形，由F 是 PC 的中点得 FAFB1PC FC5 ，又 DA DC DB 1 ，所以22△ FDA ≌△ FDC ≌△ FDB ．由 △ FDA ≌△ FDC 知 FDA FDC ，所以 FD 在面 ABCD 上的射影在 DB 上， 由 △ FDC ≌△FDB 知 FDC FDB ，所以 FD 在面 ABCD 上的射影在 DE 上，从而 FD 在面 ABCD 上的射影就是点D ，所以 FD 面 ABCD ．延伸BG 、CD 交于一点O ，连结 PO ，则 PO//DF ，所以 PO 面 ABCD ，从而POOG ． Rt △ POG 中， PO 2FD 1， PGPA2( 1AD )27 ，所以 OG 3 ，244cos321PGBcos PGO．77注：假如学习了余弦定理，以下解法更加简易：在 Rt PGA 中，PG227；在 Rt BGA中，BG212(1)23 2 (1)2；2424在 PGB 中，cos PGB PG 2BG 2PB 221 ．2PG BG725．（ 2011 江苏 16）如图，在四棱锥P ABCD 中，平面 PAD平面 ABCD ， AB AD ，BAD 60 ， E、F 分别是 AP、AD的中点．求证：（1）直线EF / /平面PCD；（2）平面BEF平面PAD【分析】简单此题观察空间想象能力和推理论证能力、线面平行和垂直的判断与性质，属简单题．（ 1）因为E、 F 分别是 AP、 AD的中点，∴ EF //PD又∵P,D面PCD，E 面 PCD，∴直线 EF / / 平面 PCD（ 2）∵AB AD ， BAD 60 ， F 是 AD 的中点，∴BF AD又平面 PAD平面 ABCD ，面 PAD I 面 ABCD＝AD∴ BF面 PAD所以，平面 BEF平面 PAD ．26．（ 2011 安徽理17）如图，ABEDFC为多面体，平面ABED与平面ACFD垂直，点O在线段AD 上， OA 1，OD 2 ，△OAB，△OAC ，△ODE ，△ ODF 都是正三角形．（1）证明直线BC∥EF；（2）求棱锥F OBED的体积．27．（ 2011 湖南理 19）如图，在圆锥PO 中，已知PO 2 ，⊙O的直径AB 2 ， C 是弧 AB 的中点， D 为 AC 的中点．（ I ）证明：平面POD平面PAC ;（ II ）求二面角B PA C 的余弦值．【分析】（ I ）连结OC，因为OA OC ，D 为的AC 中点，所以AC OD ．又 PO底面⊙O, AC底面⊙O,所以 AC PO.因为 OD , PO是平面POD 内的两条订交直线，所以AC平面 POD．而AC平面 PAC，所以平面 POD平面PAC．（ II ）在平面POD 中，过O 作OH PD 于H，由（I ）知，平面POD平面 PAC，所以OH平面PAC ,又PA平面PAC ,所以PA OH．在平面PAO 中，过O作OG PA于G连结 HG ，则有PA平面 OGH，从而PA HG ，所以OGH 是二面角B PA C 的平面角．在 Rt ODA中, OD OA sin 45222PO OD210在 Rt2POD中, OH15PO2+OD 22+2在 Rt POA中,OGPO OA 2 16PO2 +OA22+13OH101510在 Rt OHG中,sin5OGHOGH6，所以 cos．OG553故二面角 B PA C 的余弦值为10 ．S 5AB CD BC CD SAB28．（2011 全国19）如图，棱锥ABCD中，∥，⊥，侧面为等边三角形，AB = BC =2，CD = SD =1．（Ⅰ）证明：SD ⊥平面 SAB；（Ⅱ）求 AB 与平面 SBC所成的角的大小．【分析】本小题主要观察空间直线与直线、直线与平面、平面与平面的地点关系及线面角等基础知识，观察空间想象能力、推理论证能力和运算能力．（Ⅰ）证明：连BDQ AB SB BC, CD SD1, BD BD SDB BCD ,又QBCCD,BCD BSD90 ,SD SB取 AB 的中点 E ，连DE ，则AE EB CD ,又Q AB∥CD，BC⊥CD，四边形BCDE是矩形， DE AB DA DB又QSASB, SD SD SAD SBD,SD SA故 SD ⊥平面 SAB．（Ⅱ）过 S 作 SOED 于O ，过 O 作OFBC 于F ，连 SF ，则 OF ∥ AB ， AB 与平面 SBC所成的角为 OF 与平面 SBC 所成的角． 由（Ⅰ）有 DE AB ，又 SE AB ，所以 AB平面 SDE∴ SO 平面 ABCD ．所以 BC 平面 SDF ，故SFO 即为所求．在 Rt SDE 中， SE3, SD1,DEBC2 ，所以 SOg3,OFCD 11 32 23 33所以 tan SFO2 SFOarctan ．1，所以2229．（ 2011 重庆 19）如图，在四周体ABCD 中，平面 ABC ⊥ ACD ， AB ⊥ BC ， AD = CD ，∠CAD = 300 ．（Ⅰ）若 AD =2， AB =2 BC ，求四边形 ABCD 的体积．（Ⅱ）若二面角 CAB D 为 600 ，求异面直线 AD 与 BC 所成角的余弦值．【分析】（Ⅰ）以下图，设F 为 AC 的中点，因为 AD CD ，所以 DFAC ．故由平面 ABC ⊥ ACD ，知 DF平面 ABC ，即 DFAD sin 30o 1，AFAD cos30o3 ．在Rt ABC 中，因 AC2 AF 23 ，AB 2BC ，由勾股定理易得 BC2 15， AB 4 155．故5四周体 ABCD 的体积 V1gS ABC gDF1 12 15 4 15 4 ．33 2 5 5 5（Ⅱ）以下图设 G 、H 分别为边 CD ，BD 的中点， 则 FG / / AD ，GH / / BC ，，从而FGH是异面直线 AD 与 BC 所成角或其补角． 设 E 为边 AB 的中点， 则 EF / / BC ，由 AB ⊥ BC ，知 EF⊥ ABDF平面 ABC，故由三垂线定理知DE ⊥ AB，所以 DEF为二面角，又由（Ⅰ）有CAB D 的平面角，由题设知DEF 60o ，设 AD a ，则 DFAD sin CAD a2在 Rt DEF 中， EFDF gcot DEFa g 3 3a ，2 36从而 GH1BC EF3 a26因ADEBDE ，故 BDAD a ．从而，在 Rt BDF 中， FH1BD1a ，又22FG1AD1a ，从而在 FGH 中，因 FG FH ，由余弦定理得22cos FGHFG 2GH 2 FH 2 GH 3 ，2FG gGH2FG6 故异面直线 AD 与 BC 所成角的余弦值为3 ．630．（ 2011 江西 21）（ 1）如图，对于任一给定的四周体 A 1 A 2 A 3 A 4 ，找出挨次摆列的四个互相平行的平面1, 2,3 ,4 ，使得 A ii （ i=1 ， 2， 3，4），且此中每相邻两个平面间的距离都相等；（2）给定挨次摆列的四个互相平行的平面 1 , 2, 3,4 ，此中每相邻两个平面间的距离为1，若一个正四周体 A 1 A 2 A 3 A 4 的四个极点知足： A i i （ i=1 ， 2， 3， 4），求该正四周体 A 1 A 2 A 3 A 4 的体积．【分析】（ 1）将直线 A 1 A 4 三均分，此中另两个分点挨次为 A 2, A 3 ，连结 A 2 A 2 , A 3 A 3 ，作平行于A 2 A 2 , A 3 A 3 的平面，分别过 A 2 A 2 , A 3 A 3 ，即为 2,3 ．同理，过点 A 1 , A4 作平面 1, 4 即可的出结论．（ 2）现设正方体的棱长为a ，若 A 1MMN 1,则有 ， A 1M 1a，2D 1E 1A 1D 12A 1E 125a ，因为 A 1 D 1 A 1E 1A 1 MD 1E 1, 得， a5 ，2那么，正四周体的棱长为 d2a10，其体积为 V1 a 3 5 5 （即一个棱长为 a 的正方体割3 3去四个直角三棱锥后的体积）31．（ 2011 上海春天 20）某甜品店制作一种蛋筒冰激凌， 其上部分是半球形， 下半部分呈圆锥形 （如图），现把半径为 10 cm 的圆形蛋皮均分红5 个扇形，用一个蛋皮围成圆锥的侧面（蛋皮的厚度忽视不计），求该蛋筒冰激凌的表面积和体积（精准到0.01）【分析】设圆锥的底面半径为r ，高为h．由题意，圆锥的侧面扇形的周长为12104cm ，5圆锥底面周长为 2 r cm ，则2r4，r2cm．圆锥的高为102229646cm ，圆锥的侧面扇形的面积为S1141020cm2，2半球的面积为S214228．2所以该蛋筒冰激凌的表面积为S S1S22887.96 cm2；圆锥的体积为V112246166cm3，33半球的体积为 V2142316cm3，233所以该蛋筒冰激凌的体积为V V1 V2166157.80cm3．3所以该蛋筒冰激凌的表面积约为87.96cm 2，体积约为 57.80cm 3．第二章分析几何初步一、选择题1．（2011 广东理2）已知会合A{( x, y) | x ，y为实数，且 x 2y21}，B{( x, y) | x ，y为实数，且 y x }，则 AI B的元素个数为A ．0B． 1C． 2 D ． 3【答案】 C【分析】会合 A 由由圆x2y21上的全部点构成，会合 B 由直线yx 上的全部点构成，而直线经过圆内的点 O (0,0)，故直线与圆有 2 个交点．2．（ 2011 重庆 8）在圆x2y22x6y0内，过点E0,1 的最长弦和最短弦分别为AC和BD，则四边形 ABCD 的面积为A ．5 2B ．10 2C ．15 2D ．20 2【答案】 B【分析】由题意， AC 为直径，设圆心为 F ，则 FE BD ，圆的标准方程为 2210 ，x 1y3 故 F 1,3 ，由此，易得：AC 2 10 ，又 k EF3 1 2 ，所以直线 BD 的方程为 y 1 x 1 ，121 1 3F 到 BD 的距离为25，由此得， BD2 5所以四边形 ABCD 的面积为521ACgBD12521010 2．223．（ 2011 江西 10）如图， 一个直径为 1的小圆沿着直径为 2 的大圆内壁的逆时针方向转动，M 和 N 是小圆的一条固定直径的两个端点．那么，当小圆这样滚过大圆内壁的一周，点M ，N 在大圆内 所绘出的图形大概是【答案】 A【分析】 依据小圆 与大圆半径恰巧是大圆的四分之一，所以大圆的半径．1: 2 的关系， 找上下左右四个点， 依据这四个点的地点，M 点的轨迹是个大圆，而 N 点的轨迹是四条线，恰巧是点小圆转半圈，M 产生的4．（2011 上海春天17）直线l : yk x1与圆 C : x 2y 21的地点关系为2A ．订交或相切B ．订交或相离C ．相切D ．订交【答案】 D【分析】法 1：因为直线 l 过点1,0 ，而点1,0 在圆 C : x 2y 21 的内部，所以直线与圆22订交．应选 D ．法 2：圆心为0,0 ，半径为 1，圆心到直线的距离为11kk1d22 1 ，1 k 2k2所以直线与圆订交．应选D ．二、填空题5 ．（ 2011江 苏14 ） 设 集 合 A{( x, y) |m(x 2)2y 2m 2 , x, y R} ，2B {( x, y) | 2m x y 2m 1, x, y R} ， 若 A I B 则 实 数 m的取值范围是______________．【答案】 1m2 12【分析】此题综合观察会合及其运算、直线与圆的地点关系、含参分类议论、点到直线距离公式、 两条直线地点关系、解不等式，属难题．会合 B 是在两条平行线及他们的之间的部分． 当mm 2 即 0 m1 时， A ， A I B，不合题意；22当 m 0 时，会合 A 表示 (2,0) 为圆心，以mm 为半径的圆，由A I B知只要圆与直线x y2m 1有公共点，所以因为 | 2 2m 1|1 2mm ，解得 m12220 ，矛盾；2当 m1 时，会合 A 是以 (2,0) 为圆心，1为半径的圆，直线 x y 2m 1过圆心，切合题意．2 2 当 m1 时，2若m ，则2m 2 2m 1， (2,0) B ，切合题意；1若 m 12m 2，则只要2 2mm ，解得 1 m2 1．，即2综上可知，1m2 1 ．26．（ 2011 湖北 14）如图，直角坐标系 xOy 所在的平面为 ，直角坐标系 x 'Oy ' （此中 y ' 轴与 y 轴重合）所在的平面为， xOx '450 ．（Ⅰ）已知平面内有一点 P' 22,2 ，则点 P ' 在平面内的射影 P 的坐标为 ________；内的曲线 C ' 的方程是x '222 0 ，则曲线 C '在平面（Ⅱ）已知平面2 y '2 内的射影C 的方程是 ________．【答案】2,2 ； x1 2 y 21【分析】（Ⅰ）设点 P '在平面 内的射影 P 的坐标为 x, y ，则点 P 的纵坐标和 P ' 2 2,2 纵坐标同样，所以 y2，过点 P '作 P 'HOy ，垂足为 H ，连结 PH ，则 P 'HP 450， P 横坐标，x PHP ' H cos450x'cos 4502 22 2 ，所以点 P'在平面 内的射影P 的坐标为22,2 ；高考试题分类汇编数学必修2部分试题.doc（Ⅱ）由（Ⅰ）得 x x 'cos 450x '2， y 'y ，所以x '2x，代入曲线 C ' 的方程，2y 'yx '22 y' 220 ，得 2 x22 y2 2 0x 12y 21，所以射影C的方程22填 x 1 2y2 1 ．7．（ 2011 上海春天7）两条直线l1: x3y20 与l2: x y20 夹角的大小是_____________．【答案】12【分析】直线 l1的倾斜角为，直线 l2的倾斜角为，夹角为4612．64。

高一数学必修2习题(答案详解)高一数学必修2习题(答案详解)一、选择题1. 题目：已知集合A={1, 2, 3, 4}，集合B={3, 4, 5, 6}，则A∩B的最小值是（）选项：A. 0B. 1C. 2D. 3解析：集合A和集合B的交集即为A∩B。

在这里，A和B的交集为{3, 4}，共有两个元素。

因此，答案为C. 2。

2. 题目：若sinθ=1/2，θ∈（0, π），则cosθ的值为（）选项：A. 1/2B. -1/2C. √3/2D. -√3/2解析：根据三角函数的定义，sinθ=对边/斜边。

在这里，sinθ=1/2，代表一个直角三角形中，对边的长度是斜边长度的一半。

根据勾股定理，可知另外一个边的长度为√3/2。

因此，cosθ=邻边/斜边=√3/2。

答案为C. √3/2。

二、填空题1. 题目：已知事件A的概率为0.6，事件B的概率为0.4，事件A 和事件B同时发生的概率为0.3，则事件A和事件B互不独立。

事件A的补事件的概率是（）。

解析：事件A的概率为0.6，补事件即为事件A不发生的概率，即1-0.6=0.4。

2. 题目：已知函数y=2x-1，若x=3，则y的值为（）。

解析：将x=3代入函数中，得到y=2*3-1=5。

三、计算题1. 题目：已知函数y=2x+3，求当x=1时，y的值。

解析：将x=1代入函数中，得到y=2*1+3=5。

2. 题目：已知函数y=3x^2-2x+1，求当x=2时，y的值。

解析：将x=2代入函数中，得到y=3*2^2-2*2+1=13。

四、解答题1. 题目：求解方程2x-5=7。

解析：将方程两边都加上5，得到2x=12。

再将方程两边都除以2，得到x=6。

因此，方程的解为x=6。

2. 题目：求解方程3x^2-5=0。

解析：将方程两边都加上5，得到3x^2=5。

再将方程两边都除以3，得到x^2=5/3。

对方程两边取平方根，得到x=±√(5/3)。

因此，方程的解为x=±√(5/3)。

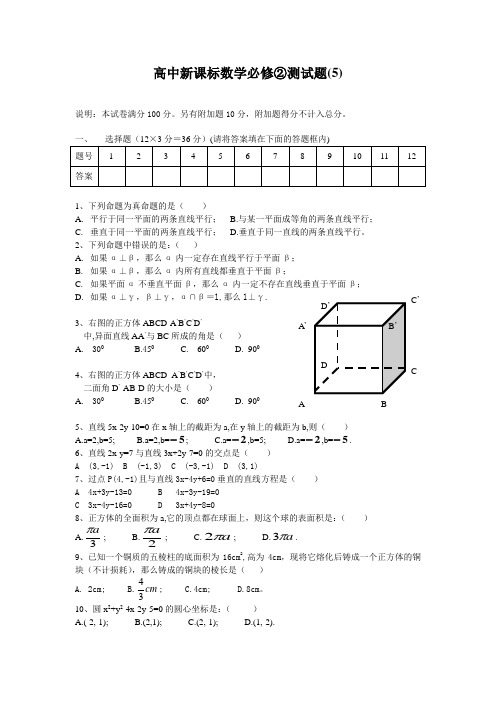
高中新课标数学必修②测试题(5)说明：本试卷满分100分。

另有附加题10分，附加题得分不计入总分。

1、下列命题为真命题的是（ ）A. 平行于同一平面的两条直线平行；B.与某一平面成等角的两条直线平行；C. 垂直于同一平面的两条直线平行；D.垂直于同一直线的两条直线平行。

2、下列命题中错误的是：（ ）A. 如果α⊥β，那么α内一定存在直线平行于平面β；B. 如果α⊥β，那么α内所有直线都垂直于平面β；C. 如果平面α不垂直平面β，那么α内一定不存在直线垂直于平面β；D. 如果α⊥γ，β⊥γ，α∩β＝l,那么l ⊥γ.3、右图的正方体ABCD-A ’B ’C ’D ’中,异面直线AA ’与BC 所成的角是（ ） A. 300 B.450 C. 600 D. 900 4、右图的正方体ABCD- A ’B ’C ’D ’中，二面角D ’-AB-D 的大小是（ ）A. 300B.450C. 600D. 9005、直线5x-2y-10=0在x 轴上的截距为a,在y 轴上的截距为b,则（ ） A.a=2,b=5; B.a=2,b=5-;C.a=2-,b=5;D.a=2-,b=5-. 6、直线2x-y=7与直线3x+2y-7=0的交点是（ ） A (3,-1) B (-1,3) C (-3,-1) D (3,1)7、过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是（ ） A 4x+3y-13=0 B 4x-3y-19=0 C 3x-4y-16=0 D 3x+4y-8=08、正方体的全面积为a,它的顶点都在球面上，则这个球的表面积是：（ ） A.3aπ; B.2aπ; C.a π2; D.a π3.9、已知一个铜质的五棱柱的底面积为16cm 2,高为4cm ，现将它熔化后铸成一个正方体的铜块（不计损耗），那么铸成的铜块的棱长是（ ） A. 2cm; B.cm 34; C.4cm; D.8cm 。

10、圆x 2+y 2-4x-2y-5=0的圆心坐标是：（ ） A.(-2,-1); B.(2,1); C.(2,-1); D.(1,-2).A B A ’ CC ’11、直线3x+4y-13=0与圆1)3()2(22=-+-y x 的位置关系是：（ ） A. 相离; B. 相交; C. 相切; D. 无法判定.12、圆C 1: 1)2()2(22=-++y x 与圆C 2:16)5()2(22=-+-y x 的位置关系是（ ） A 、外离 B 相交 C 内切 D 外切 二、填空题（5×4=20）13、底面直径和高都是4cm 的圆柱的侧面积为 cm 2。

（数学2必修）第一章 空间几何体[基础训练A 组] 一、选择题1．有一个几何体的三视图如下图所示；这个几何体应是一个( )A .棱台B .棱锥C .棱柱D .都不对2．棱长都是1的三棱锥的表面积为（ ）AB. C. D. 3．长方体的一个顶点上三条棱长分别是3,4,5；且它的8个顶点都在 同一球面上；则这个球的表面积是（ ）A ．25πB ．50πC ．125πD ．都不对 4．正方体的内切球和外接球的半径之比为（ ）AB2 C．2:D35．在△ABC 中；02, 1.5,120AB BC ABC ==∠=；若使绕直线BC 旋转一周；则所形成的几何体的体积是（ ）A.92π B. 72π C. 52π D. 32π 6．底面是菱形的棱柱其侧棱垂直于底面；且侧棱长为5；它的对角线的长 分别是9和15；则这个棱柱的侧面积是（ ） A ．130 B ．140 C ．150 D ．160二、填空题1．一个棱柱至少有 _____个面；面数最少的一个棱锥有 ________个顶点； 顶点最少的一个棱台有 ________条侧棱。

主视图 左视图 俯视图2．若三个球的表面积之比是1:2:3；则它们的体积之比是_____________。

3．正方体1111ABCD A B C D - 中；O 是上底面ABCD 中心；若正方体的棱长为a ； 则三棱锥11O AB D -的体积为_____________。

4．如图；,E F 分别为正方体的面11A ADD 、面11B BCC 的中心；则四边形E BFD 1在该正方体的面上的射影可能是____________。

5．已知一个长方体共一顶点的三个面的面积分别是2、3、6；这个长方体的对角线长是___________；若长方体的共顶点的三个侧面面积分别为3,5,15；则它的体积为___________.三、解答题1．养路处建造圆锥形仓库用于贮藏食盐（供融化高速公路上的积雪之用）；已建的仓库的底面直径为12M ；高4M ；养路处拟建一个更大的圆锥形仓库；以存放更多食盐；现有两种方案：一是新建的仓库的底面直径比原来大4M （高不变）；二是高度增加4M (底面直径不变)。

高中数学二试题库及答案一、选择题（每题3分，共30分）1. 若函数\( f(x) = ax^2 + bx + c \)（\( a \neq 0 \)）的图像与x轴有两个交点，则下列说法正确的是（）。

A. \( a > 0 \)且\( b^2 - 4ac > 0 \)B. \( a < 0 \)且\( b^2 - 4ac > 0 \)C. \( a > 0 \)且\( b^2 - 4ac < 0 \)D. \( a < 0 \)且\( b^2 - 4ac < 0 \)2. 已知\( \sin \theta = \frac{3}{5} \)，且\( \theta \)为锐角，则\( \cos \theta \)的值为（）。

A. \( \frac{4}{5} \)B. \( -\frac{4}{5} \)C. \( \frac{3}{5} \)D. \( -\frac{3}{5} \)3. 集合\( A = \{x | x^2 - 5x + 6 = 0\} \)，\( B = \{x | x^2 - 5x + 6 < 0\} \)，则\( A \cap B \)为（）。

A. \( \{2, 3\} \)B. \( \{2\} \)C. \( \{3\} \)D. 空集4. 若\( \log_2 8 = 3 \)，则\( \log_2 32 \)等于（）。

A. 3B. 5C. 6D. 95. 函数\( y = \frac{1}{x} \)的图像关于（）对称。

A. y轴B. x轴C. 原点D. 直线y = x6. 已知\( \tan \alpha = 2 \)，求\( \sin \alpha \)的值（）。

A. \( \frac{2}{\sqrt{5}} \)B. \( \frac{1}{\sqrt{5}} \)C. \( \frac{2}{\sqrt{3}} \)D. \( \frac{1}{\sqrt{3}} \)7. 函数\( f(x) = x^3 - 3x^2 + 4 \)的极大值点是（）。

数学2（必修）第一章：空间几何体[基础训练A 组] 数学2（必修）第一章：空间几何体[综合训练B 组] 数学2（必修）第一章：空间几何体[提高训练C 组] 数学2（必修）第二章：点直线平面[基础训练A 组] 数学2（必修）第二章：点直线平面[综合训练B 组] 数学2（必修）第二章：点直线平面[提高训练C 组] 数学2（必修）第三章：直线和方程[基础训练A 组] 数学2（必修）第三章：直线和方程[综合训练B 组] 数学2（必修）第三章：直线和方程[提高训练C 组] 数学2（必修）第四章：圆和方程 [基础训练A 组] 数学2（必修）第四章：圆和方程 [综合训练B 组] 数学2（必修）第四章：圆和方程 [提高训练C 组]（数学2必修）第一章 空间几何体[基础训练A 组] 一、选择题1．有一个几何体的三视图如下图所示，这个几何体应是一个( )A .棱台B .棱锥C .棱柱D .都不对2．棱长都是1的三棱锥的表面积为（ ）AB. C. D. 3．长方体的一个顶点上三条棱长分别是3,4,5，且它的8个顶点都在主视图 左视图 俯视图同一球面上，则这个球的表面积是（ ）A ．25πB ．50πC ．125πD ．都不对 4．正方体的内切球和外接球的半径之比为（ ）A ．3:1B ．3:2C ．2:3D ．3:35．在△ABC 中，02, 1.5,120AB BC ABC ==∠=,若使绕直线BC 旋转一周，则所形成的几何体的体积是（ ）A.92π B. 72π C. 52π D. 32π 6．底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长 分别是9和15，则这个棱柱的侧面积是（ ） A ．130 B ．140 C ．150 D ．160二、填空题1．一个棱柱至少有 _____个面，面数最少的一个棱锥有 ________个顶点， 顶点最少的一个棱台有 ________条侧棱。

2．若三个球的表面积之比是1:2:3，则它们的体积之比是_____________。

空间几何体1.【2012高考新课标文7】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（ ）()A 6 ()B 9 ()C 12 ()D 18【答案】B2.【2012高考新课标文8】平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π 【答案】B[3.【2012高考全国文8】已知正四棱柱1111ABCD A B C D -中 ，2AB =，122CC =，E 为1CC 的中点，则直线1AC 与平面BED 的距离为（A ）2 （B ）3 （C ）2 （D ）1【答案】D4.【2012高考陕西文8】将正方形（如图1所示）截去两个三棱锥，得到图2所示的几何体，则该几何体的左视图为 （ ）8.【答案】B.5.【2012高考江西文7】若一个几何体的三视图如图所示，则此几何体的体积为}A．112.5 C D.92【答案】D6.【2012高考湖南文4】某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能．．．是【答案】D7.【2012高考广东文7】某几何体的三视图如图1所示，它的体积为A. 72πB. 48πC. 30πD. 24π【答案】C8.【2102高考福建文4】一个几何体的三视图形状都相同，大小均等，那么这个几何体不可以是A 球B 三棱锥C 正方体D 圆柱&;图1正视图俯视图侧视图5563—563【答案】D.9.【2012高考重庆文9】设四面体的六条棱的长分别为1，1，1，1，2和a 且长为a 的棱与长为2的棱异面，则a 的取值范围是 （A ）(0,2) （B ）(0,3) （C ）(1,2)（D ）(1,3)【答案】A10.【2012高考浙江文3】已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积是A.1cm 3B.2cm 3C.3cm 3D.6cm 3 【答案】C\11.【2012高考浙江文5】 设l 是直线，a ，β是两个不同的平面A. 若l ∥a ，l ∥β，则a ∥βB. 若l ∥a ，l ⊥β，则a ⊥βC. 若a ⊥β，l ⊥a ，则l ⊥βD. 若a ⊥β, l ∥a ，则l ⊥β【答案】B12.【2012高考四川文6】下列命题正确的是（ ）A 、若两条直线和同一个平面所成的角相等，则这两条直线平行B 、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C 、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行，D 、若两个平面都垂直于第三个平面，则这两个平面平行 【答案】C13.【2012高考四川文10】如图，半径为R 的半球O 的底面圆O 在平面α内，过点O 作平面α的垂线交半球面于点A ，过圆O 的直径CD 作平面α成45角的平面与半球面相交，所得交线上到平面α的距离最大的点为B ，该交线上的一点P 满足60BOP∠=，则A 、P 两点间的球面距离为（ ）（1）2arccos4R B、4RπC、3arccos3R D、3Rπ【答案】A14.【2102高考北京文7】某三棱锥的三视图如图所示，该三棱锥的表面积是>（A）28+65B）30+65C）56+125（D）60+125【答案】B二、填空题15.【2012高考四川文14】如图，在正方体1111ABCD A B C D-中，M、N分别是CD、1CC的中点，则异面直线1A M 与DN所成的角的大小是____________。