初二数学等边三角形[人教版]
- 格式:pdf
- 大小:1.14 MB
- 文档页数:9


![初二数学等边三角形[人教版]](https://uimg.taocdn.com/e46dfea80b4e767f5acfceda.webp)
![初二数学等边三角形[人教版]](https://uimg.taocdn.com/1357a798647d27284a73518a.webp)

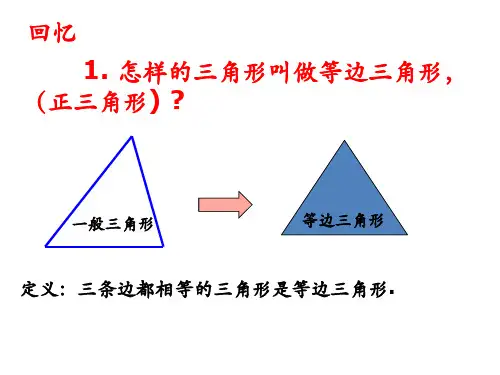

等边三角形的性质和判定知识总结:等边三角形的性质:等边三角形的判定:1、三边相等1、三边相等2、三个内角60°2、三个内角60°3、三线合一3、有一个内角为60°的等腰三角形定理:30°所对的直角边为斜边的一半逆定理:如果直角边为斜边的一半,则直角边所对的角为30°例1、如图,在△ABC中,∠BAC=90°,AB=AC,∠BAD=30°,AD=AE,则∠EDC的度数为()A、10°B、15°C、20°D、30°例2、若等腰三角形的腰长为6cm,腰上的高为3cm,则等腰三角形的顶角为()A、30°B、150°C、30°或150°D、以上都不对1、已知a、b、c是三角形的边长,且满足(a-b)2+|b-c|=0,那么这个三角形一定是()A、直角三角形B、等边三角形C、钝角三角形D、锐角三角形2、在△ABC中,∠A+∠B=120°,∠C=∠A,则△ABC是()A、钝角三角形B、等腰直角三角形C、直角三角形D、等边三角形3、如图,△ABC为等边三角形,BD是中线,延长BC到E,使CE=CD,若△ABC的周长为18,BD=a,则△BDE 的周长为()A、9+aB、12+2aC、12+aD、9+2a4、已知∠AOB=30°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1、O、P2三点构成的三角形是()A、直角三角形B、钝角三角形C、等腰三角形D、等边三角形5、等腰三角形底边长为6cm,一腰上的中线把它的周长分成两部分,差为2cm,则腰长为()A、4cmB、8cmC、4cm或8cmD、以上都不对例4、如图,△ABC是等边三角形。
D、E是△ABC外两点,连结BE交AC于M,连结AD交CE于N,AD交BE 于F,DA=EB。




等边三角形(提高)【学习目标】1. 掌握等边三角形的性质和判定.2. 掌握含30°角的直角三角形的一个主要性质.3. 熟练运用等边三角形的判定定理与性质定理进行推理和计算. 【要点梳理】【高清课堂:389303 等边三角形,知识要点】 要点一、等边三角形 等边三角形定义:三边都相等的三角形叫等边三角形.要点诠释:由定义可知,等边三角形是一种特殊的等腰三角形.也就是说等腰三角形包括等边三角形.要点二、等边三角形的性质 等边三角形的性质:等边三角形三个内角都相等,并且每一个内角都等于60°. 要点三、等边三角形的判定 等边三角形的判定:(1)三条边都相等的三角形是等边三角形;(2)三个角都相等的三角形是等边三角形;(3)有一个角是60°的等腰三角形是等边三角形. 要点四、含30°的直角三角形含30°的直角三角形的性质定理:在直角三角形中,如果有一个锐角是30°,那么它所对的直角边等于斜边的一半. 要点诠释:这个定理的前提条件是“在直角三角形中”,是证明直角三角形中一边等于另一边(斜边)的一半的重要方法之一,通常用于证明边的倍数关系. 【典型例题】类型一、等边三角形1、(2015秋·黄冈期中)如图,已知点B 、C 、D 在同一条直线上,ABC ∆和DCE ∆都是等边三角形,BE 交AC 于F ,AD 交CE 于H. (1)求证:△BCE ≌△ACD ; (2)求证:FH ∥BD.【答案与解析】(1)证明: ABC ∆和DCE ∆都是等边三角形 ∴BC =AC ,CE =CD ,∠BCA =∠ECD =60°∴∠BCA+∠ACE=∠ECD+∠ACE ,即∠BCE=∠ACD在△BCE 和△ACD 中BCE ACD CE B A D C C C ∠=∠==⎧⎪⎨⎪⎩∴△BCE ≌△ACD (SAS )(2)由(1)知△BCE ≌△ACD 则∠CBF=∠CAH ,BC=AC又∵ABC ∆和DCE ∆都是等边三角形,且点B 、C 、D 在同一条直线上, ∴∠ACH=180°-∠ACB-∠HCD=60°=∠BCF , 在△BCF 和△ACH 中CBE CAH BC ACBCF ACH ∠=∠=∠=∠⎧⎪⎨⎪⎩∴△BCF ≌△ACH (ASA ) ∴CF=CH ,又∵∠FCH =60°∴△CHF 是等边三角形 ∴∠FHC =∠HCD=60°, ∴FH ∥BD【总结升华】本题考查等边三角形的判定与性质及全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键。