长方体和正方体表面积的变化―

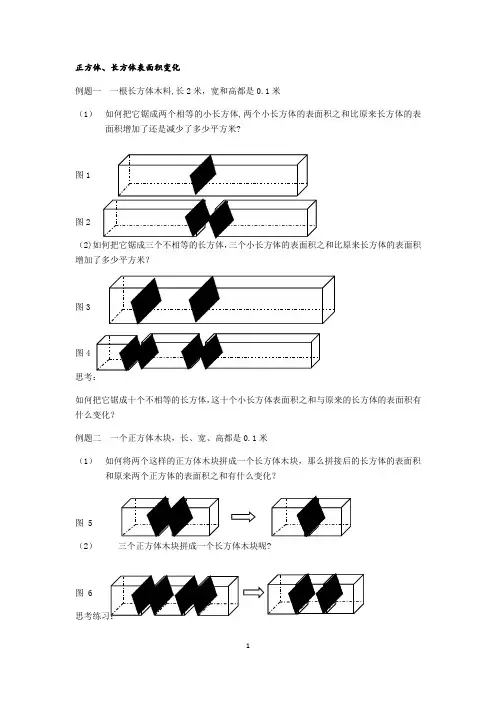
正方体、长方体表面积变化例题一一根长方体木料,长2米，宽和高都是0.1米（1）如何把它锯成两个相等的小长方体,两个小长方体的表面积之和比原来长方体的表面积增加了还是减少了多少平方米?图1图（2)如何把它锯成三个不相等的长方体，三个小长方体的表面积之和比原来长方体的表面积增加了多少平方米？图3图如何把它锯成十个不相等的长方体，这十个小长方体表面积之和与原来的长方体的表面积有什么变化？例题二一个正方体木块，长、宽、高都是0.1米（1）如何将两个这样的正方体木块拼成一个长方体木块，那么拼接后的长方体的表面积和原来两个正方体的表面积之和有什么变化？图 5（2）三个正方体木块拼成一个长方体木块呢?图 6（3）八个正方体呢?总结：对于这种长方体和正方体拼接或截取导致表面积产生变化的问题，我们要弄清楚一下问题:1.在这个演变过程中，我们能看到的立方体的表面有什么变化?2.变化过程中，表面积的改变和这些新增或消失的面有什么关系3.新增或消失的面和原来长方体或正方体哪些面的面积相等以及个数有什么变化？正方体、长方体表面积变化例题用两个长、宽、高分别是5cm、4cm、3cm的长方体可以拼成几种不同的长方体？怎么拼表面积最大？怎么拼表面积最小？方法一:出新长方体的长、宽、高，然后再求长方体表面积方法二：拼接之后长方体的表面积减少的面积的大小有什么关系?减少的表面积越小,拼成后的大长方体的表面积就越大典型例题:【例题1】有一个正方体木块，把它分成两个长方体后，表面积增加了24平方厘米,这个正方体木块原来的表面积是多少平方厘米？练习2:1。

把三个棱长都是2厘米的正方体拼成一个长方体，这个长方体的表面积是多少平方厘米?2.有一个长方体木块，长4分米、宽3分米、高6分米，现在把它锯成两个长方体，表面积最多增加多少平方分米？【例题2】一个棱长为6厘米的正方体木块，如果把它锯成棱长为2厘米的正方体若干块，表面积增加多少平方厘米?练习1.把27块棱长是1厘米的小正方体堆成一个大正方体，这个大正方体的表面积比原来所有的小正方体的表面积之和少多少平方厘米？2.用棱长是1厘米的小正方体摆成一个棱长是2厘米的正方体，至少需要多少个小正方体？如果要摆一个棱长是6厘米的正方体，需要多少个小正方体?3。

长方体和正方体的公式转换
长方体体积=长x宽x高=底面积x高=侧面积x长=前面面积x宽
长方体表面积=(长x宽+长x高+宽x高)x2=长x宽x2+长x高x2+宽x高x2
长方体棱长总和=（长+宽+高）x4=长x4+宽x4+高x4
正方体体积=棱长x棱长x棱长=底面积x棱长
正方体表面积=棱长x棱长x6
正方体棱长和=棱长x12
长方体的长=棱长总和÷4-宽-高=（棱长总和-宽x4-高x4）÷4=体积÷宽÷高=体积÷侧面积长方体的宽=棱长总和÷4-长-高=（棱长总和-长x4-高x4）÷4=体积÷长÷高=体积÷前面面积长方体的高=棱长总和÷4-宽-长=（棱长总和-宽x4-长x4）÷4=体积÷宽÷长=体积÷底面积正方体的棱长=正方体棱长和÷12 =正方体的表面积÷6的商再开方
长方体：前面（或后面）的面积=长×高左面（或右面）的面积=宽×高下面（或上面）的面积=长×宽。

关于长方体正方体的几个小问题1.长方体最多只能有4个面是正方形。

同样的最多只能有8条棱相等。

2.正方体的棱长扩大2倍，表面积会扩大4倍，体积会扩大8倍。

表面积=棱长×棱长×6体积=棱长×棱长×棱长3.长方体的高扩大2倍，表面积不会成倍增加，体积会增加2倍。

表面积=长×宽×2 + 宽×高×2 + 长×高×2体积=长×宽×高4.棱长为6的正方体表面和体积不能比较。

单位不同，没有比较的意义。

就类似1千米和1千克不能比较。

5.体积和容积的计算方式相同。

但是体积和容积不是一样的意义。

体积是占用的空间大小，容积是容纳的空间大小。

简单的说是体积是从物体的外面测量，容积是从物体的内部测量。

在有些计算题目中，体积可以等于容积。

判断易错点1、两个正方体的体积相等，表面积也一定相等。

2、两个长方体的体积相等，表面积也一定相等。

3、a3=3a（a不为0）1、关于棱长的几个考点2、长方体正方体的表面积问题（基础)关于做成一个无盖纸盒子的问题3、长、正方体切割、拼合引起的表面积体积问题4、容器里面加石块引起的问题关于棱长的问题用棱长1厘米的正方体木块摆成一个长5厘米，宽4厘米，高3厘米的长方体，共需要用多少块木块？5×4×3=60(cm3) 1×1×1=1(cm3)60÷1=60(个)一个长方体的12条棱长总和是68厘米，侧面是一个周长为18厘米的长方形，它的长是多少？（68-18×2）÷4=8 cm一个长方体和一个正方体的棱长之和相等，已知长方体的长、宽、高分别是3厘米、2厘米、1厘米，那么正方体的棱长是多少？（3+2+1）×4=24cm 24÷12=2cm一个长方体的棱长之和是60厘米，从一个顶点引出的三条棱长的和是多少？60÷4=15cm把一个正方形棱长扩大三倍，体积会扩大多少倍？表面积呢？表面积 6a2 6（3a）2=6×9a2体积 a3 (3a)3=27a32、长方体正方体的表面积问题（基础）正方体：表面积=棱长×棱长×6体积=棱长×棱长×棱长3体积棱长=长方体：表面积=（长×宽 + 长×高 + 宽×高)×2体积=长×宽×高= 底面积×高高=体积÷底面积=体积÷长÷高什么是求表面积？比如说需要贴瓷砖、贴红纸、粉刷墙面、看单位为平方。

一、高的变化引起表面积的变化。

1、一个长方体，如果高增加2厘米就成了正方体，而且表面积要增加56平方厘米，原来这个长方体的体积是多少立方厘米？2、一个长方体，如果高减少2厘米就成了正方体，而且表面积要减少56平方厘米，原来这个长方体的体积是多少立方厘米？3、一个长方体，如果长减少2厘米就成了一个正方体，而且表面积要减少56平方厘米。

原来这个长方体的体积是多少立方厘米？4、一个长方体，长a分米，宽b分米，高h分米，如果高减少3分米，这个长方体表面积比原来减少（）平方分米？体积比原来减少（）立方分米？二、段的变化1、一个长方体长2米，截面是边长3厘米的正方形，将这个长方体木料锯成五段后，表面积一共增加了多少平方厘米？2、将一个长3米的长方体木料平均截成3段，表面积一共增加了平方分米，这根木料的体积是多少立方分米？三、切1、一个正方体的表面积是48平方厘米，将它平均分成两个小长方体，每个小长方体的表面积是多少？2、一个正方体的表面积是96平方厘米，将它平均分成两个小长方体，每个小长方体的体积是多少立方厘米？3、一个正方体的体积是125立方厘米，它的表面积是多少平方厘米？四、拼。

（拼表面积发生变化，体积不变）1、用8个棱长都是2厘米的正方体拼成一个长方体，拼成的长方体的表面积最多是多少平方厘米？最少是多少平方厘米？2、用12个棱长都是2厘米的正方体拼成一个长方体，一共有多少种拼法，每种拼法拼成的长方体的表面分别是多少？3、用四个棱长都是3厘米的正方体拼成一个长方体，拼成的长方体的表面积可能是多少？五、切1、将一个长8厘米，宽6厘米，高5厘米的长方体切成两个小长方体，表面积最多增加多少平方厘米？最少增加多少平方厘米？2、将三个长8厘米，宽6厘米，高5厘米的长方体拼成一个大长方体，表面积最多减少多少平方厘米？最少减少多少平方厘米？六、扩大和增加倍数。

1、一个正方体棱长扩大2倍，表面积扩大（）倍，体积扩大（）倍，表面积增加（）倍，体积增加（）倍。

长方体与正方体必须掌握的几种题型一、高的变化引起表面积的变化。

1、一个长方体，如果高增加2厘米就成了正方体，而且表面积要增加56平方厘米，原来这个长方体的体积是多少立方厘米？2、一个长方体，如果高减少2厘米就成了正方体，而且表面积要减少56平方厘米，原来这个长方体的体积是多少立方厘米？3、一个长方体，如果长减少2厘米就成了一个正方体，而且表面积要减少56平方厘米。

原来这个长方体的体积是多少立方厘米？4、一个长方体，长a分米，宽b分米，高h分米，如果高减少3分米，这个长方体表面积比原来减少多少平方分米？体积比原来减少多少立方分米？二、段的变化1、一个长方体长2米，截面是边长3厘米的正方形，将这个长方体木料锯成五段后，表面积一共增加了多少平方厘米？2、将一个长3米的长方体木料平均截成3段，表面积一共增加了0.36平方分米，这根木料的体积是多少立方分米？三、切1、一个正方体的表面积是48平方厘米，将它平均分成两个小长方体，每个小长方体的表面积是多少？2、一个正方体的表面积是96平方厘米，将它平均分成两个小长方体，每个小长方体的体积是多少立方厘米？3、一个正方体的体积是125立方厘米，它的表面积是多少平方厘米？四、拼。

（拼表面积发生变化，体积不变）1、用8个棱长都是2厘米的正方体拼成一个长方体，拼成的长方体的表面积最多是多少平方厘米？最少是多少平方厘米？2、用12个棱长都是2厘米的正方体拼成一个长方体，一共有多少种拼法，每种拼法拼成的长方体的表面分别是多少？3、用四个棱长都是3厘米的正方体拼成一个长方体，拼成的长方体的表面积可能是多少？五、切1、将一个长8厘米，宽6厘米，高5厘米的长方体切成两个小长方体，表面积最多增加多少平方厘米？最少增加多少平方厘米？2、将三个长8厘米，宽6厘米，高5厘米的长方体拼成一个大长方体，表面积最多减少多少平方厘米？最少减少多少平方厘米？六、扩大和增加倍数。

1、一个正方体棱长扩大2倍，表面积扩大（）倍，体积扩大（）倍，表面积增加（）倍，体积增加（）倍。

第4讲聪聪和明明玩积木——长方体和正方体的表面积【教学内容】《数学》春季全国版，5年级第4讲“聪聪和明明玩积木——长方体和正方体的表面积”。

【教学目标】知识技能1．通过学生动手操作，理解长方体、正方体的特征，熟练掌握长方体和正方体表面积的计算方法，能够灵活解决一些实际问题。

2．在解决长方体和正方体表面积的实际问题过程中，学会将空间的位置关系转化成平面的位置关系来处理的解题策略。

数学思考1．通过探究长方体和正方体表面积的变化关系，培养学生分析、解决问题的能力，以及良好的思维习惯。

2．培养学生初步的空间观念、逻辑思维能力、动手操作能力。

问题解决尝试从日常生活中发现并提出简单的立体图形表面积的问题，并运用所学知识加以解决。

情感态度1．通过合作探究、归纳总结、迁移类比等数学活动，发展学生的空间观念，感悟“数学来源于生活，应用于生活”的理念。

2．向学生渗透知识之间“相互转化”的辩证唯物主义思想。

【教学重难点】教学重点掌握长方体和正方体表面积的计算方法，能够灵活解决一些实际问题。

教学难点几个长方体拼起来表面积最小。

【教学准备】动画多媒体语言课件、正方体和长方体教具。

第一课时教学过程：的这种形状不少我们学过的立体图形，要计算它的表面积，你们会想出哪些办法？（看看哪组同学聪明想出解决问题的办法）学生分组研究、交流。

教师巡视、检查，并发现典型的方法（包括正确和错误的，在学生回答问题时要找犯典型错误的学生回答）想一想：还有其他更好的方法吗？学生合作、讨论交流，寻求更好的办法。

出示解析：按上下、左右、前后的顺序数出各有多少个小正方形。

上和下相同、左和右相同、前和后相同。

（其中上、右、前、都做成按钮的形式。

点“上”的时候，图形上闪动9个小正方形，并标上数字；点“右”和“前”的时候类似。

）答案：2×2＝4（平方厘米）（9＋8＋10）×2×4＝216（平方厘米）答：它的表面积是216平方厘米。

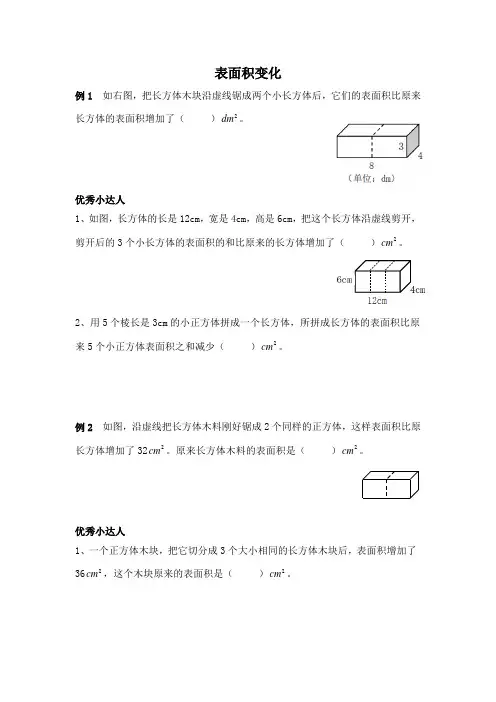
表面积变化
例1 如右图，把长方体木块沿虚线锯成两个小长方体后，它们的表面积比原来长方体的表面积增加了（ ）2dm 。

优秀小达人
1、如图，长方体的长是12cm ，宽是4cm ，高是6cm ，把这个长方体沿虚线剪开，剪开后的3个小长方体的表面积的和比原来的长方体增加了（ ）2cm 。

2、用5个棱长是3cm 的小正方体拼成一个长方体，所拼成长方体的表面积比原来5个小正方体表面积之和减少（ ）2cm 。

例2 如图，沿虚线把长方体木料刚好锯成2个同样的正方体，这样表面积比原长方体增加了322cm 。

原来长方体木料的表面积是（ ）2cm 。

优秀小达人
1、一个正方体木块，把它切分成3个大小相同的长方体木块后，表面积增加了362cm ，这个木块原来的表面积是（ ）2cm 。

2、把5个同样大小的正方体拼成一个长方体，表面积比原来减少了322cm ，则 一个正方体的表面积是（ ）2cm ，拼成的长方体体积是（ ）3cm 。

3、一根2米长的长方体钢材截成3段，表面积比原来增加了24平方分米，这跟钢材原来的体积是（ ）立方米。

综合练习
1、如右图所示，把这个长方体木块锯成三块后，
木块的表面积增加（ ）2cm 。

2、一根长方体木料，长1.5m ，宽和高都是2dm ，把它锯成4段小长方体木料，各段的表面积之和比原来的长方体的表面积最少增加（ ）2dm 。

A. 8
B. 16
C. 24
D. 32
3、有一个正方体木块，把它分成两个长方体木块后，表面积增加了242cm ，这个正方体木块原来的表面积是多少平方厘米？
20cm
5cm。

五年级数学下册典型例题系列之第三单元长方体和正方体的表面积提高部分（原卷版）编者的话：《2021-2022学年五年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的，该系列主要包含典型例题和专项练习两大部分。

典型例题部分是按照单元顺序进行编辑，主要分为计算和应用两大部分，其优点在于考题典型，考点丰富，变式多样。

专项练习部分是从常考题和期末真题中选取对应练习，其优点在于选题经典，题型多样，题量适中。

本专题是第三单元长方体和正方体的表面积提高部分。

本部分内容考察长方体和正方体的表面积的增减变化及不规则立体图形的表面积，考点和题型难度稍大，建议作为本章核心内容选择性进行讲解，一共划分为十个考点，欢迎使用。

【考点一】正方体表面积的增减变化：切片问题。

【方法点拨】1.表面积的增减变化问题主要有三种，一种是切片问题，表面积会相应增加，一种是拼接问题，表面积会相应减少，一种是高的变化引起的表面积变化。

2.切片问题，即切一刀多两个切面，沿着不同的方向切，多出的表面积一般是不一样的，但正方体比较特殊，它的表面积的增减变化都是都是正方形在进行变化，相对比较简单。

3.刀数×2=切面个数。

【典型例题】把一个棱长是2cm的正方体切成两个完全一样的长方体后，表面积比原来增加了（）平方厘米，每个小长方体的表面积是（）平方厘米。

【对应练习1】一个正方体的棱长是4厘米，把它切成两个完全相同的长方体后，表面积增大（）平方厘米，每个长方体的表面积是（）平方厘米，两个长方体的表面积和是（）平方厘米。

【对应练习2】把一个棱长是5分米的正方体木块锯成两个完全一样的长方体，表面积比原来增加了（）平方分米，每个小长方体的表面积是（）平方分米。

【对应练习3】一个正方体的表面积是20平方厘米，将它切成8个一样大小的小正方体，每个小正方体的表面积是多少平方厘米？【对应练习4】一个正方体形状的木块，棱长为1m，沿着水平方向将它锯成3片，每片又按任意尺寸锯成4条，每条再按任意尺寸锯成5小块，共得到大大小小的长方体60块，如图所示。

第02讲：长方体正方体的表面积一、熟练掌握长方体正方体表面积计算公式二、学会运用长方体正方体面积公式解决实际问题三、了解长方体正方体切割的面积变化，了解增加减少了几个面四、了解正方体的表面涂色问题，可以自己推导一般情况一、长方体与正方体的表面积一、考点： 掌握长方体、正方体面积的计算．二、难点： 应用长方体、正方体表面积的计算解决实际问题． 三、易错点：实际应用中长方体、正方体的表面积应该求几个面．一．长方体表面积计算方法1．长方体表面积：长×宽+长×宽+长×高+长×高+宽×高+宽×高； 字母公式：S 长=c b c b c a c a b a b a ⨯+⨯+⨯+⨯+⨯+⨯ 2．长方体表面积：长×宽×2+长×高×2+宽×高×2；字母公式：S 长=222⨯⨯+⨯⨯+⨯⨯c b c a b a 3．长方体表面积：（长×宽+长×高+宽×高）×2； 字母公式：S 长=2)⨯⨯+⨯+⨯c b c a b a （二．正方体表面积的计算方法 1．正方体表面积：边长×边长×6字母公式：S 正=6⨯⨯a a．三．根据实际情况求长方体或正方体的表面积1．当一组对面是正方形时求表面积公式：S长=；a242⨯⨯+⨯ba2．求粉刷墙面、无盖水箱时有时并不要求6个面；3．求一些拼接类题需要考虑“接头”部分．题模一：长方体表面积的计算方法例1黎明用240厘米长的铁丝围成一个底面边长是15厘米长方体灯笼框架，接头处不计，如果把这个灯笼糊上彩纸（上面不糊），至少需要多少平方厘米的彩纸？【答案】15×8=120cm(240-120)÷4=30cm15×30×4+15×15=2025cm2题模二：正方体表面积的计算方法例1一个正方体的棱长是8cm，这个正方体的表面积是多少平方厘米？【答案】3842cm例2求下面所示图形的表面积．（单位：cm）【答案】6642cm题模三：长方体正方体的拼接切割面积变化例1 将一个由4个棱长是8cm的正方体拼成的长方体拆开（如图），4个正方体的表面积之和是多少？与长方体的表面积相等吗？与同伴交流。

一、本周主要内容：长方体和正方体整理与复习、表面积的变化二、本周学习目标：1、知识与技能：进一步掌握长方体和正方体的基本特征；掌握常用的体积单位及容积单位间的进率；能够正确计算长方体和正方体的表面积、体积（容积）；能够正确解决有关的实际问题。

2、情感与态度：能积极主动地参与各种探索和操作活动；愿意与他人交谈自己的想法；提出不懂的问题；倾听不同的观点。

有克服困难和运用知识解决问题的成功体验。

三、考点分析：能从现实生活中发现并提出一些与长方体、正方体相关的简单的实际问题；能主动探索解决问题的有效方法；并对自己解决问题的过程作出合理的解释。

四、典型例题例1、回顾与整理回顾本单元的有关概念。

口答：1、长方体、正方体的特征。

（面、棱、顶点）2、什么叫表面积？3、什么是体积？4、什么是容积？5、常用的体积单位有哪些？常用的容积单位有哪些？它们之间有怎样的关系？6、怎样求长方体、正方体的表面积、体积？长方体的表面积=（长×宽 + 宽×高 + 长×高）×2正方体的表面积= 棱长×棱长×6长方体的体积= 长×宽×高正方体的体积= 棱长×棱长×棱长长（正）方体的体积= 底面积×高例2、请你分别计算出下面每个长方体或正方体向上、向左的面的面积。

5厘米厘米7厘米5厘米①②分析与解：首先要弄清楚每个长方体（含正方体）向上、向左的面是哪个面；如果是长方形；长和宽分别是多少厘米；如果是正方形；边长又是多少厘米；这样即可求出所求面的面积。

图①向上的面积是7×2 = 14（平方厘米）；向左的面积是2×5 = 10（平方厘米）。

图②向上、向左的面积都是5×5 = 25（平方厘米）。

例3、江宁体育馆有一个长方体形状的游泳池；长50米；宽30米；深3米；现在要在游泳池的各个面上抹上一层水泥；抹水泥的面积有多少平方米？如果每平方米用水泥12千克；22吨够吗？分析与解：求水泥的面积有多少平方米；实际就是求这个长方体游泳池的表面积。

长方体与正方体必须掌握的几种题型一、高的变化引起表面积的变化..1、一个长方体;如果高增加2厘米就成了正方体;而且表面积要增加56平方厘米;原来这个长方体的体积是多少立方厘米2、一个长方体;如果高减少2厘米就成了正方体;而且表面积要减少56平方厘米;原来这个长方体的体积是多少立方厘米3、一个长方体;如果长减少2厘米就成了一个正方体;而且表面积要减少56平方厘米..原来这个长方体的体积是多少立方厘米4、一个长方体;长a分米;宽b分米;高h分米;如果高减少3分米;这个长方体表面积比原来减少平方分米体积比原来减少立方分米二、段的变化1、一个长方体长2米;截面是边长3厘米的正方形;将这个长方体木料锯成五段后;表面积一共增加了多少平方厘米2、将一个长3米的长方体木料平均截成3段;表面积一共增加了0.36平方分米;这根木料的体积是多少立方分米三、切1、一个正方体的表面积是48平方厘米;将它平均分成两个小长方体;每个小长方体的表面积是多少2、一个正方体的表面积是96平方厘米;将它平均分成两个小长方体;每个小长方体的体积是多少立方厘米3、一个正方体的体积是125立方厘米;它的表面积是多少平方厘米四、拼..拼表面积发生变化;体积不变1、用8个棱长都是2厘米的正方体拼成一个长方体;拼成的长方体的表面积最多是多少平方厘米最少是多少平方厘米2、用12个棱长都是2厘米的正方体拼成一个长方体;一共有多少种拼法;每种拼法拼成的长方体的表面分别是多少3、用四个棱长都是3厘米的正方体拼成一个长方体;拼成的长方体的表面积可能是多少五、切1、将一个长8厘米;宽6厘米;高5厘米的长方体切成两个小长方体;表面积最多增加多少平方厘米最少增加多少平方厘米2、将三个长8厘米;宽6厘米;高5厘米的长方体拼成一个大长方体;表面积最多减少多少平方厘米最少减少多少平方厘米六、扩大和增加倍数..1、一个正方体棱长扩大2倍;表面积扩大倍;体积扩大倍;表面积增加倍;体积增加倍..2、一个正方体的棱长增加2倍;表面积增加倍;体积增加倍..3、一个大正方体的棱长是小正方体棱长的2倍;已知大正方体的体积比小正方体多21立方厘米;大小正方体的体积分别是多少七、将一个长方体或正方体切成若干个小正方体或小长方体..1、把一个棱长6厘米的正方体方块;锯成棱长2厘米的小正方体木块;表面积增加多少平方厘米2、把一个长8 厘米;宽6厘米;高4厘米的长方体木块;锯成若干个棱长2厘米的小正方体;一共可锯成多少个这样的小正方体3、把一个长16 厘米;宽12厘米;高8厘米的长方体木块;锯成若干个小正方体;没有剩余至少可以锯成多少个这样的小正方体表面积一共增加多少平方方厘米八、挖1、用8个小正方体木块拼成一个大的正方体;如果拿走1个小方块;它的表面积和原来比 ..2、在棱长1分米的正方体的顶点处挖去一个棱长1厘米的小正方体;剩下物体的表面积和体积分别是多少3、在一个棱长4厘米的正方体六个面的中心都挖去一个棱长1厘米的小正方体;剩下物体的表面积是多少平方厘米九、熔铸沉浮1、一个正方体钢坯棱长6分米;把它锻造成横截面是边长3分米的正方形的长方体钢材;钢材长多少米2、一块棱长是0.6米的正方体的钢坯;锻成横截面是0.09平方米的长方体钢材;锻成的钢材有多长3、把一块棱长是0.5米的正方体钢坯;锻成高2分米、宽4分米的长方体钢材;锻成的长方体钢材有多少长4、把两个棱长都是1分米的正方体的方钢;熔铸成一根横截面是长5厘米、宽4厘米的长方体的钢材;这根钢材的长是多少分米5、有一个完全封闭的容器;里面的长是20厘米;宽是16厘米;高是10厘米;平放时里面装了7厘米深的水..如果把这个容器竖起来放;水的高度是多少6、在一只长25厘米;宽20厘米的玻璃缸中;有一块棱长10厘米的正方体铁块;这时水深15厘米;如果把这块铁块从缸中取出来;缸中的水深多少厘米7、把一个体积为80立方厘米的铁块浸在底面积为20平方厘米的长方体容器中;水面高度为10厘米;如果把铁块捞出后;水面高多少8、一个长方体玻璃缸;从里面量长40厘米;宽25厘米;缸内水深12厘米..把一块石头浸入水中后;水面升到16厘米;求石块的体积..9、一个长方体的容器;底面积是16平方分米;装的水高6分米;现放入一个体积是24立方分米的铁块..这时的水面高多少10、一个长方体玻璃缸;底面积是200平方厘米;高8厘米;里面盛有4厘米深的水;现在将一块石头放入水中;水面升高2厘米..这块石头的体积是多少立方厘米11、一个长方体玻璃缸;最多可装水120升..已知玻璃缸里面长6分米;宽4分米;现有水深3分米..如果在玻璃缸里放入了体积为15立方分米的玻璃球;里面的水会不会溢出为什么12、红家新买一个长50厘米、宽24厘米、高30厘米金鱼缸;玻璃厚度不计放进30升水;水深多少厘米13、一个正方体玻璃缸;棱长4分米;用它装满水;再把水全部倒入一个底面积为20平方分米的长方形水槽中;槽里的水面高多少分米14、一个棱长是5分米的正方体鱼缸;里面装满水;把水倒入一个底面积48平方分米;高6分米的的长方体鱼缸里;鱼缸里水有多深15、一个长20分米、宽15分米的长方体容器内;有20分米深的水;现在在水中沉入一个棱长30厘米的长方体铁块;这时容器内的水深多少分米16、一个棱长是12厘米的正方体鱼缸;里面装满水;把水倒入一个长18厘米、宽10厘米的长方体鱼缸里;水有多深17、一个正方体玻璃容器棱长2分米;向容器中倒入5升水;再把一块石头放入水中..这时量得容器内的水深15厘米..石头的体积是多少立方厘米18、一个长方体玻璃缸;从里面量长40厘米;宽25厘米;缸内水深12厘米..把一块石头浸入水中后;水面升到16厘米;求石块的体积..19、一个房间内共铺设了1200块长40厘米;宽20厘米;厚2厘米的木地板;这个房间共占地多少平方米铺这个房间共要木材多少立方米20、一块长35厘米、宽25厘米的长方形铁皮;在它的四个角上分别剪去面积相等的四个小正方形后;正好可以制成一个高为5厘米的铁盒..求这个铁盒的体积..21、一个长方体如果高缩短3厘米;就成了一个正方体..这时表面积比原来减少了48平方厘米;原来的长方体的体积是多少立方厘米表面积是多少平方厘米22、一个长方体;高截去2厘米;表面积就减少了48平方厘米;剩下部分成为一个正方体;求原长方体的体积23、用两块大小相同的正方体木块拼成长方体;已知长方体的棱长总和是48厘米;每块正方体木块的体积是多少24、一个长方体12条棱长度的总和是48厘米;底面周长是18厘米;高是多少厘米25、一个长方体的木块;截成两个完全相等的正方体..两个正方体棱长之和比原来长方体棱长之和增加40厘米;求原长方体的长是多少厘米26、一根横截面为正方形的长方体木料;表面积为114平方厘米;锯去一个最大正方体后;表面积为54平方厘米;锯下的正方体木料表面积是多少27、一个正方体和一个长方体;拼一个新长方体;新长方体的表面积比原长方体增加60平方厘米;求正方体的表面积..28、大正方体棱长是小正方体棱长的2倍;大正方体的体积比小正方体的体积多21立方分米;小正方体的体积是多少。

长、正方体表面积的变化教学目标：1、让学生通过把几个相同的正方体或长方体拼成较大的长方体的操作活动，探索并发现拼接前后有关几何体表面积的变化规律，并让学生应用发现的规律解决一些简单实际问题。

2、培养学生的合作能力、空间想象能力和思维能力。

教学重点：探究长方体的表面积与原来两个正方体的表面积之间的关系。

教学难点：通过操作，发现、理解、运用规律。

教学准备：1、课前把全班同学合理分组，并明确分工，强调合作。

2、以小组为单位，每小组准备8个1立方厘米的正方体，2个完全相同的长方体。

教学过程：一、导入我们知道把一些小的物品包在一起的时候，会用纸、塑料等东西把它们包装起来。

老师前两天去逛超市的时候观察了一下，好多地方都用到了包装的知识。

今天，老师也带了几样包装盒，（出示三盒装的面巾纸），三盒面巾纸除了这样包装外，还可以怎样包装呢？商家为什么要这样包装呢？今天我们就来研究这普普通通的包装中蕴藏的数学知识。

二、拼拼算算操作一：相同的正方体拼接后表面积的变化情况1、教师演示操作：把两个体积是1立方厘米的正方体拼成一个长方体。

体积有没有变化？学生观察、交流、讨论（可以计算、可以用肉眼观察）。

2、再次提问：表面积有没有发生变化？是增加了还是减少了？具体是哪几个面的面积呢？想像有困难的可以让学生通过拼一拼，计算或观察的方法来发现，再小组讨论，集体交流。

3、交流发现：A、长方体的表面积比两个正方体表面积的和少2平方厘米。

B、拼成长方体后，表面积减少了原来的2个面的面积。

4、继续深入研究：（1）如果用3个、4个、5个、6个正方体拼成长方体，表面积又发生了什么变化呢？（排法要求是排成一排）（学生自己猜想、操作、探究、验证）（2）提醒学生边操作边把相关数据填在表中。

操作后填表：（3）交流填写结果。

（4）发现规律：你能从表中发现什么规律吗？给予学生充分时间讨论。

学生交流（可以有多种表述，只要符合题意即可）A、最简单的是体积不变，表面积变了。

五年级数学下册典型例题系列之第二单元：长方体和正方体表面积的增减变化方式专项练习（解析版）1．一个长12cm、宽4cm、高2cm的长方体按下图方式切割成两个长方体，表面积增加( )cm2。

【解析】根据题图可知，切割成两个长方体后表面积增加了两个侧面，用4×3×2解答即可。

4×3×2＝12×2＝24（平方厘米）2．手工课上，小石把三块小正方体粘在一起（下图），表面积比原来减少了16cm2，原来1个正方体的体积是( )cm3，粘成的这个立体图形的表面积是( )cm2。

【解析】小石把三块小正方体粘在一起，减少了4个面，每个面的面积为16÷4＝4平方厘米，得出每个小正方体的棱长是2厘米，根据体积公式得体积2×2×2＝8立方厘米；因为粘成的这个立体图形减少4个面，还剩3×6－4＝14个面，再乘每个面的面积即可。

（1）每个面的面积为16÷4＝4（平方厘米）4÷2＝2（厘米）原来1个正方体的体积是2×2×2＝8（立方厘米）（2）（3×6－4）×4＝14×4＝56（平方厘米）3．一个长方体长4分米、宽3分米、高2分米，把它切成两个小长方体，它的表面积最多增加( )平方分米，最少增加( )平方分米。

【解析】沿着最大的面切开表面积增加的最多，沿着最小的表面积切开表面积增加的最少，切一次增加两个面，据此分析。

4×3×2＝24（平方分米）3×2×2＝12（平方分米）4．把一个棱长6分米的正方体木块平均分成两个长方体后，木块的表面积增加( )平方分米。

【解析】把这个正方体分成两个完全一样的长方体时，增加了两个原正方体一个面的面积，由此即可解答。

6×6×2＝72（平方分米）5．一个正方体的表面积是18平方分米，3个这样的正方体拼成一个长方体，表面积是( )平方分米。