同济版大学物理第七章

第七章钢筋砼板的特性和分析钢筋砼板的特性和分析一、概述二、弹性理论三、塑性理论四、板的适用性五、板的冲切板的概述最普通的结构构件对板的认识不如对梁深刻普遍性：复杂性：分析法：弹塑性性能较难分析弹性分析法和塑性极限分析法一、概述一、概述板的结构类型特点：直接支撑于柱，厚度均匀。

受抗冲切强度限制一、概述板的结构类型无梁楼板特点：支撑板的柱顶有柱帽、柱顶托板等一、概述板的结构类型双向板特点：板的每个边都支承在梁上的板，可变化为单向板一、概述井式板二、弹性理论1. 适用范围板厚足够小从而剪切变形可忽略；以及板厚足够大从而平面内的力可忽略的各向同性板。

二、弹性理论2. 假定1）材料各向同性且符合虎克定律；2）挠度相比板厚很小；3）在受弯前垂直于板的中间平面的任何直线，在受弯后仍为直线且与中间平面垂直；4）与中间平面正交的正应力可忽略。

3. 分析推导过程二、弹性理论1）平衡条件（a ）作用面及剪力（b ）弯矩和扭矩矢量图作用在微小板单元上的力3. 分析推导过程二、弹性理论z 方向的平衡：0x yyX V V q ∂∂++=∂∂考虑上图所示的板的微元。

作用在微元上的力有法向外荷载q,板的剪力V x 和V y ，板的弯矩m x 和m y ，板的扭矩m xy 。

各力的符号以图示方向为正，板的剪力、弯矩和扭矩是作用在中面切割面的单位长度上的量。

3. 分析推导过程二、弹性理论所有力绕y 轴的力矩求和，得：x x yxyx m m V ∂∂+=∂∂0x x x x yx x yx yx V m m dy V dx dydx m dx m dx dyx x m m dy dx y ∂∂⎛⎞⎛⎞+++−+⎜⎟⎜⎟∂∂⎝⎠⎝⎠∂⎛⎞−+=⎜⎟∂⎝⎠略去高阶项，3. 分析推导过程二、弹性理论同理，yxy xy ym m V ∂∂+=∂∂由上三式联立，得板的平衡方程222222x x y yxy y xm m m q ∂∂∂++=−∂∂∂∂3. 分析推导过程二、弹性理论2）物理条件22()1()12(1)x x y y y x x y x y EEEσεμεμσεμεμτγμ⎧=+⎪−⎪⎪=+⎨−⎪⎪=⎪+⎩二、弹性理论3. 分析推导过程）变形协调条件33. 分析推导过程二、弹性理论3）变形协调条件221x x x R z xεωφ∂===−∂22xz xωε∂∴=−∂对于弯矩—曲率关系：曲率：式中：R x 为x 方向的曲率半径，为x 方向离中和轴z 处的纤维内的应变。

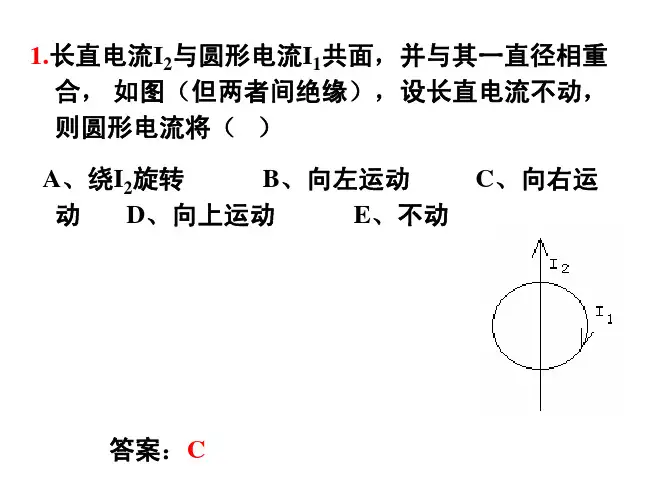
第七章 恒定磁场7 －1 两根长度相同的细导线分别多层密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管，两个螺线管的长度相同，R ＝2r ，螺线管通过的电流相同为I ，螺线管中的磁感强度大小B R 、B r 满足（ ） （A ） （B ） （C ） （D ）分析与解 在两根通过电流相同的螺线管中，磁感强度大小与螺线管线圈单位长度的匝数成正比．根据题意，用两根长度相同的细导线绕成的线圈单位长度的匝数之比因而正确答案为（C ）。

7 －2 一个半径为r 的半球面如图放在均匀磁场中，通过半球面的磁通量 为（ ）（A ） （B ） （C ） （D ）分析与解 作半径为r 的圆S ′与半球面构成一闭合曲面，根据磁场的高斯定理，磁感线是闭合曲线，闭合曲面的磁通量为零，即穿进半球面S 的磁通量等于穿出圆面S ′的磁通量；．因而正确答案为（D ）． 7 －3 下列说法正确的是（ ）（A ） 闭合回路上各点磁感强度都为零时，回路内一定没有电流穿过 （B ） 闭合回路上各点磁感强度都为零时，回路内穿过电流的代数和必定为零 （C ） 磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度必定为零（D ） 磁感强度沿闭合回路的积分不为零时，回路上任意一点的磁感强度都不可能为零分析与解 由磁场中的安培环路定律，磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度不一定为零；闭合回路上各点磁感强度为零时，穿过回路的电流代数和必定为零。

因而正确答案为（B ）．7 －4 在图（ａ）和（ｂ）中各有一半径相同的圆形回路L1 、L2 ，圆周内有电流I1 、I2 ，其分布相同，且均在真空中，但在（ｂ）图中L2 回路外有电流I3 ，P 1 、P 2 为两圆形回路上的对应点，则（ ）r R B B 2=r R B B =r R B B =2r R B B 4=21==R r n n r R B r 2π2B r 2παB r cos π22αB r cos π2S B ⋅=m Φ（A ） ，（B ） ，（C ） ，（D ） ，分析与解 由磁场中的安培环路定律，积分回路外的电流不会影响磁感强度沿回路的积分；但同样会改变回路上各点的磁场分布．因而正确答案为（C ）．*7 －5 半径为R 的圆柱形无限长载流直导体置于均匀无限大磁介质之中，若导体中流过的恒定电流为I ，磁介质的相对磁导率为μｒ （μｒ＜1），则磁介质内的磁化强度为（ ） （A ）（B ） （C ） （D ）分析与解 利用安培环路定理可先求出磁介质中的磁场强度，再由M ＝（μｒ－1）H 求得磁介质内的磁化强度，因而正确答案为（B ）．7 －6 北京正负电子对撞机的储存环是周长为240 m 的近似圆形轨道，当环中电子流强度为8 mA 时，在整个环中有多少电子在运行？ 已知电子的速率接近光速。

同济大学大学物理答案【篇一：大学物理复习题答案(同济大学课件)】>1、①r?rcos?ti?rsin?tj?htdxdyk；②vx???r?sin?t，vy??r?cos?t，2?dtdtvz?dvydvdvdzh2???r?2sin?t，az?z?0 ；③ax?x??r?cos?t，ay?dt2?dtdtdt2、在运动函数中消去t，可得轨道方程为y?x2?8 由r?2ti?(4t2?8)j，得v?drdv?2i?8tj，a??8j dtdt可得在t?1时r1?2i?4j，v1?2i?8j，a1?8j 在t?2时r2?2i?8j，v2?2i?16j，a1?8jf3?4t3?4?3???1.5m/s2， m1010v3v33?4tdva?,dv?adt,?dv??adt,?dv??dt,v?2.7m/s0000dt10f3?4x3?4?3dv3?4xdvdvdxdv???1.5m/s2，a???.?v，②a?，m1010dt10dtdxdtdxv33?4x3?4xdx?vdv，?vdv??dx，v?/s001010124、以投出点为原点，建立直角坐标系。

x?v0cos?t，y?v0sin?t?gt 23、①a?以(x,y)表示着地点坐标，则y??h??10m。

将此值和v0，?值一并代入得11?10?20??t??9.8?t222解之得，t?2.78s和t??0.74s。

取正数解。

着地点离投射击点的水平距离为：x?v0cos?t?20?cos300?2.78?48.1m 5、①?0?2?n?2??1802??180?18.8(rad/s)，v0??0r??0.5?9.42(m/s) 6060②由于均匀减速，翼尖的角加速恒定，???a??0ta?0?18.8??0.209(rad/s2) 90at??r??0.105(m/s2)负号表示切向加速度的方向与速度方向相反。

???0??t?18.8?0.209?80?2.08(rad/s)an??2r?2.16(m/s2)，a??2.16(m/s2)，??arctan0.105?2.780 2.166、x?12t?2t?4?v?t?2?a?1ms2 则： 22（1）t?2s时：v?2?2?4(s) a?1s 方向都沿x轴正方向（2）在1~2s内，a?1?f?ma?2?1?2(n)，则在1~2s内，i??212dt?2(n?s) 方向沿x轴正方向（3）在1~2s内，f所做的功：由动能定理得：11a?ek(t?2)?ek(t?1)??2?(2?2)2??2?(1?2)2?7(j)22第二章牛顿运动定律1、小球下落过程中受重力g?mg和空气阻力f?kv作用。

第七章 电磁感应选择题7－1 在闭合导线回路的电阻不变的情况下,下述正确的是 （ B ） (A) 穿过闭合回路所围面积的磁通量最大时,回路中的感应电流最大; (B) 穿过闭合回路所围面积的磁通量变化越快,回路中的感应电流越大; (C) 穿过闭合回路所围面积的磁通量变化越大,回路中的感应电流越大; (D) 穿过闭合回路所围面积的磁通量为零时,回路中的感应电流一定为零.7－2 导体细棒ab 与载流长直导线垂直.在如图所示的四种情况中,细棒ab 均以与载流导线平行的速度v 平动,且b 端到长直导线的距离都一样.在(a)、(b)和(c)三种情况中,细棒ab 与光滑金属框保持接触.设四种情况下细棒ab 上的感应电动势分别为a E 、b E 、c E 和d E ,则 （ C ）(A) a b c d ==<E E E E ; (B) a b c d ==>E E E >E ; (C) a b c d ===E E E E ;(D) a b c d >>>E E E E .7－3 如图所示,半圆周和直径组成的封闭导线,处在垂直于匀强磁场的平面内.磁场的磁感应强度的大小为B ,直径AB 长为l .如果线圈以速度v 在线圈所在平面内平动, v 与AB 的夹角为θ,则 （ A ）(A) 线圈上的感应电动势为零,AB 间的感应电动势sin AB Bl θ=E v ; (B) 线圈上的感应电动势为零,AB 间的感应电动势cos AB Bl θ=E v ;(C) 线圈上的感应电动势为i 2sin Bl θ=E v ,AB 间感应电动势为sin AB Bl θ=E v ; (D) 线圈上的感应电动势为i 2cos Bl θ=E v ,AB 间感应电动势为cos AB Bl θ=E v . 7－4 一个面积210cm S =的圆线圈,其电阻0.10R =Ω,处于垂直于匀强磁场的平面内,若磁感应强度的大小随时间的变化率1d 10T s d Bt-=⋅,则线圈中的感应电流的大小为（ D ）(A) 3i 1.010A I -=⨯; (B) 2i 1.010A I -=⨯; (C) 2i 1.010A I =⨯; (D) 1i 1.010A I -=⨯.7－5 导线元d l 在磁感应强度为B 的磁场中以速度v 运动时,其上的动生电动势为()i d d =⨯⋅B l E v（ D ） (A) 当v 与d l 垂直时,一定有i d d B l =E v ; (B) 当v 与B 垂直时,一定有i d d B l =E v ; (C) 当d l 与B 垂直时,一定有i d d B l =E v ;(D) 只有在v 、B 和d l 三者相互垂直时,才有i d d B l =E v 或i d d B l =-E v .7－6 下述正确的是 （ C ）(A) 静电场和感生电场的电场线都不闭合;(B) 静电场的电场线是闭合的,感生电场的电场线不闭合; (C) 感生电场的电场线是闭合的,静电场的电场线不闭合; (D) 静电场和感生电场的电场线都是闭合的.7－7 静止的导体中产生涡电流的原因是 （ C ） (A) 导体处于不均匀的稳恒磁场中; (B) 导体处于不均匀的静电场中; (C) 导体处于随时间变化磁场中; (D) 导体处于通有稳恒电流的线圈内. 7－8 在自感线圈中,电流i 随时间t 的变化曲线如图(a)所示.若以i 的正流向为正方向,则线圈中自感电动势L E 随时间t 的变化曲线应为图(b)中的 （ D ）7－9 尺寸相同的铜环和铝环,穿过它们所围面积的磁通量的变化率相同.设铜环上的感应电动势和感应电流分别为1E 和1I ,铝环上的感应电动势和感应电流分别为2E 和2I ,则（ C ）(A) 12=E E , 12I I =; (B) 12>E E , 12I I >; (C) 12=E E , 12I I >; (D) 12>E E , 12I I =.7－10 如图所示,若一块磁铁沿着一根竖直放置的长铜管的轴线,自管口竖直下落,如果忽略空气阻力,则 （ C ）(A) 磁铁越落越快,最后速度趋于无限大; (B) 磁铁越落越慢,最后速度趋于零; (C) 磁铁越落越快,最后达到一恒定速度; (D) 磁铁越落越慢,最后达到一恒定速度;计算题7－11 一个匝数100N =的导线圈,通过每匝线圈的磁通量41510sin10πΦt =⨯,式中1Φ的单为Wb ,t 的单位为s .求:(1) 任意时刻线圈上的感应电动势;(2) 在10s t =时,线圈上的感应电动势的大小.解 (1) 根据法拉第电磁感应定律,任意时刻线圈上的感应电动势为()41i d d100510sin10π0.5πcos10πd d ΦNt t t t-=-=-⨯=-E 式中t 的单位为s ,i E 的单位为V .(2) 10s t =时,线圈上的感应电动势为()i 0.5πcos 10π10 V 1.57 V =-⨯=-i E大小为i 1.57 V =i E7－12 若在一方向不变的磁场中,有一面积为20.03m 的平面线圈,线圈所在平面的法线与磁场的夹角为θ,磁感强度的大小为510B t =+,式中B 的单位为T ,t 的单位为s .求:(1) 当π3θ=时,线圈中的感应电动势的大小; (2) 当π2θ=,2s t =时,线圈中的感应电动势的大小; 解 穿过线圈所围平面的磁通量为()()cos 5100.03cos 0.150.3cos BS t t Φθθθ==+⨯=+线圈中的感应电动势为()i d d0.150.3cos 0.3cos d d t t tΦθθ=-=-+=-E (1) 在π3θ=的情况下,线圈中的感应电动势为 i π0.3cos V 0.15V 3⎛⎫=-=- ⎪⎝⎭E其大小为0.15V(2) 在π2θ=的情况下,2s t =时,线圈中的感应电动势为 i π0.3cos V 02⎛⎫=-= ⎪⎝⎭E7－13 如图所示,一正方形线圈与载流长直导线共面,线圈的匝数为N ,边长为a ,其两边与长直导线平行,与长直导线之间的最小距离为b .长直导线中的电流为I .(1) 求通过线圈的磁通量;(2) 若100N =,20cm a =,10cm b =,当长直导线中的电流I 以12A s -⋅的变化率增长时,求线圈中的感应电动势.解 (1) 坐标选取如图所示.以顺时针为线圈回路的正方向, 则线圈所围平面的法向单位矢量n e 垂直纸面向里.在线圈平面上,长直载流导线的磁感应强度为0n 2πIaxμ=B e .在x 处取面元dS d a x =,则面元矢量为n d d a x =S e .穿过面元的磁通量为0d d d 2πIaΦx xμ=⋅=B S穿过线圈所围平面的磁通量为00d d ln2π2πa bSaIaNIaa bΦN N x xbμμ++=⋅==⎰⎰B S(2) 若100N =，20cm a =,10cm b =,则7064π101000.200.200.10ln ln Wb2π2π0.10 4.4010WbNIaa b I Φb I μ--⎛⎫+⨯⨯⨯⨯+== ⎪⎝⎭=⨯ 线圈中的感应电动势为()666i d d 4.4010 4.40102 V 8.8010 V d d ΦIt t--=-=-⨯=-⨯⨯=-⨯E i 0<E ,表明线圈中的感应电动势沿逆时针方向.7－14 如图所示,矩形导线框ABCD 与载流为I 的长直导线共面,边长分别为b 和l ,AB 与长直导线平行.矩形线框以速度v 在其平面内向右运动,v 与直导线垂直.在时刻t ,AB 与长直导线间的距离为a .求此时线框上的感应电动势.解 在长直导线右侧的线框平面上,到长直导线的距离为r 的点上，载流长直导线的磁场,方向垂直于纸面向里,磁感应强度的大小为02πIB rμ=以顺时针为导线回路的正方向,线圈中的感应电动势为()()()()()i d d d d d ABCDAAB BC CD DA =⨯⋅=⨯⋅+⨯⋅+⨯⋅+⨯⋅⎰⎰⎰⎰⎰B l B l B l B l B lv v v v v E 在BC 和DA 段上,d l v ,()d 0⨯⋅=B l v ,因此积分为零.在时刻t ,AB 处的磁感应强度大小为012πIB aμ=,CD 处的磁感应强度大小为()022πIB a b μ=+.于是()()()i 1200000d d d d d d 11 2π2π2πAB CD AB CD llB l B lI lI l Il a a b a a b μμμ=⨯⋅+⨯⋅=+-⎛⎫=-=- ⎪++⎝⎭⎰⎰⎰⎰⎰⎰B l B l E v v v v v v vi 0>E ,表明线圈中的感应电动势沿顺时针方向.7－15 如图所示,匀强磁场的磁感应强度的大小为B ,方向垂直纸面向外.有一根长为L 的金属棒MN ,可绕点O 在纸面内逆时针旋转,角速度为ω,4LOM =.求金属棒两端之间的电动势.那一端的电势较高?解 如图所示,在棒MN 上,到点O 的距离为l 处,沿径向取位移元d l .d l 的速度v 的方向如图,既垂直于d l ,也垂直于B ,大小为l ω=v .d l 上的动生电动势为()i d d d Bl l ω=⨯⋅=B l dE vMN 上的动生电动势为32441d 4L L MN Bl l BL ωω==⎰E0MN >E ,表明动生电动势的方向为从M 到N ,N 端电势较高.7－16 如图所示,矩形导线框ABCD 与载流长直导线共面,AB 与长直导线平行,相互间的距离为a ,导线框的边长分别为b 和l .如果长直导线上的电流为0πcos 3I I t ω⎛⎫=+ ⎪⎝⎭,式中0I 和ω为常量.求在0t =时,导线框上的感应电动势.解 坐标选取如图所示.以ABCDA ,即顺时针为线框回路的正方向,则平面ABCD 的法向单位矢量n e 垂直纸面向里.在平面ABCD 上,长直载流导线的磁感应强度为0n 2πIx μ=B e .由于0πcos 3I I t ω⎛⎫=+ ⎪⎝⎭,因此B 的具体指向随时间变化.在x 处取面元dS d l x =,则面元矢量为n d d l x =S e .穿过面元的磁通量为0d d d d 2πIlΦB S x xμ=⋅==B S穿过线框所围平面的磁通量为00d d ln2π2πa bSaIlIla bΦx xaμμ++=⋅==⎰⎰B S 矩形线框ABCD 上的感应电动势为0i 0000d d ln d 2πd d ππ ln cos ln sin 2πd 32π3l a b I t a tl I l a b a b I t t a t a μΦμμωωω+=-=-+⎡⎤+⎛⎫⎛⎫=-+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦E0t =时0000i πlnsin ln2π34πI lI l a b a b a aμωω++==E i 0>E ,表明此时线框上的感应电动势沿顺时针方向.7－17 在一个长为0.6m 、直径为5.0cm 的纸筒上,密绕1200匝线圈.求这个长直螺线管的自感.解 长直螺线管的自感为()2220027223π44π101200π 5.010H 5.9210H40.6N SN d L llμμ---==⨯⨯⨯⨯⨯==⨯⨯7－18 一螺线管的自感为21.010H -⨯,流过的电流为2.0A .求其储存的磁场能.解 载流螺线管储存的磁场能为2222m 11 1.010 2.0J 2.010J 22W LI --⎛⎫==⨯⨯⨯=⨯ ⎪⎝⎭7－19 一个直径为0.01m 、长为0.10m 的长直密绕螺线管,共1000匝线圈,总电阻为7.76Ω.若把螺线管接到电动势为2V 的电池上,求电流稳定后,螺线管中储存的磁能和管内的磁能密度.解 长直螺线管的自感为()2220027223π44π101000π 1.010H 9.8710H40.1N SN d L llμμ--==⨯⨯⨯⨯⨯==⨯⨯线圈上稳定电流的强度为2A 0.258A 7.76U I R === 电流稳定后,螺线管中储存的磁能为2325m 119.87100.258J 3.2810J 22W LI --⎛⎫==⨯⨯⨯=⨯ ⎪⎝⎭载流螺线管中磁能密度为()533m m m 22244 3.2810J m 4.18J m ππ1.0100.1W W V d l ---⨯⨯===⋅=⋅⨯⨯w 7－20 在真空中,若一匀强电场中的电场能量密度与一0.5T 的匀强磁场的能量密度相等,求该电场的电场强度.解 设电场强度为E 的匀强电场的能量密度与0.5T B =的匀强磁场的能量密度相等,则有22001122B E εμ=由此可得181m 1.5010 V m E --==⋅=⨯⋅。

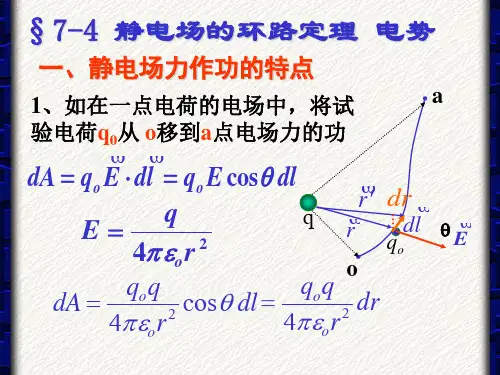
大作业解答变化的电磁场P.1一、选择题1.一导体圆线圈在均匀磁场中运动, 能使其中产生感应电流的一种情况是(A) 线圈绕自身直径轴转动, 轴与磁场方向平行.(B) 线圈绕自身直径轴转动, 轴与磁场方向垂直.(C) 线圈平面垂直于磁场并沿垂直磁场方向平移.(D) 线圈平面平行于磁场并沿垂直磁场方向平移.2.如图, 长度为l 的直导线ab 在均匀磁场中以速度移动, 直导线ab 中的电动势为(A) Bl v . (B) Bl v sin a . (C) Bl v cos a . (D) 0.B v Bva bα⎰⋅⨯ba lB d )(vP.23.如图所示, 直角三角形金属框架abc 放在均匀磁场中, 磁场平行于ab 边, bc 的长度为l . 当金属框架绕ab 边以匀角速度ω转动时, abc 回路中的感应电动势εi 和a 、c 两点间的电势差U a –U c 为B 2i 21,0)A (l B U U c a ωε=-=2i 21,0)B (l B U U c a ωε-=-=22i 21,)C (l B U U l B c a ωωε=-=22i 21,)D (l B U U l B c a ωωε-=-=Bl b acωP.34. 对于单匝线圈取自感系数的定义式为L =Φm /I . 当线圈的几何形状、大小及周围磁介质分布不变, 且无铁磁性物质时, 若线圈中的电流强度变小, 则线圈的自感系数L(A) 不变.(B) 变小.(C) 变大, 与电流成反比关系.(D) 变大, 但与电流不成反比关系.P.4VB LI W μ22m 2121==nI B μ=222πr l n V n L μμ==5.有两个长直密绕螺线管, 长度及线圈匝数均相同, 半径分别为r1和r 2, 管内充满均匀介质, 其磁导率分别为μ1和μ2. 设r 1:r 2=1:2, μ1:μ2=2:1, 当将两只螺线管串联在电路中通电稳定后, 其自感系数之比L1:L 2与磁能之比W m1:W m2分别为:(A)L1:L 2 = 1:1, W m1:W m2 = 1:1(B)L 1:L 2= 1:2, W m1:W m2= 1:1(C)L 1:L2 = 1:2, W m1:W m2 = 1:2(D)L 1:L 2 = 2:1, W m1:W m2= 2:1解: 已知自感系数与长直密绕螺线管内部磁场分别为磁场能量为P.5St B Sd ⋅∂∂=⎰ε6.在圆柱形空间内有一磁感应强度为的均匀磁场,如图所示. 的大小以速率变化. 有一长度为l 0的金属棒先后放在磁场的两个不同位置ab 和a 'b ',那么,金属棒在这两个位置时棒内的感应电动势的大小关系为(A)(B)(C)(D)Oa 'bb 'a ⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯B Bt B d d 0≠=''b a ab εεabb a εε>''abb a εε<''0==''ab b a εεB 解:P.67:电磁波的电场强度、磁场强度和传播速度的关系是(A) 三者互相垂直, 而和位相相差(B) 三者互相垂直, 而、、构成右旋系统(C) 三者中和是同方向的, 但都与垂直(D) 三者中和可以是任意方向的, 但都必须与垂直E H u u E E E E H H u u H H 2π/P.7St D S j I I l H S S d Ld d d 0⋅∂∂+⋅=+=⋅⎰⎰⎰8.如图所示, 平板电容器(忽略边缘效应)充电时, 沿环路L 1、L 2磁场强度的环流中, 必有:(A) (B) (C) (D) H⎰⎰⋅>⋅21d d L L l H l H ⎰⎰⋅=⋅21d d L L l H l H ⎰⎰⋅<⋅21d d L L l H l H 0d 1=⋅⎰L l H L 2L 1解:P.8二、填空题1.一根直导线在磁感应强度为的均匀磁场中以速度切割磁力线运动, 导线中对应于非静电力的场强(称作非静电场场强) ⎽⎽⎽⎽⎽⎽⎽⎽.B v =k E解:lE l B L Ld d )(i ⋅=⋅⨯=⎰⎰感v εB ⨯v 2.载有恒定电流I 的长直导线旁有一半圆环导线MN, 半圆环半径为b , 环面与直导线垂直, 且半圆环两端点连线的延长线与直导线相交, 如图所示.当半圆环以速度沿平行于直导线的方向平移时, 半圆环上的感应电动势的大小是⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.v abM O N 的方向I v 解:⎰⋅⨯==L l B d )(MN MN v εεba b a I -+⋅=ln π20v μP.9I o rωa 3.如图所示, 一半径为r 的很小的金属圆环, 在初始时刻与一半径为a (a >>r )的大金属圆环共面且同心. 在大圆环中通以恒定的电流I , 方向如图. 如果小圆环以角速度ω绕其任一方向的直径转动, 并设小圆环的电阻为R , 则任一时刻t 通过小圆环的磁通量Φm =⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽; 小圆环中的感应电流i = ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.解:t r a It BS Φωμωcos π2cos 20m =≈tr aR I t ΦR R i ωωμεsin π2d d 120===P.10 4.如图, 通有电流I0的长直导线旁, 有一与其共面、且相距为d 的U 形导轨, 在导轨上有电阻为R 的金属棒AB,其长度为a , 以速度向右沿导轨平动, 不计一切摩擦, 则AB 棒上的感应电动势为; AB 棒所受安培力的大小为, 方向为⎽⎽⎽⎽⎽⎽⎽⎽.v r r I l B a d d d 2πd )(00i v v ⎰⎰+=⋅⨯=με d ad I +ln 2π00vμ⎰⨯=B l I F d ⎰++⋅=ad d r r I d a d I R F d π2ln 2π0000μμv 向左Ad R aBR vIR d a d I v 200ln 2π⎥⎦⎤⎢⎣⎡+μP.115.自感系数L =0.3H 的长直螺线管中通以I =8A 的电流时, 螺线管存储的磁场能量W m =⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.解:221LI L =J6.983.0212=⨯⨯=6.将条形磁铁插入与冲击电流计串联的金属环中时,有q =2.0⨯10-5C 的电荷通过电流计. 若连接电流计的电路总电阻R =25Ω, 则穿过环的磁通量的变化∆Φm ＝⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.解:m 1ΦR q ∆-=RqΦ=∆m Wb 105.04-⨯P.127.由半径为r 的两块圆板组成的平行板电容器,在放电时两板间的电场强度的大小为,式中E 0、RC t E E -=e 0R 、C 均为常数. 则两板间的位移电流的大小为⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽; 其方向与场强方向⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.解:S t Dt ΦI d d d d d D ==St Ed d 0ε=RCtr RC E --=e π200ε流向与电场方向相反P.13试判断下列结论是包含于或者等效于哪一个麦克斯韦方程式的,将你确定的方程式用代号填在相应结论后的空白处：:(1) 变化的磁场一定伴随有电场: ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽;(2) 磁感应线是无头无尾的: ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽;(3) 电荷总伴随有电场: ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.231⎰∑==⋅s n i q S D 0i d ⎰-=⋅L t Φl E d d d m⎰=⋅sS B 0d ⎰∑+=⋅=L ni tΦI l H d d d D0i 8.反映电磁场基本性质和规律的积分形式的麦克斯韦方程组为：(1)(2)(4)(3)P.14三、计算题解:rr I l B t l a t a d 2πsin d )(0cos cos i μθεθθ⎰⎰+++-=⋅⨯=v v v v θθθμcos cosln sin 2π0t a t l a I v v v +++-=A 端电势髙a a +lO r 1. 如图所示, 一长直导线中通有电流I ，有一垂直于导线、长度为l 的金属棒AB 在包含导线的平面内, 以恒定的速度沿与棒成θ角的方向移动. 开始时, 棒的A 端到导线的距离为a , 求任意时刻金属棒中的动生电动势, 并指出棒哪端的电势高.v I a lA BvθP.15直于磁场方向,如图所示.回路的CD 段为滑动导线,以匀速远离A 端运动,且始终保持回路为等边三角形.设滑动导线CD 到A 端的垂直距离为x ,且初始x =0.试求回路ACDA 中的感应电动势ε和时间t 的关系.(其中为常矢量)的均匀磁场中,回路平面垂t B B 0=0Bv 2.将等边三角形平面回路ACDA 放在磁感应强度为⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯v A C DB x 解:⎰⎰=⋅=S S S t B S B Φd d 0mtS B S t B S 00d ==⎰320203330tan t B tx B v =︒=220m3d d t B t Φv -=-=εP.16220200013330tan d d d )d(d t B x B S B S t t B S t B v =︒===⋅∂∂-=⎰⎰⎰ ε220233230tan 2)(tB x B CD B v v v =︒⋅=⋅⨯= ε22022022021333233t B t B t B v v v =+=+=∴εεε⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯v A C D B x 另解:P.173.无限长直导线通以电流.有一与之共面的矩形线圈,其长边与长直导线平行.已知长边为L ,两长边距离长直导分别为a 、b ,位置如图所示.求:(1) 矩形线圈内的感应电动势的大小和感应电动势的方向; (2) 导线与线圈的互感系数.)4exp(0t I I -= b L Ia解: 建立坐标系Oxx L x I x BL S B Φd π2d d d 0m μ==⋅= O x abILx L x I Φb a ln π2d π200m μμ⎰==tIa bLt Φd d ln π2d d 0m i ⋅-=-=μεP.18tI t I I I 404t -0e 4d d e --== t i a b LI 400e ln π2-=∴με方向:顺时针 bLIaabLI abLI I ΦM ln π2ln π200m μμ===tIa bLt I M t Φi d d ln π2d d d d 0m ⋅-=-=-=μεP.19r L l 1R 2R I I 4.由半径为R 1和R 2的的两个薄圆筒形导体组成一同轴电缆,中间填充磁导率为μ的均匀磁介质.电缆内层导体通电流I ,外层导体作为电流返回路径,如图所示.求长度为l 的一段电缆内的磁场储存的能量.解:选图示的安培环路,由介质中的环路定理⎰∑=⋅L I l H d 得:)(π221R r R r IH <<=r IH B π2μμ==磁能密度:222m π821r I BH w μ==体积元:rrl V d π2d =磁场能量:122m m ln π4d 21R R l I V w W R R μ==⎰。

大学物理复习题答案（同济大学课件）第一章质点运动学1、①cos sin 2ht r R ti R tj k ωωπ=++；②sin t x dx v R dt ωω==-，cos t y dy v R dtωω==，h 2z dz v dt π==；③2cos t x x dv a R dt ωω==-，2sin t y y dv a R dtωω==-，0z z dv a dt == 2、在运动函数中消去t ，可得轨道方程为28y x =- 由22(48)r ti t j =+-，得28dr v i t j dt ==+，8dva j dt== 可得在1t =时124r i j =-，128v i j =+，18a j = 在2t =时228r i j =+，2216v i j =+，18a j =3、①2343431.5/1010F t a m s m ++?====， 33000034,,,, 2.7/10v v dvt a dv adt dv adt dv dt v m s dt +=====②234343 1.5/1010F x a m s m ++?====，dv a dt =，34.10x dv dv dx dv v dt dx dt dx+===，3410xdx vdv +=，3003410v x vdv dx +=??，/v s =4、以投出点为原点，建立直角坐标系。

0cos x v t θ=，201sin 2y v t gt θ=-以(,)x y 表示着地点坐标，则10y h m =-=-。

将此值和0v ，θ值一并代入得21110209.822t t -=??-??解之得， 2.78t s =和0.74t s =-。

取正数解。

着地点离投射击点的水平距离为：00cos 20cos30 2.7848.1x v t m θ==??= 5、①02180218.8(/)60n rad s πωπ?===，0021800.59.42(/)60v R m s πω?==?= ②由于均匀减速，翼尖的角加速恒定，20018.80.209(/)90A Arad s t ωωα--===- 20.105(/)t a R m s α==-负号表示切向加速度的方向与速度方向相反。

发光材料主讲：刘波同济大学物理系lbo@第七章显示技术中的荧光粉提纲¾7.1 引言¾7.2 阴极射线显示¾7.3 平板显示¾7.3.1 液晶显示（LCD）¾7.3.2等离子体显示屏（PDP）¾7.2.3 有机电致发光显示（OLED）¾7.2.4 场发射显示（FED）7.2 阴极射线显示¾定义：利用发光物质在电子束激发下产生的发光显示。

¾发光过程：电子束的电子能量通常在几千至几万电子伏特，入射到发光材料中产生大量次级电子，离化和激发发光中心产生发光。

¾用途：主要用于雷达、电视、示波器和飞点扫描等方面。

其主要部件是阴极射线管。

Cutaway rendering of a color CRT:1.Three Electron guns (for red, green, and blue phosphor dots)2.Electron beams3.Focusing coils4.Deflection coils5.Anode connection6.Mask for separating beams for red, green, and blue part of displayed image7.Phosphor layer with red, green, and blue zones8.Close-up of the phosphor-coated inner side of the screen阴极射线荧光粉阴极射线荧光粉主要用于电视示波器，雷达，计算机等各种荧光屏和显示器。

要求：¾发光色调：红,绿,蓝三基色粉应具有良好的色饱和度。

¾亮度-电流和特性：亮度-电流饱和效应是指荧光粉的发光效率随电子束电流密度的增大而下降的现象。

¾温度猝灭特性：温度对阴极射线荧光粉的影响很大,特别是大功率显示器件要求高亮度。

同济大学高等数学上册第七章常微分方程同济大学高等数学上册是大多数理工科专业的学生必修的课程，第七章是关于常微分方程的内容。

常微分方程是数学中的一个重要分支，广泛应用于物理、化学、经济等领域。

掌握常微分方程的基本理论和解法对于理解和应用这些领域的知识具有重要意义。

本章内容主要包括：一阶常微分方程、高阶常微分方程、一阶线性微分方程、可分离变量的微分方程、齐次线性微分方程和一阶齐次线性方程、一阶齐次线性非齐次方程、二阶常系数齐次线性方程、常系数非齐次方程等。

一、一阶常微分方程一阶常微分方程是指未知函数的导数只包含一阶导数的方程。

例如，dy/dx = f(x)。

常微分方程的求解可以采用分离变量法、恰当方程、公式法等。

其中分离变量法是常用的解法之一。

分离变量法的基本思想是将方程两边的变量分离开来，从而达到求解的目的。

二、高阶常微分方程高阶常微分方程是未知函数的导数包含高于一阶导数的方程。

例如，d²y/dx² + p(x) dy/dx + q(x) y = f(x)。

高阶常微分方程的求解可以采用常系数线性微分方程的方法。

常系数线性微分方程是指系数为常数的微分方程，其求解方法相对简单。

三、一阶线性微分方程一阶线性微分方程是指未知函数的导数与未知函数本身之间线性相关的方程。

例如，dy/dx + p(x) y = q(x)。

一阶线性微分方程的求解可以借助于积分因子的方法。

积分因子的选择是使方程两边的未知函数系数相等，从而将方程转化为可积分的形式。

四、可分离变量的微分方程可分离变量的微分方程是指未知函数和自变量可以在方程中分离的方程。

例如，dy/dx = f(x)/g(y)。

可分离变量的微分方程的求解可以通过对方程两边的变量分离，然后进行适当的积分得到。

这种方法常用于求解一些特殊形式的微分方程。

五、齐次线性微分方程和一阶齐次线性方程齐次线性微分方程是指未知函数的导数和未知函数本身之间构成齐次线性关系的微分方程。