高中数学题库A集合与简易逻辑简单逻辑

一. 本周教学内容：集合与简易逻辑知识结构：【典型例题】例1. 已知集合A{2，3，7}，且A中至多有一个奇数，则这样的集合共有A. 2个B. 4个C. 5个D. 6个解：集合A可有三类：第一类是空集；第二类是A中不含奇数；第三类是A中只含一小结：应充分理解“至多”两字，然后进行分类计数。

例2. 设全集I=R，集合A={x|(x－1)(x－3)≤0}，B={x|(x－1)(x－a)<0}且解：解不等式(x－1)(x－3)≤0，得1≤x≤3，故A={x|1≤x≤3}，当a<1时，是[1，3]小结：这类问题一般可采用画数轴进行分析解决。

例3.解：小结：此题将解方程与集合运算有机地结合起来，对解题能力的要求略高一些，当然例4. 解不等式|x+2|+|x|>4解法一：综上可知，原不等式的解集为{x|x<－3或x>1}解法二：不等式|x+2|+|x|>4表示数轴上与A(－2)，O(0)的距离之和大于4的点，如图所示。

小结：①我们常用脱去绝对值的方法来解含有绝对值的不等式，即零点分区间法，其实质是转化为分段求解，如解法一。

②解法二是充分考虑绝对值的几何意义，从形的方面来考虑的，解决任何一个数学问题都要养成从数、形两个方面去思考的习惯，数形结合是数学中的一种基本的思维方法。

例5. 若关于x的不等式x2－ax－6a<0的解集为一开区间，且此区间的长度不超过5，试求a的取值范围。

解：小结：解a的范围。

但韦达定理不能保证有实根，故应注意Δ>0这一条件。

例6.解：依题意有：小结：关于方程根的讨论一般用函数的观点和方法去解决会使问题简洁。

例7. 等差数列{a+bn|n=1，2，…}中包含一个无穷的等比数列，求a，b（b≠0）所需满足的充分必要条件解：设有自然数n1<n2<…，使分必要条件。

例8.（1）求证：两图象交于不同的两点A、B。

（2）求线段AB在x轴上的射影A1B1之长的范围解：（2）设方程①的两根为x1，x2，由韦达定理得：小结：此题涉及一次函数、二次函数的图象、一元二次方程、一元二次函数在区间上的取值范围等多个知识点，要注意熟练掌握二次函数与方程，不等式的相互联系和相互转化。

高一数学上学期单元测试题(三)——集合与简易逻辑1.集合运算中一定要分清代表元的含义。

[举例]已知集合P={y|y=x2，x∈R}，Q={y|y＝2x，x∈R}求P∩Q。

解析：集合P、Q均为函数值域（不要误以为是函数图象，{（x,y）| y=x2，x∈R}才表示函数图象），P=[0，+ ，Q=（0，+ ，P∩Q=Q。

[提高]A={x｜y=3x+1,y∈Z},B={y｜y=3x+1,x∈Z},求A∩B。

2.空集是任何集合的子集，空集是任何非空集合的真子集。

[举例]若A={x|x2<a} B={x|x＞2}且A∩B=Φ，求a的范围（注意A有可能为Φ）。

解析：当a>0时，集A=（- ，），要使A∩B=Φ，则≤2，得0<a≤4,当a≤0时，A=Φ，此时A∩B=Φ，综上：a≤4（A=Φ的情况很容易疏漏！）[巩固]若A={x∣ax=1},B={x∣x2=1}且B∩A=A，求a的所有可能的值的集合。

[关注]A∩B=A等价于A B3.充要条件可利用集合包含思想判定：若A B，则A是B充分条件；若A B，则A 是B必要条件；若A B且A B即A=B，则A是B充要条件。

换言之：由A B则称A是B的充分条件，此时B是A的必要条件；由B A则称B是A的充分条件，此时A是B的必要条件。

有时利用原命题与逆否命题等价，“逆命题”与“否命题”等价转换去判定也很方便。

充要条件的问题要十分细心地去辨析：“哪个命题”是“哪个命题”的充分（必要）条件；注意区分：“甲是乙的充分条件（甲乙）”与“甲的充分条件是乙（乙甲）”。

[举例] 若非空集合，则“或”是“”的（）（A）充分非必要条件（B）必要非充分条件（C）充要条件（D）既非充分又非必要条件解析：命题“或”等价于“∈”，显然是的真子集，∴“或”是“”的必要不充分条件。

[巩固]已知直线、和平面，则‖的一个必要但不充分条件是（）（）‖且‖（）且（）、与成等角（）‖且4.命题“A或B”真当且仅当“A、B中至少要一个真”；命题“A或B”假当且仅当“A、B全假”。

单元练习一 集合与简易逻辑（A ）一、选择题：1．设11},32|{=≤=a x x M ；则关系：①M a ∈；②M a ∈}{；③M a ⊆；④M a ⊆}{．其中真命题的个数是…………………………………………………………（ ）（A ）1 （B ）2 （C ）3 （D ）42．设集合},412|{Z k k x x M ∈+==；},214|{Z k k x x N ∈+==；则………………（ ） （A ）N M = （B ）N M ⊂ （C ）N M ⊃ （D ）φ=⋂N M3．设}22|{},4|3||{x x y y B x x A -+-==≤-=；则=⋂B A …………… （ ）（A ）}0{ （B ）}2{ （C ）φ （D ）}72|{≤≤x x4．不等式x x 32|12|-<-的解集是…………………………………………………………（ ）（A ）}153|{><x x x 或 （B ）}53|{<x x （C ）}532121|{<<<x x x 或 （D ）}313|{<<-x x 5．下列四个集合中；是空集的是……………………………………………………………（ ） （A ）}33|{=+x x （B ）},,|),{(22R y x x y y x ∈-=（C ）}|{2x x x < （D ）}01|{2=+-x x x6．已知关于x 的二次不等式01)13(2>+--x a ax 的解集是R ；则实数a 的取值范围是（ ） （A ）191≤≤a （B ）191<<a （C ）1910><<a a 或 （D ）1910≥≤<a a 或 7．已知},013|{},0|{2>+-=≤++=x x x B c bx x x A 且R B A =⋃； }43|{≤<=⋂x x B A ；则c b 、的值为………………………………………………（ ）（A ）4,3-=-=c b （B ）4,3=-=c b （C ）4,3-==c b （D ）4,3==c b8．对任意实数x ；若不等式k x x >-++|1||2|恒成立；则k 的取值范围是……… （ ）（A ）3≤k （B ）3-≤k （C ）3<k （D ）3-<k9．如果y x ,是实数；则“||||||y x y x +=+”是“0>xy ”成立的 …………………（ ）（A ）充分非必要条件 （B ）必要非充分条件（C ）充要条件 （D ）既非充分又非必要条件10．设命题甲：0122>++ax ax 的解集是实数集R ；命题乙：10<<a ．则命题甲是命题乙成立的 …………………………………………………………………（ ）（A ）充分非必要条件 （B ）必要非充分条件（C ）充要条件 （D ）既非充分又非必要条件二、填空题：11．若集合}3|),{(}04202|),{(b x y y x y x y x y x +=⊂=+-=-+且；则_____=b ．12．命题p 是命题q 的充分但不必要条件；命题s 是命题q 的必要不充分条件；命题t 是命题s 的充要条件；则命题p 是命题t 的 ．13．已知命题：“R d c b a ∈,,,若d c b a ==,则bd ac =”；其逆否命题是：；且逆否命题是 （填真或假）命题．14．已知全集R U =；集合}0103|{2≤--=x x x M ；}1|{>=x x N 则_________)(=⋂N M C U ．15．已知集合},1|{2R x x y y P ∈+==；},1|{R x x y y Q ∈+==；则______=⋂Q P ．16．不等式1273310522>+-+-x x x x 的解集是 ． 三、解答题：17．已知函数3)1(4)54(22+-+-+=x k x k k y 的图象都在x 轴上方；求实数k 的取值范围．18．集合}01|{},023|{22=-+-∈==+-∈=a ax x R x B x x R x A ；}02|{2=+-∈=mx x R x C ；满足C C A A B A =⋂=⋃,；求m a ,的值．单元练习一 集合与简易逻辑（A ）答案一、选择题：1．B 2．B 3．A 4．B 5．D6．B 7．A 8．C 9．B 10．B二、填空题：11．2 12．充分但不必要条件13．R d c b a ∈,,,若bd ac ≠则d c b a ≠≠或；真14．}52|{>-<x x x 或 15．}1|{≥y y16．}212131|{<<<<x x x 或 三、解答题：17．若0542=-+k k 则51-==k k 或；检验可知当1=k 时满足题意；若0542≠-+k k ；根据二次函数的图象和性质可得1910)54(34)]1(4[054222<<⇒⎩⎨⎧<-+⨯--=∆>-+k k k k k k 综上可得：191<≤k ．18． }2,1{}023|{2==+-∈=x x R x A}0)]1()[1(|{}01|{2=---==-+-∈=a x x x a ax x R x B∵C C A A B A =⋂=⋃,∴A C A B ⊂⊂, ∴32或=a若φ=C ；此时2222082<<-<-m m 即满足题意； 若φ≠C ；结合题意可知}2,1{=C 从而得到：3=m∴m 应该满足：2222<<-m 或3=m ．。

集合、简易逻辑常用数集符号自然数集N （包括0），正整数集N *或N +，整数集Z ，实数集R 集合1、互异性例：集合{a 2，0，1}与集合{b 2，0，-1}相等，根据互异性，a 2=-1、b 2=12、元素、集合间的关系（韦恩图）：元素与集合∈∉，集合与集合⊆ ⊊⊄ （注：集合A ⊆集合B ，集合A 可以是Ø，集合A 、B 可以相等）3、空集：Ø，无任何元素，是任何集合的子集（注：{Ø}与Ø不同，{Ø}包含1个元素Ø，Ø无元素）（注：空集必须分类讨论）4、交集∩，并集∪，补集（全集U 中不属于集合A 的元素集合，C U A ） 例：A={x |1≤x ≤3}，B={x |mx+1=0}，A ∩B ≠Ø，求m 的范围 补集思想，令A ∩B ＝Ø，则B ＝Ø（m=0）或-m1<1或>3，求出m 的集合M ，C R M 即所求范围5、常见元素类型（1）数集例：{x|x 2+3x-4=0}，表示方程x 2+3x-4=0的解（2）点集例：{（x ，y ）|y=x 2+3x-4}，表示函数y=x 2+3x-4图像上点的坐标6、集合子集的个数含有n 个元素的集合，子集个数为2n ，非空集合个数为2n -1简易逻辑1、复合命题：或∨、且∧、非﹁p∨q：一真即真（特称命题∃：“存在……”）p∧q：一假即假（全称命题∀：“对于所有……”）2、原命题（若p，则q）与逆否命题（若﹁q，则﹁p）同真同假3、对于命题“若p，则q”，否命题与命题的否定（否定命题）（1）否命题：若﹁p，则﹁q（2）命题的否定（否定命题）：若p，则﹁q（注：命题的否定考的多，否命题考的少）（3）全称命题、特称命题的否定例1：否定全称命题“∀实数x，x2＞0”先改为“若p，则q”，“若x为实数，则x2＞0”→否定即﹁q，“若x为实数，∃实数x，x2≤0”，即“∃实数x，x2≤0”例2：否定特称命题“∃平行四边形，不是矩形”先改为“若p，则q”，“若一个平面图形是平行四边形，∃一个平行四边形，不是矩形”→否定即﹁q，“若一个平面图形是平行四边形，则它是矩形”，即“∀平行四边形，是矩形”4、充分必要条件p是q的充分必要条件，p⇔q（1）充分条件：p⇒q（2）必要条件：p⇐q（注：利用集合理解充分必要条件p⇒q，即集合P⊆Q，p⇐q，即集合P⊇Q）。

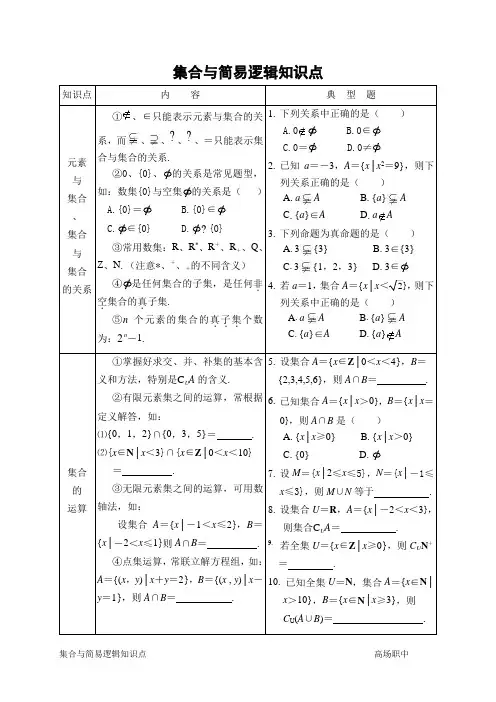
集合与简易逻辑知识点系，而、、的关系是（B.{0}∈{0} D.B.0≠}A{3}{1A Ap一个实数一个实数(p∧q)＝p∨q(q)))第一章集合与简易逻辑测试题一、选择题1.集合A={x|x≤}，a=3，则 ( )A.a AB.a AC.{a}∈AD.{a} A2.集合M={x|x=3k-2，k∈Z}，Q={y|y=3l+1，l∈Z}，S={z|z=6m+1，m∈Z}之间的关系是 ( )A.S Q MB.S=Q MC.S Q=MD.S Q=M3.若A={1，3，x}，B={x2，1}，且A∪B=A，则这样x的不同取值有 ( )A.1个B.2个C.3个D.4个4.符合条件{a}P{a，b，c}的集合P的个数是 ( )A.2B.3C.4D.55.若A={x|x2-4x+3＜0}，B={x|x2-6x+8＜0}，C={x|2x2-9x+a＜0}，(A∩B)C，则a的取值范围是 ( )A.a≤10B.a≥9C.a≤9D.9≤a≤106.若a＞0，使不等式|x-4|+|3-x|＜a在R上的解非空，则a的值必为 ( )A.0＜a＜1B.0＜a≤1C.a＞1D.a≥17.集合A={x|x2-5x+4≤0}，B={x|x2-5x+6≥0}，则A∩B= ( )A.{x|1≤x≤2，或3≤x≤4}B.{x|1≤x≤2，且3≤x≤4}C.{1，2，3，4}D.{x|1≤x≤4或2≤x≤3}8.如果方程x2+(m-3)x+m的两根都是正数，则m的取值范围是 ( )A.0＜m≤3B.m≥9或m≤1C.0＜m≤1D.m＞99.由下列各组命题构成“P或Q”，“P且Q”，“非P”形式的复合命题中，“P或Q”为真命题，“P且Q”为假命题，“非P”为真命题的是 ( )A.P：3是偶数；q：4是奇数B.P：3+2=6；q：3＞2C.P：a∈{a，b}；q：{a}{a，b}D.p：Q R；q：N=N+10.对于实数x、y，条件A：|x|≤1且|y|≤1；条件B：|x|+|y|≤1；条件C：x2+ y2≤1.则正确的是 ( )A.B是C的充分不必要条件；A是C的必要不充分条件B.B是C的必要不充分条件；A是C的充分不必要条件C.C是A的必要不充分条件；C是B的充分不必要条件D.C是A的充要条件；B是A的既不充分也不必要条件11.若a、b为实数，则ab(a-b)＜0成立的一个充要条件是 ( )A.0＜＜B.0＜＜C.＜D.＜12.给出以下四个命题：p：若x2-3x+2=0，则x=1或x=2；q：若2≤x＜3，则(x-2) (x-3)≤0；r：若x=y=0，则x2+y2=0；s：若x、y∈N，x+y是奇数，则x、y中一个是奇数一个是偶数，那么 ( )A.p的逆命题为真B.q的否命题为真C.r的否命题为假D.s的逆命题为假二、填空题13.已知集合M={x|x∈N+，且8-x∈N+}，则M中只含有两个元素的子集的个数有__ __个.14.已知集合A={x|x2-x-2≤0}，B={x|a＜x＜a+3}，满足A B=，则实数a的取值范围是____.15.“若a+b是偶数，则a、b必定同为奇数或偶数”的逆否命题为____.16.已知集合M{0，1，2，3，4}，且M{0，2，4，8}，则集合M中最多有____个元素.三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.17.已知三元素集合A={x，xy，x-y}，B={0，|x|，y}，且A=B，求x与y的值.18设集合A={|a+1|，3，5}，集合B={2a+1，a2+2a，a2+2a-1}，当A∩B={2，3}时，求A∪B.19.设A={x|-2＜x＜-1，或x＞1}，B={x|x2+ax+b≤0}，已知A∪B={x|x＞-2}，A ∩B={x|1＜x≤3}，试求a，b的值.20.已知不等式ax2+bx+c＞0的解集为{x|0＜m＜x＜n}，求关于x的不等式cx2-bx +a＜0的解.21.已知集合A={x|1＜|x-2|＜2}，B={x|(x-a)(x-1)＜0，a≠1}，且A∩B≠，试确定a的取值范围.22关于实数x的不等式与x2-3(a+1)x+2(3a+1)≤0的解集依次为A、B(1)求集合A、B(2)若A B，求此时a的取值范围.参考答案一、选择题1-12：DCCBC CACBB DA二、填空题13.21个14.a≥2或a≤-415.“若a、b不同为奇数且不同为偶数则a+b不是偶数”16.3个三、解答题17.解：∵0∈B，A=B，∴0∈A∵集合A为三元素集，∴x≠xy，∴x≠0，y≠1又∵0∈B，y∈B，∴y≠0从而，x-y=0，x=y这时，A={x，x2，0}，B={0，|x|，x}∴x2=|x|，x=0(舍去)或x=1(舍去)，或x=-1经验证x=-1，y=-1是本题的解.18.解：∵|a+1|=2，∴a=1或a=-3当a=1时，集合B的元素a2+2a=3，2a+1=3，由集合的元素的互异性可知，a≠1当a=-3时，集合B={-5，3，2}∴A∪B={-5，2，3，5}19.解：由A∪B={x|x＞-2}，A∩B={x|1＜x≤3}得B={x|-1≤x≤3}，根据二次不等式与二次方程的关系，可知-1与3是方程x2+ax+b=0的两根.∴a=-(-1+3)=-2，b=(-1)×3=-320.解：m＜x＜n(x-m)(x-n)＜0x2-(m+n)x+mn＜0，对照-ax2-bx-c＜0，∴，∴a=-k，b=k(m+n)，c=-kmn，代入cx2-bx+a＜0，∴-kmnx2-k(m+n)x-k＜0，mnx2+(m+n)x+1＞0，∵0＜m＜n，∴∴所求不等式的解集为21.解：A={x|1＜|x-2|＜2}={x|0＜x＜1，或3＜x＜4}(1)当a＞1时，B={x|1＜x＜a}∵A∩B≠∴a＞3(2)当a＜1时，B={x|a＜x＜1}∵A∩B≠∴a＜1综合(1)、(2)可知，a的取值范围是a＜1，或a＞322.解：(1)A==={x|2a≤x≤a2+1}B={x|x2-3(a+1)x+2(3a+1)≤0}={x|(x-2)(x-3a-1)≤0}当a≤时，B={x|3a+1≤x≤2}当a＞时，B={x|2≤x≤3a+1}(2)当a≤时，若，则2a≥3a+1且a2+1≤2得a=-1当a＞时，若，则2a≥2且a2+1≤3a+1得1≤a≤3∴a的取值范围是：a=-1，或1≤a≤3。

第1章集合与简易逻辑§1–1 集合一、集合的概念1.1.1 在“①难解的题目；②方程x2＋1＝0在实数集内的解；③直角坐标平面上第四象限内的所有点；④很多多项式”中，能够组成集合的是( )．(A) ②③(B) ①③(C) ②④(D) ①②④解析由集合中元素的确定性可知只有②和③能组成集合，答案为A．1.1.2 下列集合中，有限集是( )．(A) {x|x<10，x∈N} (B) {x|x<10，x∈Z}(C) {x|x2<10，x∈Q} (D) {x|x＝y＋10，y∈R}解析由N表示自然数集得{x|x<10，x∈N}＝{0，1，2，3，4，5，6，7，8，9}是有限集，答案为A．1.1.3 若集合M＝{x|x≤6}，a＝ ，则下列结论中正确的是( )．(A) {a}M(B) a M(C) {a}∈M(D) a∉M解析因为<6，则∈M，{a}M，所以，答案为A．1.1.4 已知集合A＝{0，1}，B＝{y|y2＝1－x2，x∈A}，则A与B的关系是( )．(A) A＝B(B) A B(C) A∈B(D) A B解析由已知得集合B＝{－1，0，1}，所以，A B，答案为B．1.1.5 下列四个关系中，正确的是( )．(A) ∅∈{0} (B) 0∉{0} (C) {0}∈{0，1} (D) 0∈{0，1}解析∅与{0}，{0}与{0，1}是两个集合间的关系，这种关系不应用表达元素与集合间关系的“∈”来表达；而0∈{0}，又0是集合{0，1}中的元素，所以，0∈{0，1}是正确的，答案为D．1.1.6 设a，b∈R，集合{1，a＋b，a}＝ ，，，则b－a＝( )．(A) 1 (B) －1 (C) 2 (D) －2解析由已知得0∈{1，a＋b，a}，而a≠ ，于是，只能a＋b＝0，则＝－1，又－1∈{1，a＋b，a}，所以，a＝－1，b＝1，b－a＝2，答案为C．1.1.7 用适当的方式写出下列集合：(1) 组成中国国旗的颜色名称的集合；(2) 不大于6的非负整数所组成的集合；(3) 所有正奇数组成的集合；(4) 方程x3＋6＝0的实数解构成的集合；(5) 不等式x2－5x＋4<0的解集；(6) 直角坐标平面中，第一象限内的所有点组成的集合；(7) 直角坐标平面中，直线y＝2x－1上的所有点组成的集合．解析(1) 组成中国国旗的颜色名称的集合是{红，黄}．(2) 不大于6的非负整数所组成的集合是{0，1，2，3，4，5，6}．(3) 所有正奇数组成的集合是{x|x＝2k＋1，k∈N}．(4) 方程x3＋6＝0的实数解构成的集合是{x|x3＋6＝0，x∈R}．(5) 不等式x2－5x＋4<0的解集{x|x2－5x＋4<0}或写成{x|1<x<4}．(6) 直角坐标平面中，第一象限内的所有点组成的集合是{(x，y)|x>0且y>0}．(7) 直角坐标平面中，直线y＝2x－1上的所有点组成的集合是{(x，y)|y＝2x－1}．1.1.8 已知集合A＝{1，3，x}，集合B＝{1，x2}，若有B A且x∉B，则A＝．解析由x2∈A及x∉B得x2＝3，解得x＝± ，经检验此x的值符合集合中元素的互异性，所以，集合A＝{1，3，}或{1，3，－}．1.1.9 集合A＝{x|－3≤x≤2}，B＝{x|2m－1≤x≤2m＋1}，若B⊆A，则m的取值范围是．解析由已知可得－1－ ，＋1 ，解得－1≤m≤1．1.1.10 若集合M＝{0，1，2}，N＝{(x，y)|x－2y＋1≥0且x－2y－1≤0，x，y∈M}，则N中元素的个数为( )．(A) 9 (B) 6 (C) 4 (D) 2解析将点(0，0)，(1，1)，(2，2)，(0，1)，(1，0)，(0，2)，(2，0)，(1，2)，(2，1)的坐标代入不等式组－＋1 ，－－1 ，可知只有点(0，0)，(1，1)，(1，0)，(2，1)四个点在集合N内，所以，答案为C．1.1.11 定义集合运算：A☉B＝{z|z＝xy(x＋y)，x∈A，y∈B}，设集合A＝{0，1}，B＝{2，3}，则集合A☉B的所有元素之和为( )．(A) 0 (B) 6 (C) 12 (D) 18解析由已知可得A☉B＝{0，6，12}，所以，A☉B中所有元素之和为18，答案为D．1.1.12 设⊕是R上的一个运算，A是R的非空子集，若对任意a，b∈A，有a⊕b∈A，则称A对运算⊕封闭．下列数集对加法，减法，乘法和除法(除数不等于零)四则运算都封闭的是( )．(A) 自然数集(B) 整数集(C) 有理数集 (D)无理数集解析任意两个自然数或整数的商不一定是自然数或整数，任意两个无理数的积不一定是无理数，而任意两个有理数的和、差、积、商一定都是有理数，所以，有理数集对加法，减法，乘法和除法(除数不等于零)四则运算都封闭的，答案为C．1.1.13 集合M ＝{x |a 1x >b 1}，N ＝{x |a 2x >b 2}，其中常数a 1b 1a 2b 2≠ ，则“ 1 ＝ 1”是“M ＝N ”的( )．(A) 充分不必要条件(B) 必要不充分条件 (C) 充要条件(D) 既不充分也不必要条件解析 若a 1＝b 1＝1，a 2＝b 2＝－1，则有 1 ＝ 1 ，此时，M ＝{x |x >1}，N ＝{x |x <1}，M ≠N ； 若M ＝N ，则必有a 1a 2>0，于是，M ＝ 1 1 ，N ＝， 或者，M ＝ 1 1 ，N ＝ ，于是， 1 1＝ ，即 1 ＝ 1， 所以，“ 1 ＝ 1”是“M ＝N ”的必要不充分条件，答案为B ．1.1.14 已知集合M ＝{x |x ≤a 2＋b 2}，其中a ，b 是常数．给出下列四个命题：① 2ab 一定属于M ② 2ab 一定不属于M③ －2ab 一定属于M ④ －2ab 一定不属于M其中正确命题的序号是 (写出所有正确命题的序号)．解析 由(a －b )2≥0和(a ＋b )2≥0对任意a ，b ∈R 恒成立可得2ab ≤a 2＋b 2，－2ab ≤a 2＋b 2，所以，2ab ∈M ，－2ab ∈M ，在上述四个命题中，①和③是正确的．1.1.15 已知集合A 是非零实数集的子集，并且有如下性质：对任意x ∈A ，必有3－∈A ．问： (1) 集合A 可否有且仅有一个元素?如果可以，求出所有满足要求的集合A ；若不可以，则说明理由；(2) 集合A 可否有且仅有两个元素?如果可以，求出所有满足要求的集合A ；若不可以，则说明理由．解析 (1) 若集合A 中有且仅有一个元素x ，则3－＝x ，即x 2－3x ＋2＝0，解得x ＝1或x ＝2，所以，集合{1}和{2}是两个满足要求的单元集．(2) 集合{1，2}是满足要求的二元集．若集合A ＝{a ，b }是满足要求的二元集，并且 － ＝ ， － ＝ ，即 － ＝ ， － ＝ ，则a ＝b ，矛盾，所以，满足要求的二元集只能是{1，2}．1.1.16 同时满足{1}A ⊆{1，2，3，4，5}，且A 中所有元素之和为奇数的集合A 的个数是( )．(A) 5 (B) 6 (C) 7 (D) 8解析 若A 为二元集，则A 可为{1，2}、{1，4}；若A 为三元集，则A 可为{1，2，4}、{1，3，5}；若A 为四元集，则A 可为{1，2，3，5}、{1，3，4，5}；若A 为五元集，则A 可为{1，2，3，4，5}，所以，共有7个符合条件的集合，答案为C ．1.1.17 对于集合A 和B ，当A B 时，下列集合之间的关系一定不能成立的是( )．(A) ∅⊆A (B) ∅B (C) B ＝∅ (D) A ＝∅ 解析 由于不存在集合是空集的真子集，所以，由A B 可得B ≠∅，所以，答案为C ．1.1.18 下列各组集合中，M 与P 表示同一个集合的是( )．(A) M ＝{(1，－3)}，P ＝{(－3，1)}(B) M ＝∅，P ＝{0}(C) M ＝{y |y ＝x 2＋1，x ∈R}，P ＝{(x ，y )|y ＝x 2＋1，x ∈R}(D) M ＝{y |y ＝x 2＋1，x ∈R}，P ＝{t |t ＝(y －1)2＋1，y ∈R}解析 (1，－3)与(－3，1)是平面直角坐标系中两个不相同的点；集合{0}中有一个元素，它不是空集．集合M ＝{y |y ＝x 2＋1，x ∈R}是二次函数y ＝x 2＋1的因变量的集合，它是一个数集，而集合P ＝{(x ，y )|y ＝x 2＋1，x ∈R}表示平面直角坐标系中的一条抛物线，它是点的集合．集合M ＝{y |y ＝x 2＋1，x ∈R}＝{t |t ＝(y －1)2＋1，y ∈R}＝{y |y ≥1}，所以，答案为D ．1.1.19 写出集合A ＝{(x ，y )|x 2＋y 2＝2且x ＋y ＝0}的所有子集： ．解析 集合A ＝{(1，－1)，(－1，1)}，所以，A 的所有子集是∅，{(1，－1)}，{(－1，1)}，{(1，－1)，(－1，1)}．1.1.20 用适当的方式写出下列集合并化简：(1) 方程x 2＋2＝0的全体实数解组成的集合： ；(2) 函数y ＝3x ＋2，1≤x ≤3的所有因变量组成的集合： ；(3) 函数y ＝－x 2＋4x ＋3，x ∈R 的所有因变量组成的集合： ．解析 (1) 方程x 2＋2＝0的全体实数解组成的集合是{x |x 2＋2＝0，x ∈R}＝∅；(2) 函数y ＝3x ＋2，1≤x ≤3的所有因变量组成的集合是{y |y ＝3x ＋2，1≤x ≤3}＝{y |5≤y ≤11}；(3) 函数y ＝－x 2＋4x ＋3，x ∈R 的所有因变量组成的集合是{y |y ＝－x 2＋4x ＋3，x ∈R}＝{y |y ≤7}．1.1.21 已知集合{x |ax 2＋2x ＋1＝0，a ∈R ，x ∈R}中有且仅有一个元素，则a 的值是 ．解析 要使得集合{x |ax 2＋2x ＋1＝0，a ∈R ，x ∈R}中有且仅有一个元素，则a ＝0或Δ＝22－4a ＝0，所以，a ＝0或a ＝1．1.1.22 关于x 的不等式 － ＋1 ≤ －1的解集是A ，关于x 的不等式x 2－3(a ＋1)x ＋2(3a ＋1)≤0 (其中a ∈R)的解集是B ，求使A ⊆B 的a 的取值范围．解析 不等式 － ＋1 ≤ －1 的解集A ＝[2a ，a 2＋1]． 不等式x 2－3(a ＋1)x ＋2(3a ＋1)≤0即为(x －2)(x －3a －1)≤0．若a ≥1 ，则B ＝[2，3a ＋1]；若a <1 ，则B ＝[3a ＋1，2]．由A ⊆B 得 1 ， ， ＋1 ＋1或 1 ， ＋1 ， ＋1 ，解得1≤a ≤3或a ＝－1． 所以，a 的取值范围是a ＝－1或1≤a ≤3．1.1.23 已知集合A ＝{x |x 2－3x ＋2＝0}，B ＝{x |x 2－ax ＋(a －1)＝0}，C ＝{x |x 2－bx＋2＝0，x ∈R}，若B ⊆A ，C ⊆A ，求实数a ，b 应满足的条件．解析 集合A ＝{1，2}，而x 2－ax ＋(a －1)＝0即为(x －1)(x －a ＋1)＝0，若a －1＝1，即a ＝2，则B ＝{1}满足；若a －1≠1，即a ≠ ，则B ＝{1，a －1}，由B ⊆A 知a －1＝2，即a ＝3．对于集合C ，由C ⊆A 知，若C ＝∅，则Δ＝(－b )2－8<0，解得－2 b <2 C 为单元集，则Δ＝(－b )2－8＝0，此时C ＝{ }或C ＝{－ }，与C ⊆A 矛盾；若C ＝{1，2}，即C 中方程两根为1和2，则b ＝3．所以，a ，b 应满足的条件是a ＝2或a ＝3而 －2 <b <2 或b ＝3．1.1.24 已知集合A ＝{(x ，y )|y ＝－x 2＋mx －1}，B ＝{(x ，y )|x ＋y ＝3，0≤x ≤3}，若有且仅有一个点同时属于集合A 和B ，求实数m 的取值范围．解析 由已知得抛物线与线段有且仅有一个交点．由 ＝－ ＋ －1，＋ ＝ ， 得 x 2－(1＋m )x ＋4＝0，该方程在区间[0，3]上只有一个解．若Δ＝(m ＋1)2－16＝0，则m ＝3或m ＝－5，如果m ＝3，解得x ＝2；如果m ＝－5，解得x ＝－2∉[0，3]，于是m ＝－5舍去．若Δ> ，则记f (x )＝x 2－(1＋m )x ＋4，此时，只需f (3)<0，即9－3(m ＋1)＋4<0，解得m >1．所以，m 的取值范围是m >1 或m ＝3．1.1.25 设集合M ＝{1，2，3，4，5，6}，S 1，S 2，…，S k 都是M 的含两个元素的子集，且满足：对任意的S i ＝{a i ，b i }，S j ＝{a j ，b j }(i ≠j ，i ，j ∈{1，2，3，…，k })，都有min ， ≠min ，(min{x ，y }表示两个数x ，y 中的较小者)，则k 的最大值是( )． (A) 10 (B) 11(C) 12 (D) 13解析 集合M 的所有两元子集是{1，2}，{1，3}，{1，4}，{1，5}，{1，6}，{2，3}，{2，4}，{2，5}，{2，6}，{3，4}，{3，5}，{3，6}，{4，5}，{4，6}，{5，6}，共计15个，其中，不同min ，(i ＝1，2，…，15)有1 ，1 ，1 ，1 ，1 ， ， ， ， ， ，共11个，所以，答案为B ．1.1.26 设P 是一个数集，且至少含有两个数，若对任意a ，b ∈P ，都有a ＋b ，a －b ，ab ，∈P (除数b ≠ ，则称P 是一个数域．例如有理数集Q 是数域；数集F ＝{a ＋b |a ，b∈Q}也是数域．有下列命题：①整数集是数域；②若有理数集Q⊆M，则数集M必为数域；③数域必为无限集；④存在无穷多个数域．其中正确的命题的序号是(把你认为正确的命题的序号填上)．解析因为任意两个整数的商不一定是整数，故命题①不正确；当集合M＝Q∪{}时，由于1∈Q，而∉M，故命题②不正确；由数域P的定义知，必有＝1∈P，从而2∈P，则3∈P，…，所以，整数集Z⊆P，故数域P中必有无穷多个元素，命题③正确；由于数集F＝{a＋b|a，b∈Q}是数域，则将其中的 换成 ， ，…等仍为数域，所以数域有无穷多个，命题④正确．所以，在上述四个命题中，正确命题的序号是③，④．1.1.27 非空集合G关于运算⊕满足：(1) 对任意a，b∈G，都有a⊕b∈G；(2) 存在e∈G，使得对一切a∈G，都有a⊕e＝e⊕a＝a，则称G关于运算⊕为“融洽集”．现给出下列集合和运算：①G＝{非负整数}，⊕为整数的加法；②G＝{偶数}，⊕为整数的乘法；③G＝{平面向量}，⊕为平面向量的加法；④G＝{二次三项式}，⊕多项式的乘法；⑤G＝{虚数}，⊕为复数的乘法．其中G关于运算⊕为“融洽集”的是(写出所有“融洽集”的序号)．解析对于非负整数集以及加法运算，两个非负整数之和一定是非负整数，其中e＝0；对于偶数集和乘法运算，其中不存在满足要求的元素e；对于平面向量集合以及向量的加法运算，任意两个平面向量之和仍为该平面内的向量，e＝ ；对于二次三项式集合以及多项式的乘法，其中不存在满足要求的元素e；对于虚数集和复数的乘法运算，其中不存在满足要求的元素e，所以，集合G关于运算⊕为“融洽集”的是①和③．1.1.28 已知集合S＝{x|x＝m2＋n2，m，n∈Z}．求证：若a，b∈S，则ab∈S．解析由a，b∈S得存在整数p，q，r，s，使得a＝p2＋q2，b＝r2＋s2，则ab＝(p2＋q2)(r2＋s2)＝p2r2＋q2s2＋p2s2＋q2r2＝(pr＋qs)2＋(ps－qr)2，其中pr＋qs和ps－qr都是整数，所以，ab∈S．1.1.29 已知集合A＝{x|x＝12a＋8b，a，b∈Z}，B＝{y|y＝20c＋16d，c，d∈Z}．判断集合A与集合B之间存在什么关系，并说明理由．解析若y∈B，即y＝20c＋16d＝12c＋8(c＋2d)，因为c，d∈Z，则有c＋2d∈Z，得y∈A，于是B⊆A；若x∈A，则x＝12a＋8b＝60a－48a＋40b－32b＝20(3a＋2b)＋16(－3a－2b)，因为a，b∈Z，则有3a＋2b，－3a－2b∈Z，于是A⊆B．所以，A＝B．1.1.30 若f(x)＝x2＋ax＋b，a，b∈R，A＝{x|x＝f(x)，x∈R}，B＝{x|x＝f[f(x)]，x∈C}．(1) 写出集合A与B之间的关系，并证明；(2) 当A＝{－1，3}时，用列举法表示集合B．解析(1) 任取x∈A，则f(x)＝x，于是，f [ f(x)]＝f(x)＝x，即有x∈B，所以有A⊆B，但由于x＝f[f(x)]必为四次方程，在复数集C上有4个根，所以A B．(2) 当A＝{－1，3}时，即方程x2＋ax＋b＝x的两根为－1、3，于是－1＋3＝－(a－1)，(－1 × ＝b，所以a＝－1，b＝－3，即f(x)＝x2－x－3，此时，集合B中的方程为(x2－x－3)2－(x2－x－3)－3＝x，即(x2－x－3)2－x2＝0，(x2－3)(x2－2x－3)＝0，所以，B＝{－1，3， ，－}．1.1.31 已知A＝{(x，y)|x2＋y2＋4x＋4y＋7＝0，x，y∈R}，B＝{(x，y)|xy＝－10，x，y∈R}．(1) 对于直线m和直线外的一点P，用“m上的点与点P距离的最小值”定义点P到直线m的距离与原有的点线距离概念是等价的．试以类似的方式给出一个点集A与B的“距离”的定义；(2) 依照(1)中的定义求出A与B的“距离”．解析(1) 定义：在点集A，B中分别任取一点，所取两点间的距离若有最小值，则此最小值称为点集A与B的“距离”．(2) 集合A中的点构成一个圆，其方程是(x＋2)2＋(y＋2)2＝1，圆心C(－2，－2)，半径为1，设P(x，y)为曲线xy＝－10上任意一点，则|PC|2＝(x＋2)2＋(y＋2)2＝x2＋y2＋4(x＋y)＋8＝(x＋y)2－2xy＋4(x＋y)＋8＝(x＋y)2＋4(x＋y)＋28＝(x＋y＋2)2＋24．当且仅当＋＋ ＝ ，＝－1 ，即＝－1＋11，＝－1－11或＝－1－11，＝－1＋11时，|PC最小值＝24，|PC|最小值＝2 ，所以，A与B的“距离”为2 －1．二、集合的运算1.1.32 已知全集I＝{a1，a2，a3，a4，a5，a6}，集合A＝{a1，a3，a4，a5}，B＝{a1，a4}，则A∩∁I B＝( )．(A) {a1，a4} (B) {a2，a6}(C) {a3，a5} (D) {a2，a3，a5，a6}解析∁I B＝{a2，a3，a5，a6}，所以，A∩∁I B＝{a3，a5}，答案为C．1.1.33 若集合M＝{x||x|≤2}，N＝{x|x2－3x＝0}，则M∩N＝( )．(A) {3} (B) {0} (C) {0，2} (D) {0，3}解析M＝[－2，2]，N＝{0，3}，所以M∩N＝{0}，答案为B．1.1.34 设A，B，I均为非空集合，且满足A⊆B⊆I，则下列各式中错误的是( )．(A) (∁I A)∪B＝I(B) (∁I A)∪(∁I B)＝I(C) A∩ ∁I B)＝∅(D) (∁I A ∩ ∁I B)＝(∁I B)解析集合A，B，I的关系如图所示，可知(∁I A)∪(∁I B)＝∁I A≠I，所以，答案为B．1.1.35 设全集I＝{2，3，5}，A＝{|a－5|，2}，∁I A＝{5}，则a的值为( )．(A) 2 (B) 8 (C) 2或8 (D) －2或题1.1.348解析由A∪∁I A＝I得|a－5|＝3，所以a＝2或8，答案为C．1.1.36 设集合M＝{x|a1x2＋b1x＋c1＝0}，N＝{x|a2x2＋b2x＋c2＝0}，则方程(a1x2＋b1x＋c1)(a2x2＋b2x＋c2)＝0的解集是( )．(A) M∩N(B) M∪N(C) N(D) M解析由(a1x2＋b1x＋c1)(a2x2＋b2x＋c2)＝0可得(a1x2＋b1x＋c1)＝0或(a2x2＋b2x＋c2)＝0，所以，该方程的解集是M∪N，答案为B．1.1.37 若集合M＝{(x，y)|x＋y＝0}，P＝{(x，y)|x－y＝2}，则M∩P＝( )．(A) (1，－1) (B) {x＝1}∪{y＝－1}(C) {1，－1} (D) {(1，－1)}解析由＋＝ ，－＝ ，得＝1，＝－1，所以，M∩P＝{(1，－1)}，答案为D．1.1.38 满足M⊆{a1，a2，a3，a4}，且M∩{a1，a2，a3}＝{a1，a2}的集合M的个数是( )．(A) 1 (B) 2 (C) 3 (D) 4解析由M∩{a1，a2，a3}＝{a1，a2}知a1、a2∈M，a3∉M，a4可以在集合M也可以不在集合M中，所以，满足要求的集合M的个数是2个．答案为B．1.1.39 若A，B，C为三个集合，A∪B＝B∩C，则一定有( )．(A) A⊆C(B) C⊆A(C) A≠C(D) A＝∅解析任取x∈A，则x∈A∪B＝B∩C，于是，x∈B∩C，则x∈C，所以，A⊆C，答案为A．1.1.40 已知A＝{x|x≤7}，B＝{x|x<2}，C＝{x|x>5}，则A∩B＝；A∪C＝；A∩B∩C＝．解析由已知得A∩B＝{x|x<2}，A∪C＝R，A∩B∩C＝∅．1.1.41 若集合A＝{x|－2<x<1或x>1}，B＝{x|a≤x≤b}满足A∪B＝{x|x>－2}，A∩B＝{x|1<x≤3}，则a＝；b＝．解析在数轴上画出集合A∪B和A∩B可得a＝1，b＝3．1.1.42 全集U的子集A、B、C的关系如图所示：其中三个圆分别表示集合A、B、C，试用集合A、B、C的运算结果表述图中的阴影所代表的集合：．解析图中的阴影部分表示集合∁U A∩B∩C．1.1.43 已知a>b>0，全集I＝R，集合M＝＋，N＝，P＝{x|b<x<}，则下列关系式中正确的是( )．(A) P＝M∩∁I N(B) P＝∁I M∩N 题1.1.41题1.1.42(C) P ＝M ∪N (D) P ＝M ∩N解析 由a >b >0得b < < ＋ <a ，将集合M ，N 表示在数轴上可知P ＝ M ∩∁I N ，答案为A ．1.1.44 对于集合A ，B ，C ，“A ∩C ＝B ∩C ”是“A ＝B ”的( )．(A) 充分不必要条件 (B) 必要不充分条件(C) 充要条件 (D) 既不充分也不必要条件解析 若A ＝B ，则显然有A ∩C ＝B ∩C ；反之，若C ＝{1}，A ＝{1，2}，B ＝{1，3}，此时A ∩C ＝B ∩C ＝{1}，但A ≠B ，所以，“A ∩C ＝B ∩C ”是“A ＝B ”的必要不充分条件，答案为B ．1.1.45 设全集I ＝{(x ，y )|x ，y ∈R}，集合M ＝ ， －－ ＝1 ，N ＝{(x ，y )|y ≠x ＋1}，那么∁I (M ∪N )＝( )．(A) ∅ (B) {(2，3)}(C) (2，3) (D) {(x ，y )|y ＝x ＋1}解析 集合I 表示平面上所有的点，集合M 表示直线y ＝x ＋1上除(2，3)外的所有点，集合N 表示不在直线y ＝x ＋1上的所有点，所以M ∪N 表示平面上除(2，3)外的所有点，所以，∁I (M ∪N )是集合{(2，3)}，答案为B ．1.1.46 若全集I ＝R ，f (x )，g (x )都是定义域为R 的函数，P ＝{x |f (x )<0}，Q ＝{x |g (x )≥0}，则不等式组 ，的解集用P ，Q 表示为 ． 解析 由已知可得不等式g (x )<0的解集是∁I Q ，所以，不等式组的解集是P ∩∁I Q ．1.1.47 设P 表示△ABC 所在平面上的点，则集合{P |PA ＝PB }∩{P |PB ＝PC }＝ ． 解析 由已知得点P 到△ABC 三顶点等距，所以，{P |PA ＝PB }∩{P |PB ＝PC }＝{△ABC 的外心}．1.1.48 集合A ＝{(x ，y )|ax ＋y ＝1}，B ＝{(x ，y )|x ＋ay ＝1}，C ＝{(x ，y )|x 2＋y 2＝1}，分别求使得集合(A ∪B ∩C 为含有两个元素和三个元素的集合的a 的值．解析 集合A 、B 分别表示过定点(0，1)和(1，0)的两条直线，集合C 表示单位圆，且(0，1)，(1，0)∈C ，若(A ∪B ∩C 含有两个元素，则两直线重合或同时与圆相切，可得a ＝1或a ＝0．若(A ∪B ∩C 含有三个元素，即表明两条直线与圆有且仅有三个公共点，由于两直线或同时与圆相切，或同时与圆不相切，则必须有上述两条直线的交点在圆上，两直线的交点是 11＋ ，11＋ ，则 11＋ ＋ 11＋＝1，所以，a ＝－1± ．1.1.49 若集合A 是一个有限集，我们以f (A )表示该集合中元素的个数．例如：f (∅)＝0，f ({a })＝1等等．(1) 已知集合M ＝{(x ，y )|y ＝x 2，x ∈R}，若集合N ＝{(x ，y )|y ＝b }，其中b 是实常数，求f (M ∩N )的值；(2) 已知集合M ＝{(x ，y )|y ＝x 2，x ∈Z}，若集合P ＝{(x ，y )|y ＝x ＋p }，其中p 是实常数，如果存在整数k 使得(k ，k 2)∈M ∩P ，求证：f (M ∩P )＝2．解析 (1) 若b <0，则f (M ∩N )＝0；若b ＝0，则f (M ∩N )＝1；若b >0，则f (M ∩N )＝2．(2) 由已知可得关于x 的方程x 2＝x ＋p 有一个根是k ，则k 2＝k ＋p ，即p ＝k 2－k ，于是，方程x 2＝x ＋p 即为x 2－x －(k －1)k ＝0，即(x －k )(x ＋k －1)＝0，解得x ＝k 或x ＝1－k ，所以，M ∩P ＝{(k ，k 2)，(1－k ，(1－k )2)}，由k 是整数得k ≠1－k ，则f (M ∩N )＝2．1.1.50 设全集为R ，A ＝{x |x 2－5x －6>0}，B ＝{x ‖x －5|<a }(a 是常数)，且11∈B ，则( )．(A) ∁R A ∪B ＝R (B) A ∪∁R B ＝R(C) ∁R A ∪∁R B ＝R (D) A ∪B ＝R解析 集合A ＝{x |x >6或x <－1}，由11∈B 得|11－5|<a ，即a >6，集合B ＝(5－a ，5＋a )，此时5－a <－1，5＋a >6，所以，A ∪B ＝R ，答案为D ．1.1.51 已知P ＝{y |y ＝x 2＋1，x ∈R}，Q ＝{y |y ＝x ＋1，x ∈R}，则P ∩Q ＝( )．(A) {(0，1)，(1，0)} (B) {0，1}(C) {1，2} (D) {y |y ≥1}解析 集合P ，Q 分别是函数y ＝x 2＋1，y ＝x ＋1的值域，于是P ＝[1，＋∞ ，Q ＝R ，所以P ∩Q ＝[1，＋∞ ，答案为D ．1.1.52 设A 、B 是两个非空集合，定义A 与B 的“差集”为A－B ＝{x |x ∈A ，且x ∉B }，则A －(A －B )＝( )．(A) B (B) A ∩B (C) A ∪B (D) A解析 由“差集”的定义可知集合A –B 如图中阴影部分所示，所以，A －(A －B )＝A ∩B ，答案为B ．1.1.53 已知全集U ＝A ∪B 中有m 个元素，(∁U A )∪(∁U B )中有n个元素，若A ∩B 非空，则A ∩B 的元素个数为( )．(A) mn (B) m ＋n (C) n －m (D) m －n解析 由文氏图可得A ∩B 的元素个数为m －n ，答案为D ．1.1.54 设全集U ＝N *，集合A ＝{x |x ＝2n ，n ∈N *}，B ＝{x |x ＝3n ，n ∈N *}，则∁U (A ∪B )＝( )．(A) {x |x ＝6n ，n ∈N *} (B) {x |x ＝6n ±1，n ∈N *}(C) {x |x ＝6n ± ，n ∈N *} (D) {x |x ＝6n ± ，n ∈N *}解析 对于x ＝2n ，n ∈N *，若n ＝3k (k ∈N *)，则x ＝6k ；若n ＝3k －1 (k ∈N *)，则x＝6k －2；若n ＝3k －2 (k ∈N *)，则x ＝6k －4，对于x ＝3n ，若n ＝2k (k ∈N *)，则x ＝6k ；若n ＝2k －1 (k ∈N *)，则x ＝6k －3，所以，∁U (A ∪B )＝ {x |x ＝6n ±1，n ∈N *}，答案为B ．1.1.55 我们称(P ，Q )为“有序集合对”，其中P ，Q 是集合，当P ≠Q 时，认为(P ，Q )与(Q ，P )是两个不同的“有序集合对”．那么，使得A ∪B ＝{a ，b }成立的“有序集合对”(A ，B )共有( )个．(A) 9 (B) 4 (C) 7 (D) 16解析 若A ＝∅，则只能B ＝{a ，b }；若A ＝{a }，则B 可以为{b }或{a ，b }；若A ＝{b }，则B 可以为{a }或{a ，b }；若A ＝{a ，b }，则B 可以是∅，{a }，{b }，{a ，b }这四个集合中的某一个，所以，使得A ∪B ＝{a ，b }成立的“有序集合对”(A ，B )共有9个，答案为A ． 题1.1.52题1.1.531.1.56 有限集合S 中元素的个数记做card(S )．设A ，B 都为有限集合，给出下列命题：① A ∩B ＝∅的充要条件是card(A ∪B )＝card(A )＋card(B )；② A ⊆B 的必要条件是card(A )≤card(B )；③ A ⊈B 的充分条件是card(A )≤card(B )；④ A ＝B 的充要条件是card(A )＝card(B )，其中真命题的序号是( )．(A) ③，④ (B) ①，② (C) ①，④ (D) ②，③解析 用文氏图可知，当A ∩B ＝∅时，必有card(A ∪B )＝card(A )＋card(B )．反之，若card(A ∪B )＝card(A )＋card(B )，也必有A ∩B ＝∅．于是，card(A ∪B )＝card(A )＋card(B )是A ∩B ＝∅的充要条件；若A ⊆B ，则card(A )≤card(B )；反之，当card(A )≤card(B )时，未必有A ⊆B ，于是，card(A )≤card(B )是A ⊆B 的必要条件；当card(A )≤card(B )时，有可能有A ⊆B ，于是，card(A )≤card(B )是A ⊈B 的既不充分，也不必要条件；card(A )＝card(B )是A ＝B 的必要不充分条件，所以，答案为B ．1.1.57 若非空集合A ，B ，C 满足A ∪B ＝C ，且B 不是A 的子集，则( )．(A) x ∈C 是x ∈A 的充分条件但不是必要条件(B) x ∈C 是x ∈A 的必要条件但不是充分条件(C) x ∈C 是x ∈A 的充要条件(D) x ∈C 既不是x ∈A 的充分条件，也不是x ∈A 的必要条件解析 若x ∈A ，则一定有x ∈A ∪B ＝C ，于是，x ∈C 是x ∈A 的必要条件；如果x ∈C ＝A ∪B 时必有x ∈A ，则C ⊆A ，即A ∪B ⊆A ，于是，任取y ∈B ⊆A ∪B ⊆A ，则y ∈A ，B ⊆A ，矛盾，所以，x ∈C 是x ∈A 的必要条件但不是充分条件，答案为B ．1.1.58 已知集合M ＝{2，3，m 2＋4m ＋2}，P ＝{0，7，m 2＋4m －2，2－m }满足M ∩P ＝{3，7}，则实数m 的值是 ．解析 由已知得7∈M ，则m 2＋4m ＋2＝7，解得m ＝1或m ＝－5．若m ＝1，则m 2＋4m －2＝3，2－m ＝1．若m ＝－5，2－m ＝7，与集合中元素的互异性矛盾，所以，m 的值是1．1.1.59 如果全集U ＝{a ，b ，c ，d ，e ，f }，A ＝{a ，b ，c ，d }，A ∩B ＝{a }，∁U (A ∪B )＝{f }，则B ＝ ．解析 由表示集合U，A ，B 的图形可得只有e ∈(∁U A ∩B ，所以，B ＝{a ，e }．1.1.60 如果全集U 含有12个元素，P ，Q 都是U 的子集，P ∩Q中含有2个元素，∁U P ∩∁U Q 含有4个元素，∁U P ∩Q 含有3个元素，则P 含有 个元素；Q 含有 个元素．解析 由表示集合U ，P ，Q 的图形可得P ，Q 中各有5个元素．1.1.61 集合A ＝{x |x ＝5k ＋3，k ∈N}， B ＝{x |x ＝7k ＋2，k ∈N}，则A ∩B 中的最小元素是 ．解析 由已知可得集合A ＝{3，8，13，18，23，28，33，…}， B ＝{2，9，16，23，题1.1.56 题1.1.59 题1.1.6030，…}，所以，A ∩B 中的最小元素是23．1.1.62 已知集合A ＝{x |－8≤x ≤6}，B ＝{x |x ≤m }，若A ∪B ≠B 且A ∩B ≠∅，则m 的取值范围是 ．解析 将集合A ，B 表示在数轴上可知m 的取值范围是－8≤m <6．1.1.63 已知常数a 是正整数，集合A ＝ － ＋1， ， B ＝{x ‖x |<2a ，x ∈Z}，则集合A ∪B 中所有元素之和为 ．解析 由|x －a |<a ＋1 可得－1 <x <2a ＋1 ，而x ∈Z ，于是，A ＝{0，1，2，3，…，2a －1，2a }，由|x |<2a 得－2a <x <2a ，又x ∈Z ，则B ＝{－(2a －1)，－(2a －2)，…，(2a －2)，(2a －1)}．于是，A ∪B ＝{－(2a －1)，－(2a －2)，…，－1，0，1，…，(2a －2)，(2a －1)，2a }，其中所有元素之和为2a ．1.1.64 我们将b －a 称为集合{x |a ≤x ≤b }的“长度”．若集合M ＝ ＋ ，N ＝ －1 ，且M 和N 都是集合{x |0≤x ≤1}的子集，则集合M ∩N 的“长度”的最小值是( )．(A) 1 (B) 1(C) (D) 解析 集合M 和N 的“长度”分别是和1 ，又M 和N 都是集合{x |0≤x ≤1}的子集，于是，当m ＝1，n ＝0时，集合M ∩N 的“长度”取得最小值1 －1 ＝11，答案为B ．1.1.65 已知集合A ＝{x |x 2＋(m ＋2)x ＋1＝0，x ∈R}，且A ∩R ＋＝∅，求实数m 的取值范围．解析 若A ＝∅，则Δ＝(m ＋2)2－4<0，解得－4<m <0；若A ≠∅，则由x 2＋(m ＋2)x ＋1＝0没有正数根得 ＋ － ，－ ＋ ， 1 ，解得m ≥0．所以，m 的取值范围是m >－4．1.1.66 若集合A ＝{x |x 2－2ax ＋a ＝0，x ∈R}，B ＝{x |x 2－4x ＋a ＋5＝0，x ∈R}．(1) 若A ＝B ＝∅，求a 的取值范围；(2) 若A 和B 中至少有一个是∅，求a 的取值范围；(3) 若A 和B 中有且仅有一个是∅，求a 的取值范围．解析 (1) 若A ＝∅，则4a 2－4a <0，解得0<a <1．若B ＝∅，则16－4(a ＋5)<0，解得a >－1，所以，使A ＝B ＝∅成立的a 的取值范围是0<a <1．(2) 设 A '＝(0，1)，B '＝(－1，＋∞ ，则使A 和B 中至少有一个是∅的实数a ∈ A '题1.1.62∪B'，即使A和B中至少有一个是∅的实数a的取值范围是a>－1．(3) 使A和B中有且仅有一个是∅的a∈[A'∩ ∁R B')]∪[(∁R A' ∩B']，所以，使A和B 中有且仅有一个是∅的a的取值范围是－1<a≤0或a≥1．§1–2 简易逻辑一、命题1.2.1 如果一个命题的逆命题是真命题，那么这个命题的( )．(A) 否命题必是真命题(B) 否命题必是假命题(C) 原命题必是假命题(D) 逆否命题必是真命题解析一个命题的逆命题与否命题真假相同，答案为A．1.2.2 命题“对任意的x∈R，x3－x2＋1≤0”的否定是( )．(A) 不存在x∈R，x3－x2＋1≤0(B) 存在x∈R，x3－x2＋1≤0(C) 存在x∈R，x3－x2＋1>0(D) 对任意的x∈R，x3－x2＋1>0解析“对任意的x∈R，x3－x2＋1≤0”的否定是“存在x∈R，使得x3－x2＋1>0”，答案为C．1.2.3 与命题“若a∉M，则b∉M”等价的命题是( )．(A) 若b∈M，则a∉M(B) 若b∉M，则a∈M(C) 若b∈M，则a∈M(D) 若a∉M，则b∈M解析逆否命题与原命题互为等价命题，原命题的逆否命题为“若b∈M，则a∈M”，所以，答案为C．1.2.4 设f(x)是定义在正整数集上的函数，且f(x)满足：“当f(k)≥k2成立时，总可以推出f(k＋1)≥(k＋1)2成立”，那么，下列命题总成立的是( )．(A) 若f(3)≥9成立，则当k≥1时，均有f(k)≥k2成立(B) 若f(5)≥25成立，则当k≤5时，均有f(k)≥k2成立(C) 若f(7)<49成立，则当k≥8时，均有f(k)<k2成立(D) 若f(4)＝25成立，则当k≥4时，均有f(k)≥k2成立解析由25>16得f(4)＝25使得f(4)≥42成立，由已知可得当k≥4时，均有f(k)≥k2成立，答案为D．1.2.5 命题“若x2<1，则－1<x<1”的逆否命题是( )．(A) 若x2≥1，则x≥1或x≤－1 (B) 若－1<x<1，则x2<1(C) 若x>1或x<－1，则x2>1 (D) 若x≥1或x≤－1，则x2≥1解析命题“若x2<1，则－1<x<1”的逆否命题是“若x≥1或x≤－1，则x2≥1”，答案为D．1.2.6 在原命题“若A∪B≠B，则A∩B≠A”与它的逆命题、否命题、逆否命题这四个命题中，真命题的个数是．解析原命题的逆否命题为“若A∩B＝A，则A∪B＝B”．当A∩B＝A时，任取x∈A ＝A∩B，必有x∈B，则A⊆B，必有A∪B＝B成立，所以，逆否命题和原命题都是真命题．原命题的否命题为“若A∪B＝B，则A∩B＝A”，同上，可知否命题和逆命题也都是真命题．所以，在这四个命题中，真命题的个数是4．1.2.7 若a，b都是非零实数，证明：|a|＋|b|＝|a＋b|与ab>0等价．解析若|a|＋|b|＝|a＋b|，则(|a|＋|b|)2＝|a＋b|2，a2＋b2＋2|a||b|＝a2＋b2＋2ab，于是，|ab|＝ab，可得ab>0；若ab>0，则，或，，于是，|a|＋|b|＝|a＋b|．所以，当a，b都是非零实数时，|a|＋|b|＝|a＋b|与ab>0等价．1.2.8 已知A和B都是非空集合，证明：“A∪B＝A∩B”与“A＝B”是等价的．解析若A∪B＝A∩B，则任取x∈A，必有x∈A∪B＝A∩B，于是，x∈A∩B，则x∈B，所以，A⊆B，同理可得B⊆A，于是，A＝B；若A＝B，则显然有A∪B＝A∩B，所以，“A∪B＝A∩B”与“A＝B”是等价的．1.2.9 已知a ，b ，c 是实数，则与“a ，b ，c 互不相等”等价的是( )．(A) a ≠b 且b ≠c (B) (a －b )(b －c )(c －a ≠(C) (a －b )2＋(b －c )2＋(c －a )2≠ (D) a 2，b 2，c 2互不相等解析 由于不相等关系不具有传递性，当a ≠b 且b ≠c ，a 与c 可能相等；由(a －b )2＋(b －c )2＋(c －a )2≠ 可得a ＝b ，b ＝c ，c ＝a 中至少有一个不成立，即(a－b )2＋(b －c )2＋(c －a )2≠ 等价于“a ，b ，c 不全相等”，而不能等价于“a ，b ，c 互不相等”；a ＝－1，b ＝0，c ＝1，此时a ，b ，c 互不相等，但a 2＝c 2，所以，“a ，b ，c 互不相等”与“a 2，b 2，c 2互不相等”不是等价的；a ≠b 等价于a －b ≠ ，“a ，b ，c 互不相等”等价于a －b ≠ ，b －c ≠ ，c －a ≠ 同时成立，所以，“a ，b ，c 互不相等”与“(a －b )(b －c )(c －a ≠ ”等价，答案为B ．1.2.10 命题“若ab ＝0，则a 、b 中至少有一个为零”的逆否命题为 ．解析 原命题的逆否命题为“若a 、b 均不为零，则ab ≠ ”．1.2.11 给出下列四个命题：① 若x 2＝y 2，则x ＝y ；② 若x ≠y ，则x 2≠y 2；③ 若x 2≠y 2，则x ≠y ；④ 若x ≠y 且x ≠－y ，则x 2≠y2，其中真命题的序号是 ．解析 由x 2＝y 2可得x ＝y 或x ＝－y ，命题①不成立；若x ＝－y ≠ ，此时x ≠y ，而x 2＝y 2，于是，命题②不成立；若x 2≠y 2时有x ＝y ，则可得x 2＝y 2，矛盾，于是，命题③成立；对于x ≠y 且x ≠－y ，如果x 2＝y 2，则有x ＝y 或x ＝－y ，即x ＝y 与x ＝－y 至少有一个成立，矛盾，于是，命题④成立．所以，上述四个命题中，真命题的序号是③和④．1.2.12 已知命题p ：方程x 2＋mx ＋1＝0有两个不等的负实根．命题q ：方程4x 2＋4(m －2)x ＋1＝0没有实根．若“p 或q ”为真，“p 且q ”为假，求实数m 的取值范围．解析 当命题p 为真时，应有 － ，－ ， 1 ，解得m >2．当命题q 为真时，应有Δ＝16(m －2)2－16<0，解得1<m <3．于是，使“p 或q ”为真的m 的取值范围是m >1，使“p 且q ”为假的m 的取值范围是m ≤2或m ≥3，所以，使两者同时成立的m 的取值范围是m ≥3或1<m ≤2．1.2.13 某人要在一张 × 的表格中填入9个数(填的数有正有负)，他要使得表中任意一行的三个数之和为正，而任意一列的三个数之和为负．求证：他一定不能写出满足要求的数表．解析 若此人能写出满足要求的数表，则由a 11＋a 12＋a 13>0，a 21＋a 22＋a 23>0，a 31＋a 32＋a 33>0可得数表中的九个数之和为正；同时，又有a 11＋a 21＋a 31<0，a 12＋a 22＋a 32<0，a 13＋a 23＋a 33<0，则数表中的九个数之和为负，矛盾，所以，此人一定不能写出满足要求的数表．1.2.14 设a ，b ∈R ，A ＝{(x ，y )|y ＝ax ＋b ，x ∈Z}，B ＝{(x ，y )|y ＝3x 2＋15，x ∈Z}，C ＝{(x ，y )|x 2＋y 2≤144}都是平面xOy 内的点的集合．求证：不存在a ，b ，使得A ∩B ≠∅，且点(a ，b )∈C 同时成立．解析 设满足要求的a ，b 存在，则P (a ，b )∈C ，即a 2＋b 2≤144．由＝＋，＝＋1 ，得ax＋b－(3x2＋15)＝0，在aOb平面内，原点到直线ax＋b－(3x2＋15)＝0的距离是＋1＝3＋1≥12，其中等号当且仅当3＋1，即x2＝3时成立，但它与x∈Z矛盾，所以，使A∩B≠∅成立的(a，b)必有＋>12，与a2＋b2≤144矛盾，所以，满足要求的a，b不存在．1.2.15 中学数学中存在许多关系，比如“相等关系”，“平行关系”等等，如果集合A中元素之间的一个关系“~”满足以下三个条件：(1) 自反性：对于任意a∈A，都有a~a；(2) 对称性：对于a，b∈A，若a~b，则有b~a；(3) 传递性：对于a，b，c∈A，若a~b，b~c，则有a~c，则称“~”是集合A的一个等价关系，例如：“数的相等”是等价关系，而“直线的平行”不是等价关系(自反性不成立)，请你再列出三个等价关系：．解析由集合、角、向量的性质可知，“集合相等”、“角相等”、“向量相等”都是满足要求的等价关系．1.2.16 已知函数f(x)在R上是增函数，a，b∈R．写出命题“若a＋b>0，则f(a)＋f(b)>f(－a)＋f(－b)”的逆命题，并判断其真假．若所写命题是真命题，给出证明；若所写命题是假命题，给出反例．解析所求逆命题为：已知函数f(x)在R上是增函数，a，b∈R．若f(a)＋f(b)>f(－a)＋f(－b)，则a＋b>0．该命题是真命题．证明如下：若a＋b≤0，即a≤－b，由函数f(x)在R上是增函数得f(a)≤f(－b)，同理f(b)≤f(－a)，由此可得f(a)＋f(b)≤f(－a)＋f(－b)，与已知条件矛盾．所以，a＋b>0．二、充分条件和必要条件1.2.17 两个圆“周长相等”是“面积相等”的( )．(A) 充分不必要条件(B) 必要不充分条件(C) 充要条件(D) 既不充分也不必要条件解析两个圆周长相等，则由 πr1＝ πr2得两圆半径r1＝r2，则两圆面积相等，反之亦然，所以，两个圆“周长相等”是“面积相等”的充要条件，答案为C．1.2.18 P：四边形四条边长相等，Q：四边形是平行四边形，则P是Q的( )．(A) 充分不必要条件(B) 必要不充分条件(C) 充要条件(D) 既不充分也不必要条件解析当四边形的四条边长相同时，它是菱形，一定是平行四边形；反之，一个平行四边形的四条边长不一定都相等，所以，P是Q的充分不必要条件，答案为A．1.2.19 已知a，b，c，d都是实数，则“a＝b且c＝d”是“a＋c＝b＋d”的( )．(A) 充分不必要条件(B) 必要不充分条件(C) 充要条件(D) 既不充分也不必要条件解析 对于实数a ，b ，c ，d ，如果a ＝b 且c ＝d ，则有a －b ＝0，c －d ＝0，则a ＋c －(b ＋d )＝(a －b )＋(c －d )＝0，于是，a ＋c ＝b ＋d ；反之，如果a ＝1，b ＝2，c ＝4，d ＝3，有a ＋c ＝b ＋d ，但此时a ≠b ，c ≠d ，所以，“a ＝b 且c ＝d ”是“a ＋c ＝b ＋d ”的充分不必要条件，答案为A ．1.2.20 已知a ，b ，c 是实数，则“a ＝b ”是“ac ＝bc ”的( )．(A) 充分不必要条件 (B) 必要不充分条件(C) 充要条件 (D) 既不充分也不必要条件解析 如果a ＝b ，则a －b ＝0，于是，ac －bc ＝(a －b )c ＝0，可得ac ＝bc ；反之，如果c ＝0，a ＝1，b ＝2，此时有ac ＝bc ，但a ≠b ，所以，“a ＝b ”是“ac ＝bc ”的充分不必要条件，答案为A ．1.2.21 设m ，n 是整数，则“m ，n 均为偶数”是“m ＋n 是偶数”的( )．(A) 充分不必要条件 (B) 必要不充分条件(C) 充要条件 (D) 既不充分也不必要条件解析 如果m ，n 均为偶数，则m ＋n 一定是偶数；反之，如果m ＝1，n ＝3，m ＋n ＝4为偶数，但此时m 和n 都不是偶数，所以，“m ，n 均为偶数”是“m ＋n 是偶数”的充分而不必要条件，答案为A ．1.2.22 设集合A ，B 是全集U 的两个子集，则A B 是∁U A ∪B ＝U的( )．(A) 充分不必要条件(B) 必要不充分条件(C) 充要条件(D) 既不充分也不必要条件 解析 由表示集合U ，A ，B 关系的图形可知当A B 时必有∁U A ∪B ＝U 成立，反之，当A ＝B 时，也有∁U A ∪B ＝U 成立，即A 是B 的真子集不是∁U A ∪B ＝U 成立的必要条件，所以，答案为A ．1.2.23 对于集合M 和P ，“x ∈M 或x ∈P ”是“x ∈M ∩P ”的( )．(A) 充分不必要条件(B) 必要不充分条件(C) 充要条件(D) 既不充分也不必要条件解析 由表示集合M ，P 的图形可知当x ∈M 或x ∈P 时不一定有x ∈M ∩P ，而当x ∈M ∩P 时必有x ∈M 或x ∈P ，所以，“x ∈M 或x ∈P ”是“x ∈M ∩P ”的必要不充分条件，答案为B ．1.2.24 如果x ，y 是实数，那么“cos x ＝cos y ”是“x ＝y ”的( )．(A) 充分不必要条件 (B) 必要不充分条件(C) 充要条件 (D) 既不充分也不必要条件题1.2.22题1.2.23解析 当cos x ＝cos y 时，不一定有x ＝y 如 ＝π ， ＝－π，而当x ＝y 时，必有 cos x ＝cos y ，所以，“cos x ＝cos y ”是“x ＝y ”的必要不充分条件，答案为B ．1.2.25 使不等式(1－|x |)(1＋x )>0成立的充要条件为( )．(A) x <－1或x >1 (B) －1<x <1(C) x >－1且x ≠1 (D) x <1且x ≠－1解析 此不等式等价于 1＋ ，1－ 或 1＋ ， 1－ ，解得－1<x <1或x <－1，即为x <1且x ≠－1，所以，答案为D ．1.2.26 一元二次方程ax 2＋bx ＋c ＝0有一个正数根和一个负数根的充要条件是( )．(A) ab >0 (B) ab <0 (C) ac >0 (D) ac <0 解析 若一元二次方程ax 2＋bx ＋c ＝0有一个正数根x 1和一个负数根x 2，则x 1x 2＝ <0，则ac <0；反之，若ac <0，一元二次方程的判别式Δ＝b 2－4ac >0，此方程一定有两个实数根，且两根之积为<0，这两个实数根一定是一个正数和一个负数，所以，一元二次方程ax 2＋bx ＋c ＝0有一个正数根和一个负数根的充要条件是ac <0，答案为D ．1.2.27 “x >1”是“1 <1”的( )．(A) 充分不必要条件(B) 必要不充分条件 (C) 充要条件 (D) 既不充分也不必要条件 解析 若x >1，则1 －1＝1－ <0，即1 <1；反之，如果x <0，则有1<1，此时，x >1不成立，所以，“x >1”是“1 <1”的充分不必要条件，答案为A ．1.2.28 已知x 是实数，则“x ≠1”是“x 2－4x ＋ ≠ ”的( )．(A) 充分不必要条件 (B) 必要不充分条件(C) 充要条件 (D) 既不充分也不必要条件解析 如果x ＝3，则x ≠1，此时x 2－4x ＋3＝(x －1)(x －3)＝0；反之，如果x 2－4x ＋≠ ，即(x －3)(x －1 ≠ ，则x ≠ 且x ≠1，所以，“x ≠1”是“x 2－4x ＋ ≠ ”的必要不充分条件，答案为B ．1.2.29 “一个正整数的个位数字是5”是“这个正整数是5的倍数”的( )．(A) 充分不必要条件 (B) 必要不充分条件(C) 充要条件 (D) 既不充分也不必要条件解析 如果一个正整数的个位数是5，即此正整数一定可表示成10k ＋5(k 是非负整数)，它一定是5的倍数；反之，可写成10n (n 是正整数)的正整数一定是5的倍数，但它的个位数不是5，所以，“一个正整数的个位数字是5”是“这个正整数是5的倍数”的充分不必要条件，答案为A ．1.2.30 对于集合A ，B ，下列四个命题中正确的是( )．。

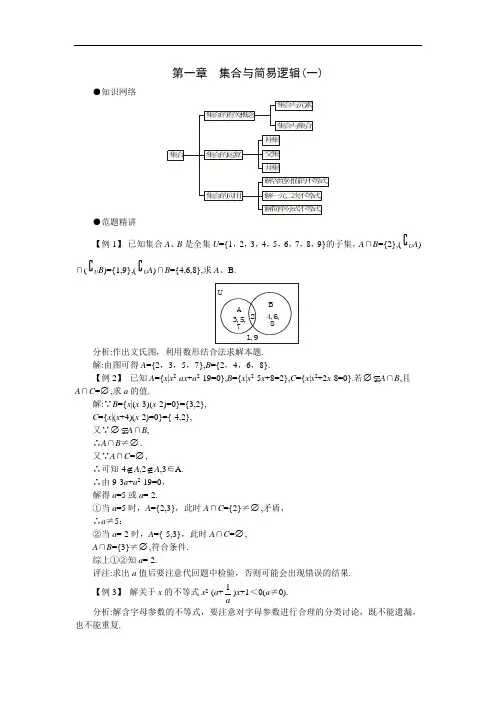
第一章 集合与简易逻辑(一)●知识网络集合集合的有关概念集合与元素补集解含绝对值的不等式并集解简单分式不等式集合与集合交集解一元二次不等式集合的运算集合的应用●范题精讲【例1】 已知集合A 、B 是全集U ={1，2，3，4，5，6，7，8，9}的子集，A ∩B ={2},(U A )∩(U B )={1,9},(U A )∩B ={4,6,8},求A 、B.UAB 4,6,83,5, 721,9分析:作出文氏图，利用数形结合法求解本题.解:由图可得A ={2，3，5，7},B ={2，4，6，8}.【例2】 已知A ={x |x 2-ax +a 2-19=0},B ={x |x 2-5x +8=2},C ={x |x 2+2x -8=0}.若∅A ∩B ,且 A ∩C =∅,求a 的值.解:∵B ={x |(x -3)(x -2)=0}={3,2}, C ={x |(x +4)(x -2)=0}={-4,2}, 又∵∅A ∩B , ∴A ∩B ≠∅. 又∵A ∩C =∅,∴可知-4∉A ,2∉A ,3∈A. ∴由9-3a +a 2-19=0， 解得a =5或a =-2.①当a =5时，A ={2,3}，此时A ∩C ={2}≠∅,矛盾， ∴a ≠5；②当a =-2时，A ={-5,3}，此时A ∩C =∅, A ∩B ={3}≠∅,符合条件. 综上①②知a =-2.评注:求出a 值后要注意代回题中检验，否则可能会出现错误的结果.【例3】 解关于x 的不等式x 2-(a +a1)x +1＜0(a ≠0). 分析:解含字母参数的不等式，要注意对字母参数进行合理的分类讨论，既不能遗漏，也不能重复.解:原不等式化为(x -a )(x -a1)＜0, ∴相应方程的根为a 、a1. 当a ＞a 1，即-1＜a ＜0或a ＞1时，解集为{x |a 1＜x ＜a }. 当a =a 1，即a =±1时，解集为∅.当a ＜a 1，即0＜a ＜1或a ＜-1时，解集为{x |a ＜x ＜a1 }.综上，当-1＜a ＜0或a ＞1时，解集为{x |a1＜x ＜a };当a =±1时，解集为∅；当0＜a ＜1或a ＜-1时，解集是{x |a1＜x ＜a }.评注:解含字母参数的不等式时，要弄清为何要分类讨论、分类讨论的标准是什么、如何分类讨论三个问题.【例4】 已知A ={x ||x -a |≤1},B ={x |3302x--x-x ≥0},且A ∩B =∅，求a 的取值范围.分析:先利用解含绝对值不等式的方法及积的符号法则解不等式，求出A 和B ，再利用数轴表示出A 和B (如下图所示)，得到A ∩B =∅时应满足的条件，从而求出a 的取值范围.解:A ={x ||x -a |≤1}={x |a -1≤x ≤a +1}.不等式3302x--x-x ≥0,即()()356x-x x +-≥0, 其解集是⎩⎨⎧≥+>05)6)(-(0,3-x x x 与⎩⎨⎧≤+-<-0)5)(6(,03x x x 的解集的并集.解得不等式3302x--x-x ≥0的解集是{x |x ≥6}∪{x |-5≤x ＜3}={x |x ≥6或-5≤x ＜3}.所以B ={x |-5≤x ＜3或x ≥6}. 要使A ∩B =∅，必须满足a +1＜-5或⎩⎨⎧<+≥-,61,31a a即a ＜-6或4≤a ＜5.所以，满足条件的a 的取值范围是a ＜-6或4≤a ＜5.评注:将集合A 、B 都标在数轴上，借助于图形直观性找到需满足的条件，再转化为与之等价的关于a 的不等式组.这种数形结合的数学思想很重要.●试题详解高中同步测控优化训练(一) 第一章 集合与简易逻辑(一)(A 卷)说明：本试卷分为第Ⅰ、Ⅱ卷两部分，请将第Ⅰ卷选择题的答案填入题后括号内，第Ⅱ卷可在各题后直接作答.共100分，考试时间90分钟.第Ⅰ卷(选择题 共30分)一、选择题(本大题共10小题，每小题3分，共30分)1.已知A ={x |x ≤32,x ∈R },a =5,b =23,则A.a ∈A 且b ∉AB.a ∉A 且b ∈AC.a ∈A 且b ∈AD.a ∉A 且b ∉A 答案:C2.设集合U ={1,2,3,4,5},A ={1,2,3},B ={2,5},则A ∩(U B )等于A.{2}B.{2,3}C.{3}D.{1,3} 解析:∵U ={1,2,3,4,5},B ={2,5}, ∴U B ={1,3,4}.∴A ∩(U B )={1,3}.答案:D3.已知集合S={a ,b ,c }中的三个元素是△ABC 的三边长,那么△ABC 一定不是 A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形 解析:由于集合中的元素是互异的,所以a 、b 、c 互不相等,即△ABC 一定不是等腰三角形. 答案:D4.集合A ={x ∈R |x (x -1)(x -2)=0}，则集合A 的非空子集的个数为A.4B.8C.7D.6解析:集合A ={0，1，2}，共有23=8个子集，其中非空子集有7个，故选C.这里特别注意{0}≠∅.答案:C5.已知集合A ={x ||2x +1|>3},B ={x |x 2+x -6≤0},则A ∩B 等于A.(-3,-2］∪(1,+∞)B.(-3,-2］∪［1,2)C.［-3,-2)∪(1,2］D.(-∞,-3］∪(1,2］ 解析:A ={x ||2x +1|>3}={x |2x +1>3或2x +1<-3}={x |x >1或x <-2}, B ={x |x 2+x -6≤0}={x |-3≤x ≤2}(如下图).答案:C6.已知集合P ={x |x 2=1}，集合Q ={x |ax =1},若Q ⊆P ，那么a 的值是A.1B.-1C.1或-1D.0，1或-1解析:因为由x 2=1得x =±1，所以P ={-1,1}.又因为Q ⊆P ，所以分Q =∅和Q ≠∅两种情况讨论.(1)若Q =∅，则a =0；(2)若Q ≠∅，则a ≠0，Q ={x |x =a1}，所以a =-1或1.综合(1)(2)可知，a 的值为0，1或-1. 答案:D7.设U 为全集，P 、Q 为非空集合，且P Q U .下面结论中不正确的是A.(U P )∪Q =UB.( U P )∩Q =∅ C.P ∪Q =Q D.P ∩(U Q )=∅UPQ解析:由文氏图知(U P )∩Q ≠∅.答案:B8.不等式组⎩⎨⎧>+>03,42a x x 的解集是{x |x ＞2}，则实数a 的取值范围是A.a ≤-6B.a ≥-6C.a ≤6D.a ≥6答案:B9.若|x +a |≤b 的解集为{x |-1≤x ≤5},那么a 、b 的值分别为A.2，-3B.-2，3C.3，2D.-3，2 答案:B10.设全集U =R ，集合E ={x |x 2+x -6≥0}，F ={x |x 2-4x -5＜0}，则集合{x |-1＜x ＜2}是A.E ∩FB.( U E )∩FC.(U E )∪(U F )D. U (E ∪F )解析:E ={x |x 2+x -6≥0}={x |x ≤-3或x ≥2}, F ={x |x 2-4x -5＜0}={x |-1＜x ＜5}. 借助数轴知{x |-1＜x ＜2}=(U E )∩F .答案:B第Ⅱ卷(非选择题 共70分)二、填空题(本大题共4小题，每小题4分，共16分)11.设T ={(x ,y )|ax +y -3=0},S ={(x ,y )|x -y -b =0}.若S ∩T ={(2,1)},则a =_______,b =_______.解析:由S ∩T ={(2,1)},可知⎩⎨⎧==1,2y x 为方程组⎩⎨⎧=--=-+0,03b y x y ax 的解，解得⎩⎨⎧==.1,1b a答案:1 112.已知集合M ={0,1,2},N ={x |x =2a ,a ∈M },则集合M ∩N =_______. 解析:∵M ={0,1,2},N ={x |x =2a ,a ∈M },∴N ={0,2,4}.∴M ∩N ={0,2}. 答案:{0,2}13.不等式1-x ax＜1的解集为{x |x ＜1或x ＞2}，则a 的值为________. 解析:由1-x ax＜1得［(a -1)x +1］(x -1)＜0，由不等式的解集为{x |x ＜1或x ＞2}知，1、2为方程［(a -1)x +1］(x -1)=0的两根，∴(a -1)×2+1=0.∴a = 21. 答案: 2114.不等式3)2(-+x x x <0的解集为_______. 解析:原不等式x (x +2)(x -3)<0.如下图,由数轴穿根法可知原不等式的解集为{x |0<x <3或x <-2}.答案:{x |0<x <3或x <-2}三、解答题(本大题共5小题，共54分.解答应写出文字说明、证明过程或演算步骤) 15.(本小题满分10分)已知集合A ={a ,a +b ,a +2b },B ={a ,ac ,ac 2}.若A =B ，求实数c 的值.解:若⎩⎨⎧=+=+22acb a ac b a ⇒a +ac 2-2ac =0, 所以a (c -1)2=0,即a =0或c =1.当a =0时，集合B 中的元素均为0，故舍去； 当c =1时，集合B 中的元素均相同，故舍去.若⎩⎨⎧=+=+acb a ac b a 22⇒2ac 2-ac -a =0. 因为a ≠0，所以2c 2-c -1=0, 即(c -1)(2c +1)=0. 又c ≠1，所以只有c =-21. 经检验，此时A =B 成立.综上所述c =-21. 16.(本小题满分10分)设集合A ={x ||x -a |<2},B ={x |212+-x x <1},若A ⊆B ,求实数a 的取值范围.解:A ={x |-2<x -a <2}={x |a -2<x <a +2},∵212+-x x <123+-x x <0(x +2)(x -3)<0-2<x <3,∴B ={x |-2<x <3}. 如下图,∵A ⊆B ,∴⎩⎨⎧≤+-≥-.32,22a a解得0≤a ≤1.17.(本小题满分10分)已知集合A ={x |x 2-3x +2=0},B ={x |x 2-ax +3a -5=0}.若A ∩B =B ，求实数a 的取值范围.解:A ={x |x 2-3x +2=0}={1,2},由x 2-ax +3a -5=0，知Δ=a 2-4(3a -5)=a 2-12a +20=(a -2)(a -10). (1)当2＜a ＜10时，Δ＜0,B =∅⊆A ;(2)当a ≤2或a ≥10时，Δ≥0，则B ≠∅. 若x =1，则1-a +3a -5=0,得a =2, 此时B ={x |x 2-2x +1=0}={1}⊆A ;若x =2，则4-2a +3a -5=0，得a =1, 此时B ={2,-1} A.综上所述，当2≤a ＜10时，均有A ∩B =B .18.(本小题满分12分)解不等式：(1)1＜|x -2|≤3;(2)|x -5|-|2x +3|＜1.分析:解含绝对值的不等式应根据绝对值的概念去掉绝对值符号，(2)中可采用零点分区间法去绝对值符号.(1)解法一:原不等式即⎪⎩⎪⎨⎧≤->-.32,12x x由①得x ＜1或x ＞3.由②得-1≤x ≤5(如图).所以原不等式的解集为{x |-1≤x ＜1或3＜x ≤5}.解法二:原不等式的解集是下面两个不等式组解集的并集.⎩⎨⎧≤-<≥-321,02x x 或⎩⎨⎧≤--<<-,3)2(1,02x x 即1＜x -2≤3或-3≤x -2＜-1,解得3＜x ≤5或-1≤x ＜1.所以原不等式组的解集为{x |-1≤x ＜1或3＜x ≤5}. (2)解:①当x ≥5时，原不等式可化为 (x -5)-(2x +3)＜1, 解得x ≥5.②当-32≤x ＜5时，原不等式可化为-(x -5)-(2x +3)＜1, 解得31＜x ＜5.① ②③当x ＜-32时，原不等式可化为 -(x -5)+(2x +3)＜1,解得x ＜-7. 综上可知，原不等式的解集为{x |x ＞31或x ＜-7}. 19.(本小题满分12分)已知U ={x |x 2-3x +2≥0},A ={x ||x -2|＞1},B ={x |21--x x ≥0},求A ∩B , A ∪B ,(U A )∪B ,A ∩(U B ).解:∵U ={x |x 2-3x +2≥0}={x |(x -2)(x -1)≥0}={x |x ≥2或x ≤1}, A ={x ||x -2|＞1}={x |x -2＞1或x -2＜-1}={x |x ＞3或x ＜1},B ={x |⎩⎨⎧≠-≥--020)2)(1(x x x }={x |x ＞2或x ≤1}.由图(1)可知,A ∩B ={x |x ＞3或x ＜1},A ∪B ={x |x ＞2或x ≤1}.图(1)由图(2)可知U A ={x |2≤x ≤3或x =1},易知U B ={x |x =2}.图(2)由图(3)可知,(U A )∪B ={x |x ≥2或x ≤1}=U .图(3)由图(4)可知,A ∩(U B )=∅.图(4)。

已知命题),0(012:,64:22>≥-+-≤-a a x x q x p 若非p 是q 的充分不必要条件，求a 的取值范围答案：.03a <≤来源：09年福建省福州市月考一题型：解答题，难度：容易求证：△ABC 是等边三角形的充要条件是a 2＋b 2＋c 2＝ab ＋ac ＋bc 。

这里a.b.c 是△ABC 的三条边。

答案：(必要性)∵△ABC 是等边三角形，且a.b.c 是其三边∴a=b=c ∴a 2+b 2+c 2=ab+ac+bc（充分性）a 2+b 2+c 2=ab+ac+bc21 (a 2+b 2)+ 21（a-c ）2+21 (b-c)2=0⇒(a-b)2+(a-c)2+(b-c)2=0 a=b=c ∵a.b.c 是△ABC 的三边∴△ABC 是等边三角形综上所述，△ABC 是等边三角形的充要条件是a 2＋b 2＋c 2＝ab ＋ac ＋bc来源：09年福建省福州市月考一题型：解答题，难度：中档设p:实数x 满足22430x ax a -+<,其中0a >,命题:q 实数x 满足2260,280.x x x x ⎧--≤⎪⎨+->⎪⎩. (Ⅰ)若1,a =且p q ∧为真，求实数x 的取值范围；(Ⅱ)若p ⌝是⌝q 的充分不必要条件,求实数x 的取值范围.答案：由22430x ax a -+<得(3)()0x a x a --<，又0a >,所以3a x a <<,当1a =时，1<3x <,即p 为真时实数x 的取值范围是1<3x <.由2260280x x x x ⎧--≤⎪⎨+->⎪⎩,得23x <≤,即q 为真时实数x 的取值范围是23x <≤. 若p q ∧为真，则p 真且q 真，所以实数x 的取值范围是23x <<. (Ⅱ) p ⌝是q ⌝的充分不必要条件，即p ⌝⇒q ⌝,且q⌝⇒/p ⌝,设A={|}x p ⌝,B={|}x q ⌝,则A B ,又A={|}x p ⌝={|3}x x a x a ≤≥或, B={|}x q ⌝={23x x ≤>或}，则0<2a ≤,且33a >所以实数a 的取值范围是12a <≤.来源：09年山东潍坊市月考一题型：解答题，难度：中档已知集合A={x | x 2-3 x +2=0}，B={ x | x 2-mx +2=0}，若A 是B 的必要不充分条件，求实数m 范围。

集合A ＝｛x ｜x 2－ax ＋a 2－19＝0｝，B ＝｛x ｜x 2－5 x ＋6＝0｝，C ＝｛x ｜x 2＋2 x －8＝0｝．（1）若A ∩B ＝A ∪B ，求a 的值；（2）若∅ A ∩B ，A ∩C ＝∅，求a 的值．答案：由已知，得B ＝｛2，3｝，C ＝｛2，－4｝.(1) A ∩B ＝A ∪B ， A ＝B于是2，3是一元二次方程x 2－ax ＋a 2－19＝0的两个根，由韦达定理知：⎩⎨⎧-=⨯=+1932322a a 解之得a ＝5. (2)由A ∩B ∅A ⇒∩≠B ∅，又A ∩C ＝∅，得3∈A ，2∉A ，－4∉A ，由3∈A ，得32－3a ＋a 2－19＝0，解得a ＝5或a=－2当a=5时，A ＝｛x ｜x 2－5x ＋6＝0｝＝｛2，3｝，与2∉A 矛盾；当a=－2时，A ＝｛x ｜x 2＋2x －15＝0｝＝｛3，－5｝，符合题意.来源：09年湖北宜昌月考一题型：解答题，难度：中档已知：集合A={x|532+-x x ≤0}， B={x|x 2－3x+2<0}，U=R ，求（1）A ∪B ；（2）（uA ）∩B.答案：A={x|532+-x x ≤0}={x|－5<x ≤23} B={x|x 2－3x+2<0}={x|1<x<2}（1）A ∪B={x|－5<x<2}（2）（uA ）={x|x ≤－5或x>23} （uA ）∩B={x|23<x<2}来源：09年湖北襄樊月考一题型：解答题，难度：中档已知全集U =R ，不等式202x x -<+的解集为A ，不等式21x -<的解集为B ． （I ）求A ，B ；（II ）求()U A B ．答案：（Ⅰ）由202-<+x x 得22x -<<.∴{}22A x x =-<<.由21x -<.得 13x <<.∴{}13B x x =<<. （Ⅱ）∵{}22A x x =-<<，U =R ，∴(][),22,U A =-∞-+∞. ∴()[)2,3U A B =.来源：09年北京海淀月考一题型：解答题，难度：容易 设},,{22Z y x y x a a M ∈-==，求证：（1）)(,12Z k M k ∈∈-；（2）)(,24Z k M k ∈∈-；（3）若M q M p ∈∈,，则.M pq ∈答案：（1）因为Z k k ∈-1,，且22)1(12--=-k k k ，所以.12M k ∈-（2）假设)(24Z k M k ∈∈-，则存在Z y x ∈,，使2224y x k -=-，由于y x -和y x +有相同的奇偶性，所以))((22y x y x y x +-=-是奇数或4的倍数，不可能等于24-k ，假设不成立，所以.24M k ∉-（3）设Z b a y x b a q y x p ∈-=-=,,,,,2222，则 ))((2222b a y x pq --=22222222a y b x b y a a --+=M ya xb yb xa ∈---=22)()(（因为Z ya xb Z ya xa ∈-∈-,）。

高中一年级数学集合与简易逻辑试题一、选择题（每小题 5 分，共 60 分）1、下列对象能构成集合的是（）A 高一年级视力较好的同学B 中国文学作品中著名的人物C 小于 8 的所有质数D 与 1 接近的数答案：C解析：选项 A 中“视力较好”没有明确的标准，不满足集合中元素的确定性；选项 B 中“著名”没有明确的界限，不满足集合中元素的确定性；选项 C 中小于 8 的质数有 2、3、5、7，是确定的，能构成集合；选项 D 中“与 1 接近”没有明确的标准，不满足集合中元素的确定性。

2、集合{1, 2, 3}的子集个数为（）A 6B 7C 8D 9答案：C解析：集合{1, 2, 3}的子集有∅，｛1}，｛2}，｛3}，｛1, 2}，｛1, 3}，｛2, 3}，｛1, 2, 3}，共 8 个。

3、设集合 A ＝｛x ｜－1 ＜ x ＜ 2}，B ＝｛x ｜ 0 ＜ x ＜ 3}，则 A ∪ B ＝（）A ｛x ｜－1 ＜ x ＜ 3}B ｛x ｜ 0 ＜ x ＜ 2}C ｛x ｜－1 ＜ x ＜ 0}D ｛x ｜ 2 ＜ x ＜ 3}答案：A解析：A ∪ B 表示 A 和 B 中所有元素组成的集合，所以 A ∪ B ＝｛x ｜－1 ＜ x ＜ 3}。

4、已知集合 A ＝｛1, 2, 3}，B ＝｛2, 3, 4}，则A ∩ B ＝（）A ｛1, 2, 3, 4}B ｛2, 3}C ｛1, 4}D ∅答案：B解析：A ∩ B 表示 A 和 B 中共有的元素组成的集合，所以A ∩ B＝｛2, 3}。

5、设全集 U ＝｛1, 2, 3, 4, 5}，集合 A ＝｛1, 2, 3}，B ＝｛2, 4}，则∁U（A ∩ B）＝（）A ｛1, 3, 4, 5}B ｛1, 2, 3, 4, 5}C ｛1, 3, 5}D ｛4, 5}答案：C解析：A ∩ B ＝｛2}，∁U（A ∩ B）表示在全集 U 中去掉A ∩ B 中的元素，所以∁U（A ∩ B）＝｛1, 3, 4, 5}。

已知命题),0(012:,64:22>≥-+-≤-a a x x q x p 若非p 是q 的充分不必要条件，求a 的取值范围答案：.03a <≤来源：09年福建省福州市月考一 题型：解答题，难度：容易若则,R a ∈“3>a ”是“方程x a y )9(22-=”表示开口向右的抛物线”的 A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案：A来源：07年浙江十校联考三 题型：选择题，难度：容易求证：△ABC 是等边三角形的充要条件是a 2＋b 2＋c 2＝ab ＋ac ＋bc 。

这里a.b.c 是△ABC 的三条边。

答案：(必要性)∵△ABC 是等边三角形，且a.b.c 是其三边 ∴a=b=c ∴a 2+b 2+c 2=ab+ac+bc （充分性）a 2+b 2+c 2=ab+ac+bc21 (a 2+b 2)+21（a-c ）2+21 (b-c)2=0⇒(a-b)2+(a-c)2+(b-c)2=0a=b=c ∵a.b.c 是△ABC 的三边∴△ABC 是等边三角形综上所述，△ABC 是等边三角形的充要条件是a 2＋b 2＋c 2＝ab ＋ac ＋bc来源：09年福建省福州市月考一 题型：解答题，难度：中档设p:实数x 满足22430x ax a -+<,其中0a >,命题:q 实数x 满足2260,280.x x x x ⎧--≤⎪⎨+->⎪⎩.(Ⅰ)若1,a =且p q ∧为真，求实数x 的取值范围； (Ⅱ)若p ⌝是⌝q 的充分不必要条件,求实数x 的取值范围.答案：由22430x ax a -+<得(3)()0x a x a --<， 又0a >,所以3a x a <<,当1a =时，1<3x <,即p 为真时实数x 的取值范围是1<3x <.由2260280x x x x ⎧--≤⎪⎨+->⎪⎩,得23x <≤,即q 为真时实数x 的取值范围是23x <≤. 若p q ∧为真，则p 真且q 真，所以实数x 的取值范围是23x <<. (Ⅱ) p ⌝是q ⌝的充分不必要条件，即p ⌝⇒q ⌝,且q ⌝⇒/p ⌝,设A={|}x p ⌝,B={|}x q ⌝,则AB ,又A={|}x p ⌝={|3}x x a x a ≤≥或, B={|}x q ⌝={23x x ≤>或}， 则0<2a ≤,且33a >所以实数a 的取值范围是12a <≤.来源：09年山东潍坊市月考一 题型：解答题，难度：中档已知集合A={x | x 2-3 x +2=0}，B={ x | x 2-mx +2=0}，若A 是B 的必要不充分条件，求实数m 范围。

集合A ＝｛x ｜x 2－ax ＋a 2－19＝0｝，B ＝｛x ｜x 2－5 x ＋6＝0｝，C ＝｛x ｜x 2＋2 x －8＝0｝．（1）若A ∩B ＝A ∪B ，求a 的值；（2）若∅ A ∩B ，A ∩C ＝∅，求a 的值．答案：由已知，得B ＝｛2，3｝，C ＝｛2，－4｝.(1) A ∩B ＝A ∪B ， A ＝B于是2，3是一元二次方程x 2－ax ＋a 2－19＝0的两个根，由韦达定理知：⎩⎨⎧-=⨯=+1932322a a 解之得a ＝5. (2)由A ∩B ∅A ⇒∩≠B ∅，又A ∩C ＝∅，得3∈A ，2∉A ，－4∉A ，由3∈A ， 得32－3a ＋a 2－19＝0，解得a ＝5或a=－2当a=5时，A ＝｛x ｜x 2－5x ＋6＝0｝＝｛2，3｝，与2∉A 矛盾；当a=－2时，A ＝｛x ｜x 2＋2x －15＝0｝＝｛3，－5｝，符合题意.来源：09年湖北宜昌月考一题型：解答题，难度：中档设A={-4，2a-1，a 2 }，B={a-5，1-a ，9}．若A∩B={9}，求a 的值．答案：解：∵A ∩B={9}，A={-4，2a-1，a 2 }，∴2a-1=9或a 2=9．解得a 1=5，a 2=3，a 3=-3．当a=5时，A={-4，9，25}，B={0，-4，9}．这时，A ∩B={-4，9}与已知A ∩B={9}矛盾，∴把a=5舍去．当a=3时，A={-4，5，9}，B={-2，-2，9}．由集合中元素的互异性，应把a=3舍去．当a=-3时，A={-4，-7，9}，B={-8，4，9}．A ∩B={9}符合要求．∴a=-3．来源：题型：证明题，难度：中档已知：集合A={x|532+-x x ≤0}， B={x|x 2－3x+2<0}，U=R ， 求（1）A ∪B ；（2）（uA ）∩B.答案：A={x|532+-x x ≤0}={x|－5<x ≤23} B={x|x 2－3x+2<0}={x|1<x<2} （1）A ∪B={x|－5<x<2}（2）（uA ）={x|x ≤－5或x>23} （uA ）∩B={x|23<x<2}来源：09年湖北襄樊月考一题型：解答题，难度：中档已知全集U =R ，不等式202x x -<+的解集为A ，不等式21x -<的解集为B ． （I ）求A ，B ；（II ）求()U A B ．答案：（Ⅰ）由202-<+x x 得22x -<<.∴{}22A x x =-<<. 由21x -<.得 13x <<.∴{}13B x x =<<.（Ⅱ）∵{}22A x x =-<<，U =R ，∴(][),22,U A =-∞-+∞. ∴()[)2,3U A B =.来源：09年北京海淀月考一题型：解答题，难度：容易 设},,{22Z y x y x a a M ∈-==，求证：（1）)(,12Z k M k ∈∈-；（2）)(,24Z k M k ∈∈-；（3）若M q M p ∈∈,，则.M pq ∈答案：（1）因为Z k k ∈-1,，且22)1(12--=-k k k ，所以.12M k ∈-（2）假设)(24Z k M k ∈∈-，则存在Z y x ∈,，使2224y x k -=-，由于y x -和y x +有相同的奇偶性，所以))((22y x y x y x +-=-是奇数或4的倍数，不可能等于24-k ，假设不成立，所以.24M k ∉-（3）设Z b a y x b a q y x p ∈-=-=,,,,,2222，则 ))((2222b a y x pq --=22222222a y b x b y a a --+=M ya xb yb xa ∈---=22)()(（因为Z ya xb Z ya xa ∈-∈-,）。

高中数学题库A集合与简易逻辑命题及其关系已知k ∈{a -1<a <1,且a ≠0},设命题p:y=kx +2008的值随x 的增大而增大；命题q:不等式x +|x －2k |>1的解集为R.当命题p.q 有且只有一个正确时，求实数k 的取值范围。

答案：将已知条件转化为等价的简单不等式.首先研究q:因为x+|x －2k|=⎩⎨⎧<≥-)2(2)2(22k x k k x k x ,所以x+|x －2k|的最小值是2k.因为x+|x －2k|>1的解集为R.所以2k>1,k>21.结合k ∈{a -1<a<1,a ≠0}知q 正确时，21<k<1.q 不正确时，-1<k ≤21且k ≠0.其次研究p:y=kx+2008的值随x 的增大而增大，k>0.反之k ≤0,所以p 正确时，0<k<1, p 不正确时，－1<k<01..综上知，当p正确且q不正确时,0<k≤2当p不正确且q正时,k∈φ.1.所以k的取值范围是0<k≤2来源：09年福建省福州市月考一题型：解答题，难度：中档判断下列命题的真假性:①.若m>0，则方程x2－x＋m＝0有实根②.若x>1,y>1,则x+y>2的逆命题③.对任意的x∈{x|-2<x<4},|x-2|<3的否定形式_____④.△>0是一元二次方程ax2＋bx＋c＝0有一正根和一负根的充要条件答案：①.假②.假③.真④.假来源：09年福建省福州市月考一 题型：填空题，难度：中档已知命题p ：函数)2(log25.0a x x y ++=的值域为R.命题q ：函数xa y )25(--=是R 上的减函数.若p 或q 为真命题，p 且q 为假命题，则实数a 的取值范围是答案：1<a<2来源：09年江苏南通月考一 题型：填空题，难度：中档有两个命题：不等式m x x ＞|1|||-+的解集为R ；函数f (x )=-（7-3m ）x 是减函数。

高三复习测试題一集合与简易逻辑1.集合A = {XI-1 <x<2),B = {X11 <x<3),那么( )A、0B、{x\-\<x<\}C、{x\\<x<2}D、{xl2<x<3}2.给出下面四个命题：①“直线a〃直线b”的充要条件是"a平行于b所在的平面”；②“直线1丄平面a所有直线”的充要条件是“1丄平面a ” ；③''直线a, b为异面直线”的充分不必要条件是“直线a, b不相交”；④“平面a 〃平面B ”的必要不充分条件是"a存在不共线三点到P的距离相等”. 其中正确命题的序号是()A. ®®B.②③C.③®D.②④3.给出下列关系①丄eR②迈已Q③一3EZ④一屁 N，其中正确的个数为()2A. 1B. 2C.3D.44.两个集合A与B之差记作"力一B”定义为A —若集合M =(¥|log2 x< 1}, N= [vx2 -4x + 3 < 0),则M _N等于( )A. {A-|0 < X < 2)B. {.v|0 < X < 1}C. {.v|0 < X < 3}D. {K|1 < X < 3}5.已知命題P：函数/(x) = |sin2x|的最小正周期为兀；命题彳：若函数/(x + 1)为偶函数，则/(x)关于x = l对称.则下列命题是真命题的是( )h. p 八 q B. p\/q C. (—1/7) A (—if?) D. p v (—»^)6.“x>2 ”是>4” 成立的()A.充分不必要条件；B.必要不充分条件；C.充要条件；D•既非充分又非必要条件；7..已知均为大于0的实数，设命题P：以a,b,c为长度的线段可以构成三角形的三边，命题Q : a2 +b2 + c2 < 2(ab + be + ca),则P 是Q 的( )A.充分但不必要条件，B.必要但不充分条件C.充要条件D.既不h充分也不必要条件8.下列命题中假命题有( )①拥wR,使f(x) = (m +丄+2)X"TE是暮函数；_________________m3②日& w R,使sin & cos & =—成立；③PciwR、使做+ 2/ + " — 2 = 0恒过定点；④Vx>0,不等式2x + -> 4成立的充要条件a>2.A. 3个B. 2个C・1个 D. 0个9.命题/八对任意XG R,2V+1> 0的否定是()A.-/?:对任意xeR , 21 +1 <0B.-/?：不存在x o eR , 2^'+1<0C.―:存在兀)G R , 2" +15 0D.―p :存在兀w R , 2" +1 > 010.已知全集U=N,集合P = {1,2,3,4,6},Q二{1,2,3,5,9}则Pri(Q2)= ()A. {1,2,3}B. {5,9}C. {4,6}D. {1,2,34,6}11.集合A = {2,5,8}, B = {1,3,5,7},那么A\JB = _______________12.定义集合运算：AOB={z! z=xy (x+y), xEA, y GB} •设集合A={0, 1}, B 二{2, 3},则集合AG)B的所有元素之和为_______ .13.命题“ \/xeR,使得x2+x + l>0 ."的否定是.14.巳知集合M={1,2,3,4},AGL集合A中所有元素的乘积称为集合A的'‘累积值”,且规定：当集合A只有一个元素时，其累积值即为该元素的数值，空集的累积值为0. 当集合A 的累积值是偶数时，这样的集合A共有_个・15.设a, 0是空间两个不同的平面，叭n是平面a及0外的两条不同直线.从“①加丄/?;②&丄0;③”丄0;④刃丄a”中选取三个作为条件，余下一个作为结论，写出你认为正确的一个命题：▲(用代号表示).16.已知集合4 = {x卜> 1} •集合B二{x|/n <x<m + 3}(1)当加=一1时，求(2)若ByA,求加的取值围.17.已知命题p： Vre[l,3],(丄)曲+加一1<0,2命題 q： e (0, +co), mx2 + x - 4 = 0.若且g”为真命题，数刃的取值围.18.已知集合A = Mx，+2x-3 = o}, B二=0},且A\JB = A ,数川的取值围.19.(本小题满分12分)已知集合A={x\x-3x+2=0},〃={”# 一财+2=0},且/1D B=B、数刃的取值围。

20XX年高中测试高中试题试卷科目：年级：考点：监考老师：日期：高一数学集合与简易逻辑测试题一、选择题（每题3分，共54分）1已知集合{}{}2,1,,0==N x M ，若{}2=⋂N M ，则=⋃N M （ ） A ．{}2,1,,0x B ．{}2,1,0,2C ．{}2,1,0D ．不能确定2不等式0)32)(1(2>+-+x x 的解集是（ ）A ．⎭⎬⎫⎩⎨⎧23B ．⎭⎬⎫⎩⎨⎧>23x x C ．⎭⎬⎫⎩⎨⎧<23x xD ．⎭⎬⎫⎩⎨⎧->23x x 3已知集合{}{}4),(,2),(=-==+=y x y x N y x y x M ，那么集合N M ⋂为（）A ．1,3-==y xB ．)1,3(-C ．{}1,3-D ．{})1,3(-4设不等式ba x <-的解集为{}21<<-x x ，则a 与b 的值为（）A ．3,1==b aB ．3,1=-=b aC ．3,1-=-=b aD ．23,21==b a5不等式032>-+x x 的解集是（ ） A ．{}23-<>x x x 或B ．{}32<<-x xC ．{}32<->x x x 或D ．{}23-<<x x 6若q p ,是两个简单命题，且“p 或q ”的否定是真命题，则必有（ ）A ．p 真q 真B ．p 假q 假C ．p 真q 假D ．p 假q 真7已知A 与B 是两个命题，如果A 是B 的充分不必要条件，那么A ⌝是B ⌝的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件8⎩⎨⎧>>3321x x 是⎩⎨⎧>>+962121x x x x 成立的（） A ． 充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件9命题“若b a >，则c b c a +>+”的逆否命题为（ ）A ．若b a <，则c b c a +<+B ．若b a ≤，则c b c a +≤+C ．若c b c a +<+，则b a <D ．若c b c a +≤+，则b a ≤10已知全集U {}2,1,0=且{}2=A C U ，则集合A 的真子集共有（） A ．3个B ．4个C ．5个D ．6个11二次函数c bx ax y ++=2中，若0<ac ，则其图象与x 轴交点个数是（ ） A ．1个 B ．2个 C ．没有交点D ．无法确定12设集合A{}13≤=x x ，32=a ，那么下列关系正确的是（）A ．A a ⊂B ．A a ∈C ．A a ∉D ．{}A a ∈13不等式321<-x 的解集是（ ）A ．{}1<x xB ．{}21<<-x xC ．{}2>x x D ．{}21>-<x x x 或14下列命题为“p 或q ”的形式的是（）A ．25>B ．2是4和6的公约数C ．{}0≠ΦD ．B A ⊆15已知全集U {}8,7,6,5,4,3,2,1=，集合A ={}5,4,3，B ={}6,3,1，那么集合C ={}8,7,2是（ ）A ．BC UB ．B A ⋂C ．)()(B C A C U U ⋂D ．)()(B C A C U U ⋃16不等式11>x 的解集是（） A ．{}1>x xB ．{}1<x xC ．{}10<<x xD ．{}01<>x x x 或17二次不等式02>++c bx ax 的解集为全体实数的条件是（ ）A ．⎩⎨⎧>∆>00aB ．⎩⎨⎧<∆>00aC ．⎩⎨⎧>∆<00aD ．⎩⎨⎧<∆<00a 18下列命题为复合命题的是（ ）A ．12是6的倍数B ．12比5大C ．四边形ABCD 不是矩形D ．222c b a =+二、填空题（每题3分，共15分）19若不等式02<-ax x 的解集是{}10<<x x ，则=a 20抛物线16)(2+-=x x x f 的对称轴方程是21已知全集U {}5,4,3,2,1=，A {}3,1=，B {}4,3,2=，那么=⋃)(B C A U二次函数)0()(2≠++=a c bx ax x f ，若)()(21x f x f =（其中21x x ≠），则)2(21x x f +等于23已知{}2,2,1x x ∈，则实数x =三、解答题（第24、25两题每题7分，第26题8分，第27题9分，共31分）24解不等式723>-x25用反证法证明：已知R y x ∈,，且2>+y x ，则y x ,中至少有一个大于1。

（完整版）集合与简易逻辑试卷及详细答案集合与简易逻辑⼀、选择题(本⼤题共12⼩题，每⼩题5分，共60分．每⼩题中只有⼀项符合题⽬要求)1．集合M＝{x|lg x>0}，N＝{x|x2≤4}，则M∩N＝( )A．(1,2) B．[1,2)C．(1,2] D．[1,2]2.已知全集U＝Z，集合A＝{x|x2＝x}，B＝{－1,0,1,2}，则图中的阴影部分所表⽰的集合等于()A．{－1,2} B．{－1,0}C．{0,1} D．{1,2}3．已知?Z A＝{x∈Z|x＜6}，?Z B＝{x∈Z|x≤2}，则A与B的关系是() A．A?B B．A?BC．A＝B D．?Z A?Z B4．已知集合A为数集，则“A∩{0,1}＝{0}”是“A＝{0}”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件5．下列选项中，p是q的必要不充分条件的是()A．p：a＋c＞b＋d，q：a＞b且c＞dB．p：a＞1，b＞1，q：f(x)＝a x－b(a＞0，且a≠1)的图像不过第⼆象限C．p：x＝1，q：x2＝x D．p：a＞1，q：f(x)＝log a x(a＞0，且a≠1)在(0，＋∞)上为增函数6．已知命题p：所有有理数都是实数；命题q：正数的对数都是负数．则下列命题中为真命题的是() A．(⾮p)或q B．p且qC．(⾮p)且(⾮q) D．(⾮p)或(⾮q) 7．下列命题中，真命题是()B．?x∈R,2x>x2C．a＋b＝0的充要条件是ab＝－1D．a>1，b>1是ab>1的充分条件8．已知命题p：“x>3”是“x2>9”的充要条件，命题q：“ac2>bc2”是“a>b”的充要条件，则()A．“p或q”为真B．“p且q”为真C．p真q假D．p，q均为假9．命题p：?x∈R，x2＋1>0，命题q：?θ∈R，sin2θ＋cos2θ＝1.5，则下列命题中真命题是()A．p∧q B．(⾮p)∧qC．(⾮p)∨q D．p∧(⾮q)10．已知直线l1：x＋ay＋1＝0，直线l2：ax＋y＋2＝0，则命题“若a＝1或a＝－1，则直线l1与l2平⾏”的否命题为() A．若a≠1且a≠－1，则直线l1与l2不平⾏B．若a≠1或a≠－1，则直线l1与l2不平⾏C．若a＝1或a＝－1，则直线l1与l2不平⾏D．若a≠1或a≠－1，则直线l1与l2平⾏11．命题“?x∈[1,2]，x2－a≤0”为真命题的⼀个充分不必要条件是() A．a≥4 B．a≤4C．a≥5 D．a≤512．设x，y∈R，则“|x|≤4且|y|≤3”是“x216＋y29≤1”的()A．充分⽽不必要条件B．必要⽽不充分条件C．充分必要条件D．既不充分也不必要条件⼆、填空题(本⼤题共4⼩题，每⼩题5分，共20分，把答案填在题中横线上)13．已知集合A＝{1，a,5}，B＝{2，a2＋1}．若A∩B有且只有⼀个元素，则实数a的值为________．14．命题“?x∈R，x2＋ax－4a<0”为假命题，是“－16≤a≤0”的________条件．15．设全集U＝A∪B＝{x∈N*|lg x<1}，若A∩(?U B)＝{m|m＝2n＋1，n＝0,1,2,3,4}，则集合B＝________.16．若f(x)＝x2－2x，g(x)＝ax＋2(a>0)，?x1∈[－1,2]，?x0∈[－1,2]，使g(x1)＝f(x0)，则a的取值范围是________．三、解答题(本⼤题共6⼩题，共70分，解答应写出⽂字说明、证明过程或演算步骤)17．(本⼩题满分10分)已知集合A＝{x|x2－2x－3≤0，x∈R}，B＝{x|x2－2mx＋m2－4≤0，x∈R，m∈R}．(1)若A∩B＝[0,3]，求实数m的值；(2)若A??R B，求实数m的取值范围．18．(本⼩题满分12分)已知命题“?x∈R，|x－a|＋|x＋1|≤2”是假命题，求实数a的取值范围．19．(本⼩题满分12分)已知集合E＝{x||x－1|≥m}，F＝{x|10x＋6>1}．(1)若m＝3，求E∩F；(2)若E∪F＝R，求实数m的取值范围．20．(本⼩题满分12分)已知全集U＝R，⾮空集合A＝{x|x－2x－(3a＋1)<0}，B＝{x|x－a2－2x－a<0}．(1)当a＝12时，求(?U B)∩A；(2)命题p：x∈A，命题q：x∈B，若q是p的必要条件，求实数a的取值范围．21．(本⼩题满分12分)设集合A为函数y＝ln(－x2－2x＋8)的定义域，集合B为函数y＝x＋1x＋1的值域，集合C为不等式(ax－1a)(x＋4)≤0的解集．(1)求A∩B；(2)若C??R A，求a的取值范围．22．(本⼩题满分12分)已知命题p：⽅程2x2＋ax－a2＝0在[－1,1]上有解；命题q：只有⼀个实数x0满⾜不等式x20＋2ax0＋2a≤0，若命题“p或q”是假命题，求a的取值范围．答案：⼀、选择题(本⼤题共12⼩题，每⼩题5分，共60分．每⼩题中只有⼀项符合题⽬要求)1．答案C解析因为M＝{x|x>1}，N＝{x|－2≤x≤2}，所以M∩N＝{x|12解析依题意知A＝{0,1}，(?U A)∩B表⽰全集U中不在集合A中，但在集合B中的所有元素，故图中的阴影部分所表⽰的集合等于{－1,2}，选A.3．答案A4．D．既不充分也不必要条件答案 B解析∵“A∩{0,1}＝{0}”得不出“A＝{0}”，⽽“A＝{0}”能得出“A∩{0,1}＝{0}”，∴“A∩{0,1}＝{0}”是“A＝{0}”的必要不充分条件．5．解析B选项中，当b＝1，a＞1时，q推不出p，因⽽p为q的充分不必要条件．C选项中，q为x＝0或1，q不能够推出p，因⽽p为q的充分不必要条件．D选项中，p、q可以互推，因⽽p为q的充要条件．故选A.6．答案D解析由于命题p是真命题，命题q是假命题，因此，命题綈q是真命题，于是(綈p)或(綈q)是真命题．7．答案D解析∵a>1>0，b>1>0，∴由不等式的性质，得ab>1.即a>1，b>1?ab>1.8．答案A解析由x>3能够得出x2>9，反之不成⽴，故命题p是假命题；由ac2>bc2能够推出a>b，反之，因为1c2>0，所以由a>b能推出ac2>bc2成⽴，故命题q是真命题．因此选A.9．答案D解析易知p为真，q为假，⾮p为假，⾮q为真．由真值表可知p∧q假，(⾮p)∧q假，(⾮p)∨q假，p∧(⾮q)真，故选D.10．答案A解析命题“若A，则B”的否命题为“若綈A，则綈B”，显然“a＝1或a ＝－1”的否定为“a≠1且a≠－1”，“直线l1与l2平⾏”的否定为“直线l1与l2不平⾏”，所以选A.11．答案C解析命题“?x∈[1,2]，x2－a≤0”为真命题的充要条件是a≥4，故其充分不必要条件是实数a的取值范围是集合[4，＋∞)的⾮空真⼦集，正确选项为C.12．答案B⼆、填空题(本⼤题共4⼩题，每⼩题5分，共20分，把答案填在题中横线上)13．答案0或－2解析若a＝2，则a2＋1＝5，A∩B＝{2,5}，不合题意舍去．若a2＋1＝1，则a＝0，A∩B＝{1}．若a2＋1＝5，则a＝±2.⽽a＝－2时，A∩B＝{5}．若a2＋1＝a，则a2－a＋1＝0⽆解．∴a＝0或a＝－2.14．答案充要解析∵“?x∈R，x2＋ax－4a<0”为假命题，∴“?x∈R，x2＋ax－4a≥0”为真命题，∴Δ＝a2＋16a≤0，即－16≤a≤0.故为充要条件．15．答案{2,4,6,8}解析A∪B＝{x∈N*|lg x<1}＝{1,2,3,4,5,6,7,8,9}，A∩(?U B)＝{m|m＝2n＋1，n ＝0,1,2,3,4}＝{1,3,5,7,9}，∴B＝{2,4,6,8}．16．答案(0，1 2]解析由于函数g(x)在定义域[－1,2]内是任意取值的，且必存在x0∈[－1,2]，使得g(x1)＝f(x0)，因此问题等价于函数g(x)的值域是函数f(x)值域的⼦集．函数f(x)的值域是[－1,3]，函数g(x)的值域是[2－a,2＋2a]，则有2－a≥－1且2＋2a≤3，即a≤12，⼜a>0，故a的取值范围是(0，12]．三、解答题(本⼤题共6⼩题，共70分，解答应写出⽂字说明、证明过程或演算步骤)17 答案 (1)2。