概率统计试题及答案一份2016(仅供参考)

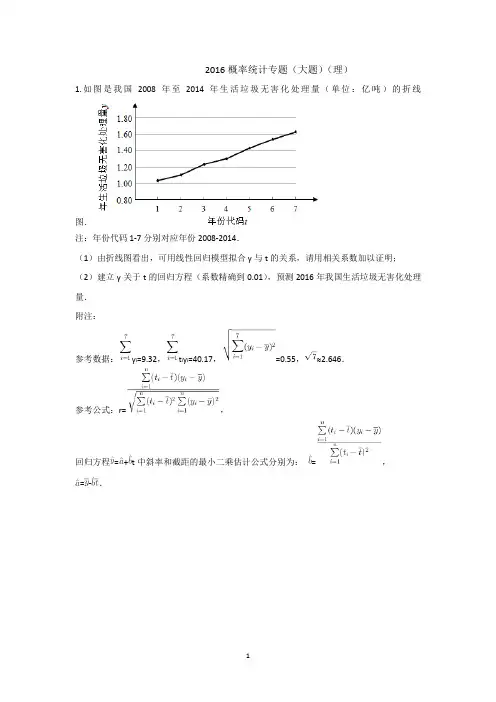
2016概率统计专题（大题）（理）1.如图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图．注：年份代码1-7分别对应年份2008-2014．（1）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以证明；（2）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量．附注：参考数据：y i=9.32，t i y i=40.17，=0.55，≈2.646．参考公式：r=，回归方程=+t中斜率和截距的最小二乘估计公式分别为：=，=-．2． A，B，C三个班共有100名学生，为调查他们的体育锻炼情况，通过分层抽样获得了部分学生一周的锻炼时间，数据如表（单位：小时）：（Ⅰ）试估计C班的学生人数；（Ⅱ）从A班和C班抽出的学生中，各随机选取一个人，A班选出的人记为甲，C班选出的人记为乙．假设所有学生的锻炼时间相对独立，求该周甲的锻炼时间比乙的锻炼时间长的概率；（Ⅲ）再从A，B，C三班中各随机抽取一名学生，他们该周锻炼时间分别是7，9，8.25（单位：小时），这3个新数据与表格中的数据构成的新样本的平均数记为μ1，表格中数据的平均数记为μ0，试判断μ0和μ1的大小．（结论不要求证明）3.甲、乙两人组成“星队”参加猜成语活动，每轮活动由甲、乙各猜一个成语，在一轮活动中，如果两人都猜对，则“星队”得3分；如果只有一个人猜对，则“星队”得1分；如果两人都没猜对，则“星队”得0分．已知甲每轮猜对的概率是，乙每轮猜对的概率是；每轮活动中甲、乙猜对与否互不影响．各轮结果亦互不影响．假设“星队”参加两轮活动，求：（I）“星队”至少猜对3个成语的概率；（II）“星队”两轮得分之和为X的分布列和数学期望EX．4.我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超出x的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），…，[4，4.5）分成9组，制成了如图所示的频率分布直方图．（Ⅰ）求直方图中a的值；（Ⅱ）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；（Ⅲ）若该市政府希望使85%的居民每月的用水量不超过标准x（吨），估计x的值，并说明理由．。

2016 年高考数学理试题分类汇编统计与概率一、1、（ 2016 年北京高考）袋中装有偶数个球，其中球、黑球各占一半.甲、乙、丙是三个空盒 .每次从袋中任意取出两个球，将其中一个球放入甲盒，如果个球是球，就将另一个球放入乙盒，否就放入丙盒.重复上述程，直到袋中所有球都被放入盒中，（）A. 乙盒中黑球不多于丙盒中黑球B. 乙盒中球与丙盒中黑球一多C.乙盒中球不多于丙盒中球D. 乙盒中黑球与丙盒中球一多【答案】 C2、（ 2016 年山高考）某高校了200 名学生每周的自（位：小），制成了如所示的率分布直方，其中自的范是[17.5,30] ，本数据分[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30] .根据直方，200 名学生中每周的自不少于22.5 小的人数是（A ） 56（B）60（C）120（D）140【答案】 D3、（ 2016 年全国 I 高考）某公司的班在7:30，8:00，8:30 ，小明在 7:50 至 8:30 之到达站乘坐班，且到达站的刻是随机的，他等不超10 分的概率是（ A）1123 3（ B ）2（ C）3（D ）4【答案】 B4、（ 2016 年全国 II 高考）从区0,1随机抽取 2n 个数x1,x2，⋯， x n， y1， y2，⋯， y n，构成 n 个数x, y， x , y x , y，其中两数的平方和小于 1 的数共有m个，则用随机模拟的方法得到的圆周率的近似值为（A）4n（B）2n（C）4m（D）2m m m n n【答案】 C5、（ 2016 年全国III 高考）某旅游城市为向游客介绍本地的气温情况，绘制了一年中月平均最高气温和平均最低气温的雷达图。

图中 A 点表示十月的平均最高气温约为150C，B 点表示四月的平均最低气温约为50C。

下面叙述不正确的是(A)各月的平均最低气温都在00C 以上(B)七月的平均温差比一月的平均温差大(C)三月和十一月的平均最高气温基本相同(D)平均气温高于200C 的月份有 5 个【答案】 D二、填空题1 、（ 2016年山东高考）在[－1,1]上随机的取一个数k，则事件“ 直线y = kx与圆(x－5)2 + y2 = 9 相交”发生的概率为3【答案】．42、（ 2016 年上海高考）某次体检， 6 位同学的身高（单位：米）分别为 1.72,1.78,1.75,1.80,1.69,1.77则这组数据的中位数是_________（米）【答案】 1.763、（ 2016 年四川高考）同时抛掷两枚质地均匀的硬币，当至少有一枚硬币正面向上时，就说这次试验成功，则在 2 次试验中成功次数X 的均值是.【答案】3 2三、解答题1、（ 2016 年北京高考）A、 B、C 三个班共有100 名学生，为调查他们的体育锻炼情况，通过分层抽样获得了部分学生一周的锻炼时间，数据如下表（单位：小时）；A 班6 6.577.58B 班6789101112C 班3 4.567.5910.51213.5（ 1）试估计 C 班的学生人数；（ 2）从 A 班和 C 班抽出的学生中，各随机选取一人， A 班选出的人记为甲， C 班选出的人记为乙，假设所有学生的锻炼时间相对独立，求该周甲的锻炼时间比乙的锻炼时间长的概率；（ 3）再从 A 、 B、 C 三个班中各随机抽取一名学生，他们该周的锻炼时间分别是7， 9， 8.25（单位：小时），这 3 个新数据与表格中的数据构成的新样本的平均数记1，表格中数据的平均数记为0 ，试判断0 和 1 的大小，（结论不要求证明）解析】⑴8100 40 ， C班学生40 人20⑵在 A 班中取到每个人的概率相同均为15设 A 班中取到第 i 个人事件为 A i, i1,2,3,4,5C 班中取到第j 个人事件为C j,j 1,2,3,4,5,6,7,8A 班中取到 A i C j的概率为 P i所求事件为 D则 P( D )1P11P21P31P41P5555551213131314585858585838⑶ 10三组平均数分别为 7 , 9 , 8.25 , 总均值08.2但 1 中多加的三个数据7 , 9 , 8.25 , 平均值为 8.08 ，比0小，故拉低了平均值2、（ 2016 年山东高考）甲、乙两人组成“星队”参加猜成语活动，每轮活动由甲、乙各猜一个成语，在一轮活动中，如果两人都猜对，则“星队”得 3 分；如果只有一人猜对，则“星队”得 1 分；如果两人都没猜对，则“星队”得0 分．已知甲每轮猜对的概率是3，乙每轮4猜对的概率是2；每轮活动中甲、乙猜对与否互不影响，各轮结果也互不影响．假设“星队”3参加两轮活动，求：( Ⅰ )“星队”至少猜对 3 个成语的概率；( Ⅱ )“星队”两轮得分之和X 的分布列和数学期望EX ．【解析】 ( Ⅰ ) “至少猜对 3 个成语”包括“恰好猜对 3 个成语”和“猜对 4 个成语”．设“至少猜对 3 个成语”为事件 A ；“恰好猜对 3 个成语”和“猜对 4 个成语”分别为事件B,C ，则 P( B) C213 3 2 1C21 3 1 2 25 ；443344331233221．P(C )43344所以 P( A)P( B)P(C )512．1243( Ⅱ )“星队”两轮得分之和X 的所有可能取值为0,1,2,3,4,6于是 P( X0)11111；4343144P( X 1) C211 2 1 1C21 1 1 3 110 5 ；4343434314472P( X 2) 1 12 2 3 3 1 1C21 1 3 2 125 ；443344334433144 P( X3) C21 3 2 1 1 12 1 ；434314412P( X 4) C2132( 1 2 3 1)60 5 ；43434314412P( X6)3232361；43431444X012346P1525151 14472144121241525154155223X 的数学期望 EX01236144．144721441212463、（ 2016 年四川高考）我国是世界上重缺水的国家，某市政府了鼓励居民用水，划整居民生活用水收方案，确定一个合理的月用水量准x （吨）、一位居民的月用水量不超 x 的部分按平价收，超出 x 的部分按价收.了了解居民用水情况，通抽，得了某年 100 位居民每人的月均用水量（位：吨），将数据按照 [0,0.5) ，[0.5,1) ，⋯，[4,4.5)分成 9 ，制成了如所示的率分布直方.（ I）求直方中 a 的；（ II ）市有30 万居民，估全市居民中月均用水量不低于 3 吨的人数，并明理由；（ III ）若市政府希望使85%的居民每月的用水量不超准x （吨），估x 的，并明理由 .【解析】（ I ）由概率相关知，各率之和的1∵ 率 =(率 /距 )* 距∴ 0.50.080.160.40.520.120.080.042a1得 a0.3（ II ）由，不低于3吨人数所占百分比0.50.120.080.04 =12%∴全市月均用水量不低于3吨的人数：3012%=3.6 (万 )（ III ）由可知，月均用水量小于 2.5吨的居民人数所占百分比：0.50.080.160.30.40.520.73即 73% 的居民月均用水量小于 2.5吨 ,同理， 88%的居民月均用水量小于3吨，故 2.5x3假月均用水量平均分布，x 2.50.585%73%0.52.9 （吨） .0.3注：本次估计默认组间是平均分布，与实际可能会产生一定误差。

湖北汽车工业学院概率论与数理统计考试试卷一、(本题满分24，每小题4分)单项选择题（请把所选答案填在答题卡指定位置上): 【C 】1．已知A 与B 相互独立，且0)(>A P ，0)(>B P ．则下列命题不正确的是 )(A )()|(A P B A P =． )(B )()|(B P A B P =． )(C )(1)(B P A P -=． )(D )()()(B P A P AB P =． 【B 】2．已知随机变量X 的分布律为则)35(+X E 等于)(A 8． )(B 2． )(C 5-． )(D 1-．【A 】3．设随机变量X 与Y 均服从正态分布2~(,4)X N μ，2~(,5)Y N μ，而}5{},4{21+≥=-≤=μμY P p X P p ,则)(A 对任何实数μ，都有21p p =． )(B 对任何实数μ，都有21p p <． )(C 只对μ的个别值，才有21p p =． )(D 对任何实数μ，都有21p p >．【C 】4．在总体X 中抽取样本,,,321X X X 则下列统计量为总体均值μ的无偏估计量的是)(A 3213211X X X ++=μ． )(B 2223212X X X++=μ． )(C 3333213X X X ++=μ． )(D 4443214X X X++=μ． 【D 】5。

设)(~n t X ,则~2X)(A )(2n χ． )(B )1(2χ． )(C )1,(n F ． )(D ),1(n F ．【B 】6．随机变量)1,0(~N X ,对于给定的()10<<αα,数αu 满足αα=>)(u u P ， 若α=<)(c X P ，则c 等于)(A 2αu ． )(B 2)1(α-u ． )(C α-1u ． )(D 21α-u ． 二、（本题满分24，每小题4分）填空题(请把你认为正确的答案填在答题卡指定位置上):1. 设样本空间{},2,3,4,5,61=Ω,{},21=A ，{},32=B ，{},54=C ，则=)(C B A {},3,4,5,61。

2016年1月全国自考概率论与数理统计（经管类）模拟试卷和答案一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

第1题【正确答案】 A【你的答案】本题分数2分第2题【正确答案】 C【你的答案】本题分数2分第3题每次试验的成功概率为p(0＜p＜1),则在3次重复试验中至少成功一次的概率为（）【正确答案】 C【你的答案】本题分数2分第4题甲、乙、丙三人独立地破译一密码，若每人能译出的概率均为0.25，则密码能译出的概率为（）【正确答案】 B【你的答案】本题分数2分第5题【正确答案】 D【你的答案】本题分数2分第6题【正确答案】 A【你的答案】本题分数2分第7题下面说法正确的是（）A. 如果备择假设是正确的，但做出的决策是拒绝备择假设，则犯了弃真错误B. 如果备择假设是错误的，但做出的决策是接受备择假设，则犯了采伪错误C. 如果原假设是正确的，但做出的决策是接受备择假设，则犯了弃真错误D. 如果原假设是错误的，但做出的决策是接受备择假设，则犯了采伪错误【正确答案】 C【你的答案】本题分数2分第8题 100件产品中有5件次品，从中任取5件，则这5件全是正品的概率为（）【正确答案】 A【你的答案】本题分数2分第9题【正确答案】 D【你的答案】本题分数2分第10题【正确答案】 C二、填空题（本大题共15小题，每小题2分，共30分）请在每小题的空格中填上正确答案。

错填、不填均无分。

第1题若二维随机变量（X,Y）的概率密度为（如下图）则A=___.【正确答案】【你的答案】修改分数本题分数2分你的得分第2题若随机变量X与Y相互独立，其分布分别为（如图所示）则（X，Y）的分布为___.【正确答案】【你的答案】本题分数2分修改分数你的得分第3题若随机变量X的可能取值为1与a,且P{X=1}=0.4,E(X)=0.2,则a=___.【正确答案】【你的答案】修改分数本题分数2分你的得分第4题若E（X）=25，E（Y）=5，则E（5X-25Y）=___.【正确答案】 0【你的答案】修改分数本题分数2分你的得分第5题一批产品中有10个正品2个次品，现随机抽取两次，每次取一件，取后放回，则第二次取到正品的概率为___.【正确答案】【你的答案】修改分数本题分数2分你的得分第6题如果X与Y独立，且都服从［0，1］上的均匀分布，则二维随机变量（X，Y）的密度函数为___.【正确答案】【你的答案】本题分数2分修改分数你的得分第7题 X服从参数为λ的泊松分布,则E［(X-1)(X-2)］=___.【正确答案】【你的答案】修改分数本题分数2分你的得分第8题图中空白处答案应为：___【正确答案】 16【你的答案】修改分数本题分数2分你的得分第9题图中空白处答案应为：___【正确答案】 0.4【你的答案】修改分数本题分数2分你的得分第10题图中空白处答案应为：___【正确答案】【你的答案】修改分数本题分数2分你的得分第11题图中空白处答案应为：___【正确答案】【你的答案】本题分数2分修改分数你的得分第12题 ___【正确答案】 3【你的答案】修改分数本题分数2分你的得分第13题【正确答案】【你的答案】修改分数本题分数2分你的得分第14题某地区成年人患A，B种病的概率分别为0.015和0.08，设这两种病的发生量是相互独立的，则该地区任一成年人同时患有这两种病的概率为.___【正确答案】【你的答案】修改分数本题分数2分你的得分第15题 ___【正确答案】三、计算题（本大题共2小题，每小题8分，共16分）第1题【正确答案】【你的答案】本题分数8分修改分数你的得分第2题【正确答案】【你的答案】四、综合题（本大题共2小题，每小题12分，共24分）第1题2016年1月全国自考概率论与数理统计（经管类）模拟试卷和答案【正确答案】【你的答案】五、应用题（10分）第1题2016年1月全国自考概率论与数理统计（经管类）模拟试卷和答案【正确答案】【你的答案】。

《概率与统计》专项练习（解答题）1．（2016全国Ⅰ卷，文19，12分）某公司计划购买1台机器，该种机器使用三年后即被淘汰．机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元．在机器使用期间，如果备件不足再购买，则每个500元．现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：记x表示1台机器在三年使用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用（单位：元），n表示购机的同时购买的易损零件数．（Ⅰ）若n＝19，求y与x的函数解析式；（Ⅱ）若要求“需更换的易损零件数不大于n”的频率不小于0.5，求n的最小值；（Ⅲ）假设这100台机器在购机的同时每台都购买19个易损零件，或每台都购买20个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买19个还是20个易损零件？解：（Ⅰ）当x≤19时，y＝3800当x＞19时，y＝3800＋500(x－19)＝500x－5700∴y与x的函数解析式为y＝，，＞(x∈N)（Ⅱ）需更换的零件数不大于18的频率为0.46，不大于19的频率为0.7∴n的最小值为19（Ⅲ）①若同时购买19个易损零件则这100台机器中，有70台的费用为3800，20台的费用为4300，10台的费用为4800∴平均数为(3800×70＋4300×20＋4800×10)＝4000②若同时购买20个易损零件则这100台机器中，有90台的费用为4000，10台的费用为4500∴平均数为(4000×90＋4500×100)＝4050∵4000＜4050∴同时应购买19个易损零件2．（2016全国Ⅱ卷，文18，12分）某险种的基本保费为a（单位：元），继续购买该险种的投保人称为（Ⅱ）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160％”，求P(B)的估计值；（Ⅲ）求续保人本年度的平均保费估计值．解：（Ⅰ）若事件A发生，则一年内出险次数小于2则一年内险次数小于2的频率为P(A)＝＝0.55∴P(A)的估计值为0.55（Ⅱ）若事件B发生，则一年内出险次数大于1且小于4一年内出险次数大于1且小于4的频率为P(B)＝＝0.3∴P(B)的估计值为0.3（Ⅲ）续保人本年度的平均保费为(0.85a×60＋a×50＋1.25a×30＋1.5a×30＋1.75a×20＋2a×10)＝1.1925a3．（2016全国Ⅲ卷，文18，12分）下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图（Ⅰ）由折线图看出，可用线性回归模型拟合y 与t 的关系，请用相关系数加以说明； （Ⅱ）建立y 关于t 的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量． 附注：参考数据：719.32i i y ==∑，7140.17i i i t y ==∑，∑=-712)(i iy y＝0.55， ≈2.646．参考公式：相关系数r ＝∑∑∑===----ni ni i ini i iy y t ty y t t11221)()())((．回归方程 ＝ ＋ t 中斜率和截距的最小二乘估计公式分别为：＝∑∑==---ni ini i it ty y t t121)())((， ＝ －解：（Ⅰ）由折线图中数据得 ＝(1＋2＋3＋4＋5＋6＋7)＝4………………1分由附注中参考数据得∑=--71))((i i iy y t t＝∑=71i i i y t －∑=71i i y t ＝40.17－4×9.32＝2.89………………………………………………………………………2分 ＝27262424232221)4()4()4()4()4()4()4(-+-+-+-+-+-+-t t t t t t t ＝28………………………………………………………………3分∑=-712)(i i y y ＝0.55………………………………………………4分r ＝∑∑∑===----ni ni iini i iy yt ty y t t11221)()())((＝∑∑==-⨯-ni ini iy yt t1212)()(89.2＝55.02889.2⨯≈0.99………………………………………………………………………5分 ∵y 与t 的相关关系r 近似为0.99，说明y 与t 的线性相关程度相当高 ∴可以用线性回归模型拟合y 与t 的关系…………………………6分（Ⅱ） ＝771∑=i iy＝≈1.331………………………………………………7分＝∑∑==---ni ini i it ty y t t121)())((＝≈0.103…………………………………8分＝ －≈1.331－0.103×4≈0.92…………………………………9分 ∴y 关于t 的回归方程为 ＝0.92＋0.103t …………………………10分 2016年对应的t ＝9…………………………………………………11分 把t ＝9代入回归方程得 ＝0.92＋0.103×9＝1.82∴预测2016年我国生活垃圾无害化处理量将约1.82亿吨………12分4．（2015全国Ⅰ卷，文19，12分）某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x (单位：千元)对年销售量y (单位：t )和年利润z (单位：千元)的影响．对近8年的年宣传费x i 和年销售量y i (i ＝1，2，…，8)数据作了初步处理，得到下面的散点图及一些统计量的值．表中w i ＝ ， ＝＝w i ．（Ⅰ）根据散点图判断，y ＝a ＋bx 与y ＝c ＋d 哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型？(给出判断即可，不必说明理由)（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y 关于x 的回归方程；（Ⅲ）已知这种产品的年利润z 与x ，y 的关系为z ＝0.2y －x ．根据（Ⅱ）的结果回答下列问题：（ⅰ）年宣传费x ＝49时，年销售量及年利润的预报值是多少？ （ⅱ）年宣传费x 为何值时，年利润的预报值最大？附：对于一组数据(u 1，v 1)，(u 2，v 2)，…，(u n ，v n )，其回归直线v ＝α＋βu 的斜率和截距的最小二乘估计分别为＝＝－ － ＝－，＝ －．解：（Ⅰ）y ＝c ＋d 适宜作为y 关于x 的回归方程类型………………………………………………………………………………………2分 （Ⅱ）令w ＝ ，先建立y 关于w 的回归方程由于＝＝18－ － ＝18－＝.81.＝ 8…………………3分＝ － ＝563－68×6.8＝100.6…………………4分 ∴y 关于w 的回归方程为＝100.6＋68w …………………5分 ∴y 关于x 的回归方程为 ＝100.6＋68 ………………… 分 （Ⅲ）（ⅰ）由（Ⅱ）知，当x ＝49时y 的预报值＝100.6＋68 49＝576.6…………………7分 z 的预报值 ＝576.6×0.2－49＝66.32…………………9分（ⅱ）根据（Ⅱ）的结果知z 的预报值 ＝0．2(100.6＋68 )－x ＝－x ＋13.6 ＋20.12……10分∴当 ＝13.2＝6.8，即x ＝46.24时，取得最大值…………………11分 ∴年宣传费为46.24千元时，年利润的预报值最大…………………12分5．（2015全国Ⅱ卷，文18，12分）某公司为了解用户对其产品的满意度，从A ，B 两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频数分布表．值及分散程度(不要求计算出具体值，给出结论即可)； 解：（Ⅰ）…………4分B 地区的平均值高于A 地区的平均值…………5分 B 地区比较集中，而A 地区比较分散………… 分 （Ⅱ）A 地区不满意的概率大…………7分记C A 表示事件：“A 地区用户的满意度等级为不满意”C B 表示事件：“B 地区用户的满意度等级为不满意” …………9分 由直方图得P (C A )＝(0.01＋0.02＋0.03)×10＝0.6…………10分P (C B )＝(0.005＋0.02)×10＝0.25…………11分∴A 地区不满意的概率大…………12分6．（2014全国Ⅰ卷，文18，12分）从某企业生产的某种产品中抽取100件，测量这些产品的一项质量（Ⅱ）估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表)； （Ⅲ）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定？解：（Ⅰ）…………4分（Ⅱ）平均数为 ＝80×0.06＋90×0.26＋100×0.38＋110×0.22＋120×0.08＝100方差为S 2＝1100[6×(80－100)2＋26×(90－100)2＋38×(100－100)2＋22×(110－100)2＋8×(120－100)2]＝104∴平均数为100，方差为104…………8分（Ⅲ）质量指标值不低于95的比例为0.38＋0.22＋0.08＝0.68…………10分∵0.68＜0.8…………11分∴不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定…………12分7．（2014全国Ⅱ卷，文19，12分）某市为了考核甲、乙两部门的工作情况，随机访问了50位市民．根（Ⅱ）分别估计该市的市民对甲、乙两部门的评分高于90的概率； （Ⅲ）根据茎叶图分析该市的市民对甲、乙两部门的评价． 解：（Ⅰ）甲的评分由小到大排序，排在第25，26位的是75，75∴样本中位数为75＋752＝75∴甲的中位数是75乙的评分由小到大排序，排在第25，26位的是66，68 ∴样本中位数为＋ 82＝67∴乙的中位数是67（Ⅱ）甲的评分高于90的概率为550＝0.1乙的评分高于90的概率为850＝0.16∴甲、乙的评分高于90的概率分别为0.1，0.16 （Ⅲ）甲的中位数高于对乙的中位数甲的标准差要小于对乙的标准差甲的评价较高、评价较为一致，对乙的评价较低、评价差异较大8．（2013全国Ⅰ卷，文18，12分）为了比较两种治疗失眠症的药(分别称为A 药，B 药)的疗效，随机地选取20位患者服用A 药，20位患者服用B 药，这40位患者在服用一段时间后，记录他们日平均增加的睡眠时间(单位：h )．试验的观测结果如下： 服用A 药的20位患者日平均增加的睡眠时间： 0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5 2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4 服用B 药的20位患者日平均增加的睡眠时间： 3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4 1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5（Ⅰ）分别计算两组数据的平均数，从计算结果看，哪种药的疗效更好？ （Ⅱ）根据两组数据完成下面茎叶图，从茎叶图看，哪种药的疗效更好？ 解：（Ⅰ）设A 的平均数为 ，B 的平均数为＝120(0.6＋1.2＋1.2＋1.5＋1.5＋1.8＋2.2＋2.3＋2.3＋2.4＋2.5＋2.6＋2.7＋2.7＋2.8＋2.9＋3.0＋3.1＋3.2＋3.5)＝2.3 ＝120(0.5＋0.5＋0.6＋0.8＋0.9＋1.1＋1.2＋1.2＋1.3＋1.4＋1.6＋1.7＋1.8＋1.9＋2.1＋2.4＋2.5＋2.6＋2.7＋3.)＝1.6 ∴ ＞∴A 药的疗效更好 （Ⅱ）茎叶图如下：从茎叶图可以看出A 的结果有710的叶集中在茎2，3上B 的结果有710的叶集中在茎0，1上∴A 药的疗效更好9．（2013全国Ⅱ卷，文19，12分）经销商经销某种农产品，在一个销售季度内，每售出1t 该产品获利润500元，未售出的产品，每1t 亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130t 该农产品，以X (单位：t ，100≤X ≤150 表示下一个销售季度内的市场需求量，T (单位：元)表示下一个销售季度内经销该农产品的利润． （Ⅰ）将T 表示为X 的函数；（Ⅱ）根据直方图估计利润T 不少于57 000元的概率． 解：（Ⅰ）当X ∈[100，130)时，T ＝500X －300(130－X )＝800X －39000当X ∈[130，150]时，T ＝500×130＝65000∴T ＝800 －39000，100≤ ＜130 5000，130≤ ≤150（Ⅱ）由（Ⅰ）知利润T 不少于57000元，当且仅当120≤X ≤150由直方图知需求量X ∈[120，150]的频率为0.7∴下一个销售季度内的利润T 不少于57000元的概率的估计值为0.710．（2012全国卷，文18，12分）某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售．如果当天卖不完，剩下的玫瑰花作垃圾处理．（Ⅰ）若花店一天购进17枝玫瑰花，求当天的利润y (单位：元)关于当天需求量n (单位：枝，n ∈N )的函数解析式；（ⅰ）元)的平均数； （ⅱ）若花店一天购进17枝玫瑰花，以100天记录的各需求量的频率作为各需求量发生的概率，求当天的利润不少于75元的概率．解：（Ⅰ）当日需求量n ≥17时，利润y ＝85当日需求量n ＜17时，利润y ＝10n －85所以y 关于n 的函数解析式为y ＝ 10 －85， ＜1785， ≥17(n ∈N )（Ⅱ）（ⅰ）解法一：由表格可得有10天的日利润为5×14－5×3＝55元 有20天的日利润为5×15－5×2＝65元 有16天的日利润为5×16－5×1＝75元有16＋15＋13＋10＝54天的日利润为85元∴这100天的日利润的平均数为1100(55×10＋65×20＋75×16＋85×54)＝76.4（ⅰ）解法二：由（Ⅰ）y ＝ 10 －85， ＜1785， ≥17(n ∈N )得当n ＝14时，10天的日利润为10n －85＝10×14－85＝55元 当n ＝15时，20天的日利润为10n －85＝10×15－85＝65元 当n ＝16时，16天的日利润为10n －85＝10×16－85＝75元 当n ≥17时，54天的日利润为85元∴这100天的日利润的平均数为1100(55×10＋65×20＋75×16＋85×54)＝76.4（ⅱ）利润不低于75元，当且仅当日需求量不少于16枝∴当天的利润不少于75元的概率为P ＝0.16＋0.16＋0.15＋0.13＋0.1＝0.711．（2011全国卷，文19，12分）某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品．现用两种新配方(分别称为A 配方和B 配方)做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：（Ⅱ）已知用B 配方生产的一件产品的利润y (单位：元)与其质量指标值t 的关系式为y ＝ －2， ＜942，94≤ ＜1024， ≥102，估计用B 配方生产的一件产品的利润大于0的概率，并求用B 配方生产的上述100件产品平均一件的利润．解：（Ⅰ）A 配方的优质品的频率为22＋8100＝0.3 ∴A 配方的优质品率为0.3B 配方的优质品的频率为32＋10100＝0.42∴B 配方的优质品率为0.42（Ⅱ）用B 配方的利润大于0，当且仅当t ≥94∵t ≥94的频率为0.96∴B 配方的利润大于0的概率为0.96B 配方的利润为1100×[4×(－2)＋54×2＋42×4]＝2.68(元)。

2．D 7．A
3．B 8．B
4．B 9．C
5．D 10．C
二、填空题（本大题共 15 小题，每小题 2 分，共 30 分）

1 4
25． 0 1 x0
三、计算题（本大题共 2 小题，每小题 8 分，共 16 分）
26．解 设事件 B 表示“取出 1 件次品”， 事件A 则由题设知 P(A ) = ,P(A ) = P( )= ……2 ,考法分别表示“取出的是由甲、乙、两厂生产的产品”，
解设事件b表示取出1件次品事件a考法分别表示取出的是由甲乙两厂生产的产品则由题设知四综合题本大题共2小题每小题12分共242一个此型号电子元件工作超过8000小时的概率为3一台仪器能正常工作8000小时以上的概率为30
2016 年 10 月高等教育自学考试全国统命题考试 概率论与数理统计(经管类)试题答案及评分参考 (课程代码 04183)
F x =P X≤x =
=
䁞000
䁞000
… … 4
（2）一个此型号电子元件工作超过 8000 小时的概率为 分 P X > 8000 = F 8000 = 0.7㌍; （3）一台仪器能正常工作 8000 小时以上的概率为 (P{X > 8000}) = 0.㌍䁞 ㌍
+
… … 8
… … 12
分
29．解 （1）由 分 （2） P （3）E
分
（1）由全概率公式得
分
= × % + × % + × % = 0.0 （2）由贝叶斯公式得 =P A B =
Hale Waihona Puke P=P B =P A P BA
+P A P B A
+ P(

解题思路：从概率的统计性定义及几何意义出发回答此问题。
2. 论随机变量及其分布
（1）我们通常用随机变量 来刻划一个随机试验中的所有可能的随机事件.讨论随机变量可分为
连续型与离散型两种基本类型.设 是连续型随机变量，则它的概率密度函数 是概率吗？它
的概率分布函数
是概率吗？两者有什么关系？
（2）设随机变量 满足正态分布
，方差 的无偏估计是
.
解题思路：
第2/2页
的现象；
（2）一般地，我们称随机试验E的样本空间的子集为E的随机事件，简称事件；依照随机事件的 统计规律性知，事件A发生的频率随试验的不同而改变，但是当试验的次数越来越大时，频率会 稳定在某个数值ｐ附近，则称ｐ为事件A的概率，即概率是频率的稳定值. (3) P(A)=c; P(B)=d;P(C)=a;P(D)=b;P(E)=e.
的依据是中心极限定理.即独立随机变量序列的和
服从或近似服从正态分布.
解题思路：
5. 论参数估计的基本知识
(1)什么是参数估计？通常分为哪两种形式？它们最大的区别在那里？
(2)矩估计法和极大似然估计法是最常用的点估计法，请问矩估计法的具体做法是什么？
(3)在点估计中，什么是无偏估计？你知道在一般情况下，其数学期望 与方差 的无偏估计是
.大数定理和中心极限定理是极限定理中最重要的两种.请问：
(1)什么是切比雪夫大数定理？有什么意义？
(2)伯努利大数定理是切比雪夫大数定理的特殊情况，它有什么意义？
(3)在数理统计中，不论总体 服从什么分布，只要样本容量 充分大，我们总是利用标准正态
分布讨论其含样本均值
的统计量
，这是依据什么原理？(20分)
分布、泊松分布，连续型的有：均匀公布、指数分布、正态分布等等.

概率统计期末考试试题及答案试题一：随机变量的概率分布某工厂生产的产品合格率为0.9，不合格率为0.1。

假设每天生产的产品数量为100件，求下列事件的概率：1. 至少有80件产品是合格的。

2. 至多有5件产品是不合格的。

试题二：连续型随机变量的概率密度函数设随机变量X的概率密度函数为f(x) = 2x，0 ≤ x ≤ 1，0 其他，求：1. X的期望E(X)。

2. X的方差Var(X)。

试题三：大数定律与中心极限定理假设某银行每天的交易量服从均值为100万元，标准差为20万元的正态分布。

求：1. 该银行连续5天的总交易量超过500万元的概率。

2. 根据中心极限定理，该银行连续20天的总交易量的平均值落在90万元至110万元之间的概率。

试题四：统计推断某工厂生产的零件长度服从正态分布，样本数据如下：95, 96, 97, 98, 99, 100, 101, 102, 103, 104求：1. 零件长度的平均值和标准差。

2. 零件长度的95%置信区间。

试题五：假设检验某公司对两种不同品牌的打印机进行了效率测试，测试结果如下：品牌A：平均打印速度为每分钟60页，标准差为5页。

品牌B：平均打印速度为每分钟55页，标准差为4页。

样本量均为30台打印机。

假设两种打印机的平均打印速度没有显著差异，检验假设是否成立。

答案一：1. 至少有80件产品是合格的，即不合格的产品数少于或等于20件。

根据二项分布，P(X ≤ 20) = Σ[C(100, k) * (0.1)^k *(0.9)^(100-k)]，k=0至20。

2. 至多有5件产品是不合格的，即不合格的产品数不超过5件。

根据二项分布，P(X ≤ 5) = Σ[C(100, k) * (0.1)^k * (0.9)^(100-k)]，k=0至5。

答案二：1. E(X) = ∫[2x * x dx]，从0到1，计算得 E(X) = 2/3。

2. Var(X) = E(X^2) - [E(X)]^2 = ∫[2x^2 * x dx] - (2/3)^2，从0到1，计算得 Var(X) = 1/18。

概率统计试题及答案概率统计是数学中的一个重要分支，它在自然科学、社会科学、工程技术等多个领域都有着广泛的应用。

本文将提供一套概率统计的试题及答案，以供学习和复习之用。

一、选择题1. 概率论中，如果事件A和B是互斥的，那么P(A∪B)等于：A. P(A) + P(B)B. P(A) - P(B)C. P(A) / P(B)D. 1 - (1 - P(A))(1 - P(B))答案：A2. 以下哪项不是随机变量的典型性质？A. 可测性B. 有界性C. 随机性D. 独立性答案：D3. 标准正态分布的数学期望和方差分别是：A. 0和1B. 1和0C. 1和1D. 0和0答案：A4. 若随机变量X服从参数为λ的指数分布，其概率密度函数为f(x) = λe^(-λx), x > 0，则λ的值为：A. E(X)B. Var(X)C. E(X)^2D. 1 / Var(X)答案：D5. 在贝叶斯定理中，先验概率是指：A. 基于经验或以往数据得到的概率B. 基于主观判断得到的概率C. 事件实际发生的概率D. 事件未发生的概率答案：B二、填空题1. 事件的空间是指包含所有可能发生的事件的集合，其记作______。

答案：Ω2. 若随机变量X服从均匀分布U(a,b)，则X在区间[a, b]上的概率密度函数是______。

答案：1 / (b - a)3. 两个事件A和B相互独立的必要不充分条件是P(A∩B) = ______。

答案：P(A)P(B)4. 若随机变量X服从正态分布N(μ, σ^2)，则其概率密度函数为f(x) = (1 / (σ * √(2π))) * e^(- (x - μ)^2 / (2σ^2))，其中μ是______，σ^2是______。

答案：数学期望，方差5. 拉普拉斯定理表明，对于独立同分布的随机变量序列，当样本容量趋于无穷大时，样本均值的分布趋近于______分布。

答案：正态三、简答题1. 请简述条件概率的定义及其计算公式。

概率论与数理统计习题集第一章 随机事件及其概率一、填空题1、袋中有a 只白球，b 只红球，k 个人（k a b ≤+）依次在袋中取一只球，在不放回抽样下，求第2个人取到白球的概率_______.2、设B A ,是两个事件，已知1()4P A =，1()2P B =，1()8P AB =，则()P AB =_______.3、袋中装有10只球，其编号为1,2,,10 .从中任取3只球，则取出的球中最大号码为5的概率是_______.4、设A 与B 为两个事件，()0.4P A B ⋃=，则()P AB =____.5、设A 与B 为两个互不相容的事件，()0.4,()0.5P A P B ==，则()P AB =____.6、某一治疗方法对一个患者有效的概率为0.9，今对3个患者进行了治疗，对各个患者的治疗效果是相互独立的，则对3个患者的治疗中，至少有一人是有效的概率_____.7、设B A ,两事件相互独立，6.0)(=⋃B A P ，4.0)(=A P ，则=)(B P _________.8、3个人独立地破译一份密码，已知各人能译出的概率分别为111,,,543则三人能同时译出密码的概率是________.9、设事件B A ,相互独立，()0.3,()0.18P A P AB ==，则()P B =_______. 10、设C B A ,,为事件，B A ,至少有一个发生，但C 不发生的事件可以表示为_______.11、甲、乙两人分别独立破译某个密码，设甲、乙单独译出的概率是0.4，0.7，则密码能译出的概率是_______.12、设C B A ,,为事件，B A ,发生，但C 不发生的事件可以表示为_______. 二、选择题1、向指定的目标射三枪，以321,,A A A 分别表示事件“第一、二、三枪击中目标”，则“只击中第一枪”用321,,A A A 表示为_______.（A ） 1A (B) 321A A A (C) 321A A A (D) 321A A A ⋃⋃2、设事件A ，B ，()0,()0,P A P B >>且A B ⊂，则下列命题正确的是_____. (A)()()()P A B P A P B ⋃=+ (B)()()()P AB P A P B =(C)()()()P A P A B P B =(D)()()()P A B P A P B -=- 3、设A ，B 是任意两个事件，则()P A B -=_____. (A)()()P A P B - (B)()()()P A P B P AB -+ (C)()()P A P AB - (D) ()()()P A P B P AB +-4、设A 与B 互不相容，0)(,0)(>>B P A P ，则___________一定成立.（A ） )(1)(B P A P -= （B ） 0)(=B A P （C ） 1)(=B A P （D ） 0)(=AB P 5、向指定的目标射击三枪，若以321,,A A A 分别表示事件“第一、二、三枪击中目标”，则“至少击中一枪”用321,,A A A 表示为_________. （A ）1A （B ）321A A A ⋃⋃ （C ）321A A A （D ）321A A A6、设事件A 与B 互不相容，()0P B >，则_______一定成立.（A ） ()0P B A > （B ）()()P A B P A = （C ）()0P A B = （D ）()()()P AB P A P B = 7、从5双不同型号的鞋中任取4只，则至少有2只鞋配成1双的概率为_______.（A ） 121 （B ）1221 （C ）821 （D ）13218、设A 与B 是两个事件，已知()0.5,()0.7,()0.8P A P B P A B ==⋃=，则()P AB =_______.（A ）0.1 （B ）0.3 （C ）0.5 （D ）09、设事件A 与B 相互独立，()0>A P ，()0P B >，则_______一定不成立.（A ） ()0P B A > (B) ()()P A B P A = (C) ()0P A B = (D) ()()()P AB P A P B =10、设每次试验成功的概率是)10(<<p p ，则3次重复独立试验都失败的概率为_______.（A ） 3p (B) 3)1(p - (C))1()1(22p p p p -+- (D) 1-3p11、设事件A 与B 互不相容，0)(,0)(>>B P A P ，则_______一定成立.（A ） )(1)(B P A P -= (B) 1)(=B A P (C) 1)(=B A P (D) 1)(=AB P12、设A 与B 是两个事件，已知()0.5,()0.7,()P A P B P A B ==⋃=，则()AB P =_______.（A ） 0.1 (B) 0.3 (C)0.5 (D) 0.4三、综合计算题1、计算机中心有三台打字机A,B,C ，程序交与各台打字机打字的概率依次为0.6,0.3,0.1，打字机发生故障的概率依次为0.01,0.05,0.04.已知一程序因打字机发生故障而被破坏了，求该程序是在A,B,C 上打字的概率分别为多少？ 2、一种用来检验50岁以上的人是否患有关节炎的检验法，对于确实患关节炎的患者有85%给出了正确结果；而对于已知未患关节炎的人有4%会认为他患关节炎.已知人群中有10%的人患有关节炎.问一名被检验者经检验，认为他没有患关节炎，而他却患有关节炎的概率？3、某地区居民的肝癌发病率为0.0004，现用甲胎蛋白法进行普查，医学研究表明，化验结果是存在错误的.已知患有肝癌的人其化验结果99%呈阳性（有病），而没有患有肝癌的人其化验结果99.9%呈阴性（无病），现某人的检验结果为阳性，问他真的患肝癌的概率是多大.4、设一仓库中有10箱同种规格的产品，其中由甲、乙、丙三厂生产的分别为5箱、3箱、2箱，三厂产品的次品率依次为0.1，0.2，0.3，从这10箱中任取一箱，再从这箱中任取一件，求这件产品为正品的概率.若取出的产品为正品，它是甲厂生产的概率是多少.5、一在线计算机系统，有4条输入通讯线，其性质如下表，求一随机选择的进入讯号无误差地被接受的概率.通讯线 通讯量的份额 无误差的讯息的份额 1 0.4 0.9998 2 0.3 0.9999 3 0.1 0.9997 4 0.20.99966、甲袋中有3个白球2个黑球，乙袋中有4个白球4个黑球，今从甲袋中任取2球放入乙袋，再从乙袋中任取一球，求该球是白球的概率.7、假设有同种零件两箱，第一箱内装50件，其中10件一等品；第二箱内装30件，其中18件一等品。

02197概率论与数理统计一、单项选择题（在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

） 1．将一枚硬币连抛两次，则此随机试验的样本空间为 【 B 】A ．{（正，正），（反，反），（一正一反）}B ．{ (反，正)，（正，反），（正，正），（反，反）}C ．{一次正面，两次正面，没有正面}D ．{先得正面，先得反面}2. 设A 与B 互不相容，且()0P A >，()0P B >则有 【 D 】A. ()1()P A P B =-B. ()()()P AB P A P B =C. ()1P AB =D. ()()()P AB P A P B =+3. 若φ≠AB ，则下列各式中错误的是 【 C 】A ．0)(≥AB PB.1)(≤AB PC. P(A+B)=P(A)+P(B)D. P(A-B)≤P(A)4. 若A B ⊂，则下面答案错误的是 【 A 】A. B 未发生A 可能发生B. ()B-A 0P ≥C. ()B P A P ≤)(D. B 发生A 可能不发生5. 袋中有a 个白球,d 个黑球,从中任取一个,则取得白球的概率是 【 C 】A.21B. 1a d +C. a a d +D. da d + (c5)6. 设A,B,C 是三个相互独立的事件,且,1)(0<<C P 则下列给定的四对事件中,不独立的是【 C 】 A.C AUB 与 B. B A -与C(B5)C. C AC 与D. C AB 与 7. 设,1)()|(,1)(0,1)(0=+<<<<B A P B A P B P A P 且则 【 D 】A. A 与B 不相容B. A 与B 相容C. A 与B 不独立D. A 与B 独立8. 四人独立地破译一份密码,已知各人能译出的概率分别为61,31,41,51则密码最终能被译的概率为【 D 】A. 1B. 21(B8\c8)C. 52D. 329. 已知11()()(),()0,()(),416P A P B P C P AB P AC P BC ======则事件A,B,C 全不发生的概率为 【 B 】A.81B. 83C. 85D.87 10. 设随机变量X 服从参数为λ的泊松分布，且},2{}1{===X P X P 则}2{>X P 的值为【 B 】A.2-e B.251e -C.241e-D.221e-. 11. 设),4,(~μN X 则 【 C 】A.)1,0(~4N X μ-B.21}0{=≤X PC.)1(1}2{Φ-=>-μX PD.0≥μ12. 设随机变量X 的概率密度函数为(),23X f x Y X =-+则的密度函数为 。

概率统计试题及答案在概率统计学中，试题和答案的准确性和清晰度非常重要。

下面将给出一系列关于概率统计的试题和详细的解答，以帮助读者更好地理解和应用概率统计的基本概念和技巧。

试题一：基础概率计算某餐厅有3个主菜，每个主菜又有4种不同的配菜。

如果顾客在选择主菜和配菜时是随机的，那么一个顾客会选择哪种搭配的概率是多少？解答一：根据概率统计的基本原理，计算顾客选择搭配的概率可以使用“事件数除以样本空间”的方法。

在这个问题中，总共有3个主菜和4种配菜，所以样本空间的大小为3 × 4 = 12。

而一个顾客选择一种特定的搭配可以有1种选择，因此事件数为1。

因此，顾客选择某种搭配的概率为1/12。

试题二：概率的加法规则某班级有25名男生和15名女生。

从中随机选择一名学生，那么选择一名男生或选择一名女生的概率分别是多少？解答二：根据概率统计的加法规则，选择一名男生或选择一名女生的概率可以通过计算每个事件的概率然后相加来得到。

在这个问题中，男生和女生分别属于两个互斥事件，因此可以直接相加。

男生的概率为25/40，女生的概率为15/40。

因此，选择一名男生或选择一名女生的概率为25/40 + 15/40 = 40/40 = 1。

试题三：条件概率计算某电子产品的退货率是0.05，而该产品是有瑕疵的情况下才会退货。

对于一台已经退货的产品，有0.02的概率是有瑕疵的。

那么一台被退货且有瑕疵的电子产品占所有退货产品的比例是多少？解答三：根据条件概率的定义，求一台被退货且有瑕疵的电子产品占所有退货产品比例的问题，可以用有瑕疵且被退货的产品数除以所有被退货的产品数来得到。

假设有1000台电子产品被退货，根据退货率的定义，有5%的产品会被退货，即退货的产品数为0.05 * 1000 = 50台。

而在这50台退货产品中，有2%有瑕疵，即有瑕疵且被退货的产品数为0.02 * 50 = 1台。

因此，一台被退货且有瑕疵的电子产品占所有退货产品的比例为1/50，即0.02。

2016年4月全国自考概率论与数理统计（经管类）真题试卷(题后含答案及解析)题型有：1. 单项选择题 2. 填空题 3. 计算题 4. 综合题 5. 应用题单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．设A，B为随机事件，A B，则～( )正确答案：B解析：2．设随机事件A，B相互独立，且P(A)=0．2，P(B)=0．6，则= ( )A．0．12B．0．32C．0．68D．0．88正确答案：B解析：3．设随机变量X的分布律为F(x)为X的分布函数，则F(0．5)= ( )A．0B．0．2C．0．25D．0．3正确答案：D解析：F(0．5)=P(x≤0．5)=P(X=－1)+P(X=0)=0．3．4．设二维随机变量(X，Y)的分布函数为F(x，y)，则(X，Y)关于X的边缘分布函数FX(x)= ( )A．F(x，+∞)B．F(+∞，y)C．F(x，－∞)D．F(－∞，y)正确答案：A解析：边缘概率密度fX(x)=∫－∞+∞f(x，y)dy，－∞＜x＜+∞．FX(x)=F(x，+∞)．5．设二维随机变量(X，Y)的分布律为则P{X+Y=3}= ( )A．0．1B．0．2C．0．3D．0．4正确答案：D解析：P{X+Y=3}=P(X=1，Y=2)+P(X=2，Y=1)=0．3+0．1=0．4．6．设X，Y为随机变量，E(X)=E(Y)=1，Cov(X，Y)=2，则E(2XY) ( ) A．－6B．－2C．2D．6正确答案：D解析：E(XY)=Cov(X，Y)+E(X)E(Y)=3．E(2XY)=2E(XY)=6．7．设随机变量X～N(0，1)，Y～χ2(5)，且X与Y相互独立，则( )A．t(5)B．t(4)C．F(1，5)D．F(5，1)正确答案：A解析：随机变量X1～N(0，1)，X2～χ2(n)，则t=为自由度为n的t 分布．8．设总体X～B(1，p)，x1，x2，…，xn为来自X的样本，n＞1，为样本均值，则未知参数p的无偏估计=( )A．B．C．D．正确答案：C解析：X～B(1，P)，参数P无偏估计为其样本均值．9．在假设检验过程中，增大样本容量，则犯两类错误的概率( ) A．都增大B．都减小C．都不变D．一个增大，一个减小正确答案：B解析：要同时降低两类错误的概率，需增大样本容量n．10．依据样本(xi，yi)(i=1，2，…，n)得到一元线性回归方程为样本均值．令，则回归系数= ( )A．B．C．D．正确答案：A解析：回归系数β1最小二乘估计为填空题请在每小题的空格中填上正确答案。

全国2016年10月高等教育自学考试 概率论与数理统计（经营类）试题课程代码：04183一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其选出并将“答题纸”的相应代码涂黑。

错涂、多涂或未涂均无分。

1．设A 与B 是两个随机事件，则P （A-B ）＝（D ） A ．P （A ） B ．P （B ） C ．P （A ）-P （B ） D ．P （A ）-P （AB ）第1章第5个知识点。

2．设随机变量X 的分布律为10120.10.20.30.4X P-，则P{－1＜X ≤1}＝（D ）A ．0.1B ．0.2C ．0.3D ．0.5第2章第1个知识点。

3．设二维随机变量（X ，Y ）的分布律为0100.20.21Y Xab且X 与Y 相互独立，则下列结论正确的是（B ） A ．a ＝0.2，b ＝0.2 B ．a ＝0.3，b ＝0.3 C ．a ＝0.4，b ＝0.2 D ．a ＝0.2，b ＝0.4第3章第6个知识点。

4．设二维随机变量（X ，Y ）的概率密度为1,04,04,(,)160x y f x y ⎧<<<<⎪=⎨⎪⎩，其他，则{02,02}P X Y <<<<=（B ）A ．1/16B ．1/4C ．9/16D ．1第3章第3个知识点。

5．设随机变量X 服从参数为1/2的指数分布，则D （X ）＝（D ） A ．1/4 B ．1/2 C ．2D ．4第4章第6个知识点。

6．设随机变量X 服从二项分布B （10，0.6），Y 服从均匀分布U （0，2），则E （X －2Y ）＝（A ） A ．4 B ．5 C ．8D ．10第4章第6个知识点。

7．设（X ，Y ）为二维随机变量，且D （X ）＞0，D （Y ）＞0，ρXY 为X 与Y 的相关系数，则Cov （X ，Y ）＝（A ）A ．XY ρB ．()()XY D X D Y ρ⋅⋅C ．()()E X E Y ⋅D ．()()D X D Y ⋅第4章第8个知识点。

习 题 一1．写出下列随机试验的样本空间：(1)记录一个班级一次概率统计考试的平均分数(设以百分制记分)。

(2)同时掷三颗骰子，记录三颗骰子点数之和。

(3)生产产品直到有10件正品为止，记录生产产品的总件数。

(4)对某工厂出厂的产品进行检查，合格的记上“正品”，不合格的记上“次品”，如连续查出2个次品就停止检查，或检查4个产品就停止检查，记录检查的结果。

(5)在单位正方形内任意取一点，记录它的坐标。

(6)实测某种型号灯泡的寿命。

解：（1）{|0,1,2,,100}i i n nΩ==，其中n 为小班人数。

（2）Ω={3, 4,…,18}。

（3）Ω={10，11，…}。

（4）Ω={00，100，0100，0101，0110，1100，1010，1011，0111，1101，1110，1111}，其中0表示“次品”，1表示“正品”。

（5）{(,)|01,01}x y x y Ω=<<<<。

（6）{|0}t t Ω=≥。

2．设A ，B ，C 为三事件，用A ，B ，C 的运算关系表示下列各事件。

X(1)A 发生，B 与C 不发生。

(2)A 与B 都发生，而C 不发生。

(3)A ，B ，C 中至少有一个发生。

(4)A ，B ，C 都发生。

(5)A ，B ，C 都不发生。

(6)A ，B ，C 中不多于一个发生。

(7)A ，B ，C 至少有一个不发生。

(8)A ，B ，C 中至少有两个发生。

解：（1）C B A ；（2）C AB ；（3）A ∪B ∪C 或C B A ；（4）ABC ；（5）C B A ； （6）C B C A B A ⋃⋃或C B A BC A C B A C B A C B A ⋃⋃⋃⋃；（7）C B A ⋃⋃；（8）AB ∪AC ∪BC 或ABC BC A C B A C AB ⋃⋃⋃.3．指出下列命题中哪些成立，哪些不成立，并作图说明。

(1)B B A B A =； (2)AB B A =；(3)若A B ⊂，则AB B =； (4)若B A ⊂，则A B ⊂； (5)C B A C B A = ； (6) 若Φ=AB 且A C ⊂， 则Φ=BC 。

概率统计考试试卷及答案一、 填空题（每小题4分，共20分）1. 设)(~λP X ,且)()(21===X P X P ,则_________)(==3X P .2. 设随机变量X 的分布函数)(,)(+∞<<-∞+=-x eA x F x1，则___=A3. 已知,)|(,)|(,)(213141===B A P A B P A P 则_____)(=⋃B A P 4. 已知随机变量),,(~10U X 则随机变量X Y ln 2-=的密度函数___)(=y f Y5. 设随机变量X 与Y 相互独立，且,2σ==DY DX 则____)(=-Y X D 42 二、 计算下列各题（每小题8分，共40分)1. 设随机变量X 的概率密度为⎪⎩⎪⎨⎧≤>=-000x x e x f x ,,)( 已知Y=2X ，求E(Y ）， D(Y ）.2. 两封信随机地投入标号为I ，II,III ，IV 的四个邮筒，求第二个邮筒恰好投入1封信的概率.3. 设X,Y 是两个相互独立的随机变量,X 在（0，1）上服从均匀分布,Y的概率密度为⎪⎩⎪⎨⎧≤>=-000212y y e y f yY ,,)( 求含有a 的二次方程022=++Y Xa a 有实根的概率。

4. 假设91X X ,, 是来自总体),(~220N X 的简单随机样本,求系数a,b ，c 使 298762543221)()()(X X X X c X X X b X X a Q ++++++++=服从2χ分布，并求其自由度.5. 某车间生产滚珠，从长期实践知道,滚珠直径X 服从正态分布。

从某天产品里随机抽取6个,测得直径为（单位：毫米)14.6, 15。

1， 14。

9， 14。

8， 15.2, 15.1 若总体方差0602.=σ， 求总体均值μ的置信区间（9610502.,./==ααz ）三、（14分）设X,Y 相互独立，其概率密度函数分别为⎩⎨⎧≤≤=其他 ,,)(0101x x f X ，⎪⎩⎪⎨⎧≤>=-000y y e y f y Y ,,)( 求X+Y 的概率密度四、（14分）设⎪⎩⎪⎨⎧≤<-=其它,),()(~0063θθθx x xx f X ,且n X X ,, 1是总体X的简单随机样本，求 (1）θ的矩估计量θ，(2) )(θD五、（12分）据以往经验，某种电器元件的寿命服从均值为100小时的指数分布，现随机地取16只,设它们的寿命是相互独立的,求这16只元件的寿命的总和大于1920小时的概率.（7881080.).(=Φ）普通本科概率统计期末考试试卷答案：一、填空题(每小题4分，共20分)1、243e -；2、 1；3、13；4、/21,020,0y e y y -⎧>⎪⎨⎪≤⎩； 5、220σ二、计算下列各题（每小题8分，共40分） 1、解：2()EY xf x dx +∞-∞=⎰。

2016年10月全国自考概率论与数理统计（经管类）真题试卷(题后含答案及解析)题型有：1. 单项选择题 2. 填空题 3. 计算题 4. 综合题 5. 应用题单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．设A，B为随机事件，且B A，P(A)=0．4，P(B)=0．2，则P(B｜A)=【】A．0．2B．0．4C．0．5D．1正确答案：C解析：因B A，故P(AB)=P(B)，则P(B｜A)==0．5．2．设随机变量X～B(3，0．2)，则P{X＞2}= 【】A．0．008B．0．488C．0．512D．0．992正确答案：A解析：因为X～B(3，0．2)，故P{X＞2}=P{X=3}=C33×(0．2)3×(1－0．2)0=0．008．3．设随机变量X的概率密度为f(x)=，则X～【】A．N(－2，2)B．N(－2，4)C．N(2，2)D．N(2，4)正确答案：B4．设随机变量X的分布函数为F(x)，则下列结论中不一定成立的是【】A．F(－∞)=0B．F(+∞)=1C．0≤F(x)≤1D．F(x)是连续函数正确答案：D5．设二维随机变量(X，Y)的分布律为则P{X≤Y}= 【】A．0．25B．0．45C．0．55D．0．75正确答案：D解析：P{X≤Y}=P{X=1，Y=1}+P{X=1，Y=2}+P{X=2，Y=2}=0．2+0．25+0．3=0．75．6．设随机变量X服从参数为的指数分布，则E(2X－1)= 【】A．0B．1C．3D．4正确答案：C解析：X～，则E(X)=2．故E(2X－1)=2E(X)－1=3．7．设随机变量X与Y相互独立，且D(X)=D(Y)=4，则D(3X－Y)= 【】A．8B．16C．32D．40正确答案：D解析：因为X与Y相互独立，所以D(3X－Y)=9D(X)+D(Y)=9×4+4=40．8．设总体X服从正态分布N(0，1)，x1，x2，…，xn是来自X的样本，则x12+x22+…+xn2～【】A．N(0，)B．N(0，1)C．χ2(n)D．t(n)正确答案：C9．设x1，x2，x3，x4为来自总体X的样本，且E(X)=μ．记，则μ的无偏估计是【】A．B．C．D．正确答案：B解析：10．设总体X～N(μ，σ02)，σ02已知，x1，x2，…，xn为来自X的样本，为样本均值．假设H0：μ=μ0，H1：μ≠μ0，μ0已知，检验统计量u=，给定检验水平α，则拒绝H0的理由是【】A．B．C．D．正确答案：B填空题请在每小题的空格中填上正确答案。