xC桁架的内力计算学习资料

桁架内力桁架内力是指桁架结构在受到外部力作用时所承受的内部力。

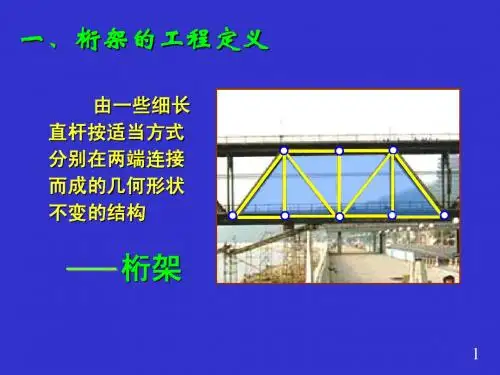
桁架结构是由多根互相连接的直线构成的一种空间结构形式，常见于建筑和机械工程中，用于支撑和分担结构的载荷。

了解桁架内力对于设计和分析桁架结构的稳定性和安全性非常重要。

以下是一些相关参考内容：1. 桁架结构和内力分析基本原理桁架结构的原理是将力沿桁架的元素进行传递和分担。

在受力分析中，通过应用平衡原理和静力学等基本原理，可以推导出桁架结构中各个桁架元素所受的内力。

这些内力包括张力、压力和剪力等。

了解这些基本原理对于理解桁架内力分析的方法和原则非常重要。

2. 桁架内力的计算方法桁架内力的计算可以通过静力平衡和弹性力学原理进行。

一般来说，可以根据桁架结构的几何形状和外部荷载，采用基本的力平衡原理和弹性力学公式，推导出各个桁架元素所受的内力。

计算方法包括节点法、截面法、力法和位移法等。

这些方法在不同场景和结构要求下应用于桁架结构的内力计算和分析。

3. 桁架内力的影响因素桁架内力的大小和分布受到多个因素的影响，包括结构的几何形状、荷载情况、边界条件和材料性能等。

通过对这些因素的研究和分析，可以更好地了解和预测桁架内力的变化规律。

例如，在分析桁架结构的受力性能时，需要考虑荷载的大小、方向和分布情况，以及桁架元素的尺寸和刚度等。

4. 桁架内力的应用案例桁架内力的计算和分析在实际工程中有广泛的应用。

例如，在建筑结构设计中，桁架结构常用于大跨度的屋顶、桥梁和支撑结构中。

通过分析桁架结构的内力，可以评估其受力性能和稳定性，并确保结构的安全性。

在机械工程中，桁架结构常用于起重机、吊车和机械臂等设备中，用于承载和分担重物。

通过分析桁架内力，可以评估结构的承载能力和运动性能。

总结来说，桁架内力是桁架结构在受到外部荷载作用时所承受的内部力。

了解桁架内力对于设计和分析桁架结构的稳定性和安全性非常重要。

通过应用平衡原理和弹性力学等基本原理，可以计算出桁架内力的大小和分布。

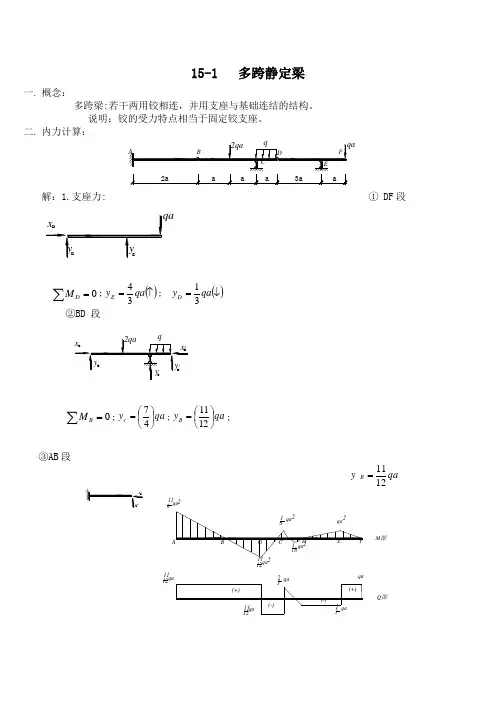
15-1 多跨静定梁031=+-=+'=qx qa qx y Q DX a x 31=2当lX = αcos 2l q Q B -=αα0sin sin =--qx y N A X因在梁上的总载不变：ql l q =11 αcos 11111ql l q q l l q ===()()()11122112211111d p l V fH MH H x a p a p lV M b p b p l V A A CBA B A A -⋅====+==+=∑∑∑fMHVVVVCABBAA===f=0时，HA=∞，为可弯体系。

简支梁：①1PVQA-=()axPV A--1H=+HA，（压为正）②()yHaxpxVMAA---=11即yHMMA-=D截面M、Q、N()yHaxpxVMAAx⋅---=11即yHMMAx-=ϕϕϕϕsinsinsincosHQNHQQxx+=-=说明：ϕ随截面不同而变化，如果拱轴曲线方程()xfy=已知的话，可利用dxdytg=ϕ确定ϕ的值。

二.三铰拱的合理轴线（拱轴任意截面==QM）据：yHMMA⋅-= 当0=M时，AHMy=M是简支梁任意截面的弯矩值，为变值。

说明：合理拱轴材料可得到充分发挥。

fMH cA=（只有轴力，正应力沿截面均匀分布）cM 为简支跨中弯矩。

由于 M 、A H 荷载不同，其结果不同，故不同荷载有不同的合理拱轴方程。

弯矩时则使刚架内侧受拉b. 内力校核：取出刚架中任一部分（如刚结点），按∑∑∑===000M Y X 校核。

四. 讲书上例题及补充例题。

15-4 静定平面桁架一 .桁架特点：1. 结构中所有杆为二力杆;2. 杆与杆之间是移铰连接二.桁架类型：1. 简单桁架；2.联合桁架；3.复杂桁架；举例 三.求内力方法及原理：1. 方法:①结点法②截面法2. 原理 ：①结点法----汇交力系平衡条件∑∑==00y x∑=0x11;01;022--==--=∑y yy。

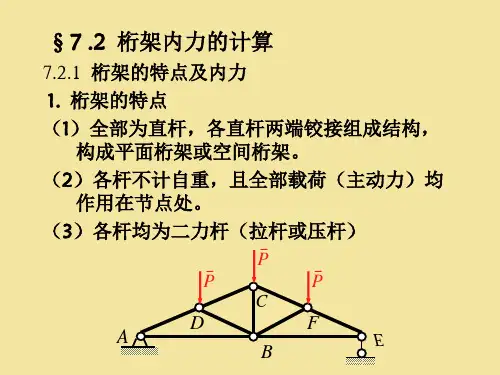
截面法‹1截面法可以快速求出某一内力，通常取结构 的一部分为隔离体，其上力系为平面一般力系。

每个隔离体上有3个独立平衡方程。

一般表示 为： ∑ FX = 0 投影法 ∑ FY = 0 力矩法 ∑M = 0 计算要点： 尽量使一个方程解一个未知数，避免求解 联立方程。

一. 力矩法例：求图示桁架1、2、3杆的轴力。

2VAVB解：由整体平衡条件求得支座反力 VA=VB HA=0作Ⅰ--Ⅰ截面,截开1、2、3杆的轴力 取截面以左为隔离体。

Ⅰ3Ⅰ（1）求1杆轴力N1K14选取未知力N2和N3 延长线的交点K1作 为取矩点。

N1 对K1点取矩，由 ∑MK1 = 0 从而求出所求未知 力N1。

VA（2）求2杆轴力N2N2 K2 VAY252X2由∑MK2 = 0 ,比例关系从而求出所求未知力Y2。

2杆轴力N2（3）求3杆轴力N3Y3 N3 X3K3 VA6由 ∑MK3 = 0比例关系从而求出所求未知力X3。

3杆轴力N3力矩法要点：„7„„欲求某指定杆内力，则作一截面，截开待求 杆； 隔离体上除所求未知力外，其余未知力的延 长线均交于某一点K。

对K点取矩，从而求出所求未知力 。

（1）选择其余未知力延长线的交点K作为取矩 点，从而用∑MK=0，求出指定杆内力。

（2）将斜杆的内力放在某一个合适的点上分 解，使其一个分力通过取矩点K。

例1. 求图示桁架杆件a、b、c的轴力890kN30kN作Ⅰ—Ⅰ截面Ⅰ9Ⅰ求NaNa 求Na时，对另 外两个未知力的 交点C取矩，10C由 ΣMc＝0，得 Na×4＋30×8＝030kN解得： Na =－ 60kN求NbD Xb E Yb Nb30kN11求Nb时，对点D取矩。

将Nb 其在E点处分解 为水平和竖向分量。

由ΣMD＝0，得 Yb×12＋40×4 － 30×12＝0 解得 Yb＝16.67 kN由比例关系得到：N b = 2Yb = 2 × 16.67 = 23.57kN求NcYc XcD Nc12求Nc时，对点E取矩。

15-1 多跨静定梁031=+-=+'=qx qa qx y Q DX a x 31=2当lX =αcos 2l q Q B -=αα0sin sin =--qx y N A X因在梁上的总载不变：ql l q =11 αcos 11111q l l q q l l q ===()()()11122112211111d p l V fH MH H x a p a p lV M b p b p l V A A CBA B A A -⋅====+==+=∑∑∑fMHVVVVCABBAA===f=0时，HA=∞，为可弯体系。

简支梁：①1PVQA-=()axPV A--1H=+HA，（压为正）②()yHaxpxVMAA---=11即yHMMA-=D截面M、Q、N()yHaxpxVMAAx⋅---=11即yHMMAx-=ϕϕϕϕsinsinsincosHQNHQQxx+=-=说明：ϕ随截面不同而变化，如果拱轴曲线方程()xfy=已知的话，可利用dxdytg=ϕ确定ϕ的值。

二.三铰拱的合理轴线（拱轴任意截面==QM）据：yHMMA⋅-= 当0=M时，AHMy=是简支梁任意截面的弯矩值，为变值。

说明：合理拱轴材料可得到充分发挥。

fMH cA=（只有轴力，正应力沿截面均匀分布）cM 为简支跨中弯矩。

由于M、AH荷载不同，其结果不同，故不同荷载有不同的合理拱轴方程。

弯矩时则使刚架内侧受拉 b. 内力校核：取出刚架中任一部分（如刚结点），按∑∑∑===000M Y X 校核。

四. 讲书上例题及补充例题。

15-4 静定平面桁架一 .桁架特点：1. 结构中所有杆为二力杆;2. 杆与杆之间是移铰连接二.桁架类型：1. 简单桁架；2.联合桁架；3.复杂桁架；举例三.求内力方法及原理：1. 方法:①结点法②截面法2. 原理 ：①结点法----汇交力系平衡条件∑∑==00y x∑=0x11;01;022--==--=∑y yy。