固体物理 第二章 晶体的结合知识讲解

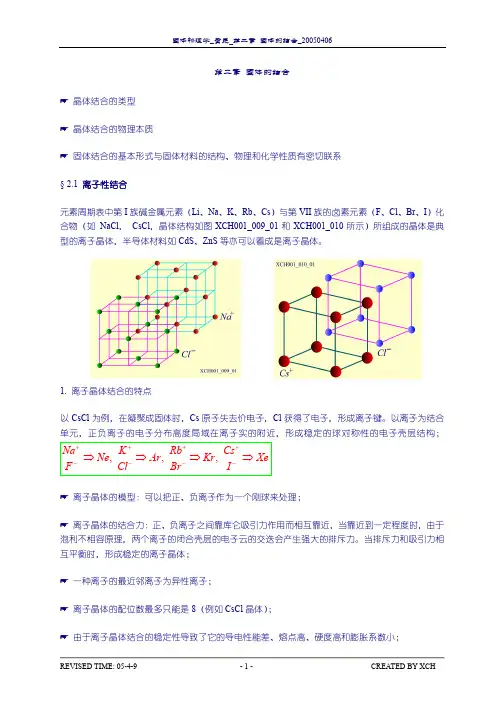
第二章 固体的结合晶体结合的类型 晶体结合的物理本质固体结合的基本形式与固体材料的结构、物理和化学性质有密切联系 § 2.1 离子性结合元素周期表中第I 族碱金属元素（Li 、Na 、K 、Rb 、Cs ）与第VII 族的卤素元素（F 、Cl 、Br 、I ）化合物（如 NaCl ， CsCl ，晶体结构如图XCH001_009_01和XCH001_010所示）所组成的晶体是典型的离子晶体，半导体材料如CdS 、ZnS 等亦可以看成是离子晶体。

1. 离子晶体结合的特点以CsCl 为例，在凝聚成固体时，Cs 原子失去价电子，Cl 获得了电子，形成离子键。

以离子为结合单元，正负离子的电子分布高度局域在离子实的附近，形成稳定的球对称性的电子壳层结构；,,,Na K Rb Cs Ne Ar Kr Xe FClBrI++++−−−−⇒⇒⇒⇒离子晶体的模型：可以把正、负离子作为一个刚球来处理；离子晶体的结合力：正、负离子之间靠库仑吸引力作用而相互靠近，当靠近到一定程度时，由于泡利不相容原理，两个离子的闭合壳层的电子云的交迭会产生强大的排斥力。

当排斥力和吸引力相互平衡时，形成稳定的离子晶体； 一种离子的最近邻离子为异性离子；离子晶体的配位数最多只能是8（例如CsCl 晶体）；由于离子晶体结合的稳定性导致了它的导电性能差、熔点高、硬度高和膨胀系数小；大多数离子晶体对可见光是透明的，在远红外区有一特征吸收峰。

氯化钠型(NaCl 、KCl 、AgBr 、PbS 、MgO)(配位数6) 氯化铯型(CsCl 、 TlBr 、 TlI)（配位数8）离子结合成分较大的半导体材料ZnS 等（配位数4） 2. 离子晶体结合的性质 1）系统内能的计算晶体内能为所有离子之间的相互吸引库仑能和重叠排斥能之和。

以NaCl 晶体为例，r 为相邻正负离子的距离，一个正离子的平均库仑能：∑++−++321321,,2/122322222102)(4)1('21n n n n n n r n r n r n q πε ——遍及所有正负离子，因子1/2—库仑作用为两个离子所共有，一个离子的库伦能为相互作用能的一半。

第二章 固体的结合晶体中粒子的相互作用力可以分为两大类，即吸引力和排斥力，前者在远距离是主要的，后者在近距离是主要的；在某一适当的距离，两者平衡，使晶格处于稳定状态。

吸引作用来自于异性电荷的库仑作用；排斥作用源于：一、同种电荷之间的库仑作用，二、泡利原理所引起的作用。

固体的结合根据结合力的性质分为四种基本形式：⎪⎪⎩⎪⎪⎨⎧范德瓦尔结合金属性结合共价性结合离子性结合 实际结合可能是兼有几种结合形式或者具有两种结合之间的过渡性质。

§2-1 离子性结合离子性结合的基本特点是以离子而不是以原子为结合的单位，结合的平衡依靠较强的静电库仑力，要求离子间相间排列。

其结构比较稳定，结合能为800千焦耳/摩尔数量级。

结合的稳定性导致导电性能差、熔点高、硬度高和膨胀系数小等特点。

以N a Cl 晶体为例，由于N a +和 Cl -离子满壳层的结构，具有球对称结构，可以看成点电荷，若令r 表示相邻离子的距离，则一个正离子的平均库仑能为：∑++-++321321,,2122322222102)(4)1(21n n n n n n r n r n r n q πε这里n 1，n 2，n 3为整数且不能同时为零。

一个元胞的库仑能为：απεπεr q n n n r q n n n n n n 02,,21232221024)()1(4321321-≡∑++-++上式中α为无量纲量，称为马德隆常数。

当邻近离子的电子云显著重叠时，将出现排斥，其能量可以由下式描述：n r rr bbe 或者0-因此含N 个元胞的晶体的系统内能可以表示为：)(nr B r A N U +-= 其和体积或者晶格常数的关系如下图（1） 晶格常数结合最稳定时的原子间距即为晶格常数，由下式决定0)(0=∂∂=r r r r U（2） 压缩系数压缩系数定义为单位体积的改变随单位压强的变化的负值，即：T pV V )(1∂∂-=κ 由热力学第一定律有：pdV dU -=（这里忽略了热效应），则压缩系数为：TV UV )(122∂∂=κ 体弹性模量为：κ1=K（3） 抗张强度晶体能够承受的最大张力，叫抗张强度。

固体物理讲义第二章2.1 晶体结构的实验确定晶体的结构可以通过衍射的方法来确定，即利用入射的射线束受晶体内部原子的相干散射产生衍射。

目前常用的衍射方法有X射线衍射、电子衍射和中子衍射。

其中，X射线衍射是最常用的方法，可以用于测量晶体内部结构，而电子衍射则适用于表面结构的测量，中子衍射则适用于磁性物质结构的测量。

晶体衍射的条件是波长与晶格常数同数量级。

现在，我们可以利用高分辨电子显微镜、场粒子显微镜和扫描透射电子显微镜直接观察原子排列和晶格结构。

虽然往往只能看到表面和局部的原子排列，但无论如何这是一种直接的观察，一种对原子规则结构的周期排列的直接验证。

2.2 晶体的倒格子和布里渊区晶体的倒格子是通过___格子的基矢量定义三个新的基矢量得到的，它们之间的关系为：b1 = 2π(a2×a3)/Ω，b2 =2π(a3×a1)/Ω，b3 = 2π(a1×a2)/Ω。

其中，a1、a2、a3为构成晶体正格子的基矢，Ω为正格子的体积。

倒格子中每个格点的位置为：Kh = h1b1 + h2b2 + h3b3，其中Kh称为倒格矢量，简称倒格矢。

倒格子空间也叫倒易点阵，每一个___正格子都有与之对应的倒格子。

正格子中的一族晶面(h1h2h3)和倒格矢Kh = h1b1 + h2b2+ h3b3正交，即d(h1h2h3)·Kh = 2π。

晶面族(h1h2h3)面间距d(h1h2h3)的长度正比于倒格矢Kh的倒数：d(h1h2h3) = 2π/|Kh|。

正格子原胞体积与倒格子原胞体积之间的关系为Ω = b1·b2×b3.倒格点与晶体中的一晶面相对应。

晶体中任一处r的物理量具有晶格周期性，可以展开为___级数。

比较展开式可得，周期为l的函数的倒格矢量一定是GG。

倒格子和正格子互相是对应的傅立叶空间。

每个晶体结构都有两套格子与之相联系，倒格子是与真实空间相联系的傅立叶空间中的格子，一定是___点阵。

第二章晶体的结合填空体1.晶体的结合类型为：离子结合分子结合、金属结合和氢键结合。

2.共价结合的特点—方向性和饱和性。

3.晶体中原子的相互作用力可分为两类吸引力—和排斥力。

4.一般固体的结合可概括为范德瓦耳斯结合、金属结合、离子结合和共价结合四种基本类型。

5.金属具有延展性的微观根源是金属原子容易相对滑动。

6.石墨晶体的结合涉及到的结合类型有共价结合、氢键结合和金属结合。

7.GaAs晶体的结合涉及到的结合类型有共价结合和离子结合。

二、基本概念1.电离能始原子失去一个电子所需要的能量。

2.电子的亲和能电子的亲和能：一个中性原子获得一个电子成为负离子所释放出的能量。

3.电负性描述化合物分子中组成原子吸引电子倾向强弱的物理量。

4.共价键原子间通过共享电子所形成的化学键。

5.离子键两个电负性相差很大的元素结合形成晶体时，电负性小的原子失去电子形成正离子，电负性大的得到电子形成负离子，这种靠正、负离子之间库仑吸引的结合成为离子键。

6.范德瓦尔斯力答：分子晶体的粒子间偶极矩相互作用以及瞬时偶极矩相互诱生作用力称为范德瓦耳斯力。

7.氢键答：氢原子处于两个电负性很强的原子（如氟、氧、氮、氯等）之间时，可同时受两个原子的吸引而与它们结合，这种结合作用称为氢键。

8.金属键答：在金属中，组成金属的原子的价电子已脱离母原子而成为自由电子，自由电子为整个晶体共有，而剩下的离子实就好像沉浸在自由电子的海洋中。

自由电子与离子实间的互相吸引作用具有负的势能，使势能降低形成稳定结构。

这种公有化的价电子（自由电子）与离子实间的互作用称为金属键。

三、简答题1.共价结合为什么有“饱和性”和“方向性”答：饱和性：当一个原子与其它原子结合时，能够形成共价键的数目有一个最大值，这个最大值决定于它所含的未配对的电子数，这个特性称为共价键的饱和性。

方向性：两个原子在以共价键结合时，必定选取尽可能使其电子云密度为最大的方位，电子云交迭得越厉害，共价键越稳固。

固体物理晶体结合晶体是具有高度有序结构的固体，其原子或分子排列有规律的空间网络。

固体物理研究的对象之一就是晶体结构及其性质。

晶体的结构决定了其物理性质，因此研究晶体结构对于理解材料的性能至关重要。

晶体的基本结构在固体物理学中，晶体被定义为原子或分子以有规则排列组成的空间网络。

最简单的晶体结构是立方晶体，其中原子在空间中排列成立方体网格。

除了立方晶体，还有多种晶体结构，如六方晶体、正交晶体等。

每种晶体结构都具有特定的对称性和周期性。

晶体的结合方式晶体的结合方式决定了其性质。

晶体中的原子或分子通过共价键、离子键、金属键等方式结合在一起。

其中，离子晶体是由正负离子构成的，它们之间通过静电力相互作用，形成离子键。

共价晶体是由原子通过共享电子而形成的，其中共价键是强有力的化学键。

金属晶体则是由金属原子通过金属键相互结合形成的，金属键是一种电子云的共享。

晶体的性质晶体的结合方式直接影响其性质。

离子晶体通常具有高熔点、硬度大、脆性等性质，共价晶体则更加稳定，具有较高的硬度和导电性。

金属晶体具有良好的导电性和可塑性。

此外，晶体还会表现出光学性质，如双折射、偏振等现象。

应用与展望固体物理中对晶体结合的研究不仅有助于理解材料的性质，还可以为材料设计和应用提供重要依据。

随着科学技术的不断发展，人们对晶体结构和性质的认识也在深化，预计在材料科学、电子学等领域会有更多的应用发展。

通过对固体物理中晶体结合的了解，可以看出晶体结构与材料性能之间的密切关系。

进一步的研究和应用将有助于开发出更多优异的材料，推动材料科学领域的发展，促进科学技术的进步和创新。

第二章 晶体中的衍射主要内容：● 晶体的倒格子和布里渊区 ● 晶体衍射的条件✓ 劳厄方程、布拉格反射● 原子散射因子和几何结构因子 2.1 晶体结构的实验确定方法：利用入射的射线束受晶体内部原子的相干散射－衍射。

● X 射线衍射光子与电子作用，晶体内部结构测量● 电子衍射电子与电子作用，表面结构测量● 中子衍射中子与原子核作用，磁性物质结构测量● 一般性地讨论波动在晶体中的衍射 衍射的条件：波长与晶格常数同数量级现在，我们可以利用高分辨电子显微镜、场粒子显微镜和扫描遂穿显微镜直接观察原子排列和晶格结构，虽然往往只能看到表面和局部的原子排列，但无论如何这是一种直接的观察，一种对原子规则结构的周期排列的直接验证。

X 射线衍射：有关晶体在0.1纳米尺度结构的主要知识主要来源于此。

本课程的核心－周期结构中传播的波。

2.2 晶体的倒格子和布里渊区 倒格子的定义根据布拉菲格子的基矢量定义三个新的基矢量，它们之间的关系为：以 为基矢构成的格子称为正格子以 为基矢构成的格子称为倒格子正格子中每个格点的位置为：倒格子中每个格点的位置为：K h 称为倒格矢量，简称倒格矢倒格子空间也叫倒易点阵，每一个布拉菲正格子都有与之对应的倒格子。

[]321a a a ⨯=Ω∙321a a a 、、321b b b 、、()()⎩⎨⎧≠==⋅j i i=j j i j i 0 22 ππδb a[][][]Ω⨯=Ω⨯=Ω⨯=213132321222a a b a a b a a b πππ倒格子的性质1 正格子中的一族晶面(h 1h 2h 3)和倒格矢332211b b b Kh h h h ++= 正交2 倒格矢332211b b b K h h h h ++= 的长度正比于晶面族(h 1h 2h 3)面间距321h h h d 的倒数：34 倒格点与正格子中的一晶面相对应周期性物理量的傅里叶变换晶体中任一处r 的物理量具有晶格周期性:将其展开为傅里叶级数：比较以上两式，可得R,r+R 对于晶格平移保持不变的任何函数，都可以展成傅立叶级数 倒格子和正格子互相是对应的傅立叶空间。

固体物理二章知识点总结固体物理第二章是关于晶体结构的内容，围绕着晶体的结晶结构、晶体点阵和基本晶胞的概念来展开讨论。

晶体是由周期性排列的原子或分子组成的，具有高度有序的结构，其结晶结构决定了晶体的性质和行为。

在这一章中，我们将从晶体的基本概念出发，逐步展开对晶体结构的探讨。

晶体的结晶结构是指晶体中原子或分子的排列方式和规律。

晶体的结晶结构包括晶体点阵和晶体的基本晶胞。

晶体点阵描述了晶体原子或分子的周期性排列方式，而晶体的基本晶胞则是由最小的重复单元构成，可以描述晶体的整体结构。

在这一部分，我们将介绍常见的晶体点阵和基本晶胞的类型以及它们之间的关系。

晶体点阵包括简单立方晶体、体心立方晶体和面心立方晶体等多种类型。

这些不同类型的晶体点阵具有不同的原子或分子排列方式和周期性，从而导致了晶体具有不同的性质和行为。

而晶体的基本晶胞则由部分晶胞和全部晶胞构成，它们决定了晶体的整体结构和周期性。

在这一章中，我们将深入探讨不同类型的晶体点阵和基本晶胞的性质和特点，并对它们进行详细的介绍和比较。

此外，我们还将介绍晶体缺陷和晶体生长的原理。

晶体缺陷是指晶体中存在的一些不规则排列的原子或分子，这些缺陷对晶体的性质和行为有着重要的影响。

晶体生长则是指晶体通过物质的沉积和积累形成有序结构的过程，它是晶体的产生和发展的基本原理。

在这一章中，我们将对晶体缺陷和晶体生长的机制和规律进行详细的阐述和分析。

总的来说，固体物理第二章是关于晶体结构的内容，围绕着晶体的结晶结构、晶体点阵和基本晶胞的概念展开讨论，同时还包括晶体缺陷和晶体生长的原理。

这些知识点对于理解固体物质的结构和性质，以及相关材料的性能和应用有着重要的意义。

在今后的学习和研究中，我们需要深入掌握这些知识点，并不断拓展和深化自己的理解，以便更好地应用和发展固体物理的相关理论和方法。