3.7 数据校验码

校验码的计算方法一、为什么要设置给原代码设置校验码？代码是数据的重要组成部分，它的正确性将直接影响系统的质量。

当人们抄写、录入时，发生错误的可能性很大，如抄写错（把1234写成1235）、易位错（1234记为1243）、隔位易位错（1234记为1432）等等。

因此，为了验证输入代码的正确性，要在代码本体的基础上，再外加校验码（通常算出后置于补在原代码的最后面），使它成为代码的一个组成部分。

二、补上校验码后系统怎么确认其正确与否？（工作原理）校验码是根据事先规定好的数学方法及代码本体计算出来的。

当计算后的自检码输入系统，系统将按照同样的数学方法，也对代码本体进行计算，将它得出的结果与原来计算出来的校验位比较，检验输入的代码是否正确（只要双方一致就说明是正确的）。

三、校验码的生成过程如下：（计算方法）（1）对代码本体的每一位加权求和设代码本体为C1、C2^Cn，权因子为P1、P2^Pn，加权求和：S=ΣCi Pi。

其中权因子可取自然数1，2，3，…，几何级数2，4，8，16，32，…，质数2，3，5，7，11，…，等等。

（2）以模除和得余数R=Smod(M)其中：R表示余数；M表示模数，可取M=10，11，等等。

（3）模减去余数得校验位四、实例：代码本体为123456，权因子为1，7，3，1，7，3，模为10，则：S=ΣCi Pi=1×1+2×7+3×3+4×1+5×7+6×3=81R=S MOD M=81 mod (10)=1校验位为：J=M–R=10—1=9所以自检码为1234569，其中9为校验位。

（这个实例惟一缺的就是公式的规范性，请用课本p154－155的公式然后才算）关键点：P自然数请反过来从7 ――― 1，得出余数后直接用余数作校验位，不要用模10去减它了。

2、原编码： 5 8 9 6 4 3 7权因子： 7 6 5 4 3 2 1乘积之和：S=35 + 48 +45 +24 +12 +6 +7 = 177R= S MOD M = 177 MOD 10 =7J = M – R=10-7=3原代码加校验码：58964377。

校验码的原理
校验码是指在信息传递过程中为了确认数据的正确性和完整性而采用
的一种技术手段。

校验码的原理是基于一定的算法对原始数据进行加
工处理，生成一段特定的代码值，发送方将处理后的数据和代码值一
并发送给接收方。

接收方收到数据后，同样通过相同的算法对接收到
的数据进行处理，生成相应的校验码，然后将生成的校验码与发送方
提供的校验码进行对比，如果两者相同，就说明数据传输的过程中没
有出现错误。

在计算机传输和存储数据时，往往伴随着误码、漏码等问题，这些问
题会导致数据的不完整或者错误。

为了解决这个问题，人们发明了校
验码。

校验码的生成方式具有一定的算法规律，通常采用的是异或、
倒置码、加权和等数学算法。

通过对原始数据进行操作，生成了一段
固定的校验码，将这段校验码与发送方发送的数据一同传输到接收方，接收方通过同样的算法对收到的数据进行加工，得到一个校验码，与
发送的校验码进行对比，如果两个码值一致，就说明数据传输过程中
没有出现问题。

如果校验码不一致，则说明在数据传输或者储存过程
中发生了错误，需要重新传输或者修复数据。

在实际应用中，各种不同的校验码算法被广泛采用，例如CRC校验码、LRC校验码、累加和校验码等等。

校验码技术在数据传输、存储等方
面的应用非常广泛，不仅在计算机领域，而且在通信网络、物联网、车联网等领域中也都有广泛的应用。

总之，校验码是一种验证数据正确性的技术手段，可以有效地避免因数据传输过程中的误码、漏码等问题导致数据的不完整或者错误。

校验码的选择需要根据具体的应用场景进行考虑，选择合适的算法以确保数据传输过程的可靠性。

各种校验码校验算法分析校验码校验算法是一种用于数据传输或存储中验证数据完整性和准确性的技术，它能够检测出数据在传输或存储过程中是否发生了错误或损坏，从而确保数据的可靠性。

在实际应用中，校验码校验算法广泛应用于通信、网络传输、存储和数据处理等领域，其设计和选择对数据可靠性和安全性至关重要。

常见的校验码校验算法包括奇偶校验码、循环冗余校验码（CRC）、校验和、哈希校验码等。

下面将对这几种常见的校验码校验算法进行详细分析：1.奇偶校验码：奇偶校验码是最简单的一种校验码校验算法，它通过检测数据中的奇偶位来判断数据是否正确。

在奇偶校验中，通常规定数据中的位数为偶数个或奇数个，如果数据中出现奇数个1，则在校验位中加上1，使总的1的数量为偶数；如果数据中出现偶数个1，则在校验位中加上0，使总的1的数量仍为偶数。

在数据传输或存储中，接收方会通过比较校验位和数据位的和是否为偶数来判断数据的正确性。

奇偶校验码虽然简单易实现，但只能检测出奇数个错误位（例如一个错误的位），并不能检测出多个错误位或连续错误的情况。

因此，奇偶校验码一般用于对数据传输的基本错误进行检测。

2.循环冗余校验码（CRC）：CRC是一种基于多项式除法的校验码校验算法，它通过对数据进行特定的多项式运算来计算出校验码。

接收方在收到数据后，也会对数据进行相同的多项式运算，然后比较计算出的校验码与发送方发送的校验码是否一致，从而判断数据是否正确。

CRC校验码具有较高的检错能力和容错率，能够有效地检测出多个位错误和定位错误的位置，因此广泛应用于计算机网络传输、磁盘存储、通信协议等领域。

3.校验和：校验和是一种简单的校验码校验算法，它通过对数据中所有位进行求和操作来计算出校验码。

接收方在接收到数据后，也会对数据进行相同的求和操作，然后比较计算出的校验和与发送方发送的校验和是否一致，从而判断数据是否正确。

校验和算法比较简单，计算速度较快，但只能检测出简单的错误情况，对于复杂的错误或多位错误检测能力有限。

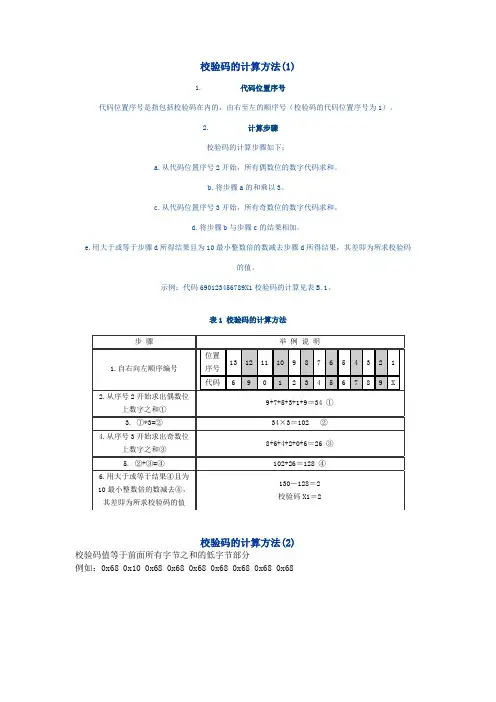
校验码的计算方法(1)
1.代码位置序号
代码位置序号是指包括校验码在内的，由右至左的顺序号（校验码的代码位置序号为1）。

2.计算步骤
校验码的计算步骤如下：
a.从代码位置序号2开始，所有偶数位的数字代码求和。

b.将步骤a的和乘以3。

c.从代码位置序号3开始，所有奇数位的数字代码求和。

d.将步骤b与步骤c的结果相加。

e.用大于或等于步骤d所得结果且为10最小整数倍的数减去步骤d所得结果，其差即为所求校验码
的值。

示例：代码690123456789X1校验码的计算见表B.1。

表1 校验码的计算方法
校验码的计算方法(2)
校验码值等于前面所有字节之和的低字节部分
例如：0x68 0x10 0x68 0x68 0x68 0x68 0x68 0x68 0x68。

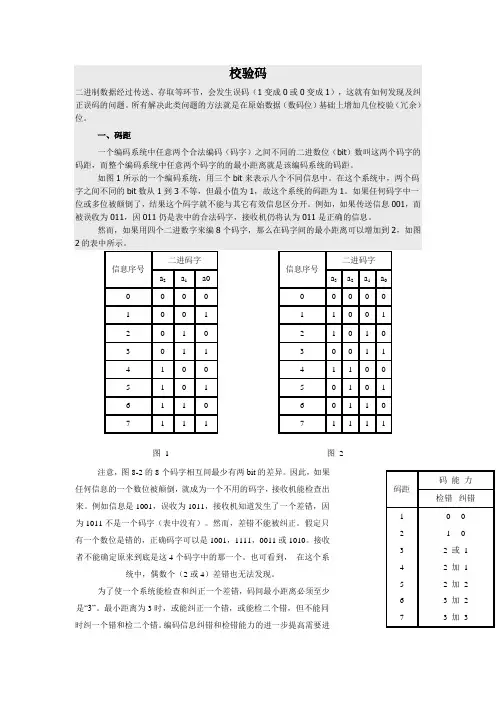
图 1 图 2注意，图8-2的8个码字相互间最少有两bit 的差异。

因此，如果任何信息的一个数位被颠倒，就成为一个不用的码字，接收机能检查出来。

例如信息是1001，误收为1011，接收机知道发生了一个差错，因为1011不是一个码字（表中没有）。

然而，差错不能被纠正。

假定只有一个数位是错的，正确码字可以是1001，1111，0011或1010。

接收者不能确定原来到底是这4个码字中的那一个。

也可看到， 在这个系统中，偶数个（2或4）差错也无法发现。

为了使一个系统能检查和纠正一个差错，码间最小距离必须至少是“3”。

最小距离为3时，或能纠正一个错，或能检二个错，但不能同时纠一个错和检二个错。

编码信息纠错和检错能力的进一步提高需要进一步增加码字间的最小距离。

图8-3的表概括了最小距离为1至7的图3码的纠错和检错能力。

码距越大，纠错能力越强，但数据冗余也越大，即编码效率低了。

所以，选择码距要取决于特定系统的参数。

数字系统的设计者必须考虑信息发生差错的概率和该系统能容许的最小差错率等因素。

要有专门的研究来解决这些问题。

二、奇偶校验奇偶校验码是一种增加二进制传输系统最小距离的简单和广泛采用的方法。

例如，单个的奇偶校验将使码的最小距离由一增加到二。

一个二进制码字，如果它的码元有奇数个1，就称为具有奇性。

例如，码字“10110101”有五个1，因此，这个码字具有奇性。

同样，偶性码字具有偶数个1。

注意奇性检测等效于所有码元的模二加，并能够由所有码元的异或运算来确定。

对于一个n位字，奇性由下式给出：奇性=a0⊕a1⊕a2⊕…⊕a n奇偶校验可描述为：给每一个码字加一个校验位，用它来构成奇性或偶性校验。

例如，在图8-2中，就是这样做的。

可以看出，附加码元d2，是简单地用来使每个字成为偶性的。

因此，若有一个码元是错的，就可以分辨得出，因为奇偶校验将成为奇性。

奇偶校验编码通过增加一位校验位来使编码中1个个数为奇数（奇校验）或者为偶数（偶校验），从而使码距变为2。

校验码（海明码）
海明码⼀般指汉明码，与其他的错误校验码类似，汉明码也利⽤了的概念，通过在后⾯增加⼀些⽐特，可以验证数据的有效性。

利⽤⼀个以上的校验位，汉明码不仅可以验证数据是否有效，还能在数据出错的情况下指明错误位置。

　确定校验码的位数x
设数据有n位，校验码有x位。

则校验码⼀共有2x种取值⽅式。

其中需要⼀种取值⽅式表⽰数据正确，剩下2x-1种取值⽅式表⽰有⼀位数据出错。

因为编码后的⼆进制串有n+x位，因此x应该满⾜
2x-1 ≥　n+x
使不等式成⽴的x的最⼩值就是校验码的位数。

在本例中，n=7，解得x=4。

就是说，当n=校验位的值的时候，X等于多少？
题⽬⼀般会说给出⼀定位数的数据。

⾸先根据下⾯这个表格，⼆进制次⽅表。

看看这个位数对应多少次⽅，只能⼤不能⼩
⽐如说32位的校验码。

根据上⾯的公式，2x ≥ 32+1+X ,将位数代⼊到N⾥。

将1移到右边。

简化公式就是：2x ≥ 33+X 根据这个简化公式，其实就可以理解为，2的多少次⽅可以⼤于等于33
根据2次⽅表就可以知道，6个次⽅！！
最后代⼊公式，26 ≥ 33+6 即26 ≥ 39 ，即X=6 就是说需要加⼊6位校验码
遇到此种题⽬，⾸先看给出的信息位是多少，⽐如16，那么2的多少个次⽅可以⽐16⼤？。

2的4次⽅刚好是16，2的5次⽅⽐16⼤。

那么就代⼊公式看看，答案是5次⽅。

excel 字母数字的校验码计算方法Excel中的校验码是一个非常有用的功能，它可以帮助我们验证数据的准确性和完整性。

校验码的计算方法是基于字母和数字的组合，通过一定的规则来生成校验码。

在本文中，我将介绍校验码的计算方法，并给出一些实际应用的例子。

我们需要了解校验码的生成规则。

校验码的计算方法有很多种，其中比较常见的有两种：一种是基于模运算的算法，另一种是基于权重的算法。

基于模运算的算法是将字母和数字转换为对应的ASCII码，然后将它们相加，再取模运算的结果作为校验码。

这种算法的优点是简单易懂，计算速度较快。

但是，它的缺点是容易出现冲突，即不同的字母和数字组合可能生成相同的校验码。

基于权重的算法则是给每个字母和数字赋予一个权重，然后将它们相乘再相加，最后取结果的模运算作为校验码。

这种算法的优点是能够保证生成的校验码的唯一性，但计算过程相对复杂一些。

举个例子来说明校验码的计算方法。

假设我们要生成一个包含字母和数字的校验码，其中包含的字符为A、B、C、1、2、3。

我们可以使用基于模运算的算法来计算校验码。

首先，将字母和数字转换为对应的ASCII码，A对应的ASCII码为65，B对应的ASCII码为66，以此类推。

然后，将它们相加，即65+66+67+49+50+51=342。

最后，取342的模运算结果，假设我们取模97，那么342 mod 97=51，所以校验码为51。

校验码的计算方法可以应用于很多实际场景中。

比如，在身份证号码中，最后一位通常是校验码，用于验证身份证号码的合法性。

在银行卡号码中，最后一位也是校验码，用于验证银行卡号码的正确性。

在商品条码中，校验码可以用来检查条码是否输入正确。

除了校验码的计算方法，我们还可以通过校验码来进行数据的验证。

比如，我们可以将校验码与输入的数据进行比较，如果两者不一致，则说明数据输入错误。

这样可以帮助我们减少数据错误带来的麻烦和损失。

总结一下，校验码是一种用于验证数据准确性和完整性的方法，它可以通过一定的规则来生成。

常⽤校验码（奇偶校验码、海明校验码、CRC校验码）计算机系统运⾏时,各个部之间要进⾏数据交换. 为确保数据在传送过程正确⽆误,常使⽤检验码. 我们常使⽤的检验码有三种. 分别是奇偶校验码、海明校验码和循环冗余校验码(CRC)。

奇偶校验码（Parity Codes）奇偶校验码最简单,但只能检测出奇数位出错. 如果发⽣偶数位错误就⽆法检测. 但经研究是奇数位发⽣错误的概率⼤很多. ⽽且奇偶校验码⽆法检测出哪位出错.所以属于⽆法矫正错误的校验码。

奇偶校验码是奇校验码和偶校验码的统称. 它们都是通过在要校验的编码上加⼀位校验位组成. 如果是奇校验加上校验位后,编码中1的个数为奇数个。

如果是偶校验加上校验位后,编码中1的个数为偶数个。

例:原编码奇校验偶校验0000 0000 1 0000 00010 0010 0 0010 11100 1100 1 1100 01010 1010 1 1010 0如果发⽣奇数个位传输出错,那么编码中1的个数就会发⽣变化. 从⽽校验出错误，要求从新传输数据。

⽬前应⽤的奇偶校验码有3种.⽔平奇偶校验码对每⼀个数据的编码添加校验位,使信息位与校验位处于同⼀⾏.垂直奇偶校验码把数据分成若⼲组,⼀组数据排成⼀⾏,再加⼀⾏校验码. 针对每⼀⾏列采⽤奇校验或偶校验例: 有32位数据10100101 00110110 11001100 10101011垂直奇校验垂直偶校验10100101 10100101 数据00110110 0011011011001100 1100110010101011 1010101100001011 11110100 校验⽔平垂直奇偶校验码就是同时⽤⽔平校验和垂直校验例:奇校验奇⽔平偶校验偶⽔平10100101 1 10100101 0 数据00110110 1 00110110 011001100 1 11001100 010101011 0 10101011 100001011 0 11110100 1 校验我们把传送过来的1100111000逐位相加就会得到⼀个1，应该注意的的，如果在传送中1100111000变成为0000111000，通过上⾯的运算也将得到1，接收⽅就会认为传送的数据是正确的，这个判断正确与否的过程称为校验。

各种校验码校验算法分析校验码是一种用于验证数据完整性和准确性的算法。

在计算机科学中，常见的校验码算法包括纵向冗余校验(VRC)，横向冗余校验(HRC)，循环冗余校验(CRC)，校验和和哈希校验等。

下面将对这些校验码算法进行分析。

VRC是一种最简单的校验码算法，它将数据位分为数据位和校验位两部分。

数据位按照一定的规则进行编码，校验位是根据数据位计算得到的。

当数据接收方收到数据后，它也会按照相同的规则计算校验位，并将计算得到的校验位与发送方传来的校验位进行比较，如果两者一致，则认为数据传输正确。

然而，VRC算法只能检测数据传输中的单比特错误，无法检测到多比特错误。

HRC是一种通过对数据进行按位求和来计算校验位的算法。

它与VRC算法类似，只是校验位的计算方法不同。

与VRC算法相比，HRC算法更加复杂，但也能检测到更多的错误。

然而，HRC算法仍然无法检测到多比特错误。

CRC是一种更为强大的校验码算法，它通过对数据进行除法运算来计算校验位。

CRC算法将数据视为二进制数，将除法运算看作一个模2整除的过程。

发送方在传输数据之前，计算数据的CRC校验位并将其附加在数据末尾。

接收方在接收数据后，也计算接收到的数据的CRC校验位，并与接收到的校验位进行比较。

如果两者一致，则认为数据传输正确。

与VRC和HRC算法相比，CRC算法具有更高的错误检测能力。

校验和是一种将数据按照一定规则进行求和来计算校验位的算法。

校验和算法将数据视为一系列数值，按照一定的规则进行求和，然后将求和结果的低位部分作为校验位。

校验和算法简单易实现，但其错误检测能力有限，无法检测到一些错误。

哈希校验是一种借助哈希函数来计算校验位的算法。

哈希函数将数据映射为一个固定长度的哈希值，该哈希值称为校验值。

发送方在发送数据之前，计算数据的哈希值并将其附加在数据末尾。

接收方在接收数据后，也计算接收到的数据的哈希值，并与接收到的校验值进行比较。

如果两者一致，则认为数据传输正确。