2012年学而思四年级超常班选拔考试

第五讲简单的统计20、【例8不超过最低额度a立方米时，只付基本费3元和每户每月额定c保险费；如果每月用气量超过最低额度a立方米时，超过部分应按b元/立方米的标准付费，并知道保险费c不超过5元。

试根据以上提供的资料确定a，b，c的值。

第六讲定义新运算21、【学案4】小明来到红毛族探险，看到下面几个红毛族的算式：8×8＝8，9×9×9＝5，9×3＝3，（93＋8）×7＝837。

老师告诉他，红毛族算术中所用的符号“＋、－、×、÷、（）、＝”与我们算术中的意义相同，进位也是十进制，只是每个数字虽然与我们写法相同，但代表的数却不同。

请你按红毛族的算术规则，完成算式：89×57＝______。

22、【例7】定义a*b为a与b之间（包括a、b）所有与a奇偶性相同的自然数的平均数，例如：7*14=(7+9+11+13)÷4=10，18*10=(18+16+14+12+10)÷5=14。

在算式口*(19*99)=80的方格中填入恰当的自然数后可使等式成立，那么所填的数是多少？23、【例8】如有a#b新运算，a#b表示a、b中较大的数除以较小数后的余数。

例如：2#7=1，8#3=2，9#16=7，21#2=1。

如21#(21#x)=5，则x可以是______(x 小于50)。

第七讲游戏与策略本讲是博弈论的入门，例如：①大自然是平衡的，保护平衡就可以胜利，破坏平衡就会失败；②寻找制胜点；③当无法找到胜利的方法时保证自己不输也是对策，保证了自己不输，最终的结果就是对方输；④增强自己或者削弱对手是两种很有意思的对策，有时增强自己可以获胜，但有时增强自己却无法获胜必须削弱对手24、【作业1】甲乙二人轮流报数，报出的数只能是1～７的自然数。

同时把所报数一一累加起来，谁先使这个累加和达到80，谁就获胜。

问怎样才能确保获胜？25、【学案3】15个小球围成一圈，甲、乙两人轮流从中取一个或者相邻的两个，如果两球中间有一个空位置，则不难将这两个球同时拿走，谁取走最后一个球谁就获胜，甲先拿，谁将获胜？26、【作业6】100个“+”号排成一排，甲乙轮流将“+”号改成“-”号，每次只能改一个或相邻的两个，谁将最后一个“+”改成“-”，谁获胜，获胜的策略是什么？27、【作业5】在一个6×5的棋盘上，甲乙二人轮流往棋盘的方格内放棋子。

育民小学超常班选拔考试复试题第一部分神经类测试题目1、根据图示中心球的颜色填空，第一行红色填写数字1，非红色填写数字01；第二行蓝色填写数字2，非蓝色填写数字02，；第三行绿色填写数字3，非绿色填写数字03。

提示：题目分为3小题，下图仅为每一题的例图，根据孩子回忆，出示例图后老师提出要求：黑板上会出现图片，请小朋友看图写数字，与例图一样，中心球为红色的填写1，非红色的填写01，以此类推。

2、在图形队伍中，找出左边的图形。

第二部分思维题目1、听故事，做判断。

《躲雨》三只猴子下山，去看风景，它们没注意到已经快下雨了。

走在路上的时候开始下雨了，它们看到了一座木屋。

第一只猴子过去看了看，回来说“门是关着的”；第二只猴子过去看了看，回来说“窗户也是关着的”；接下来，它们开始讨论，怎么才能进木屋，最后一口决定：它们准备回山上。

突然，一阵大风刮来，把门给吹开了，原来木屋的门根本就没有锁。

①这个故事的名字是叫“下雨”么？（）②猴子们是上山看风景，对么？（）③第一只猴子看了看，说“窗户是关着的”，对么？（）④大风把门给吹开了，对么？（）2、看图找不同。

风景找不同，河边有房子和果树，河里有鱼儿，河对面有花。

不同之处有5处：①两幅图果树上的果子数量不同；②河里的鱼儿数量不同；③房子一座有门，一座没有门；④河对面的花数量不同；⑤花的叶子上图案不同。

3、故事排顺序连线。

提示：原题是图片呈现形式。

4、找到规律，选择填空。

①钢笔文具老虎（）1、大象2、动物3、凶猛4、害怕杨树（）1、植物2、动物3、松树4、叶子②冰冷火（）1、温暖2、火苗3、燃烧4、冰床（）1、木床2、枕头3、睡觉4、被子5、图形推理6、解绳问题出示6个铁环，每个环上系着一些绳子，有的绳子还打着结，请孩子观察，找到能解开绳结的2个环。

7、代换推理题目一条件①3个小瓶+1个中瓶+2个大瓶=6个中瓶+1个小瓶条件②13个小瓶=6个中瓶+1个小瓶条件③3个大瓶+1个小瓶=6个中瓶+1个小瓶问：1个大瓶=（）小瓶1个大瓶=（）中瓶题目二条件①1个梨+2个桃=11条件②1个菠萝+1个梨+1个苹果=10问：梨=（）桃=（）菠萝=（）苹果=（）题目三有个正方体的每个面上分别写着数学1、2、3、4、5、6，有4个不同角度观察，结果如下图所示。

学校________________ 班级________________ 姓名_________________ 联系电话__________________密 封 线 内 不 要 答 题2016年学而思数学超常班选拔考试 四年级一、 填空题（每题6分，共96分，将答案填在下面的空格处）1. 计算：666666666666666+-⨯÷=__________．2. 规定图形表示运算a b c +-，图形表示运算y w x z +--，则计算＋＝__________．3. 珂珂老师带着20名学生围成一圈做游戏：从某一个同学开始顺时针从1开始依次连续报数，报含有数字7的数（如7，17，71等）或7的倍数的同学击1次掌．如此进行下去，当报到100时，所有同学共击掌__________次．4.四个非零自然数的和为38，四个自然数的乘积的最小值是__________，最大值是_________．5. 如图，大平行四边形ABCD 的面积是48平方厘米，小平行四边形CEFG 的面积是6平方厘米，则阴影三角形BDF 的面积是__________平方厘米．6. 家具厂生产一批桌椅，原计划每天生产30套，12天完成．实际只用原来时间的一半就完成了任务，那么实际每天比原计划多生产__________套．7. 如图所示，一个小正方形和6个一样的小长方形组成一个大正方形，已知小长方形的长比宽长2厘米，则大正方形的面积是__________平方厘米．8. 在一条笔直的公路上，可可和凡凡从相距100米的地方同时出发，相向跑步，以后方向都不变，可可每秒跑6米，凡凡每秒跑4米．出发__________秒时，他们相距200米.9. 将48本书分给两组小朋友，已知第二组比第一组多5人．如果把书全部分给第一组，那么每人4本，有剩余；每人5本，书不够．如果把书全分给第二组，那么每人3本，有剩余；每人4本，书不够．问第二组有__________人．10. 若干名棋手进行单循环赛，即任两名棋手间都要赛一场．胜利者得2分，平局各得1分，负者得0分．比赛完成后，前4名依次得8、7、5、4分，则一共有__________名棋手．11. 如图，含有字母A 或者字母B 的平行四边形有__________个．BA12. 如图，在三角形ABC 中，已知3BC DC =，并且三角形ABC 的面积是24平方厘米，则三角形ADB 的面积是__________平方厘米．13. 箱子里红、白两种玻璃球，红球数是白球数的3倍多2个，每次从箱子里取出7个白球、15个红球．取若干次以后，箱子里剩下3个白球、53个红球．那么箱子里原有红球__________个．14. 已知五位数2016□能被9整除，则“□”中填上合适的数字是__________．15. 有A 、B 、C 三个人，每人戴一顶帽子，帽子上写有一个不为0的数，已知其中有1个数为其它2个数之和，每个人都可以看见其他人帽子上的数但看不到自己帽子上的数．他们都很聪明不会有失误的推理，他们所说的话均为真话，并且会将当时已经确知的事全部说出来． A 说：“我不知道我帽子上的数．”B 说：“我帽子上的数是10．”C 帽子上的数是__________．DCBA16. 套娃是俄罗斯的一种民间工艺品．大套娃里面有小套娃，小套娃里面有更小的套娃．现在有一个特产商店里出售这种六重套娃，一整套套娃的价格是8700元，当然也可以单卖，而且相邻大、小套娃的差价是300元．请问：在这种六重套娃之中，最小的套娃要卖__________元钱．二、 解答题（17、18题每题12分，19、20题每题15分，共54分，写出必要步骤，否则不得分）17. 在长方形ABCD 中，E 是AB 的中点，F 是ED 的中点．已知AB 等于6厘米，AD 等于4厘米．求：（1） 长方形ABCD 的面积? （2） 梯形ADCE 的面积?（3） 阴影部分三角形AEF 的面积?D18. 四位数的数字顺序重新排列后，可以得到一些新的四位数．现有一个四位数码互不相同，且没有0的四位数M ，它比重排的新数中最大的小3834，比新数中最小的大4338．求这个四位数．19. 如图，线段AB 和CD 垂直且相等，点E 、F 、G 是线段AB 的四等分点，点E 、H 是线段CD的三等分点，从A 、B 、C 、D 、E 、F 、G 、H 这8 个点中任选3个作为顶点构成三角形．（1）已知CFE △面积为2，则三角形CDB △的面积是多少． （2）面积是CFE △面积2倍的三角形有多少个．（3）面积与CFE △面积相等的三角形（不包括CFE △）有多少个．20. 三个环行跑道如图排列，每个环行跑道周长为210厘米；甲、乙两只爬虫分别从A 、B 两地按箭头所示方向出发，甲爬虫绕1、2号环行跑道作“8”字形循环运动，乙爬虫绕3、2号环行跑道作“8”字形循环运动，已知甲、乙两只爬虫的速度分别为每分钟20厘米和每分钟15厘米.则：甲、乙两爬虫第二次相遇时，甲爬虫爬了多少厘米?学校________________ 班级________________ 姓名_________________ 联系电话__________________密 封 线 内 不 要 答 题321BA（1） 经过多长时间，甲、乙两爬虫第一次相遇?（2） 甲、乙两爬虫第二次相遇时，甲爬虫爬了多少厘米?学校________________ 班级________________ 姓名_________________ 联系电话__________________密 封 线 内 不 要 答 题2016年学而思数学超常班选拔考试 四年级一、 填空题（每题6分，共96分，将答案填在下面的空格处）1.计算：666666666666666+-⨯÷=__________．【答案】6662. 规定图形表示运算a b c +-，图形表示运算y w x z +--，则计算＋＝__________．【答案】23. 珂珂老师带着20名学生围成一圈做游戏：从某一个同学开始顺时针从1开始依次连续报数，报含有数字7的数（如7，17，71等）或7的倍数的同学击1次掌．如此进行下去，当报到100时，所有同学共击掌__________次． 【答案】304. 四个非零自然数的和为38，四个自然数的乘积的最小值是__________，最大值是_________．【答案】35；81005. 如图，大平行四边形ABCD 的面积是48平方厘米，小平行四边形CEFG 的面积是6平方厘米，则阴影三角形BDF 的面积是__________平方厘米．【答案】246. 家具厂生产一批桌椅，原计划每天生产30套，12天完成．实际只用原来时间的一半就完成了任务，那么实际每天比原计划多生产__________套． 【答案】30套7. 如图所示，一个小正方形和6个一样的小长方形组成一个大正方形，已知小长方形的长比宽长2厘米，则大正方形的面积是__________平方厘米．【答案】648. 在一条笔直的公路上，可可和凡凡从相距100米的地方同时出发，相向跑步，以后方向都不变，可可每秒跑6米，凡凡每秒跑4米．出发__________秒时，他们相距200米. 【答案】309. 将48本书分给两组小朋友，已知第二组比第一组多5人．如果把书全部分给第一组，那么每人4本，有剩余；每人5本，书不够．如果把书全分给第二组，那么每人3本，有剩余；每人4本，书不够．问第二组有__________人．【答案】15人10. 若干名棋手进行单循环赛，即任两名棋手间都要赛一场．胜利者得2分，平局各得1分，负者得0分．比赛完成后，前4名依次得8、7、5、4分，则一共有__________名棋手． 【答案】611. 如图，含有字母A 或者字母B 的平行四边形有__________个．BA【答案】4812. 如图，在三角形ABC 中，已知3BC DC =，并且三角形ABC 的面积是24平方厘米，则三角形ADB 的面积是__________平方厘米． 【答案】16DCBA13. 箱子里红、白两种玻璃球，红球数是白球数的3倍多2个，每次从箱子里取出7个白球、15个红球．取若干次以后，箱子里剩下3个白球、53个红球．那么箱子里原有红球__________个．【答案】158只14. 已知五位数2016□能被9整除，则“□”中填上合适的数字是__________．【答案】915. 有A 、B 、C 三个人，每人戴一顶帽子，帽子上写有一个不为0的数，已知其中有1个数为其它2个数之和，每个人都可以看见其他人帽子上的数但看不到自己帽子上的数．他们都很聪明不会有失误的推理，他们所说的话均为真话，并且会将当时已经确知的事全部说出来．A 说：“我不知道我帽子上的数．”B 说：“我帽子上的数是10．”C 帽子上的数是__________． 【答案】516. 套娃是俄罗斯的一种民间工艺品．大套娃里面有小套娃，小套娃里面有更小的套娃．现在有一个特产商店里出售这种六重套娃，一整套套娃的价格是8700元，当然也可以单卖，而且相邻大、小套娃的差价是300元．请问：在这种六重套娃之中，最小的套娃要卖__________元钱． 【答案】700二、 解答题（17、18题每题12分，19、20题每题15分，共54分，写出必要步骤，否则不得分）17. 在长方形ABCD 中，E 是AB 的中点，F 是ED 的中点．已知AB 等于6厘米，AD 等于4厘米．求：（1） 长方形ABCD 的面积? （2） 梯形ADCE 的面积?（3） 阴影部分三角形AEF 的面积?D【答案】24平方厘米 ；（4分）18平方厘米；（4分）（3）连接AC ，11348S AEF S ABC S ABCD D D ===正（平方厘米）．（4分） 18. 四位数的数字顺序重新排列后，可以得到一些新的四位数．现有一个四位数码互不相同，且没有0的四位数M ，它比重排的新数中最大的小3834，比新数中最小的大4338．求这个四位数． 【答案】设组成这个四位数的四个数码为a ，b ，c ，d (91a b c d ≥>>>≥)，则有383443388172abcd dcba -=+=，（4分） 可得999()90()81727992180a dbc -+⨯-==+，（4分） 则8ad -=，2b c -=，9a =，1d =，194338M cb =+，且M 的四位数字分别为1、c 、b 、9，由于8917+=的个位数字为7，所以b ，c 中有一个为7，但2b c -=，所以c 不能为7，故7b =，5c =，157943385917M =+=．（4分）19. 如图，线段AB 和CD 垂直且相等，点E 、F 、G 是线段AB 的四等分点，点E 、H 是线段CD的三等分点，从A 、B 、C 、D 、E 、F 、G 、H 这8 个点中任选3个作为顶点构成三角形．（1）已知CFE △面积为2，则三角形CDB △的面积是多少． （2）面积是CFE △面积2倍的三角形有多少个．（3）面积与CFE △面积相等的三角形（不包括CFE △）有多少个．【答案】（1）9（4分）（2）三角形三个顶点不能共线，所以不能三个点都在AB 上，一定有一个或两个点在CD 上．只含C 点：CFB △、CFA △、CEG △ 3个 只含H 点：HAB △1个只含D 点：DAB △ 1个含C 、H 点：0个 含H 、D 点：HDG △1个学校________________ 班级________________ 姓名_________________ 联系电话__________________密 封 线 内 不 要 答 题共有31116+++=个．（5分）（3）只含C 点：CAE △、CFG △、CGB △ 3个 只含H 点：1HAF △、HEG △、HFB △ 3个 只含D 点：DAF △、DEG △、DFB △ 3个 含C 、H 点：CHG △1个 含H 、D 点：AHD △、FHD △2个共有3331212++++=个．（6分）20. 三个环行跑道如图排列，每个环行跑道周长为210厘米；甲、乙两只爬虫分别从A 、B 两地按箭头所示方向出发，甲爬虫绕1、2号环行跑道作“8”字形循环运动，乙爬虫绕3、2号环行跑道作“8”字形循环运动，已知甲、乙两只爬虫的速度分别为每分钟20厘米和每分钟15厘米.则：甲、乙两爬虫第二次相遇时，甲爬虫爬了多少厘米?321BA（1） 经过多长时间，甲、乙两爬虫第一次相遇?（2） 甲、乙两爬虫第二次相遇时，甲爬虫爬了多少厘米?【答案】（1）根据题意，甲爬虫爬完半圈需要210220 5.25÷÷=分钟，乙爬虫爬完半圈需要2102157÷÷=分钟．由于甲第一次爬到1、2之间要5.25分钟，第一次爬到2、3之间要10.5分钟，乙第一次爬到2、3之间要7分钟，所以第一次相遇的地点在2号环形跑道的上半圈处．(210105)(2015)9+?=（分钟）（6分）（2）由于甲第一次爬到2、3之间要10.5分钟，第二次爬到1、2之间要15.75分钟，乙第一次爬到1、2之间要14分钟，所以第二次相遇的地点在2号环形跑道的下半圈处． 第二次相遇时，两只爬虫爬了(2102105)(2015)15⨯+÷+=分钟．所以甲、乙两爬虫第二次相遇时，甲爬虫爬了2015300⨯=厘米．（8分）。

2013年学而思四年级秋季超常班选拔考试参考答案一、填空题1、10047407400740007++++=个________． 【答案】原式114941104040040004000711444077444517=+++++⨯=+=个个个2、甲、乙两人同时从A 、B 两地出发，相向而行．出发3分钟后，两人相距300米；出发7分钟后，两人也相距300米．那么A 、B 两地相距________米．【答案】750米3、甲、乙两人在笔直的公路上练习跑步，若甲让乙先跑20米，则甲跑5秒可追上乙；若让乙先跑2秒，则甲跑4秒可追上乙．甲的速度是________米/秒．【答案】124、如图，大正方形的每条边长都被截成6厘米和8厘米两部分，如图连接后内部构成一个小正方形．那么三角形②的面积比三角形①大________平方厘米． （提示：在一个直角三角形中，两条直角边的长度分别为a 和b ，斜边的长度为c ，那么它们一定满足：222a b c +=．这就是著名的勾股定理）【答案】1平方厘米5、一天，小慧和刘老师一起谈心，小慧问：“老师，您今年有多少岁啊？”刘老师 回答说：“你猜猜，当我像你这么大时，你才1岁；当你到我这么大时，我就34 岁了．”那么刘老师今年的年龄是________岁．【答案】小慧和刘老师的年龄差是一定的，设为1倍量，那么两人的年龄差是：(341)311-÷=（岁），所以，刘老师今年的年龄是：111223+⨯=（岁）．6、下图中共有________个正方形．【答案】16941(41)240+++++⨯=（个）7、黑板上写着200以内的所有偶数．擦去其中一个后，余下的所有偶数之和为9998．那么擦去的数字是________．【答案】1028、定义两种新运算[]a 和{}a ，[]a 表示求a 的整数部分；{}a 表示求a 的小数部分．如[7.23]7=，{7.23}0.23=．若[]{}8.24 4.28x x +=+，那么x =________．【答案】12.52二、简答题1、200个苹果分给一些小朋友，要求：（1）每个小朋友都分到了苹果，且个数都为偶数个；（2）小朋友分得的苹果个数各不相同．按照上述条件，这些苹果最多可以分给多少个小朋友？【答案】最小的13个偶数之和24626182++++= ；最小的14个偶数之和24628210++++= ．因此最多可以分给13个小朋友．2、有四张数字卡片0、1、2、3，利用它们可以组合出一些一位或多位数，如2，32，102，3012等．那么共可组合出多少个小于2000的数？【答案】将组合的数按位数分类：一位数4个；两位数339⨯=个；三位数33218⨯⨯=（个）；四位数13216⨯⨯⨯=（个）共4918637+++=（个）．3、请在内填上合适的数，使除法算式成立．【答案】97080120809÷=4、16支队伍参加羽毛球比赛．比赛分为小组赛和淘汰赛，赛程如下：（1）每4支队伍分为一个小组，共4小组．小组赛采取单循环赛制（任意两队赛且只赛一次），按积分决出小组第一、二名的队伍，获得出线权；（2）8支获得出线权的队伍通过淘汰赛决出冠、亚、季军．按这样的赛制，一共需要进行了多少场比赛？【答案】小组赛共进行了6424⨯=（场），淘汰赛共进行了8场，共32场．注意：决出季军还需再进行一场比赛．08三、解答题1、小琦和大琦在400米的环形跑道上跑步锻炼．小琦在前，大琦在后，相距100米．哨声一向，两人同时、同向开始跑步．已知小琦的速度是4米/秒，大琦的速度是6米/秒．那么大琦第10次追上小琦时，他离自己的出发点多远？【答案】第一次追上需要100(64)50÷-=（秒）；之后每次追上需要400(64)200÷-=（秒）． 第10次追上，用时5092001850+⨯=（秒），大琦共跑了1850611100⨯=（米）． 1110040027300÷= ，即大琦回到出发点后又多跑了300米．考虑到环形跑道，离出发点的距离为400300100-=（米）．2、有六张完全相同的直角三角形卡片，将每个三角形的一个锐角拼在一起，可以拼出240︒．有多少种形状的直角三角形卡片满足条件？（两个三角形的三个内角对应相等，那么它们是同一种形状的三角形）【答案】设两个角度分别为x 、y ，那么90x y +=︒．拼成240︒有四种情况：6x ；5x y +，42x y +，33x y +．（1）6240x =︒，解得40x =︒，50y =︒，符合条件．（2）5240x y +=︒，解得37.5x =︒，62.5y =︒，符合条件．（3）42240x y +=︒，解得30x =︒，60y =︒，符合条件．（4）33240x y +=︒，但由90x y +=︒知，33270x y +=︒，无解．因此共有三种形状的直角三角形满足条件．。

考试总分120分，填空题10题，每题5分1 计算：(12342010201120104321)2011++++++++++++÷=解答：2011.2 学校排练节目，如果每行排8人，则有一行少2人，如果每行排9人，则有一行少7人，一共有 人。

（两次排队行数一样）【分析】 两种分配方案只所以相差725-=人，是因为两种分配方案每行相差981-=人，对应的求出一共排了515÷=行，一共有58238⨯-=人。

3停车场停了三轮车和小轿车共20辆，车轮总共72个，那么三轮车有 辆【分析】三轮车有8辆4甲、乙、丙三人今年的年龄分别为12、15、34岁，那么 年后甲的年龄等于乙与丙的年龄之差。

【分析】7年 5观察下面排列的规律，第9行各个数之和与第10行各个数之和相差... (6)12345512341234321【分析】 答案：126 长方形的长是50厘米，截去一个最大的正方形后，余下一个长方形，这个长方形的周长是 厘米。

【分析】 截去的最大的正方形边长等于长方形的宽，余下的长方形的周长502100⨯=（厘米） 712011之间同时被3、5、7除都余2的数有 个。

【分析】 [3,5,7]105=，所以这些数为2、107、212⋅⋅⋅⋅⋅⋅，20111051916÷=⋅⋅⋅⋅⋅⋅，所以总共有19120+=2011学而思 乐加乐 超常班选拔考试（三升四）（个）.8某书的页码是连续的自然数1，2，3，4，…9，10…当将这些页码相加时，某人把其中一个页码错加了两次，结果和为2011，则这书共有______页。

【分析】如果这本书的页数超过62页，那么页码之和超过12362632016+++⋅⋅⋅++=。

所以页数不大于+++⋅⋅⋅+=，无论将62页，又因为如果这本书的页数不到62页，那么页码之和小于123611891哪个页码重复加两遍，都不会使页码和达到2011，所以这本书有62页。

因为-=。

学而思六年级超常班选拔考试·答案一、简答题（共10题，每题6分，要求写出简要过程）1. 【考点】分数计算 【答案】29419；111636【分析】 ⑴19101011901001190010001989810198101019801001980010001191910119191998989898981919199898398191929419⨯⨯⨯⨯⎛⎫=++⨯⨯ ⎪⨯⨯⨯⨯⎝⎭⎛⎫=++⨯⨯ ⎪⎝⎭=⨯⨯⨯=原式 ⑵()()()11199412345199219939979972399719941993199219912169979976111636=-+-+-++-+⨯-⨯=-+-++-+=+=原式2. 【考点】不定方程【答案】13平方厘米【分析】 设上面长方形的未知边长为x ，下面长方形的未知边长为y ，则有：7543x y +=，由于()433mod5≡，55y ，因此有：()73mod5x ≡，又743x <，所以728x =，即4x =．代入原方程有：3y =．那么两个矩形的面积之差为：281513-=平方厘米．3. 【考点】计数【答案】12个【分析】 21世纪即为20□□年，那么这个八位数即为2002□□□□，也就是说日已经定了，接下来只要月份定下来，相应的年份也就确定了．一年12个月，所以共12个世界对称日．分别是：20100102、20200202、20300302、20400402、20500502、20600602、20700702、20800802、20900902、20011002、20111102、20211202．4. 【考点】因倍质合【答案】()A 428=；()4296B =；24【分析】 分解质因数，42237=⨯⨯，即42的约数个数有2228⨯⨯=个，()A 428=，()()()()01010122337734896B n =+⨯+⨯+=⨯⨯=．由于()A 8n =，而8824222==⨯=⨯⨯，所以7n p =或13n p q =⨯或111n p q r =⨯⨯，三种情况下n 的最小值分别为128、24、30，因此n 的最小值是24．5. 【考点】等差数列【答案】4组【分析】 首先1000为一个解．连续数的平均值设为x ，1000必须是x 的整数倍．假如连续数的个数为偶数个，x 就不是整数了．x 的2倍只能是5，25，125才行．因为平均值为12.5，要连续80个达不到．62.5是可以的．即62，63；61，64；…．连续数的个数为奇数时，平均值为整数．1000为平均值的奇数倍．1000=2×2×2×5×5×5；x 可以为2，4，8，40，200排除后剩下40和200是可以的．所以答案为平均值为62.5，40，200，1000的4组整数．6. 【考点】立体几何【答案】942平方厘米【分析】 如下图所示将圆柱倾斜，此时可以多装一部分水．水的体积为：221π59π56300π9422V =⨯⨯+⨯⨯⨯==平方厘米．7. 【考点】概率【答案】13【分析】 四人入座的不同情况有432124⨯⨯⨯=种．A 、B 相邻的不同情况，首先固定A 的座位，有4种，安排B 的座位有2种，安排C 、D 的座位有2种，一共有42216⨯⨯=种．所以A 、B 不相邻而座的概率为()12416243-÷=．8. 【考点】比例行程【答案】25:18【分析】 乙45分钟的路程=丙50分钟的路程，因此有:50:4510:9v v ==乙丙，同理，甲60分钟的路程=乙75分钟的路程，因此有：:75:605:4v v ==乙甲，所以::25:20:18v v v =乙丙甲，即:25:18v v =丙甲．9. 【考点】数列数表【答案】991118590【分析】 将原数列按照每组1个、2个、3个…分组，有：12132143212011201011121231234122011⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，，，，，，，，，，，，，，，我们假设第2012个数在第()1n +组，有前n 组的个数小于2012且最接近2012，即()120122n n +<，估算得62n =，此时已经有1953个数了，因此第2012个数是第63组的第59个数，即559．而倒数第2012个数就是12010．两数之差为519991592010118590-=．10. 【考点】构造与论证【答案】见分析【分析】 本题答案不止一种，下面给出一种方法：二、解答题（共4题，每题10分，要求写出详细过程）11. 【考点】行程问题【答案】100米【分析】 甲只可能在DC 上追上乙，当乙到达D 点时，我们可以推算一下此时甲在什么地方才有可能追上乙．如果乙走到C 点时，甲恰好追上，那么甲的追击时间就是120430÷=秒，追击路程为()305430⨯-=米．当乙第一次到达C 点时，用时180445÷=秒，甲走了455225⨯=米，甲还没有到达B 点，此时肯定追不上；当乙第二次到达C 点时，用时4804120÷=秒，甲走了1205600⨯=米，甲刚好回到A 点，此时也不可能；当乙第三次到达C 点时，用时7804195÷=秒，甲走了1955975⨯=米，此时甲从B 地返回且距离D 点25米，追及路程小于30米．可以追上．()255425÷-=秒后，甲第一次追上了乙，此时乙在距离D 点254100⨯=米处．12. 【考点】工程问题【答案】3204小时 【分析】 据已知条件，四管按甲乙丙丁顺序各开1小时，共开4小时，池内灌进的水是全池的11117345660-+-=，加上池内原来的水，池内有水171766060+=． 再过四个4小时，即20小时后，池内有水1773460604+⨯=，还需灌水14，此时可由甲管开113434÷=小时． 所以在3204小时后，水开始溢出水池．13. 【考点】逻辑推理【答案】C【分析】 因为ABC 三人得分共40分，三名得分都为正整数且不等，所以前三名得分最少为6分，4058410220140=⨯=⨯=⨯=⨯，不难得出项目数只能是5．即M 5=．A 得分为22分，共5项，所以每项第一名得分只能是5，故A 应得4个一名一个二名．22542=⨯+，第二名得1分，又B 百米得第一，所以A 只能得这个第二． B 的5项共9分，其中百米第一5分，其它4项全是1分，951111=++++．即B 除百米第一外全是第三，跳高第二必定是C 所得．14. 【考点】直线型面积【答案】1:2【分析】 如下图，过点E 、点F 作AD 的平行线，两条平行线间的距离为h ，∵:2:3EF FC =，∴:2:3DEF S S =乙△，∴:4:22:1DEF S S ==甲△ 又12DEF ADF ADE S S S AD h =-=⨯⨯△△△ 12BCE BCF S S S BC h =-=⨯⨯甲△△ ∴:1:2AD BC =。

学而思2012年春季四年级超常123班难题汇总第一讲小数本讲是小数的入门，主要是小数的计算，难度不大，掌握一些常用方法即可。

小数计算常用的方法有：(1)凑数、(2) 扩大再缩小、(3)提取公因数、 (4)平方和平方差公式、 (5)解方程、 (6)换元法。

希望孩子领会各种方法的要领。

作业看了一遍，没有太大难度。

在此分析几道张老师课堂上讲解的补充题目，会对大家有用途的。

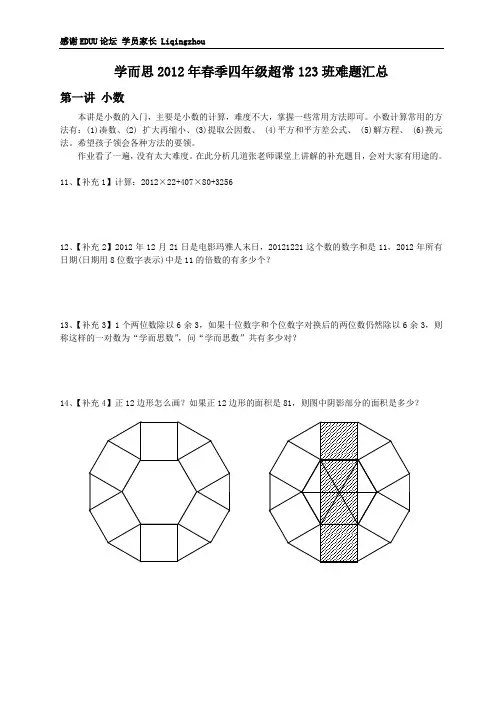
11、【补充1】计算：2012×22+407×80+325612、【补充2】2012年12月21日是电影玛雅人末日，20121221这个数的数字和是11，2012年所有日期(日期用8位数字表示)中是11的倍数的有多少个？13、【补充3】1个两位数除以6余3，如果十位数字和个位数字对换后的两位数仍然除以6余3，则称这样的一对数为“学而思数”，问“学而思数”共有多少对？14、【补充4】正12边形怎么画？如果正12边形的面积是81，则图中阴影部分的面积是多少？15、【补充5】某船往返甲乙两岸，共用12小时，前6小时比后6小时多走80千米，顺水速度比逆水速度大16千米/小时，求甲乙两岸距离。

第二讲 长度与角度综合 21、【学案3】如图，正五边形ABCDE ，若△CDF 为正三角形，试求∠BFE 的度数。

22、【例4】已知一正多边形，其内角小于160°，且大于150°，试求出此多边形可能是哪几种正多边形？ 23、【作业8】华罗庚爷爷说：数学是中国人民所擅长的学科。

请小朋友求解《九章算术》中一个古老问题：“今有木长二丈，围之三尺。

葛生其下，缠木七周，上与木齐。

问葛长几何？”白话译文：如图，有圆柱形木棍直立地面，高20尺，圆柱地面周长3尺。

葛藤生于圆柱底部A 点，等距缠绕圆柱七周恰好长到圆柱上底面的B 点，则葛藤的长度是__。

A BCD EF1 2 3 20 2120/7 324、【例7】如图，点P 在锐角∠AOB 的内部，在OB 边上求作一点D ，在OA 边上求作一点C ，使△PCD 的周长最小。

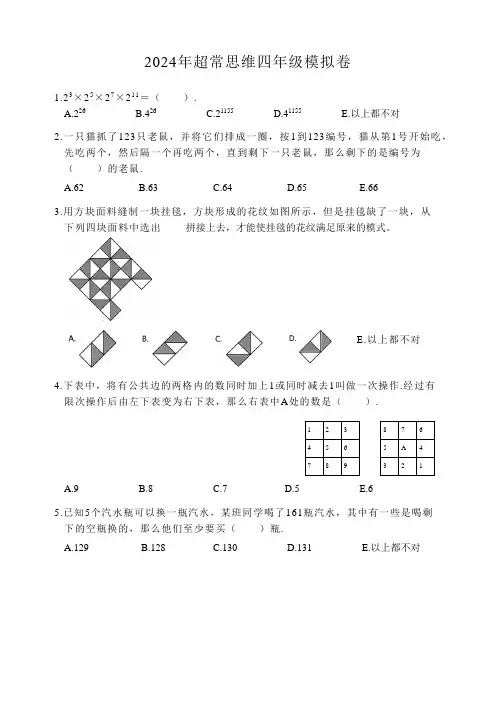
2024年超常思维四年级模拟卷1.23×25×27×211＝（ ）.A.226B.426C.21155D.41155E.以上都不对2.一只猫抓了123只老鼠，并将它们排成一圈，按1到123编号，猫从第1号开始吃，先吃两个，然后隔一个再吃两个，直到剩下一只老鼠，那么剩下的是编号为（ ）的老鼠.A.62B.63C.64D.65E.663.用方块面料缝制一块挂毯，方块形成的花纹如图所示，但是挂毯缺了一块，从下列四块面料中选出_____拼接上去，才能使挂毯的花纹满足原来的模式。

E.以上都不对4.下表中，将有公共边的两格内的数同时加上1或同时减去1叫做一次操作.经过有限次操作后由左下表变为右下表，那么右表中A 处的数是（ ）.A.9B.8C.7D.5E.65.已知5个汽水瓶可以换一瓶汽水，某班同学喝了161瓶汽水，其中有一些是喝剩下的空瓶换的，那么他们至少要买（ ）瓶.A.129B.128C.130D.131E.以上都不对1 2 3 45 6 7898 7 6 5A 4 3216.摩托车骑手甲和自行车骑手乙同时由A地去B地.走过全程的1时，乙停下来休息，3.甲到达B地后一刻也不当他休息完准备继续出发时，发现甲距B地还有全程的13停留，马上向A地返回.究竟是甲先到达A地，还是乙先到达B地，以下正确的说法是（）A.谁先到取决于两人的速度B.谁先到取决于A，B之间的距离C.两人同时到达D.甲先到A地E.乙先到B地7.下列图中能够相互补充成圆的图形对是（）8.如图，第1个方格内放着一个正方体木块，木块的六个面上分别标有A、B、C、D、E、F六个字母.其中A与D相对，B与E相对，C与F相对.现在将木块标有字母A的那个面朝上，标有字母D的那个面朝下，放在如图所示位置，然后让木块按照编号从小到大沿着方格滚动，当木块滚到图中最后一个位置时（第14号位置），木块向上的面上标的字母是（）A.AB.BC.CD.DE. E9.下列立体图形是由一些棱长为1的小立方体粘合而成的，一个5×5×5的立方体，所有面的中心正方形被打通，求它的体积以及表面积.（）A.体积111，表面积190B.体积112，表面积190C.体积111，表面积192D.体积112，表面积192E.以上都不对10.如图所示，大矩形由4个相同的矩形组成.如果小矩形的周长为144厘米，请问阴影区域的面积是多少（以平方厘米表示）？A.1944cm2B.3888cm2C.972cm2D.1494cm2E.以上都不对11.将一条纸带的两头粘连起来，形成的纸带圈叫作圆环.再沿着纸带的二等分线剪开这个圆环，就得到2个小圆环.将一条纸带扭转180°后两头再粘连起来，形成的纸带圈叫作莫比乌斯环.再沿着这个莫比乌斯环的二等分线剪开，得到1个更长的环.再沿着这个环的二等分线剪开，将会得到（）A.2个环B.3个环C.4个环D.6个环E.8个环12.13.在一次射箭练习中，小戴的6支箭都落在了靶上.靶上的数字表示落到这个区域内的每支箭的得分.如果小戴射的箭都没有落在这三个圆的边界上，那么她的总分可能是（）A.44B.31C.26D.16E.以上都不对14.一列快车和一列慢车相向而行，快车的车长是270米，慢车的车长是360米，坐在快车上的人看见慢车驶过的时间是12秒，那么坐在慢车上的人看见快车驶过的时间是（）秒.A.9B.10C.11D.12E.以上都不对15.三个盒子里的奖牌数不等.第一次从甲盒里拿出一些奖牌放入乙、丙两盒里，使乙、丙两盒里的奖牌数增加一倍;第二次从乙盒里拿出一些奖牌放入甲、丙两盒里，又使得甲、丙两盒里的奖牌数增加一倍;第三次从丙盒里拿出一些奖牌放入甲、乙两盒里，又使得甲、乙两盒里的奖牌数增加一倍.这时三个盒里都是64块奖牌.最初三个盒里各有奖牌（）块.A.32B.56C.64D.104E.以上都不对16.“蓝天杯”足球赛采用双循环赛制，即每4支球队每2队之间都要比赛2场.每场比赛胜者得3分，负者得0分，打平双方各得1分.比赛结束后4队得分互不相同，从高到低依次是B，C，D，但A两场比赛都战胜了B，并且C是4支球队中负的最少的队（不与其他队并列），那么，4队得分的乘积是（）.A.4320B.3360C.3024D.1680E.以上都不对17.牧羊人给每只羊都编了号:1，2，3，4，5，…一天，他计算羊的编号之和时发现与以往不同，是1145.经清点，他知道丢失了两只羊，那么这两只羊的编号可能是（）.A.15，16B.16，17C.39，41D.40，42E.以上都不对18.爷爷比爸爸大27岁，妈妈比小超也大27岁，小超一家4口今年的年龄之和为132岁，而5年前是113岁.则爸爸今年的年龄是（）岁.A.29B.32C.35D.38E.以上都不对19.103+117+131+145+159+…+2021＝？（）A.135784B.103482C.128430D.146556E.11203120.下表中，将每列中上下两个字组成一组，例如第一组为“我真”，第二组为“爱有”…那么第150组是（）.A.数真B.学趣C.爱趣D.爱真E.我真21.22.2021名解放军战士面向教官站成一列，教官先让大家从前往后按1，2，3，…，2020，2021依次报数，再让报数是4的倍数的战士出列，接着又让报数是6的倍数的战士出列.那么，现在留在原地的解放军战士还有（）人.A.1345B.1346C.1347D.1348E.以上都不对22.按英国人的记法，2021年5月15日记作5-15-2021;按美国人的记法，2021年5月15日记作15-5-2021.那么，2021年全年中共有（）天会让英、美两国人在记法上产生误会A.12B.66C.132D.144E.以上都不对23.把奇数按以下规律分组:（1），（1，3），（1，3，5），…其中第1组有1个数，第2组有2个数，第3组有3个数，第4组有4个数…那么第100组中的100个数之和为（）.A.1000B.10000C.100000D.1000000E.以上都不对24.四（1）班开表彰会，买了苹果、梨子和橘子共250个，其中梨子比橘子的2倍少10个，苹果比梨子的3倍多20个.则苹果、梨子分别有（）个.A.20B.50C.150D.170E.以上都不对25.图1和2是两张原来一样的长方形纸，在图1中，从一边减去宽12厘米的部分后，纸张的面积减少288平方厘米.在图2中，从两边剪去宽8厘米的部分后，纸张的面积减少了464平方厘米.原来一张纸的面积是多少平方厘米？A.1008B.918C.960D.810E.86426.2020年7月23日到08月08日将在日本东京举行第32届奥林匹克运动会，下面是奥运会五环标志.请将1~9分别填入五个环相互分割的9个区域，使每个环内的数字和都相等.则x的可能值为（）A.2B.3C.4D.6E.827.n张扑克牌，全部正面朝上放在桌子上，每次翻动k张，经过若干次翻动，使得n张扑克牌全部背面朝上.以下正确的是（）.A.n＝71，k＝5B.n＝7,k＝6C.n＝2021，k＝5D.n＝2021，k＝6E.以上都不对。

2012 年学而思四年级超常班选拔考试一、填空题（每题 7 分，共 28 分）1.计算： 5×2012÷503×15=__________2.某一个等差数列的第 3 项是 14，第 18 项是 23，那么，这个等差数列从第一项到2010 项中有 _______项是整数。

3.如下图，小正六边形沿着大正六边形的边，按顺时针方向滚动。

小正六边形的边长是大正六边形边长的一半。

如果小正六边形沿着大正六边形的边滚动了一周后返回出发时的位置，那么在这个过程中，线段 OA 围着 O 点旋转了 _______圈？OA4.“学学”用写有数字的卡片分别摆出 4 个数（如下图），但是，有部分卡片上的数字被遮挡，已知这 4 个数的平均数是 2012，那么，这 4 个数被遮挡部分的数字之和是 __________□，□ 8，□ 97，□ 825二、填空题（每题 9 分，共 36 分）5.如下图所示，大正方形的边长为 10cm，小正方形的边长为 5cm，那么阴影部分的面积是 ________平方厘米。

6.有长 3 米和 4 米的圆木共 30 根，它们长度的和等于 100 米，现在将它们全部锯成长为 1 米的圆木，如果每次只能锯一块圆木，那么，一共要锯 ____________次。

5 卷到7. 5 本百科全书按从第 1 卷到第 5 卷的递增序号排列，现在要将它们变为反序排列，即从第第 1 卷。

如果每次只能调换相邻的两卷，那么，最少要调换_____________次。

8.一群骗子和一群老实人围成一圈开圆桌会议，老实人只说真话儿，骗子只说假话，每一个老实人两边都是骗子，而每一个骗子两边都是老实人，一个过路人问小明，你们一共有多少人啊？小明说，25 人，那么聪明的小朋友们小明是 _______________? (1)老实人（2）骗子横线上只填序号。

三、填空题（每题 10 分，共 40 分）9.9. 数一数，右图中一共有 ____________个三角形。

一、简答题（共10题，每题6分，请写出简要步骤）⨯-⨯计算：98766987689876598769数字谜：在下面的算式里，相同的汉字表示相同的数字，不同的汉字表示不同的数字，问：每个汉字各代表什么数字？学而思教育⨯数=育教思而学盈亏问题：有红、白球若干，若每次拿出1个红球和1个白球，拿到没有红球时，还剩下50个白球；若每次拿走1个红球和3个白球，则拿到没有白球时，红球还剩下50个，那么这堆红球、白球共有多少个？位值原理：小花爷爷的年龄是一个两位数，将此两位数的数字交换得到的数就是小花爸爸的年龄，又知道他们的年龄的差是小花年龄的4倍，那么小花的年龄是多少？还原问题：陈老师、魏老师、卢老师各有一些糖，陈老师用一半平均给魏老师、卢老师，然后魏老师用一半平均给陈老师、卢老师，然后卢老师用一半平均给陈老师、魏老师，最后各有32块，陈老师、魏老师、卢老师原各有多少块？简单推理：请在右图44⨯表格的每格中填入l，2，3，4中的一个，使得每行，每列，每条对角线的四个数各不相同，且满足图中三个不等的关系．平均数问题：每次考试满分是100分，小明4次考试的平均成绩是89分，为了使平均成绩尽快达到94分（或更多），他至少再要考多少次？图形面积：如图，边长是整数的四边形AFED 的面积是48平方厘米，FB 为8厘米．那么，正方形ABCD 的面积是多少平方厘米？A BC DEF 488等差数列：一本书的页码是连续的自然数1，2，3，4，…，9，10，……灰太狼把这些页码相加时，他把其中一个页码错加了两次，结果和为2001，则这书共有多少页？一半模型：已知四边形AGPE 的面积与四边形PFCH 的面积相等，两块阴影部分的面积已说明，求矩形ABCD 的面积多少？P GB 393二、 解答题（共4题，每题10分，请写出详细步骤）整除性质：连续写出从1开始的自然数，写到2008时停止，得到一个多位数：123456789101120072008，请说明：这个多位数除以3，得到的余数是几？为什么？简单行程：陈老师、魏老师两人分别以每小时6千米，每小时4千米的速度从相距30千米的两地向对方的出发地前进．当两人之间的距离是10千米时，他们走了多少小时？数列应用：80名学生分成24个组，各个组的人数允许相同，分组完后发现，最多的有n 个组的人数都相同，求n 的最小值.。

2012年理科实验班自主招生考试数学试卷（一）参考答案与试题解析一、选择题1．（3分）在﹣0.3168中，用数字4替换其中的一个非0数字后，使所得的数最大，则被替换的数字是（）A．1B．3C．6D．8考点：有理数大小比较．专题：存在型．分析：先用4替换该数中任一不等于0的数，再根据负数比较大小的法则进行解答即可．解答：解：若使所得数最大，则替换后的数的绝对值应最小，当4替换3时所得数为：﹣0.4168；当4替换1时所得数为：﹣0.3468；当4替换6时所得数为：﹣0.3148；当4替换8时所得数为：﹣0.3164；∵0.4168＞0.3468＞0.3164＞0.3148，∴﹣0.4168＜﹣0.3468＜﹣0.3164＜﹣0.3148，∴﹣0.3148最大，∴被替换的数字是6．故选C．点评：本题考查的是有理数的大小比较，解答此题的关键是熟知两负数比较大小时，绝对值大的反而小．2．（3分）如图，线段AF中，AB=a，BC=b，CD=c，DE=d，EF=e．则以A，B，C，D，E，F为端点的所有线段长度的和为（）A．5a+8b+9c+8d+5e B．5a+8b+10c+8d+5eC．5a+9b+9c+9d+5e D．10a+16b+18c+16d+10e考点：比较线段的长短．分析：首先求出以A为端点线段的长度，类比依次求出B、C、D、E为端点的线段的长度，然后求出这些线段的长度总和．解答：解：以A为端点线段有AB、AC、AD、AE、AF，这些线段长度之和为5a+4b+3c+2d+e，以B为端点线段有BC、BD、BE、BF，这些线段长度之和为4b+3c+2d+e，以C为端点线段有CD、CE、CF，这些线段长度之和为3c+2d+e，以D为端点线段有DE、DF，这些线段长度之和为2d+e，以E为端点线段有EF，线段的长度为e，故这些线段的长度之和为5a+8b+9c+8d+5e，故选A．点评：本题主要考查比较线段的长短的知识点，解答本题的关键是求出A，B，C，D，E，F为端点的所有线段的条数，本题不是很难．3．（3分）二次函数y=ax2+bx+c的图象如图所示，则点P（ac，b）所在象限是（）A．第一象限B．第二象限C．第三象限D．第四象限考点：二次函数图象与系数的关系．专题：计算题．分析：根据二次函数的图象判断a、b、c的符号，再判断点P所在的象限．解答：解：抛物线开口向上，∴a＞0，抛物线对称轴y=﹣＞0，且a＞0，∴b＜0，抛物线与y轴交于正半轴，∴c＞0，∴点P（ac，b）在第四象限．故选D．点评：本题考查了二次函数的图象与系数的关系．二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定．4．（3分）如图，四边形ABCD中，∠A=∠C=90°，∠ABC=60°，AD=4，CD=10，则BD的长等于（）A．B．C．12 D．考点：勾股定理；特殊角的三角函数值．分析：分别延长AD、BC，两条延长线相交于点E，构造特殊三角形ABE，其中有一个锐角是60°，∠A是90°，那么另一个锐角是30°，在Rt△CDE中，∠E=30°，有CD=10，可求DE，那么AE的长就求出，在Rt△ABE中，利用∠E的正切值可求出AB，在Rt△ABD中，再利用勾股定理可求斜边BD的长．解答：解：延长AD、BC，两条延长线相交于点E，∵在Rt△ABE中，∠A=90°，∠B=60°，∴∠E=90°﹣60°=30°．∴在Rt△DCE中，∠E=30°，CD=10，∴DE=2CD=20，∴AE=AD+DE=20+4=24．∴在Rt△ABE中，AB=AE•tan∠E=AE•tan30°=×24=8，∴在Rt△ABD中，BD====4．故选A．点评：关键是作辅助线，构造特殊直角三角形，然后利用了勾股定理、特殊三角函数值解题．5．（3分）给出一列数，在这列数中，第50个值等于1的项的序号是（）A．4900 B．4901 C．5000 D．5001考点：规律型：数字的变化类．专题：规律型．分析：观察数字可知分子分母的和为k的分数的个数为k﹣1，并且分子分母的和为偶数的项中，有一个值等于1，依此即可求出第50个值等于1的项的序号．解答：解：第50个值等于1的项的分子分母的和为2×50=100，由于从分子分母的和为2到分子分母的和为99的分数的个数为：1+2+…+98=4851．第50个值等于1的项为．故4851+50=4901．故选B．点评：本题考查了规律型：数字的变化，有一定的难度，找到分子分母的和与分数的个数的关系，以及分子分母的和为偶数的项中，有一个值等于1的规律是解题的关键．6．（3分）如图，⊙O1与⊙O2外切于P，⊙O1，⊙O2的半径分别为2，1．O1A为⊙O2的切线，AB 为⊙O2的直径，O1B分别交⊙O1，⊙O2于C，D，则CD+3PD的值为（）A．B．C．D．考点：相切两圆的性质．专题：计算题．分析：分别求出CD和PD的长度，再计算CD+3PD：（1）由相似关系求PD的长度．连接O1O2，则O1O2过P点，三角形O1PD相似于O1BO2，由相似关系求出PD；（2）由切割线定理求CD的长度．这个要分两步做：①由勾股定理求出O1A、O1B的长度．在直角三角形O1O2A和O1AB中，分别用勾股定理求出O1A、O1B的长度；②由切割线定理求O1D的长度．由切割线定理O1A2=O1D•O1B，所以O1D可求出来．而解答：解：连接O1O2，∵AO2=1，O1O2=3，∴AO1==2，∴BO1===2，∴由切割线定理O1A2=O1D•O1B，得O1D==，∴CD=O1D﹣O1C=﹣2，又∵cos∠O2O1B==，则PD2=4+﹣cos∠O2O1B=4+﹣×=，∴PD=，∴CD+3PD=﹣2+3×=．故选D．点评：本题考查了相切两圆的性质，三角形的相似以及性质，是重点知识，要熟练掌握．二、填空题7．（5分）已知，且a+b+c≠0，那么直线y=mx﹣m一定不通过第二象限．考点：一次函数的性质；等式的性质；比例的性质．专题：计算题．分析：根据比例的性质得到3a+2b=cm，3b+2c=am，3c+2a=bm，相加即可求出m的值是5，得出y=5x ﹣5，即可得出答案．解答：解：∵，∴3a+2b=cm，3b+2c=am，3c+2a=bm，∴5a+5b+5c=（a+b+c）m，∵a+b+c≠0，∴m=5，∴y=mx﹣m=5x﹣5，∴不经过第二象限．故答案为：二．点评：本题主要考查对一次函数的性质，比例的性质，等式的性质等知识点的理解和掌握，能根据已知求出m的值是解此题的关键．题型较好．8．（5分）如图，在△ABC中，AB=AC，AD=AE，∠BAD=60°，则∠EDC=30°．考点：等腰三角形的性质；三角形内角和定理；三角形的外角性质．专题：数形结合．分析：根据三角形外角的性质，可得：∠ADE+∠EDC=∠B+∠BAD，∠AED=∠EDC+∠C．解答：解：∵△ADE中，AD=AE，∴∠ADE=∠AED；∵∠AED=∠EDC+∠C①，而∠ADE+∠EDC=∠B+∠BAD②；∴②﹣①得：2∠EDC=∠B﹣∠C+∠BAD；∵AB=AC，∴∠B=∠C；∴∠EDC=∠BAD=30°．故答案为：30°．点评：此题主要考查了等腰三角形的性质以及三角形外角的性质，难度不大，注意等腰三角形性质的掌握与运用．9．（5分）如图，在直角△ABC中，AB=AC=2，分别以A，B，C为圆心，以为半径做弧，则三条弧与边BC围成的图形（图中阴影部分）的面积为．考点：扇形面积的计算；等腰三角形的性质．专题：计算题．分析：阴影部分的面积=三角形ABC的面积减去三个扇形的面积，然后根据扇形的面积公式和三角形的面积公式计算即可．解答：解：三个扇形的面积S==，∴S阴影部分=S△ABC﹣S=•2•2﹣=2﹣．故答案为2﹣．点评：本题考查了扇形的面积公式：S=．也考查了三角形的面积公式．10．（5分）分解因式：2m2﹣mn+2m+n﹣n2=（2m+n）（m﹣n+1）．考点：因式分解-分组分解法．专题：计算题．分析：多项式有5项，采用分组分解法，1，2，5项结合，因式分解，再与3，4两项提公因式．解答：解原式=（2m2﹣mn﹣n2）+（2m+n）=（2m+n）（m﹣n）+（2m+n）=（2m+n）（m﹣n+1）．故答案为：（2m+n）（m﹣n+1）．点评：本题考查了分组解法进行因式分解，关键是分组后组与组之间可以继续进行因式分解．11．（5分）如图：四边形EFGH是一个长方形台球桌面，有白、黑两球分别位于A，B两点的位置上．试问，怎样撞击白球A，才能使白球A先碰撞台边GH，再碰撞FG，经两次反弹后再击中黑球B？（将白球A移动路线画在图上，不能说明问题的不予计分）考点：作图—应用与设计作图．专题：作图题．分析：分别作出点A关于HG的对称点A′，点B关于FG的对称点B′，然后连接A′B′，交HG、FG 于点M，N，再连接AM、BN，则白球A移动路线图可得．解答：解：（1）作出点A关于HG的对称点A′，点B关于FG的对称点B′，（2）连接A′B′，分别交HG、FG于点M、N，（3）连接AM，BN，所以白球A的移动路线为A→M→N→B．点评：本题是考查了作图问题的应用与设计作图，利用轴对称的性质作出对称点是解题的关键，难度中等．12．（5分）有三位学生参加两项不同的竞赛，则每位学生最多参加一项竞赛，每项竞赛只许有两位学生参加的概率为．考点：列表法与树状图法．分析：先根据题意画出树状图，从图上可知每项竞赛只许有两位学生参加的情况有6种，共有8种解答：解：用A、B分别表示两项不同的竞赛，如图所示：每项竞赛只许有两位学生参加的情况是AAB，ABA，ABB，BAA，BAB，BBA，共6种，则每项竞赛只许有两位学生参加的概率为=．故答案为：．点评：本题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．13．（5分）设[x]表示不超过x的最大整数（例如：[2]=2，[1.25]=1），则方程3x﹣2[x]+4=0的解为﹣4或﹣或﹣．考点：取整计算．分析：首先令[x]=n，可得方程3x﹣2n+4=0，即可求得x的值，然后由[x]≤x＜[x]+1，可得关于n的不等式组，解不等式组即可求得n的值，则代入方程即可求得x的值，注意要检验．解答：解：令[x]=n，代入原方程得3x﹣2n+4=0，即x=，又∵[x]≤x＜[x]+1，∴n≤＜n+1，整理得：3n≤2n﹣4＜3n+3，即﹣7＜n≤﹣4，∴n=﹣4或n=﹣5或n=﹣6，∴当n=﹣4时，x=﹣4，当n=﹣5时，x=﹣，当n=﹣6时，x=﹣，经检验，x=﹣4或x=﹣或x=﹣是原方程的解．故答案为：﹣4或﹣或﹣．点评：此题考查了取整函数的知识．注意[x]≤x＜[x]+1性质的应用是解此题的关键．14．（5分）如图，是一个挂在墙壁上时钟的示意图．O是其秒针的转动中心，M是秒针的另一端，OM=8cm，l是过点O的铅直直线．现有一只蚂蚁P在秒针OM上爬行，蚂蚁P到点O的距离与M 到l的距离始终相等．则1分钟的时间内，蚂蚁P被秒针OM携带的过程中移动的路程（非蚂蚁在秒针上爬行的路程）是16πcm．考点：弧长的计算．分析：作出辅助线得出△OMN≌△Q2OP，进而得出∠OPQ2=∠NOM=90°，得出从而蚂蚁P在1分钟时间内被秒针OM携带的过程中移动的轨迹就是分别以OQ1，OQ2为直径的两个圆，求出即可．解答：解：过M作MN⊥L于点N，过O作L的垂线交于点Q1，Q2，连接PQ2，则MN∥OQ2，∠M=∠MOQ2，∵OM=OQ2，MN=OP，∴△OMN≌△Q2OP，∴∠OPQ2=∠MNO=90°，∴点P在以OQ1为直径的圆上，同理点P在以OQ2为直径的圆上，从而蚂蚁P在1分钟时间内被秒针OM携带的过程中移动的轨迹就是分别以OQ1，OQ2为直径的两个圆，移动的路程为：2×8π=16π．故答案为：16π．点评：此题主要考查了弧长的计算以及物体移动路线问题，此题综合性较强得出从而蚂蚁P在1分钟时间内被秒针OM携带的过程中移动的轨迹就是分别以OQ1，OQ2为直径的两个圆是解决问题的关键．三、解答题15．（12分）已知A、B两地相距45千米，骑车人与客车分别从A、B两地出发，往返于A、B两地之间．如图中，折线表示某骑车人离开A地的距离y与时间x的函数关系．客车8点从B地出发，以45千米/时的速度匀速行驶．（乘客上、下车停车时间忽略不计）①在阅读如图的基础上，直接回答：骑车人共休息几次？骑车人总共骑行多少千米？骑车人与客车总共相遇几次？②试问：骑车人何时与客车第二次相遇？（要求写出演算过程）．考点：一次函数的应用．专题：应用题；图表型．分析：（1）看图可知，折线图中有两段水平的线，故休息了两次，时间是两次之和（看横轴）；（2）根据题意，客车一小时行驶45千米，故它的图象是两小时一个来回．从左向右看，两条折线的第二个交点就是它们第二次相遇．求出EF的函数解析式就可以了，找到特殊点（9，0）和（10，45）用待定系数法可求出．解答：解：（1）依题意得：骑车人共休息2次；骑车人总共骑行90千米；骑车人与客车总共相遇8次；（2）已知如图：设直线EF所表示的函数解析式为y=kx+b．把E（9，0），F（10，45）分别代入y=kx+b，得，解得，∴直线EF所表示的函数解析式为y=45x﹣405，把y=20代入y=45x﹣405，得45x﹣405=20，∴．答：时骑车人与客车第二次相遇．点评：本题考查了一次函数的应用：通过表格当中的信息是解题关键；根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．此题比较复杂，首先是正确理解题意，这要求仔细观察图象，从图象中得到需要的信息，关键知道它们走的方向不同．此外还用到了待定系数法求函数解析式．16．（12分）如图1：等边△ADE可以看作由等边△ABC绕顶点A经过旋转相似变换得到．但是我60°形成的．于是我们得到一个结论：如果两个正三角形存在着公共顶点，则该图形可以看成是由一个三角形绕着该顶点旋转60°形成的．①利用上述结论解决问题：如图2，△ABC中，AB=3，AC=4，BC=5，△ABD，△ACE，△BFC 都是等边三角形，求四边形ADFE的面积；②图3中，△ABC∽△ADE，AB=AC，∠BAC=∠DAE=θ，仿照上述结论，推广出符合图3的结论．（写出结论即可）考点：旋转的性质；等边三角形的性质；相似三角形的判定与性质．专题：计算题．分析：①最外沿大五边形等于一个正三角形+2个直角三角形，故可求其面积；用大五边形面积减去3个三角形面积即可求得结果（三角形ABD、三角形ACE、三角形ABC）；②结论应该是：如果两个等腰三角形有公共顶点，则该图形可以看成是一个三角形绕着该顶点旋转θ度形成的．解答：解：①S FDAE=S DFECB﹣S△ABD﹣S△ABC﹣S△ACE，=S△BCF+S△BDF+S△CEF﹣S△ABD﹣S△ABC﹣S△ACE，=××5+﹣××3﹣×2×4﹣×3×4，=6；②结论：如果两个等腰三角形有公共顶角顶点，顶角均为θ，则该图形可以看成一个三角形绕着该顶点旋转θ形成的．点评：本题考查了旋转的性质，等边三角形的性质和三角形面积的计算，解题的关键是要把握图形的变换．17．（12分）在三角形ABC中，∠C=90°，∠A，∠B，∠C对应的边分别是a，b，c，其中a﹣b=2，CD⊥AB于D，BD﹣AD=2，求△ABC三边的长．考点：勾股定理．专题：计算题．分析：设出斜边长和斜边上的高，利用锐角三角函数表示出a与b的和，再利用已知条件中的两边之差求得a和b的值即可．解答：解：设AB=c，CD=hBD=a×sinA=a×，AD=b×cosA=b×，BD﹣AD=﹣==2a﹣b=2a+b=（）×c两边同时平方得：c2+2ab=c2 ∴2ab=c2，∵ab=ch，∴ab=ch=c2，∴4h=ca2+b2﹣2ab=8c2﹣2ch=8c2﹣c2=8c=4a=+b=﹣点评：本题考查了勾股定理的知识，解题的关键是利用锐角三角函数值表示出两直角边的和，然后利用已知条件求得两直角边的值．18．（12分）按下面规则扩充新数：已有a和b两个数，可按规则c=ab+a+b扩充一个新数，而a，b，c三个数中任取两数，按规则又可扩充一个新数，…，每扩充一个新数叫做一次操作．现有数2和3．①求按上述规则操作三次得到扩充的最大新数；②能否通过上述规则扩充得到新数5183？并说明理由．考点：因式分解的应用．分析：①将2与3分别代入求解，再取其最大的两个值依次代入即可求得答案；②找到规律：设扩充后的新数为x，则总可以表示为x+1=（a+1）m•（b+1）n，式中m、n为整数，即可得当a=2，b=3时，x+1=3m×4n，然后求解即可．解答：解：①∵a=2，b=3，c1=ab+a+b=6+2+3=11，∴取3和11，∴c2=3×11+3+11=47，取11与47，∴c3=11×47+11+47=575，∴扩充的最大新数575；②5183可以扩充得到．∵c=ab+a+b=（a+1）（b+1）﹣1，∴c+1=（a+1）（b+1），取数a、c可得新数d=（a+1）（c+1）﹣1=（a+1）（b+1）（c+1）（a+1）﹣1=（a+1）2（b+1），即d+1=（a+1）2（b+1），同理可得e=（b+1）（c+1）=（b+1）（a+1）﹣1，∴e+1=（b+1）2（a+1），设扩充后的新数为x，则总可以表示为x+1=（a+1）m•（b+1）n，式中m、n为整数，当a=2，b=3时，x+1=3m×4n，又∵5183+1=5184=34×43，故5183可以通过上述规则扩充得到．点评：此题考查了因式分解的应用，解题的关键是找到规律设扩充后的新数为x，则总可以表示为x+1=（a+1）m•（b+1）n，式中m、n为整数．19．（14分）如图，二次函数y=ax2+bx（a＞0）的图象与反比例函数图象相交于点A，B，已知点A的坐标为（1，4），点B在第三象限内，且△AOB的面积为3（O为坐标原点）．①求实数k的值；②求二次函数y=ax2+bx（a＞0）的解析式；③设抛物线与x轴的另一个交点为D，E点为线段OD上的动点（与O，D不能重合），过E点作EF∥OB交BD于F，连接BE，设OE的长为m，△BEF的面积为S，求S于m的函数关系式；④在③的基础上，试说明S是否存在最大值？若存在，请求出S的最大值，并求出此时E点的坐标；若不存在，说明理由．考点：二次函数综合题；解二元一次方程；反比例函数图象上点的坐标特征；二次函数的最值；待定系数法求二次函数解析式；平行线的性质；三角形的面积；勾股定理；锐角三角函数的定义．专题：计算题．分析：①把A（1，4）代入即可；②过B作BM⊥x轴于M，BN⊥y轴于N，过A作AH⊥x轴于H，两线BN和AH交于Q，设OM=c，ON=d，c＞0，d＞o，根据S=S△ABQ﹣S△AOH﹣S△BNO﹣S矩形ONQH，和cd=4，求出c=2，d=2，得到B（﹣2，﹣2），把A（1，4）和B（﹣2，﹣2）代入抛物线得出方程组，求出方程组得解即可；③充分利用（﹣2，﹣2）这一坐标，由△DFE相似于△DBO求得EF的长（含m），再表示出F到x轴的距离，利用△EDB的面积减去△EDF的面积即可建立S与m的函数关系④S=m（1+﹣m），当m=时，S最大，把m=代入即可求出s，从而得到E的坐标．解答：解：①把A（1，4）代入得：k=xy=4，答：实数k的值是4．②过B作BM⊥x轴于M，BN⊥y轴于N，过A作AH⊥x轴于H，两线BN和AH交于Q，设OM=c，ON=d，c＞0，d＞o，则：S=S△ABQ﹣S△AOH﹣S△BNO﹣S矩形ONQH，即：3=（1+c）（4+d）﹣×1×4﹣cd﹣d×1，cd=k=4，解得：c=2，d=2，∴B（﹣2，﹣2），把A（1，4）和B（﹣2，﹣2）代入抛物线得：，解得：，∴y=x2+3x，答：二次函数y=ax2+bx（a＞0）的解析式是y=x2+3x．⑨把y=0代入y=x2+3x得：x2+3x=0，解得：x1=0，x2=﹣3，∴D（﹣3，0），即OD=3，∵B（﹣2，﹣2），∴由勾股定理得：OB=2，∵EF∥OB，∴△DFE∽△DBO，∴=，∴=，∴EF=2﹣m，过F作FC⊥x轴于C，根据相似三角形的对应高之比等于相似比得：=，∴=，FC=S=S△EDB﹣S△EDF=DE×BM﹣FC×DE，即S=﹣m2+m，∴S与m的函数关系S=﹣m2+m．④S=﹣m2+m．当m=时，S最大，是，∴，答：在③的基础上，S存在最大值，S的最大值是，此时E点的坐标是（﹣，0）．点评：本题主要考查对用待定系数法求二次函数的解析式，反比例函数的图象上点的坐标特征，解二元一次方程，三角形的面积，平行线的性质，勾股定理，函数的最值，锐角三角函数的定义等知识点的理解和掌握，能熟练地运用这些性质进行计算是解此题的关键，此题是一个拔高的题目，有一定的难度．。

学校________________ 班级________________ 姓名_________________ 联系电话__________________密 封 线 内 不 要 答 题2017年学而思数学超常班选拔考试 四年级一、 填空题（每题6分，共96分，将答案填在下面的空格处）1. 2006＋200.6＋20.06＋2.006＋994＋99.4＋9.94＋0.994＝__________．【答案】原式=（2006+994）+（200.6+99.4）+（20.06+9.94）+（2.006+0.994）=3000+300+30+3 =3333．2. 定义x ☆37y x y ．（1☆1）+（2☆2）+（3☆3）+…+（10☆10）=__________． 【答案】（1☆1）+（2☆2）+（3☆3）+…+（10☆10）31713272337331071010(12310) 5503.M 是两位数，如果11M A B ，当A B 的和最大时，M __________．【答案】984. 五位打工者一天的辛苦劳动后共获得330元工资，由于工种不同，获得最高工资者比其他四位分别多得12、14、21和28元，获得最低工资者的工资是__________元． 【答案】获得最高工资者的工资是 33012142128581 元，所以获得最低工资者的工资是812853 元．5. 一次足球赛比赛中，所有参赛队的每两个队比赛一场，共比赛了15场，那么有__________个队参赛． 【答案】66. 春节前夕，一个富翁向一些乞丐施舍一笔钱．一开始他准备给每人100元，结果剩下350元，他决定每人多给20元．这时从其他地方闻讯赶来了5个乞丐，如果他们每个人拿到的钱和其他乞丐一样多，富翁还需要再增加550元．原有__________名乞丐．【答案】题目可以转化为：每个乞丐（一开始的个数）给100元，多350元，每个乞丐（一开始的个数）给120元，多12×50-550=50元.根据盈亏问题一开始乞丐个数（350-50）÷（120-100）=15（个）．7. A 、B 两地相距90千米，甲骑自行车每小时行15千米，乙开汽车，每行1千米比甲少用3分钟，甲、乙两人同时从A 出发去B 地，乙到B 地后立即返回，当乙遇到甲时，他们距离B 地__________千米．【答案】因为甲骑自行车每小时行15千米， 所以甲骑车行1千米需要4分钟．因为乙每行1千米比甲少用3分钟，’所以乙每分钟行1千米，即每小时行60千米． 因为A 、B 两地相距90千米，所以从甲、乙同时从A 出发，到乙从B 地返回遇到甲， 两人共行了90×2 =180（千米），所花的时间是180÷(15 +60)=2.4(小时)．所以当乙遇到甲时，他们距离B 的距离是90-15×2.4=54(千米)．8. 如图，用8个相同的小长方形拼成一个大长方形，求阴影部分的面积是__________平方厘米． 【答案】阴影部分面积是900平方厘米．9. 如图，三角形ABC 面积为90平方厘米，BD =2DC ，AE :EC =2:3，求阴影部分三角形CDE 的面积__________平方厘米．BC【答案】18平方厘米.10. 如图，请在右图每个方框中填入一个不是8的数字，使乘法竖式成立．则乘积的结果为__________．888×【答案】11. 有若干根长度相等的火柴棒，把这些火柴棒摆成如图的图形．照这样摆下去，到第10行为止一共用了__________根火柴棒．【答案】1行：4根；2行：10根：3行：18根规律为：4、10、18 相邻两个数之间的差构成等差数列6、8、10所以10行的图形用了 4681022130 根火柴棒．12. 一天，红太狼和灰太狼同时从“野猪林”出发，到“天堂镇”．红太狼一半路程溜达，一半路程奔跑．灰太狼一半时间溜达，一半时间奔跑．如果它们溜达的速度相同，奔跑的速度也相同，则先到“天堂镇”是__________． 【答案】由最简单的平均速度公式可以知道灰太狼的平均速度要高于红太狼的平均速度，那么先到“天堂镇”的应该是灰太狼．13. 将一个能被5整除的三位数的首、末数字交换后，还是三位数，它的5倍也是三位数，它的后两住数字的和是60的约数，求满足条件的最大的三位数是__________． 【答案】由三位数能被5整除，可知这个三位数的末位数字是0或5．由这个三位数的首、末数字交换后还是三位数，可知这三位数的末位数字5． 由三位数的5倍也是三位数，可知这三位数的首位数字是1．故设该三位数是15xx 可能是1，2，3，…，8，9．因为x +5是60的约数，且z 要尽可能大，所以x =7． 故所求的三位数是175．14. 下面的算式是按规律排列的：11 、23 、35 、47 、19 、211 、313 、415 、117 、219 、321 、423 、125 ⋯⋯那么，第__________个算式的两数之和是2008． 【答案】1003这个和的前项是一个周期数列1，2，3，4循环，后项是一个奇数数列．和为2008，那么后项要在2004～2007之间，只能是2005和2007．分别看一下他们前面的数是不是所需要的数即可．2005是第1003项，前面是3，2005+3=2008满足题意． 2007是第1004项，前面是4，和不满足．所以只能是第1003．15. 在一张四边形的纸上共有10个点，如果把四边形的顶点算在一起，则一共有14个点．已知这些点中的任意三个点都不在同一直线上．按下面规定把这张纸剪成一些三角形： ⑴ 每个三角形的顶点都是这14个点中的3个； ⑵ 每个三角形内，都不再有这些点． 那么，这张四边形的纸最多可以剪出__________个三角形．【答案】当四边形内只有1个点时，则可剪出4个三角形；当四边形内只有2个点时，则可以剪出6个三角形；当四边形内只有3个点时，则最多可以剪出8个三角形；由此可见，四边形内每增加1个点，就可以多剪出2个三角形．因此，四边形内有10个点时，最多可剪出三角形42922 （个）．16. 老罗在退休时共有264万元的积蓄，他将这些钱分为4份，除了三个儿子各给一份外，另有一份自己留做养老金．若他把这份养老金给大儿子，则大儿子所得的钱等于二儿子及三儿子所得的钱之总和；若他把这份养老金给二儿子，则二儿子所得的钱等于大儿子及三儿子所得的钱之总和的两倍；若他把这份养老金给三儿子，则三儿子所得的钱等于大儿子及二儿子所得钱之总和的三倍．请问老罗准备拿来当养老金的部分为__________万元． 【答案】121万元二、 解答题（17、18题每题12分，19、20题每题15分，共54分，写出必要步骤，否则不得分）1. 妈妈带儿子小虎到超市买了两件商品，小虎把一件商品标价中个位上的零忽略了，他付给收银员162元，但是收银员说应当付270元．求这两种商品的单价差是多少元？ 【答案】收银员要收的钱与小虎算出的价格相差270-162=108(元)．因为小虎将一件商品标价中个位上的零忽略了， 所以这件商品被他错看成了 108÷（10-1）=12（元）， 于是这件商品的真实价格应是 12×10=120(元)．所以另外一件商品的价格是 270 -120 =150（元）． 于是两件商品的单价分别是120元和150元．1501203088888×学校________________ 班级________________ 姓名_________________ 联系电话__________________密 封 线 内 不 要 答 题2. 将1分、2分、5分和1角的硬币投入19个盒子中，使每个盒子里都有硬币，且任何两个盒子里的硬币的钱数都不相同．问： （1）至少需要投入多少硬币？（2）这时，所有的盒子里的硬币的总钱数至少是多少？ 【答案】只取一枚有1分、2分、5分、10分（1角）4种；取二枚有1＋1＝2（分），2＋2＝4（分），5＋5＝10（分），10＋10＝20（分）（2角）， 1＋2＝3（分），1＋5＝6（分），1＋10＝11（分）（1角1分），2＋5＝7（分），2＋10＝12（分）（1角2分），5＋10＝15（分）（1角5分）， 共10种，其中重复2种（2分、10分），加上只取一枚的共12种不同币值；取三枚时，可将以上取两枚的10种情况，分别加1分、2分、5分、10分，共有40种情况．从小到大取出7种不重复的币值为：8分、9分、13分、14分、16分、17分、21分，加上上述12种共19种．公用硬币的枚数为：1×4＋2×8＋3×7＝41（枚）． 总钱数为：1＋2＋3＋…＋17＋20＋21＝194（分）．3. 6条谜语让50人猜，每条谜语每人猜一次，共猜对了178次，已知每人至少猜对了2条，只猜对2条的有16人，只猜对4条的有9人，只猜对3条和只猜对5条的人数一样多．那么6条谜语全猜对的有多少人？【答案】因为50个人猜6条谜语，每条谜语每人猜一次，所以共有506300 （条）因为共猜对了178次，所以共猜错了300178122 （次）．因为只猜对2条的有16人，所以这16人共猜错了16(62)64 （次），因为猜对4条的有9人，所以这9人猜错了9(64)18（次），于是还剩122641840 （次）被猜错．而猜对6条的人猜错0条，所以这40条是被猜对3条的人或猜对5条的人猜错的．因为猜对3条和猜对5条的人数一样，所以猜对3条和猜对5条的都各有40[(63)(65)]10 (人) ．于是6条谜语全猜对的人数是5016910105 （人）．4. 8点10分，有甲、乙两人以相同的速度分别从相距60米的A ，B 两地顺时针方向沿着长方形ABCD （见图）的边走向D 点，甲8点20分到D 后，丙、丁两人立即以相同的速度从D 点出发，丙由D 逆时针向A 走去，8点24分与乙在E 点相遇，丁由D 顺时针向C 走去，8点30分在F 点被乙追上，则连接三角形BEF 的面积为多少平方米．A BCD【答案】2497.5平方米【分析】如下图所示，假设8点20分时，乙走到了M 点，由于甲、乙两人速度相同，因此有AB AM AD ，也即60MD AB 米，此时丙、丁从D 点出发．单独看乙和丙，两人做了一个相遇运动，相遇的时间是4分钟，相遇路程是60米，因此两人的速度和为15米/分．单独看乙和丁，两人做了一个追及运动，追及的时间是10分钟，追及路程也是60米，因此两人的速度差为6米/分．又因为丙和丁的速度相同，因此有乙的速度为 156210.5 米/分．乙花了14分钟走到E 点，走了10.514147 米，AE 长度为1476087 米．同理乙花了20分钟走到F 点，走了10.520210 米，DF 长度为2106010545 米．因此有：63002610405787.52497.5BEF ABCD ABE BCF DEF S S S S S △△△平方米。

第1页 共4页 第2页 共4页2015—2016年深圳学而思 超常班选拔考试四年级 数学考 生 须 知1．本试卷共4页，20道题，满分150分，考试时间90分钟． 2．在试卷上认真填写学校名称、班级和姓名．3．答案填写在答题卡上，写在试卷上无效，请用黑色字迹签字笔作答．16题，每题6分，共96分，将答案填在下面的空格处） ．计算：27 3.6 6.427=⨯+⨯____________． ．小乐四次测试的成绩分别为98分，95分，90分和93分，这四次测试的平均分是__________分． ．4名工人3小时一共做了60个零件，按照这样的速度，12名工人8小时能做__________个零件． ．数一数，下图中共有__________个三角形．．如图，边长为10厘米的正方形ABCD 里有一个三角形BEF ，AE =4厘米，FC =6厘米，三角形BEF 的面积是_________平方厘米．．一个长方形的长和宽都是整数厘米，周长是30厘米，这个长方形的面积最大是__________平方厘米． ．如图，点D 是BC 边上的中点，AE 的长度是EC 长度的3倍，如果三角形ABC 的面积是48平方厘米，那么三角形EDC 的面积是__________平方厘米．8．下图中包含☆的长方形有__________个.9．小超家和小越家相距2880米，小超每分钟走48米，小越每分钟走32米，两人同时出发相向而行，经过__________分钟两人相遇．10．用数字1、4、5、8、0能组成__________个没有重复数字的三位偶数．11．在一个宽为1米的长方形花坛周围铺上边长为1米的正方形石板路，如下图，如果花坛长2米，则会用到10块石板，如果花坛长度是3米，则会用到12块石板，如果花坛长度为a 米（a 为整数），则会用到__________块石板．（用含有a 的式子表示）12．四位数462a 既是3的倍数，又是8的倍数，a =_________．13．1~100中，所有4的倍数的和是_________．14．一个数的所有数字和是23，每个数位上的数字各不相同，且不为0，这个数最大是__________．15．四年级2班布置联欢会的现场，每位男生吹12个气球，每位女生吹8个，全班45个人一共吹了460个气球，这个班有_________名女生．16．甲、乙两人现在的年龄和是63岁，当甲年龄等于乙现在年龄一半时，乙当时的年龄等于甲现在的岁数，那么甲现在__________岁．FED CBAEDCBA☆第3页 共4页 第4页 共4页二、解答题（17题12分，18题12分，19题15分，20题15分，共54分，写出必要步骤，否则不得分） 17．如图，长方形ABCD 的长9cm AB =，12cm CF =，阴影部分ACE ∆的面积是218cm ．（1）三角形ACF 的面积是多少平方厘米？（4分） （2）CE 的长度是多少厘米？（5分）（3）长方形ABCD 的面积是多少平方厘米？（6分）18．数列：21，34，67，210，313，616，219……按照一定的规律排列． （1）这个数列的第20个是什么？（4分）（2）数列中157□的分子是几？（5分）（3）数列中第几个数的分子和分母之和是418？（6分）19．如图，宁宁、涛涛和浩浩三人合坐一辆出租车从学校回家．他们约定：共同乘坐的部分所产生的费用由乘坐者平均分摊；单独乘坐部分所产生的费用由乘坐者单独承担．（如：一段路程有3人乘坐，一共花费12元，则每人分担4元；一段路程只有1人乘坐，花费5元，则这5元由这1人承担．）此出租车没有起步价，且每公里的价格一样．结果三人承担的费用分别是6元、15元、21元．宁宁家离学校12公里． （1）这次坐车的一共花了多少元？（4分）（2）图中三段路程，每段路程的费用分别是多少元？（6分） （3）浩浩家离学校有多少公里？（5分）20．甲、乙、丙三人沿湖边练习跑步，三人同时从湖边的某一点出发，乙、丙两人顺时针跑，甲逆时针跑，在甲与乙第一次相遇后5分钟第一次遇到丙，再过15分钟第二次遇到乙．已知甲的速度是乙的1.5倍，湖的周长为8000米．（1）甲、乙两人经过几分钟第一次相遇？（3分） （2）甲、丙两人经过几分钟第一次相遇？（3分） （3）甲、乙、丙三人的速度分别是多少？（6分） （4）丙沿湖边跑一圈需要多长时间？（3分）912FED CBA学校 班级 姓名 考号 指导老师密 封 线 内 禁 止 答 题2015年深圳学而思秋季超常班选拔考试四年级考 生 须 知1. 本试卷共4页，20题2. 本试卷满分150分，考试时间90分钟3. 在试卷密封线内填上填写学校、班级、姓名、联系电话一、填空题（共16题，每题6分，共96分，将答案填在下面的空格处）1. 计算：27 3.6 6.427=⨯+⨯____________．【解析】270．2. 小乐四次测试的成绩分别为98分，95分，90分和93分，这四次测试的平均分是__________分． 【解析】()98+95+90+934=94÷分．3. 4名工人3小时一共做了60个零件，按照这样的速度，12名工人8小时能做__________个零件．【解析】1名工人1小时做6043=5÷÷个，12名工人8小时能做5128=480⨯⨯个．4. 数一数，下图中共有__________个三角形．【解析】13个．5. 如图，边长为10厘米的正方形ABCD 里有一个三角形BEF ，AE =4厘米，FC =6厘米，三角形BEF的面积是_________平方厘米．【解析】38．6. 一个长方形的长和宽都是整数厘米，周长是30厘米，这个长方形的面积最大是__________平方厘米． 【解析】78=56⨯平方厘米．7. 如图，点D 是BC 边上的中点，AE 的长度是EC 长度的3倍，如果三角形ABC 的面积是48平方厘米，那么三角形EDC 的面积是__________平方厘米．【解析】488=6÷平方厘米．8. 下图中包含☆的长方形有__________个.【解析】412=48⨯个．9. 小超家和小越家相距2880米，小超每分钟走48米，小越每分钟走32米，两人同时出发相向而行，经过__________分钟两人相遇．【解析】()288048+32=36÷分钟．10. 用数字1、4、5、8、0能组成__________个没有重复数字的三位偶数． 【解析】431+332=30⨯⨯⨯⨯．11. 在一个宽为1米的长方形花坛周围铺上边长为1米的正方形石板路，如下图，如果花坛长2米，则会用到10块石板，如果花坛长度是3米，则会用到12块石板，如果花坛长度为a 米（a 为整数），则会用到__________块石板．（用含有a 的式子表示）【解析】26a +．12. 四位数462a 既是3的倍数，又是8的倍数，a =_________． 【解析】3a =．13. 1~100中，所有4的倍数的和是_________． 【解析】()4+100252=1300⨯÷．14. 一个数的所有数字和是23，每个数位上的数字各不相同，且不为0，这个数最大是__________． 【解析】1+2+3+4+5+6=21，最大的数为854321．15. 四年级2班布置联欢会的现场，每位男生吹12个气球，每位女生吹8个，全班45个人一共吹了460个气球，这个班有_________名女生．【解析】20名．FEDCBAECBA☆学理科到学而思16. 甲、乙两人现在的年龄和是63岁，当甲年龄等于乙现在年龄一半时，乙当时的年龄等于甲现在的岁数，那么甲现在__________岁．【解析】27岁．二、解答题（17题12分，18题12分，19题15分，20题15分，共54分，写出必要步骤，否则不得分）17. 如图，长方形ABCD 的长9AB cm =，12CF cm =，阴影部分ACE ∆的面积是218cm ．（1） 三角形ACF 的面积是多少平方厘米？（4分） （2） CE 的长度是多少厘米？（5分）（3） 长方形ABCD 的面积是多少平方厘米？（6分）【解析】（1）29122=54cm ⨯÷．（2）()54182126CE cm =-⨯÷=．（3）1826=6AD cm =⨯÷，长方形的面积是96=54⨯平方厘米．18. 数列：21，34，67，210，313，616，219……按照一定的规律排列．（1） 这个数列的第20个是什么？（4分）（2） 数列中157□的分子是几？（5分）（3） 数列中第几个数的分子和分母之和是418．（6分）【解析】此数列的分子是一个周期数列，分母是一个等差数列．（1）分子：203=62÷ ，分子为3；分母：1+193=58⨯，第20个是358．（2）157是这个数列的第()15713+1=53-÷个，分子是533=172÷ ，分子为3．（3）418=2+416=3+415=6+412，其中416不在分母是数列中，415是第139个，412是第138个；对于分子来说，第139个分子是2，第138个分子是6，所以6412满足要求，是第138个．19. 如图，宁宁、涛涛和浩浩三人合坐一辆出租车从学校回家．他们约定：共同乘坐的部分所产生的费用由乘坐者平均分摊；单独乘坐部分所产生的费用由乘坐者单独承担．（如：一段路程有3人乘坐，一共花费12元，则每人分担4元；一段路程只有1人乘坐，花费5元，则这5元由这1人承担．）此出租车没有起步价，且每公里的价格一样．结果三人承担的费用分别是6元、15元、21元．宁宁家离学校12公里．（1） 这次坐车的一共花了多少元？（4分）（2） 图中三段路程，每段路程的费用分别是多少元？（5分） （3） 浩浩家离学校有多少公里？（6分）【解析】（1）6+15+21=42元．（2）第①段：63=18⨯元，第②段：()15-62=18⨯元，第③段：21156-=元．（3）前两段花的钱一样，说明前两段都是12公里，第③段花了6元，所以为123=4÷公里，浩浩家离学校有12+12+4=28公里．20. 甲、乙、丙三人沿湖边练习跑步，三人同时从湖边的某一点出发，乙、丙两人顺时针跑，甲逆时针跑，在甲与乙第一次相遇后5分钟第一次遇到丙，再过15分钟第二次遇到乙．已知甲的速度是乙的1.5倍，湖的周长为8000米．（1） 甲、乙两人经过几分钟第一次相遇？（3分） （2） 甲、丙两人经过几分钟第一次相遇？（3分） （3） 甲、乙、丙三人的速度分别是多少？（6分） （4） 丙沿湖边跑一圈需要多长时间？（3分）【解析】（1）5+15=20分．（2）20+5=25分．（3）甲、乙两人的速度和为800020=400÷米/分，甲的速度是乙的1.5倍，乙的速度为()4001+1.5=160÷米/分，甲的速度是160 1.5=240⨯米/分，甲、丙的速度和是800025=320÷米/分，丙的速度是32024080-=米/分．（4）800080=100÷分．912FED CBA。

第四届“学而思”杯综合素质测评 A 卷四年级姓名：_____________ 成绩：_____________ 考试时间：120分钟数学部分【考试说明】数学部分分为填空题（10小题）和动手动脑思维题（5小题），共15小题，满分为100分。

一、 填空题。

（本大题共10小题，每小题5分，共50分，要求直接写出答案。

）1、 12345678987654321(123456789)___⨯++++++++=2、若2010A B =+，并且12A B ÷=÷，则B = 。

3、有10种颜色的袜子（除颜色外其余相同）各20只混装在箱内, 黑暗中从箱内至少取出_______只才能保证有两双颜色相同的袜子。

4、小明家住在一条小胡同里,各家号码从1号连着排下去,全胡同所有家的号码之和再减去小明家号码后是60。

小明家是_______号.5、一张烙饼，（直着切，不能横剖），要是切4刀，最多能切出_______块。

6、 甲、乙、丙三人打靶，每人打三枪。

三人各自中靶的环数之积都是60，且环数是不超过10的自然数。

把三个人按个人总环数由高到低排列，依次是甲、乙、丙。

请问：靶子上4环的那一枪是_______打的？7、 在练习口算时，小朱按照正整数的顺序从1开始求和，当加到某个数时，和为1301。

验算时发现，她重复加了一个数。

请问这个多加一次的数是_______。

8、 甲、乙、丙、丁四人同时到一个小水龙头处用水，甲洗拖布需要3分钟，乙洗抹布需要2分钟，丙用桶接水需要1分钟，丁洗衣服需要10分钟，怎样安排四人的用水顺序，才能使他们在这个水龙头处用水花费的总时间最少，这个总时间是_______。

9、计算机上编程序打印出前10000个正整数：1、2、3、4……、10000时，不幸打印机有毛病，每次打印数字3时，它都打印出x ，问其中被错误打印的共有_______个数。

10、不是零的自然数的平方按照从小到大的顺序接连排列是：149162536，则从左向右的第100个数字是。