第二章1信号与系统,课后答案

⑺
对⑺式求一阶导，有：
de(t ) d 2 i 2 (t ) di (t ) du (t ) =2 +2 2 + c 2 dt dt dt dt de(t ) d 2 i2 (t ) di (t ) =2 + 2 2 + 2i1 (t ) + 2i 2 (t ) 2 dt dt dt
⑻
将⑸式代入⑻式中，有：
λ 2 + 2λ + 1 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1
y h (t ) = C1e −t + C2 te− t
由初始状态为 y (0 ) = 1, y ' (0 ) = 0 ，则有：
C1 = 1 − C 1 + C 2 = 0
由联立方程可得 故系统的零输入响应为：
由联立方程可得 故系统的零输入响应为：
A1 = 2, A2 = −1
y zi (t ) = 2e − t − e −2 t
（2）由原微分方程可得其特征方程为
λ 2 + 2λ + 2 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1 ± i
y h (t ) = e −t (C1 cos t + C2 sin t )
(− 3C1 + 3C2 )δ (t ) + (C1 + C2 )δ ' (t ) − (− 2C1 + C 2 )δ (t ) = δ (t )
(
(
( + C e )δ (t ) + (C e
2 1
)
−2 t
+ C2 e t δ ' (t )

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD （15,6）=3 Hz 。

因此，公共周期3110==f T s 。

(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD （5, 15）=5 Hz 。

因此，公共周期5110==f T s 。

(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数，因此无法找出公共周期。

所以是非周期的。

(d) 两个分量是同频率的，基频 =0f 1/π Hz 。

因此，公共周期π==01f T s 。

1-2 解 (a) 波形如图1-2(a)所示。

显然是功率信号。

t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。

显然是能量信号。

3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号，显然有 1=P W1-3 解 周期T=7 ，一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+； (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。

1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。

i1(t) = i2 (t) + i3 (t) , i2 (t) R2 − L 有 8i2 `(t) + 3i2 (t) = 2e`(t) ˆ ˆ 由 h`(t) + 3h(t) = 2δ (t)
0
h
(−1) t 3
T
t
t 3E − τ E (t) = ∫ δ (τ )dτ − ∫ e 8 u(τ )dτ −∞ 4 −∞ 32
x(t)
1
2 t
yx(t)
1 2 3 4 t
0
1
0
Qh(0) = 0, t ≤ 0, 有 0 ≤ t <1 , h(t) + h(t −1) + h(t − 2) = h(t) = t 时 1≤ t < 2时 h(t) + h(t −1) + h(t − 2) = h(t) + h(t −1) =1 , h(t) =1− h(t −1) =1− (t −1) = 2 −t 2 ≤ t < 3 , h(t) + h(t −1) + h(t − 2) =1 时 h(t) =1− h(t −1) − h(t − 2) =1− (2 − (t −1)) − (t − 2) = 0 3 ≤ t < 4时 h(t) = 4 − t − h(t −1) − h(t − 2) =4 −t − 0 − (2 − (t − 2)) = 0 , t, 0 ≤ t < 1 ∴h(t) = 2 − t, 1 ≤ t ≤ 2 0, t < 0,2 < t
解: (e) 特征方程为 λ2+4λ+4=0 得 λ1=-2， λ2=-2。 则 h(t)= (c1eλ1 t+ c2eλ2t)u(t)=( c1e- 3 t+ c2e-2 t)u(t) h`(t)= (c1+ c2)δ(t)+(-3c1e- 3 t-2c2e- 2t)u(t) h``(t)= (c1+ c2)δ`(t)+(-3c1-2c2) δ(t)+ (9c1e- 3 t+4c2e- 2t)u(t) 将x(t)= δ(t), y(t)=h(t)代入原方程得：

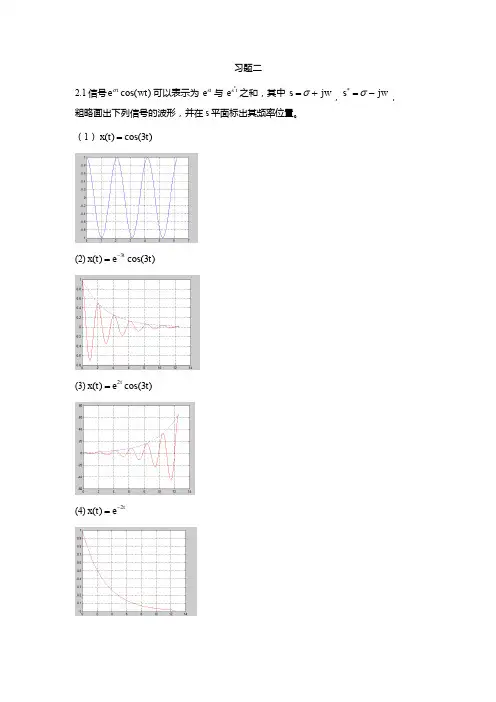
习题二2.1信号cos()t e wt σ可以表示为 st e 与 *s t e 之和，其中 s jw σ=+，*s jw σ=-， 粗略画出下列信号的波形，并在s 平面标出其频率位置。

（1）()cos(3)x t t =(2)3()cos(3)t x t e t -=(3)2()cos(3)t x t e t =(4)2()t x t e -=(5)3()t x t e =(6)()5x t =x (t )50t2.2粗略画出下列信号。

（1）()(3)(5)x t u t u t =---012345tx (t )1（2）()(3)(5)x t u t u t =-+-（3）2(){(3)(5)}x t t u t u t =--- x (t )902535t（4）()2(3)(5)(7)x t u t u t u t =-----2.3简化下列表达式（1）2sin ()()2t x t t t δ=+=0 （2）2()()9jw x jw ωδω+=+=2()9δω (3) ()()2sin 22()14t x t t t πδ⎧⎫-⎨⎬⎩⎭=-+=-1(1)5t δ- (4) sin()()()kw x t w wδ==k ()w δ 2.4 求下列积分（1）()()()x t x t d δτττ+∞-∞=-⎰=()()x t d δττ+∞-∞⎰=x(t) (2) ()()()x t x t d τδττ+∞-∞=-⎰=()()()x t t d x t δττ+∞-∞-=⎰ (3) 313()(23)sin()(23)sin()()222x t t t dt t dt t dt δπδπδ+∞+∞+∞-∞-∞-∞=-=-=--⎰⎰⎰=-12(4) ()()()1jwt x t t e dt t dt δδ+∞+∞-∞-∞===⎰⎰(5) ()(2)(3)(1)(3)(1)x t x t t dt x t dt x δδ+∞+∞-∞-∞=--=--=-⎰⎰(6) ()()()()t tjw x t e d d u t τδττδττ-∞-∞===⎰⎰(7) 3()(1)cos[(3)]sin[(3)]|0t x t t w t dt w w t δ+∞=-∞'=--=-=⎰(8)()(2)cos[(2)]cos[(2)](2)t tx t t w t dt w t d t δδ-∞-∞'=--=--=⎰⎰cos[(2)](2)|(2)cos[(2)]tt w t t t d w t δδ-∞-∞-----⎰1(2)sin[(2)]1tw t w t dt δ-∞=----=⎰2.5(1)求信号2()()t x t e u t -=的偶部与奇部2()()t x t e u t -=-偶部 {}{}2211()()(){()()}22t t Ev x t x t x t e u t e u t -=+-=+- 奇部{}{}2211{()}()()()()22t t Od x t x t x t e u t e u t -=--=--（2）2401|()|4t E x t dt e dt +∞+∞-∞-∞===⎰⎰ 总能量422220111|||()()|2448t t t E Ev dt e u t e u t dt e dt -+∞+∞+∞-∞-∞-∞==+-=⨯⨯=⎰⎰⎰偶部能量 422220111|||()()|2448t t t E Od dt e u t e u t dt e dt -+∞+∞+∞-∞-∞-∞==--=⨯⨯=⎰⎰⎰奇部能量 （3）由第二问可以得出信号的总能量等于其奇部与偶部能量之和。

第二章部分习题参考答案2-6 试求下列各函数1()f t 与2()f t 之卷积。

121212(-)01(1) ()() ()() (0) ()()()(-) ()(-)11(1) 0(2) ()t tt t tt t f t u t f t e u t f t f t f f t d u eu t d e e d e e e t f t ααταατααταατττττττααδ-+∞-∞+∞---∞--==>*===⋅=⋅=-≥=⎰⎰⎰，解：，2121212() ()cos(45)()()()cos[()45] cos(45)(3) ()(1)[()(1)] ()(1)(2) ()()t f t t f t f t t d t f t t u t u t f t u t u t f t f t ωδτωττω+∞-∞=+*=-+=+=+--=---*⎰，解：，解：ττ222221211211()(-1)(-1)-2(-2)(-2)(-1)(-1)-(-2)(-2)2211-(-2)(-2)(-3)(-3)-(-2)(-2)(-3)(-3)22()*()()1,()0123, (1-)(1)21(1)--(12ttf t t u t t u t t u t t u t t u t t u t t u t t u t f t f t f t t f t t t dt t ft t t t τττ=+++=<=<<+=+-=++⎰222-112222212111)-222123, (1-)(1)-221()2(1)-2(1-)(-1)211121---152223, ()*()0.t t t t t t d t f t t t t t t t t t t t f t f t ττττ-+=<<+=+=+++=+++=++>=⎰121221--(4) cos , (1)-(-1)()*()()(-) [(1)-(-1)][cos(-)] cos[(1)]-cos[(-1)]f t t f t t t f t f t f f t d t t t d t t ωδδτττδδωττωω+∞∞+∞∞==+==+⋅=+⎰⎰ -212-212--2-220(5) ()(), ()sin ()()()*()()sin(-)(-) sin(-)sin t t ttt tf t e u t f t t u t f t f t f t e u t u t d e t d ee d τττττττττ+∞∞==⋅==⋅⋅⋅=⋅=⋅⎰⎰⎰-12-(-)--0022-(-)-33-2-3(6) ()2[()-(-3)], ()4()-(-2)0, ()0.02,()2488-825, 88()8(-)5, ()0.t tt t t tt t t t t f t e u t u t f t u t u t t f t t f t e d e e e t ft ed ef t e e e t f t ττττττ-==<=<<==⋅=<<===>=⎰⎰2-8 求阶跃响应为32()(21)()t t s t e e u t --=-+的LTI （线性时不变）系统对输入()()t x t e u t =的响应。

第2章 习 题2-1 求下列齐次微分方程在给定起始状态条件下的零输入响应（1）0)(2)(3)(22=++t y t y dt d t y dt d ；给定：2)0(,3)0(==--y dt dy ； （2）0)(4)(22=+t y t y dt d ；给定：1)0(,1)0(==--y dtd y ；（3）0)(2)(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dt dy ； （4）0)()(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy ； （5）0)()(2)(2233=++t y dt d t y dt d t y dt d ；给定：2)0(,1)0(,1)0(22===---y dt d y dt d y 。

（6）0)(4)(22=+t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy 。

解：（1）微分方程的特征方程为：2320λλ++=，解得特征根：121, 2.λλ=-=- 因此该方程的齐次解为：2()t th y t Ae Be --=+.由(0)3,(0)2dy y dt--==得:3,2 2.A B A B +=--=解得:8, 5.A B ==- 所以此齐次方程的零输入响应为:2()85tty t e e--=-.（2）微分方程的特征方程为：240λ+=，解得特征根：1,22i λ=±.因此该方程的齐次解为：()cos(2)sin(2)h y t A t B t =+.由(0)1,(0)1d y y dx --==得:1A =,21B =,解得:11,2A B ==. 所以此齐次方程的零输入响应为:1()cos(2)sin(2)2y t t t =+.（3）微分方程的特征方程为：2220λλ++=，解得特征根:1,21i λ=-± 因此该方程的齐次解为：()(cos()sin())th y t e A t B t -=+.由(0)1,(0)2dy y dx--==得:1,2,A B A =-= 解得:1,3A B ==.所以齐次方程的零输入响应为:()(cos()3sin())ty t e t t -=+.（4）微分方程的特征方程为：2210λλ++=，解得二重根:1,21λ=-.因此该方程的齐次解为：()()th y t At B e -=+. 由(0)1,(0)2dy y dx--==得:1,2,B A B =-=解得:3, 1.A B == 所以该方程的零输入响应为:()(31)ty t t e -=+.（5）微分方程的特征方程为：3220λλλ++=，解得特征根: 1,21λ=-,30λ=. 因此该方程的齐次解为：()()th y t A Bt C e -=++.由22(0)1,(0)1,(0)2d d y y y dx dt---===得:1,1,22A C B C C B +=-=-=. 解得:5,3,4A B C ==-=-.所以方程的零输入响应为:()5(34)ty t t e -=-+.（6）微分方程的特征方程为：240λλ+=，解得特征根:120,4λλ==-. 因此该方程的齐次解为：4()th y t A Be -=+.由(0)1,(0)2d y y dx --==得:1,42A B B +=-=.解得:31,22A B ==-. 所以此齐次方程的零输入响应为:431()22ty t e -=-.2-2 已知系统的微分方程和激励信号，求系统的零状态响应。

信号与系统第三版郑君里课后习题答案第一章习题参考解1，判刑下列信号的类型解：()sin [()];y t A x t = 连续、模拟、周期、功率型信号 。

()()tt y t x ed τττ--∞=⎰连续、模拟、非周期、功率型信号。

()(2y n x n =） 离散、模拟、非周期、功率型信号。

()()y n n x n = 离散、模拟、非周期、功率型信号。

1－6，示意画出下列各信号的波形，并判断其类型。

(1) 0()s in ()x t A t ωθ=+ 连续、模拟、周期、功率型(2) ()t x t A e -= 连续、模拟、非周期、只是一个函数，不是物理量。

(3) ()c o s 0tx t ett -=≥ 连续、模拟、非周期、能量型 (4) ()2112,x t t t =+-≤≤ 连续、模拟、非周期、能量型(5) 4()(),0.5k x k k =≥ 离散、模拟、非周期、能量型(6) 0().j kx k eΩ= 离散、模拟、周期、功率型()s i n [()];()()()(2);()()tt y t A x t y t x ed y n x n y n n x n τττ--∞====⎰1－6题，1－4图。

t=-pi:1/200:pi;y1=1.5*sin(2*t+pi/6);subplot(4,1,1),plot(t,y1),title('1.5sin(2*t+pi/6)'),gridy2=2*exp(-t);subplot(4,1,2),plot(t,y2),title('2exp(-t)'),gridt1=0:1/200:2*pi;y3=10*exp(-t1).*cos(2*pi*t1);subplot(4,1,3),plot(t1,y3),title('10exp(-t1)cos(2*pi*t1)'),grid t2=-1:1/200:2;y4=2*t2+1;subplot(4,1,4),plot(t2,y4),title('2x+1'),grid习题1－6 5－6题n=0:pi/10:2*pi;y=(0.8).^n;subplot(4,1,1),stem(n,y,'fill'),title('(0.8)^n'),gridn1=0:pi/24:2*pi;y1=cos(2*pi*n1);y2=sin(2*pi*n1);subplot(4,1,2),stem3(y1,y2,n1,'fill'),title('exp[2*pi*n1'),gridsubplot(4,1,4),stem(n1,sin(2*pi*n1),'fill'),title('sin2pin1'),gridsubplot(4,1,3),stem(n1,cos(2*pi*n1),'fill'),title('cos2pin1)'),grid1－8，判断下列系统的类型。

1口 7 -, 刀、歹L
2.25
CD CD
f(t) = IOcosl 11(1) 证明： J(t)关8(1-1。) =f(t-1。)
@ f(t) = e-''u(t) (?) f(t)
状态响应可以表示力
2.26
已知线性时不变系统的输入力f(t)'系统的阶跃响应力g(t)'试证明系统的零 汕） = Lf'(,!)g(t-,!)d儿 2.27 2.28 2.29 用MATLAB求题2.7的全响 应。 用MATLAB求题2. 9的零输入响应。 （此式称为杜阿美尔积分）
=
心Yx (/)=7e-'-5e-2'(t汃0)
(2)yx (1)=6e-'-(4+5/)e-3'(t;>O) CZ) /,(1)= te-'11(1) 3 @i,(1) = -e-2'sin(21)11(1) 2
2.11 2.12
CD /,(1)�(-2e-'+2e-")的）+ 0(1)
心yx (t)�ze-" -2e-" (1;;, O) I 5 8 3 y(t) � - 3 e- '+ 2e-" + 6
第1章信号与系统概述
习题1
心f(t)=cost+2 sin(2 兀t) @ f(t)=e _,, srn(2 亢I) (J) f(k)=sm(2忒） 心f(t)=cos( 兀 I) ＠ 1.2 1.1 判断 下列信号是否是周期信号。若是周期信号，则确定信号周期。 @ f(t)= costu(t) CZ) f(t)= sin(3 兀t)+cos(2 兀t) @八I)= sin'[

信号与系统课后习题参考答案1试分别指出以下波形就是属于哪种信号？题图1-11-2试写出题1-1图中信号得函数表达式。

1-3已知信号与波形如题图1-3中所⽰,试作出下列各信号得波形图,并加以标注。

题图1-3⑴⑵⑶⑷⑸⑹⑺⑻⑼1-4已知信号与波形如题图1-4中所⽰,试作出下列各信号得波形图,并加以标注。

题图1-4⑴⑵⑶⑷⑸⑹⑺⑻⑼1-5已知信号得波形如题图1-5所⽰,试作出信号得波形图,并加以标注。

题图1-51-6试画出下列信号得波形图:⑴⑵⑶⑷1-7试画出下列信号得波形图:⑴⑵⑶⑷⑸⑹1-8试求出以下复变函数得模与幅⾓,并画出模与幅⾓得波形图。

⑴⑵⑶⑷1-9已知信号,求出下列信号,并画出它们得波形图。

1-10试作出下列波形得奇分量、偶分量与⾮零区间上得平均分量与交流分量。

题图1-101-11试求下列积分:⑴⑵⑶⑷⑸⑹1-12试求下列积分:⑴⑵⑴(均为常数)⑵⑶⑷⑸⑹⑺⑻1-14如题图1-14中已知⼀线性时不变系统当输⼊为时,响应为。

试做出当输⼊为时,响应得波形图。

题图1-14 1-15已知系统得信号流图如下,试写出各⾃系统得输⼊输出⽅程。

题图1-151-16已知系统⽅程如下,试分别画出她们得系统模拟框图。

⑴⑵⑶1-17已知⼀线性时不变系统⽆起始储能,当输⼊信号时,响应,试求出输⼊分别为与时得系统响应。

第⼆章习题2-1试计算下列各对信号得卷积积分:。

⑴(对与两种情况)⑵⑶⑷⑸⑹2-2试计算下列各对信号得卷积与:。

⑴(对与两种情况)⑵⑶⑷⑸⑹2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。

题图2-32-4试计算下图中各对信号得卷积与:,并作出结果得图形。

题图2-42-5已知,试求:⑴⑵⑶2-7系统如题图2-7所⽰,试求系统得单位冲激响应。

已知其中各⼦系统得单位冲激响应分别为:题图2-72-8设已知LTI 系统得单位冲激响应,试求在激励作⽤下得零状态响应。

2-9⼀LTI 系统如题图2-9所⽰,由三个因果LTI ⼦系统级联⽽成,且已知系统得单位样值响应如图中。

0 sin(2 t ) (t 3)dt 0
5


+ + 2.22
概率画出结果。
< 有三种解法，建议用图解法
2.22
概率画出结果。
2.28 下面均为离散时间线性时不变系统的单位脉冲响应，试判定每一系统是 否是因果和/或稳定的。陈述理由。 (a)ℎ ������ = (5)������ ������[������] (c) ℎ ������ = (2)������ ������ −������
4 5
y
长度为 M
y
x
而 N ≤n ≤N 长度为 M ，试用M 和 M 来表示 M 。
h x
(c) 考虑一个离散线性时不变系统，它具有这么一个特点，即若对 全部 n ≥10, x[n] = 0 ，则对所有的 n ≥15 都有 y[n] = 0 。系统单 位脉冲响应 h[n] 必须满足什么条件才有此特性？ (a) (c) (b)
(d) 有一个线性时不变系统的单位脉冲响应如图P2.44所示。为了确定 y (0) ，必须要知道在什么一个区间上的 x(t ) ？
2.50 图P2.50所示为两个系统的级联，其中一个系统 A 是线性时不变的，
y (t ) 而第二个系统 B 是系统 A 的逆系统，若 y (t )是系统 A 对 x (t )的响应，
5 ������ −5 1
1 − ������ cos 2������������ ������������
������0 ������ = ������ ������
(a) (b) (c)
u0 (t ) cos(t )dt (t ) cos(t )dt cos(0) 1
第二章
2.4 计算并画出y[n]=x[n]*h[n]，其中

与奇分量的波形，相应如图题 1.12 中所示。
1-13 已知信号 f(t)的偶分量 fe(t)的波形如图题 1-13(a)所示， 信号 f(t+1)×U(-t-1)的波形如图题 1-13(b) 所示。求 f(t)的奇分量 fo(t)，并画出 fo(t)的波形。
解 因
f (t ) = f e (t ) + f 0 (t )
∫
t
−∞
δ (τ )dτ ，故根据现行系统的积分性有
y (t ) = ∫ h(τ (dτ = ∫ [δ (τ ) − δ (τ − 1) − δ (τ − 2) + δ (τ − 3)]dτ = u (t ) − u (t − 1) − u (t − 2) + u (t − 3)
1-2 已知各信号的波形如图题 1-2 所示，试写出它们各自的函数式。
解： f 1 (t ) = t[u (t ) − u (t − 1)] + u (t − 1)
f 2 (t ) = −(t − 1)[u (t ) − u(t − 1)]
f 3 (t ) = (t − 2)[u(t − 2) − u(t − 3)]
y 2 (t ) 的波形如图题 1.17(c)所示.
1-18 图题 1-18(a)所示为线性时不变系统，已知 h1(t)=δ(t)-δ(t-1), h2(t)=δ(t-2)-δ(t-3)。（1）求响 应 h(t)； （2） 求当 f(t)=U(t)时的响应 y(t)（见图题 1-18(b))。
解（1） h(t ) = h1 (t ) − h2 (t ) = δ (t ) − δ (t − 1) − δ (t − 2) + δ (t − 3) (2) 因 f (t ) = u (t ) =

c xt x0t 2 ht h0t 1 yt y0t 1
d xt x0 t ht h0t
yt
1
01
2
t
We have not enough information to determine the output
e xt x0 t ht h0 t
yt
x0 t h0 t
0
2
t
Information to determine the output yt
yt
a xt 2x0t ht h0t
2
yt 2 y0 t
0
2
t
b xt x0 t x0 t 2 ht h0 t yt y0 t y0 t 2
yt
1
0
2
4t
19Chapter 2来自Problems Solution
xt
1
(a) yt et ut x 2d
1 0
yt et 2u t 2x d
ht et2ut 2
ht
2t
b yt xt ht xt h1t
h1t 1 h1t 2 16
Chapter 2
Problems Solution
h1 t t e 2u 2 d t e 2d
discontinuities,what is the value of a?
Solution ： xt
ht
1
1
0 1 t 0a t
yt
a
0 a 1 1+a t
5
Chapter 2
d yt dt
1
0 a 1 1+a t
-1
Problems Solution

第一章测试1【判断题】(10分)正弦连续函数一定是周期信号A.对B.错2【判断题】(10分)正弦离散函数一定是周期序列。

A.错B.对3【判断题】(10分)余弦连续函数一定是周期信号。

A.错B.对4【判断题】(10分)余弦离散序列一定是周期的A.对B.错5【判断题】(10分)两个离散周期序列的和一定是周期信号。

A.对B.错6【判断题】(10分)两个连续周期函数的和一定是周期信号。

A.对B.错7【判断题】(10分)两个连续正弦函数的和不一定是周期函数。

A.对B.错8【判断题】(10分)取样信号属于功率信号。

A.对B.错9【判断题】(10分)门信号属于能量信号。

A.错B.对10【判断题】(10分)两个连续余弦函数的和不一定是周期函数。

A.错B.对第二章测试1【判断题】(10分)微分方程的齐次解称为自由响应。

A.对B.错2【判断题】(10分)微分方程的特解称为强迫响应。

A.错B.对3【判断题】(10分)微分方程的零状态响应是稳态响应的一部分A.对B.错4【判断题】(10分)微分方程的零输入响应是稳态响应的一部分A.对B.错5【判断题】(10分)微分方程的零状态响应包含齐次解部分和特解两部分。

A.错B.对6【判断题】(10分)微分方程的零状态响应中的特解部分与微分方程的强迫响应相等。

A.错B.对7【判断题】(10分)对LTI连续系统，当输入信号含有冲激信号及其各阶导数，系统的初始值往往会发生跳变。

A.对B.错8【判断题】(10分)对线性时不变连续系统，当输入信号含有阶跃信号，系统的初始值往往会发生跳变A.对B.错9【判断题】(10分)冲激函数匹配法是用于由零负初始值求解零正初始值。

A.对B.错10【判断题】(10分)LTI连续系统的全响应是单位冲激响应与单位阶跃响应的和。

A.对B.错第三章测试1【判断题】(10分)LTI离散系统的响应等于自由响应加上强迫响应。

A.错B.对2【判断题】(10分)LTI离散系统的响应等于齐次解加上零状态响应的和。

分析：响应中 不含齐次解 ，所以答案(a)(b)(c)都不是
题2、两线性时不变系统分别为S1和S2，初始状态均为零。将激励信号 先通过S1再通过S2，得到响应 ；将激励信号 先通过S2再通过S1，得到响应 。则 与 的关系为_________________。
答案：
分析：该题是考查级联系统的交换率：两级联系统交换保持不变
特征方程为 ，
特征根为 ，
所以
代入初始条件 ， ，解得 ，
所以，
（2）求零状态响应
（3）
2.6 已知某线性时不变系统的方程式为
试求系统的冲激响应h(t)。
解：方程右端的冲激函数项最高阶数为 ，设
，
则有： ，将其代入原系方程，得
2.7若描述系统的微分方程为
试求系统的阶跃响应。
解：由题可知：
阶跃响应：
2.8已知某线性时不变(LTI)系统如题图2.8所示。已知图中 ， ， ,试求该系统的冲激响应 。
（7）理解卷积运算在信号与系统中的物理意义和运算规律，会计算信号的卷积。；
2.2 本章重点
（1）系统（电子、机械）数学模型（微分方程）的建立；
（2）用时域经典法求系统的响应；
（3）系统的单位冲激响应及其求解；
（4）卷积的定义、性质及运算，特别是 函数形式与其它信号的卷积；
（5）利用零输入线性与零状态线性，求解系统的响应。
2.4.4系统的零输入响应与零状态响应
（1）零输入响应
系统的零输入响应是当系统没有外加激励信号时的响应。
零输入响应 是满足
及起始状态 的解,它是齐次解的一部分
由于没有外界激励作用，因而系统的状态不会发生跳变， ，所以 中的常数 可由 确定。
（2）零状态响应

A1e −2t
+
2 A2e−8t
故有
uc (0+ ) = A1 + A2 = 6
i(0+ )
=
1 2
A1
+
2 A2
=
0
联解得 A1-=8,A2=-2。故得
uc (t) = 8e−2t − 2e−8t V t ≥ 0
又得
i(t) = −C duc = 4e−2t − 4e−8t A t ≥ 0 dt
1 1
+
p u2 (t)
=
0
即
1 3
p
+ 1u1 (t )
− u2 (t)
=
pf
(t)
( ) − u1(t) + p2 + p +1 u2 (t) = 0
联解得
u2 (t) =
p2
3 + 4p + 4
f (t) =
H ( p) f (t)
故得转移算子为
H（p) =
u2 (t) f (t)
=
p2
3 + 4p + 4
f1(t −1) − f1(t − 2) + f1(t − 3)
y2(t)的波形如图题 2.10(d)所示 2-11．
d f (t)
试证明线性时不变系统的微分性质与积分性质，即若激励 f(t)产生的响应为 y(t)，则激励 dt
产生
∫ ∫ d
的响应为 dt
y(t)
（微分性质），激励
t −∞
f (τ )dτ
故得
3 3
进一步又可求得 uc(t)为
uc
(t )

绪论单元测试1【判断题】(1分)信号到的运算中，若a>1，则信号的时间尺度缩小a倍，其结果是将信号的波形沿时间轴放大a倍。

A.错B.对第一章测试1【判断题】(1分)信号到的运算中，若a>1，则信号的时间尺度缩小a倍，其结果是将信号的波形沿时间轴放大a倍。

A.对B.错2【判断题】(1分)如果某连续时间系统同时满足叠加性和齐次性，则称该系统为线性系统。

A.错B.对3【判断题】(1分)直流信号与周期信号都是功率信号。

A.错B.对4【单选题】(1分)将信号变换为（）称为对信号的平移或移位。

A.B.C.D.5【单选题】(1分)下列各表达式正确的是（）。

A.B.C.D.6【单选题】(1分)积分的结果为（）。

A.3B.C.1D.97【单选题】(1分)设输入为、时系统产生的响应分别为、，并设、为任意实常数，若系统具有如下性质：，则系统为（）。

A.时不变系统B.因果系统C.非线性系统D.线性系统8【单选题】(1分)（）。

A.B.C.D.9【单选题】(1分)，该序列是（）。

A.非周期序列B.周期C.周期D.周期10【多选题】(1分)连续时间系统系统结构中常用的基本运算有（）。

A.微分器B.标量乘法器C.积分器D.加法器11【多选题】(1分)下列等式成立的是（）。

A.B.C.D.12【判断题】(1分)一系统，该系统是线性系统。

()A.错B.对第二章测试1【判断题】(1分)强迫响应是零状态响应与部分自由响应之差。

（）A.对B.错2【判断题】(1分)连续时间系统的单位阶跃响应是系统在单位阶跃信号作用下的响应。

（）A.对B.错3【判断题】(1分)零状态响应是由激励引起的响应。

（）A.错B.对4【判断题】(1分)某连续时间系统是二阶的，则其方框图中需要两个积分器。

（）A.错B.对5【单选题】(1分)若系统的输入信号为，冲激响应为，则系统的零状态响应是()。

A.B.C.D.6【单选题】(1分)卷积的结果是()。

A.B.C.D.7【单选题】(1分)卷积积分等于（）。

5t −∞
e2
(τ
)
dτ
= c1r1 (t ) + c2r2 (t )
∫ ∫ ∫ ( ) ( ) ( ) ( ) ( ) 时变：输入 e t − t0
，输出
5t
e
−∞
τ
− t0
τ −t0 = x
dτ =
e 5t −t0
−∞
x
dx ≠
e 5(t−t0 )
−∞
x
dx = r
t − t0
非因果： t
= 1时，
解题过程： （1）方法一：
f (t)
1
f (t − 2)
1
→
-2
-1
f (3t − 2)
0
1
→
1
2
f (−3t − 2)
1
→
3
2/3 1
-1 -2/3
方法二：
f (t)
f (3t )
1
1
→
→
-2
-1
f (3t − 2)
0
1
-2/3
→
1/3
f (−3t − 2)
2/3 1 方法三：
-1 -2/3
1
f (t)
（2） r (t ) = e(t )u (t )
线性：设 r1 (t ) = e1 (t )u (t ) 、 r2 (t ) = e2 (t )u (t ) ， 则 ⎡⎣c1e1 (t ) + c2e2 (t )⎤⎦ u (t ) = c1r1 (t ) + c2r2 (t )
6
时变：输入 e (t − t0 ) ，输出 e (t − t0 )u (t ) ≠ e (t − t0 )u (t − t0 ) = r (t − t0 ) 因果： r (t ) 仅与此时刻 e (t ) 有关 （3） r (t ) = sin ⎡⎣e(t )⎤⎦ u (t ) 非线性：设 r1 (t ) = sin ⎡⎣e1 (t )⎤⎦ u (t ) 、 r2 (t ) = sin ⎡⎣e2 (t )⎤⎦ u (t ) ， 则 sin ⎡⎣c1e1 (t ) + c2e2 (t )⎤⎦ u (t ) ≠ sin ⎡⎣c1e1 (t )⎤⎦ u (t ) + sin ⎡⎣c2e2 (t )⎤⎦ u (t ) 时变：输入 e (t − t0 ) ，输出 sin ⎡⎣e (t − t0 )⎤⎦ u (t ) ≠ sin ⎡⎣e(t − t0 )⎤⎦ u (t − t0 ) = r (t − t0 ) 因果： r (t ) 仅与此时刻 e (t ) 有关 （4） r (t ) = e (1− t ) 线性：设 r1 (t ) = e1 (1− t ) 、 r2 (t ) = e2 (1− t ) ，则 c1e1 (1− t ) + c2e2 (1− t ) = c1r1 (t ) + c2r2 (t ) 时变：设 e1 (t ) = u (t ) − u (t −1.5) ，则 r1 (t ) = u (t + 0.5) − u (t ) e2 (t ) = e1 (t − 0.5) = u (t − 0.5) − u (t − 2) ，则 r2 (t ) = u (t +1) − u (t − 0.5) ≠ r1 (t − 0.5) 非因果：取 t = 0 ，则 r (0) = e (1) ，即 t = 0 时刻输出与 t = 1时刻输入有关。 （5） r (t ) = e(2t ) 线性：设 r1 (t ) = e1 (2t ) 、 r2 (t ) = e2 (2t ) ，则 c1e1 (2t ) + c2e2 (2t ) = c1r1 (t ) + c2r2 (t ) 时变：设 e1 (t ) = u (t ) − u (t − 2) ，则 r1 (t ) = u (t ) − u (t −1) e2 (t ) = e1 (t − 2) = u (t − 2) − u (t − 4) ，则 r2 (t ) = u (t −1) − u (t − 2) ≠ r1 (t − 2) 非因果：取 t = 1，则 r (1) = e (2) ，即 t = 1时刻输出与 t = 2 时刻输入有关。 （6） r (t ) = e2 (t ) 非线性：设 r1 (t ) = e12 (t ) 、 r2 (t ) = e22 (t ) ， 则 ⎡⎣c1e1 (t ) + c2e2 (t )⎤⎦2 = c12e12 (t ) + c22e22 (t ) + 2c1c2e1 (t ) e2 (t ) ≠ c1r1 (t ) + c2r2 (t ) 时不变：输入 e (t − t0 ) ，输出 e2 (t − t0 ) = r (t − t0 ) 因果： r (t ) 仅与此时刻 e (t ) 有关