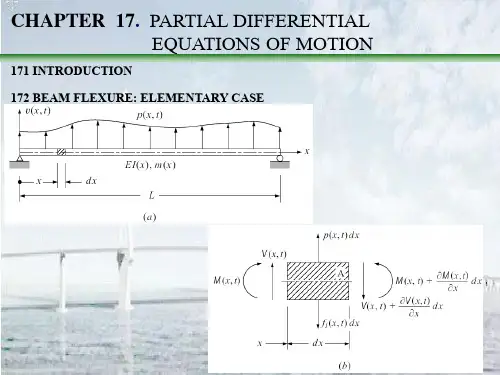
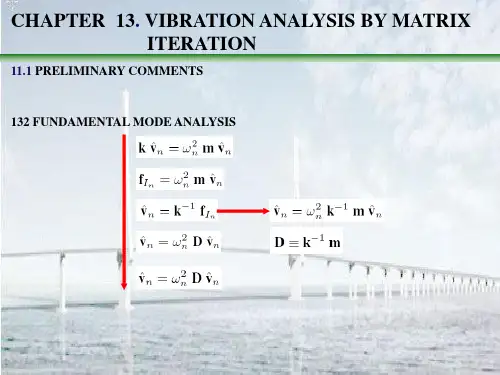
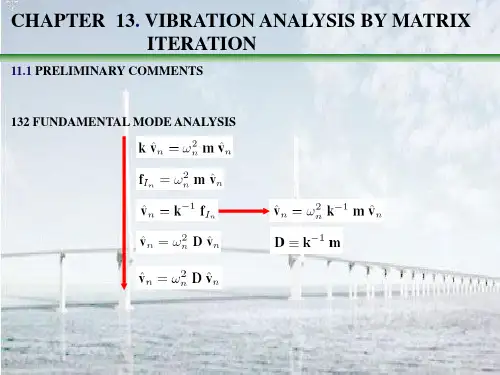
For most problems in structural dynamics it may be assumed that mass does not vary with time, in which case Eq. (13) may be written
the second term is called the inertial force resisting the acceleration of the mass.
The equation of motion for the simple system is most easily formulated by directly expressing the equilibrium of all forces acting on the mass using d'Alembert's principle.
FIGURE 1-3 Sine-series representation of simple beam deflection.
CHAPTER 1. OVERVIEW OF STRUCTURAL DYNAMICS
Discrete Models
FIGURE 1-4 Lumped-mass id(ea)a1l9i9z9a年t台io湾n集o集f地a震集si鹿m大p桥l破e坏b状e态am.
(a) 1999年台湾集集地震集鹿大桥破坏状态
Tasman Bridge Derwent River, Hobart, Australia (1975)
CHAPTER 1. OVERVIEW OF STRUCTURAL DYNAMICS
1.2 ESSENTIAL CHARACTERISTICS OF A DYNAMIC PROBLEM • timevarying nature of the dynamic problem • inertial forces (more fundamental distinction)