矮塔斜拉桥研究的新进展

矮塔斜拉桥索塔锚固区应力分布规律及计算模型研究作者：张涛李伟俊朱东邓韬李永明来源：《甘肃科技纵横》2024年第06期摘要：文章依据某矮塔斜拉桥，通过现场试验探究索塔锚固区应力分布规律，明确索塔锚固区混凝土在施工过程中的应力变化特征。

文章提出底部设置弹性支撑的局部有限实体计算分析模型，并通过实测值和理论值的对比分析验证该计算分析模型的可行性。

研究结果表明：施工过程中，索塔锚固区端部位置出现了拉应力，最大为1.2 MPa，施工时应考虑在锚固区端部增加横向钢筋；索塔锚固区混凝土横向应力呈现出端部小中间位置大的规律；索塔锚固区实测应力值和理论值基本吻合，验证了该计算分析模型用于计算索塔锚固区应力分析的可行性，为索塔锚固区的受力分析提供了技术支撑。

关键词：矮塔斜拉桥；索塔锚固区；计算分析模型；应力分布；试验中图分类号：U24文献标志码：A0引言矮塔斜拉桥的力学特性不同于斜拉桥和梁式桥，而是介于两者之间。

斜拉桥的拉索多数是单侧和索塔直接固结，而矮塔斜拉桥拉索多是直接穿过索塔作用在主梁上，索塔处直接作用在索鞍处形成一根通长的拉索。

索塔锚固区是矮塔斜拉桥的一个主要传力部位，主梁重量通过拉索将自重作用在索塔锚固区，然后通过桥塔传递给桥墩和基础，索塔锚固区在整个施工过程中受力较为复杂，为确保整个施工过程中斜拉桥的安全，需要掌握锚固区在整个施工过程中的受力特征。

为此，国内不少学者对其进行了研究。

周晖[1]通过对主塔索鞍区的计算分析，发现中间大向两边逐渐减小。

张海文等[2-3]通过数值分析探究了拉索与索鞍之间的接触关系，并研究了拉索的半径对锚固区混凝土应力的影响，认为施工中应对索鞍的安装定位进行严格控制。

部分学者依托实际工程对索塔区混凝土进行受力分析。

张树清和屈计划[4]依托实际工程，建立索塔锚固区计算分析模型，得到索塔锚固区混凝土的应力分布规律。

肖子旺[5]以常山大桥为依托建立全桥分析模型，基于等效原则通过变换索鞍结构形式，探究了索鞍形式对锚固区混凝土受力的影响规律。

China Highway111预应力混凝土矮塔斜拉桥设计研究文/重庆交建工程勘察设计有限公司 皇甫全显 敖建辉矮塔斜拉桥通常也被称为部分斜拉桥, 其雏形是反拱形梁桥，由于这种桥型具有索塔高度比较低的特点，所以在国内有的文章又把这种桥称作是矮塔斜拉桥，这种桥型介于斜拉桥和连续梁（刚构）桥两者间，其在结构性能以及经济指标上都有着相当良好的表现，在近几年发展非常迅速。

矮塔斜拉桥最初起源于国外，由Christian Menn 设计并在1981年建造的Ganter 大桥，是矮塔斜拉桥最初出现的形式，甘特大桥为其后矮塔斜拉桥的出现奠定了基础。

继甘特大桥之后，美国、墨西哥、葡萄牙等国家也建造了此种形式的桥梁。

世界上第一座矮塔斜拉桥是1994年在日本的建造小田原港桥，而后这种桥型在日本迅速发展。

我国在矮塔斜拉桥领域之中的第一次应用是2000年8月竣工通车的芜湖长江公铁两用大桥，其主梁使用的是连续桁组合梁，这也是世界上首次采用这种主梁结构。

修建于2001年的福州漳州战备桥，是国内的第一座属于预应力混凝土矮塔斜拉桥。

随后，矮塔斜拉桥在我国得到了快速地推广。

随着矮塔斜拉桥不断地在国内修建，所积累的工程经验和教训都为这种桥型在我国的发展打下了较好的基础。

本桥为预应力混凝土梁矮塔斜拉桥公路桥，汽车荷载等级为公路一级，双向六车道，无人行道。

只考虑系统升温和降温（±20℃），不考虑梯度温差。

设计内容为桥式方案拟定、预应力筋估算、斜拉索索力确定及进行桥梁检算。

结构设计结合设计要求、设计指标及同类已建桥梁的设计经验，本桥采用的设计方案为图1所示。

材料三种混凝土材料C60、C50和C40分别用于主梁、索塔和桥墩。

纵向及横向预应力筋均使用的是高强度的低松弛钢绞线，其单根公称直径为Φs15.24，标准强度1860MPa，竖向预应力筋为Φ32精轧螺纹钢筋，标准强度为750Mpa。

纵向预应力采用OVM15型锚具，竖向预应力采用YGM 锚具，预应力管道均按塑料波纹管成孔设计。

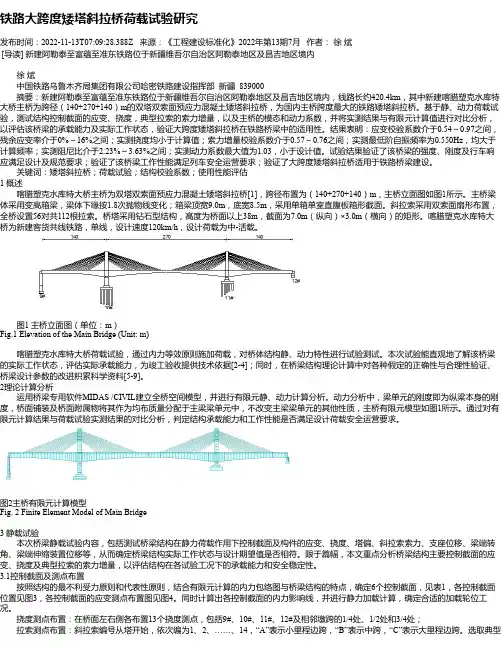
铁路大跨度矮塔斜拉桥荷载试验研究发布时间：2022-11-13T07:09:28.388Z 来源：《工程建设标准化》2022年第13期7月作者：徐斌[导读] 新建阿勒泰至富蕴至准东铁路位于新疆维吾尔自治区阿勒泰地区及昌吉地区境内徐斌中国铁路乌鲁木齐局集团有限公司哈密铁路建设指挥部新疆 839000摘要：新建阿勒泰至富蕴至准东铁路位于新疆维吾尔自治区阿勒泰地区及昌吉地区境内，线路长约420.4km，其中新建喀腊塑克水库特大桥主桥为跨径（140+270+140）m的双塔双索面预应力混凝土矮塔斜拉桥，为国内主桥跨度最大的铁路矮塔斜拉桥。

基于静、动力荷载试验，测试结构控制截面的应变、挠度，典型拉索的索力增量，以及主桥的模态和动力系数，并将实测结果与有限元计算值进行对比分析，以评估该桥梁的承载能力及实际工作状态，验证大跨度矮塔斜拉桥在铁路桥梁中的适用性。

结果表明：应变校验系数介于0.54～0.97之间，残余应变率介于0%～16%之间；实测挠度均小于计算值；索力增量校验系数介于0.57～0.76之间；实测最低阶自振频率为0.550Hz，均大于计算频率；实测阻尼比介于2.23%～3.63%之间；实测动力系数最大值为1.03，小于设计值。

试验结果验证了该桥梁的强度、刚度及行车响应满足设计及规范要求；验证了该桥梁工作性能满足列车安全运营要求；验证了大跨度矮塔斜拉桥适用于铁路桥梁建设。

关键词：矮塔斜拉桥；荷载试验；结构校验系数；使用性能评估1 概述喀腊塑克水库特大桥主桥为双塔双索面预应力混凝土矮塔斜拉桥[1]，跨径布置为（140+270+140）m，主桥立面图如图1所示。

主桥梁体采用变高箱梁，梁体下缘按1.8次抛物线变化；箱梁顶宽9.0m，底宽8.5m，采用单箱单室直腹板箱形截面。

斜拉索采用双索面扇形布置，全桥设置56对共112根拉索。

桥塔采用钻石型结构，高度为桥面以上38m，截面为7.0m（纵向）×3.0m（横向）的矩形。

双索面宽幅矮塔斜拉桥的动力特性及地震反应研究的开题
报告
题目：双索面宽幅矮塔斜拉桥的动力特性及地震反应研究
作者：XXX
导师：XXX
摘要：
双索面宽幅矮塔斜拉桥是一种新型的桥梁结构，具有结构简单、造价低廉、适用范围广等优点。

然而，由于该结构的动力特性和地震反应尚未得到深入研究，因此无
法准确评估其在各种工况下的运行安全性，未来的研究将采用动力分析和地震反应模
拟的方法，探讨双索面宽幅矮塔斜拉桥的动力特性及地震反应。

本文的研究目标是：通过建立模型，模拟双索面宽幅矮塔斜拉桥在重载、风载和地震等外部工况下的动力特性和地震反应，探讨其动力特性和结构响应的规律，并提
出相应的抗震设计建议。

本文的研究内容包括：1）双索面宽幅矮塔斜拉桥的建模方法；2）重载、风载和地震工况下的动力分析方法；3）双索面宽幅矮塔斜拉桥的动力特性分析；4）地震工
况下的结构响应分析；5）提出相应的抗震设计建议。

本研究的意义在于：通过深入研究双索面宽幅矮塔斜拉桥的动力特性及地震反应，可以准确评估其在各种工况下的运行安全性，指导该类型桥梁的设计和施工。

此外，
本文的研究方法和结论对于其他类似结构的研究，具有一定的参考价值。

关键词：双索面宽幅矮塔斜拉桥；动力特性；地震反应；模拟分析；抗震设计。

预应力混凝土矮塔斜拉桥长悬臂箱梁应力分布研究的开题报告1.研究背景预应力混凝土斜拉桥作为现代桥梁的一种新型桥梁，具有结构简洁、施工方便、经济性高、使用寿命长等优点，在国内外得到广泛应用。

其中，矮塔斜拉桥作为一种常见的斜拉桥类型，结构比较简单，施工容易，运输方便，不仅在城市道路的建设中应用广泛，同时也被广泛应用于跨越河流和山峡的交通建设中。

然而，斜拉桥在使用过程中需要承受较大的荷载，因此对桥梁结构的疲劳性能和可靠性有着更高的要求。

在设计矮塔斜拉桥时，需要考虑结构的受力情况，特别是箱梁结构的受力状况对桥梁的稳定性和安全性有着至关重要的影响。

因此，对矮塔斜拉桥长悬臂箱梁应力分布进行研究，对于提高斜拉桥的设计质量和安全性具有重要意义。

2.研究目的本研究旨在探究矮塔斜拉桥长悬臂箱梁应力分布规律，分析箱梁结构受力情况，并运用预应力技术，提高长悬臂箱梁的承载能力和安全性能。

3.研究内容本研究将围绕以下几个方面展开研究：（1）矮塔斜拉桥的结构特点及其受力情况的分析。

（2）长悬臂箱梁受力分析和应力计算方法的研究。

（3）预应力技术在斜拉桥梁中的应用及其优缺点。

（4）利用有限元软件建立长悬臂箱梁的数值模型，模拟矮塔斜拉桥的受力情况，分析箱梁应力分布规律。

（5）针对研究结果，提出针对性强的改进措施，进一步提高斜拉桥结构的质量和安全性能。

4.研究意义通过对矮塔斜拉桥长悬臂箱梁应力分布的研究，可以更好地了解矮塔斜拉桥的结构特点及其受力情况，为斜拉桥的设计、施工和维护提供科学依据和技术支持。

同时，本研究可以探索预应力技术在斜拉桥梁中的应用，提高长悬臂箱梁的承载能力和安全性能，保障斜拉桥的运行安全。

四塔单索面矮塔斜拉桥施工过程仿真分析及设计参数研究的开题报告一、研究背景和意义在交通建设中，桥梁作为一项重要的基础设施，起到了连接地区、畅通交通的作用。

随着交通运输需求的增加，对桥梁的要求也越来越高。

斜拉桥作为一种新型的桥梁结构，具有自重轻、跨径大、美观等特点，已成为桥梁建设的主要趋势之一。

在设计斜拉桥时，需要考虑许多因素，如桥梁跨度、索塔高度、斜拉角度、拉索数量等。

这些因素都会影响桥梁的承载力和稳定性。

因此，对于斜拉桥的设计参数研究和施工过程仿真分析具有重要的意义，可以为斜拉桥的建设提供有力的支持和保障。

本文拟研究四塔单索面矮塔斜拉桥的设计参数和施工过程仿真分析，以期为实际建设提供参考和指导。

二、研究内容和方法1. 研究内容（1）矮塔斜拉桥结构原理和设计参数分析以四塔单索面矮塔斜拉桥为研究对象，分析其结构原理和设计参数对桥梁性能的影响。

（2）施工过程仿真分析在MATLAB/Simulink环境下，对四塔单索面矮塔斜拉桥在不同施工阶段的行为和响应进行分析和仿真。

包括斜拉索张拉、索塔吊装、主梁安装等施工过程的仿真分析。

2. 研究方法（1）文献综述通过查阅相关文献，了解矮塔斜拉桥的结构原理、设计方法和施工技术等方面的研究成果，为后续研究提供理论依据。

（2）结构参数计算根据《公路斜拉桥设计规范》等国家标准，对四塔单索面矮塔斜拉桥的结构参数进行计算和分析，确定设计参数。

（3）MATLAB/Simulink仿真建立四塔单索面矮塔斜拉桥的仿真模型，通过MATLAB/Simulink进行施工过程的仿真分析。

包括斜拉索张拉、索塔吊装、主梁安装等施工过程的仿真分析。

三、预期研究成果和意义1. 预期研究成果（1）掌握矮塔斜拉桥的结构原理和设计参数计算方法。

（2）建立矮塔斜拉桥的施工过程仿真模型，并进行实际仿真分析。

（3）得出四塔单索面矮塔斜拉桥的合理设计参数和稳定施工方案。

2. 研究意义（1）为斜拉桥的设计和施工提供参考和指导，提高桥梁的安全性和稳定性。

基于BIM技术的矮塔斜拉桥索塔施工工法基于BIM技术的矮塔斜拉桥索塔施工工法一、前言矮塔斜拉桥作为一种新型的跨越杂乱界面的桥梁形式，在城市中得到了广泛的应用。

为了提高施工效率和质量，减少施工风险，近年来出现了基于BIM技术的矮塔斜拉桥索塔施工工法。

本文将对该工法进行详细的分析和介绍。

二、工法特点基于BIM技术的矮塔斜拉桥索塔施工工法具有以下特点：1. 施工计划的精确性：通过使用BIM技术，可以在计算机模型中建立三维的施工计划，精确地确定各个工序的执行顺序和时间，避免了传统施工过程中可能存在的人为操作和误差。

2. 工艺优化：通过BIM技术，可以对施工过程进行模拟和优化，减少施工时间和资源的浪费，提高施工效率。

3. 施工过程可视化：使用BIM技术可以将施工过程以图形化的方式展示给施工人员，使他们更好地理解和掌握施工过程，提高施工质量和安全性。

4. 数据共享与协同：基于BIM技术的矮塔斜拉桥索塔施工工法可以实现与设计、工程管理、监理等各个部门的数据共享和协同，提高工程的整体效能。

三、适应范围基于BIM技术的矮塔斜拉桥索塔施工工法适用于各种大小规模的矮塔斜拉桥工程，特别适用于复杂的交通环境和狭窄的建筑界面条件下的工程项目。

四、工艺原理基于BIM技术的矮塔斜拉桥索塔施工工法的工艺原理是将矮塔斜拉桥的施工过程与BIM技术紧密结合，实现施工过程的数字化、模拟化和可视化。

具体来说，施工工法与实际工程存在以下联系和技术措施：1. BIM模型的构建和管理：通过使用BIM软件，建立矮塔斜拉桥的三维模型，并对模型进行管理和更新，以便及时反映施工过程的变化。

2. 施工计划的制定和优化：在BIM模型中建立施工计划，将各个工序按照理想的顺序和时间进行排列，并优化施工过程，减少不必要的等待和冲突。

3. 施工资源的管理和调度：在BIM模型中加入施工资源的信息，包括材料、人力和机械设备等，以实现施工资源的最佳配置和调度。

4. 施工过程的模拟和可视化：通过BIM技术对施工过程进行模拟和可视化，将施工过程以图形化的方式展示给施工人员，以便他们更好地理解和掌握施工过程。

中国预应力技术五十年暨第九届后张预应力学术交流会论文2006年矮塔斜拉桥在桥梁建设中的应用分析王胜（铁道第一勘察设计院西安 710043）提要：矮塔斜拉桥是介于连续梁与斜拉桥之间的一种过渡桥梁，具有结构性能优越，经济指标良好，施工方便的优势。

本文结合兰州小西湖黄河大桥三跨预应力混凝土矮塔斜拉桥的设计实践，对矮塔斜拉桥在中、长跨度桥梁中的应用前景进行了分析和探讨。

关键词：矮塔斜拉桥设计实践应用1 前言近年来，在PC箱梁桥和PC斜拉桥之间出现了一种新的桥梁结构形式，这种新的桥梁结构是法国工程师J.Matlivat 1988年提出并将之命名为超配量(extradosed)体外索PC桥，日本的桥梁界将其统称为斜拉桥，1995年我国著名桥梁专家严国敏先生首次把它定义为“部分斜拉桥”，后来，国内一些文章根据这种桥型塔高较矮的特点，又把这种桥型定义为矮塔斜拉桥或低塔斜拉桥。

由于该桥型结构性能优越，经济指标良好，在许多国家作为中、长桥梁的主流桥型之一被广泛应用。

矮塔斜拉桥在我国起步虽然较晚，但发展速度较快，自2001年国内第一座矮塔斜拉桥——漳州战备桥建成之后，兰州、太原、厦门等地也陆续兴建。

由我院设计的山东惠青黄河公路大桥主跨220m，为国内已建或正建的最大跨度预应力混凝土矮塔斜拉桥。

本文结合兰州小西湖黄河大桥三跨预应力混凝土矮塔斜拉桥的设计实践，参考国内外矮塔斜拉桥的经验总结，对矮塔斜拉桥在中、长跨度桥梁中的应用前景进行了分析和探讨。

2 工程背景小西湖黄河大桥是兰州市小西湖黄河大桥工程的一部分，大桥北起黄河北岸与北滨河王胜，男，1962.6出生，工程硕士，教授级高工度预应力混凝土箱梁，支点梁高4.5m(L/30)，跨中梁高2.6m(L/52)，梁体下缘按二次抛物线变化。

斜拉索布置在箱梁的中室，索梁锚固处均设有隔墙。

主塔采用实心矩形截面，横桥向宽2.0m，顺桥向2.6～3.0m，塔高17m（L/8）。

斜拉索为单面双排索，布置在中分带上，塔根附近无索区长46 m，有索区长36 m ，跨中无索区长18m，梁上索间距4.0 m，塔上索距0.7m。

矮塔斜拉桥的结构行为分析及施工控制的开题报告题目：矮塔斜拉桥的结构行为分析及施工控制一、研究背景随着交通运输业的迅速发展，大跨度桥梁的建设已经成为一个热门领域。

斜拉桥作为一种结构优美、技术难度较大的大跨度桥梁，已经成为众多建筑师和工程师的心头之好。

矮塔斜拉桥是在斜拉桥中的一种，其矮小的塔身使得它更加适合建设在城市中心。

矮塔斜拉桥因其特殊的结构和工艺而受到了广泛的关注。

然而，矮塔斜拉桥的结构和施工方式具有很大的复杂性，需要进行深入的研究和探讨。

本课题旨在对矮塔斜拉桥的结构行为进行分析，并就其施工控制进行探讨，以对该类型桥梁的设计和施工提供一定的技术支持。

二、研究内容1. 矮塔斜拉桥的结构特点与设计原理2. 矮塔斜拉桥的结构分析方法3. 矮塔斜拉桥的静力特征分析4. 矮塔斜拉桥的动力特征分析5. 矮塔斜拉桥施工控制策略研究三、研究方法本研究将采用与该类型桥梁建设有关的文献和标准，结合实际案例，对矮塔斜拉桥的结构行为进行分析和模拟。

同时，采用数值计算和现场试验相结合的方法，对矮塔斜拉桥进行静力和动力特征分析。

最后，对矮塔斜拉桥的施工控制策略进行研究，提出有效的施工方案。

四、预期成果本研究的成果包括以下几个方面：1. 对矮塔斜拉桥结构行为进行深入的分析；2. 对矮塔斜拉桥的施工控制策略进行研究，提出有效的施工方案；3. 探索矮塔斜拉桥的设计与建设理念，提高大跨度桥梁工程的水平。

五、研究意义通过本研究，可以进一步提高矮塔斜拉桥的设计和建设的水平，丰富我国大跨度桥梁结构领域的研究成果。

同时，本研究也可为其他类型桥梁的设计和施工提供参考。

小议大跨度斜拉桥施工技术发展现状及发展趋势大跨度斜拉桥施工技术发展的现状如下：1、斜拉索材料的发展：传统的斜拉索材料主要采用钢材，但随着新材料的发展，现在也有采用碳纤维、高强度钢丝等材料作为斜拉索的新型斜拉桥。

这些新材料具有重量轻、强度高、耐腐蚀等特点，能够提高斜拉桥的承载能力和使用寿命！2、斜拉索施工技术的改进：传统的斜拉索施工主要采用吊索法或者拉索法，但这些方法存在一定的施工难度和风险。

现在，一些新的斜拉索施工技术被引入，如预应力张拉法、预制张拉法等，能够提高斜拉索的施工效率和质量。

3、斜拉桥结构设计的创新：传统的斜拉桥结构设计主要采用单塔单索或者双塔双索的形式，但这些结构存在一定的限制。

现在，一些新型的斜拉桥结构被提出，如多塔多索、斜塔斜索等，能够适应更大跨度和更复杂的地形条件。

4、斜拉桥施工技术的自动化和智能化：随着科技的发展，大跨度斜拉桥施工技术也在向自动化和智能化方向发展。

例如，施工机械的自动化控制、无人机的应用、人工智能的辅助设计等，能够提高施工效率和质量。

大跨度斜拉桥施工技术的发展趋势主要包括以下几个方面：1、施工工艺的优化：随着施工技术的不断发展，施工工艺也在不断优化。

传统的大跨度斜拉桥施工通常需要大量的人力和物力投入，而现代化的施工工艺可以通过使用先进的机械设备和自动化技术来提高施工效率，减少施工时间和成本。

2、材料的创新：大跨度斜拉桥的施工需要使用高强度、轻质的材料，以保证桥梁的结构稳定性和承载能力。

随着材料科学的不断进步，新型材料的开发和应用将为大跨度斜拉桥的施工提供更多选择，例如高强度钢材、碳纤维等。

3、结构设计的优化：大跨度斜拉桥的结构设计是保证桥梁安全可靠的关键。

随着计算机技术的发展，结构设计分析软件的应用越来越广泛，可以对桥梁的结构进行更加精确和详细的分析，优化结构设计，提高桥梁的承载能力和抗震性能。

4、施工监测技术的应用：大跨度斜拉桥的施工过程需要进行实时的监测和控制，以确保桥梁的安全性和稳定性。

第４３卷㊀第１期２０２１年１月地㊀震㊀工㊀程㊀学㊀报C H I N A E A R T H Q U A K EE N G I N E E R I N GJ O U R N A LV o l ．４３㊀N o ．１J a n u a r y,２０２１㊀㊀收稿日期:２０１９Ｇ０８Ｇ２７㊀㊀基金项目:国家自然基金(５２０６８０４１)㊀㊀第一作者简介:彭文礼(１９９１－),男,甘肃天水人,硕士研究生,研究方向为桥梁与隧道工程.E Ｇm a i l :７７４０７２７４２＠q q．c o m .㊀㊀通信作者:季日臣(１９６９－),男,山西朔州人,教授,研究方向为桥梁工程.E Ｇm a i l :１１６５２５１５３３＠q q．c o m .彭文礼,季日臣．摩擦摆支座在矮塔斜拉桥中减震效果研究[J ]．地震工程学报,２０２１,４３(１):２１３Ｇ２１８．d o i :１０．３９６９/j．i s s n ．１０００－０８４４．２０２１．０１．２１３P E N G W e n l i ,J IR i c h e n ．V i b r a t i o nR e d u c t i o nE f f e c t o f F r i c t i o nP e n d u l u mB e a r i n g s i nL o w Ｇt o w e rC a b l e Ｇs t a y e dB r i d g e s [J ]．C h i n a E a r t h q u a k eE n g i n e e r i n g J o u r n a l ,２０２１,４３(１):２１３Ｇ２１８．d o i :１０．３９６９/j．i s s n ．１０００－０８４４．２０２１．０１．２１３摩擦摆支座在矮塔斜拉桥中减震效果研究彭文礼,季日臣(兰州交通大学土木工程系,甘肃兰州７３００７０)摘要:矮塔斜拉桥有着良好的受力性能与美观性能,因此抗震设计对矮塔斜拉桥至关重要.摩擦摆式减隔震设计能够将桥梁上部结构与下部结构分离,从而延长结构的自振周期和摩擦耗能机理来降低和耗散传递到桥梁上部结构的能力.本文以靖远金滩黄河大桥(１００＋１６８＋１００)m 矮塔斜拉桥为分析模型,利用摩擦摆式减隔震支座对矮塔斜拉桥的墩身进行减隔震研究,运用M I D A S 有限元软件输入不同的地震波以检验摩擦摆系统的减震效果.分析结果证明了在矮塔斜拉桥中应用摩擦摆减隔震支座系统的有效性.关键词:矮塔斜拉桥;摩擦摆式支座;地震波;减震效果中图分类号:U ４４７㊀㊀㊀㊀㊀㊀文献标志码:A㊀㊀㊀文章编号:１０００－０８４４(２０２１)０１－０２１３－０６D O I :１０．３９６９/j．i s s n ．１０００－０８４４．２０２１．０１．２１３V i b r a t i o nR e d u c t i o nE f f e c t o f F r i c t i o nP e n d u l u mB e a r i n gs i nL o w Ｇt o w e rC a b l e Ｇs t a y e dB r i d ge s P E N G W e n l i ,J IR i c h e n(D e p a r t m e n t o f C i v i lE n g i n e e r i n g ,L a n z h o uJ i a o t o n g U n i v e r s i t y ,L a n z h o u７３００７０,G a n s u ,C h i n a )A b s t r a c t :E a r t h q u a k e i s an a t u r a l d i s a s t e r p h e n o m e n o n ．T h e l o w Ｇt o w e r c a b l e Ｇs t a y e db r i d ge ,f o r i t sg o o dm e ch a ni c a l a n da e s t h e t i c p e r f o r m a n c e ,h a s b e e nw i d e l y u s e d i n r e c e n t y e a r s ．T h e r e f o r e ,s e i s m i c d e s i g n i s v e r y i m p o r t a n t f o r l o w Ｇt o w e r c a b l e Ｇs t a y e db r i d g e s ．T h e f r i c t i o n p e n d u l u ms ys Ｇt e mc a ns e p a r a t e t h e s u p e r s t r u c t u r e f r o mt h e s u b s t r u c t u r eo f b r i d g e ,t h u s e x t e n d i n g t h en a t u r a l v i b r a t i o n p e r i o da n d f r i c t i o ne n e r g y d i s s i p a t i o no f t h e s t r u c t u r e ,r e d u c i n g a n dd i s s i p a t i n g t h e e n Ｇe r g y t r a n s f e r r e d t ot h es u p e r s t r u c t u r eo f t h eb r i d g e ．I nt h i s p a p e r ,t h e l o w Ｇt o w e rc a b l e Ｇs t a ye d b r i d g e i nJ i n t a nY e l l o w R i v e rB r i d g eof J i ng y u a nw a s t a k e na s th ea n a l y si sm o d e l ,a n d t h e f r i c Ｇt i o n p e n d u l u mb e a r i n g w a s u s e d t o s t u d y t h e s e i s m i c i s o l a t i o n e f f e c t o f t h e p i e r b o d y o f l o w Ｇt o w Ｇe r c a b l e Ｇs t a y e db r i d g e ．D i f f e r e n t s e i s m i cw a v e sw e r e i n p u t t o t e s t t h ed a m p i n g e f f e c t o f t h e f r i c Ｇt i o n p e n d u l u ms y s t e m b y u s i n g t h e M i d a s f i n i t ee l e m e n t s o f t w a r e ．T h ea n a l ys i s r e s u l t ss h o w e d t h a t t h e a p p l i c a t i o no f f r i c t i o n p e n d u l u m b e a r i n g s y s t e mi n l o w Ｇt o w e r c a b l e Ｇs t a y e db r i d ge i sef Ｇf e c t i v e．K e y w o r d s:l o wＧt o w e rc a b l eＧs t a y e db r i d g e;f r i c t i o n p e n d u l u m b e a r i n g;s e i s m i c w a v e;d a m p i n ge f f e c t０㊀引言地震是一种自然灾害现象,给人类带来的灾难很大,抵御地震成为人类防御灾害的长期工作.为了减轻地震的影响,就需要对地震有较深入的了解.因此我们要掌握工程结构抗震设计原理和方法,研究如何防止或减少建筑物的地震破坏,通过对建筑物的抗震设防,将地震造成的人员伤亡和经济损失降到最低限度[１Ｇ２].矮塔斜拉桥有着良好的受力性能与美观性能,近年来得到广泛应用,摩擦摆式减隔震支座关键是将桥梁上部结构与下部结构分离,从而延长结构的自振周期和摩擦耗能机理来降低和耗散传递到桥梁上部结构的能力.文献[２]主要研究了结构地震反应与抗震验算,指出了桥梁延性抗震设计.文献[３]主要进行了桥梁抗震的计算与抗震性能评述.文献[４Ｇ５]主要研究了摩擦摆式支座在桥梁中的应用,未研究矮塔斜拉桥中的应用.文献[６]研究了桥梁抗震设计的理论与方法.文献[７Ｇ８]研究了隔震装置的技术发展,如普通橡胶支座,高阻尼橡胶支座,铅芯橡胶支座以及摩擦摆式隔震支座,对于具体隔震效果分析未进行深入研究.我国对斜拉桥的抗震研究较早,文献[９]采用反应谱法对天津永和桥进行了地震反应分析,并研究了行波效应的影响.文献[１０]指出对斜拉桥地震波分量独立作用㊁共同作用下的地震反应对比分析,结果表明行波效应的影响与斜拉桥的结构形式和地震波的传播速度有关.文献[１１]指出摩擦摆支座是Z a y a s在１９８５年开发出来的,其具有良好的隔振效果,而且工作性能也比较稳定,近年来在我国得到了广泛的应用,如苏通大桥㊁上海长江大桥以及港珠澳大桥等重点工程.综上所述,矮塔斜拉桥减震研究以及摩擦摆支座在桥梁应用的研究都很多,但是在矮塔斜拉桥中摩擦摆式支座的减震效果的研究很少,因此对比分析摩擦摆式支座的减震效果研究很有必要.本文以靖远金滩黄河大桥(１００＋１６８＋１００)m为例,通过数值分析探讨了摩擦摆式支座在矮塔斜拉桥中的减震效果.１㊀摩擦摆式支座的介绍１．１㊀摩擦摆式支座简介摩擦摆隔震支座是另一种有效的摩擦滑移隔震体系,１９８５年由美国的D r．V i c t o rZ a y a s首先提出.由于其具有良好的工作性质,国内外学者进行了较深入的研究,并已被成功应用于实际工程中.F P S 隔震支座是利用弧形滑动面的周期来延长结构物的振动周期,大幅度减少结构物因受地震作用而引起的放大效应.此外,还可以利用F P S滑动面与滑块之间的摩擦来达到消耗地震能量㊁减少地震力输入的目的.F P S摩擦摆滑动隔震的方法造价低㊁施工简单㊁不受上部结构重量影响,除具有一般平面滑动隔震系统的特点外,还具有良好的稳定性㊁自复位功能和抗平扭能力.目前,F P S摩擦摆已在国外建筑中得到了广泛的应用,尤其在美国,采用F P S摩擦摆隔震系统的建筑物已达数百座.[２]１．２㊀摩擦摆式支座工作原理桥跨结构中的抗震理论基本上都是选取各类减震的体系,结构物在来回发生运动的过程中,摩擦摆式支座的活动面和滑块之间将会出现摩阻力来抵消一大部分地震作用的能量,从而降低地震的破坏作用[３],其工作原理如图１所示,利用减震体系本身的滞回特性来消耗地震波的输入能量,以达到地震力对下部构造影响减弱的目的[４].摩擦摆支座的承载能力高㊁施工简单,而且造价又低,除了有一般的平面滑动隔震系统的特点之外,其还具有良好的稳定性㊁复位功能以及抗平扭能力[５Ｇ６],其构造示意图如图２所示.图１㊀单摆工作原理F i g．１㊀P e n d u l u m p r i n c i p l e４１２㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀地㊀震㊀工㊀程㊀学㊀报㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀２０２１年图２㊀摩擦摆支座构造F i g．２㊀F P Bs t r u c t u r e 根据能量守恒原理,传统抗震结构:E i n ＝E R ＋E D ＋E S ㊀(１)㊀㊀消能减震结构E i n ＝E R ＋E D ＋E S ＋E A ㊀(２)式中:E i n 为地震发生时输入结构的全部能量;E R 为结构做出对地震反应的能量,包括结构的动能和势能;E D 为结构体本身阻尼部分抵消的能量(ɤ５％);E S 为主要构件的塑性变形甚至损坏所抵消的能量;E A 为摩擦摆抵消的能量[７].２㊀工程背景及有限元模型参数确定靖远金滩黄河大桥主桥结构为预应力混凝土矮塔斜拉桥,全长３６８m ,跨径布置为(１００＋１６８＋１００)m .主桥箱梁采用单箱五室斜腹板断面,顶板宽度为３６．５m ,主桥通过箱梁顶结构找坡,箱梁中支点外缘梁高６．８m ,跨中及边跨合拢段箱梁外缘梁高为３．３m ,箱梁底板下缘按１．８次抛物线变化.桥塔外形采用A 型,总高３０m ,桥塔截面为实心矩形截面,桥塔横向宽度为２．４m ,顺桥向为变宽度.下塔柱截面为２４０c mˑ２４０c m ,上塔柱(锚索区)顺向宽度从５４１c m 变化至３００c m .主桥桥墩支座布置如图３所示,从左至右分别为６~９号墩,其中７㊁８号主墩位于主河槽内.桥墩采用横桥向设置三肢实体墩身;中肢５mˑ７m 矩形截面,边肢５mˑ４m 矩形截面.墩身下接承台,承台尺寸为１５．７mˑ３３．７mˑ５m .承台底布置１８根直径２ ２m 的桩基础,桩长６０m .主桥６㊁９号过渡墩采用横桥向设置三肢实体墩身,墩身为２mˑ４m 矩形截面,墩身下设置承台,承台尺寸为８mˑ２８mˑ３m .承台底布置１２根直径１．８m 的桩基础,桩长为３５m .场地土类型为中硬土,场地类别为Ⅱ类.根据«中国地震动参数区划图»(G B １８３０６Ｇ２０１５),场址区地震动峰值加速度为０．２g ,相应的地震烈度为Ⅷ度,地震动加速度反应谱特征周期为０．４５s.图３㊀靖远金滩黄河大桥矮塔斜拉桥桥墩支座布置图F i g ．３㊀L a y o u t o f p i e r b e a r i n g s o f t h e l o w Ｇt o w e r c a b l e Ｇs t a y e db r i d g e i n J i n t a nY e l l o w R i v e rB r i d g e o f J i n g yu a n ㊀㊀全桥模型共３５９１个节点,单元３４９２个,其中梁单元３４４４个,只受拉单元４８个.模拟结构的摩擦摆式支座参数为:位移速度较慢时的摩擦系数为０ ０５,位移速度较快时摩擦系数为０．０３,主墩支座摩擦面曲率半径为９m ,过渡墩支座摩擦面曲率半径为５m ,减隔震位移为３００mm .靖远金滩黄河大桥矮塔斜拉桥的有限元模型如图４所示.３㊀减震结构与原结构动力特性对比分析３．１㊀自振频率对比分析地震波的周期与频率成反比关系,其频率大小可以直接的反应减震效果的有效性.减震模型的频率减小就说明周期增大,说明减震模型的桥梁进行减震是可行的.表１是减震结构与原结构的前二十阶频率对比的情况.图４㊀靖远金滩黄河大桥矮塔斜拉桥有限元模型F i g．４㊀F i n i t e e l e m e n tm o d e l o f t h e l o w Ｇt o w e r c a b l e Ｇs t a y e d b r i d g e i n J i n t a nY e l l o wR i v e rB r i d g e o f J i n g yu a n 限于篇幅,本文只附了前３阶的模态图(图５~７),任一阶态的频率列于表１.通过表１可以发现:当为第一阶时,原来模型的频率为１．０１１１,减震模５１２第４３卷第１期㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀彭文礼,等:摩擦摆支座在矮塔斜拉桥中减震效果研究㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀型的频率为０．５５５１,延长周期０．８１２s,有明显的减震效果;当为第五阶时,原来模型的频率为１．９２８７,减震模型的频率为１．１７４４,延长周期０．３３３s ;当为第十阶时,原来模型的频率为２．４７３３,减震模型的频率为２．１７８０,延长周期０．０５５s;当为第十五阶时,原来模型的频率为４．６４２７,减震模型的频率为３．９７８８,延长周期０．０３６s;当为第二十阶时,原来模型的频率为６．４２０７,减震模型的频率为４．０９３１,延长周期０．０８９s .任何一阶的频率增大,周期都有所减小,说明减震结构的地震反应都有所减小.表１㊀减震结构与原结构前二十阶自振频率Ta b l e １㊀T h e f i r s t t w e n t y n a t u r a l f r e q u e n c i e s o f v i b r a t i o n Ｇa b s o r b i n g s t r u c t u r e s a n do r i gi n a l s t r u c t u r e s 阶数频率/H z减震结构原结构延长周期/s 阶数频率/H z减震结构原结构延长周期/s １０．５５５１１．０１１１０．８１２１１２．７３６５３．１５０００．０４８２０．８１４１１．２２２５０．４１０１２３．２８４２３．５６１１０．０２４３１．１１６０１．５５２５０．２５２１３３．９３２６４．５６７１０．０３５４１．１２４４１．７２２３０．３０９１４３．９３８２４．５８７９０．０３６５１．１７４４１．９２８７０．３３３１５３．９７８８４．６４２７０．０３６６１．３１７４１．９５５４０．２４８１６３．９８９６４．８８９００．０４６７１．５３７６２．００１００．１５１１７４．０１４２５．４４６１０．０６５８１．９２４０２．０４７７０．０３１１８４．０４９５６．０６３００．０８２９１．９８６０２．０７５８０．０２２１９４．０４９６６．０７６６０．０８２１０２．１７８０２．４７３３０．０５５２０４．０９３１６．４２０７０．０８９图５㊀减隔震与普通支座主梁纵飘＋一阶对称竖弯图F i g ．５㊀L o n g i t u d i n a l f l o a t i n g a n d f i r s t Ｇm o d e s y mm e t r i c a l l o n g i t u d i n a l b e n d i n g of t h e m a i ng i r d e rw i t hs e i s m i c i s o l a t i o na n do r d i n a r y b e a r i n gs 图６㊀减隔震与普通支座主梁纵飘＋二阶反对称竖弯图F i g ．６㊀L o n g i t u d i n a l f l o a t i n g a n d s e c o n d Ｇm o d e a n t i Ｇs y mm e t r i c a l l o n g i t u d i n a l b e n d i n g of t h e m a i ng i r d e rw i t hs e i s m i c i s o l a t i o na n do r d i n a r y b e a r i n gs 图７㊀减隔震与普通支座主梁三阶对称侧弯图F i g ．７㊀L o n g i t u d i n a l f l o a t i n g a n d t h i r d Ｇm o d e s y mm e t r i c a l l o n g i t u d i n a l b e n d i n g of t h e m a i ng i r d e rw i t hs e i s m i c i s o l a t i o na n do r d i n a r y b e a r i n gs ６１２㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀地㊀震㊀工㊀程㊀学㊀报㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀２０２１年３．２㊀减震性能对比分析３．２．１㊀地震波输入地震波根据地震动参数选取E l c e n t 波㊁T a f t 波及S a n f e r 波三条地震波,地面加速度分别为横桥向与纵桥向同时输入地震波.其波形时程函数图如图８~１０.３．２．２㊀墩顶㊁墩底㊁桩基减震性能比较为了便于比较,现将靖远金滩黄河大桥在摩擦摆式减隔震支座的作用下将８号墩顺桥向中肢墩顶的位移,以及８号墩中肢墩底的剪力与弯矩的减震率列于表２.采用摩擦摆支座的减隔震结构墩顶位图８㊀E l c e n t 波时程函数图F i g ．８㊀T i m e Ｇh i s t o r y f u n c t i o nd i a gr a mo fE l c e n tw a v e 图９㊀T a f t 波时程函数图F i g ．９㊀T i m eh i s t o r y fu n c t i o no fT a f tw a v e 图１０㊀S a n f e r 波时程函数图F i g ．１０㊀T i m eh i s t o r y fu n c t i o no f S a n f e rw a v e 移明显减小,墩身内力也明显减小,隔震率均在７０％以上,本文定义减震率如下式所示:减震率＝原结构的地震反应 有减震支座时的地震反应原结构的地震反应ˑ１００％.表２㊀减震结构与原结构在地震波的影响下的减震效果T a b l e ２㊀S e i s m i c a b s o r p t i o n e f f e c t o f d a m p i n g s t r u c t u r e s a n do r i gi n a l s t r u c t u r e s u n d e r t h e i n f l u e n c e o f s e i s m i cw a v e s 项目地震波１地震波２地震波３原结构４０．９２７．８４３．１顺桥向８＃墩顶位移/mm减震结构１０．６７．８７．９减震率７４．１％７１．９％８１．７％原结构５１．６２２．１１８．３横桥向８＃墩顶位移/mm减震结构９．３３．９４．６减震率８２．０％８２．４％７４．９％原结构１０７９３８８７７１０７７．７１１４３３２７．２顺桥向８＃墩中肢墩底弯矩/k N m减震结构２２９６２６．５１７００１０．９１７３９６２．２减震率７８．７％７８．０％８４．８％原结构４６１４９１１．３１９５８４４６１６３１９８０横桥向８＃墩中肢墩底弯矩/k N m减震结构５５０３６６．５２３５８６７２６８８５５．２减震率８８．１％８８．０％８３．５％原结构１０７４０６．１８４７４３．４１１４７５６．３顺桥向８＃墩中肢墩底剪力/k N减震结构２４１１２１８７０９．３２１０８１．３减震率７７．６％７７．９％８１．６％原结构１５６９０８．３６９６８６．６５７６２７．２横桥向８＃墩中肢墩底剪力/k N减震结构３１５４０．９１１４３７１５６７６．４减震率７９．９％８３．６％７２．８％㊀㊀对比以上结果可以得出以下结论:在地震作用下,摩擦摆式支座对桥梁下部结构有明显的减震效果,隔震率在７０％以上.采用摩擦摆支座的隔震结构墩底的内力远小于非隔震结构的７１２第４３卷第１期㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀彭文礼,等:摩擦摆支座在矮塔斜拉桥中减震效果研究㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀墩底内力,并且采用摩擦摆支座的隔震结构墩顶位移远小于非隔震结构的墩顶位移.桥墩的地震力一部分来自梁体传来的地震力,另一部分是桥墩本身所受的地震力,在摩擦摆式支座的作用下,梁体与桥墩发生了动力的相互作用,削弱了地震的作用,合理的配置摩擦摆式支座可以有效地利用桥梁体系各部分的动力相互作用.４㊀结语摩擦摆式支座可以将桥梁上部结构与下部结构分开,进而抵消掉大量的地震波能量,降低结构的地震反应.桥墩是桥梁的主要受力构件,摩擦摆支座可使墩身内力大大减小,从而使矮塔斜拉桥受力良好.设计桥梁结构的摩擦摆式支座减隔震的系统时,应该从多种内力出发分别进行研讨,以能够正确的判断减震的幅度,从而最大程度的实现减震的效果.参考文献(R e f e r e n c e s)[１]㊀袁增嵘,肖建春,廖德,等．地震作用下超高大悬挑雕塑的抗倾覆分析[J]．贵州大学学报(自然科学版),２０１９,３６(１):９４Ｇ１００．Y U A NZ e n g r o n g,X I A OJ i a n c h u n,L I A O D e,e t a l．A n t iＧO v e rＧt u r n i n g A n a l y s i so fS u p e rT a l lC a n t i l e v e r e dS c u l p t u r eu n d e rE a r t h q u a k eA c t i o n[J]．J o u r n a l o fG u i z h o uU n i v e r s i t y(N a t u r a lS c i e n c e),２０１９,３６(１):９４Ｇ１００．[２]㊀王显利．工程结构抗震设计[M]．北京:机械工业出版社,２０１５．WA N GX i a n l i．A s e i s m i cD e s i g no f E n g i n e e r i n g S t r u c t u r e s[M]．B e i j i n g:C h i n aM a c h i n eP r e s s,２０１５．[３]㊀王克海,李茜．桥梁抗震的研究进展[J]．工程力学,２００７,２４(增刊２):７５Ｇ８２,１２８．WA N G K e h a i,L IQ i a n．R e s e a r c hP r o g r e s s o nA s e i s m i cD e s i g no f B r i d g e s[J]．E n g i n e e r i n g M e c h a n i c s,２００７,２４(S u p p２):７５Ｇ８２,１２８．[４]㊀郭俊伟．摩擦摆减隔震支座在高烈度区高架桥的减震效果分析[J]．城市道桥与防洪,２０１３(４):１８７Ｇ１９０．G U OJ u n w e i．A n a l y s i so n D a m p i n g E f f e c to fF r i c t i o nP e n d uＧl u m B e a r i n g s(F P B)f o rE l e v a t e dB r i d g e i n H i g h E a r t h q u a k eI n t e n s i t y R e g i o n[J]．U r b a n R o a d sB r i d g e s&F l o o dC o n t r o l,２０１３(４):１８７Ｇ１９０．[５]㊀杨允表．摩擦摆支座在桥梁抗震设计中的应用[J]．中国市政工程,２０１４(５):８８Ｇ９１．Y A N G Y u n b i a o．A p p l i c a t i o n o f F r i c t i o n P e n d u l u m B e a r i n g(F P B)i nB r i d g eA s e i s m a t i cD e s i g n[J]．C h i n a M u n i c i p a lE n g iＧn e e r i n g,２０１４(５):８８Ｇ９１．[６]㊀范立础,王志强．我国桥梁隔震技术的应用[J]．振动工程学报,１９９９(１):２６Ｇ３４．F A NL i c h u,WA NG Z h i q i a n g．A p p l i c a t i o no fS e i s m i c I s o l a t i o nT e c h n o l o g y f o r B r i d g e s i nC h i n a[J]．J o u r n a l o fV i b r a t i o nE n g iＧn e e r i n g,１９９９(１):２６Ｇ３４．[７]㊀薛彦涛,常兆中,高杰．隔震建筑设计指南[M]．北京:中国建筑工业出版社,２０１６．X U EY a n t a o,C HA N G Z h a o z h o n g,G A OJ i e．D e s i g n G u i d eo fI s o l a t i o n B u i l d i n g[M]．B e i j i n g:C h i n a C o n s t r u c t i o nI n d u s t r yP r e s s,２０１６．[８]㊀李宏男．地震工程学[M]．北京:机械工业出版社,２０１３．L IH o n g n a n．E a r t h q u a k eE n g i n e e r i n g[M]．B e i j i n g:C h i n a M aＧc h i n eP r e s s,２０１３．[９]㊀项海帆．斜拉桥在行波效应作用下的地震反应分析[J]．同济大学学报,１９８３,１１(３);２４Ｇ２７．X I U A N G H a i f a n．S e i s m i cR e s p o n s e A n a l y s i so fC a b l eＧs t a y e dB r i d g e u n d e rT r a v e l i n g W a v eE f f e c t[J]．J o u r n a l o fT o n g j iU n iＧv e r s i t y,１９８３,１１(３):２４Ｇ２７．[１０]㊀陈幼平,周宏业．斜拉桥地震反应的行波效应[J]．土木工程学报,１９９６,２９(６):６１Ｇ６８．C H E N Y o u p i n g,Z H O U H o n g y e．S e i s m i cB e h a v i o r o fG a b l eＧs t a y e dB r i d g e su n d e rT r a v e l l i n g W a v eE x c i t a t i o n[J]．C h i n aC i v i l E n g i n e e r i n g J o u r n a l,１９９６,２９(６):６１Ｇ６８．[１１]㊀Z A Y A S V A,L OW SS,MA H I N S A．A S i m p l eP e n d u l u m T e c h n i q u ef o r A c h i e v i n g S e i s m i cI s o l a t i o n[J]．E a r t h q u a k eS p e c t r a,１９９０,６(２):３１７Ｇ３３３．８１２㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀地㊀震㊀工㊀程㊀学㊀报㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀２０２１年。

矮塔斜拉桥方案设计论文清晨的阳光透过窗帘的缝隙，洒在我的设计图纸上，那些曲线和结构在光影的映照下，仿佛活了过来。

十年的方案写作经验，让我对矮塔斜拉桥的设计有着独特的理解。

一、设计背景与目标这座矮塔斜拉桥位于繁忙的都市，连接着两岸的经济与文化。

我们的目标是打造一座既实用又美观的桥梁，它不仅要满足交通需求，更要成为城市的标志性建筑。

二、设计理念在设计之初，我们就明确了几个核心理念：简约、现代、和谐。

简约不仅仅是一种美学，更是一种对材料、结构和成本的合理控制；现代意味着我们要运用最新的设计理念和技术；和谐则是指桥梁与周围环境的协调统一。

三、总体布局桥梁全长3.2公里，主桥跨度达到560米。

矮塔采用钢结构，塔身高60米，倾斜角度为10度。

桥面宽度为双向六车道，两侧设有人行道和自行车道。

这样的布局既保证了交通的流畅，又为行人提供了安全舒适的通行环境。

四、结构设计矮塔斜拉桥的结构设计是其核心部分。

我们采用了高强度钢材和特种混凝土，确保了桥梁的稳定性和耐久性。

斜拉索的布置采用扇形，从塔顶向桥面两侧延伸，形成了一种动态的美感。

五、技术创新在设计中，我们运用了几项技术创新。

是采用了自振频率控制技术，通过在桥梁中设置特殊的阻尼装置，有效减少了风振和地震对桥梁的影响。

是运用了智能监测系统，通过传感器实时监测桥梁的健康状况，确保其安全运行。

六、视觉效果矮塔斜拉桥的设计充分考虑了视觉效果。

桥梁的线条流畅，塔身与斜拉索形成了一种韵律感。

夜幕降临，桥上的灯光亮起，宛如一道彩虹横跨在都市之上，成为夜晚的一道亮丽风景。

七、环保与可持续发展在设计中，我们也注重了环保和可持续发展。

桥梁采用了环保材料，减少了施工过程中的污染。

同时，桥梁的设计也考虑了未来可能的扩建需求，确保其能够适应城市发展的需要。

八、经济效益矮塔斜拉桥的建设不仅是一项工程，更是一项投资。

通过精确的成本控制和高效的施工方案，我们确保了项目的经济效益。

桥梁的建成将促进两岸经济的交流与发展，为城市带来长期的回报。