第一章三角形的证明复习资料

八年级下册数学第一章三角形的证明第一部分：知识点1、等腰三角形（1）三角形全等的性质及判定全等三角形的对应边相等，对应角也相等判定：SSS、SAS、ASA、AAS、（2）等腰三角形的判定、性质及推论性质：等腰三角形的两个底角相等（等边对等角）判定：有两个角相等的三角形是等腰三角形（等角对等边）推论：等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合（即“三线合一”）（3）等边三角形的性质及判定定理性质定理：等边三角形的三个角都相等，并且每个角都等于60度；等边三角形的三条边都满足“三线合一”的性质；等边三角形是轴对称图形，有3条对称轴。

判定定理：有一个角是60度的等腰三角形是等边三角形。

或者三个角都相等的三角形是等边三角形。

（4）含30度的直角三角形的边的性质定理：在直角三角形中，如果一个锐角等于30度，那么它所对的直角边等于斜边的一半。

2、直角三角形（1）勾股定理及其逆定理定理：直角三角形的两条直角边的平方和等于斜边的平方。

逆定理：如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形。

（2）直角三角形两个锐角之间的关系定理：直角三角形两个锐角互余。

逆定理：有两个锐角互余的三角形是直角三角形。

（3）含30度的直角三角形的边的定理定理：在直角三角形中，如果一个锐角等于30度，那么它所对的直角边等于斜边的一半。

逆定理：在直角三角形中，一条直角边是斜边的一半，那么这条直角边所对的锐角是30度。

（4）命题与逆命题命题包括已知和结论两部分；逆命题是将倒是的已知和结论交换；正确的逆命题就是逆定理。

（5）直角三角形全等的判定定理定理：斜边和一条直角边对应相等的两个直角三角形全等（HL） 3、线段的垂直平分线（1）线段垂直平分线的性质及判定性质：线段垂直平分线上的点到这条线段两个端点的距离相等。

判定：到一条线段两个端点距离相等的点在这条线段的垂直平分线上。

（2）三角形三边的垂直平分线的性质三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等。

B A 第一章 三角形的证明 知识点归纳与复习[知识点1] 等腰三角形（1）定义：有两条边 的三角形是等腰三角形。

（2）性质：①等腰三角形的两个底角 。

（简写为“等边对等角”）②等腰三角形的顶角平分线、底边上的 、底边上的 互相重合。

(简写为“ ”)③等腰三角形是 图形,对称轴是 ；（3）判定： ①定义：有两条边相等的三角形是 ；②有两个角 的三角形是等腰三角形。

(简写为 “ ”)练习：1.已知等腰三角形的两条边长分别是7和3，则第三条边的长是（ ）A ．3或7B ．7C ． 4D ．32.等腰三角形的两边长为4、9，则它的周长是（ ）A ．17B ．17或22C ．20D ．223.若等腰三角形的一个内角为50°，则这个等腰三角形顶角的度为 °；4. 等腰三角形的对称轴有（ ）A ．1条 B. 2条 C. 3条 D. 1条或3条5.等腰三角形的顶角是120°，底边上的中线长为4cm, 则它的腰为 cm6.△ABC 中，若∠A =80o ， ∠B =50o ，AC =5，则AB = ;7.如图，正方形网格中，网格线的交点称为格点．已知A 、B 是两格点，如果C 也是图中的格点，且使得ABC 为等腰三角形．．．．．，则点C 的个 数是（ ） A ．6 B ． 7 C ． 8D ．9 8. 如图,在△ABC 中, AB=AC, BD 平分角ABC,交AC 于点D.若BD=BC, 则∠A ＝ 。

[知识点2] 等边三角形定义： 的三角形是等边三角形；性质：①三条边都 ，三个角都等于 °，有 条对称轴；②等边三角形有没有“”三线合一”？ 。

判定：①定义： 的三角形是等边三角形;②有一个角等于 °的等腰三角形是等边三角形;练习：1．顺次连接等边△ABC 各边的中点，可得到一个 三角形。

2.已知等边△ABC 的边长为4，则它的面积是（ ）A ．8B ．83 C ．42 D ． 433.已知a,b,c是三角形的三条边，若（a-b）2+(b-c)2=0,则这个三角形是（）A．等腰三角形 B．等边三角形 C．直角三角形 D．锐角三角形4.用反证法证明“一个三角形中不能有两个角是直角”，应假设___________________;5. 如图，在等边三角形ABC中，AB=6，D是BC上一点，且BC=3BD，△ABD绕点A旋转后得到△ACE，则CE的长度为．[知识点3] 直角三角形1.直角三角形的性质定理与判定:(1)直角三角形的两锐角________；(2)在直角三角形中，30°角所对的直角边等于___________________;(3）有两个角互余的三角形是_______________.2．勾股定理及其逆定理：（1）直角三角形的两直角边的__________等于____________________；（2）如果三角形两边的___________等于第三边的平方，那么这个三角形是_________.定理：斜边和一直角边相等的两个三角形_________.简述为“________、______”或“______”练习：1．下列长度的三条线段能构成直角三角形的是（）①8、15、17 ②4、5、6、③7.5、4、8.5 ④ 24、25、7 ⑤ 5、8、10A：①②④ B：②④⑤ C：①③⑤ D：①③④2. “平行四边形的对角线互相平分”的逆命题是___________________________．3．在直角三角形中，如果一个锐角为30°，而斜边与较小直角边的和为12，那么斜边长为．4.如图，在四边形BCDE中，∠C=∠BED=90°，∠B=60°，延长CD、BE得到Rt△ABC，已知CD=2，DE=1，求Rt△ABC的面积为．5．如图,在四边形ABCD中, AB∥CD, E为BC上的一点, 且∠BAE=25°,∠CDE=65°,AE=2,DE=3,则AD的长度是 .6．已知：如图1-2-4，△ABC中，CD⊥AB于D，AC=4，BC=3，DB=59. （1）求DC的长；（2）求AD的长；（3）求AB的长；（4）求证：△ABC是直角三角形.图1-2-47.如图1-2-9，已知∠ABC=∠ADC=90°，E 是AC 上一点，AB=AD ，求证：EB=ED.[知识点4] 线段垂直平分线 1.线段的垂直平分线上的点到这条线段的两个端点的距离_______；这个定理的逆定理是 _______________ _______________ _______________。

《三角形的证明》全章复习与巩固（基础）知识梳理【要点】要点一、等腰三角形1.三角形全等的性质及判定全等三角形的对应边相等，对应角也相等.判定：SSS、SAS、ASA、AAS、HL.2.等腰三角形的判定、性质及推论性质：等腰三角形的两个底角相等（等边对等角）判定：有两个角相等的三角形是等腰三角形（等角对等边）推论：等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合（即“三线合一”）3.等边三角形的性质及判定定理性质定理：等边三角形的三个角都相等，并且每个角都等于60°；等边三角形是轴对称图形，有3条对称轴.判定定理：有一个角是60°的等腰三角形是等边三角形；三个角都相等的三角形是等边三角形.4.含30°的直角三角形的边的性质定理：在直角三角形中，如果一个角等于30°，那么它所对的直角边等于斜边的一半. 要点诠释：等边三角形是中考中常考的知识点，并且有关它的计算也很常见，因此对于等边三角形的特殊数据要熟记于心，比如边长为a的等边三角形它的高是32a，面积是234；含有30°的直角三角形揭示了三角形中边与角的关系，打破了以往那种只有角或边的关系，同时也为我们学习三角函数奠定了基础.要点二、直角三角形1.勾股定理及其逆定理定理：直角三角形的两条直角边的平方和等于斜边的平方.逆定理：如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形.2.命题与逆命题命题包括题设和结论两部分；逆命题是将原命题的题设和结论交换位置得到的；3.直角三角形全等的判定定理定理：斜边和一条直角边对应相等的两个直角三角形全等（HL）.要点诠释：①勾股定理的逆定理在语言叙述的时候一定要注意，不能说成“两条边的平方和等于斜边的平方”，应该说成“三角形两边的平方和等于第三边的平方”.②直角三角形的全等判定方法，还有SSS,SAS,ASA,AAS,HL一共有5种判定方法.要点三、线段的垂直平分线1.线段垂直平分线的性质及判定性质：线段垂直平分线上的点到这条线段两个端点的距离相等.判定：到一条线段两个端点距离相等的点在这条线段的垂直平分线上.2.三角形三边的垂直平分线的性质三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等.3.如何用尺规作图法作线段的垂直平分线分别以线段的两个端点A、B为圆心，以大于12AB的长为半径作弧，两弧交于点M、N；作直线MN，则直线MN就是线段AB的垂直平分线.要点诠释：①注意区分线段的垂直平分线性质定理和判定定理,注意二者的应用范围；②利用线段的垂直平分线定理可解决两条线段的和距离最短问题.要点四、角平分线1.角平分线的性质及判定定理性质：角平分线上的点到这个角的两边的距离相等；判定：在一个角的内部，且到角的两边的距离相等的点，在这个角的平分线上.2.三角形三条角平分线的性质定理性质：三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等.3.如何用尺规作图法作出角平分线要点诠释：①注意区分角平分线性质定理和判定定理,注意二者的应用范围；②几何语言的表述，这也是证明线段相等的一种重要的方法.遇到角平分线时，要构造全等三角形.【典型例题】类型一、三角形的证明1. 已知：点D是△ABC的边BC的中点，DE⊥AC，DF⊥AB，垂足分别为E，F，且BF=CE．求证：△ABC是等腰三角形．【思路点拨】欲证△ABC 是等腰三角形，又已知DE ⊥AC ，DF ⊥AB ，BF=CE ，可利用三角形中两内角相等来证明．【答案与解析】证明：∵D 是BC 的中点，∴BD=CD ，∵DE ⊥AC ，DF ⊥AB ，∴△BDF 与△CDE 为直角三角形，在Rt △BDF 和Rt △CDE 中，,BF CE BD CD=⎧⎨=⎩ ∴Rt △BFD ≌Rt △CED （HL ），∴∠B=∠C ，∴AB=AC ，∴△ABC 是等腰三角形．【总结升华】考查等腰三角形的判定方法及全等三角形的判定及性质；充分利用条件证明三角形全等是正确解答本题的关键．举一反三：【变式1】（2015秋•江阴市校级期中）已知：如图，△AMN 的周长为18，∠B ，∠C 的平分线相交于点O ，过O 点的直线MN ∥BC 交AB 、AC 于点M 、N ．求AB+AC 的值．【答案】解：∵MN ∥BC ，∴∠BOM=∠OBC ，∠CON=∠OCB ，∵∠B ，∠C 的平分线相交于点O ，∴∠MBO=∠OBC ，∠NCO=∠OCB ，∴∠MBO=∠BOM ，∠NCO=∠CON ，∴BM=OM ，CN=ON ，∵△AMN 的周长为18，∴AM+MN+AN=AM+OM+ON+AN=AM+BM+CN+AN=AB+AC=18．【变式2】如图，在△ABC 中，AB=AC ，D 、E 在BC 上，且AD=AE ，求证：BD=CE ．【答案】证明：∵AB=AC ，AD=AE ，∴∠B=∠C ，∠ADE=∠AED ，∵∠ADE=∠B+∠BAD ，∠AED=∠C+∠EAC ，∴∠BAD=∠CAE ，∵AB=AC ，AD=AE ，∴△ABD ≌△ACE ，∴ BD=CE ．类型二、直角三角形2. 如图，已知，在Rt △ABC 中，∠C=90°，沿过B 点的一条直线BE 折叠这个三角形，使C 点与AB 边上的一点D 重合．（1）当∠A 满足什么条件时，点D 恰为AB 的中点写出一个你认为适当的条件，并利用此条件证明D 为AB 的中点；（2）在（1）的条件下，若DE=1，求△ABC 的面积．【思路点拨】（1）根据折叠的性质：△BCE ≌△BDE ，BC=BD ，当点D 恰为AB 的重点时，AB=2BD=2BC ，又∠C=90°，故∠A=30°；当添加条件∠A=30°时，由折叠性质知：∠EBD=∠EBC=30°，又∠A=30°且ED ⊥AB ，可证D 为AB 的中点；（2）在Rt △ADE 中，根据∠A 及ED 的值，可将AE 、AD 的值求出，又D 为AB 的中点，可得AB 的长度，在Rt △ABC 中，根据AB 、∠A 的值，可将AC 和BC 的值求出，代入S △ABC =AC ×BC 进行求解即可．【答案与解析】解：（1）添加条件是∠A=30°．证明：∵∠A=30°，∠C=90°，所以∠CBA=60°，∵C 点折叠后与AB 边上的一点D 重合，∴BE 平分∠CBD ，∠BDE=90°，∴∠EBD=30°，∴∠EBD=∠EAB ，所以EB=EA ；∵ED 为△EAB 的高线，所以ED 也是等腰△EBA 的中线，∴D 为AB 中点．（2）∵DE=1，ED ⊥AB ，∠A=30°，∴AE=2．在Rt △ADE 中，根据勾股定理，得22213-=∴AB=23，∵∠A=30°，∠C=90°，∴BC=12AB=3． 在Rt △ABC 中，AC=22AB BC -=3，∴S △ABC =12×AC ×BC=332． 【总结升华】考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，根据轴对称的性质，折叠前后图形的形状和大小不变．3. 小林在课堂上探索出只用三角尺作角平分线的一种方法：如图，在已知∠AOB 的两边上分别取点M ，N ，使OM=ON ，再过点M 作OB 的垂线，过点N 作OA 的垂线，垂足分别为C 、D ，两垂线交于点P ，那么射线OP 就是∠AOB 的平分线．老师当场肯定他的作法，并且表扬他的创新．但是小林不知道这是为什么．①你能说明这样做的理由吗？也就是说，你能证明OP 就是∠AOB 的平分线吗？②请你只用三角板设法作出图∠AOB 的平分线，并说明你的作图方法或设计思路．【思路点拨】①在Rt △OCM 与Rt △ODN 中，依据ASA 得出OC=OD;在Rt △OCP 与Rt △ODP 中，因为OP=OP ，OC=OD 得出Rt △OCP ≌Rt △ODP （HL ），所以∠COP=∠DOP ，即OP 平分∠AOB ． ②可作出两个直角三角形，利用HL 定理证明两角所在的三角形全等．【答案与解析】①证明：在Rt △OCM 和Rt △ODN 中，COM DON OCM ODN OM ON ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△OCM ≌△ODN （AAS ），∴OC=OD ，在△OCP 与△ODP 中，∵,OC OD OP OP=⎧⎨=⎩∴Rt △OCP ≌Rt △ODP （HL ），∴∠COP=∠DOP ，即OP 平分∠AOB ；②解：①利用刻度尺在∠AOB 的两边上分别取OC=OD ；②过C ，D 分别作OA ，OB 的垂线，两垂线交于点E ；③作射线OE ，OE 就是所求的角平分线．∵CE ⊥OA ，ED ⊥OB ，∴∠OCE=∠ODE=90°，在Rt△OCE与Rt△ODE中，∵OC OD OE OE=⎧⎨=⎩，∴Rt△OCE≌Rt△ODE（HL），∴∠EOC=∠EOD，∴OE为∠AOB的角平分线．【总结升华】主要考查了直角三角形的判定，利用全等三角形的性质得出∠EOC=∠EOD是解题关键．类型三、线段垂直平分线4.（2015秋•麻城市校级期中）如图所示：在△ABC中，AB＞BC，AB=AC，DE是AB的垂直平分线，垂足为D，交AC于E．（1）若∠ABE=50°，求∠EBC的度数；（2）若△ABC的周长为41cm，边长为15cm，△BCE的周长．【思路点拨】（1）由DE是AB的垂直平分线，根据线段垂直平分线的性质，可得AE=BE，继而求得∠A的度数，又由AB=AC，即可求得∠ABC的度数，则可求得答案；（2）由△BCE的周长=AC+BC，然后分别从腰等于15cm与底边等于15cm去分析求解即可求得答案．【答案与解析】解：（1）∵DE是AB的垂直平分线，∴AE=BE，∴∠ABE=∠A=50°，∵AB=AC，∴∠ABC=∠C=65°，∴∠EBC=∠ABC﹣∠ABE=15°；（2）∵AE=BE，∴△BCE的周长=BE+CE+BC=AE+CE+BC=AC+BC；∵△ABC的周长为41cm，∴AB+AC+BC=41cm，若AB=AC=15cm，则BC=11cm，则△BCE的周长为：15+11=26cm；若BC=15cm，则AC=AB=13cm，∵AB＞BC，∴不符合题意，舍去．∴△BCE的周长为26cm．【总结升华】此题考查了线段垂直平分线的性质以及等腰三角形的性质．此题难度适中，注意掌握数形结合思想的应用．举一反三：【变式】如图所示，AD是△ABC中∠BAC的平分线，AD的垂直平分线EF交BC的延长线于F，试说明∠BAF=∠ACF的理由．【答案】解：∵EF垂直平分AD，∴AF=DF，∴∠FAD=∠FDA．又∵AD平分∠BAC，∴∠BAD=∠CAD，∵∠BAF=∠BAD+∠FAD，∠ACF=∠DAC+∠FDA，∴∠BAF=∠ACF．类型四、角平分线5. 如图，在△ABC中，∠BAC=80°，延长BC到D，使AC=CD，且∠ADB=20°，DE平分∠ADB交AC于F，交AB于E，连接CE，求∠CED的度数．【思路点拨】作EG⊥DA，EH⊥BD，EP⊥AC，根据角平分线的性质得到EG=EH，根据△EGA≌△EPA，得出∠ECB，就可以得到∠CED的度数．【答案与解析】证明：作EG⊥DA交DA的延长线于G，再作EH⊥BD，EP⊥AC，垂足分别为H，P，则EG=EH ∵∠ADC=20°，AC=CD，∴∠CAD=20°，而∠BAC=80°，∴∠GAE=180°﹣20°﹣80°=80°，∴Rt△EGA≌Rt△EPA，∴EG=EP∴EP=EH，∴∠ECB=∠ECA=12∠BCA=12×40°=20°∴∠CED=∠BCE﹣∠BDE=20°﹣10°=10°【总结升华】主要考查了角平分线的性质定理及逆定理、三角形全等的性质和判定；做题中两次用到角平分线的知识是正确解答本题的关键．举一反三：【变式】如图，直线l1、l2、l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有（）A．1处B．2处 C．3处 D．4处【答案】D．解：满足条件的有：（1）三角形两个内角平分线的交点，共一处；（2）三个外角两两平分线的交点，共三处．。

第一章三角形的证明第一讲：1.等腰三角形(1)——等腰三角形的性质(知识回顾)知识点一三角形全等的证明方法：1、 2、 3、 4、例1如图所示,分别过点C,B作△ABC的BC边上的中线AD及其延长线的垂线,垂足分别为E,F.求证:BF=CE1.如图,AC与BD交于点O,AB∥CD,若用“ASA”或“AAS”判定△AOB≌△COD,还需要添加的一个条件是.2、两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O 为边AC和DF的交点.求证:OF=OC.知识点二等腰三角形的性质定理定理:等腰三角形的两底角相等.这个定理简称为等边对等角.例2如图所示,在△ABC中,AB=AC,点D在BC上,且BD=AD,DC=AC,求∠B的度数3、若等腰三角形底边上的高与底边的比为1∶2,则它的顶角等于（）A.90°B.60°C.120°D.150°4.已知等腰三角形的一个内角为50°,则这个等腰三角形顶角的度数是( )A.50°B.80C.50°或80°D.40°或65°知识点三等腰三角形性质定理的推论等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.这条性质通常称为等腰三角形的“三线合一”.是证明那三条线证明: 等腰三角形两底角的平分线相等，高线相等已知：如图，在△ABC中， AB=AC， BD、CE是△ABC的角平分线．求证：BD=CE．拓展点一等腰三角形特殊性质的证明例1求证:等腰三角形两腰上的高的交点到底边两端的距离相等.已知:如图,在△ABC中,AB=AC,CE⊥AB于点E,BD⊥AC于点D,CE,BD交于点O,求证:OB=OC.知识点四等边三角形的性质定理定理:等边三角形的三个内角都相等,并且每个角都等于60°.例4 如图,点P,Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.拓展点二等边三角形与三角形全等的综合题5、如图,已知△ABC和△ADE都是等边三角形,连接CD,BE.求证:CD=BE习题1、下列各组几何图形中，一定全等的是（）A、各有一个角是550的两个等腰三角形；B、两个等边三角形；C、腰长相等的两个等腰直角三角形；D、各有一个角是500，腰长都为6cm的两个等腰三角形.2、如图，已知：AB∥CD，AB=CD，若要使△ABE≌△CDF,仍需添加一个条件，下列条件中，哪一个不能使△ABE≌△CDF的是（）A、∠A=∠B ;B、BF=CE;C、AE∥DF;D、AE=DF.3、如果等腰三角形的一个内角等于50°，则其余两角的度数为。

第一章 三角形的证明（性质）1.等腰三角形的性质定理；（1）等腰三角形的两个底角相等；（ ）∵ ∴（2）等腰三角形顶角的平分线、底边中线、底边上高三条线重合。

（ ）①∵ ∴ ②∵ ∴ ③∵ ∴2．等边三角形三个 都相等，且每个角都是 。

3.直角三角形的性质定理；（1）勾股定理： （2）Rt △中 （3）Rt △中，30°角。

数学符号∵∴ 4.线段的垂直平分线性质；线段垂直平分线上的点到 。

∵∴5.角平分线性质定理。

角平分线上的点到 ． ∵∴第一章 三角形的证明（判定）1. 等腰三角形的判定定理；有两个角相等的三角形是等腰三角形（ ）∵ ∴ ∴2．三个角都相等的三角形是 三角形。

3.直角三角形的判定定理；（1）勾股逆定理：数学符号∵∴（2）若 ，则△ABC 是Rt △。

4.线段的垂直平分线判定定理；到一条线段两个端点的距离相等个点在 。

∵∴5.角平分线判定定理。

在一个角的内部且到角的两边距离相等的点，在 ．∵∴6．全等三角形的判定定理① ② ③ ④ 特别地在Rt △中， （ ）在∴ （ ）NAPBC M 21EDCPOB A NAPBC M 21EDCPOBA巩固基础习题1 姓名1．在△ABC 中，AB ＝AC ，∠A ＝44°,则∠B ＝ ° 2．已知等腰三角形两条边的长分别是3和6，则它的周长等于 ．3．在△ABC 中，AB ＝AC ，∠BAC ＝120°，延长BC 到D ，使CD ＝AC ，则∠C DA ＝ 度. 4．一个正三角形的边长为a ，它的高是（ ） A ． 3 a B ．32 a C ．12 a D ．34a5．至少有两边相等的三角形是( )A ．等边三角形B ．等腰三角形C ．等腰直角三角形D ．锐角三角形 6．已知：如图，点D 是△ABC 内一点，AB ＝AC ，∠1＝∠2．求证：AD 平分∠BAC ．7．如图，若∠A ＝15°，AB =BC =CD =DE =EF ，则∠DEF 等于多少？ F D ECBA8．在ΔABC 中，DB 平分∠ABC ，DC 平分∠ACB ，过D 作直线EF //BC ，交AB 、AC 于E 、F ，若AB =8，AC =7，则ΔAEF 的周长等于多少？巩固基础习题2 姓名1.已知：如图，在等腰△ABC 中，AB=AC ∠BAC=120° D 为BC 中点，DE ⊥AB 于E.2．已知，如图，△ABC 中，AB=AC ，AD 是角平分线，BE=CF ，则下列说法正确的有几个（ ） 1）AD 平分∠EDF ；2）△EBD ≌△FCD ；3）BD=CD ；4）AD⊥BC ．（A ）1个 （B ）2个（C ）3个 （D ）4个 3．如图，在△ABC 和△ABD 中，∠C=∠D=90°，若利用“AAS ”证明△ABC ≌△ABD ，则需要加条件 _______或 ； 若利用“HL ”证明△ABC ≌△ABD ，则需要加条4.如图，有一个直角△ABC ，∠C=90°，AC=10，BC=5，一条线段PQ=AB ，P.Q 两点分别在AC 和过点A 且垂直于AC 的射线AX 上运动，当AP= 时,才能使ΔABC ≌ΔPQA.5.如图,在△ABC 中，∠C ＝90°，AC ＝BC ，AD 平分∠CAB ，交BC 于 D,DE ⊥AB 于E ，且AB ＝6 cm ，则△DEB 的周长为________cm.6.如图，在△ABC 中，已知D 是BC中点，DE ⊥AB ，DF ⊥AC ，垂足分别是E 、F ，DE ＝DF . 求证：AB=ACFDECBA求证： AB AE 41巩固基础习题3 姓名1.已知：如图，AC 平分∠BAD ，CE ⊥AB 于E ，CF⊥AD 于F ，且BC ＝DC .你能说明BE 与DF 相等吗？2．已知：如图，在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，∠A=30°.求证:BD=14AB3.如图，在△ABC 中，AB =AC ，DE 是过点A 的直线，BD ⊥DE 于D ，CE ⊥DE 于E ． （1）若BC 在DE 的同侧（如图①）且AD =CE ，说明：BA ⊥A C ．（2）若BC 在DE 的两侧（如图②）其他条件不变，问AB 与AC 仍垂直吗？若是请予证明，若不是请说明理由．巩固基础习题4 姓名1.已知AB 是线段CD 的垂直平分线，E 是AB 上的一点，如果EC=7cm ，那么ED= cm ；如果∠ECD=60°，那么∠EDC=2．已知：△ABC 中，AB=AC ，AD 是BC 边一上的中线，AB 的垂直平分线交AD 于O求证：OA=OB=OC ．3.已知：如图，P 是么AOB 平分线上的一点，PC ⊥OA ，PD ⊥OB ，垂足分别为C 、D ．求证：(1)OC=OD ；(2)OP 是CD 的垂直平分线．P DAE COBA B C DE F12 CADBE。

第一章三角形的证明—重要知识点：1、全等三角形(1)性质=辛等三角飛的対应功、対应角相罢。

(2)判定=“SAS”、SSS 、 AAS ASA 、HL(直角三角形)。

2、二免(1)性质：①^睽三角形的两底角相等。

(“等边对等角”)@腰三角形的顶角平分线、底边b的中线、底边上的髙线互相重合 (三线合一)。

(2)判定：① 有两边相等的三角形是等腰三角形②有两个角相等的三角形是等腰三角形(等角对等边)(3)反证法：先假设令题的结说不成立，然后推导出与已知条件相矛盾的结果命題：由条件和结论组成逆錄：由结轮和条件组成3、等边三角形(1) 定义：的三角形是等边三角形。

(2) 性质：①三个内角都等于60度，三条边都相等②具有等腰三角形的一^性质。

(3) 判定：①三个角都相等的三角形是等边三角形②个角等于6Q度的等瞪三角形是等边三角形。

4、直角三角形(1)定理：在直角三角形中，如果一个锐角是30度，那么它所对的直角边等于斜边的一半。

(2)定理：在直角三角中，斜边上的中线等于斜边的一半(3)直角三角形的两锐角互余。

有两个角互余的三角形是直角三角形(4)勾股定理；直角三角形两条直角垃的平方和等于斜边的平方勾股定理的逆定理：如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形(5) “斜边、直角垃”或“HL”直角三角形全等的判定定理：斜边和一条直角边分别相等的两个直角三角形全等定理的作用：判定两个直角三角形全等5、线段的垂i平分线C1)线段的垂直平分线上的点到送条线段的两个端点的距离相等(2)到一条线段两个端点距离相等的点，在这条线段的垂直平分线上6、角平分线(1)角平分线上的点到送个叫的两边的距离相等(2)在一个角的内部，到角的两边距离相等的点在送个角的平分线上二、考点：考点1等腰三角形的性质1-己知等腰三角形的一个底角为80°，则这个等腰三角形的顶角为( )A. 20°B. 40°C. 50°D. 80 °2.等腰三角形的两条边长分别为5 on和6 cm，则它的周长是3.已知等腰三角形.4BC的腰4B=AC=10 cm，底边BC=12 cm，则八4BC的角平分线AD的长是考点2等腰三角形的判定1.如图15 — 4,在中，ZB = ZC, AB=S,贝［（AC 的长为（）A* 2 B. 3 C. 4 D. 52. 如图15—5，在AABC 中，AB=AC,点£＞，£在忍6：途上，^ABD = ^DAE=^EAC=36a ,则图中共有等腰三角形的个数是（）A. 4B. 5C. 6D. 7考点3等垃三角形的性质1.边长为6 cni的等边三角形中，其一边上高的长度.2.如圈15—6,己知A.4BC是等逊三角形，点B r C, D, E在同一直线上，且CGr = CD, DF=DE,贝度.考点3等边三角形的性质1.边长为6 的等边三角形中，其一边上高的长度.2.如图15—6,已知AABC是等边三角形，点忍，C, D, E在同一直线上，且CG=CD, DF=DE,贝 _____________________________ 度.1.在RtAASC 中，^ACB = 90°、AB = 10, CD 是AB 逊上的中线，贝CD 的长是（）A. 20B. 10C. 5D.-2.在AASC 中，^C=90°，^ABC=60°，SD 平分交AC 于点Z>，若A/> = 6，则CD= .考点5勾股定理及其逆定理1.在RtAABC 中，ZC = 90。

第一章三角形的证明1.1等腰三角形导学案基础知识基本技能1．等腰三角形(1)概念：有两边相等的三角形叫等腰三角形，其中相等的两边叫腰，另一条边叫底边，两腰的夹角叫做顶角，腰与底边的夹角叫做底角．(2)理解：①等腰三角形是特殊的三角形，它具备三角形所有的性质，如内角和是180°，两边之和大于第三边等．②等腰三角形是轴对称图形，这既是等腰三角形的特点也是研究它的重要方法．破疑点等腰三角形有关概念的认识(1)对于等腰三角形问题，我们说角或边时，一般都要指明是顶角还是底角，是底边还是腰，没说明则都有可能，要讨论解决，这是解决等腰三角形最容易忽视和错误的地方；(2)等腰三角形顶角可以是直角，是钝角或锐角，而底角只能是锐角．【例1】等腰三角形两边长分别是5 cm和11 cm，则它的周长是()．A．27 cm B．22 cmC．27 cm或22 cm D．无法确定2．等腰三角形性质1(1)性质1：等腰三角形的两个底角相等(简写成“等边对等角”)．(2)理解：这是等腰三角形的重要性质，它是证明角相等常用的方法，它的应用可省去三角形全等的证明，因而更简便．(3)适用条件：必须在同一个三角形中．(4)应用模式：在△ABC中，因为AB＝AC，所以∠B＝∠C.【例2－1】已知等腰三角形的一个角为40°，则其顶角为()．A．40°B．80°C．40°或100°D．100°哦，不指明是底角还是顶角时，要分类讨论，还要看三角形内角和是否是180°啊！【例2－2】如图，AD、BC相交于O，AB∥CD，OA＝OB，求证：∠C＝∠D.3.等腰三角形性质2(1)性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．习惯上称作等腰三角形“三线合一”性质．(2)含义：这是等腰三角形所特有的性质，它实际上是一组定理，应用过程中，只要是在等腰三角形前提下，知道是其中“一线”，就可以说明是其他的“两线”，性质中包含有线段相等、角相等、垂直等关系，所以应用非常广泛．(3)对称性：等腰三角形是轴对称图形，顶角平分线(或底边上的高、底边上的中线)所在的直线是它的对称轴．(4)应用模式：如图，在△ABC中，解技巧“三线合一”的应用因为题目的证明或计算所求结果大多都是单一的，所以“三线合一”性质实际的应用也是单一的，一般得出一个结论，因此应用要灵活．【例3】如图，在△ABC中，AB＝AC，AD⊥BC，交BC于D，BD＝5 cm，求底边BC的长．分析：因为是等腰三角形，所以底边上的高也是底边上的中线，所以BC＝2BD，即可求出BC的长．4．等腰三角形的判定(1)判定定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等(简写成“等角对等边”)．(2)与性质的关系：判定定理与性质定理是互逆的，性质：→；判定：→.(3)理解：性质和判定应用的前提都是在同一三角形中，并且不经过三角形全等的证明，直接由等边得等角或由等角得等边，所以应用起来更简单、便捷．破疑点等腰三角形的判定方法的理解教材中涉及等腰三角形的判定方法主要有两种：一是判定定理；二是定义．另外还有很多方法，如在同一个三角形中，三线中两线重合，也能说明是等腰三角形．但不常用，一般是通过推理得出角相等或边相等，再得出是等腰三角形．【例4】如图，BE平分∠ABC，交AC于E，过E作DE∥BC，交AB于D.试证明△BDE是等腰三角形．5．等边三角形的概念和性质(1)等边三角形①概念：三边都相等的三角形是等边三角形．②认识：它是特殊的等腰三角形，具备等腰三角形的所有性质．(2)性质：等边三角形的三个内角都相等，并且每一个角都等于60°.(3)拓展：等边三角形是轴对称图形，它有三条对称轴，它三边相等，三个内角相等，各边上的高、中线，对应的角平分线重合，且长度相等．【例5】如图，点M、N分别在等边△ABC的边BC、AC上，且BM＝CN，AM、BN交于点Q.求证：∠BQM＝60°.6．等边三角形的判定(1)判定定理：①三个角都相等的三角形是等边三角形；②有一个角是60°的等腰三角形是等边三角形．(2)判定方法：等边三角形的判定方法有三种：一是定义，另运用两个定理．(3)拓展理解：对于判定定理①，有时候在一个三角形中只要有两个角是60°也可判定是等边三角形．解技巧巧用条件证明等边三角形在证明三角形是等边三角形时，根据所给已知条件确定选择用哪个方法证明．若已知三边关系，一般选定义法；若已知三角关系，一般选判定定理①；若已知该三角形是等腰三角形，则选判定定理②.【例6】如图，等边△ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP＝∠ACQ，BP ＝CQ，问△APQ是什么形状的三角形？试说明你的结论．基本方法基本能力7．等腰三角形性质和判定的综合应用类似于全等三角形的性质和判定的关系，等腰三角形的性质和判定很多时候也是综合运用的．一方面等腰三角形是特殊的三角形，由等腰三角形性质，可以知道许多相等的线段，相等的角，还能知道垂直关系，成倍数关系的线段或角，所以有时通过判定是等腰三角形来证明角相等、线段相等或垂直关系等；另一方面通过等腰三角形性质和判定的运用，直接由线段相等得到角相等，由角相等到线段相等，省去了全等的证明，简化了过程，因此很多时候，等腰三角形性质和判定的应用更广泛．注意：等腰三角形性质和判定的应用前提是在同一个三角形中．【例7】如图1，在△ABC中，∠B＝2∠C，AD是BC边上的高，求证：CD＝AB＋BD.图1 图28.巧用“三线合一”性质解题(1)性质：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合，简称“三线合一”性质；(2)应用：它是等腰三角形特有的性质，这条线段是中线、高，也是角平分线，它包含有线段相等、角相等、垂直等关系，涉及量多，应用广泛，是证明线段相等、线段的倍数关系、角相等、角的倍数关系、垂直等常用的方法．构造“三线合一”解决等腰三角形问题在等腰三角形问题中，最常添加的辅助线就是作底边上的高，或作顶角的平分线，或作底边上的中线，这样就可以由其中一线得到其他两线，从而知道更多的条件，以便更好地完成计算、证明．【例8】已知：如图a所示，△ABC中，AB＝AC，BF是AC边上的高，求证：∠FBC＝∠BAC.图a 图b9.等边三角形的应用等边三角形也称正三角形，它是最特殊的三角形，它除了三边相等，三个内角相等，且每个角都是60°外，还具有很多特殊的性质：如，证明两个等边三角形全等只要有一边相等即可；同一个等边三角形的高、中线、角平分线都相等，并且任何一条高(或中线、顶角的平分线)将等边三角形都分成全等的两个含有30°角的直角三角形；它的高和边长也存在着特殊的比例关系，因此已知是等边三角形，就可以知道其中的许多等量关系．等边三角形的判定也具有自己独特的特点，可以由普通三角形满足条件直接判定，也可以在等腰三角形的基础上进行判定．【例9】(学科内综合题)如下图所示，在等边三角形ABC中，∠B、∠C的角平分线交于点O，OB和OC的垂直平分线分别交BC于E、F，试用你所学的知识说明BE＝EF＝FC的道理．思维拓展创新应用10．面积法证明等腰三角形的性质面积法是解决几何问题常用的一种的方法，它巧妙地运用面积之间的关系，通过计算的方式，求线段的长度，或用来证明线段之间的数量关系，有时它比运用线段之间的等量关系证明、计算更简捷，更巧妙，因而在特定条件下能出奇制胜，是一种很好的方法．面积法的运用，一般以同一个三角形的面积是相等的为基础，运用不同求法，即底不同、高不同、但面积都等于底×高的一半，或将一个图形分解成不同的图形来求面积，但面积之和相等．通过面积相等联系起各量之间的关系，再运用等式的性质，通过化简求出某些线段的长，或计算出某些线段之间的数量(如比例)关系．解技巧巧用面积法证明线段的关系因为直角三角形的特殊性，所以面积法最常用在直角三角形中求斜边上的高，有时也用在等腰三角形中证明线段相等或求线段的和．11．等腰三角形中的“二推一”模式应用在等腰三角形问题中，“等边、角平分线(等角)、平行”是出现最多，最常见的数量与位置关系，若这三个关系出现在同一图中，一般以其中任意两个条件为题设，推导、证明出第三个条件成立，因此我们称它为等腰三角形中的“二推一”．(1)基本图形：等腰三角形中的“二推一”一般有两种情况，一种是角平分线在外，要用到一个外角等于和它不相邻的两内角和；另一种是角平分线在内，基本图形如图①和图②所示，演变图形类型较多，主要有以下几种：(2)方法：通过角相等作为纽带，将线段相等、线段平行联系起来，在此过程中要用到等量代换得出的角相等，方式一般是：→→；→→.【例11-1】如图1，已知，在△ABC中，AB＝AC，BD为腰AC上的高，G为底边BC上任一点，GF⊥AB，GE⊥AC，垂足分别为F、E.求证：GF＋GE＝BD.分析：要证明BD＝GF＋GE，按常规思路将BD分成两段，如图2，证明BH＝GF，DH＝GE.所以过G作BD的垂线，通过证明三角形全等和判定是矩形完成，既复杂又超出现在所学，但用面积法却简单得多．如图3，连接AG，运用面积法，分别表示出△ABG和△ACG的面积，由于同一三角形面积是相等的，所以S△ABC＝S△ABG＋S△ACG，所以AB·GF＋AC·GE＝AC·BD，由于AB ＝AC，经过等量代换和化简即可得到GF＋GE＝BD.【例11-3】如图，已知△ABC中，AC＋BC＝24，AO、BO分别是∠BAC、∠ABC的角平分线，MN过O点，且MN∥BA，分别交AC于N、BC于M，则△CMN的周长为___．【例11-4】如图，△ABC中，∠ABC、∠ACB的平分线BO、CO相交于点O，OE∥AB，OF ∥AC，△OEF的周长＝10，求BC的长．直角三角形学习过程：一、课前准备1.每个命题都是由、两部分组成。

第一章三角形的证明知识点在几何学中，三角形是最基本的图形之一，其性质和证明方法在数学中有着重要的地位。

本章将介绍一些与三角形相关的证明知识点，帮助我们更好地理解三角形的性质和特点。

一、三角形的性质：1. 三角形的定义：三角形是由三条线段组成的图形，这三条线段称为三角形的边，而由这三条边所确定的三个内角则称为三角形的内角。

2. 三角形的分类：根据三角形的边长和角度大小，三角形可以分为三种不同类型：等边三角形、等腰三角形和普通三角形。

- 等边三角形的三条边的长度相等。

- 等腰三角形的两条边的长度相等。

- 普通三角形的三条边的长度各不相等。

3. 三角形的角度和边长关系：- 三角形的内角和等于180度（即∠A + ∠B + ∠C = 180°）。

- 三角形的任意两边之和大于第三边（即 AB + BC > AC，AC+ BC > AB，AB + AC > BC）。

二、三角形的证明知识点：1. 等腰三角形的性质：- 等腰三角形的底角相等，顶角相等。

- 等腰三角形的腰上的高线相等。

证明：设ΔABC 是一个等腰三角形，其中 AB = AC。

连接 A 到三角形的底边 BC，构造垂直于 BC 的高线 AD。

由于 AB = AC，所以∠ABC = ∠ACB。

同时，AD 为高线，所以 AD ⊥ BC，故∠BAC = ∠CAD。

因此，我们可以得出等腰三角形的底角相等并且顶角相等的结论。

同样，由于 AB = AC，所以 AD = AD，即等腰三角形的腰上的高线相等。

2. 直角三角形的性质：- 直角三角形的两条边之间满足勾股定理：c^2 = a^2 + b^2。

- 直角三角形的两条直角边之间满足勾股定理。

证明：设ΔABC 是一个直角三角形，其中∠ABC = 90°。

根据勾股定理，我们可以得出 c^2 = a^2 + b^2。

同时，直角三角形的两条直角边是相互垂直的，即∠ABC = 90°。

A B CD E F 八数下导学案——11 第一章：三角形的证明（知识点复习）一、梳理知识： 1、全等三角形（1）定义： 能够完全 的三角形是全等三角形。

（2）性质：全等三角形的 、 相等。

（3）判定：“SAS ”、 、 、 、 。

2、等腰三角形（1）定义：有两条 的三角形是等腰三角形。

（2）性质：①等腰三角形的 相等。

（“等边对等角”）②等腰三角形的顶角平分线、 、 互相重合。

( ) ③等腰三角形是 图形。

（3）判定：①定义 ②“ ”（4）等边三角形 定义： 的三角形是等边三角形。

性质：①三角都等于 ②具有等腰三角形的一切性质。

判定：①定义 ②有一个角 是等边三角形。

3、直角三角形（1）定义：有一个角是 的三角形是直角三角形。

（2）性质：①“勾股定理” 。

②直角三角形两锐角 。

③直角三角形斜边上的中线等于 。

④在直角三角形中，30°角所对直角边等于 。

（3）判定：①定义 ②两锐角 的三角形是直角三角形③“勾股定理逆定理” 。

4、命题：判断一件事的句子叫命题。

命题有 与 两部分。

互逆命题：在两个命题中，如果一个命题的 是另一个命题的 ，那么这两个命题成为互逆命题，其中一个命题称为另一个命题的 。

5、逆定理：如果一个定理的逆命题是真命题，那么这个逆命题就叫原定理的逆定理． 6、线段的垂直平分线（1）定义： 一条线段的 叫线段的垂直平分线。

（2）性质：①线段垂直平分线上一点 相等。

②三角形三边的垂直平分线 ，且到 相等。

（3）判定：到一条线段两个端点 的点，在这条线段的垂直平分线上。

（4）线段的垂直平分线的作法： 7、角平分线（1）定义： 。

（2）性质：①角平分线上的点 相等。

②三角形的三条角平分线 ，且到 相等。

（3）判定：到角的两边 的点，在这个角的平分线上。

（4）角平分线的作法：二、典型例题： 一、选择题1、到△ABC 的三条边距离相等的点是△ABC 的（ ）A.三边中线的交点B.三条角平分线的交点C.三边上高的交点D.三边中垂线的交点 2、已知等腰三角形的两边长分别为4㎝和2㎝，则其周长是（ ） A. 6㎝ B. 10㎝ C. 10㎝或8㎝ D. 8㎝3、如图，从等腰△ABC 底边BC 上任意一点分别作两腰的平行线DE 、DF ，分别交AC 、AB 于点E 、F ，则□AFDE 的周长等于这个等腰三角形的( )A. 周长B. 周长的一半C. 一条腰长的2倍D. 一条腰长4、如图，△ABC 中，AD ⊥BC 于D ，BE ⊥AC 于E ，AD 与BE 相交于F ，若BF=AC ，则∠ABC 的大小是（ ） A.45° B.50° C.55° D.60°5、如图，在△ＡＢＣ，∠Ｃ＝90°，∠Ｂ＝15°，ＡＢ的中垂线ＤＥ交ＢＣ于Ｄ，Ｅ为垂足，若ＢＤ＝10ｃｍ，则ＡＣ等于（ ） Ａ．10ｃｍ Ｂ．8ｃｍ Ｃ．5ｃｍ Ｄ．2．5ｃｍ 6、等边三角形的高为23，则它的边长为（ ） A.4 B.3 C.2 D.57、下列由线段a 、b 、c 组成的三角形，不是直角三角形的是（ ） A.a =3，b =4，c =5B.a =1，b =34，c =35C.a =9，b =12，c =15D.a =3，b =2，c =58、△ABC 中，∠A ∶∠B ∶∠C =1∶2∶3，最小边BC =4 cm ，最长边AB 的长是（ ） A.5 cm B.6 cm C.5 cm D.8 cm9、如图，已知在△ＡＢＣ中，ＡＢ＝ＡＣ，∠Ｃ＝30°，ＡＢ⊥ＡＤ，ＡＤ＝3ｃｍ，则AC 的长等于（ ）Ａ．22 ｃｍ Ｂ．32 ｃｍ Ｃ．23 ｃｍ Ｄ．33ｃｍ 10、下列定理中逆定理不存在的是（ ） A.同位角相等，两直线平行 B.全等三角形的对应角相等.C.角平分线上的点到这个角的两边距离相等D.在一个三角形中，如果两边相等，那么它们所对的角也相等 11、在Rt △ABC 中,∠C=90° ,D 是BC 边上一点,且BD=AD=10, ∠ADC=60°,求△ABC 的面积.。

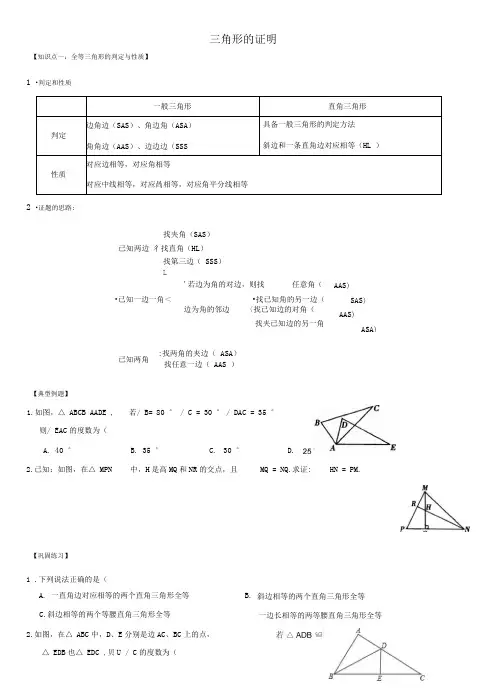
【知识点一：全等三角形的判定与性质】1 •判定和性质一般三角形直角三角形判定边角边（SAS）、角边角（ASA）角角边（AAS）、边边边（SSS具备一般三角形的判定方法斜边和一条直角边对应相等（HL ）性质对应边相等，对应角相等对应中线相等，对应咼相等，对应角平分线相等2 •证题的思路:找夹角（SAS）已知两边彳找直角（HL）找第三边（SSS）L'若边为角的对边，则找任意角（•已知一边一角＜•找已知角的另一边（边为角的邻边〈找已知边的对角（找夹已知边的另一角:找两角的夹边（ASA）找任意一边（AAS ）【典型例题】【巩固练习】1 .下列说法正确的是（三角形的证明AAS)SAS)AAS)ASA)已知两角1.如图，△ ABCB AADE , 若/ B= 80 ° / C = 30 °/ DAC = 35 °则/ EAC的度数为（A. 40 °B. 35 °C. 30 °2.已知：如图，在△ MPN 中，H是高MQ和NR的交点，且MQ = NQ.求证:A. 一直角边对应相等的两个直角三角形全等B. 斜边相等的两个直角三角形全等C.斜边相等的两个等腰直角三角形全等一边长相等的两等腰直角三角形全等2.如图，在△ ABC中，D、E分别是边AC、BC上的点，△ EDB也△ EDC ,贝U / C的度数为（HN = PM.D.A . 0 V xv 3B . x > 3如图，在△ ABC中，BO 平分/ ABC , CO 平分/ ACB , DE10cm , BC 的长为5 cm ,求厶ABC 的周长.3.在△ ABC 中，/ ACB = 90° AC = BC ,直线I 经过顶点C ,过A 、B 两点分别作I 的垂线AE 、BF , E 、F 为垂足.（1）当直线I 不与底边 AB 相交时，求证：EF = AE + BF .③ 等腰三角形两底角的平分线相等，两腰上的高、中线也相等.【典型例题】1 .等腰三角形的两边长分别为3和6 ,则这个等腰三角形的周长为（）C . 12 或 152 .等腰三角形的一个角是80 °则它顶角的度数是（）B . 80。

第一章三角形的证明1．1等腰三角形第1课时全等三角形和等腰三角形的性质1．如图，△ABC≌△BAD.若AB＝6，AC＝4，BC＝5，则AD的长为( ) A．4 B．5C．6 D．以上都不对2．如图，若能用AAS来判定△ACD≌△ABE，则需要添加的条件是( ) A．∠ADC＝∠AEB，∠C＝∠BB．∠ADC＝∠AEB，CD＝BEC．AC＝AB，AD＝AED．AC＝AB，∠C＝∠B3．(2016·成都)如图，△ABC≌△A′B′C′，其中∠A＝36°，∠C′＝24°，则∠B＝．4．(2017·怀化)如图，AC＝DC，BC＝EC，请你添加一个适当的条件：，使得△ABC≌△DEC.5．如图，点B，E，C，F在同一条直线上，AB∥DE，AB＝DE，BE＝CF，AC＝6，则DF＝．6．(2016·宜宾)如图，已知∠CAB＝∠DBA，∠CBD＝∠DAC.求证：BC＝AD.7．(2017·黄冈)已知：如图，∠BAC＝∠DAM，AB＝AN，AD＝AM，求证：∠B＝∠ANM.8．若等腰三角形的顶角为50°，则它的底角度数为( )A．40°B．50°C．60°D．65°9．(2017·平顶山市宝丰县期末)等腰三角形的一边长为4，另一边长为5，则此三角形的周长为( )A．13 B．14 C．15 D．13或14 10．(2017·江西)如图1是一把园林剪刀，把它抽象为图2，其中OA＝OB.若剪刀张开的角为30°，则∠A＝度．第11题第12题11．如图，在△ABC中，AB＝AC，AD⊥BC于点D.若AB＝6，CD＝4，则△ABC的周长是．12．如图，在△ABC中，AD⊥BC，垂足为D，AD＝BD＝CD，则下列结论错误的是( ) A．AB＝AC B．AD平分∠BACC．AB＝BC D．∠BAC＝90°13．(2017·朝阳市建平县期末)若等腰三角形的一个内角等于15°，则这个三角形为( ) A．钝角等腰三角形B．直角等腰三角形C．锐角等腰三角形D．钝角等腰三角形或锐角等腰三角形14．(2016·泰安)如图，在△PAB中，PA＝PB，M，N，K分别是PA，PB，AB上的点，且AM＝BK，BN＝AK.若∠MKN＝44°，则∠P的度数为( )A．44°B．66°C．88°D．92°15．如图，已知点A，F，E，C在同一直线上，AB∥CD，∠ABE＝∠CDF，AF＝CE.(1)从图中任找两组全等三角形；(2)从(1)中任选一组进行证明．第2课时等边三角形的性质1．在△ABC中，AB＝AC，BD，CE分别为边AC，AB上的中线．若BD＝5，则CE＝．2．证明：等腰三角形两腰上的高相等．解：已知：如图，在△ABC中，AB＝AC，CE⊥AB于点E，BD⊥AC于点D.3．如图，△ABC是等边三角形，则∠1＋∠2＝( )A．60°B．90°C．120°D．180°4．(2017·南充)如图，等边△OAB的边长为2，则点B的坐标为( )A．(1，1) B．(3，1)C．(3，3) D．(1，3)5．如图，△ABC为等边三角形，AC∥BD，则∠CBD= ．6．如图，等边△ABC中，AD为高，若AB＝6，则CD的长度为．7．等边△ABC的边长如图所示，则y＝．8．如图，△ABC和△ADE是等边三角形，AD是BC边上的中线．求证：BE＝BD.10．下列说法：①等边三角形的每一个内角都等于60°；②等边三角形三条边上的高都相等；③等腰三角形两底角的平分线相等；④等边三角形任意一边上的高与这条边上的中线互相重合；⑤等腰三角形一腰上的高与这条腰上的中线互相重合．其中正确的有( ) A．1个B．2个C．3个D．4个11．如图，△ABC是等边三角形，AD⊥BC，垂足为D，点E是AC上一点，且AD＝AE，则∠CDE 等于( )A．30°B．20°C．15°D．10°12．如图，已知△ABC是等边三角形，点B，C，D，E在同一直线上，且CG＝CD，DF＝DE，则∠E＝度．13．如图，在等边△ABC中，点D，E分别是边AB，AC的中点，CD，BE交于点O，则∠BOC 的度数是．14．如图，已知等边△ABC纸片，点E在AC边上，点F在AB边上，沿EF折叠，使点A落在BC边上的点D的位置，且ED⊥BC，则∠EFD＝．15．如图，在等边△ABC中，D是BC上的一点，延长AD至E，使AE＝AC，∠BAE的平分线交△ABC的高BF于点O.求∠E的度数．第3课时等腰三角形的判定与反证法1．在△ABC中，已知∠B＝∠C，则( )A．AB＝BC B．AB＝ACC．BC＝AC D．∠A＝60°2．如图，在△ABC中，AD平分外角∠EAC，且AD∥BC，则△ABC一定是( ) A．任意三角形B．等边三角形C．等腰三角形D．直角三角形3．如图，AC，BD相交于点O，∠A＝∠D，如果请你再补充一个条件，使得△BOC是等腰三角形，那么你补充的条件不能是( )A．OA＝OD B．AB＝CDC．∠ABO＝∠DCO D．∠ABC＝∠DCB4．(易错题)下列能判定△ABC为等腰三角形的是( )A．∠A＝30°，∠B＝60°B．∠A＝50°，∠B＝80°C．AB＝AC＝2，BC＝4D．AB＝3，BC＝7，周长为105．如图，已知OC平分∠AOB，CD∥OB.若OD＝3 cm，则CD＝cm.6．如图，在△ABC中，AD⊥BC于D，若添加下列条件中的一个：①BD＝CD；②AD平分∠BAC；③AD＝BD.其中能使△ABC成为等腰三角形的有．7．已知：如图，AB＝BC，DE∥AC，求证：△DBE是等腰三角形．11．(2017·郑州月考)已知，如图，在△ABC中，OB和OC分别平分∠ABC和∠ACB，过O作DE∥BC，分别交AB，AC于点D，E.若BD＋CE＝5，则线段DE的长为( )A．5 B．6 C．7 D．812．已知△ABC中，AB＝AC，求证：∠B＜90°.若用反证法证这个结论，应首先假设．13．如图，在一张长方形纸条上任意画一条截线AB，将纸条沿截线AB折叠，所得到△ABC的形状一定是三角形．14．某轮船由西向东航行，在A处测得小岛P的方位是北偏东70°，又继续航行7海里后，在B 处测得小岛P的方位是北偏东50°，则此时轮船与小岛P的距离BP＝海里．15．(2017·内江)如图，AD平分∠BAC，AD⊥BD，垂足为点D，DE∥AC.求证：△BDE是等腰三角形．16．如图，在等边△ABC中，BD平分∠ABC，延长BC到E，使CE＝CD，连接DE.(1)成逸同学说：BD＝DE，她说得对吗？请你说明理由；(2)小敏同学说：把“BD平分∠ABC”改成其他条件，也能得到同样的结论，你认为应该如何改呢？第4课时等边三角形的判定1．△ABC中，AB＝AC，∠A＝∠C，则△ABC是( )A．等腰三角形B．等边三角形C．不等边三角形D．不能确定2．下列说法不正确的是( )A．有两个角分别为60°的三角形是等边三角形B．顶角为60°的等腰三角形是等边三角形C．底角为60°的等腰三角形是等边三角形D．有一个角为60°的三角形是等边三角形3．如图，在△ABC中，AB＝BC＝6，∠B＝60°，则AC等于( )A．4 B．6 C．8 D．104．如图，将两个完全相同的含有30°角的三角板拼接在一起，则拼接后的△ABD的形状是．5．如图，已知OA＝a，P是射线ON上一动点，∠AON＝60°，当OP＝时，△AOP 为等边三角形．6．如图，点D，E在线段BC上，BD＝CE，∠B＝∠C，∠ADB＝120°，求证：△ADE为等边三角形．7．(2017·平顶山市宝丰县期中)在Rt△ABC中，∠C＝90°，∠A＝30°，BC＝9，则AB＝．8．(2017·郑州月考)如图，∠C＝90°，∠ABC＝75°，∠CDB＝30°.若BC＝3 cm，则AD＝cm.9．如图，这是某超市自动扶梯的示意图，大厅两层之间的距离h＝6.5米，自动扶梯的倾角为30°，若自动扶梯运行速度为v＝0.5米/秒，则顾客乘自动扶梯上一层楼的时间为秒．10．如图，铁路AC与铁路AD相交于车站A，B区在∠CAD的平分线上，且距车站A为20千11．如图，在△ABC中，∠ACB＝90°，∠A＝30°，CD⊥AB于点D，BC＝8 cm，求AD的长．12．在下列三角形中：①三边都相等的三角形；②有一个角是60°且是轴对称图形的三角形；③三个外角(每个顶点处各取1个外角)都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有( )A．①②③B．①②④C．①③D．①②③④13．如图，折叠直角三角形纸片的直角，使点C落在斜边AB上的点E处，已知CD＝1，∠B＝30°，则BD的长是( )A．1 B．2 C. 3 D．2 314．已知∠AOB＝30°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1，O，P2三点所构成的三角形是( )A．直角三角形B．钝角三角形C．等腰三角形D．等边三角形15．如图，已知∠AOB＝60°，点P在边OA上，OP＝12，点M，N在边OB上，PM＝PN.若MN＝2，则OM＝( )A．3 B．4 C．5 D．616．如图，△ABC是等边三角形，D，E，F分别是AB，BC，CA边上一点，且AD＝BE＝CF，则△DEF的形状是．17．如图，在△ABC中，AB＝AC，∠BAC＝120°，AD是BC边的中线，点E，F分别是AB，AC的中点，连接DE，DF.(1)求证：△AED是等边三角形；(2)若AB＝2，则四边形AEDF的周长是．∴△ADE是等边三角形．1．2直角三角形第1课时勾股定理及其逆定理1．在一个直角三角形中，有一个锐角等于60°，则另一个锐角的度数是( ) A．120°B．90°C．60°D．30°2．由下列条件不能判定△ABC是直角三角形的是( )A．∠A＝37°，∠C＝53°B．∠A－∠C＝∠BC．∠A∶∠B∶∠C＝3∶4∶5D．∠A∶∠B∶∠C＝2∶3∶53．(2017·安徽)直角三角板和直尺如图放置．若∠1＝20°，则∠2的度数为( )A．60°B．50°C．40°D．30°4．(2017·西安期中)下列各组数中，以它们为边长的线段能构成直角三角形的是( ) A．2，4，5 B．6，8，11C．5，12，12 D．1，1， 25．如图，点D在△ABC的边AC上，将△ABC沿BD翻折后，点A恰好与点C重合．若BC＝5，CD＝3，则BD的长为( )A．1 B．2 C．3 D．46．(2017·阿坝)直角三角形斜边长是5，一直角边的长是3，则此直角三角形的面积为6．7．(2017·成都)如图，数轴上点A表示的实数是．8．如图，在四边形ABCD中，AB＝3，BC＝4，CD＝12，AD＝13，AC⊥CD，求四边形ABCD 的面积．9．下列命题中，其逆命题成立的是 ．(只填写序号) ①同旁内角互补，两直线平行；②如果两个角是直角，那么它们相等；③如果两个实数相等，那么它们的平方相等；④如果三角形的三边长a ，b ，c(c 为最长边)满足a 2＋b 2＝c 2，那么这个三角形是直角三角形． 10．写出下列命题的逆命题，并判断它们是真命题还是假命题． (1)两直线平行，同位角相等；(2)如果a 是偶数，b 是偶数，那么a ＋b 是偶数． 11．已知下列命题： ①若a ＋b ＝0，则|a|＝|b|；②等边三角形的三个内角都相等；③底角相等的两个等腰三角形全等．其中原命题与逆命题均为真命题的个数是( )A ．1个B ．2个C ．3个D ．4个12．如图，正方形网格中的△ABC ，若小方格边长为1，则△ABC 的形状为( )A ．直角三角形B ．锐角三角形C ．钝角三角形D ．以上答案都不对13．(2017·陕西)如图，将两个大小、形状完全相同的△ABC 和△A ′B ′C ′拼在一起，其中点A′与点A 重合，点C′落在边AB 上，连接B′C.若∠ACB ＝∠AC ′B ′＝90°，AC ＝BC ＝3，则B′C 的长为( )A ．3 3B ．6C ．3 2 D.21 14．(2017·平顶山市宝丰县期中)如图，在△ABC 中，∠A ＝45°，∠B ＝30°，CD ⊥AB ，垂足为D ，CD ＝1，则AB 的长为( )A ．2B ．2 3 C.33＋1 D.3＋1 15．在△ABC 中，AB ＝10，AC ＝210，BC 边上的高AD ＝6，则另一边BC 等于( )A ．10B ．8C ．6或10D ．8或1016．如图，圆柱形容器高为18 cm ，底面周长为24 cm ，在杯内壁离杯底4 cm 的点B 处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2 cm 与蜂蜜相对的点A 处，则蚂蚁从外壁A 处到达内壁B 处的最短距离为 cm.第2课时直角三角形全等的判定1．如图，点P是∠BAC内一点，PE⊥AC于点E，PF⊥AB于点F，PE＝PF，则直接得到△PEA≌△PFA的理由是( )A．HL B．ASAC．AAS D．SAS2．如图，已知AD是△ABC的边BC上的高，下列能使△ABD≌△ACD的条件是( ) A．AB＝AC B．∠BAC＝90°C．BD＝AC D．∠B＝45°3．如图，∠B＝∠D＝90°，BC＝CD，∠1＝40°，则∠2＝( )A．40°B．50°C．60°D．75°4．如图，点D，A，E在直线l上，AB＝AC，BD⊥l于点D，CE⊥l于点E，且BD＝AE.若BD ＝3，CE＝5，则DE＝．5．如图所示，AD⊥BE于点C，C是BE的中点，AB＝DE，求证：AB∥DE.6．(2017·平顶山市宝丰县期中)下列条件不能判断两个直角三角形全等的是( ) A．两条直角边分别对应相等B．斜边和一个锐角分别对应相等C．两个锐角对应相等D．斜边和一直角边分别对应相等7．如图，AC⊥BC，AD⊥DB，要使△ABC≌△BAD，还需添加条件：．(只需写出一种情况)8．如图，在Rt△ABC中，∠ABC＝90°，点D在边AB上，使DB＝BC，过点D作EF⊥AC，分别交AC于点E，交CB的延长线于点F.求证：AB＝BF.9．如图，点C是路段AB的中点，小明和小红两人从C同时出发，以相同的速度分别沿两条直线行走，并同时到达D，E两地，并且DA⊥AB于A，EB⊥AB于B.此时小明到路段AB的距离是50米，则小红到路段AB的距离是多少米？10．已知在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝4，则下列图中的直角三角形与Rt△ABC 全等的是( )11．如图，在△ABC中，AB＝AC，BD⊥AC于点D，CE⊥AB于点E，BD和CE交于点O，AO 的延长线交BC于点F，则图中全等的直角三角形有( )A．3对B．4对C．5对D．6对12．如图所示，过正方形ABCD的顶点B作直线a，过点A，C作a的垂线，垂足分别为点E，F.若AE＝1，CF＝3，则AB的长度为．13．如图，在Rt△ABC中，∠C＝90°，AC＝10，BC＝5，线段PQ＝AB，P，Q两点分别在AC 和过点A且垂直于AC的射线AO上运动，当AP＝时，△ABC和△PQA全等．14．如图，在△ABC中，AB＝CB，∠ABC＝90°，F为AB延长线上一点，点E在BC上，且AE＝CF.(1)求证：Rt△ABE≌Rt△CBF；(2)若∠CAE＝30°，求∠ACF的度数．15．如图1，E，F分别为线段AC上的两个动点，且DE⊥AC于E，BF⊥AC于F，若AB＝CD，BF＝DE，BD交AC于点M.(1)求证：AE＝CF，MB＝MD；(2)当E，F两点移动到如图2的位置时，其余条件不变，上述结论能否成立？若成立，请给予证明；若不成立，请说明理由．1.3线段的垂直平分线第1课时线段垂直平分线的性质定理及其逆定理1．如图，直线CD是线段AB的垂直平分线，P为直线CD上的一点，已知线段PA＝3 cm，则线段PB的长为( )A．6 cm B．5 cm C．4 cm D．3 cm2．如图，AB是CD的垂直平分线，若AC＝2.3 cm，BD＝1.6 cm，则四边形ACBD的周长是( ) A．3.9 cm B．7.8 cm C．4 cm D．4.6 cm3．如图，在四边形ABCD中，AC垂直平分BD，垂足为E，下列结论不一定成立的是( ) A．AB＝AD B．AC平分∠BCDC．AB＝BD D．△BEC≌△DEC4．(2017·西安期中)如图所示，线段AC的垂直平分线交线段AB于点D，∠A＝50°，则∠BDC ＝( )A．50°B．100°C．120°D．130°5．如图，在△ABC中，∠B＝30°，ED垂直平分BC，ED＝3，则CE的长为．6．如图，在Rt△ABC中，∠C＝90°，AB边的垂直平分线DE交BC于点E，垂足为D.求证：∠CAB＝∠AED.7．如图，AC＝AD，BC＝BD，则有( )A．AB垂直平分CDB．CD垂直平分ABC．AB与CD互相垂直平分D．CD平分∠ACB8．如图，D是△ABC的边BC的延长线上一点，且BD＝BC＋AC，则点C在线段的垂直平分线上．9．如图，在△ABC 中，∠C ＝90°，∠A ＝30°，BD 平分∠ABC 交AC 于点D.求证：点D 在AB 的垂直平分线上．10．平面直角坐标系中，已知A(－1，3)，B(－1，－1)．下列四个点中，在线段AB 的垂直平分线上的点是( )A ．(0，2)B ．(－3，1)C ．(1，2)D ．(1，0)11．下列说法：①若直线PE 是线段AB 的垂直平分线，则EA ＝EB ；②若PA ＝PB ，EA ＝EB ，则直线PE 是线段AB 的垂直平分线；③若EA ＝EB ，则直线EP 是线段AB 的垂直平分线；④若PA ＝PB ，则点P 在线段AB 的垂直平分线上．其中正确的有( )A ．1个B ．2个C ．3个D ．4个 12．如图，在Rt △ABC 中，∠B ＝90°，分别以A ，C 为圆心，大于12AC 长为半径画弧，两弧相交于点M ，N ，连接MN ，与AC ，BC 分别交于点D ，E ，连接AE ，则：(1)∠ADE ＝ ；(2)AE EC ；(填“＝”“＞”或“＜”)(3)当AB ＝3，AC ＝5时，△ABE 的周长＝ ．13．如图，AD ⊥BC 于点D ，D 为BC 的中点，连接AB ，∠ABC 的平分线交AD 于点O ，连接OC.若∠AOC ＝125°，则∠ABC ＝ ．14．如图，在Rt △ABC 中，∠BAC ＝90°，AD ⊥BC 于点D ，将AB 边沿AD 折叠，发现B 点的对应点E 正好在AC 的垂直平分线上，则∠C ＝ ．15．(2017·朝阳市建平县期中)如图，Rt △ABC 中，∠ACB ＝90°，BC ＝3，AC ＝4，AB 的垂直平分线DE 交BC 的延长线于点E ，则CE 的长为 ．16．如图，在△ABC中，∠ACB＝90°，D是BC延长线上一点，E是BD垂直平分线与AB的交点，DE交AC于点F.求证：点E在AF的垂直平分线上．17．(1)如图，在△ABC中，AB＝AC，AB的垂直平分线交AB于点N，交直线BC于点M，∠A ＝40°，求∠NMB的大小；(2)如果将(1)中的∠A的度数改为70°，其余条件不变，再求∠NMB的大小；(3)你发现了什么样的规律？试证明；(4)将(1)中的∠A改为钝角，对这个问题的规律性认识是否需要修改．第2课时三角形三边的垂直平分线1．三角形纸片ABC上有一点P，量得PA＝3 cm，PB＝3 cm，则点P一定( ) A．是边AB的中点B．在边AB的中线上C．在边AB的高上D．在边AB的垂直平分线上2．(2017·郑州期末)在三角形的内部，有一个点到三角形三个顶点的距离相等，则这个点一定是三角形( )A．三条中线的交点B．三条角平分线的交点C．三条边的垂直平分线的交点D．三条高的交点3．如图，∠BAC＝110°，若MP和NQ分别垂直平分AB和AC，则∠PAQ的度数是( ) A．20°B．40°C．50°D．60°4.△ABC中，AB，AC的垂直平分线相交于点P，那么P点必定在BC的，且PA＝＝．5.如图，O为△ABC三边垂直平分线的交点，点O到顶点A的距离为5 cm，则AO＋BO＋CO＝．6．如图，在△ABC中，∠B＝32°，∠C＝48°，AB和AC的垂直平分线分别交BC于点D，E，BC＝6 cm，请计算出∠DAE的度数和△ADE的周长．7．在同一平面内，过直线上一点作已知直线的垂线，能作( )A．1条B．2条C．3条D．无数条8．下列作图语句正确的是( )A．过点P作线段AB的中垂线B．在线段AB的延长线上取一点C，使AB＝ACC．过直线a和直线b外一点P作直线MN，使MN∥a∥b9．如图，已知线段a，h，作等腰△ABC，使AB＝AC，且BC＝a，BC边上的高AD＝h.张红的作法是：①作线段BC＝a；②作线段BC的垂直平分线MN，MN与BC相交于点D；③在直线MN上截取线段h；④连接AB，AC，则△ABC为所求的等腰三角形．上述作法的四个步骤中，你认为有错误的一步是( )A．①B．②C．③D．④10．为了推进农村新型合作医疗制度改革，准备在某镇新建一个医疗点P，使P到该镇A村，B 村，C村所属的村委会所在地的距离都相等(A，B，C不在同一直线上，地理位置如图)，请你用尺规作图的方法确定点P的位置．要求：写出已知、求作；不写作法，保留作图痕迹．11．在平面内，到三点A，B，C距离相等的点( )A．只有一个B．有两个C．有三个或三个以上D．有一个或没有12．等腰三角形的底角为40°，两腰的垂直平分线交于点P，则( )A．点P在三角形内B．点P在三角形外C．点P在三角形底边上D．点P的位置与三角形的边长有关13．(2017·西安期中)如图，已知点O为△ABC三边垂直平分线的交点，∠BAC＝80°，则∠BOC ＝.14．如图所示，在△ABC中，∠BAC＝76°，EF，MN分别是AB，AC的垂直平分线，点E，M 在BC上，则∠EAM＝．15．如图，由于水资源缺乏，B，C两地不得不从黄河上的扬水站A引水，这就需要A，B，C之间铺设地下输水管道，有人设计了三种铺设方案：如图①②③，图中实线表示管道铺设线路，在图②中，AD垂直BC于点D；在图③中，OA＝OB＝OC.为减少渗漏，节约水资源，并降低工程造价，铺设线路应尽量缩短，已知△ABC恰好是一个边长为a的等边三角形，那么通过计算，你认为最好的铺设方案是方案．1．4角平分线第1课时角平分线的性质定理及其逆定理1．(2017·台州)如图，点P是∠AOB平分线OC上一点，PD⊥OB，垂足为D.若PD＝2，则点P到边OA的距离是( )A．2 B．3 C. 3 D．42．下列各图中，OP是∠MON的平分线，点E，F，G分别在射线OM，ON，OP上，则可以解释定理“角平分线上的点到角的两边的距离相等”的图形是( )3．(2016·怀化)如图，OP为∠AOB的平分线，PC⊥OA，PD⊥OB，垂足分别是C，D，则下列结论错误的是( )A．PC＝PD B．∠CPO＝∠DOP C．∠CPO＝∠DPO D．OC＝OD4．如图，∠AOC＝∠BOC，点P在OC上，PD⊥OA于点D，PE⊥OB于点E.若OD＝8，OP＝10，则PE的长为( )A．5 B．6 C．7 D．85．如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点．若PA＝2，则PQ的最小值为( )A．1 B．2 C．3 D．46．(2017·西安期中)在Rt△ABC中，∠C＝90°，AD平分∠BAC，AD＝5，AC＝4，则D点到AB的距离是．7．如图，在Rt△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于点E，若AC＝6，BC＝8，CD＝3.(1)求DE的长；(2)求△ADB的面积．小专题(一)等腰三角形中常见的数学思想类型1方程思想1．如图，在△ABC中，AB＝AC，BC＝BD＝ED＝EA，求∠A的度数．类型2分类讨论思想2．如图，在Rt△ABC中，∠ACB＝90°，AB＝2BC，在直线BC或AC上取一点P，使得△PAB 为等腰三角形，则符合条件在点P共有( )A．7个B．6个C．5个D．4个3．若实数x，y满足|x－5|＋y－10＝0，则以x，y的值为边长的等腰三角形的周长为．4．如图，∠BOC＝60°，点A是BO延长线上的一点，OA＝10 cm，动点P从点A出发沿AB 以2 cm/s的速度移动，动点Q从点O出发沿OC以1 cm/s的速度移动．如果点P，Q同时出发，用t(s)表示移动的时间，当t＝时，△POQ是等腰三角形．5．已知O为等边△ABD的边BD的中点，AB＝4，E，F分别为射线AB，DA上一动点，且∠EOF ＝120°，若AF＝1，求BE的长．章末复习(一)三角形的证明知识点1三角形全等1．如图，△ABC≌△BAD，A和B，C和D是对应顶点．如果AB＝5，BD＝6，AD＝4，那么BC等于( )A．4 B．6C．5 D．无法确定2．(2017·黔东南)如图，点B，F，C，E在一条直线上，已知FB＝CE，AC∥DF，请你添加一个适当的条件，使得△ABC≌△DEF.知识点2等腰三角形3．(2016·赤峰)等腰三角形有一个角是90°，则另两个角分别是( )A．30°，60°B．45°，45°C．45°，90°D．20°，70°4．如图，在△ABC中，AB＝AC，D为BC中点，∠BAD＝35°，则∠C的度数为．5．如图，△ABC是等边三角形，BD平分∠ABC，点E在BC的延长线上，且CE＝1，∠E＝30°，则DC＝．知识点3直角三角形6．如图，BD平分∠ABC，CD⊥BD，D为垂足，∠C＝55°，则∠ABC的度数是( )A．35°B．55°C．60°D．70°7．如图，在△ABC中，∠C＝90°，AC＝2，点D在BC上，∠ADC＝2∠B，AD＝5，则BC 的长为( )A.3－1B.3＋1C.5－1D.5＋18．如图，BE，CD是△ABC的高，且BD＝EC，判定△BCD≌△CBE的依据是“”．知识点4线段的垂直平分线和角平分线9．(2017·西安期中)如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，AB的垂直平分线交BC 于点D，连接AD，则△ACD的周长是( )A．7 B．8 C．9 D．1010．如图所示，在△ABC中，∠C＝90°，AB＝8，AD是△ABC的一条角平分线．若CD＝2，则△ABD的面积为．11．如图，在△ABC中，BD是∠ABC的平分线，EF垂直平分BD.求证：∠ABD＝∠BDF.12．在△ABC中，∠B＝∠C，与△ABC全等的三角形有一个角是100°，那么在△ABC中与这100°角对应相等的角是( )A．∠A B．∠BC．∠C D．∠B或∠C13．如图，在单位正方形组成的网格图中标有AB，CD，EF，GH四条线段，其中能构成一个直角三角形三边的线段是( )A．CD，EF，GH B．AB，EF，GHC．AB，CD，EF D．AB，CD，GH14．(2016·枣庄)如图，在△ABC中，AB＝AC，∠A＝30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为( )A．15°B．17.5°C．20°D．22.5°15．如图，在△ABC中，AB＝AC＝5，BC＝8，D是线段BC上的动点(不含端点B，C)．若线段AD的长为正整数，则点D的个数共有( )A．5个B．4个C．3个D．2个16．如图，四边形ABCD中，AB＝AD，∠BAD＝90°，∠CBD＝30°，∠BCD＝45°.若AB＝22，则四边形ABCD的面积为．17．如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE，BE，BE⊥AE，延长AE 交BC的延长线于点F.求证：(1)FC＝AD；(2)AB＝BC＋AD.18．如图，在△ABC中，AD平分∠BAC，且BD＝CD，DE⊥AB于点E，DF⊥AC于点F.(1)求证：AB＝AC；(2)若DC＝4，∠DAC＝30°，求AD的长．周周练(1.1～1.2)(时间：45分钟满分：100分)一、选择题(每小题4分，共32分)1．如图，在△ABC中，AB＝AC，∠B＝65°，则∠A的度数是(C)A．70°B．55°C．50°D．40°2．若△ABC是直角三角形，且∠C＝90°，则必有(D)A．∠A＝2∠B＝3∠CB．∠A＝∠B＝∠CC．∠A＝∠B＋∠CD．∠A＋∠B＝∠C3．下列命题的逆命题不正确的是(D)A．若a2＝b2，则a＝bB．两直线平行，内错角相等C．等腰三角形的两个底角相等D．对顶角相等4．如图，△ABC中，AB＝AC，D是BC中点，下列结论中不正确的是(D) A．∠B＝∠C B．AD⊥BCC．AD平分∠BAC D．AB＝2BD5．(2017·平顶山市宝丰县期中)若等边三角形的一条高为3，其边长为(A)A．2 B．1 C．3 D．46．(2017·陕西西北大学附属学校期中)如图，△ABC中，AC＝3，∠C＝90°，∠B＝30°，点P 是BC边上的动点，则AP的长不可能是(D)A．3.5 B．4.2 C．5.8 D．77．(2017·西安期中)如图，在△ABC中，∠A＝36°，AB＝AC，BD是△ABC的角平分线．若在边AB上截取BE＝BC，连接DE，则图中等腰三角形共有(D)A．2个B．3个C．4个D．5个的垂线，两线相交于点D，连接AD.若AB＝3，DC＝4，则AD的长是(C)A．5 B．7 C．5 2 D．无法确定二、填空题(每小题4分，共24分)9．如图，在△ABC和△DFE中，∠A＝∠D＝90°，AC＝DE，若要用“斜边、直角边(HL)”直接证明Rt△ABC≌Rt△DFE，则还需补充条件答案不唯一，如：BC＝FE．10．在证明命题“一个三角形中至少有一个内角不大于60°”成立时，我们利用反证法，先假设三角形的三个内角都大于60°，则可推出三个内角之和大于180°，这与三角形内角和定理相矛盾．11．如图，在△ABC中，已知∠1＝∠2，BE＝CD，AB＝5，AE＝2，则CE＝3．12．如图，在高3米，坡面线段距离AB 为5米的楼梯表面铺地毯，则地毯长度至少需7米．13．如图，△ABC 和△DCE 都是边长为4的等边三角形，点B ，C ，E 在同一条直线上，连接BD ，则BD 的长为14．在平面直角坐标系中，点A ，B 的坐标分别为A(3，0)，B(8，0)，若点P 在y 轴上，且△PAB 是等腰三角形，则点P 的坐标为(0，4)或(0，－4)．三、解答题(共44分) 15．(8分)(2017·平顶山市宝丰县期中)如图，在△ABC 和△DCB 中，∠A ＝∠D ＝90°，AC ＝BD ，AC 与BD 相交于点O.(1)求证：△ABC ≌△DCB ；(2)△OBC 是何种三角形？证明你的结论．解：(1)证明：∵在△ABC 和△DCB 中，∠A ＝∠D ＝90°， ∴△ABC 和△DCB 都为直角三角形．在Rt △ABC 和Rt △DCB 中，⎩⎨⎧AC ＝DB ，BC ＝CB ，∴Rt △ABC ≌Rt △DCB(HL)． (2)△OBC 是等腰三角形．证明：∵Rt △ABC ≌Rt △DCB ，∴∠ACB ＝∠DBC. ∴OB ＝OC.∴△OBC 是等腰三角形．16．(10分)(2017·苏州)如图，∠A ＝∠B ，AE ＝BE ，点D 在AC 边上，∠1＝∠2，AE 和BD 相交于点O.(1)求证：△AEC ≌△BED ；(2)若∠1＝42°，求∠BDE 的度数．解：(1)证明：∵AE 和BD 相交于点O ， ∴∠AOD ＝∠BOE. ∵∠A ＝∠B ， ∴∠BEO ＝∠2. 又∵∠1＝∠2，∴∠1＝∠BEO.∴∠1＋∠AED ＝∠BEO ＋∠AED ，即∠AEC ＝∠BED. 在△AEC 和△BED 中，⎩⎨⎧∠A ＝∠B ，AE ＝BE ，∠AEC ＝∠BED ，∴△AEC ≌△BED(ASA)． (2)∵△AEC ≌△BED ， ∴EC ＝ED ，∠C ＝∠BDE. 在△EDC 中，∵EC ＝ED ，∠1＝42°，∴∠C ＝∠EDC ＝69°. ∴∠BDE ＝∠C ＝69°.17．(12分)如图，已知A ，B ，C ，D 四个城镇(除B ，C 外)都有笔直的公路相接，公共汽车行驶于城镇之间，公共汽车票价与路程成正比，已知各城镇间公共汽车票价如下：为了B ，C 间的交通方便，打算在B ，C 之间建一条笔直公路，请按上述标准预算出B ，C 之间的公共汽车票价．解：AD 为16，AB 为20，BD 为12，∵122＋162＝202， ∴∠ADB ＝90°.∵AC ＝25，AD ＝16，CD ＝9，即AC ＝AD ＋DC ，∴A，D，C三个点在一条直线上，可知∠BDC＝90°.又∵BD＝12，DC＝9，∴BC＝122＋92＝15.故B，C之间的公共汽车票价为15元．18．(14分)如图，在等边△ABC中，∠ABC与∠ACB的平分线相交于点O，且OD∥AB，OE∥AC.(1)求证：△ODE是等边三角形；(2)线段BD，DE，EC三者有什么数量关系？写出你的判断过程；(3)数学学习不但要能解决问题，还要善于提出问题．结合本题，在现有的图形上，请提出两个与“直角三角形”有关的问题．(只要提出问题，不需要解答)解：(1)证明：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°.∵OD∥AB，OE∥AC，∴∠ODE＝∠ABC＝60°，∠OED＝∠ACB＝60°.∴△ODE是等边三角形．(2)BD＝DE＝EC.理由：∵OB平分∠ABC，且∠ABC＝60°，∴∠ABO＝∠OBD＝30°.∵OD∥AB，∴∠BOD＝∠ABO＝30°.∴∠OBD＝∠BOD.∴DB＝DO.同理，EC＝EO.由(1)知，△ODE是等边三角形，∴DE＝OD＝OE.∴BD＝DE＝EC.(3)答案不唯一，如：①连接AO，并延长交BC于点F，求证：△ABF是直角三角形；②若等边△ABC的边长为1，求BC边上的高．。

第一章 三角形的证明1、 等腰三角形一、主要知识点1、 进一步巩固全等的判定和性质。

2、 等腰三角形的性质：（1）底角相等；（2）三线合一；拓展（学生可以自己证明）（3）两底角的平分线相等；（4）两腰上的中线相等；（5）两腰上的高相等；…… 3、 等边三角形的性质（1）边 ；（2）角 ；（3）对称性；对称轴。

4、 等腰三角形的判定：(1)定义；（2）等角对等边；等边三角形的判定：（1）三个角都相等的三角形；（2）有一个角等于60°的等腰三角形； 5、6、 反证法证明命题的一般步骤：（1）假设；（2）推理，得出与已知、定理、基本事实或定理相矛盾的结论；（3）否定假设；（4）肯定原命题。

7、 含30°的直角三角形，30°所对的直角边等于斜边的一半。

二、基本知识技能巩固与应用1、 如图1.1，AB=AE ，∠1=∠2，∠C=∠D ，求证：BC=DE2、 如图1.2，AB=AC ，点D 、E 在BC 上，且AD=AE ，求证：∠BAD=∠CAE.3、 如图1.3，D 、E 分别是等边△ABC 的边AB 、BC 上的点，且AD=BE ，求证：△AEC ≌△CDB4、 如图1,5，△ABC 中，AB=AC ，E 是CA 延长线上的点，EG ⊥BC于G ，交AB 于F ，求证：△AEF 是等腰三角形。

5、 求证，一个三角形中至少有一个内角不小于60°。

6、 如图1.6，△ABC 中，D 是AB 上的点， AD=DB=CD ，∠B=30°。

求证：（1）△ACD 是等边三角形。

；（2）∠ACB=90°（没有∠B=30°的条件，∠ACB=90°的结论是否成立？）7、 证明：在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于30°。

8、 如图1.7，在△ABC 中，∠A : ∠Ｂ: ∠ACB=1: 2: 3，求证：AB=4BD9、 如图1.8，已知等边△ABC ，BD ⊥AC 于D ，延长BC 到E ，使CE=CD=1，连接DE,求：DE 长ABC D E 1.1图1 2 A B CD E 1.2图三、深度拓展1、如图1，△ABC中，AB=AC, D在BC上，且BD=AD，DC=爱吃，则：∠Ｂ= 度2、如图2，△ABC中，BC=8，BP,CP分别是∠ABP，∠ACP的平分线，PD∥AB，PE∥AC.则△PDE的周长等于。

三角形的证明知识点超详细一、全等三角形的证明。

1. 全等三角形的性质。

- 全等三角形的对应边相等。

例如，若ABC≅ DEF，则AB = DE，BC=EF，AC = DF。

- 全等三角形的对应角相等。

即∠ A=∠ D，∠ B=∠ E，∠ C=∠ F。

2. 全等三角形的判定方法。

- SSS（边边边）- 内容：三边对应相等的两个三角形全等。

- 示例：在ABC和DEF中，若AB = DE，BC = EF，AC=DF，则ABC≅DEF。

- SAS（边角边）- 内容：两边和它们的夹角对应相等的两个三角形全等。

- 示例：在ABC和DEF中，若AB = DE，∠ B=∠ E，BC = EF，则ABC≅DEF。

- ASA（角边角）- 内容：两角和它们的夹边对应相等的两个三角形全等。

- 示例：在ABC和DEF中，若∠ A=∠ D，AB = DE，∠ B=∠ E，则ABC≅ DEF。

- AAS（角角边）- 内容：两角和其中一角的对边对应相等的两个三角形全等。

- 示例：在ABC和DEF中，若∠ A=∠ D，∠ B=∠ E，BC = EF，则ABC≅ DEF。

- HL（斜边、直角边）（适用于直角三角形）- 内容：斜边和一条直角边对应相等的两个直角三角形全等。

- 示例：在Rt ABC和Rt DEF中，若AB = DE（斜边），AC = DF（直角边），则Rt ABC≅ Rt DEF。

二、等腰三角形的证明与性质。

1. 等腰三角形的性质。

- 等腰三角形的两腰相等。

例如，在ABC中，若AB = AC，则ABC是等腰三角形。

- 等腰三角形的两底角相等（等边对等角）。

即若AB = AC，则∠ B=∠ C。

- 等腰三角形三线合一：等腰三角形底边上的高、底边上的中线、顶角平分线互相重合。

例如，在等腰ABC（AB = AC）中，AD是底边BC上的高，则AD也是BC边上的中线和∠ BAC的平分线。

2. 等腰三角形的判定。

- 定义法：有两边相等的三角形是等腰三角形。

第一章三角形的证明一．全等三角形相关1.性质：全等三角形的对应边，对应角。

2.判定定理及推论（1）；（2）；（3）；（4）；（5）。

二．等腰三角形1.定义：。

2.性质（1）定理：等腰三角形的两个底角相等。

简称（“”）几何语言：（2）推论：三线合一几何语言：——————————————————————————————————————————————————————————3.判定：（1）定义（2）定理：有两个角相等的三角形是等腰三角开。

简称（“”）三．等边三角形1.定义：三条边都相等的三角形是等边三角形。

2.性质：（1）边：；（2）角：；（3）三线合一：。

3.判定（1）定义：（2）三个角都相等的三角形是等边三角形；（3）有一个角是 60 度的等腰三角形是等边三角形。

四，直角三角形1.定义：有一个角是 90 度的三角形叫做直角三角形。

2.表示：3.性质：（1）角：；（2）边：勾股定理（3）定理：在直角三角形中，如果有一个锐角等于30 度，那么它所对的直角边等于斜边的一半。

（4）在直角三角形中，斜边上的中线等于斜边的一半。

4.判定（1）定义：（2）定理：有两个角互余的三角形是直角三角形。

（3）勾股定理的逆定理：如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形。

五．线段的垂直平分线1.性质定理：线段垂直平分线上的点到这条线段两端点的距离相等。

几何语言：2.判定定理：到一条线段两端点距离相等的点，在这条线段的垂直平分线上。

几何语言：3.尺规作图（1）已知底边和底边上的高作等腰三角形；（2）过直线上一点作直线的垂线；（3）过直线外一点作直线的垂线；六．角平分线1.性质定理：角平分线上的点到这个角两边的距离相等。

几何语言：2.判定定理：在一个角的内部，到角两边距离相等的点在这个角的角平分线上。

几何语言：。