当前位置：文档之家 › 理论力学第二章

理论力学第二章

  • 格式：docx
  • 大小：579.08 KB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

理论力学第二章

理论力学第二章
1 1 1 3
M F d F d
2 2 2 4
F F F
3
4
F F F
3 4
3 4 3 4 1 2
M Fd F F d F d F d M M
平面内任意力偶可以合成一个合力偶，该合力偶系的平衡条件
尾相接，合力沿反方向构成封闭边。
二.平面汇交力系平衡的几何条件
平面汇交力系平衡的充要条件：

Fi 0

平面汇交力系平衡的几何条件：该力系各分力组成的力多边形自行封闭
例2.1 已知AC=CB，P=10kN，求铰链A的约束力和杆DC所受的力。支架
的横梁AB与斜杆DC以铰链C相连，并以铰链A、D连接于铅直墙上。杆DC
三.平面汇交力系合成的解析法
1.力在坐标轴上的投影与力沿轴的分解
FR=FRx+FRy=FRxi+FRy j
2.合矢量投影定理
合矢量投影定理：合力在某一轴上的投影，等于各分力在
同一轴上投影的代数和。
即：FRx=Fx1+Fx2+…+Fxn =∑Fx FRy=Fy1+Fy2+…+Fyn =∑Fy
3.平面汇交力系合成的解析法
2、力偶矩
力偶中两力所在平面称为力偶作用面. 力偶两力之间的垂直距离称为力偶臂.
两个要素 a.大小：力与力偶臂乘积
b.方向：转动方向
力偶矩：M=±Fd=±2A△ABC，代数量， 逆为正，顺为负。单位：N· m，或kN· m
力偶不能合成为一个力，或用一个力来等效替换； 力偶也不能用一个力来平衡。
四.同平面内力偶的等效定理
ix

例2.4 图示踏板，各杆自重不计，已知：F、α、l、B点坐标 (xB、yB)。求(1)力F对A点之矩；(2)平衡时杆CD的拉力。

理论力学第二章.

理论力学第二章.

(a)
(b) 图2.1 力多边形
(c)
3
从图2—1b可见，在合成该平面汇交力的合力时，也可不必将中间力矢量
FR1 、 FR 2 一一求出。只需从力 F1 的终点B作出与力 F2 相等的矢量 BC ，再从
BC 的终点C作出一个与力 F3相等的矢量 CD ，最后从CD 的终点D作出一个与 F4 力相等的矢量力相等的矢量 DE 。连接 F1 的始点A与最后一个矢量的终点
FR F1 F2 Fn Fi
（2-1）
三、平面汇交力学平衡的几何条件
当力多边形自行闭合，即合力 FR 0，于是平面汇交力系平衡；反之，若平面汇 交力系平衡，即合力 FR 0。所以，平面汇交力系平衡的充分必要条件是：力多边形 自行闭合，或平面汇交力系的合力等于0，即
例2.1 AC和BC两杆用铰链C连接，两杆的另一端分别铰支在墙上，如 图2-2(a)示。在点C悬挂重10kN的物体，已知AB=AC=2m,BC=1m,如杆重 不计，求两杆所受的力。 解（1）取销钉C为研究对象； （2）画销钉C的受力图，如图2-2（b)示； （3）作封闭力三角形，如图2-2(c)示。 由于封闭的力三角形与三角形ABC相似，故
所以
F=11.5kN , NB=23.1kN
由作用力和反作用力的关系，碾子对障碍物的压力等于 23.1kN。
此题也可用力多边形方法用比例尺去量。
例2-3 已知： AC CB, F 10 kN ,各杆自重不计； 求：CD 杆及铰链 A 的受力.
解：CD 为二力杆，取 AB杆，画受力图. 用几何法，画封闭力三角形.
求：在中心作用的水平力F的大小和碾子对障碍物的压力。
解： ①选碾子为研究对象 ②取分离体画受力图

理论力学第二章

理论力学第二章
得 h 2l 3
Ph

l
q dx x
0

l

0
x2 l
q dx
§2-4 平面力偶理论
一.力偶和力偶矩 1.力偶
由两个等值、反向、不共线的（平行）力组
成的力系称为力偶，记作 F, F
2.力偶矩 力偶中两力所在平面称为力偶作用面 力偶两力之间的垂直距离称为力偶臂 两个要素 a.大小：力与力偶臂乘积 b.方向：转动方向 力偶矩
力对点之矩是一个代数量，它的绝对值等于力的 大小与力臂的乘积，它的正负：力使物体绕矩心逆时 针转向时为正，反之为负.常用单位N·m或kN·m
二、合力矩定理 平面汇交力系
MO FR MO Fi
该结论适用于任何合力存在的力系
三、力矩与合力矩的解析表达式
MO F MO Fy MO Fx
求： 光滑螺柱AB所受水平力. 解：由力偶只能由力偶平衡的性 质，其受力图为
M 0
FAl M1 M2 M3 0
解得
FA

FB

M1 M2 l
M3

200N
例2-10 已知 M 2kN m,OA r 0.5m,θ 30 ;
1
求：平衡时的 M 2及铰链O，B处的约束力. 解：取轮,由力偶只能由力偶平衡的性质,画受力图.
例2-1
已知： P=20kN，R=0.6m， h=0.08m 求：
1.水平拉力F=5kN时，碾子对地面及障碍物的压力？ 2.欲将碾子拉过障碍物，水平拉力F至少多大？
3.力F沿什么方向拉动碾子最省力，及此时力F多大？？
解： 1.取碾子，画受力图. 用几何法，按比例画封闭力四边形

理论力学第2章

理论力学第2章

则： (0.2785 FR F )i (0.1691 F ) j (0.9463 F )k ;
求力系的主矩：即求各力对 在坐标轴上的矩 M xi , M yi , M zi 方法一：利用分力计算力矩：
x 3F
z
F3 y
3F
M x ( F3 ) M x ( F3 x ) M x ( F3 y ) M x ( F3z ) 6 6 0( F )(2b) 0 Fb; F3 z 6 3 M y ( F3 ) 0;
2 2
m
y
12420 3420
FR

o
x
对A、D点的主矩分别为：
M A M Ai 0.3F2 0.2F3 25N m M D M Di 0.4F1 sin 60 0.3F2 0.2F3 4.282N m
m
A

O M O
d
M d F
一个力不仅可以分解为几个力， 还可以分解为力和力偶。
2.2.2 力系等效定理
充要条件：两力系的主矢相等， 对同一点的主矩相等. 1 2 FR FR 1 2 Mo Mo
矩心O是任意选择的
1 1 1 M o M o OO FR 2 2 2 M o M o OO FR 1 2 Mo Mo
1. 几何法（力多边形法） 注意：主矢没有 作用点！
F3
F2
F4
F 1
F3
F4
F1

' FR F22 解析法力系的主矢
' FR 的三个投影为：
Fi Fxii Fyi j Fzi k

理论力学第二章

理论力学第二章
cos T1 T2 P 2P 1 2
(1)
(2)
0
60
T2
T1 α
由(2)式解得：
N D Q - T2 sin
Q
Q 2 P sin 60
0
Q
3P
ND
END
(b)
[习题2-1] B
600
A
SAB SAC
A
B SAB
300
W (a)
W
200 700
C
∑X=0：
2.1 平面汇交力系合成与平衡的几何法 一、合成的几何法 1. 两个共点力的合成 公理3：作如右图所示。
A
F1
R α φ
F2
也可用力的三角形法则来作， 如右下图所示R ： 合力R大小和方向可直接由图上
按比例尺寸量取，此法叫图解法。
除了上面介绍的图解法之外，也可用三角函数来计算 合力R的大小和方向: 由余弦定理求合力R的大小：
C
解: 2)用解析法求解
a. 取AC杆为分离体: b.画其受力图:
600
(二力体)
c.选择坐标系:
(1)
B y A RA
W = 5kN (三力体)
d.列平衡方程: ΣX=0: SBC = RA
ΣY=0: SBC· sin30o+RA· sin30o= W C x 将(1)代入得: SBC = RA 0 30 = W/(2· sin30o) SBC = W = 5 kN
第一篇
静力学
Statics
第2章
平面汇交力系 与平面力偶理论
引 言
力系的概念：
平面力系 ------ ? ...... 在同一平面上。 空间力系 ------ ???

理论力学 第二章

理论力学 第二章

扭矩扳手
2-3 平面力对点之矩的概念及计算
一、力对点的矩（力矩） 力对点的矩（力矩）
M O ( F ) = ± F ⋅ d ，单位N•m或KN•m 单位N KN•
→
→
① ②
是代数量。 M O ( F ) 是代数量。
M O ( F ) 正负判定： 正负判定：
→
→
M O (F ) (F
+
→ →
-
③ 当F=0或d=0时， O (F ) =0。 =0或 =0时 M =0。 点O为矩心，d为力臂。 为矩心， 为力臂。 角 形面积，或是矢量积的模。 面积，或是矢量积的模。 ④ M O (F ) = ± 2⊿AOB= r × F 2⊿AOB= 力对点0矩的大小等于2 力对点0矩的大小等于2倍三
Fx = X i , F y = Y j
F = X +Y
2 2
→
→ →
→
X cos α = F
Y cos β = F
2-2 平面汇交力系合成与平衡的解析法
区分力沿轴的分力和力在两轴上的投影： 区分力沿轴的分力和力在两轴上的投影： 力沿轴的分力和力在两轴上的投影 • 分力是矢量，投影是代 分力是矢量， 数量，二者性质不同。 数量，二者性质不同。 • 在直角坐标系中，投影 在直角坐标系中， 的大小与分力的大小相 但在斜角坐标系中， 同，但在斜角坐标系中， 二者不等。 二者不等。
∑F = 0 ix
− FBA + F cos60 − F2 cos30 = 0 1
o o
∑F =0 iy
FBC − F cos30 − F cos60 = 0 1 2
o o
F = F2 = P 1
解得： FC = 27 32kN 解得： B .

理论力学第2章平面任意力系

理论力学第2章平面任意力系

空载时轨道A 、 B的约束反力，并问此起重机在使用过程中有无翻
倒的危险。
解：
（1）起重机受力图如图
（2）列平衡方程 ：
MA 0:
Q
Q(6 2) RB 4 W 2 P(12 2) 0
MB 0:
Q(6 2) W 2 P(12 2) RA 4 0
6m
解方程得:
W
P
12m
RA 170 2.5P
FR' Fi Fxi Fy j
MO MO (Fi )
3. 平面任意力系的简化结果
（1）FR´= 0，Mo ≠ 0, （2）FR´ ≠ 0，Mo = 0, （3）FR´≠ 0，Mo ≠ 0, （4）FR´= 0，Mo = 0,
合力偶，合力偶矩，MO MO (Fi )
合力，合力作用线通过简化中心O。
3
F2
j
F3
x
(437.6)2 (161.6)2
F1
1 1
100
Oi
1 2
466.5N
200
MO 21.44N m
y
合力及其与原点O的距离如图(c) 。 MO
x
y
d
x
O
FR FR′ 466.5N FR´
FR
O
d MO 45.96mm
(b)
(c)
FR
10
例11 水平梁AB受按三角形分布的载荷作用，如图示。载荷的
M
l
l
30
B
D
° F
3l
P
q
A
21
解：T字形刚架ABD的受力如图所示。
M
l
l
Fx 0
30
B
FAx 1 • q • 3a Fcos30 0

理论力学第二章汇交力系与平面力偶系

理论力学第二章汇交力系与平面力偶系

FBC= 224.23 kN 代入（3）、（4）解得
tan θ = 1.631 , θ = 58.5°
FA= 303.29 kN
y
FBC
FD
C
45°
30°
x
W2
y
FA
θB
x
45°
W1 F'BC
第二章 汇交力系与平面力偶系
§2–1 平面汇交力系的合成与平衡
投影法的符号法则： 当由平衡方程求得某一未知力的值
y
FBC
B 30°
x
FAB
FD 30° W
b
联立求解,得
FAB= －54.5kN , FBC= 74.5kN
反力FAB为负值，说明该力实际指向与图上假定指向相反。 即杆AB实际上受拉力。
第二章 汇交力系与平面力偶系
§2–1 平面汇交力系的合成与平衡
例2–5 如图已知W1=100 kN， W2=250 kN。不计各
Fx F cos
Fy
Fy F cos
O 2、力在空间直角坐标轴上的投影：
F
Fx x
一次投影法：
Z
Fx F cos Fy F cos
F
O
y
FZ F cos
第二章 汇交力系与平面力偶系
x
★§2–2 空间汇交力系的合成与平衡 二次投影法：
已知力F 和某一平面（oxy)的夹
角为θ，又已知力F 在该平面
杆自重，A，B，C，D各点均为光滑铰链。试求平衡状
态下杆AB内力及与水平的夹角。
A
θB
D
W1
45° C
30°
W2 第二章 汇交力系与平面力偶系
§2–1 平面汇交力系的合成与平衡

理论力学第二章

理论力学第二章

rm2 h
rm
p 1 e
p mh2 k2
r p
E k 4 (e2 1)
1 e cos
2mh2
e 1 2mh2 E k4
质点的总 机械能与 轨道偏心 率的关系
e<1, 则 E<0, 则轨道为椭圆 e=1, 则 E=0, 则轨道为抛物线 e>1, 则 E>0, 则轨道为双曲线
r r2 F (r)
m
r 2 h
r
dr
d
d
dt
dr d
h r2
dr
d
h d
d
(1) r
进行变换 u 1 r
将
r h du
d hu2
代入 r r 2 F(r)
m
r
h
d 2u
d 2
h 2u 2
d 2u
d 2
mh2u
2
(
d 2u
d 2
u)
F (u)
有心运动的轨道微分方程 --- Binet （比内)公式
• 有心力的特性：
– ◆ 质点做有心运动时角动量守恒（质点所受到的力 始终沿着力心，导致其对力心的力矩始终为0）
– ◆ 质点做有心运动时，机械能守恒（有心力是保守 力，质点在保守力的作用下运动，只发生势能和动 能的相互转化，总的机械能保持恒定）
dL
M
dt
E T V
• 有心运动的运动方程
– 在平面极坐标系下面考虑有心运动，则质点的动量 矩（角动量）与极坐标平面垂直，质点运动微分方 程为：
p
mh2 p
u2
mh2 p
1 r2
§2.2 距离平方反比引力下的质点运动
•

理论力学第二章

理论力学第二章
即
M O FR M O Fi
平面汇交力系 M 0 FR M 0 Fi 合力矩定理：平面汇交力系的合力对于平面内任一点之矩等于 所有各分力对于各点之矩的代数和
三、力矩的解析表达式
M O F M O Fy M O Fx x F sin y F cos x Fy y Fx
重点：平面汇交力系可简化为一个合力，其合力的大小与方向 等于各分力的矢量和（几何和）合力作用线通过汇交点
特例：共线力系合成：作用线在一条直线上，矢量和即为代数和
力系合成的目的：简化力系，研究平衡问题
二.平面汇交力系平衡的几何条件
平衡条件
Fi 0
FR 0
平面汇交力系平衡的必要和充分条件是：该力系的力 多边形自行封闭. 力的多边形起点和终点重合
平衡方程
F 0 Fyi 0
xi
平面汇交力系平衡的 充要条件是：各力在两个坐标轴 上的投影的代数和分别等于零。
i可省，两个独立方程，可求两个未知量。
例2-3求图示支座的AB的反力，各杆的自重忽略，
ABC BAC 300
解：
取坐标如图，取C点为 研究对象进行受力分析
FA
A
B
FA1
三.平面力偶系的合成和平衡条件
已知：M1 , M 2 , M n ;
任选一段距离d
M1 F1 d
M2 F2 d
M1 F1d
M 2 F2d
Mn Fn d
M n Fnd
= =
=
FR F1 F2 Fn
FR F1 F2 Fn
平面内力矩的解析表达式
M O FR M O Fi

理论力学第二章(汇交力系)

理论力学第二章(汇交力系)
力多边形 各分力矢与合力矢构成的多边形。
2) 合力
力矢量合成的力多边形法则： 1) 各分力首尾相接，次序可变；
R 为封闭边。
z F3 FR F2 F1 x
5
2、空间汇交力系合成的几何法
r r r r r r FR = F1 + F2 + F3 + F4 = Σ Fi ,
合成为一个合力，合力的大小与方向等于 各分力的矢量和，合力的作用线过汇交点.
FR = F1 + F2 + L + Fn = ∑ Fi
向两个坐标轴投影，
FR = FRx + FRy = (∑ Fix ) + (∑ Fiy )
2 2 2
2
FR
合力方向 FRx ∑ Fix FRy cos θ = = , sin θ = = FR FR FR 合力投影定理：
∑F
FR
iy
10 合力在任一轴上的投影等于各分力在同一轴上投影的代数和。
FDA
P
FDB=FDC=289N。
18
例 ：起重机起吊重量P = 1 kN， ABC 在 yz 平面内，求：立柱 x’ AB、绳BC，BD，BE 的拉力。 解：B点有四个未知力汇 交，故先从C点求解，
[C] 平面汇交力系 z 750
B 450 E FBE FBD 450 450 D x A y 450 F BA 450 FCB FBC 300 FCA
汇交力系的平衡条件为：力系中各力在x、y、z三个坐标 轴的每一轴上投影之代数和均为零。 14 汇交力系平衡的几何条件为：力多边形自行封闭。
汇交力系平衡条件的应用
例：园柱物置于光滑的燕尾槽内，已知：P 为 500 N,求： 接触处A、B的约束力。

理论力学 第二章

理论力学 第二章

平面任意力系1第二章平面力系第二部分平面任意力系平面任意力系：各力的作用线在同一平面内，既不汇交于一点，又不相互平行的力系。

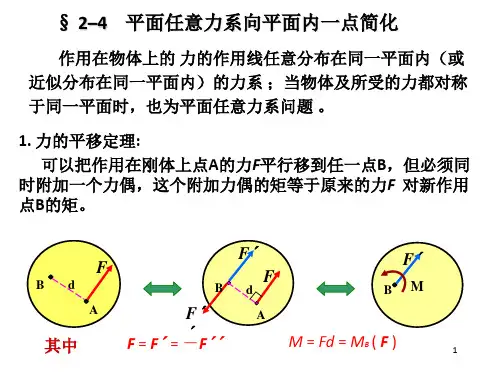
[例]第二章平面力系第二部分平面任意力系§2–5 力的平移定理§2–6 平面任意力系向一点简化§2–7 平面任意力系的简化结果• 合力矩定理§2–8 平面任意力系的平衡条件和平衡方程§2–9 平面平行力系的平衡方程§2–10 静定与超静定问题的概念•物体系统的平衡§2–11 平面简单桁架的内力分析平面任意力系习题课§2-5 力的平移定理力的平移定理：作用在刚体上点A的力可以平行移到任一点B，但必须同时附加一个力偶。

这个力偶的矩等于原来的力对新作用点B的矩。

FF[证] 力力系），力偶（力FFF''+'FFF''',,F说明：①力的平移定理揭示了力与力偶的关系：力力+力偶（例断丝锥）②力平移的条件是附加一个力偶M，且M与d有关，M=F•d③力的平移定理是力系简化的理论基础。

任意力系向一点简化汇交力系+力偶系未知力系）（已知力系）汇交力系力，F R '(主矢) ，(作用在简化中心)力偶系力偶，M O (主矩) ，(作用在该平面上)§2-6平面任意力系向一点简化大小：主矢方向：与简化中心的关系：'R F 123'R iF F F F F =+++=∑ 主矢12312 ()()()O O O O i M M M M M F M F M F =+++=++=∑主矩2222'''()()R Rx Ry x y F F F F F =+=+∑∑11tg tg xRyRx yF F F F α--==∑∑（移动效应）(与简化中心位置无关)[因主矢等于各力的矢量和]大小：主矩M O 方向：与简化中心的关系：()O O i M M F =∑（转动效应）固定端（插入端）约束在工程中常见的雨搭车刀方向规定+ —(与简化中心有关)[因主矩等于各力对简化中心取矩的代数和]固定端（插入端）约束说明①认为F i 这群力在同一平面内;②将F i 向A 点简化得一力和一力偶;③F RA 方向不定可用正交分力F Ay ,F Ax 表示;④F Ay ,F Ax , M A 为固定端约束力;⑤F Ay , F Ax 限制物体平动, M A 限制转动。

理论力学第二章

理论力学第二章

3．用解析法求平面汇交力系的合力
合力FR的大小和方向可由下式确定 ：
FR FRx FRy tan FRy FRx F F
y 2 2
y F1 A
F F
2 2 x y
x

α
F2 FR
x
F3
式中 α为合力FR与x轴所夹的锐角。
四、平面汇交力系的平衡条件
作用在同一平面内的力偶系称为平面力偶系。
1.平面力偶系的合成
平面力偶系可以合成为一个合 力偶，合力偶矩等于平面力偶系中 各个力偶矩的代数和。用式子表示 为：
M M1 M2
Mn M
M1、M 2、 、M n表示原力
式中 M表示合力偶矩,
偶系中各力偶的力偶矩。
2.平面力偶系的平衡条件
难点：主矢和主矩的概念；物体系平衡问题的求 解
力 系
平 面 力 系
各力的作用线都在 同一平面内的力系 称为平面力系。
平面汇交力系 平面平行力系 平面力偶系 平面任意力系
作用线汇交 于一点
2-1
平面汇交力系
一、平面汇交力系合成的几何法
1.
两个汇交力的合成
F1 FR F1 A F2
b
F2
c
o
FR
力三角形法则。
力偶特点：
1．力偶中的二力不满足二力平衡公理，故不是平衡力系。 2.力偶不能合成为一个合力，所以不能用一个力来代替。 3．力偶在任何坐标轴上的投影都等于零。
4．力偶不会引起物体的移动效应，只能使物体发生转动效应
（纯转动）。
力偶与单个力一样，是构成力的基本元素。
2.力偶矩
力偶对物体的转动效应由组成力偶的力的大小与力偶 臂的乘积，即力偶矩确定。记作：记作M（F，F′）或M， 即 M（F，F′）= M =±Fd 方向：逆正，顺负。 单位：KN.m或N.m 力偶对物体的转动效应取决于力偶矩的大小、力偶的 转向及力偶的作用面，此即力偶的三要素。

理论力学第2章-汇交力系

理论力学第2章-汇交力系

Fz F k
（2-5）
力在某一轴上的投影，等于该力与沿该轴方向的单 位矢量之标积。
这结论也适用于在任何一轴上的投影。
例如，设有一轴，沿该轴正向的单位矢量为n， 则力F在 轴上的投影为
F F n
设n在坐标系Oxy 中的方向余弦为l1 、l2 、l3 ，则
F Fxl1 Fyl2 Fzl3
F Fxi Fy j Fzk
（2-3）
i、j、k是沿坐标轴正向的单位
矢量，
Fx、Fy、Fz分别是力F在x、y、
z轴上的投影。
2.3.1.1 直接投影法
已知F与坐标轴正向的夹角分别为、、 ， cos
Fz F cos
（2-4）
Fx Fy
F F
i j
cos FR ,
k
FR z FR
F
z
FR
（2-12）
例2-2 如图所示平面汇交力系，已知： F1 20kN F2 30kN
F3 10kN F4 25kN 试求汇交力系的合力矢。
解 (1)求合力矢FR在坐标轴上的投影：
FRx F1 cos 30 F2 cos 60 F3 cos 45 F4 cos 45 10 3 15 5 2 12.5 2 12.93 kN
平面汇交力系：各力作用线在同一平面内且 汇交于同一点的力系。
空间汇交力系：各力作用线不在同一平面内 且汇交于同一点的力系。
2.1 汇交力系合成的几何法
2.1.1 合成的几何法
F1
A
F2 FR F3
F4
b F3
c
F2 a FR1
FR2 F4
F1 o FR
d
FR = F1 + F2 + F3 + F4

理论力学第2章

理论力学第2章

力作用线通过三角形的几何中心。
★力对点之矩与力对轴之矩
★力偶系
F1r1 rBA r2
F2
力 偶(couple): 大 小相等,方向相反,不 共线的两个力所组成 的力系.
F1
力偶作用面(acting plane of
F2
a couple) : 二力所在平面。
力偶臂(arm of couple):二力作用线之间的垂直距离。
■空间任意力系简化
主矢的特点： ◆ 对于给定的力系，主矢唯一； ◆ 主矢仅与各力的大小和方向有关，主矢不 涉及作用点和作用线,因而主矢是自由矢。
主矩的特点:
◆力系主矩MO与矩心( O )的位置有关；
◆ 力系主矩是定位矢,其作用点为矩心。
■空间任意力系简化
FB
MC
MD
FC
FA
ME
怎样判断不同力系的 运动效应是否相同？
M rBA F
★力偶系
MO = MO(F) + MO(F´)
= rA×F + rB× F´
= rA× F - rB× F
=( rA - rB )× F
O1
= rBA× F
？ MO1 =
其方向亦可由 右手定则确定。
★力偶系
●力偶的性质
性质一 : 力偶无合力,即主矢FR=0. 性质二 : 力偶对刚体的运动效应
FA 8.66kN
FA为正值，表明所设的 F
AB
A方向正确， 为 压 杆。
力对点的矩
■力偶系
★力对点之矩与力对轴之矩 ★力偶系
★力对点之矩与力对轴之矩
1、力对点之矩
( m o ment of a force about a
力对点之矩是力使物体绕某点转动效果的度量。

理论力学第二章

理论力学第二章
静力学的理论和方法，特别是对物体进行受力分析和画受力 图的方法是学习理论力学及后续许多课程的基础，在工程技术中也 有广泛的应用。
返回
第二章 刚体静力分析基础
第二章 刚体静力分析基础
本章介绍刚体、力、平面内力对点之矩、力偶、力系等基本概念及静力学公 理，并在介绍约束和约束反力概念的基础上，具体分析工程实际中常见的几种典 型约束的特点及其约束力的性质，着重阐述物体受力分析的方法和受力图的画法， 为学习静力学打下必要的基础。
目录
第二章 刚体静力分析基础\刚体和力的概念 分布在狭长面积上的力可看作线分布力，其集度单位为N/m或
kN/m。图示在梁AB上沿长度方向作用着向下的均匀分布力，其集 度为q=2 kN/m。
目录
第二章 刚体静力分析基础\刚体和力的概念 5.力系、平衡力系等效力系、合力的概念 作用于一个物体上的若干个力称为力系。 如果作用于物体上的力系使物体处于平衡状态，则称该力系为
目录
第二章 刚体静力分析基础\刚体和力的概念
4.集中力和分布力
作用于物体上某一点处的力称为集中 力。对于集中力，可以用一个矢量来表示 （如图）。该矢量的长度AB按一定比例尺 绘出表示力的大小；矢量的方向表示力的 方向；矢量的始端（点A）或终端（点B） 表示力的作用点；矢量AB所沿的直线（图 上的虚线）表示力的作用线。由于表示力 的矢量不仅有大小和方向还有确定的始端 （或终端），所以常称其为定位矢量。规 定用黑体字母F表示力的矢量，而用普通 字母F表示力的大小。在国际单位制(SI)中， 力的单位为牛顿(N)或千牛顿(kN)。
目录
第二章 刚体静力分析基础\刚体和力的概念 物体之间相互接触时，其接触处多数情况下并不是一个点，而
是一个面。因此，无论是施力物体还是受力物体，其接触处所受的 力都是作用在接触面上的，这种分布在一定面积上的力称为分布力。 分布力的大小用力的集度表示，例如，水对容器壁的压力是作用在 一定面积上的分布力，其大小用面积集度表示，单位为N/m2或 kN/m2。

理论力学第二章

理论力学第二章

T
T1
T2
二、平面汇交力系合成的几何法
设有一个平面汇交力系 F1、F2、F3、F4作用于汇交点，如图2-1a
所示。我们可以依次地应用力三角形法则来求该平面汇交力系的
合力。即先将力 F1与 F2合成为一个力 FR1，再将力FR1与F3 合成 为一个力 FR2，最后将力FR2 与F4合成，即得该平面汇交力系的合 力 FR ，且合力的作用线通过汇交点，如图2-1b所示。
第二章 平面汇交力系和平面力偶系
2.1 平面汇交力系合成与平衡的几何法 2.2 平面汇交力系合成与平衡的解析法 2.3 平面力对点之矩的概念与计算 2.4 平面力偶
武汉大学出版社
1
§2-1 平面汇交力系合成与平衡的几何法
一.平面汇交力系的概念
平面汇交力系：各力在同一平面内，作用线交于一
点的力系。
例：起重机的挂钩。
例2-3
已知：图示平面共点力系； 求：此力系的合力.
解：用解析法
FRx
F ix

F1
cos 30

F2
cos 60

F3
cos 45

F4
cos 45
129.3N
FRy
F iy

F1
sin
30

F2
sin
60

F3
sin
45

F4
sin
45
112.3N
FR
FCA AC 1 P AB
FCB BC 1 P AB 2
图2-2
解得
FCA 10 kN, FCB 5 kN
也可给P一定比例，量出FCA和FCB的大小，如取比例尺为1cm=5kN，作
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第2章 力系的等效与简化2－1试求图示中力F 对O 点的矩。

解：（a ）l F F M F M F M M y O y O x O O ⋅==+=αsin )()()()(F （b ）l F M O ⋅=αsin )(F（c ）)(sin cos )()()(312l l Fl F F M F M M y O x O O +--=+=ααF （d ）2221sin )()()()(l l F F M F M F M M y O y O x O O +==+=αF2－2 图示正方体的边长a =0.5m ，其上作用的力F =100N ，求力F 对O 点的矩及对x 轴的力矩。

解：)(2)()(j i k i Fr F M +-⨯+=⨯=Fa A O m kN )(36.35)(2⋅+--=+--=k j i k j i Fam kN 36.35)(⋅-=F x M2－3 曲拐手柄如图所示，已知作用于手柄上的力F =100N ，AB =100mm ，BC =400mm ，CD =200mm ，α = 30°。

试求力F 对x 、y 、z 轴之矩。

解：)cos cos sin (sin )4.03.0()(2k j i k j F r F M αααα--⨯-=⨯=F D Ak j i αααα22sin 30sin 40)sin 4.03.0(cos 100--+-=力F 对x 、y 、z 轴之矩为：m N 3.43)2.03.0(350)sin 4.03.0(cos 100)(⋅-=+-=+-=ααF x M m N 10sin 40)(2⋅-=-=αF y Mm N 5.7sin 30)(2⋅-=-=αF z M2—4 正三棱柱的底面为等腰三角形，已知OA=OB =a ，在平面ABED 内沿对角线AE 有一个力F ， 图中θ =30°，试求此力对各坐标轴之矩。

习题2-1图A r A习题2-2图（a ）习题2-3图(a)ABr 解：)sin 45sin cos 45cos cos ()(k j i i F r F M θθθ+︒+︒-⨯=⨯=F a A O )45sin cos sin (k j ︒+-=θθaF 力F 对x 、y 、z 轴之矩为：0)(=F x M230sin )(aF aF M y -=︒-==F Fa aF M z 4645sin 30cos )(=︒︒=F2－5 如图所示，试求力F 对A 点之矩及对x 、y 、z 轴之矩。

解：F r F M ⨯=AB A )(5354F F d d d-k j i = =)743(51k j i -+-Fd)34(5)(j i j F M +⨯=Fd O力F 对x 、y 、z 轴之矩为：0)(=F x M ；0)(=F y M ；Fd M z 54)(-=F2—6 面。

求这四个力偶的合力偶。

解：4321M M M M M+++=k j i )53()54(43241M M M M M +--+-=m N 8.1284.14⋅---=k j i2－7 已知一平面力系对A （3,0），B A B = 0，M C =–10kN ·m 。

试求该力系合力的大小、方向和作用线。

解：由已知M B = 0知合力F R 过B 点； 由M A = 20kN ·m ，M C = -10kN ·m 知F R 位于A 、C 间，且CD AG 2=（图a ）在图（a ）中，设 OF = d ，则 θcot 4=dCD AG d 2)sin 3(==+θ （1）θθsin )25.4(sin dCE CD -== （2）即 θθsin )25.4(2sin )3(dd -=+d d -=+93， 3=d F 点的坐标为（-3, 0） 合力方向如图（a ），作用线如图过B 、F 点；习题2－4图习题2－5图习题2－6图 （a ） 43 M 1M 2 M 3M 4习题2－7图34tan =θ 8.4546sin 6=⨯==θAG8.4R R ⨯=⨯=F AG F M AkN 6258.420R ==F 即 )kN 310,25(R =F作用线方程：434+=x y讨论：本题由于已知数值的特殊性，实际G 点与E 点重合。

2－8 已知F 1 = 150N ，F 2 = 200N ，F 3 = 300N ，F =F '= 200N 。

求力系向点O 的简化结果，并求力系合力的大小及其与原点O 的距d 。

80200100131121FFF'1yRF 'o2.7xoM yRF oxd解：N .64375210145cos 321-=--︒-=∑F F F F xN .61615110345sin 321-=+-︒-=∑F F F F ym N 44.2108.02.0511.045sin )(31⋅=-⨯+⨯︒=∑F F F M O F向O 点简化的结果如图（b ）；合力如图（c ），图中N 5.466)()(22'R =∑+∑=y x F F F ，m N 44.21⋅=O M合力N 5.466'R R ==F F ，mm 96.45R==F M d O2－9 图示平面任意力系中F 1 = 402N ，F 2 = 80N ，F 3 = 40N ，F 4 = 110M ，M = 2000 N ·mm 。

各力作用位置如图所示，图中尺寸的单位为mm 。

求（1）力系向O 点简化的结果；（2）力系的合力的大小、方向及合力作用线方程。

FFFF (0,30)(20,20)(20,-30)(-50,0)45yxRF 'ooM yxoRF (0,-6)解：N 15045cos 421R -=--︒=∑=F F F F F x x045sin 31R =-︒=∑=F F F F y y(a)yxRF O θθCG ADEF423d5.4-习题2－8图习题2－9图N 150)()(22'R =∑+∑=y x F F Fm m N 900305030)(432⋅-=--+=∑=M F F F M M O O F向O 点简化结果如图（b ）；合力如图（c ），其大小与方向为N 150'R R i F F -==设合力作用线上一点坐标为（y x ,），则x y O O yF xF M M R R R )(-==F将O M 、'R y F 和'R x F 值代入此式，即得合力作用线方程为：mm 6-=y2－10 图示等边三角形板ABC ，边长a ，今沿其边缘作用大小均为F P 的力，方向如图（a ）所示，求三力的合成结果。

若三力的方向改变成如图（b ）所示，其合成结果如何？解（a ）0'R =∑=i F Fa F a F M A P P 2323=⋅=（逆） 合成结果为一合力偶a F M P 23=（逆） （b ）向A 点简化i F P 'R 2F -=（←）a F M A P 23=（逆） 再向'A 点简化，a F M d A 43'R==合力i F P R 2F A -=（←）2－11 图示力系F 1 = 25kN ，F 2 = 35kN ，F 3 = 20kN ，力偶矩m = 50kN ·m 。

各力作用点坐标如图。

试计算（1）力系向O 点简化的结果；（2）力系的合力。

解（1）向O 点简化 kN 10'R k F F =∑=i)(F M M O O ∑=mkN )10580(200 002 3- 35- 0 00 2 2 250 00 2- 3 50⋅+-=+++=j i kj i k j i k j i j（2）合力kN 10R k F =设合力作用线过点)0,,(y x ，则F F FF F F 习题2－10图 F F F A 'A d R F F 'A M 习题2－11图z xoM M a)0,0,(a A RF 'RFj i M kj i 10580100 00 +-==O x y 5.10-=x ，0.8-=y ，0=z合力作用线过点（-10.5，-8.0，0）。

2－12 图示载荷F P =1002N ， F Q =2002N ，分别作用在正方形的顶点A 和B 处。

试将此力系向O 点简化，并求其简化的最后结果。

解：N )(100P k i F +-=N )(200Q k j i F +--=mN )300200(200200- 20001 1 1000 1000 0 1 )(⋅-=-+-=j i kj i k j i F O MN )300200300('R k j i F F +--=∑=iQ P F F F r M ⨯+⨯=B A O合力 N )300200300('R R k j i F F +--== 设合力过点（0,,y x ），则j i M kj i 300200300200- 3000 -==-O y x得 1=x ，32=y ，0=z 即合力作用线过点（0,32,1）。

2－13 图示三力F 1、 F 2和 F 3的大小均等于F ，作用在正方体的棱边上，边长为a 。

求力系简化的最后结果。

解：先向O 点简化，得k F F ='R ， k j M Fa Fa O +=因0'R ≠⋅O M F ，故最后简化结果为一力螺旋。

该力螺旋k F F ='R ，k M Fa = 设力螺旋中心轴过)0,,(y x O '，则 j M F r Fa O ==⨯'1R即j k j i Fa Fy x = 0 00 得 a x -=，0=y ，0=z即合成最后结果的力螺旋中心轴上一点坐标为（0,0,a -）。

习题2－12图习题2－13图2－14 某平面力系如图所示，且F 1=F 2=F 3=F 4= F ，问力系向点A 和B 简化的结果是什麽？二者是否等效？解：（1）先向A 点简化，得)(2Rj i F -='F ；Fa M A 2= （2）再向B 点简化，得)(2Rj i F -='F ；0=B M 二者等效，若将点B 处的主矢向点A 平移，其结果与（1）通。

2－15 某平面力系向两点简化的主矩皆为零，此力系简化的最终结果可能是一个力吗？可能是一个力偶吗？可能平衡吗？解：可能是一个力，也可能平衡，但不可能是一个力偶。

因为（1），平面力系向一点简化的结果为一主矢和一主矩，而由已知是：向两点简化的主矩皆为零，即简化结果可能为（0,R ='A M F ），（0,R ='B M F ）（主矢与简化中心无关），若0R≠'F ，此时已是简化的最后结果：一合力'R R F F =经过A 点，又过B 点。