第11章外排序第2讲-磁盘排序-生成初始归并段

一、单项选择题1. 下列对顺序存储的有序表（长度为n）实现给定操作的算法中平均时间复杂度为O(1)的是（）。

A、查找包含指定值元素的值B、插入包含指定值元素的算法C、删除第i(1≤i≤n)个元素的算法D、获取第i(1≤i≤n)个值的算法2、现有非空双向链表L，其结点结构为，prev是指向直接前驱结点的指针，next是指向直接后继结点的指针。

若要在L中指针p 所指向的结点（非尾结点）之后插入指针s指向的新结点，则在执行了语句序列：“s->next=p->next;p->next=s;”，后，还要执行（）。

A、s->next->prev=p;s->prev=p;B、p->next->prev=s;s->prev=p;C、s->prev=s->next->prev; s->next->prev=s;D、p->next->prev=s->prev;s->next->prev=p;3、若采用三元组表存储结构存储稀疏矩阵M，则除三元组外，下列数据中还需要保存的是（）。

I. M的行数；II.M中包含非零元素的行数；III.M的列数；IV.M中包含非零元素的列数。

A、仅I、IIIB、仅I、IIC、仅III、IVD、I、II、III、IV4、在由6个字符组成的字符集S中，各个字符出现的频次分别为3，4，5，6，8，10，为S构造的哈夫曼树的加权平均长度为（）。

A、2.4B、2.5C、2.67D、2.75注：每个关键字的查找长度为：图片加权平均长度为：(3×3+3×4+3×5+3×6+2×8+2×10)/(3+4+5+6+8+10)=2.5。

如果不考虑权重，会错误计算为(3+3+3+3+2+2)/6≈2.67，从而误选C。

5、已知一棵二叉树的树形如下图所示，若其后序遍历为fdbeca，则其先序列为（）。

【外排序】外排序算法（磁盘排序、磁带排序） 外存设备结构分析 败者树多路归并 最佳归并树白话讲解列队猫2020-06-20 21:15:46外排序外排序概述外排序的基本方法是归并排序法例子总结存储设备（可忽略）磁带磁带结构磁盘硬盘结构块硬盘上的数据定位磁盘排序磁盘排序过程1.生成初始顺串方法1(常规方法）：方法2：置换－选择排序方法2.处理顺串形成有序文件1.多路平衡归并2.利用败者树实现k路平衡归并过程利用败者树实现k路平衡归并的过程是：最佳归并树最佳归并树概念存在的问题当进行k路归并时最后进行归并的归并段小于k个构造步骤磁带排序磁带多路平衡归并排序磁带多阶段归并排序外排序概述(本章设计内容后续会具体讲解)外排序是指数据存放在外存中，数据排序时涉及内、外存数据交换的排序方法。

存储在外存上的数据以文件为基本单位，由文件系统进行读写操作，读写操作的基本单位为物理块外排序的基本方法是归并排序法一、生成若干初始归并段（顺串）：这一过程也称为文件预处理。

一种常规的方法如下：1. 把含有n个记录的文件，按内存大小w分成若干长度为w的子文件（归并段）；2. 分别将各子文件（归并段）调入内存，采用有效的内排序方法排序后送回外存。

产生m=[n/w]个初始归并段。

此时产生的若干子文件称为顺串二、多路归并：（所谓多路归并，具体使用几路归并是看计算机内存大小的，如计算机内存为2则只能使用2路归并） 对这些初始归并段进行多遍归并，使得有序的归并段逐渐扩大，最后在外存上形成整个文件的单一归并段，也就完成了这个文件的外排序。

例子1. 将一个大文件分成M个小文件，每个小文件是有序的2. 然后我们从M个子文件中各取一个数字进入内存处理（将该数字打上队列编号标记方便后续处理）3. 比较中转站中的数据，当从中转站出来的最小数字（升序排列）就是我们最后要排序的数字之一，将其写入到归并结果文件 因为该数字打上了队列编号，所以方便我们通知对应的编号队列继续出数字进入中转站队列（保证从中转站中取出的数据是所有文件中最小的），可以看出中转站一直保存了M个记录，当中转站中的所有数字都出队完毕，则本次归并结束。

归并排序的详细过程归并排序是一种常见的排序算法，它通过将待排序序列分成若干个子序列，分别对每个子序列进行排序，然后再将排好序的子序列合并成最终的有序序列。

下面将详细介绍归并排序的过程。

1. 分解阶段：将待排序的序列不断二分，直到每个子序列只剩下一个元素为止。

这个过程可以使用递归来实现。

例如，对于序列[8, 4, 2, 5, 1, 3, 6, 7]，先将其二分为[8, 4, 2, 5]和[1, 3, 6, 7]两个子序列，再将这两个子序列继续二分，直到每个子序列只剩下一个元素。

2. 合并阶段：将相邻的两个子序列合并成一个有序序列。

具体的合并过程如下：- 创建一个临时数组来存放合并后的序列。

- 初始化两个指针，分别指向两个子序列的起始位置。

- 依次比较两个子序列中的元素，将较小的元素放入临时数组中，并将指向该元素的指针后移一位。

- 当其中一个子序列的指针移到末尾时，将另一个子序列中剩余的元素依次放入临时数组中。

- 将临时数组中的元素复制回原始序列的对应位置。

以序列[8, 4, 2, 5, 1, 3, 6, 7]为例，将其分解为[8, 4, 2, 5]和[1, 3, 6, 7]两个子序列，然后对这两个子序列进行合并。

首先比较两个子序列的第一个元素，4小于8，将4放入临时数组中，并将指向4的指针后移一位。

接着比较2和8，2小于8，将2放入临时数组中，并将指向2的指针后移一位。

继续比较5和8，5小于8，将5放入临时数组中，并将指向5的指针后移一位。

此时第一个子序列中的元素已经全部放入临时数组中。

接下来比较两个子序列的第一个元素，3小于1，将3放入临时数组中，并将指向3的指针后移一位。

继续比较6和1，6大于1，将1放入临时数组中，并将指向1的指针后移一位。

接着比较6和3，6大于3，将3放入临时数组中，并将指向3的指针后移一位。

最后比较6和7，7小于6，将7放入临时数组中，并将指向7的指针后移一位。

此时第二个子序列中的元素已经全部放入临时数组中。

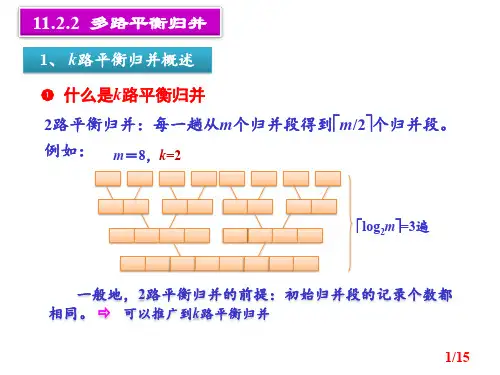
第11章外排序1、什么是外排序外排序是指数据存放在外存中，数据排序时涉及内、外存数据交换的排序方法。

内存数据交换文件存储在外存上的数据以文件为基本单位。

（1）生成若干初始归并段（顺串）：这一过程也称为文件预处理。

一种常规的方法如下：❶把含有n 个记录的文件，按内存大小w 分成若干长度为w 的子文件（归并段）；❷分别将各子文件（归并段）调入内存，采用有效的内排序方法排序后送回外存。

产生⎡n /w ⎤个初始归并段。

外排序的基本方法是归并排序法。

它分为以下两个步骤：2、外排序的基本方法内存abc.databc 1.dat abc 2.dat …abc n .dat均有序某内排序算法（2）多路归并：对这些初始归并段进行多遍归并，使得有序的归并段逐渐扩大，最后在外存上形成整个文件的单一归并段，也就完成了这个文件的外排序。

内存abc 1.dat abc 2.dat …abc n .databc.dat有序采用归并算法示例文件abc.dat：5，6，3，4，9，8，1，7，10，2递增排序应用程序可用的内存空间大小w=2。

5，6，3，4，9，8，1，7，10，2外排序过程：w =2内存abc.dat（1）生成5个初始归并段①abc1.dat ：5，6②abc2.dat ：3，4③abc3.dat ：8，9④abc4.dat ：1，7⑤abc5.dat ：2，10外排序过程：k =2内存abc1.dat abc2.databc12.dat ：3，4，5，6（2）多路归并：w =2 2路归并（k =2）abc1.dat ：5，6abc2.dat ：3，4abc1.dat ：abc2.dat ：5634比较abc12.dat ：内存∞ ∞u （u =4）个记录需要进行u -1次操作（不考虑∞ ）k （k =2）路归并每次需要k -1次关键字比较大致分析总的关键字比较次数：(u -1)(k -1)段1记录段2记录结果段内存abc3.databc4.dat abc34.dat：1，7，8，9abc3.dat：8，9abc4.dat：1，7w =2内存abc12.databc34.dat abc1234.dat：1，3，4，5，6，7，8，9abc12.dat：3，4，5，6abc34.dat：1，7，8，9k =2内存abc1234.databc5.dat abc.dat：1，2，3，4，5，6，7，8，9，10abc1234.dat：1，3，4，5，6，7，8，9abc5.dat：2，10k =2归并过程对应的归并树5，6abc1.dat 3，4abc2.dat 3，4，5，6abc12.dat 8，9abc3.dat 1，7abc4.dat 1，7，8，9abc34.dat 1，3，4，5，6，7，8，9abc1234.dat 1，2，3，4，5，6，7，8，9，10abc.dat2，10abc5.dat 归并过程的性能：记录读写次数。

排序算法所用的辅助空间一、引言在计算机科学中，排序算法是数据处理的基本技术之一。

排序算法可以分为内部排序和外部排序两大类。

内部排序是指待排序数据全部加载到内存中进行排序，而外部排序则是针对大规模数据，需要借助外部存储设备进行排序。

本文将重点讨论排序算法中所使用的辅助空间。

二、排序算法概述1.内部排序内部排序算法是指待排序数据可以完全加载到内存中进行排序的算法，如快速排序、归并排序、堆排序等。

这些算法的特点是时间复杂度较低，但在处理大规模数据时，空间复杂度成为瓶颈。

2.外部排序外部排序算法针对的是大规模数据，其特点是数据规模超过内存容量。

外部排序需要借助外部存储设备，如磁盘等，进行排序。

常见的外部排序算法有归并排序、快速排序等。

三、辅助空间的作用1.空间复杂度辅助空间是指在排序过程中，除待排序数据外，还需要使用的额外空间。

辅助空间的大小直接影响到排序算法的性能。

一般来说，我们希望辅助空间尽量小，以提高排序效率。

2.实例分析以归并排序为例，归并排序需要使用额外的空间存储中间结果。

当待排序数据规模较大时，辅助空间的需求也随之增加。

此时，可以考虑使用外部排序算法，将数据分块，依次加载到内存中进行排序，最后合并排序结果。

四、常见排序算法的辅助空间使用1.快速排序快速排序算法采用递归策略，其辅助空间主要用于存储子序列。

在递归过程中，快速排序会创建一个新的序列，将原序列分为两个子序列。

这个过程会递归进行，直到序列长度为1。

快速排序的辅助空间与递归深度成正比。

2.归并排序归并排序算法的辅助空间主要用于存储临时数据。

在归并过程中，需要将两个已排序的序列合并成一个有序序列。

这个过程需要额外的空间存储临时数据，以便进行合并操作。

归并排序的辅助空间与序列数量成正比。

3.堆排序堆排序算法在排序过程中，需要构建最大堆或最小堆。

堆排序的辅助空间主要用于存储堆结构的数据。

堆排序的辅助空间与堆的大小成正比。

4.计数排序计数排序是一种非比较排序算法，其原理是根据键值统计每个键值出现的次数，然后将计数结果存储在辅助空间中。

归并排序算法图⽂详解（模版使⽤）算法介绍引⽤百度百科的介绍。

归并排序（Merge Sort）是建⽴在操作上的⼀种有效，稳定的排序算法，该算法是采⽤（Divide and Conquer）的⼀个⾮常典型的应⽤。

将已有序的⼦合并，得到完全有序的序列；即先使每个⼦序列有序，再使⼦序列段间有序。

若将两个有序表合并成⼀个有序表，称为⼆路归并。

算法描述归并排序，采⽤是分治法，先将数组分成⼦序列，让⼦序列有序，再将⼦序列间有序，合并成有序数组。

算法描述：（1）把长度为n的输⼊序列分成长度 n/2的⼦序列；（2）对两个⼦序列采⽤归并排序；（3）合并所有⼦序列。

算法实现void mergeSortInOrder(int[] arr,int bgn,int mid, int end){int l = bgn, m = mid +1, e = end;//相当于对⼀个数组的前半部分和后半部分进⾏排序排序，从开始的只有两个数，到后⾯//因为基本有序，所以只需要进⾏合并就⾏int[] arrs = new int[end - bgn + 1];int k = 0;//进⾏有序合并while(l <= mid && m <= e){if(arr[l] < arr[m]){arrs[k++] = arr[l++];}else{arrs[k++] = arr[m++];}}//如果前半部分⼤的⽐较多，直接接在后⾯while(l <= mid){arrs[k++] = arr[l++];}//如果后半部分⼤的⽐较多，直接接在后⾯while(m <= e){arrs[k++] = arr[m++];}//对我们原来的数组进⾏值的覆盖for(int i = 0; i < arrs.length; i++){arr[i + bgn] = arrs[i];}}void mergeSort(int[] arr, int bgn, int end){//如果开始指针⼤于结束指针，结束if(bgn >= end){return;}//通过分治将我们的数组分成多个⼩数组int mid = (bgn + end) >> 1;mergeSort(arr,bgn,mid);mergeSort(arr,mid + 1, end);//对我们的⼩数组进⾏排序mergeSortInOrder(arr,bgn,mid,end);}算法分析稳定排序外排序（需要消耗额外的内存）时间复杂度O(nlogn)，空间复杂度为O(1)。

第11章外排序教材中练习题及参考答案1. 外排序中两个相对独立的阶段是什么？答：外排序中两个相对独立的阶段是产生初始归并段和多路归并排序。

2.给出一组关键字T=（12，2，16，30，8，28，4，10，20，6，18），设内存工作区可容纳4个记录，给出用置换-选择排序算法得到的全部初始归并段。

答：置换-选择排序算法的执行过程如表11.1所示。

共产生两个初始归并段，归并段1为（2，8，12，16，28，30），归并段2为（4，6，10，18，20）。

表11.1 初始归并段的生成过程3. 设输入的关键字满足k1>k2>…>k n，缓冲区大小为m，用置换-选择排序方法可产生多少个初始归并段？答：可产生⎡n/m⎤个初始归并段。

设记录R i的关键字为k i（1≤i≤n），先读入m个记录R1、R2、…、R m，采用败者树选择最小记录R m，将其输出到到归并段1，R min=k m，在该位置上读入R m+1，采用败者树选择最小记录R m-1，将其输出到到归并段1，R min=k m-1，在该位置上读入R m+2，采用败者树选择最小记录R m－2，将其输出到到归并段1，R min=k m-2，…，以此类推，产生归并段1：（R m，R m-1，…，R1）。

同样产生其他归并段（R2m，R2m-1，…，R m+1），（R3m，R3m-1，…，R2m+1），…，一共有⎡n/m⎤个初始归并段。

4. 什么是多路平衡归并，多路平衡归并的目的是什么？答：归并过程可以用一棵归并树来表示。

多路平衡归并对应的归并树中，每个结点都是平衡的，即每个结点的所有子树的高度相差不超过1。

k路平衡归并的过程是：第一趟归并将m个初始归并段归并为⎡m/k⎤个归并段，以后每一趟归并将l个初始归并段归并为⎡l/k⎤个归并段，直到最后形成一个大的归并段为止。

m个归并段采用k路平衡归并，总的归并趟数s=⎡log k m⎤。

其趟数是所有归并方案中最少的，所以多路平衡归并的目的是减少归并趟数。

前言1.1排序的重要性生活中，无时不刻不充满这排序，比如：班级同学的成绩排名问题，公司产值高低的问题等等，解决这些问题的过程中，都涉及到了一个数据结构的构造思想过程。

数据结构中的排序，也有很多种，如：插入排序、交换排序、选择排序等等，此时我们就要注意选择具有优解的算法，将一个数据元素（或记录）的任意序列，重新排列成一个有序的排列，便于我们查找。

假设含有n个记录的序列为{R1,R2,Rn},其相应的关键字序列为{K1,K2,…,Kn}需确定1，2…n的一种排序P1,P2…Pn,使其相应的关键字满足如下的非递减的关系：Kp1≤Kp2≤…≤Kpn,即按关键字{Rp1,Rp2,…,Rpn}有序的排列，这样的一种操作称为排序。

一般情况下，排序又分为内部排序和外部排序。

而在内部排序中又含有很多排序方法，就其全面性能而言，很难提出一种被认为是最好的方法，因为每一种方法都有它的优缺点，适合在不同的环境下使用。

我们学习的排序有:直接插入排序、折半插入排序、希尔排序、快速排序、基数排序、归并排序等。

本次课题研究中，我主要进行了二路归并排序的研究和学习。

1.2设计的背景和意义排序是计算机领域的一类非常重要的问题，计算机在出来数据的过程中，有25%的时间花在了排序上，有许多的计算机设备，排序用去计算机处理数据时间的一半以上，这对于提高计算机的运行速度有一定的影响。

此时排序算法的高效率显得尤为重要。

在排序算法汇中，归并排序（Merging sort）是与插入排序、交换排序、选择排序不同的另一类排序方法。

归并的含义是将两个或两个以上的有序表组合成一个新的有序表。

归并排序可分为多路归并排序，两路归并排序，既可用于内排序，也可以用于外排序。

这里仅对内排序的两路归并排序进行讨论。

而我们这里所探究学习的二路归并排序，设计思路更加清晰、明了，程序本身也不像堆结构那样复杂，同时时间复杂度仅为0(N)，同时在处理大规模归并排序的时候，排序速度也明显优于冒泡法等一些排序算法，提高排序算法的效率。