2018-2019初中数学竞赛专题复习极限几何100题
- 格式:pdf
- 大小:1.27 MB
- 文档页数:33

城郊初中2018-2019学年度第一学期八年级数学竞赛试卷(答案)一.选择题(每小题4分,共8小题满分32分)1.7条长度均为正整数的线段a1、a2、……、a7满足a1<a2<……<a7,且这7条线段中的任意三条都不能构成三角形,则a7的最小值为()A.19 B.20 C.21 D.22【解答】解:因为三角形任意两边之和大于第三边,任意两边之差小于第三边,而且7条长度不同,但都是整数的线段.设最短的一条长1,则第二条线段长为2,所以只要满足任意两条线段之和等于下一个数字即可,此时最长的线段也最短,2+1=3 3+2=5 5+3=8 8+5=13 13+8=21即这七条线段为:1,2,3,5,8,13,21,任意三条都不能作为边构成三角形,所以a7的最小值为21,故选:C.2.下列说法中,正确的个数是()①三角形的中线、角平分线、高都是线段;②三角形的三条角平分线、三条中线、三条高都在三角形内部;③直角三角形只有一条高;④三角形的三条角平分线、三条中线、三条高分别交于一点.A.1 B.2 C.3 D.4【解答】解:①三角形的中线、角平分线、高都是线段,故正确;②钝角三角形的高有两条在三角形外部,故错误;③直角三角形有两条直角边和直角到对边的垂线段共三条高,故错误;④三角形的三条角平分线、三条中线分别交于一点是正确的,三条高线所在的直线一定交于一点,高线指的是线段,故错误.所以正确的有1个.故选:A.3.在△ABC中,如果∠A﹣∠B=90°,那么△ABC是()A.直角三角形B.钝角三角形C.锐角三角形D.以上三种都可能【解答】解:∵∠A﹣∠B=90°,∴∠A=90°+∠B,∴∠A大于90°.根据三角形性质可知大于90°的角为钝角,∴此三角形为钝角三角形.故选:B.4.长为l的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为()A .B .C .D .【解答】解:∵围成两个全等的三角形可得两个三角形的周长相等∴x+y+z=,∵y+z>x ∴可得x <,又因为x 为最长边大于∴x ≥综上可得≤x <故选:A.5.已知一个圆的半径为Rcm,若这个圆的半径增加2cm,则它的面积增加()A.4cm2B.(2R+4)cm2C.(4R+4)cm2D.以上都不对【解答】解:∵S2﹣S1=π(R+2)2﹣πR2,=π(R+2﹣R)(R+2+R),=4π(R+1),∴它的面积增加4π(R+1)cm2.故选:D.6.如图是由10把相同的折扇组成的“蝶恋花”(图1)和梅花图案(图2)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为()A.36°B.42°C.45°D.48°【解答】解:如图,梅花扇的内角的度数是:360°÷3=120°,180°﹣120°=60°,正五边形的每一个内角=(5﹣2)•180°÷5=108°,∴梅花图案中的五角星的五个锐角均为:108°﹣60°=48°.故选:D.7.如图,地面上有三个洞口A、B、C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口(到A、B、C三个点的距离相等),尽快抓到老鼠,应该蹲守在()A.△ABC三边垂直平分线的交点B.△ABC三条角平分线的交点C.△ABC三条高所在直线的交点D.△ABC三条中线的交点【解答】解:∵三角形三边垂直平分线的交点到三个顶点的距离相等,∴猫应该蹲守在△ABC三边垂直平分线的交点处.故选:A.8.为了求1+2+22+23+…+22011+22012的值,可令S=1+2+22+23+…+22011+22012,则2S=2+22+23+24+…+22012+22013,因此2S﹣S=22013﹣1,所以1+22+23+…+22012=22013﹣1,仿照以上方法计算1+5+52+53+…+52012的值是()A.52013﹣1 B.52013+1 C .D .【解答】解:令S=1+5+52+53+ (52012)则5S=5+52+53+…+52012+52013,5S﹣S=﹣1+52013,4S=52013﹣1,则S=.故选:D.二.填空题(每小题4分,共8小题满分32分)9.314×(﹣)7= ﹣1 .【解答】解:314×(﹣)7=(32)7×(﹣)7=(﹣×9)7=(﹣1)7=﹣1,10.若一个三角形的三边长分别是m+2,10,2m﹣1,则m的取值范围为3<m<13 .【解答】解:根据三角形的三边关系,得即,解不等式组得,3<m<13.11.如图,△AOB≌△COD,∠B=29°,∠C=90°,则∠COD的度数是61°.【解答】解:∵△AOB≌△COD,∠B=29°,∴∠D=∠B=29°,∵∠C=90°,∴∠COD=180°﹣∠C﹣∠D=180°﹣90°﹣29°=61°,故答案为:61°.12.如图,在△ABC中,边BC的垂直平分线分别与AC、BC交于点D、E,如果AB=CD,∠C=20°,那么∠A= 40 度.【解答】解:连接DB,∵DE是边BC的垂直平分线,∴DB=DC,∴∠DBC=∠C,∴∠BDA=2∠C,∵AB=CD,DB=DC,∴BA=BD,∴∠A=∠BDA,∴∠A=2∠C,∵∠C=20°,∴∠A=40°,故答案为40.13.一个多边形的一个外角为α,且该多边形的内角和与α的和等于840°,则这个多边形的边数为六,α= 120 度.【解答】解:∵840÷180=4…120,∴这个多边形的边数为:4+2=6,α=120°,故答案为:六;120.14.如图,把一个三角尺的直角顶点D放置在△ABC内,使它的两条直角边DE,DF分别经过点B,C,如果∠A=30°,则∠ABD+∠ACD= 60°.【解答】解:∵∠A=30°,∴∠ABC+∠ACB=150°,∵∠D=90°,∴∠DBC+∠DCB=90°,∴∠DBA+∠DCA=150°﹣90°=60°.故答案为:60°.15.如图,已知△ABC中,∠C=90°,AD平分∠BAC,且CD:BD=3:4.若BC=21,则点D到AB边的距离为9 .【解答】解:如图,∵CD:BD=3:4.设CD=3x,则BD=4x,∴BC=CD+BD=7x,∵BC=21,∴7x=21,∴x=3,∴CD=9,过点D作DE⊥AB于E,∵AD是∠BAC的平分线,∠C=90°,∴DE=CD=9,∴点D到AB边的距离是9,故答案为:9.16.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为48【解答】解:由平移的性质知,BE=6,DE=AB=10,∴OE=DE﹣DO=10﹣4=6,∴S四边形ODFC=S梯形ABEO =(AB+OE )•BE=(10+6)×6=48.故答案为48.三.解答题(共6小题满分56分)17.(8分)如图,在△ABC中,∠BFE=∠BDC,∠1=∠2,且∠3=115°,求∠ACB的度数.【解答】解:∵∠BFE=∠BDC,∴CD∥EF,∴∠2=∠BCD,∵∠1=∠2,∴∠1=∠BCD,∴DG∥BC,∴∠ACB=∠3=115°.18.(8分)如图,在等边三角形ABC中,∠ABC,∠ACB的平分相交于点O,BO,CO的垂直平分线分别交BC于点E、F,判断△OEF的形状,并说明理由.【解答】解:△OEF是等边三角形,∵E为BO垂直平分线上的点,且∠OBC=30°,∴BE=OE,∠EBO=∠EOB=30°,∴∠OEF=∠EBO+∠EOB=60°,同理,∠OFE=∠FCO+∠FOC=60°,∴△OEF为等边三角形,19.(10分)如图,点M是线段AB中点,AD、BC交于点N,连接AC、BD、MC、MD,∠l=∠2,∠3=∠4.(1)求证:△AMD≌△BMC;(2)图中在不添加新的字母的情况下,请写出除了“△AMD≌△BMC”以外的所有全等三角形,并选出其中一对进行证明.【解答】(1)解:∵点M是AB中点,∴AM=BM,∵∠1=∠2,∴∠AMD=∠BMC,在△AMD和△BMC中,,∴△AMD≌△MBC(ASA);(2)△AMC≌△BMD,△ABC≌△BAD,△ACN≌△BDN.理由:∵△AMD≌△MBC,∴AD=BC,∵∠3=∠4,AB=BA,∴△BAD≌△ABC(SAS),∴AC=BD,∠BDN=∠ACN,∵∠ANC=∠BND,∴△ANC≌△BND(AAS),∵AC=BD,∠CAM=∠DBM,AM=BM,∴△AMC≌△BMD(SAS).20.(10分)近年来,为减少空气污染,北京市一些农村地区实施了煤改气工程,某燃气公司要从燃气站点A向B,C两村铺设天然气管道,经测量得知燃气站点A到B村距离约3千米,到 C村距离约4千米,B,C两村间距离约5千米.下面是施工部门设计的三种铺设管道方案示意图.请你通过计算说明在不考虑其它因素的情况下,下面哪个方案所用管道最短。




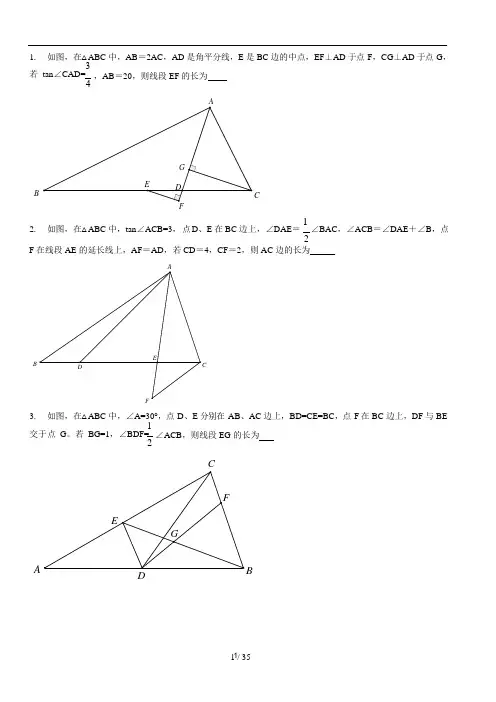
EDFEG1. 如图,在△ABC 中,AB =2AC ,AD 是角平分线,E 是 BC 边的中点,EF ⊥AD 于点 F ,CG ⊥AD 于点 G , 3若 tan ∠CAD= 4,AB =20,则线段 EF 的长为GEDC2. 如图,在△ABC 中,tan ∠ACB=3,点D 、E 在 BC 边上,∠DAE = 1∠BAC ,∠ACB =∠DAE +∠B ,点2F 在线段 AE 的延长线上,AF =AD ,若 CD =4,CF =2,则 AC 边的长为3. 如图,在△ABC 中,∠A=30°,点 D 、E 分别在 AB 、AC 边上,BD=CE=BC ,点 F 在 BC 边上,DF 与 BE 1交于点 G 。
若 BG=1,∠BDF= 2 ∠ACB ,则线段 EG 的长为D4. 如图,在△ABC 中,∠A =60°,角平分线 BD 、CE 交于点 F ,若 BC =3CD ,BF =2,则 BC 边的长为EB5. 如图,在△ABC 中,AB =AC ,∠ACD =45°,点 E 在射线 BD 上,AE//CD ,AE =DE ,若 BD =1,CD = 5,则 AE 的长为6. 如图,△ABC 中,∠AB =90°,CD 是 AB 边上的中线,点 F 在线段 AD 上,点 F 在 CD 延长线上,AE = DF ,连接 CE 、BF ,若∠AEC =∠DFB ,AC = 2 3 ,DF = 1,则线段 CE 的长为A B7. 如图,在等边△ABC 中,D 为 AB 边上一点,连接 CD ,在 CD 上取一点E ,连接BE ,∠BED =60°,若3CE =5,△ACD 的面积为35 43 ,则线段 DB 的长为B8. 如图,在Rt △ABC 中,∠BAC =90°,AC =6,点 D 是 AB 的中点,DE//BC , 点 F 为 BC 上一动点,连接 AF 交 DG 于 E ,∠AEC 恰好为 90°,连接 CE ,当 DE =2 时,线段AB 的长为BFC9. 如图,在Rt △ADB 中,∠ADB =90°,点C 为∠ADB 的角平分线上一点,连接 AC 、DC ,过点 A 作DB 的 平行线,分别交 DC 、BC 于点E 、F ,若 BE =BF ,AC = 2 5 ,则 AE 的长为N10. 已知:在△ABC 中,∠ACB =2∠ABC ,AD 为∠BAC 的平分线,E 为线段 AC 上一点,DE =DB ,过E 作 AD 的垂线交直线AB 于 F ,取BF 的中点 M ,连接 DM 。

初中几何证明中考压轴全国初中数学联赛必做100题第一部一、想一想、思一思、多种方法全等证明之割补法,(截取或延长)。
例1、(想一想、思一思、多种方法全等)如图,点E是BC中点,∠BAE=∠CDE ,求证:AB=CD证明:把CE绕C点顺时针旋转交DE于F,如图,∴CE=CF,∴∠1=∠2,∴∠4=∠3,∵点E是BC的中点,∴BE=CE=CF,在△BAE和△CDF中∠BAE=∠CDF∠3=∠4BE=CF∴△BAE≌△CDF(AAS),∴AB=CD.证明二:延长DE到G,使BE=BG证明三:延长DE到G,使AB=BG例2、(想一想、思一思、多种方法相似)如图,点E是BC上一点,BE=k·EC,∠BAE=∠CDE ,猜想 AB、CD 的数量关系.证明:把CE绕C点顺时针旋转交DE于F,如图,∴CE=CF,∴∠1=∠2,∴∠4=∠3,∴△BAE∽△CDF∴AB= k·CD例3、(想一想、思一思、多种方法全等)如图,在△ABC中,∠BAC=90°,AB= AC,CD∥BA,,点P是BC上一点,连结AP,过点P做PE⊥AP交CD于E. 想一想、思一思、咱来探究PE与PA的数量关系.答:PE=PA,理由如下:证明:过点P作PM⊥AC,垂足为M,过点P作PN⊥CD,垂足为N,∵△ABC中,∠BAC=90°,AB=AC,∴∠B=∠ACB=45°,∵CD∥BA,∴∠B=∠BCN=45°,∴∠ACB=∠BCN=45°,∵PM⊥AC,PN⊥CD,∴PM=PN,∵∠PMC=∠PNC=90°,∠ACB=∠BCN=45°,∴△PMC与△PNC都为等腰直角三角形,∴∠MPC=∠NPC=45°,即∠MPN=90°,∵∠APE=90°,∴∠APE-∠MPE=∠MPN-∠MPE,即∠APM=∠EPN,在△APM和△EPN中,∠AMP=∠EPN=90°PM=PN∠APM=∠EPN∴△APM≌△EPN(ASA),∴AP=EP.例4、(想一想、思一思、多种方法相似)如图,在△ABC中,∠BAC=90°,AB= k·AC,CD∥BA,,点P是BC上一点,连结AP,过点P做PE⊥AP交CD于E.想一想、思一思、咱来探究PE与PA的数量关系.证明:连接AE∵∠APE=∠ACE=90°∴APCE四点共圆∴∠ACP=∠AEP∴△ABC∽△PAE∴k·PE=PA证明二:过点P作AC,CD垂线,垂足F、G∴△ABC∽△FPC△APF∽△EPGPG=CF∴k·PE=PA如图,在△ABC中,AI为BC边上的中线。

第二题:证明四点共圆 (5)第三题:证明角的倍数关系 (6)第四题:证明线与圆相切 (7)第五题:证明垂直 (8)第六题:证明线段相等 (9)第七题:证明线段为比例中项 (10)第八题:证明垂直 (11)第九题:证明线段相等 (12)第十题:证明角平分 (13)第十一题:证明垂直 (14)第十二题:证明线段相等 (15)第十三题:证明角相等 (16)第十四题:证明中点 (17)第十五题:证明线段的二次等式 (18)第十六题:证明角平分 (19)第十七题:证明中点 (20)第十八题:证明角相等 (21)第十九题:证明中点 (22)第二十题:证明线段相等 (23)第二十一题:证明垂直 (24)第二十二题:证明角相等 (25)第二十三题:证明四点共圆 (26)第二十四题:证明两圆相切 (27)第二十五题:证明线段相等 (28)第二十六题:证明四条线段相等 (29)第二十七题:证明线段比例等式 (30)第二十八题:证明角的倍数关系 (31)第二十九题:证明三线共点 (32)第三十题:证明平行 (33)第三十一题:证明线段相等 (34)第三十二题:证明四点共圆 (35)第三十三题:证明三角形相似 (36)第三十四题:证明角相等 (37)第三十五题:证明内心 (38)第三十六题:证明角平分 (39)第三十七题:证明垂直 (40)第三十八题:证明面积等式 (41)第三十九题:证明角平分 (42)第四十题:证明角相等 (43)第四十一题:证明中点 (44)第四十二题:证明中点 (45)第四十三题:证明角相等 (46)第四十四题:证明垂直 (47)第四十六题:证明垂直 (49)第四十七题:证明四点共圆 (50)第四十八题:证明四点共圆 (51)第四十九题:证明四点共圆 (52)第五十题:证明角平分 (53)第五十一题:证明线段相等 (54)第五十二题:证明两圆外切 (55)第五十三题:证明垂直 (56)第五十四题:证明垂直 (57)第五十五题:证明垂直 (58)第五十六题:证明垂直 (59)第五十七题:证中点 (60)第五十八题:证明角相等 (61)第五十九题:证明角相等 (62)第六十题:证明四点共圆 (63)第六十一题:证明四点共圆 (64)第六十二题:证明四点共圆 (65)第六十三题:证明角相等 (66)第六十四题:证明角的倍数关系 (67)第六十五题:证明中点 (68)第六十六题:伪旁切圆 (69)第六十七题:证明垂直 (70)第六十八题:证明平行 (71)第六十九题:证明圆心在某线上 (72)第七十题:证明三线共点 (73)第七十一题:证明垂直 (74)第七十二题:证明垂直 (75)第七十三题:证明中点 (76)第七十四题:证明垂直 (77)第七十五题:证明垂直 (78)第七十六题:证明三线共点 (79)第七十七题:证明平行 (80)第七十八题:证明平行 (81)第七十九题:证明三线共点、证明垂直 (82)第八十题:证明三点共线(牛顿定理) (83)第八十一题:证明角平分 (84)第八十二题:证明角相等 (85)第八十三题:证明三点共线 (86)第八十四题:证明四圆共点 (87)第八十五题:证明角平分 (88)第八十六题:证明线段相等 (89)第八十七题:证明角相等 (90)第八十八题:证明线段相等 (91)第九十题:证明线段相等 (93)第九十一题:证明中点 (94)第九十二题:证明四点共圆 (95)第九十三题:证明西姆松定理及逆定理 (96)第九十四题:证明线段的和差关系等式 (97)第九十五题:证明角相等 (98)第九十六题:证明托勒密定理及逆定理 (99)第九十七题:证明线段的和差关系等式 (100)第九十八题:证明角相等 (101)第九十九题:证明四点共圆 (102)第一百题:证明两三角形共内心 (103)已知PE 、PF 是⊙ O 的切线,A 、B 是一组对径点,PB 交⊙O 于另一点C ,直线AF 、BE 交于D 点。

中考数学超百分特训--几何图形求极值类题目(教师版)1.如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE上的动点,过点N作NP//EM交MC于点P,则MN+NP 的最小值为.解析:作点P关于CE的对称点,P’,连接MP’,交CE于N,此时MP’=MN+NP,∴当MP’CD 时,MP’最小,连接DM交CE于H,则DM CE,DH=MH== ,CH= ,DM ・CH=CD・MP’∴MP’=∴MN+NP的最小值为2.如图,在矩形中,,,为中点,为上一动点,则的最小值为.解析:作点E关于CD的对称点,连接AE’,AF+EF的最小值即为AE’,CE’=CE=2,BE’=6,由勾股定理可得AE’=33.如图,正方形ABCD的边长为8,∠DAC的平分线交DC于点E.若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是.解析:作点P关于AE的对称点P’,DQ+PQ的最小值为DP’,而DP’与AC垂直时最小,所以DQ+PQ的最小值是=44.如图,点为矩形的对角线上一动点,点为的中点,连接,,若,,则的最小值为.解析:作点B关于AC的对称点,连接BC’,由,,可得∠BCA=30°,故△B’BC为等边形三角形,BP=B’P,当B’E BC时,B’E最小,此时B’E=6,故的最小值为6.5.已知:点E是正方形ABCD边上的一点,将线段AE绕点E顺时针旋转90°,得到线段EA′,若AB=2,则线段DA′的最小值为解析:过点D作DH CA’于H,在AB上取点F,使AF=CE,∠EAF=∠A’EC,AE=A’E,∴△EAF≌△A’EC∴∠AFE=∠A’CE∵AF=CE∴BF=BE,∴∠BFE=45°,∴∠AFE=∠A’CE=135°∴∠DCA’=45°,无论E点怎样运动,∠DCA’=45°保持不变,∴DA’的最小值即DH,DH==6.如图,在Rt△ABC中,∠BAC=90°,且BA=6,AC=8,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为.解析:连接AD,∵四边形AMDN为矩形,∴MN=AD,当AD最小时,即MN最小,当AD CB时,AD最小,此时AD==4.87.如图,点是内任意一点,,点和点分别是射线和射线上的动点,,则周长的最小值是.解析:分别作点P关于OA、OB的对称点F、E,连接OE,OF,EN,FM,EF由对称可知OE=OP=OF,∠BOE=∠BOP,∠AOP=∠AOF,∴∠EOF=2∠AOB=60°,△EOF为边长是3的等边三角形,由对称可知,PN=EN,PM=FM,∴周长的最小值是EF,EF=38.如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为()解析:分别作点C关于直线AB及Y轴的对称点M,N,连接AM,FN,EM,由对称知ME=CE,FN=CF,∴周长的最小值是MN;一次函数的图象与x轴夹角∠BAO=45度∴∠MAC=90°,AM=AC=2,∴M(-4,2)∵N(2,0)∴MN的解析式为y= - x+ ∴,9.如图,和都是等腰直角三角形,,,O为AC 中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是()解析:连接CE,由题意可知△ACE≌△ABD,∴∠ABD=∠ACE=45°∴CE BC当OE CE时,OE最小,此时△OCE为等腰三角形,∵OC=2,∴OE=10.如图,在矩形中,,,动点满足,则点到、两点距离之和的最小值为()A.B.C.D.解析:过点P作AB的平行线,交AD于M,BC于N,作点B关于MN的对称点B’,连接AB’交MN 于P,AP+BP的最小值为AB’,∵,AD=BC=3∴BN=2,∴BB’=4∴AB’=∴AP+BP的最小值为11.如图,在矩形ABCD中,AB=4,BC=8,E为CD边的中点,P,Q为BC边上两个动点,且PQ=2,当四边形APQE的周长最小时,BP的长为()解析:将AP沿AD方向平移2个单位,使点A落在A’点,作点E关于BC的对称点E’,连接A’E’,当A’E’交BC于点Q时,AP+QE最小,此时AP+QE=A’E’,AE、PQ的长度一定,所以此时四边形APQE的周长最小。

中考数学平面几何 100 题难度排行:红字偏难,黑字为常见难度1.在锐角△ABC中,AB<AC,AB 是BC 边上的高,P 是线段 AD上一点,过 P 作PE⊥AC,垂足为 E,作PF⊥AB,垂足为 F,O1,O2 分别是△BDF,△CDE外心.证明:O1.O2.E.F 共圆的充要条件为 P 是△ABC的垂心.2.设 H 是△ABC 的垂心,D.E.F 分别是△ABC 外接圆上三点,且AD∥BE∥CF,S.T.U 分别为 D.E.F 关于 BC.CA.AB 的对称点,证明:S.T.U.H 四点共圆3.在△PAB中,E.F 分别是边PA.PB 上的点,在AP.BP 的延长线上分别取点 C.D 使得 PC=AE,PD=BF,点 M.N 分别是△PCD,△PEF 的垂心,证明:MN⊥AB4.过△ABC外心O 任作直线,交边 AB.AC 于M.N;E.F 分别是BN.CM 的中点.证明:∠EOF=∠A5.P 为△ABC 内一点, D.E.F 分别是 BC.CA.AB 上的点,且PD⊥BC,PE⊥CA,PF⊥AB,△ABC内的一点 H 满足∠HAB =∠PAC,∠HCB=∠PCA,证明:DE⊥EF,当且仅当 H 是△BDF 垂心.6.锐角△ABC三边长互不相等,其垂心为 H,D 是BC 中点,直线BH 与AC 交于E,直线 CH 与AB 交于F,直线 AH 与BC 交于T,BDE 与○CDF 交于G,直线 AG 与○BDE.○CDF分别交于 M.N,证明:(1)AH 平分∠MTN,(2)ME.NF.AH 三线共点.7.凸四边形 ABCD 的外接圆圆心为 O,已知AC≠BD,且 AC 与 BD交于E,若P 为ABCD 内部一点,且∠PAB+∠PCB=∠PBC+∠PDC=90°,证明:P.O.E 共线8.与等腰△ABC两腰AB.AC 都相切的圆ω交BC 与K 和L,联结AK,交圆ω于一点另一点 M,点 P.Q 分别是点 K 关于点B 和点C 的对称点,证明:△PMQ的外接圆和圆ω相切9.在△ABC中,D 是 BC 边上一点,O1.O2.分别是△BAD.△ACD外心,O′是经过 A.O1.O2 三点的圆的圆心.记△ABC的九点圆心为V,作O′E⊥BC于E,证明:VE∥AD10.在△ABC中,AB>AC,内心为 I,内切圆分别切BC.CA.AB 于D.E.F,M是B C中点,A H是高,直线A I与D E.D F分别交于K.L,证明:M.L.H.K 四点共圆11.○O为△ABC 外接圆 AM.AD 分别为中线与角平分线,过B.C 分别作切线相交于P,A P交B C于E,交○O于F,证明:D是△A M F内心.12.锐角△ABC,点 D.E.F 分别是 BC.CA.AB 上的高的垂足,I1,I2,I3 分别是△AEF,△BDF,△CDE的内心,L1 是○I2 与圆I3 不同于BC 的外公切线,类似定义 L2.L3,证明:L1,L2.L3 共点,且此点是△I1I2I3 外心13.锐角△ABC中,AB<AC,M 为边 BC 中点,点 D 和点 E 分别是△ABC 外接圆弧 BAC 和 BC 中点,F 为△ABC 内切圆在AB 上的切点,AE 和 BC 交于 G,N 点在线段 EF 上,满足NB⊥AB,证明:若 BN=EM,则DF⊥FG14.两圆内切.ABCD 为大圆上顺次四点,AC.BD 分别切小圆于E.F,B 与小圆在 AC 同侧,证明:EF 过△ABC 内心15.在△ABC中,D.E 分别在 AB.AC 上,ED∥BC,BD.CE 交于 F,证明:△AEF.△ADF,△EFB,△DFC四个外心共圆16.D.E.F 分别在△ABC 边 BC.CA.AB 上,并且 AD.BE.CF 交于一点G,△AFG,△BFG,△BGD,△GDC,△CGE,△AGE的外心分别为O i(i=1,2,3,4,5,6),且他们互不相同,证明:O i六点共圆的充要条件为 G 是△ABC 重心17.○O是△ABC 的外接圆,D 在弧 AB 上,△CAD,△CBD的内心分别为 E.F,○DEF与○O 的另一个交点为 X,证明:当 D 点在弧AB 上运动时,X 是一个定点18.四边形 ABCD 的边AD.BC 交于P,AB 与CD 不平行,△ABP,△CDP的外心分别为 O1,O2,垂心分别为 H1,H2,O1H1,O2H2 中点分别为 E1,E2,过 E1.E2 分别作 CD.AB 的垂线.证明:两条垂线和H1H2 共点19.△ABC外心为 O,BO 与 AC 交于 F,CO 与 AB 交于 E,EF的垂直平分线交B C于D,D E与B F交于M,D F与C E交于N,若E M.F N的垂直平分线交于 EF 上一点 K,证明:∠BAC=90°20.点 P 在以△ABC 垂心 H 为圆心的圆上运动,P 在三边的射影分别是D.E.F,证明:s i n(2A)·P D2+s i n(2B)·P E2+s i n(2C)·P F2为定值.21.△A B C内接于圆O,I为内心,M为弧 B C中点,A′是A关于O 的对径点,D 为△ABC 内切圆和 BC 的切点,AE⊥BC于E,直线A′D和M E交于K,证明:D M⊥I K22.P 为△ABC 内一点,满足∠PAC=∠PCB=∠PBA=30°,证明:△ABC 为等边三角形23.在△ABC中,点A1 在边 BC 上,点B1 在边 AC 上,点P 和点Q 分别在 AA1 和 BB1 上,且PQ∥AB,在直线 PB1 上取点 P1 使得 B1 严格位于 P 和P1 之间,且∠PP1C=∠BAC,类似地,在直线 QA1 上取点 Q1 使得使得 A1 严格位于点 Q 和点 Q1 之间,且∠CQ1Q=∠CBA,证明:P.Q.P1.Q1 共圆24.凸五边形 ABCDE 内接于○O,且 AB=CD=EA,对角线BE.CE 相交于点 P,点 H 为△ABE 垂心,M.N 分别是 BC.DE中点,G 是△AMN 重心,直线 PH,OG 相交于 T,证明:AT⊥CD25.在锐角三角形 ABC 中,AB>AC,点 E.F 分别在 AC.AB 上,满足B F+C E=B C,点I B,I C分别是∠B,∠C内的旁心,直线E I C,F I B 相交于点T,点K为弧B A C中点,直线K T与△A B C的外接圆交于 K.P,证明:T.F.P.E 四点共圆.26.等腰△ABC 中,AB=AC,AC 边上一点 D 及 BC 延长线上一点 E,满足2AD·CE=DC·BC,以 AB 为直径的圆ω与线段 DE 交于一点 F,证明:BCFD 共圆27.在△ABC平面内,存在唯一一组点(P.Q)使得 P.Q 关于△ABC 互为等角共轭,且满足 PA+QA=PB+QB=PC+QC28.在△ABC中,P1,P2 为一组等角共轭点,点 P1 在 BC.CA.AB 上的射影分别是 D1.E1.F1,直线 D1P1 与 E1F1 交于点 K1,直线 AK1 与BC 交于点 X1 类似定义 X2,证明 BX1=CX229.△ABC的内切圆○I 分别与 BC.CA.AB 相切于 D.E.F 联结AD 交○I 于点P ,联结BP 交○I 于点H ,证明:PH·DE·DF=EF·DP·DH30.在△ABC中,以 AB.AC 为直径的圆ω1,ω2,M 是∠BAC 角平分线 AD 的中点,BK 的延长线分别交ω1,ω2 于 E.F,CK 的延长线分别交ω1,ω2 于点 F.G 证明:○AEF 和○AFG 外切31.在△ABC 中,∠A ,∠B 均为锐角,CD⊥AB于,且CD2·BC2+AC2·CD2=AC2·BC2,证明:∠ACB=90°32.△ABC和△AB′C′共外接圆,P 为外接圆上任一点,证明:P 关于△ABC 和 P 关于△AB′C′的西姆森线平行的充要条件是BC∥B′C′33.凸四边形ABCD 中,对角线BD,AC 交于M,△AMB,△CMD 的垂心分别是S.R ,△A M D,△B M C的重心分别是I.Q,证明:I Q⊥S R34.△ABC中,AD⊥BC于D,BF⊥AC于E,CG⊥AB于F,联DE.EF.DF,证明:△AEF,△BDE,△CDF的欧拉线共点,且交点在九点圆上35.△ABC中,AY⊥BC于 Y,记 O 为外心,A O交 BC 于 X,过B.C 引外接圆切线交于 L,D 为内切圆在 BC 上的切点,I 为内心,PQ 是过O I的外接圆直径(P.Q端点),证明:P X Y Q共圆当且仅当A D L共线36.△A B C中,P为∠B A C平分线上一点,O1,O2,O3分别是△A P B,△APC,△BPC外心,K 为△O1O2O3 外心,证明:OK∥AP(其中O 是△ABC外心)37.圆 O1,O2 相交于 A.B 两点,CD 是两圆靠近 B 的外公切线,P 是圆 O1 上一点,Q 是圆 O2 上一点,PC.QD 延长线交于 R,若 AR平分∠PAQ,证明:PQ∥CD或PBQ 共线38.已知圆 O1 和圆 O2 相交于 P.Q 两点,O 是连心线 O1O2 的中点,过P 作两条不重合的割线 AB 和CD,(其中 A.C 在圆O1 上,B.D 在圆O2上),联结A D并取其中点M,联C B 并取其中点N,证明:O到直线 MN 的距离小于 O 到PQ 的距离.39.四边形 ABCD 内接于圆,O 是外心,E 是对角线交点,P 是平面内任一点,O1,O2,O3,O4 分别是△PAB,△PBC,△PCD,△PDA 外心,证明:OE,O1O3,O2O4 共点40.平面内有七个圆,其中六个圆含于一个大圆内,且没个圆都和大圆相切,六个圆两两相切,记六个圆在大圆上的切点依次为A i(i=1.2.3.4.5.6),证明:A1A4.A2A5.A3A6共点41.△ABC内切圆与 BC.AC.AB 相切于点 D.E.F,一圆与△ABC 内切圆切于 D,与△ABC 外接圆切于 K,M.N 类似定义,证明:DK,EM.FN 共点,且此点在△DEF 的欧拉线上42.圆O1,O2分别是△A B C的C-旁切圆,B-旁切圆,O1与A C.B C分别相切于 G.H,圆 O2 分别与 AB.BC 相切于 L.K,直线O1L 和直线O2G 相交于 P,证明:AP⊥GL43.从圆Ω外一点 P 作圆Ω的切线 PA.PB,AA′,BB′分别是圆Ω的两条直径,点 C.D 分别在切线 PA.PB 上,过 C 且垂直于 AB 的直线与∠ABB′的平分线交于 C′,过 D 且垂直于AB 的直线与∠A′AB的平分线交于 D′,证明:C,D′,A′共线当且仅当C′DB′共线44.四条直线相交成四个三角形,这四个三角形的垂心共线45.已知△ABC,A1,A2,A3 分别在高线 AD.BE.CF 上若 S△ABC =S△ABC1+S△BCA1+S△CAB1,证明:△A1B1C1 外接圆通过△ABC的垂心46.四边形 ABCD 内接于圆, E 为 BC 上一点, E 在直线A B.B D.A C.C D上的射影分别是M.N.Q.P,直线M N与P Q交于点K,直线 EK 与AD 交于F,证明:KE=KF47.等腰三角形A B C中,A B=A C,三角形内存在一点P使得∠P B C=45°,∠PCB=15°,且 AP=BP+CP,求∠ABC48.在梯形 ABCD 中,AD∥BC,P 为 BC 上任一点,PE∥AC交AB 于 E,PF∥BD交 CD 于 F,EF 分别交 BD.AC 于点 G.H,证明:EG=FH49.在不等腰锐角三角形ABC 中,三条高线 AD.BE.CF 的中点依次为 P.S.T,内心为 I,外心为 O,内切圆○I 与边BC.CA.AB 分别相切于M.N.L,证明:P M.S N.T L共点,且此交点和O I共线50.△ABC中,M 是BC 中点,点E.F 分别是M 关于AC.AB 的对称点,直线FB.EC 交于P,点 Q 满足QA=QM,∠QAP=90°,O 是△PEF 外心,证明:AO⊥OQ51.△ABC中,AB>AC,∠BAC的角平分线交 BC 于D,线段AD的垂直平分线与 AB.AC 分别交于 E.F,点 X 在 BC 上,且BX·CF=XC·BE,AX 交△ABC 外接圆于 Y,已知 BC=a,CA=b,AB= c,求△ADY外接圆半径52.△ABC 中,BC>CA>AB,BE.CF 是角平分线,外接圆弦BQ∥EF,QP∥AC,证明:PC=PA+PB53.已知△ABC 为给定三角形,D 在 BC 上,E 在 AB 上,F 在AC 上,且△DEF为正三角形,求 S△DEF 最小值54.设F是双曲线定点,A是右焦点,△H I J的内切圆是以A为圆心A F为半径的圆.过H.I作双曲线的切线交于K,证明:K A J 共线55.已知正△XYZ 的顶点分别在△ABC 的边 BC.CA.AB 上,证明:△ABC 的内心在△XYZ 的内切圆的内部56.△ABC 内接于圆 O,∠ABC>90°,M 是边 BC 中点,点 P在△ABC内,满足PB⊥PC,过P 作AP 的垂线,D.E 是该垂线上不同于 P 的两点,满足 BD=BP,CE=CP,若四边形 ADOE 是平行四边形,证明:∠OPE=∠AMB57.设 A 为○Ω外一点,直线 AB.AC 分别与圆Ω相切于 B.C 两点,设 P 是劣弧 BC 上的一个动点,过点 P 作Ω的切线分别于A B.A C相交于点D.E,直线B P.C P分别与∠B A C的内角平分线交于点 U.V,过点 P 作 AB 的垂线,与直线 DV 交于 M,过点 P 作A C的垂线,与直线 EU 交于点 N,证明:存在一个与点P 无关的定点 L,使得 MNL 共线58.△ABC中,AB>AC,M 是边 BC 的中点,○M 以 BC 为直径,直线 AB.AC 分别与○M 交于点 D(异于 B),E(异于 C),已知在△ABC内的点 P 满足∠PAB=∠ACP,∠CAP=∠ABP,BC²=2DE·MP,在○M外的点 X 满足XM∥AP,XB·AC=XC·AC,证明:∠BXC+∠BAC=90°59.锐角三角形 ABC 中,AB<AC,AD 是 BC 边上的高,D 是垂足,I 是△ABC内心,J 是A-旁心,点 E 在边 AB 上,点 F 在AB 延长线上满足 BE=BF=BD,证明:在△ABC 外接圆上存在两点P.Q(可以重合),满足P B=Q C,并且△P E I∽△Q FJ60.锐角△ABC中,作出角平分线 BL,D.E 分别是△ABC 外接圆上弧 AB 和弧 BC 中点,线段 BD 的延长线上取一点 P,在线段BE 的延长线上取一点 Q,使得∠APB=∠CQB=90°,证明:线段 BL 的中点与 P.Q 共线61.锐角△ABC 内有 P.Q 两点满足∠ACP=∠BCQ,∠CAP=∠BAQ,过点 P 作 BC.CA.AB 的垂线,垂足为 D.E.F,证明:∠DEF=90°当且仅当 Q 是△BFD 垂心62.在△ABC周围作3 个任意三角形△DBC,△ECA,△FAB,他们的顶点围成△DEF ,再向△DEF 周围作三个三角形△A′FE,△B′DF,△C′ED 相应地,使他们与△DBC,△ECA,△FAB 顺向相似,证明:△A′B′C′∽△ABC63.圆周上有 ABCD 四点,证明:其中一点关于另三点围成的三角形的三条西姆森线共点64.设○O1,O2 交于 P.Q 两点,过点 P 任作两条直线 APB,CPD,其中A.C在○O1上,点B.D在○O2上,M.N分别是A D.B C中点,O为O1O2 中点,∠APC=θ为锐角,设 h 为点O 到MN 的距离,K 为PQ 中点,证明:h=OK·cosθ65.锐角△ABC 中,I 是内心AB≠AC,△ABC的内切圆ω与边BC.CA.AB 分别相切于点 D.E.F 过D 点且垂直于 EF 的直线与ω另一个交点为 R.直线 AR 与ω另一个交点为 P,△PCE 和△PBF 的外接圆交于另一点Q.证明:直线D I和P Q的交点在过A且垂直于A I的直线上.66.在△A B C中,I为内心,T为A I与B C的交点,J为A-胖切圆与边 BC 的切点,△AJT 的外接圆和△ABC 的外接圆第二个交点为F,过I作I S⊥A T,与B C交于点S,A S与△A B C外接圆的第二个交点为 E,证明:EF∥BC.67.已知五角星形A B C D E F G H I J,△I B C,△J B A,△E A G,△F E D,△HDC的外接圆轮回相交,两两交点分别是 K.O.N.M.L,记LB 和 AN 交于 Q 类似定义 T.S.R.P,记 JO 与 FN 交于 U 类似定义W.Z.V.A1.证明:K O N M L Q TS R P U W Z V A1共圆∠XAY为一个固定的角,B.C 分别是射线 AX.AY 上的动点,∠XAY内有一点P 满足PA.PB.PC 的长均为定值,求△ABC 的最大值答:设P是△A B C内的任意点,O.O A.O B.O C分别是△A B C,△P B C,△P C A,△P A B 外心,O B C,O C A,O A B 分别是△P O B O C,△P O C O A,△P O A O B的外心, O′,O′分别是△O A O B O C ,△O BC O CA O AB 外心,证明:OP∥OO′′68.设△ABC 的外心为 O,在∠A 的角平分线上取一点 P,分别作P在A B.B C.C A.上的射影D.E.F,若△D E F的外接圆交B C于另外一点 G,设 H 为△EFG 垂心,求证:O.P.H 共线。

第17章 几何不等式与极值问题17.1.1★ 一个凸行边形的内角中,恰好有4个钝角,求n 的最大值.解析考虑这个凸行边形的n 个外角,有4n -个角90︒≥,故有()490360n -⨯︒<︒(严格小于是由于4个钝角的外角和大于0︒),因此8n <,n 的最大值是7.易构造这样的例子。
如果恰好有k 个钝角,则n 的最大值是3k +. 17.1.2★ 在ABC △中,A B A C >,P 为BC 边的高AD 上的一点,求证:AB AC PB PC -<-.PCDB A解析易知AB AC PB PC +>+,又2222AB AC BD CD -=- 22PB PC =-,故有AB AC PB PC -<-.评注 读者不妨考虑AD 是角平分线与中线的情况.17.1.3 已知四边形ABCD ,AC 、BD 交于O ,ADO △和BCO △的面积分别为3、12,求四边形ABCD 面积的最小值.CB ODA解析易知ABO BCOADO DCOS S BO S DO S ==△△△△,故36ABO CDO ADO BCO S S S S ⋅=⋅=△△△△.从而12ABO CDO S S +=△△≥,且当ABO CDO S S =△△(此时四边形ABCD 为一梯形)时等号成立,所以此时四边形ABCD 面积达到最小值27.17.1.4★ 已知:直角三角形ABC 中,斜边BC 上的高6h =. (1)求证:BC h AB AC +>+; (2)求()()22BC h AB AC ++-. 解析()()22BC h AB AC +-+222222BC h BC h AB AC AB AC =++⋅---⋅,由条件,知242ABC BC h S AB AC ⋅==⋅△,且222AB AC BC +=, 于是()()22236BC h AB AC h +-+==.注意:这同时解决了(1)和(2).17.1.5★ 设矩形ABCD ,10BC =,7CD =,动点F 、E 分别在BC 、CD 上,且4BF ED +=,求AFE △面积的最小值.B FCED A解析设 BF x=,()4DE y x ==-,则()()()117101077022ABF ADE ECF S S S x y x y xy ++=++--=+⎡⎤⎣⎦△△△。
数学初中竞赛几何专题训练1.如图,在正方形ABCD中,N为边AD上一点,连接BN.过点A作AP⊥BN于点P,连接CP,M为边AB上一点,连接PM,∠PMA=∠PCB,连接CM,有以下结论:①△PAM∽△PBC;②PM ⊥PC;③M、P、C、B四点共圆;④AN=AM.其中正确的个数为()A.4 B.3 C.2 D.1解:∵AP⊥BN,∴∠PAM+∠PBA=90°,∵∠PBA+∠PBC=90°,∴∠PAM=∠PBC,∵∠PMA=∠PCB,∴△PAM∽△PBC,故①正确;∵△PAM∽△PBC,∴∠APM=∠BPC,∴∠CPM=∠APB=90°,即PM⊥PC,故②正确;∵∠MPC+∠MBC=90°+90°=180°,∴B、C、P、M四点共圆,∴∠MPB=∠MCB,故③正确;∵AP⊥BN,∴∠APN=∠APB=90°,∴∠PAN+∠ANB=90°,∵∠ANB+∠ABN=90°,∴∠PAN=∠ABN,∵∠APN=∠BPA=90°,∴△PAN∽△PBA,∴,∵△PAM∽△PBC,∴,∴,∵AB=BC,∴AM=AN,故④正确;故选:A.2.如图①,若BC是Rt△ABC和Rt△DBC的公共斜边,则A、B、C、D在以BC为直径的圆上,则叫它们“四点共圆”.如图②,△ABC的三条高AD、BE、CF相交于点H,则图②中“四点共圆”的组数为()A.2 B.3 C.4 D.6解:如图,以AH为斜边的两个直角三角形,四个顶点共圆(A、F、H、E),以BH为斜边的两个直角三角形,四个顶点共圆(B、F、H、D),以CH为斜边的两个直角三角形,四个顶点共圆(C、D、H、E),以AB为斜边的两个直角三角形,四个顶点共圆(A、E、D、B),以BC为斜边的两个直角三角形,四个顶点共圆(B、F、E、C),以AC为斜边的两个直角三角形,四个顶点共圆(A、F、D、C),共6组.故选:D.3.如图,在四边形AOBC中,若∠1=∠2,∠3+∠4=180°,则下列结论正确的有()(1)A、O、B、C四点共圆(2)AC=BC(3)cos∠1==(4)S四边形AOBCA.1个B.2个C.3个D.4个解:∵∠3+∠4=180°,∴A、O、B、C四点共圆,(1)正确;作CD⊥OA于D,CE⊥OB于E,如图所示:则∠CDA=∠CEB=90°,∵∠1=∠2,∴CD=CE,∵∠3+∠4=180°,∠3+∠CAD=180°,∴∠CAD=∠4,在△ACD和△BCE中,,∴△ACD≌△BCE(AAS),∴AD=BE,AC=BC,(2)正确;∵cos∠1==,cos∠2==,∴cos∠1+cos∠2=+==,∵∠1=∠2,∴cos∠1=cos∠2,∴2cos∠1=,∴cos∠1=,(3)正确;∵CD=CE,sin∠1=,∴CD=c×sin∠1,∴S四边形AOBC =S△OAC+S△BOC=a×CD+b×CE=(a+b)CD=(a+b)×c×sin∠1=,(4)正确;正确的结论有4个,故选:D.4.点C是半径为1的半圆弧AB的一个三等分点,分别以弦AC、BC为直径向外侧作2个半圆,点D、E也分别是2半圆弧的三等分点,再分别以弦AD、DC、CE、BE为直径向外侧作4个半圆.则图中阴影部分(4个新月牙形)的面积和是()A.B.C.D.解:易知D、C、E三点共线,点C是半径为1的半圆弧AB的一个三等分点,∴对的圆心角为=60°,∴∠ABC=30°,∵AB是直径,∴∠ACB=90°,∴AC=AB=1,BC=AB•COS30°=,BE=BC•COS30°=,CE=DC=,AD=,且四边形ABED为直角梯形,外层4个半圆无重叠.从而,S阴影=S梯形ABED+S△ABC﹣,=S△ADC +S△BCE,=.故选:B.5.如图,已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M,过D任作一条与直线BC不重合的直线l,直线l分别与直线MB、M C交于点P、Q,下列判断错误的是()A.无论直线l的位置如何,总有直线PM与△ABD的外接圆相切B.无论直线l的位置如何,总有∠PAQ>∠BACC.直线l选取适当的位置,可使A、P、M、Q四点共圆D.直线l选取适当的位置,可使S△APQ <S△ABC解:假设A、P、M、Q四点共圆,根据相交弦定理可得:DA•DM=DP•DQ,∵A、B、M、C四点共圆,∴根据相交弦定理可得:DA•DM=DB•DC,∴DP•DQ=DB•DC,即=,∵∠BDP=∠QDC,∴△DBP∽△DQC,∴∠BPD=∠QCD,∵AM平分∠BAC,∴∠BAM=∠MAC,∵∠MBC=∠MAC,∠MCB=∠BAM,∴∠MBC=∠MCB,∴∠BPD=∠MBC.与∠MBC=∠BPD+∠BDP矛盾,故假设不成立,因而命题C错误,故选:C.6.已知,在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合的一动点,Q是边BC上的任意一点,连结AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ 交DQ于F.则△PEF面积的最大值是()A.B.C.D.解:设PD =x ,S △PEF =y ,S △AQD =z ,梯形ABCD 的高为h ,∵AD =3,BC =4,梯形ABCD 面积为7, ∴, 解得:,∵PE ∥DQ , ∴∠PEF =∠QFE ,∠EPF =∠PFD ,又∵PF ∥AQ ,∴∠PFD =∠EQF ,∴∠EPF =∠EQF ,∵EF =FE ,∴△PEF ≌△QFE (AAS ),∵PE ∥DQ ,∴△AEP ∽△AQD ,同理,△DPF ∽△DAQ , ∴=()2,=()2,∵S △AQD =3,∴S △DPF =x 2,S △APE =(3﹣x )2,∴S △PEF =(S △AQD ﹣S △DPF ﹣S △APE )÷2,∴y =[3﹣x 2﹣(3﹣x )2]×=﹣x 2+x ,∵y 最大值==,即y 最大值=.∴△PEF 面积最大值是,故选:D .7.如图,正ABC 中,P 为正三角形内任意一点,过P 作PD ⊥BC 、PE ⊥AB ,PF ⊥AC ,连AP 、BP 、CP ,如果S △AFP +S △PCD +S △BPE =,那么△ABC 的内切圆半径为( )A .1B .C .2D .解:过P 点作正三角形的三边的平行线,于是可得△MPN ,△OPQ ,△RSP 都是正三角形,四边形ASPM ,四边形NCDP ,平行四边形PQBR 是平行四边形,故可知黑色部分的面积=白色部分的面积,又知S △AFP +S △PCD +S △BPE =, 故知S △ABC =3,S △ABC =AB 2sin60°=3, 故AB =2,三角形ABC 的高h =3,△ABC 的内切圆半径r =h =1.故选:A .8.如图所示,已知△ABC 面积为l ,点D 、E 、F 分别在BC 、CA 、AB 上,且BD =2DC ,CE =2EA ,AF =2FB ,AD 、BE 、CF 两两相交于P 、Q 、R ,则△PQR 的面积为( )A .B .C .D .解:连接BR ,设△CDR 的面积为a ,△BRF 的面积为b ,∵BD =2DC ,AF =2FB ,∴△BDR 的面积为2a ,△ARF 的面积为2b ,∵已知△ABC 面积为l ,∴S △CDR +S △B DR +S △BRF =,S △BDR +S △BRF +S △ARF = ∴,解得,∴△CDR 的面积为,同理可得S △APE =S △BFQ =, S △PQR =S △BCE ﹣(S △BCF ﹣S △BFQ )﹣(S △ACD ﹣S △APE ﹣S △CDR )=﹣+S △BFQ ﹣+S △APE +S △CDR =S △BFQ +S △APE +S △CDR =×3=.故选:C .9.观察图(1),容易发现图(2)中的∠1=∠2+∠3.把图(2)推广到图(3),其中有8个角:∠1,∠2,…,∠8.可以验证∠1=∠2+∠5+∠8成立.除此之外,恰好还有一组正整数x ,y ,z ,满足2≤x ≤y ≤z ≤8,使得∠1=∠x +∠y +∠z ,那么这组正整数(x ,y ,z )=( )A .(3,4,7)B .(3,5,7)C .(3,3,7)D .(4,6,7) 解:∵小正方形的边长为1,∴∠1=45°,∵∠1=∠x +∠y +∠z ,∴∠x +∠y +∠z =45,∵一组正整数x ,y ,z ,满足2≤x ≤y ≤z ≤8,“第二条对角线和第三条对角线形成的三角形”与“第二条对角线和第七条对角线形成的三角形”相似,∠2是“第二条对角线和第七条对角线形成的三角形”的外角,∠2=∠7+∠α(∠α是∠3的对应角),而∠1=∠2+∠3,∴∠1=∠2+∠3=∠3+∠3+∠7.∴这组正整数(x ,y ,z )=3,3,7;故选:C .10.如图,在Rt △ABC 中,∠ACB =90°,内切圆⊙I 切AC 、BC 于E 、F ,射线BI 、AI 交直线EF 于点M 、N ,设S △AIB =S 1,S △MIN =S 2,则的值为( )A .B .2C .D .3解:连接IE 、IF 、IG ,IC 与EF 交于H ,设内切圆⊙I 的半径为r ,∵∠C =90°,它的内切圆⊙I 分别与边AC 、BC 相切于点E 、F ,∴四边形CEIF 是正方形,HI =IC =r , ∴△CEF 是等腰直角三角形,∴∠CEF =∠CFE =45°,∴∠NFB =∠CFE =45°,∠MEA =∠CEF =45°,∴∠NIB =∠AIM =∠IAB +∠IBA =(∠CAB +∠CBA )=45°,∴∠M =∠CAN =∠IAB ,∠N =∠CBM =∠IBA ,∴△NIM ∽△BIA , ∴=()2=()2=2,故选:B .11.如图,若干个正三角形的一边在同一条直线a 上,这边对的顶点也在同一条直线b 上,它们的面积依次为S 1,S 2,S 3,S 4…若S 1=1,S 2=2,则S 6等于( )A .16B .24C .32D .不能确定解:∵△AEF 、△BFG 、△CGH 都是等边三角形, ∴∠AFE =∠BGF =60°,∠BFG =∠CGH =60°, ∴AF ∥BG ,BF ∥CG ,∴∠BAF =∠CBG ,∠ABF =∠BCG , ∴△ABF ∽△BCG , ∴=.∵△AEF 、△BFG 、△CGH 都是等边三角形, ∴△AEF ∽△BFG ∽△CGH , ∴=()2,=()2,∴=,∴=,∴S22=S1•S3.∵S1=1,S2=2,∴S3=4.同理S32=S2•S4,则有S4=8;S 42=S3•S5,则有S5=16;S 52=S4•S6,则有S6=32.故选:C.12.如图,在四边形ABCD中,AC、BD为对角线,点M、E、N、F分别为AD、AB、BC、CD边的中点,下列说法:①当AC=BD时,M、E、N、F四点共圆.②当AC⊥BD时,M、E、N、F四点共圆.③当AC=BD且AC⊥BD时,M、E、N、F四点共圆.其中正确的是()A.①②B.①③C.②③D.①②③解:连接EM、MF、FN、NE,连接EF、MN,交于点O,如图所示.∵点M、E、N、F分别为AD、AB、BC、CD边的中点,∴EM∥BD∥NF,EN∥AC∥MF,EM=NF=BD,EN=MF=AC.∴四边形ENFM是平行四边形.①当AC=BD时,则有EM=EN,所以平行四边形ENFM是菱形.而菱形的四个顶点不一定共圆,故①不一定正确.②当AC⊥BD时,由EM∥BD,EN∥AC可得:EM⊥EN,即∠MEN=90°.所以平行四边形ENFM是矩形.则有OE=ON=OF=OM.所以M、E、N、F四点共圆,故②正确.③当AC=BD且AC⊥BD时,同理可得:四边形ENFM是正方形.则有OE=ON=OF=OM.所以M、E、N、F四点共圆,故③正确.故选:C.13.如图,已知△ABC的面积是1,D、E、F和G、H、I分别是BC和AC边上的4等分点,则图中阴影部分的面积是()A.B.C.D.解:连结IF,如图,设S△IFK的面积为S,∵D、E、F和G、H、I分别是BC和AC边上的4等分点,∴==,而∠ICF=∠ACB,∴△CIF∽△CAB,∴=()2,∴S△CIF=,∵△CIF∽△CAB,∴∠CIF=∠CAB,==,∴IF∥AB,∴△IFK∽△BKA,∴=,∴S△ABK=16S,∵BF=3CF,∴S△IBF =3S△ICF,即S+S△KBF=3×,∴S△KBF=﹣S,∴S△ABF =S△ABK+S△KBF=16S+﹣S,∵BF=BC,∴S △ABF =S △ABC =, ∴16S +﹣S =, ∴S =,∴图中阴影部分的面积=S △IFK +S △CIF =+=.故选:A .14.如图,正方形ABCD 中线段A 1A 、AA 2、B 1B 、BB 2、C 1C 、CC 2、D 1D 、DD 2的长度分别等于边长的、、、、、、、,则正方形面积是阴影面积的多少倍( )A .B .C .D .2解:设正方形的边长为a ,则线段A 1A 、AA 2、B 1B 、BB 2、C 1C 、CC 2、D 1D 、DD 2的长度分别为a 、a 、a 、a 、a 、a 、a 、a ,正方形面积的面积为a 2,直角三角形的面积之和为a 2(×+×+×+×)=a 2, 阴影面积为a 2,则正方形面积是阴影面积倍.故选:C.15.如图,直角△ABC的直角边BC=6,AC=5.把BC六等分,等分点是D1,D2,D3,D4,D 5;把AC五等分,等分点是E1,E2,E3,E4.连AD1,AD2,AD3,AD4,AD5.过E1,E2,E3,E 4作BC边的平行线E1F1,E2F2,E3F3,E4F4,交AB边于F1,F2,F3,F4.那么图中所有可以数得出来的三角形的面积的总和为()A.115.5 B.462 C.420 D.231解:由底边一格组成的三角形的个数为5×5=25,面积为33,由底边两格组成的三角形的个数为4×5=20,面积为48+,由底边三格组成的三角形的个数为3×5=15,面积为54+,由底边四格组成的三角形的个数为2×5=10,面积为48+,由底边五格组成的三角形的个数为1×5=5,面积为33,图中所有可以数得出来的三角形的面积的总和为33×2+48×2+54+×2+=231,故选:D.16.有一塔形几何体由若干个正方体构成,构成方式如图所示:上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形几何体的全面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是()A.4 B.5 C.6 D.7解:设有n个正方体构成,其表面积由两部分组成:(1)俯视图、表面只有一个正方形,其边长为2.(2)侧面则由4n个正方形构成,且各层(从下往上看)正方形面积构成一个首项为4,公比为的等比数列.∴表面积为:4+4+4×[4+4×+4×+…+4×]>39,∴8+4×>39,∴n的最小值为6.故选:C.17.如图,正方形ABCD的面积为2,现进行如下操作:第1次:分别延长AB、BC、CD、DA至点E、F、G、H,使得BE=AB,CF=BC,DG=CD,AH=DA,顺次连接E、F、G、H四点得四边形EFGH;第2次:分别延长EF、FG、GH、HE至点J、K、L、M,使得JF=EF,KG=GF,LH=HG,EM=EH,顺次连接J、K、L、M四点得四边形JKLM,…按此方法操作,要使所得到的四边形面积超过2007,则这样的操作至少需要()A.7次B.6次C.5次D.4次解:设正方形ABCD的边长为a,第一次操作后得到正方形的边长为a,第二次操作后得到正方形的边长为5a,故第n次操作后正方形的边长为a,故知第n次操作后正方形的面积S=5n a2,若要使所得到的四边形面积超过2007,即5n a2>2007,a2=2,解得n>4,这样的操作至少需要5步,故选:C .18.某住宅小区的圆形花坛如图所示,圆中阴影部分种了两种不同的花,O 1,O 2,O 3,O 4分别是小圆的圆心,且小圆的直径等于大圆的半径.设小圆的交叉部分所种花的面积和为S 1.在小圆外、大圆内所种花的面积和为S 2,则S 1和S 2的大小关系是( )A .S 1>S 2B .S 1<S 2C .S 1=S 2D .无法确定解:设大圆的半径为2,则小圆半径是1,S 2=4π﹣(π+π+π+π﹣S 1)即S 1=S 2. 故选:C .19.在一堂“探索与实践”活动课上,小明借助学过的数学知识,利用三角形和长方形为班里的班报设计了一个报徽,设计图案如下:如图,两条线段EF 、MN 将大长方形ABCD 分成四个小长方形,已知DE =a ,AE =b ,AN =c ,BN =d ,且S 1的面积为8,S 2的面积为6,S 3的面积为5,则阴影三角形的面积为( )A .B .3C .4D .解:根据题意:DE =a ,AE =b ,AN =c ,BN =d ,且S 1的面积为8,S 2的面积为6,S 3的面积为5, 故知ac =8…①ad =6…② bd =5…③,②÷③得:a =b …④,把④代入①可得bc =,∵阴影三角形的面积=bc =.故选:A .20.如图,已知凸四边形ABCD 的面积为S ,四边AB ,BC ,CD ,DA 的第1个三等分点是E 、F 、G 、H ,连AF 、BG 、CH 、DE ,相邻两连线交于I 、J 、K 、L ,又△AEL 、△BFI 、△CGJ 、△DHK 的面积分别为a 、b 、c 、d ,S 1=a +b +c +d ,则四边形IJKL 的面积为( )A .B .C .D .解:如图,连接EF 、FG 、GH 、HE ,设△EFL 、△FGI 、△GKJ 、△HLK 的面积分别为a ′、b ′、c ′、d ′则 a ′=S △AEF ﹣a=S △ABF ﹣a =S △ABC ﹣a同理,b ′=S △BCD ﹣b 、c ′=S △CDA ﹣c 、d ′=S △DAB ﹣d . 四式相加得:a ′+b ′+c ′+d ′=S ﹣(a +b +c +d ) 又S 四边形EFGH =S ﹣(S △AHE +S △BEF +S △CGF +S △DGH )=S ﹣(×S △ABD +×S △ABD +×S △BCD +×S △BCD ) =S ﹣S =S∴S 四边形IJIKL =S 四边形EFGH ﹣(a ′+b ′+c ′+d ′) =S ﹣[S ﹣(a +b +c +d )] =S +a +b +c +d=S+S1故选:D.。
2018年中考数学复习试题汇编----几何综合1.已知,△ABC中,∠ACB=90°,AC=BC,点D为BC边上的一点.(1)以点C为旋转中心,将△ACD逆时针旋转90°,得到△BCE,请你画出旋转后的图形;(2)延长AD交BE于点F,求证:AF⊥BE;(3)若AC= ,BF=1,连接CF,则CF的长度为.527.(1)补全图形……………………2分(2)证明:∵ΔCBE由ΔCAD旋转得到,∴ΔCBE≌ΔCAD,………………3分∴∠CBE=∠CAD,∠BCE=∠ACD=90°,……………4分∴∠CBE+∠E=∠CAD+∠E,∴∠BCE=∠AFE=90°,∴AF⊥BE.……………………………………5分(3)2………………………………………………7分2.△ACB中,∠C=90°,以点A为中心,分别将线段AB,AC逆时针旋转60°得到线段AD,AE,连接DE,延长DE交CB于点F.(1)如图1,若∠B=30°,∠CFE的度数为;(2)如图2,当30°<∠B<60°时,①依题意补全图2;②猜想CF与AC的数量关系,并加以证明.图1 图23.如图1,在Rt△AOB中,∠AOB=90°,∠OAB=30°,点C在线段OB上,OC=2BC,AO)得到边上的一点D满足∠OCD=30°.将△OCD绕点O逆时针旋转α度(90°<α<180°△OC D,C,D两点的对应点分别为点C,D,连接AC,BD,取AC的中点M,连接OM.(1)如图2,当C D∥AB时,α=°,此时OM 和BD之间的位置关系为;(2)画图探究线段OM和BD之间的位置关系和数量关系,并加以证明.图1 图2备用图4.如图,∠BAD=90°,AB=AD,CB=CD,一个以点C为顶点的45°角绕点C旋转,角两边与BA,DA交于点M,N,与BA,DA延长线交于点E,F,连接AC.(1)在∠FCE旋转的过程中,当∠FCA=∠ECA时,如图1,求证:AE=AF;(2)在∠FCE旋转的过程中,当∠FCA≠∠ECA时,如图2,如果∠B=30°,CB=2,用等式表示线段AE,AF之间的数量关系,并证明.图1 图227.解:(1)证明:∵AB=AD ,BC=CD ,AC=AC ,∴△ABC ≌△ADC .…1分∴∠BAC =∠DAC =45°,可证∠FAC =∠EAC =135°.……2分又∵∠FCA =∠ECA ,∴△ACF ≌△ACE .∴AE=AF .……3分其他方法相应给分.(2)过点C 作CG ⊥AB 于点G ,求得AC =2.……4分∵∠FAC =∠EAC =135°,∴∠ACF +∠F=45°.又∵∠ACF +∠ACE =45°,∴∠F=∠ACE .∴△ACF ∽△AEC.……5分∴AC AF AE AC ,即AF AE AC 2. ……6分∴2AF AE .……7分5.在等腰△ABC 中,AB=AC ,将线段BA 绕点B 顺时针旋转到BD ,使BD ⊥AC 于H ,连结AD 并延长交BC 的延长线于点P.(1)依题意补全图形;(2)若∠BAC=2α,求∠BDA 的大小(用含α的式子表示);(3)小明作了点D 关于直线BC 的对称点点E ,从而用等式表示线段DP 与BC 之间的数量关系.请你用小明的思路补全图形并证明线段DP 与BC 之间的数量关系.27.解:(1)如图……………………………………………1分(2) ∵∠BAC =2α,∠AHB =90°∴∠ABH=90°-2α (2)分∵BA=BD∴∠BDA =45°+α………………………………………………………………………………3分(3)补全图形,如图………………4分。