第8章高斯光束

格式：ppt
大小：1.08 MB
文档页数：3

下载文档原格式

第8章高斯光束

l2 f 2
f
2
1
l f
(3) F 1 R(l) 1 (l f 2 )时,
2
2l
(4)F
时，
w0 w0
1
lim w0 lim
F
w F 0
F (l F )2 f 2
lim F
1
1
(l
- F)2 F
f F
2 2
w0 1 w0
w0 w0
1
l f
2
1
RR
2
F
25
结论
只有 F 1 R(l) ,才有聚焦作用
F15 q
五、透镜对高斯光束的变换规律
q=l+if q=-l+if
q Fq Fq
q、q:透镜处物、像高斯光束q参数
l、l :物、像高斯光束腰到透镜距离
f、f :物像高斯光束焦参数
q q
f(w0)
O
f(w0) Z
O
l F l
16
例1 某高斯光束焦参数为f=1m,将焦距F=1m 的凸透镜置於其腰右方l=2m处,求经透镜变换后的像光束的焦参数f及其腰距透镜的距离l
解 (1)
0
f
f
02
3.14 106 3.14 106
1m
z=0.5m
q(z) பைடு நூலகம் if 0.5 i(m)
(2)
w(z) w0
1
z2 f2
w0
1
0.52 12
1.12mm
f2
12
R(z) z 0.5 2.5m
z
0.5
8
例8-2 高斯光束在某处的光斑半径为w=1mm, 等相

高斯光束

为光波波前的曲率半径；
束宽：对于在自由空间传播的高斯光束，其腰斑位置的半径在光轴方向总大于一个最小值，这个最小值被称为束腰。波长为的光波的腰斑位置在轴上的分布为这里将定为束腰位置。被称为瑞利长度。
瑞利距离和共Байду номын сангаас参数：与束腰轴向距离等于瑞利距离处的束宽为这两点之间的距离称作是共焦参数或光束的焦深
高斯光束
钱朝阳
在光学中，高斯光束（Gaussian beam）是横向电场以及辐照度分布近似满足高斯函数的电磁波光束，所以称为高斯光束。是激光在光学谐振腔里基模条件下发出的光，许多激光都近似满足高斯光束的条件。
麦克斯韦方程组（1）
物质方程（5）
（2）
（3）（4）
（6）
（7）
对光频电磁场, 主要关心电场E,我们所讲的光场均指电磁场的电场分量。
谢谢观赏
曲率半径：光束偏移：当
是光束波前的曲率半径，它是轴向距离的函数，参数趋于一条直线。这条直线与中央光轴的夹角被称为光束的偏移，即远场发散角。
综上所述，可知高斯光束在其轴线附近可以看做是一种非均匀高斯球面波，周期传输过程中曲率中心不断改变，其振幅在横截面内为一高斯函数，强度集中在轴线及其附近，且等相面为球面（特殊范围内为平面）。
（13）
式（13）为在近轴近似下的波动方程，高斯光束就是缓变振幅近似下的一个特解。
高斯光束作为电磁波，其电场的振幅为：
r为场点距离光轴中的径向距离；z为光轴上光波最狭窄位置束腰的位置坐标为激光的束腰宽度为波数；为电磁场振幅降到轴向的1/e、强度降到轴向的1/e2的点的半径为轴对称光波的Gouy相位，对高斯光束的相位也有影响，在近轴条件下可以忽略。

2.6 高斯光束基本性质及特征参数详解

a、光腰半径
x方向：m2 2m 102 02 y方向：n2 2n 102 02
b、z处光斑半径
x方向： m2z 2m 1z2 z2 y方向： n2z 2n 1z2 z2
(5) 远场发散角
x方向： m
lim
z
2m z
z
y方向：
n
lim
z
2n z
z
2m 1 2 0
2n 1 2 0
1
2
z
R
z 1
R z w2 z
2
1
00 x,
y, z
c
wz
exp
ik
r2 2
1
Rz
i w2 z
e
i
kztg
1
z f
1
qz
1
Rz
i
2 z
1/q(z) —高斯光束的复曲率半径
知道q(z)可以求R (z)和 z
1
Rz
Re q1z
1
2 z
Im
q
1
z
特例：
自由空间为例
r2 Ar1 B1 近轴光 ,
2 Cr1 D1 r2 R22 r1 R11
R2
r2
2
AR1 B CR1 D
—ABCD公式
二、高斯光束q参数的变换规律——ABCD公式 1、高斯光束与普通球面波参数与传输规律的对应
描述传播
普通球面波曲率半径
R2
AR 1 CR 1
B D
高斯光束
2.9 高斯光束基本性质和特征参数
在高斯近似下，稳定腔和共焦腔都输出高斯光束，对方形镜和圆形镜腔，分别是厄米—高斯(高阶或基模)和拉盖尔—高斯(高阶或基模)光束。

[整理版]高斯光束透镜变换

在这个例子中，我们将考虑高斯光束在一个简单的成像系统中的传播。

在第一章中，关联物像平面的ABCD 矩阵可写为⎥⎦⎤⎢⎣⎡-=m f m M /1/10 其中m 为透镜的横向放大率，f 是成像透镜的焦距。

用ABCD 定律，并假设1'==n n ，我们用q 描述物面上的高斯光束，通过透镜后，用q ’描述在像面上的高斯光束m a f m qq 11'+-=使用q 参数，可以方便地把上式分为实部和虚部。

聚焦点'ω和近轴像面的波面曲率半径为ωωm ='10.76mR f Rf m R -=2'10.77从上述关系中可以得出几个结论。

像物聚焦点大小的比率就是近轴横向放大率。

考虑将激光束腰放置在物方平面的情况，这时∞=R 。

将10.77的极值放在这个情况下，可得mf R -='对于正透镜的通常情况，它有实的物距和像距，f 为正，m 为负，因此R ’是正的，按照光束符号惯例表示像空间光束在通过它的近轴像面之前已经通过了它的束腰，例如，束腰位于近轴像的位置。

这种现象叫做“焦移”，因为最大近轴发光点不在几何焦点处。

为了在近轴像面处得到光束束腰（∞='R ）我们必须在物面处有m f R /=。

焦移现象对于有很小发散角的“慢”光束而言更生动，换句话说，对于有小的菲涅尔数的光束而言。

（孔径半径为a 和波前曲率半径为R 的菲涅尔数为R a λ/2）。

我们可以用OSLO中的交互式ABCD 分析数据表来阐明这一现象。

我们在目录数据库中选择一个焦距为500mm 的透镜，用近轴设置数据表来设置近轴放大率为-1。

将主波长设为0.6328m μ，在设置放大率前删除波长2和3，如下图所示使用交互式ABCD 分析表，我们可以考察穿过这个透镜的高斯光束。

用束腰直径为0.25mm ，束腰离第0面距离为0。

在OSLO 中使用高斯光束数据表时有几个惯例：1 使用这个数据表，你必须在4个区域（w,w0,z,R ）中的两个中添入数据。

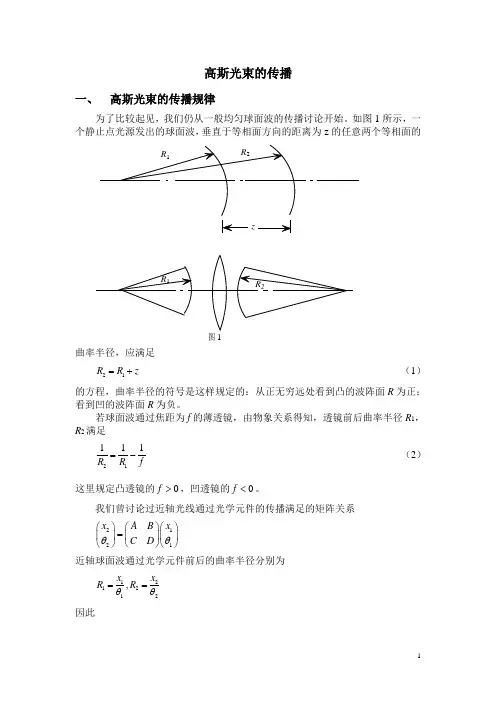
高斯光束的传播讲义

高斯光束的传播一、高斯光束的传播规律为了比较起见，我们仍从一般均匀球面波的传播讨论开始。

如图1所示，一个静止点光源发出的球面波，垂直于等相面方向的距离为z 的任意两个等相面的z图1曲率半径，应满足21R R z =+（1）的方程，曲率半径的符号是这样规定的：从正无穷远处看到凸的波阵面R 为正；看到凹的波阵面R 为负。

若球面波通过焦距为f 的薄透镜，由物象关系得知，透镜前后曲率半径R 1，R 2满足21111R R f=- （2）这里规定凸透镜的0f >，凹透镜的0f <。

我们曾讨论过近轴光线通过光学元件的传播满足的矩阵关系2121x x AB CD θθ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭近轴球面波通过光学元件前后的曲率半径分别为121212,x x R R θθ==因此1211112121111x A Bx Ax B AR B R x C x D C R DCDθθθθθ+++====+++ （3）所以对于一般均匀球面波，只用一个参数——曲率半径R 就可完全描述其传播和变换的特性。

与普通球面波不同，高斯光束必须由两个量即R （z ）和w (z)来描写。

但下面将看到，对于高斯光束——非均匀的、曲率中心不断变化的球面波——也具有一个与一般球面波曲率半径R 的作用类似的复曲率半径q (z )，它可被用来描述高斯光束的传播行为。

在推导高斯光束表达式时，我们已经得出复曲率半径在均匀空间传播的表达式，具体过程可以参考伍长征编写的《激光原理》书中的（3.3-14）式，即21q q z=+ （4）这里21,q q 分别为传播方向上任意两点21,z z 处的复曲率半径，z 为两点间距离，21z z z =-，参见图2(a)。

再看高斯光束通过薄透镜的变换，如图2(b)。

令薄透镜焦距为f ，由于是近轴光线，波阵面是一球面，透镜前后曲率半径应满足21111R R f=-,000(,)q w R 111(,)q w R 222(,)qwR z 1z 2图2(a)f 20w 10w q 1q 2图2(b)又透镜足够薄，两侧光斑尺寸相等，即12w w =，与上式合并，可以变形为22222112121()i iR kwR kw f-=-- (5)由复曲率半径定义式2112()()()i q z R z kw z =-，可得21111q q f=-（6）比较（4）式和（6）式与（1）式和（2）式知道，利用复曲率半径q ，形式上完全可等价于球面波的曲率半径R 。

11-12讲高斯光束

+ z0 )
与上式相比，位相之差一常数。与上式相比，位相之差一常数。 Z>0处波阵面是球面，曲率半径处波阵面是球面，处波阵面是球面
πW02 2 R ( z 0 ) = z 0 1 + ( ) > z0 > 0 zλ
x R(z) z W0 W(z0) y W(z) z
为有限大小的高斯光束，无论F 对w01为有限大小的高斯光束，无论和z1如何取都不可能使 w02→∞，也不可能使 2→0，说明单个透镜不能将高斯光束变换，也不可能使θ ，成平行光束。成平行光束。
方向性，提高准直性，单透镜可以改善高斯光束的方向性，提高准直性，就有θ 尽可能使w 当w01 > w02，就有 2 <θ1,尽可能使 02达到极大值尽可能使
x θ R(z) z W0 W(z0) y W(z) z
在z=0处，发散角为，光斑最小 0称为腰斑，远离腰束光斑逐处发散角为0，光斑最小W 称为腰斑，渐增大，增大而增大。渐增大，W(z) 随z增大而增大。增大而增大
dW ( z ) 2 zλ 2θ = 2 = πW0 dz
当z=0时，2θ=0，平面波时，
平面波
A0 E(x, y,0) = A(x, y, z = 0) = e W0
r2 − 2 W0
表明和，坐标相关的相位部分消失了坐标相关的相位部分消失了，的平面是等相位面，表明和x，y坐标相关的相位部分消失了，即z=0的平面是等相位面，的平面是等相位面和平面光波一样，和平面光波一样，振幅部分是高斯函数
W01 W02 = = 2 f W01 2 1 + ( )2 1+ ( ) F λF
W01

高斯光束传输方程及其解法

高斯光束传输方程及其解法光学是研究光的物理现象和规律的科学，光在自然界中广泛存在并起到重要作用，对于现代科技的发展也有着不可替代的作用。

高斯光束是一种常见的光束形式，其具有良好的传输性质和应用前景，因此得到广泛应用。

一、高斯光束的定义和特性高斯光束是指在自由空间中横向至少二次可微、纵向一次可微的光束，其光强分布和相位分布都可用高斯函数表征。

高斯光束具有如下的重要特性：1. 具有良好的射程特性，能够在传输过程中保持约束的形态；2. 横向光强分布呈高斯分布，纵向呈指数分布，能够满足许多光学应用中对于光束形态和光强的要求；3. 光束通过透镜进行聚焦后，仍然是高斯光束，具有良好的自聚焦能力；4. 具有相干性，能够满足干涉、衍射等光学现象的要求。

二、高斯光束传输方程的推导在光学应用中，高斯光束的传输是一个重要的问题，需要准确描述其传输过程。

高斯光束传输方程可以描述高斯光束在自由空间中传输的过程，其推导如下：设高斯光束的累计相位为φ(x,y,z)，其横向强度分布为I(x,y)，则光强的分布可以表示为：I(x,y,z)=|A(x,y,z)|^2其中，A(x,y,z)是高斯光束的复振幅，其表示为：A(x,y,z)=u(x,y,z)exp(jφ(x,y,z))其中u(x,y,z)表示高斯光束的复场，根据标量波动方程可以得到：△u+k^2u=0其中k=2π/λ为波数，λ为波长。

将复场u分解为实部和虚部，可得到：u=u1+ju2则标量波动方程可以分解为实部和虚部的两个方程：△u1+k^2u1=-△u2-k^2u2△u2+k^2u2=△u1-k^2u1再利用高斯光束的对称性和横向可微性，可以得到：▽^2u1+k^2u1=0▽^2u2+k^2u2=0则高斯光束的传输方程可以写为：∂A(x,y,z)/∂z+iβ(x,y,z)A(x,y,z)=0其中β(x,y,z)为传输因子，可以表示为：β(x,y,z)=k/2n[∂^2φ(x,y,z)/∂x^2+∂^2φ(x,y,z)/∂y^2]则高斯光束的累计相位和传输因子分别代表了光束的位相和弯曲程度，通过方程可以描述光束在自由空间中传输时的演化形态。

第八章--激光准直技术

2、四象限PSD工作原理（平恒电桥法）如图8-15所示，
图8-15 1、当四象限硅光电池中心和准直线同轴时，四块硅光电池输出电压相同，电桥平衡。 2、若输出不平衡，测准直中心变化，根据其变化规律，可判断其方向。
要求：四象限硅光电池光电特性完全一致，一般不易保证，其差值多达 20% ，可采用以下平衡电阻法来解决。（图8-16）
中心光效的直径近似为：d0
2 4
n1
例，设θ=0.01rad，R=5mm，n=1.5，λ=0.6328×10-3mm
则 Zma xn R 10.5 50.0 110m 00 m
d02.4 1.05.6 132 01 .080 13 0.1mm
§8-2 位相测量型激光准直系统
如图8-11所示：
图8-11
部分资料从网络收集整理而来，供大家参考，
感谢您的关注！
J0
r
位相振幅
其 r2 中 x2y2 ， 22k2, k2
如果光波为高斯光束则：
E2ejzJ0rex p r20 2
当上二式中时：
E1 ejz ——平面波
E2 expr202ejz ——一般高斯光束
从Bessel-Gaussian光束的表达式可以看出，
其振幅 J0arexpr202 只与X、Y有关，而与Z无关，
Df d
其产生零阶Bessel-Gaussian光束的条件为：
Δd<<2λF（F为透镜的F数：
F
1 D
f
f D
）
例：设d=φ2.5mm，fˊ=305mm，D=φ7mm
则 Zma x7 2.350585m 4m
此时产生零级Bessel-Gaussian光束的条件为：

第八章高斯光束全

基模光斑半径随z按双曲线规律的变化
２、w(z)和R(z)参数
观察点z处光斑半径w(z)与等相位面曲率半径R(z)
w(z) w0
1
z2 f2
(f
z2 )
f
R(z) z f 2 z
３、q参数
(1)定义
1 q(z)
1 R(z)
i
w 2 (z)
1 R(z)
Re 1 q(z)
(2)计算 q(z) z if
T
1 F
1
R
1 1
R
0 R 1
R 1 R
FR F R
F
F
或
Ru
11 1 uv F
R v 1 1 1 R R F
R R
o u v o z
F
1 1 1 FR R R F FR
R FR FR
四、高斯光束q参数的传输规律
1、传播L距离
q q L
证传播L距离的光学变换矩阵
q 1 q L q L 0q 1
共焦谐振腔
共焦谐振腔的性能介于平行平面腔与球面腔之间，其特点如下： 1）镜面较易安装、调整； 2）较低的衍射损耗； 3）腔内没有过高的辐射聚焦现象； 4）模体积适度；
共焦谐振腔一般应用于连续工作的激光器
共焦场等相面的分布
如果在场的任意一个等相位面处放上一块具有相应曲率的反
射镜片,则入射在该镜片上的场将准确地沿着原入射方向返
2
T P P
0
0 2
I (r)2 rdrd I (r)2 rdrd
1
exp
2 2 2
0 0
孔径半径a ω/2
ω
3ω/2
2ω
功率透过比 39.3% 86.5% 98.89% 99.99%

高斯光束

1
1．亥姆霍兹方程的波束解
波束场强在横截面上的分布形式是由具体激发条件确定的．现在我们研究一种比较简单和常见的形式．这种波束能量分布具有轴对称性，在中部场强最大，靠近边缘处强度迅速减弱．设波束对称轴为z轴，在横截面上具有这种分布性质的最简单的函数是高斯函数
e−
x
2+y w2
2
2
x2 + y2
（6.2）
ψ(x,y,z)是z的缓变函数．所谓缓变是相对于eikz而言的 .因子eikz当z≤λ时已有显著变化，我们假设ψ(x,y,z),当z~λ时
变化很小，因此在它对z的展开式中可以忽略高次项5 .
电磁场的任一直角分量u(x,y)满足亥姆霍兹方程
∇2u + k 2u = 0
把
µ(x, y, z) = ψ (x, y, z)eikz
2
2
e −iφ
= µ0
w0 w
e−iφ
φ = arc tg 2z kw02
（6.14）（6.15）
11
把（6 .13）和（6 .14）代人（6 .2）和（6. 4）式得光束场强函数
( ) µ
x, y, z
µ =
w0
−
x
2+y ω2
2
iΦ
w e e 0
( ) Φ
=
kz
+
§6 高斯光束
第一节所讨论的平面电磁波是具有确定传播方向，但却广延于全空间中的波动 . 实际上应用的定向电磁波除了要求它具有大致确定的传播方向外，一般还要求它在空间中形成比较狭窄的射束，即场强在空间中的分布具有有限的宽度 . 特别是在近年发展激光技术中，从激光器发射出来的光束一般是很狭窄的光束 . 研究这种有限宽度的波束在自由空间中传播的特点对于激光技术和定向电磁波传播问题都具有重要意义 . 本节我们从电磁场基本方程研究波束传播的特性 .

高斯光束的基本性质及特征参数PPT课件

§2.8 高斯光束的自再现变换
自再现变换：如果一个高斯光束通过透镜后其结构不发生变化，即参数0或f不变，
或同时满足0 = 0、 l=l。
•利用透镜实现自再现变换：
令 •当透镜的焦距等于高斯光束入射在透镜表面
该高斯光束
l F
作
自(l
(l F
• 参数q将(z)和R(z)统一在一个表达式中，知道了高斯光束在某位置处的q参数值，可由下式求出该位置处(z)和R(z)的数值
1 Re[ 1 ]
R(z)
q(z)
1 2 (z)
Im[ 1 ] q(z)
用q0=q(0)表示z=0处的参数值（purely
imaginary），得出
1 q0
1 q(0)
如果知道了某给定位置处的(z)和R(z)，可决
定高斯光束腰斑的大小0和位置z
00
(高x, y斯, z)光束c 的exqp参{i数k r2
(z)
2
[
1 R(z)
i
2 (
z)
]
}ex
p
[i(kz
arctg
z f
)]
引入一个新的参数q(z)，定义为
1 q(z)
1 R(z)
i
2 (z)
第6页/共40页
0 >>f
F ，l
0
l F
不l=论F，l的值0为达多到大极，大只值要，F<f满足，就能，实现一定的且聚焦作用，。仅当F<f时，透镜才有聚焦作用。
第20页/共40页
l 确定， 0随F变化情况
当 F R(l) 2 ，透镜才能对高斯光束起聚焦作用。F 愈小，聚集效果愈好

2-5高斯光束

Aq1 B q2 Cq1 D
曲率半径R
复曲率半径q
例1 某高斯光束焦参数为f=1m,将焦距F=1m 的凸透镜置於其腰右方l=2m处,求经透镜变换后的像光束的焦参数f及其腰距透镜的距离l 解 q=2+i
q f(w0)
O
q f(w0) Z
O
l F l
研究对象
普通球面波
高斯球面波
特点
曲率中心固定的曲率中心变化的
q2=q1+L
1 1 1 q2 q1 F
在自由空间的传 R2=R1+L 输规律通过薄透镜的变 1 1 1 R2 R1 F 换总的变换规律 AR1 B
R2 CR1 D
高斯光束q参数的传输规律
1、传播L距离
q q L
1 T 0 L 1
证
传播L距离的光学变换矩阵
1 q L q qL 0 q 1
2、通过透镜
q、q:透镜处物、像高斯光束q参数 l、l :物、像高斯光束腰到透镜距离 f、f :物像高斯光束焦参数
1 T 1 F 0 1
• 研究对象：高斯球面波—非均匀的、曲率中心不断改变的球面波 • q参数在自由空间的传输规律q(z)=q0+z，q2=q1+L 1 1 1 • 通过薄透镜的变换
q2
q1
F
• q参数的变换规律可统一表示为
Aq1 B q2 Cq1 D
• 结论：高斯光束经任何光学系统变换时服从ABCD公式，由光学系统对傍轴光线的变换矩阵所决定。 • 优点：能通过任意复杂的光学系统追踪高斯光束的q参数值 (将q称为复曲率半径the complex radius of curvature)

高斯光束的振幅和强度分布

器
的输出特
2.一般的激光器是向着数量级约为10－6 sr的立体角范围内输出激光光束的。而普通光源发光(如电灯光)是朝向空间各个可能的方向的，它的发光立体角为4πsr。相比之下，普通光源的发光立体角是激光的约百万倍。
性
3.小结一下高斯光束的主要特征参量：
§3.3
高斯光
0
L 2
R0
z
[1
y2
2z0
x2 y2
1
L 2z0
2
可知：
输
➢当 z0 f L 2时，R(z0 ) 2 f L
出特性
➢当 z0 0时，R(z0) ; z0 时，R(z0 )
➢共焦腔反射镜面是共焦场中曲率最大的等相位面
§3.3
4.共焦场中等相位面的分布如图(3-9)所示。
高
斯
第三章
激光器
4.
( 0
z)
1 2
L [1 2 s
(
1 2
2z )2] L
L
(
z)
0
1
z
(
2 0
)2
2 02
z2
(
2 0
)2
1
的输
5. 基模光斑半径随 z 按双曲线规律变化，如图(3-8)。
出
特
性
§3.3
高
斯
光束
图(3-8) 基模光斑半径随z按双曲线规律的变化
传
播
特
性
上一页回首页下一页回末页回目录
3.3.1 高斯光束的振幅和强度分布
第三
1. 基横模TEM00的场振幅U00和强度I00分布分别为：

高斯光束的传播特性课件

高斯光束的未来发展趋势
01 发展现状分析
前景广阔
02 未来趋势探讨
挑战与机遇并存
03 科学研究发展
跨学科交叉
高斯光束在工业应用中的创新
制造工艺
高效精准节约成本
设备应用
智能控制自动化生产
材料加工
高质量快速加工
能源利用
节能环保绿色生产
● 07
第7章高斯光束的传播特性课件
高斯光束的重要性
折射率与热效应
热效应
高斯光束在介质中传播时会产生热效
应。
折射率变化
热效应会导致折射率发生变化，影响高斯光束的传播和聚焦效
果。
总结
高斯光束的传播特性受到折射率、衍射效应、非线性光学和热效应等因素的影响。理解这些因素对于光学应用和光束传输具有重要意义。
● 03
第3章高斯光束的光学系统
高斯光束的聚焦系统
● 04
第四章高斯光束的传播实验
高斯光束的干涉实验
迈克尔逊干涉仪观测
利用迈克尔逊干涉仪观测高斯光束的
干涉条纹
分析干涉条纹
分析干涉条纹的形状和对比度，验证高斯
光束的传播特性
高斯光束的衍射实验
在衍射光栅实验中，观测高斯光束的衍射效应是探究光栅对高斯光束的光斑形状和光强分布的影响。通过实验，可以进一步了解光的衍射现象，验证高斯光束在衍射过程中的特性。
衍射效应
光束传播中的衍射现象
散射效应
光束在物质中传播时的散射现象
折射效应
光束在介质中传播时的折射规律
高斯光束的调制特性
高斯光束可以通过调制改变其传播特性，例如调制频率、相位等参数可以实现对光束的精准控制。调制技术在光通信和激光加工中有着重要的应用价值。

3.8高斯光束

第八节高斯光束
一、高斯光束的基本性质
1.基模高斯光束
沿z轴传播的基模高斯光束的表达式
x2 + y2 ⎡ z k x2 + y2 ⎤ −i ⎢ kz − arctg + ⎥ zR 2 R(z ) ⎥ ⎢ ⎣ 14444244443 4 4⎦
相位因子
(
)
C 00 − w2 ( z ) ψ 00 ( x, y , z ) = e e w( z ) 14243
U ( x, y , z ) ∝ 1 −ikR 1 e ≈ e R R
⎛ x2 + y2 −ik ⎜ z + ⎜ 2z ⎝ ⎞ ⎟ ⎟ ⎠
=
1 e R
⎛ x2 + y2 −ik ⎜ z + ⎜ 2R ⎝
⎞ ⎟ ⎟ ⎠
因此，q(z)称为高斯光束的复曲率半径，也称为q参数
q(z)将w(z)和R(z)统一起来，已知q(z)可求出w(z) 和R(z)
Q 高斯光束的q的变换规律同球面波R的变换规律相同 ∴ Aq1 + B q2 = Cq1 + D
（1）高斯光束q参数在自由空间的传播由
⎧ 1 1 λ ⎪ = −i q( z ) R( z ) πω 2 ( z ) ⎪ ⎪ ⎡ ⎛ πω 2 ⎞ 2 ⎤ ⎪ 0 ⎨ R( z ) = z ⎢1 + ⎜ ⎟ ⎜ λz ⎟ ⎥ ⎢ ⎝ ⎠ ⎥ ⎪ ⎦ ⎣ ⎪ ⎡ ⎛ λz ⎞ 2 ⎤ ⎪ω 2 ( z ) = ω 2 ⎢1 + ⎜ 0 ⎟ ⎜ πω 2 ⎟ ⎥ ⎪ ⎢ ⎝ 0⎠ ⎥ ⎦ ⎣ ⎩
（3）普通球面波的ABCD定律
光学系统 R1
θ1
P1 R2
r1
r2
θ2
P2

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例3 高斯光束波长为=3.14m,某处的q参数为q=1+i(m),求(1)此光束腰斑半径w0及腰位置 (2)该处光斑半径w与等相位面曲率半径R
解 (1) z=1m f=1m
w0
f
3.14 106 1 1mm 3.14
腰位置为在该处左方1m处
(2) 1 1 1 i 1 i 1
q 1i 2 2 2
2i
q 1 2 i 2 i 0.4 0.2i(m) 2i 41 5
(2)
w(z) w0
1
z2 f2
( f z2 )
f
R(z) z f 2 z
z f 2 0.5 z
f z2 1 f
z2 f 2 0.5 ① z
f 2 z2 1 ②
f
z2 f 2 0.5 z
f 2 z2 1 f
R=R(z) R=R(z)
z
0 z z
L
2、通过透镜 R FR
FR
F:透镜焦距(凸透镜为正)
证透镜的光学变换矩阵
T
1
1 F
0 1
R
1 1
R
R
0
1
R 1 R
FR F R
F
F
或
Ru
11 1 uv F
R v 1 1 1 R R F
R R
o u v o z
F
1 1 1 FR R R F FR
例1 某高斯光束波长为=3.14m,腰斑半径为 w0=1mm,求腰右方距离腰50cm处的(1)q参数 (2)光斑半径w与等相位面曲率半径R
解 (1)
w0
f
z=0.5m
f
w
2 0
3.14 106 3.14 106
1m
q=0.5+i(m)
(2)
w(z) w0
1 z2 f2
w0
1 0.52 12
1 1 R2
R 2m
W 2
1 2
W 2 2 3.14106 1.414mm
3.14
§2 高斯光束的传输规律
一、球面波的R参数 R(z)=z
R(z):等相位面曲率半径(凸向z轴为正)
R(z) z
0
z
二、ABCD定律
若某元件的光学变换矩阵为
A C
B D
，则通过
此元件前、后的球面波R参数和高斯光束q参数满足关系
1.12mm
R(z) z f 2 0.5 12 2.5m
z
0.5
例2 高斯光束在某处的光斑半径为w=1mm, 等相位
面曲率半径为R=0.5m, 求此高斯光束(1)该处的q参
数 (2)腰斑半径w0及腰位置(光波长为=3.14m)
解 (1)
1 q
1 R
i w2
1 0.5
i
3.14 106 3.14 (103)2
f
R(z) z f 2 z
３、q参数
(1)定义
1 q(z)
1 R(z)
i
w 2 (z)
(2)计算
q(z) z if
证
w(z) ( f z2 )
f
1 W2
f f 2 z2
R(z) z f 2 z
1z R z2 f 2
1 1 i z i f z if q R W 2 z2 f 2 z2 f 2 z2 f 2
f 2 4 f 2 1 f
f 0 (舍去)
①
②/①: z 2
②
f
5f2 f
5f2 f 0
f 0.2m
z2f
f (5 f 1) 0
0.22 z2 1 0.2
z2 0.2 0.22 0.16
w0
f
3.14106 0.2 0.447mm 3.14
腰位置在该处左方0.4m
z 0.4m
q=l+if q=-l+if
q Fq Fq
q、q:透镜处物、像高斯光束q参数
l、l :物、像高斯光束腰到透镜距离
f、f :物像高斯光束焦参数
q q
f(w0)
O
f(w0) Z
O
l F l
例1 某高斯光束焦参数为f=1m,将焦距F=1m 的凸透镜置於其腰右方l=2m处,求经透镜变换后的像光束的焦参数f及其腰距透镜的距离l
R AR B CR D
q Aq B Cq D
R、q:通过元件前的参数 R、q:通过元件后的参数
三、球面波R参数的传输规律
1、传播L距离 R=R+L
证传播L距离的光学变换矩阵
T
1 0
L 1
R 1 R L R L 0 R 1
或 R=R(z)=z R=R(z)=z
R-R=z-z=L ∴R=R+L
第八章高斯光束 §1 高斯光束的特征参数一、定义
可以完全确定高斯光束形状与位置的物理量
二、参数类型
１、fz参数
焦参数f (或腰斑半径w0)与腰位置z(观察点坐标)
w0
f
f w02
２、wR参数
观察点z处光斑半径w(z)与等相位面曲率半径R(z)
z2
z2
w(z) w0 1 f 2
(f )
解
q=2+i
q Fq 2 i (2 i)( 1 i) 2 i 2i 1 3 i
F q 1 2 i (1 i)( 1 i) Nhomakorabea11
2
1.5 0.5i
l =1.5m f =0.5m
§3 高斯光束的聚焦与准直一、透镜对高斯光束的变换公式
(已知l、f、F,求l 、f )
f
R FR FR
四、高斯光束q参数的传输规律
1、传播L距离
q q L
证传播L距离的光学变换矩阵
q 1 q L q L 0q 1
T
1 0
L 1
或 q=q(z)=z+if
q=q(z)=z+if
q-q=z-z=L ∴q=q+L
2、通过透镜
q Fq Fq
证透镜的光学变换矩阵
1 0
T
(l
F2 F)2
f
2
f
w0
F (l F)2
f2
w0
l
l(l F) (l F)2
f f
2 2
F
证 q=l+if
q F(l if) (F l) if
(l if)[(F l) if] [(F l) if][(F l)
if]
F
[l(F l) f 2 ] (F l)2 f 2
q z2 f 2 (z2 f 2 )(z if ) z if z if (z if )(z if )
讨论腰处的q参数 q0=q(0)=if
w(z)
(f
z2 )
f
R(z) z f 2 z
fz参数
q(z) z if
WR参数
q参数
1 q(z)
1 R(z)
i
w 2 (z)
1 F
1
q
1 1
q q
0 1
q 1 q
Fq F q
F
F
或
1 1 i q R w 2
1 q
1 R
i
w2
q q w w
Z
R FR FR
1 1 1 R R F
w w
R R F
1 1 1 1 1 q q R R F
1 1 1 F q q Fq
q q F Fq
Fq
五、透镜对高斯光束的变换规律

第8章高斯光束

合集下载