2.2平行四边形的性质与判定练习题 Microsoft Office Word 97-2003 文档 (3)

（一) 平行四边形的判定一、教学目的：1．在探索平行四边形的判别条件中，理解并掌握用边、对角线来判定平行四边形的方法．2．会综合运用平行四边形的判定方法和性质来解决问题．3．培养用类比、逆向联想及运动的思维方法来研究问题．二、重点、难点1．重点：平行四边形的判定方法及应用．2．难点：平行四边形的判定定理与性质定理的灵活应用．平行四边形的判定方法平行四边形判定方法1(与边相关) 两组对边分别相等的四边形是平行四边形。

平行四边形判定方法2 (与边相关) 两组对边分别平行的四边形是平行四边形平行四边形判定方法3 （与边相关) 一组对边平行且相等的四边形是平行四边形平行四边形判定方法4 (与角相关) 两组对角分别相等的四边形是平行四边形平行四边形判定方法5 (与对角线相关）对角线互相平分的四边形是平行四边形。

三、练习题1．如图，在四边形ABCD中，AC、BD相交于点O，（1)若AD=8cm,AB=4cm,那么当BC=___ _cm，CD=___ _cm时，四边形ABCD为平行四边形;（2)若AC=10cm，BD=8cm,那么当AO=__ _cm，DO=__ _cm时，四边形ABCD为平行四边形．（3）．（选择)下列条件中能判断四边形是平行四边形的是( ）．（A）对角线互相垂直 (B）对角线相等(C）对角线互相垂直且相等（D）对角线互相平分2．判断题：（1)相邻的两个角都互补的四边形是平行四边形；（）（2）两组对角分别相等的四边形是平行四边形; ( ）（3)一组对边平行，另一组对边相等的四边形是平行四边形； ( ）（4)一组对边平行且相等的四边形是平行四边形； ( ）(5）对角线相等的四边形是平行四边形； ( ）（6)对角线互相平分的四边形是平行四边形．（）3．（选择）在下列给出的条件中,能判定四边形ABCD为平行四边形的是（）．（A）AB∥CD，AD=BC （B)∠A=∠B,∠C=∠D（C）AB=CD，AD=BC (D）AB=AD，CB=CD4．已知:如图，AC∥ED，点B在AC上，且AB=ED=BC，找出图中的平行四边形，并说明理由．5．已知：如图，ABCD中，点E、F分别在CD、AB上，DF∥BE，EF交BD于点O．求证:EO=OF．6．已知：如图,△ABC，BD平分∠ABC，DE∥BC,EF∥AC，求证：BE=CF7。

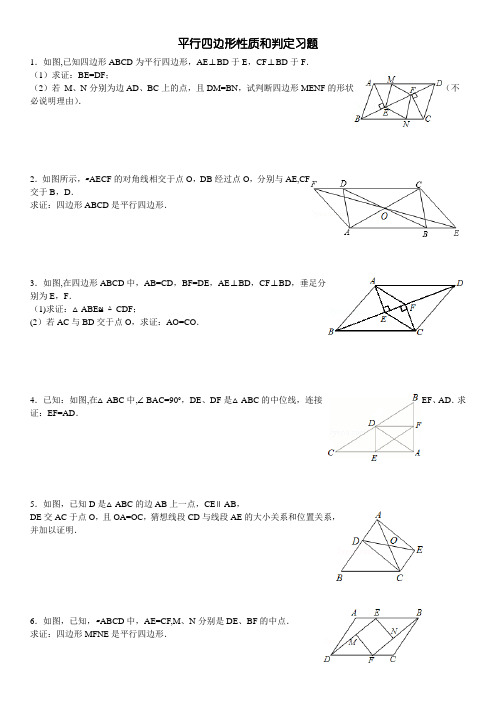
平行四边形性质和判定习题1．如图,已知四边形ABCD为平行四边形，AE⊥BD于E，CF⊥BD于F．（1）求证：BE=DF；（2）若M、N分别为边AD、BC上的点，且DM=BN，试判断四边形MENF的形状（不必说明理由）．2．如图所示，▱AECF的对角线相交于点O，DB经过点O，分别与AE,CF交于B，D．求证：四边形ABCD是平行四边形．3．如图,在四边形ABCD中，AB=CD，BF=DE，AE⊥BD，CF⊥BD，垂足分别为E，F．（1)求证：△ABE≌△CDF；(2）若AC与BD交于点O，求证：AO=CO．4．已知：如图,在△ABC中,∠BAC=90°，DE、DF是△ABC的中位线，连接EF、AD．求证：EF=AD．5．如图，已知D是△ABC的边AB上一点，CE∥AB，DE交AC于点O，且OA=OC，猜想线段CD与线段AE的大小关系和位置关系，并加以证明．6．如图，已知，▱ABCD中，AE=CF,M、N分别是DE、BF的中点．求证：四边形MFNE是平行四边形．7．如图，平行四边形ABCD，E、F两点在对角线BD上，且BE=DF，连接AE,EC，CF，FA．求证：四边形AECF是平行四边形．8．在▱ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF，连接BE、DF．求证：四边形BEDF是平行四边形．9．如图所示，DB∥AC，且DB=AC，E是AC的中点，求证：BC=DE．10．已知：如图,在梯形ABCD中，AD∥BC，AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，直线PQ截梯形为两个四边形．问当P，Q同时出发,几秒后其中一个四边形为平行四边形？11．如图：已知D、E、F分别是△ABC各边的中点，求证：AE与DF互相平分．12．已知：如图，在▱ABCD中,对角线AC交BD于点O，四边形AODE是平行四边形．求证:四边形ABOE、四边形DCOE都是平行四边形．13．如图,已知四边形ABCD中，点E，F，G，H分别是AB、CD、AC、BD的中点，并且点E、F、G、H有在同一条直线上．求证:EF和GH互相平分．14．如图：▱ABCD中，MN∥AC，试说明MQ=NP．15．已知：如图所示,平行四边形ABCD的对角线AC，BD相交于点O，EF经过点O并且分别和AB,CD相交于点E，F，点G，H分别为OA,OC的中点．求证:四边形EHFG是平行四边形．16．如图,已知在▱ABCD中，E、F是对角线BD上的两点，BE=DF,点G、H分别在BA和DC的延长线上，且AG=CH，连接GE、EH、HF、FG．（1)求证：四边形GEHF是平行四边形;（2）若点G、H分别在线段BA和DC上，其余条件不变，则（1)中的结论是否成立？（不用说明理由）17．如图，在△ABC中,D是AC的中点，E是线段BC延长线一点，过点A作BE的平行线与线段ED的延长线交于点F，连接AE、CF．(1）求证：AF=CE；（2)如果AC=EF,且∠ACB=135°，试判断四边形AFCE是什么样的四边形，并证明你的结论．18．如图平行四边形ABCD中，∠ABC=60°,点E、F分别在CD、BC的延长线上，AE∥BD，EF⊥BF，垂足为点F，DF=2(1）求证：D是EC中点;（2)求FC的长．19．如图，已知△ABC是等边三角形，点D、F分别在线段BC、AB上,∠EFB=60°，DC=EF．(1）求证：四边形EFCD是平行四边形；（2)若BF=EF，求证：AE=AD．20．如图,四边形ABCD，E、F、G、H分别是AB、BC、CD、DA的中点．（1)请判断四边形EFGH的形状？并说明为什么；（2）若使四边形EFGH为正方形，那么四边形ABCD的对角线应具有怎样的性质?21．如图，△ACD、△ABE、△BCF均为直线BC同侧的等边三角形．（1）当AB≠AC时,证明:四边形ADFE为平行四边形；（2）当AB=AC时，顺次连接A、D、F、E四点所构成的图形有哪几类？直接写出构成图形的类型和相应的条件．22．如图，以△ABC的三边为边，在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF，那么，四边形AFED是否为平行四边形？如果是,请证明之，如果不是，请说明理由．23．在△ABC中,AB=AC，点P为△ABC所在平面内一点，过点P分别作PE∥AC交AB于点E，PF∥AB交BC 于点D,交AC于点F．若点P在BC边上(如图1），此时PD=0，可得结论：PD+PE+PF=AB．请直接应用上述信息解决下列问题:当点P分别在△ABC内(如图2）,△ABC外（如图3）时，上述结论是否成立？若成立,请给予证明；若不成立，PD,PE，PF与AB之间又有怎样的数量关系，请写出你的猜想，不需要证明．24．如图1,P为Rt△ABC所在平面内任意一点（不在直线AC上），∠ACB=90°,M为AB边中点．操作：以PA、PC为邻边作平行四边形PADC，连续PM并延长到点E，使ME=PM，连接DE．探究:（1）请猜想与线段DE有关的三个结论；(2）请你利用图2,图3选择不同位置的点P按上述方法操作;(3）经历(2）之后，如果你认为你写的结论是正确的,请加以证明;如果你认为你写的结论是错误的,请用图2或图3加以说明;(注意:错误的结论，只要你用反例给予说明也得分)（4）若将“Rt△ABC"改为“任意△ABC”，其他条件不变，利用图4操作，并写出与线段DE有关的结论（直接写答案）．25．在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD分割成四个部分,使含有一组对顶角的两个图形全等；（1）根据小强的分割方法，你认为把平行四边形分割成满足以上全等关系的直线有_________组;(2）请在图中的三个平行四边形中画出满足小强分割方法的直线；(3）由上述实验操作过程,你发现所画的两条直线有什么规律？26．如图，在直角梯形ABCD中，AB∥CD,∠BCD=Rt∠，AB=AD=10cm，BC=8cm．点P从点A出发，以每秒3cm 的速度沿折线ABCD方向运动,点Q从点D出发，以每秒2cm的速度沿线段DC方向向点C运动．已知动点P、Q 同时发，当点Q运动到点C时，P、Q运动停止，设运动时间为t．（1）求CD的长；(2）当四边形PBQD为平行四边形时，求四边形PBQD的周长；（3）在点P、点Q的运动过程中，是否存在某一时刻，使得△BPQ的面积为20cm2？若存在，请求出所有满足条件的t的值;若不存在，请说明理由．27．已知平行四边形的三个顶点的坐标分别为O（0,0）、A（2，0）、B（1，1），则第四个顶点C的坐标是多少？28．已知平行四边形ABCD的周长为36cm，过D作AB，BC边上的高DE、DF，且cm，，求平行四边形ABCD的面积．29．如图，在平面直角坐标系中，已知O为原点，四边形ABCD为平行四边形,A、B、C的坐标分别是A（﹣3，），B(﹣2,3)，C（2，3），点D在第一象限．（1）求D点的坐标；（2）将平行四边形ABCD先向右平移个单位长度，再向下平移个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少？（3）求平行四边形ABCD与四边形A1B1C1D1重叠部分的面积？30．如图所示．▱ABCD中,AF平分∠BAD交BC于F，DE⊥AF交CB于E．求证：BE=CF．答案与评分标准1．如图，已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F．（1)求证:BE=DF;（2）若M、N分别为边AD、BC上的点，且DM=BN,试判断四边形MENF的形状（不必说明理由）．考点：平行四边形的判定与性质；全等三角形的判定与性质。

第一部分 平行四边形的性质练习题 例题1、平行四边形得周长为50cm ，两邻边之差为5cm,求各边长。

变题1.平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2：3，则AB=_______,BC=________. 变题2.四边形ABCD 是平行四边形，∠BAC=90°,AB=3,AC=4,求AD 的长。

例题2.平行四边形ABCD 中，∠A-∠B=20°,求平行四边形各内角的度数。

变题3.平行四边形ABCD 中，AE 平分∠DAB, ∠DEA=20°,则∠C=_________,∠B_________. 变题4.如图，在平行四边形ABCD 中，∠BAC=34°, ∠ACB=26°，求∠DAC 与∠D 的度数。

例题3.如图，在平行四边形ABCD 中，CE ⊥AD,CF ⊥BA 交BA 的延长线于F ，∠FBC=30°,CE=3cm,CF=5cm,求平行四边形ABCD 的周长。

变题5.如图，平行四边形ABCD 的周长为50，其中AB=15，∠ABC=60°，求平行四边形面积。

1、如图，四边形ABCD 是平行四边形，AB=6cm,BC=8cm ，∠B=70°,则AD=________,CD=______,∠D=_______,∠A=______,∠C=_______.2、平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2：3，则AB=_______,BC=________.3、平行四边形得周长为50cm ，两邻边之差为5cm,则长边是________ ，短边是__________.4、平行四边形ABCD 中，∠A-∠B=20°, 则∠A=_______ ∠B=________5、.平行四边形ABCD 中，AE 平分∠DAB, ∠DEA=20°,则∠C=____,∠B_____.6、平行四边形 ABCD 中，∠A+∠C=200°.则：∠A= _______，∠B= _________ .7、如图，平行四边形ABCD 的周长为50，其中AB=15，∠ABC=60°，求平行四边形面积。

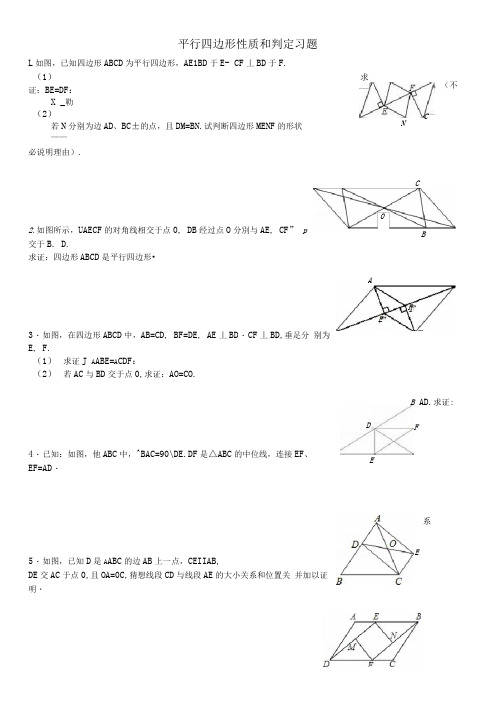
平行四边形性质和判定习题L如图，已知四边形ABCD为平行四边形，AE1BD于E- CF丄BD于F.（1）求证：BE=DF：X _勒（2）若N分别为边AD、BC±的点，且DM=BN.试判断四边形MENF的形状——必说明理由）.2.如图所示，UAECF的对角线相交于点0, DB经过点O分別与AE, CF” p交于B. D.求证：四边形ABCD是平行四边形•3・如图，在四边形ABCD中，AB=CD, BF=DE, AE丄BD・CF丄BD,垂足分别为E, F.（1）求证J A ABE=A CDF：（2）若AC与BD交于点0,求证：AO=CO.4・已知：如图，他ABC中，^BAC=90\DE.DF是△ABC的中位线，连接EF、EF=AD・5・如图，已知D是A ABC的边AB上一点，CEIIAB,DE交AC于点0,且OA=0C,猜想线段CD与线段AE的大小关系和位置关并加以证明・B AD.求证:。

（不CNCBAFED FE系E6・如图，已知，UABCD中，AE=CF, M、N分别是DE、BF的中点.求证：四边形MFNE是平行四边形•7・如图，平行四边形ABCD, E 、F 两点在对角线BD 上，且BE=DF,连接AE. EG CF, FA ・求证：四边形AECF 是平行四边形•& 在UABCD 中，分别以AD 、BC 为边向内作等边△ADE 和等边△BCF,连接BE. DF ・求证：四边形BEDF 是平 行四边形・DBIIAC,且DB 丄AC. E 是AC 的中点，求证：BC=DE ・2如图，在梯形ABCD 中，ADIIBC, AD=24cm. BC=30cm,点P 自点A 向D 以IcmZs 的速度运动，到D 点Q 自点C 向B 以2cm/s 的速度运动，到B点即停止，直线PQ 截梯形为两个四边形•问当P. Q同时10. 已知脣 点即停止. 出发，几秒后其中一个四边形为平行四边形？IL 如图：已知D 、E 、F 分别是A ABC 各边的中点, 求证：AE 仃DF 互相平分.如图所示, 9・ED13.如图，已知四边形ABCD中，点E, F. G, H分别是AB、CD、AC. BD的中点，并且点E、F、G、H有在同一条直线上.求证：EF和GH互相平分・14.如图J oABCD 中，MNIIAC.试说明MQ=NP.15.已知：如图所示「平行四边形ABCD的对角线AC, BD柑交于点6 EF经过点0并且分别和AB. CD相交于点E, F,点G, H分别为OA, 0C的中点.求证：四边形EHFG是平行四边形.-46 如制已知的ABCD中,E、F是对角线BD上的两点，BE=DF,点G、H分别在BA和DC的延长线上，且AG=CH. 连接GE、EH、HF、FG.（1）求证：四边形GEHF是平行四边形；（2）若点G、H分别在线段BA和DC上，尖余条件不变，则（1）中的结论是否成立？（不用说明理由）17.如图，在A ABC中，D是AC的中点，E是线段BC延长线一点，过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.（1）求证J AF=CE：（2）如果AC=EF,且ZACB=135\试判断四边形AFCE是什么样的四边形，并证明你的结论・18,如图平行四边形ABCD 中.mBC=6（几 点E 、F 分別在CD.BC 的延长线上，AE||BD ・ EEhBB 垂足为点F, DF=2 （1） 求证：D 是EC 中点； （2） 求FC 的长.19.如图，已知A ABC 是等边三角形，点D 、F 分别在线段BC 、AB 匕 厶EFB=60。

初 2017 级寒假培训（八） A 层----平行四边形的性质与判定班级： 姓名：1.定 ：两 互相平行的四 形叫做平行四 形，平行四 形 ABCD 作： □ ABCD几何 言：AB // CD , AD // BC , 四边形 ABCD 是平行四边形AD2.性 ：平行四 形的 平行且相等， 角相等， 角互 ， 角 互相平分；几何 言：∵四 形 ABCD 是平行四 形O∴ AD ∥ BC, _________ （ 平行）； AD=BC ,__________（ 相等）；BCBAC BCD ， _________（ 角相等）； BACABC 180 ⋯（ 角互 ） ；OA OC ，（ 角 互相平分） 。

平行四边形的判定：判定 1.两 分 平行的四 形是平行四 形 判定 2.两 分 相等的四 形是平行四 形 判定 3.两 角分 相等的四 形是平行四 形 判定 4. 角 互相平分的四 形是平行四 形 判定 5. 一 平行且相等的四 形是平行四 形； 几何 言判定 1.AB // CD , AD // BC , 四边形 ABCD 是平行四边形判定 2. AB DC , AD BC ， 四边形 ABCD 是平行四边形判定 3. ABCADC , BADBCD , 四边形 ABCD 是平行四边形 判定 4. AO CO, BO DO , 四边形 ABCD 是平行四边形 判定 5.AB // CD , AB CD ,四边形 ABCD 是平行四边形夯 基 ：1. 如 ，将 □ ABCD 的一 BC 延 至 E ，若∠ A =110°， ∠ 1=________．ADABADB E1 D C BCCE242. 如 ，在 □ ABCD 中， A 120，D ＝°．3. 在平行四 形ABCD 中， AB6cm ， BC 8cm ， 平行四 形ABCD 的周cm ．4. 如 ，在 □ ABCD 中，已知 AD 8CM , AB 6CM , ，DE 平分 ADC 交 BC 于点 E ，则 BE 等于（）A.2CMB.4CMC.6CM D .8CM5．平行四边形中一边的长为10cm，那么它的两条对角线的长度可以是（）A.4cm和 6cmB.20cm和30cmC.6cm和8cmD.8cm和12cm6.在□ABCD中，对角线 AC，BD相交于点 O，若 BD与 AC的和为 18cm，CD： DA=2：3，AOB的周长为 13cm，那么 BC的长为（）A. 6cmB. 9cm C .3cm D .12cm7.如图， ?ABCD 中， AC 、 BD 为对角线， BC=6 ， BC 边上的高为4，则阴影部分的面积为．8. 在下面给出的条件中，能判定四边形ＡＢＣＤ是平行四边形的是（）A. AB BC, AD CDB.AB // CD, AD BCC.AB // CD , B DD. AB, C D9. 一个四边形的三个相邻内角度数依次如下，那么其中是平行四边形的是（）A.88 ,108 ,88B.88 ,104 ,108 C .88 ,92 ,92 D.108 ,72 ,10810.点 A， B，C， D 在同一平面内，从①AB∥CD，② AB=CD，③ BC∥ AD，④ BC=AD 这四个条件中任选两个，能使四边形ABCD是平行四边形的选法有（）种A． 3 B．4 C．5 D． 6 ADB C8.如图，在平行四边形 ABCD 中，若 AB=6 ，AD=10 ，?ABC 的平分线交 AD 于点 E，交 CD 的延长线于点 F，求 DF 的长．9. 已知：如图a，ABCD 的对角线 AC 、 BD 相交于点 O ， EF 过点 O 与 AB 、 CD 分别相交于点 E 、 F ．（1）求证：OE OF , AE CF , BE DF .（2）若上题中的条件都不变，将EF 转动到图 b 的位置，那么结论是否成立？若将EF向两方延长与平行四边形的两对边的延长线分别相交（图 c 和图 d），结论是否成立，说明你的理由．10.已知如图， O 为平行四边形 ABCD的对角线 AC 的中点， EF 经过点 O，且与 AB 交于 E，与 CD 交于 F，求证：四边形 AECF是平行四边形。

平行四边形性质与判定练习题1. 平行四边形的定义平行四边形是指有四条边对两对相邻边均平行的四边形。

2. 平行四边形的性质根据平行四边形的定义，我们可以得出以下性质：- 对边相等：平行四边形的对边相等，即两对相邻边的长度相等。

- 对角线互相平分：平行四边形的两条对角线互相平分，即把平行四边形分成四个相等的三角形。

- 对角线长的一半为高：平行四边形的两条对角线交点到任意边的距离等于对角线的一半，即为平行四边形的高。

3. 判定平行四边形的条件可以利用以下条件来判定一个四边形是否为平行四边形：- 边对边平行：四边形的对边必须互相平行。

- 对角线相等：四边形的对角线必须相等。

4. 练题请回答以下平行四边形的判定练题：1. 判断四边形ABCD是否为平行四边形：- A(2, 3), B(4, 7), C(8, 5), D(6, 1)- AB = 5, BC = 3, CD = 5, DA = 3- AC ≠ BD2. 判断四边形EFGH是否为平行四边形：- E(-1, -3), F(3, -3), G(5, 1), H(1, 1)- EF = 4, FG = 5, GH = 5, HE = 4- EG = FH, EF ≠ GH3. 判断四边形IJKL是否为平行四边形：- I(-2, 1), J(-2, 4), K(2, 4), L(2, 1)- IJ = KL = 3, JK = LI = 5- IJ ≠ KL, JK = LI根据以上判定条件，我们可以得出：- 题目1的四边形ABCD不是平行四边形；- 题目2的四边形EFGH不是平行四边形；- 题目3的四边形IJKL是平行四边形。

以上是关于平行四边形性质与判定的练习题。

希望能帮助你更好地理解平行四边形和判定条件。

G B A DCEF平行四边形练习1．判断题：（1）平行四边形的一组邻角的平分线互相垂直。

（ ） （2）有一组对边平行，且两个角是直角的四边形是矩形。

（ ） （3）两条对角线相等的四边形是矩形。

（ ） （4）两组对边分别相等的四边形是矩形。

（ ） （5）有一个角是60°的平行四边形是菱形。

（ ） （6）有两边相等的平行四边形是菱形。

（ ） （7）有一组邻边相等的矩形是正方形。

（ ）（8）有三边相等，且有一个角是直角的四边形是正方形。

（ ）（9）对角线相等，且互相垂直平分的四边形是正方形。

（ ） （图1）2.已知矩形的一条对角线长是8cm ，两条对角线的一个交角为60°，则矩形的周长为3.直角三角形斜边上的高与中线分别是5cm 和6cm ，则它的面积为4．如图1所示，两张等宽的纸条交叉重叠在一起，重叠部分的四边形ABCD 是 形．5. 如图所示，将两条等宽的纸条重叠在一起，若AB=8，∠ABC=600，则AC=______________.6.如图所示，矩形ABCD 的对角线AC 和BD 相交于点O ，过点O 的直线分别交AD 和BC 于点E,F,AB=3,BC=4,则图中阴影部分的面积为 .7.若菱形的周长为12cm ，较长对角线所对的角为120°，那么较短的对角线为 cm.8.如图所示,正方形ABCD 的周长是20cm,则矩形EFGH 的周长为 cm.AD9．如图，已知在四边形ABCD 中，AC ⊥DB ，交于O 、E 、F 、G 、H 分别是四边的中点，求证:四边形EFGH 是矩形．10.如图所示,在△ABC 中,AD 平分∠BAC,且DE ∥AC,DF ∥AB,试说明四边形AEDF 为菱形17．如图，矩形ABCD 中，AC 与BD 交于O 点，BE ⊥AC 于E ，CF ⊥BD 于F. 求证：BE=CF.23、如图，延长正方形ABCD 的边BC 到点E ，使得CE=CA,连接AE 交CD 于点F 。

E DCBA 平行四边形的性质与判定（练习）【知识点】：1. 平行四边形的定义：2．平行四边形性质：⑴边： ；⑵角： ； ⑶对角线： ；(3)对称性：___________________________. 3．平行四边形判定：边：①___________________ ___②_____________ ___________③ ； 角： ； 对角线： ； 【基础训练】一．填空题 (3分×10 = 30分)1．在□ABCD 中，如果∠A +∠C =120°，那么∠B = °．2．已知平行四边形的周长为56㎝，两邻边之比为3:1，则四边形较长的边长为 ． 3．已知□ABCD 中，AB = 6，BC 、AB 边上的高分别为6、4，则BC 边长为 ． 4．已知□ABCD 中，∠A =60°，AB = 4㎝，AD = 6㎝，则□ABCD 的面积为 ． 5．已知□ABCD 中，若∠B 的2倍与∠A 的补角的和为90°，则∠B = 度．6．已知□ABCD 的周长为20cm ，对角线相交于点O ，且△BOC 的周长比△AOB 的周长多2cm ，则AB = cm ．7．如图1，已知□ABCD 中，AE ＝CF ，则图中有 对全等三角形．8．如图2，已知□ABCD 中，BC =12，AB =10，AE ⊥BC 于点E ，且AE =8，则AB 与CD 两边之间的距离为 ．9．如图3，已知□ABCD 中，AB =6，AD =8，AE 平分∠BAD 交BC 于E ，则EC = ．图1 图2 图310．在四边形ABCD 中，AB =CD ，要使这个四边形成为平行四边形，则可添加的一个条件可以是 ． 二．选择题 (3分×6 = 18分)E DCB A1．平行四边形是 ( )（A ）轴对称图形 （B ）既是轴对称图形，又是中心对称图形 （C ）中心对称图形 （D ）既不是轴对称图形，也不是中心对称图形2．用两个全等的三角形（三边互不相等）拼成不同的四边形，其中不同的平行四边形的个数是 ( ) （A ）1个 （B ）2个 （C ）3 个 （D ）4个 3．下列条件中，能判断四边形是平行四边形的条件是（ ） （A ）一组对边平行 （B ）四条边相等 （C ）一组对边平行，另一组对边相等 （D ）两条对角线相等4．已知□ABCD 的周长为40cm ，△ABC 的周长为25cm ，则对角线AC 长为（ ） （A ）5cm （B ）15cm （C ）6cm （D ）16cm 5．如图4，已知四边形ABCD 和CEFG 都是平行四边形， 则下列等式中正确的是（ ）（A ）∠1+∠8=1800（B ）∠1+∠5=180° （C ）∠4+∠6=180° （D ）∠2+∠8=180°6．已知P 为□ABCD 的边AB 上的任一点，则△PCD 与 图4□ABCD 的面积的比S △PCD :S □ABCD 为（ ）（A ）1:2 （B ）1:3 （C ）1:4 （D ）不能确定 三、几何证明1.已知：如图，D 、F 分别是ΔABC 的边BC 、AC 的中点，点E 在线段DF 的延长线上，FE ＝DF 。

平行四边形性质和判定综合习题一．解答题（共30小题）1．如图，已知四边形ABCD为平行四边形，AE⊥BD于E，CF⊥BD于F．（1）求证:BE=DF；(2）若M、N分别为边AD、BC上的点，且DM=BN，试判断四边形MENF的形状（不必说明理由)．2．如图所示，▱AECF的对角线相交于点O,DB经过点O，分别与AE,CF交于B，D．求证：四边形ABCD是平行四边形．3．如图，在四边形ABCD中，AB=CD，BF=DE，AE⊥BD，CF⊥BD，垂足分别为E，F．（1）求证:△ABE≌△CDF；（2)若AC与BD交于点O，求证：AO=CO．4．已知：如图，在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线，连接EF、AD．求证：EF=AD．5．如图，已知D是△ABC的边AB上一点，CE∥AB,DE交AC于点O，且OA=OC，猜想线段CD与线段AE的大小关系和位置关系，并加以证明．6．如图,已知，▱ABCD中，AE=CF,M、N分别是DE、BF的中点．求证：四边形MFNE是平行四边形．7．如图，平行四边形ABCD，E、F两点在对角线BD上，且BE=DF，连接AE，EC，CF，FA．求证:四边形AECF是平行四边形．8在▱ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF，连接BE、DF．求证：四边形BEDF是平行四边形．9如图所示,DB∥AC，且DB=AC，E是AC的中点，求证：BC=DE．10．已知：如图,在梯形ABCD中，AD∥BC，AD=24cm，BC=30cm,点P自点A向D以1cm/s的速度运动，到D 点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，直线PQ截梯形为两个四边形．问当P，Q同时出发，几秒后其中一个四边形为平行四边形？11如图:已知D、E、F分别是△ABC各边的中点，求证：AE与DF互相平分．12．已知：如图，在▱ABCD中，对角线AC交BD于点O，四边形AODE是平行四边形．求证：四边形ABOE、四边形DCOE都是平行四边形．13．如图，已知四边形ABCD中，点E，F，G，H分别是AB、CD、AC、BD的中点，并且点E、F、G、H有在同一条直线上．求证:EF和GH互相平分．14．如图:四边形ABCD中，MN∥AC，试说明MQ=NP．15．已知：如图所示，平行四边形ABCD的对角线AC，BD相交于点O,EF经过点O并且分别和AB，CD相交于点E，F,点G，H分别为OA，OC的中点．求证：四边形EHFG是平行四边形．16．如图，已知在▱ABCD中，E、F是对角线BD上的两点，BE=DF，点G、H分别在BA和DC的延长线上，且AG=CH,连接GE、EH、HF、FG．（1）求证：四边形GEHF是平行四边形;（2）若点G、H分别在线段BA和DC上，其余条件不变，则(1）中的结论是否成立？（不用说明理由）17．如图，在△ABC中，D是AC的中点，E是线段BC延长线一点，过点A作BE的平行线与线段ED的延长线交于点F，连接AE、CF．（1）求证:AF=CE；(2）如果AC=EF，且∠ACB=135°，试判断四边形AFCE是什么样的四边形,并证明你的结论．18．如图平行四边形ABCD中,∠ABC=60°，点E、F分别在CD、BC的延长线上,AE∥BD，EF⊥BF，垂足为点F，DF=2（1）求证：D是EC中点；(2）求FC的长．19如图，已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF．（1）求证：四边形EFCD是平行四边形；（2）若BF=EF，求证：AE=AD．20如图，四边形ABCD，E、F、G、H分别是AB、BC、CD、DA的中点．(1）请判断四边形EFGH的形状？并说明为什么；（2）若使四边形EFGH为正方形，那么四边形ABCD的对角线应具有怎样的性质？21．如图，△ACD、△ABE、△BCF均为直线BC同侧的等边三角形．（1)当AB≠AC时，证明：四边形ADFE为平行四边形；(2）当AB=AC时,顺次连接A、D、F、E四点所构成的图形有哪几类？直接写出构成图形的类型和相应的条件．22．如图,以△ABC的三边为边，在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF，那么,四边形AFED 是否为平行四边形?如果是，请证明之，如果不是,请说明理由．23．在△ABC中，AB=AC，点P为△ABC所在平面内一点，过点P分别作PE∥AC交AB于点E，PF∥AB交BC 于点D，交AC于点F．若点P在BC边上（如图1），此时PD=0，可得结论：PD+PE+PF=AB．请直接应用上述信息解决下列问题:当点P分别在△ABC内（如图2),△ABC外(如图3)时，上述结论是否成立？若成立，请给予证明；若不成立，PD，PE，PF与AB之间又有怎样的数量关系,请写出你的猜想,不需要证明．26．如图,在直角梯形ABCD中,AB∥CD，∠BCD=Rt∠，AB=AD=10cm，BC=8cm．点P从点A出发，以每秒3cm 的速度沿折线ABCD方向运动，点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动．已知动点P、Q 同时发，当点Q运动到点C时，P、Q运动停止，设运动时间为t．（1）求CD的长；（2）当四边形PBQD为平行四边形时，求四边形PBQD的周长;（3)在点P、点Q的运动过程中，是否存在某一时刻，使得△BPQ的面积为20cm2？若存在,请求出所有满足条件的t的值；若不存在,请说明理由．27．已知平行四边形的三个顶点的坐标分别为O（0,0)、A（2，0）、B（1，1），则第四个顶点C的坐标是多少？28．已知平行四边形ABCD的周长为36cm，过D作AB，BC边上的高DE、DF，且cm，，求平行四边形ABCD的面积．29．如图，在平面直角坐标系中，已知O为原点，四边形ABCD为平行四边形，A、B、C的坐标分别是A（﹣3，），B(﹣2，3)，C（2，3)，点D在第一象限．（1）求D点的坐标；(2）将平行四边形ABCD先向右平移个单位长度，再向下平移个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少？（3）求平行四边形ABCD与四边形A1B1C1D1重叠部分的面积？30．如图所示．四边形ABCD中，AF平分∠BAD交BC于F，DE⊥AF交CB于E．求证：BE=CF．。

平行四边形性质和判定习题(答案详细)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（平行四边形性质和判定习题(答案详细)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为平行四边形性质和判定习题(答案详细)的全部内容。

平行四边形性质和判定习题1．如图，已知四边形ABCD为平行四边形，AE⊥BD于E，CF⊥BD于F．（1）求证：BE=DF；（2）若 M、N分别为边AD、BC上的点，且DM=BN，试判断四边形MENF的形状（不必说明理由）．2．如图所示，▱AECF的对角线相交于点O，DB经过点O，分别与AE,CF交于B，D．求证：四边形ABCD是平行四边形．3．如图，在四边形ABCD中，AB=CD，BF=DE，AE⊥BD，CF⊥BD，垂足分别为E,F．(1)求证：△ABE≌△CDF；（2)若AC与BD交于点O，求证:AO=CO．4．已知:如图，在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线，连接EF、AD．求证：EF=AD．5．如图，已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O，且OA=OC，猜想线段CD与线段AE的大小关系和位置关系，并加以证明．6．如图，已知，▱ABCD中，AE=CF，M、N分别是DE、BF的中点．求证：四边形MFNE是平行四边形．7．如图,平行四边形ABCD,E、F两点在对角线BD上，且BE=DF,连接AE，EC，CF,FA．求证：四边形AECF是平行四边形．8．在▱ABCD中，分别以AD、BC为边向内作等边△ADE和等边△BCF，连接BE、DF．求证：四边形BEDF是平行四边形．9．如图所示,DB∥AC,且DB=AC，E是AC的中点，求证:BC=DE．10．已知：如图，在梯形ABCD中，AD∥BC，AD=24cm，BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止．点Q自点C向B以2cm/s的速度运动,到B点即停止，直线PQ截梯形为两个四边形．问当P，Q同时出发，几秒后其中一个四边形为平行四边形？11．如图：已知D、E、F分别是△ABC各边的中点,求证：AE与DF互相平分．12．已知:如图，在▱ABCD中，对角线AC交BD于点O，四边形AODE是平行四边形．求证：四边形ABOE、四边形DCOE都是平行四边形．13．如图，已知四边形ABCD中，点E,F，G,H分别是AB、CD、AC、BD的中点，并且点E、F、G、H有在同一条直线上．求证:EF和GH互相平分．14．如图:▱ABCD中，MN∥AC，试说明MQ=NP．15．已知：如图所示，平行四边形ABCD的对角线AC，BD相交于点O，EF经过点O并且分别和AB,CD相交于点E，F，点G，H分别为OA，OC的中点．求证:四边形EHFG是平行四边形．16．如图，已知在▱ABCD中,E、F是对角线BD上的两点，BE=DF,点G、H分别在BA和DC的延长线上，且AG=CH，连接GE、EH、HF、FG．（1)求证：四边形GEHF是平行四边形;（2)若点G、H分别在线段BA和DC上，其余条件不变，则（1）中的结论是否成立？（不用说明理由）17．如图，在△ABC中，D是AC的中点,E是线段BC延长线一点，过点A作BE的平行线与线段ED的延长线交于点F，连接AE、CF．（1）求证：AF=CE；（2）如果AC=EF，且∠ACB=135°,试判断四边形AFCE是什么样的四边形,并证明你的结论．18．如图平行四边形ABCD中,∠ABC=60°，点E、F分别在CD、BC的延长线上，AE∥BD，EF⊥BF，垂足为点F，DF=2（1）求证:D是EC中点；（2）求FC的长．19．如图，已知△ABC是等边三角形，点D、F分别在线段BC、AB上，∠EFB=60°,DC=EF．（1)求证：四边形EFCD是平行四边形;（2)若BF=EF，求证:AE=AD．20．如图，四边形ABCD，E、F、G、H分别是AB、BC、CD、DA的中点．（1）请判断四边形EFGH的形状？并说明为什么;（2）若使四边形EFGH为正方形,那么四边形ABCD的对角线应具有怎样的性质？21．如图，△ACD、△ABE、△BCF均为直线BC同侧的等边三角形．(1）当AB≠AC时，证明：四边形ADFE为平行四边形；（2）当AB=AC时，顺次连接A、D、F、E四点所构成的图形有哪几类？直接写出构成图形的类型和相应的条件．22．如图，以△ABC的三边为边，在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF，那么,四边形AFED是否为平行四边形？如果是，请证明之,如果不是，请说明理由．23．在△ABC中，AB=AC，点P为△ABC所在平面内一点，过点P分别作PE∥AC交AB于点E，PF∥AB交BC于点D,交AC于点F．若点P在BC边上（如图1),此时PD=0，可得结论：PD+PE+PF=AB．请直接应用上述信息解决下列问题:当点P分别在△ABC内（如图2)，△ABC外（如图3)时,上述结论是否成立？若成立,请给予证明；若不成立,PD，PE，PF与AB之间又有怎样的数量关系，请写出你的猜想,不需要证明．24．如图1，P为Rt△ABC所在平面内任意一点（不在直线AC上），∠ACB=90°,M为AB边中点．操作：以PA、PC为邻边作平行四边形PADC，连续PM并延长到点E,使ME=PM,连接DE．探究：(1）请猜想与线段DE有关的三个结论；（2）请你利用图2，图3选择不同位置的点P按上述方法操作；(3)经历（2)之后，如果你认为你写的结论是正确的，请加以证明；如果你认为你写的结论是错误的，请用图2或图3加以说明;(注意：错误的结论,只要你用反例给予说明也得分)(4）若将“Rt△ABC"改为“任意△ABC”，其他条件不变，利用图4操作,并写出与线段DE有关的结论（直接写答案）．25．在一次数学实践探究活动中，小强用两条直线把平行四边形ABCD分割成四个部分，使含有一组对顶角的两个图形全等;（1)根据小强的分割方法，你认为把平行四边形分割成满足以上全等关系的直线有_________组;(2）请在图中的三个平行四边形中画出满足小强分割方法的直线；（3）由上述实验操作过程，你发现所画的两条直线有什么规律？26．如图,在直角梯形ABCD中，AB∥CD，∠BCD=Rt∠，AB=AD=10cm，BC=8cm．点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发，以每秒2cm的速度沿线段DC 方向向点C运动．已知动点P、Q同时发，当点Q运动到点C时，P、Q运动停止，设运动时间为t．(1）求CD的长；（2）当四边形PBQD为平行四边形时,求四边形PBQD的周长；（3）在点P、点Q的运动过程中，是否存在某一时刻,使得△BPQ的面积为20cm2?若存在，请求出所有满足条件的t的值；若不存在,请说明理由．27．已知平行四边形的三个顶点的坐标分别为O（0，0)、A（2，0）、B(1，1），则第四个顶点C的坐标是多少?28．已知平行四边形ABCD的周长为36cm,过D作AB,BC边上的高DE、DF，且cm,，求平行四边形ABCD的面积．29．如图，在平面直角坐标系中，已知O为原点，四边形ABCD为平行四边形，A、B、C的坐标分别是A（﹣3，),B(﹣2，3），C（2，3)，点D在第一象限．(1)求D点的坐标；（2）将平行四边形ABCD先向右平移个单位长度，再向下平移个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少？（3)求平行四边形ABCD与四边形A1B1C1D1重叠部分的面积？30．如图所示．▱ABCD中，AF平分∠BAD交BC于F，DE⊥AF交CB于E．求证：BE=CF．答案与评分标准1．如图，已知四边形ABCD为平行四边形,AE⊥BD于E，CF⊥BD于F．（1）求证：BE=DF;（2)若 M、N分别为边AD、BC上的点，且DM=BN，试判断四边形MENF的形状（不必说明理由）．考点：平行四边形的判定与性质；全等三角形的判定与性质。