26.1.3_二次函数y=ax2+c_的图象和性质

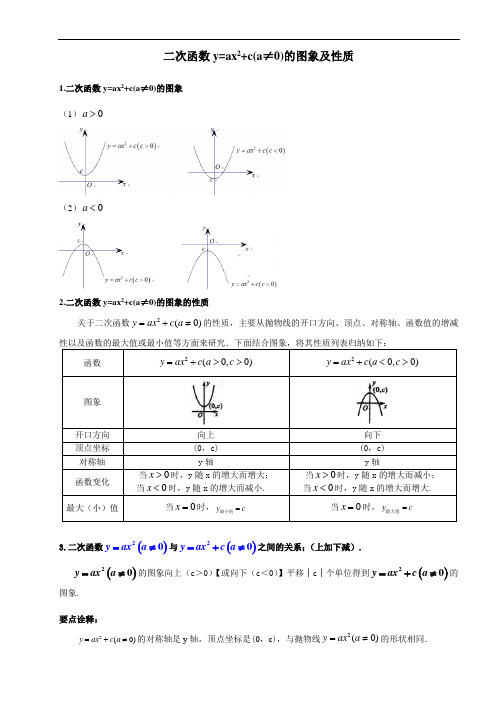
二次函数y=ax 2+c(a ≠0)的图象及性质1.二次函数y=ax 2+c(a ≠0)的图象 （1）0a >（2）0a <2.二次函数y=ax 2+c(a ≠0)的图象的性质关于二次函数2(0)y ax c a =+≠的性质，主要从抛物线的开口方向、顶点、对称轴、函数值的增减3.二次函数()20y axa =≠与()20y ax c a =+≠之间的关系；（上加下减）. ()20y ax a =≠的图象向上（c ＞0）【或向下（c ＜0）】平移│c │个单位得到()20y ax c a =+≠的图象.要点诠释：2(0)y ax c a =+≠的对称轴是y 轴，顶点坐标是(0，c )，与抛物线2(0)y axa =≠的形状相同．函数2(0)y ax c a =+≠的图象是由函数2(0)y ax a =≠的图象向上（或向下）平移||c 个单位得到的，顶点坐标为(0，c )．抛物线y ＝ax 2(a ≠0)的对称轴、最值与顶点密不可分，其对称轴即为过顶点且与x 轴垂直的一条直线，其顶点横坐标x ＝0，抛物线平移不改变抛物线的形状，即a 的值不变，只是位置发生变化而已．例1．求下列抛物线的解析式：（1）与抛物线2132y x =-+形状相同，开口方向相反，顶点坐标是（0，-5）的抛物线；（2）顶点为（0，1），经过点（3，-2）并且关于y 轴对称的抛物线． 【答案与解析】（1）由于待求抛物线2132y x =-+形状相同，开口方向相反，可知二次项系数为12， 又顶点坐标是（0，-5），故常数项5k =-，所以所求抛物线为2152y x =-． （2）因为待求抛物线顶点为（0，1），所以其解析式可设为21y ax =+，又∵ 该抛物线过点（3，-2），∴ 912a +=-，解得13a =-．∴ 所求抛物线为2113y x =-+．【总结升华】抛物线形状相同则||a 相同，再由开口方向可确定a 的符号，由顶点坐标可确定k 的值，从而确定抛物线的解析式2y ax k =+．．在同一直角坐标系中，画出2y x =-和21y x =-+的图象，并根据图象(如图所示)回答下列问题．(1)抛物线21y x =-+向________平移________个单位得到抛物线2y x =-；(2)抛物线，21y x =-+开口方向是________，对称轴为________，顶点坐标为________；(3)抛物线21y x =-+，当x________时，随x 的增大而减小；当x________时，函数y 有最________值，其最________值是________．【答案】 (1)下； l ； (2)向下； y 轴； (0，1)； (3)＞0； ＝0； 大； 大 ； 1. 【解析】在同一平面直角坐标系内画出两条抛物线，利用图象回答问题．(1)抛物线21y x =-+向 下 平移 1__个单位得到抛物线2y x =-；(2)抛物线，21y x =-+开口方向是 向下 ，对称轴为___ y 轴_____，顶点坐标为_ (0，1)__；(3)抛物线21y x =-+，当x ＞0时，y 随x 的增大而减小； 当x ＝0__时，函数y 有最 大 值，其最 大__值是 1 ．【总结升华】本例题把函数21y x =-+与函数2y x =-的图象放在同一直角坐标系中进行对比，易得出二次函数2(0)y a x k a =+≠与2(0)y ax a =≠的图象形状相同，只是位置上下平移的结论．2(0)y ax k a =+≠可以看作是把2(0)y ax a =≠的图象向上(0)k >或向下(0)k <平移||k 个单位得到的．练习1．在同一坐标系中，一次函数y=﹣mx +n 2与二次函数y=x 2﹣m 的图象可能是（ ）A ．B ．C ．D ．2．在直角坐标系中，函数y=3x 与y=﹣x 2+1的图象大致是（ ）A ．B ．C ．D ．3．如图，在同一直角坐标系中，y=ax +c 与y=ax 2+c 的图象为（ ）A ．B ．C ．D ．4．函数y=ax 2+c 与y=ax +c （a ≠0）在同一坐标系内的图象是图中的（ ）A ．B ．C ．D ．5．在同一平面直角坐标中，直线y=ax+b与抛物线y=ax2+b的图象可能是（）A． B．C． D．6．已知一次函数y=ax﹣c的图象如图所示，则二次函数y=ax2+c的图象大致是（）A．B．C． D．7．已知函数y=a（x+1）和y=a（x2+1），那么它们在同一坐标系内图象的示意图是（）A．B． C．D．8．函数y1=ax+3和y2=ax2﹣2（a≠0）的图象在同一象限内的图象可能是（）A．B．C．D．9．抛物线y=﹣x2﹣1的顶点坐标为（）A．（1，0） B．（﹣1，0）C．（0，﹣1）D．（2，3）10．下列函数中，图象形状、开口方向相同的是（）①y=﹣3x2；②y=﹣x2；③y=﹣x2﹣1；④y=2x2+1；⑤y=5x2﹣3；⑥y=﹣5x2．A．①④B．②③C．⑤⑥D．②③④11．抛物线y=x2+1的对称轴是（）A．直线x=1 B．直线x=﹣1 C．y轴D．直线x=﹣212．函数y=x2+1与y=x2图象不同之处是（）A．对称轴B．开口方向C．顶点D．形状13．如图所示是二次函数y=﹣x2+2的图象在x轴上方的一部分，对于这段图象与x轴所围成的阴影部分的面积，你认为与其最接近的值是（）A．4 B．C．2πD．814．关于函数y=2x2﹣3，y=﹣的图象及性质，下列说法不正确的是（）A．它们的对称轴都是y轴B．对于函数，当x＞0时，y随x的增大而减小C．抛物线y=2x2﹣3不能由抛物线y=﹣平移得到D．抛物线y=2x2﹣3的开口比y=﹣的开口宽15．已知二次函数y=﹣﹣3，其图象的对称轴是（）A．直线B．直线C．直线D．直线x=016．二次函数y=x2﹣2的图象的顶点是（）A．（2，﹣2）B．（﹣1，0）C．（1，9） D．（0，﹣2）17．函数y=﹣x2﹣1的开口方向和对称轴分别是（）A．向上，y轴B．向下，y轴C．向上，直线x=﹣1D．向下，直线x=﹣118．对于函数y=x2+1，下列结论正确的是（）A．图象的开口向下B．y随x的增大而增大C．图象关于y轴对称D．最大值是019．若在同一直角坐标系中，作y=﹣x2，y=﹣x2+1，y=x2﹣1的图象，则对它们图象的说法正确的是（）A．都关于y轴对称B．开口方向相同C．都经过原点D．互相可以通过平移得到二．填空题（共16小题）20．已知二次函数y=﹣2x2+4的图象如图所示，那么，当﹣2＜x≤1时，y的取值范围是．21．抛物线y=x2+的开口向，对称轴是．22．二次函数y=﹣x2+4的图象的顶点坐标是．23．抛物线y=2x2﹣1的顶点坐标是．24．抛物线y=﹣﹣3的顶点坐标是．25．抛物线y=﹣2x2﹣5的开口方向，对称轴是，顶点坐标是．26．抛物线y=﹣2x2+4的顶点坐标为．27．二次函数y=2x2+4的对称轴为．28．给出下列三个函数：①y=﹣2x，②y=2x﹣1，③y=﹣x2+3（x＞0），其中y随x的增大而减小的函数有．29．对于抛物线y=﹣x2+3，下列说法：①开口向下；②对称轴是y轴；③顶点在x轴上；④顶点是（0，3）；⑤顶点是（0，﹣3）；⑥有最低点，其中正确的说法有（填序号）30．函数y=x2﹣2的顶点坐标是，当x时函数值y随x的增大而增大．31．函数y=ax2﹣2中，当x=1时，y=﹣4，则函数的最大值是．32．二次函数y=﹣x2+3的最大值是．33．二次函数y=x2+2017的最小值是．34．已知抛物线y=3x2﹣6，则该抛物线的最低点的坐标为．35．函数y=9﹣4x2的最大值是．。