材料力学第06章作业刘06

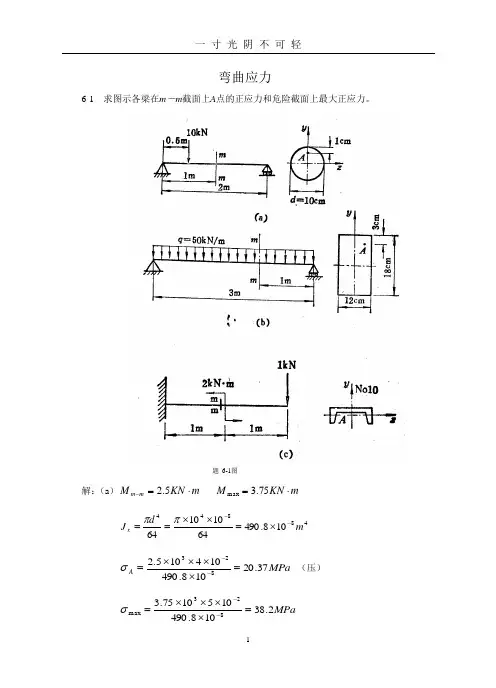
弯曲应力6-1 求图示各梁在m－m截面上A点的正应力和危险截面上最大正应力。

题6-1图解：（a）mKNMmm⋅=-5.2mKNM⋅=75.3max48844108.49064101064mdJx--⨯=⨯⨯==ππMPaA37.20108.490104105.2823=⨯⨯⨯⨯=--σ（压）MPa2.38108.4901051075.3823max=⨯⨯⨯⨯=--σ（b ）m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ （压） MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ （c ）m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ （压） MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D ＝6 cm 的圆轴，其外伸段为空心，内径d ＝4cm ，求轴内最大正应力。

解：)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。

试求梁内最大拉应力与最大压应力。

已知I z =10170cm 4，h 1=9.65cm ，h 2=15.35cm 。

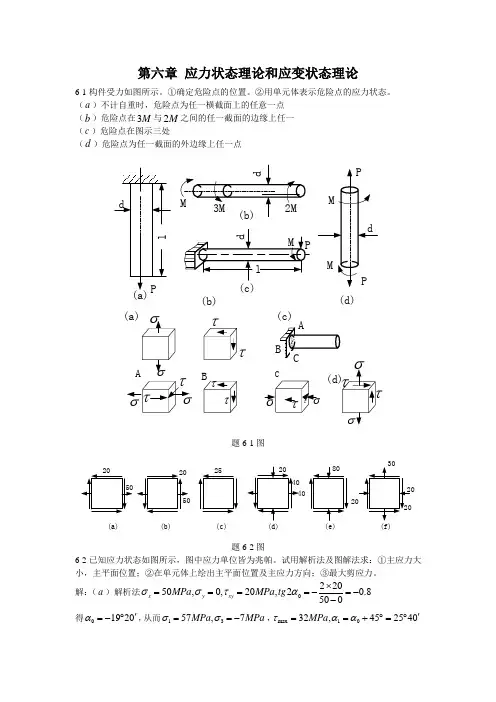
《材料力学》第6章简单超静定问题习题解.第六章简单超静定问题习题解[习题 6-1] 试作图示等直杆的轴力图解:把 B 支座去掉,代之以约束反力B R (↓。

设 2F 作用点为 C , F 作用点为 D ,则:B BD R N =F R N B CD +=F R N B AC 3+=变形谐调条件为:0=?l02=?+?+?EAa N EA a N EA a N BD CD AC 02=++BD CD AC N N N03 (2=++++F R F R R B B B45F R B -=(实际方向与假设方向相反,即:↑ 故:45F N BD-= 445F F F N CD-=+-= 47345F F F N AC =+-= 轴力图如图所示。

[习题 6-2] 图示支架承受荷载 kN F 10=, 1, 2, 3各杆由同一种材料制成,其横截面面积分别为21100mm A =, 22150mm A =, 23200mm A =。

试求各杆的轴力。

解:以节点 A 为研究对象,其受力图如图所示。

∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N032132=+-N N N ……… (1∑=0Y030sin 30sin 0103=-+F N N2013=+N N ………… (2变形谐调条件:设 A 节点的水平位移为x δ,竖向位移为y δ,则由变形协调图(b 可知: 00130cos 30sin x y l δδ+=?x l δ=?200330cos 30sin x y l δδ-=?03130cos 2x l l δ=?-?231l l l ?=?-?设 l l l ==31,则 l l 232= 2233113EA l N EA l N EA l N ??=- 22331123A N A N A N =- 150 23200100231?=-N N N23122N N N =-21322N N N -=……………… (3(1、 (2、 (3联立解得:kN N 45. 81=; kN N 68. 22=; kN N 54. 111=(方向如图所示,为压力,故应写作:kN N 54. 111-=。

材料⼒学习题第六章应⼒状态分析答案详解第6章应⼒状态分析⼀、选择题1、对于图⽰各点应⼒状态，属于单向应⼒状态的是（A ）。

20（MPa ）20d20（A ）a 点；（B ）b 点；（C ）c 点；（D ）d 点。

2、在平⾯应⼒状态下，对于任意两斜截⾯上的正应⼒αβσσ=成⽴的充分必要条件，有下列四种答案，正确答案是（ B ）。

（A ）,0x y xy σστ=≠；（B ）,0x y xy σστ==；（C ）,0x y xy σστ≠=；（D ）x y xy σστ==。

3、已知单元体AB 、BC ⾯上只作⽤有切应⼒τ，现关于AC ⾯上应⼒有下列四种答案，正确答案是（ C ）。

（A ）AC AC /2,0ττσ==；（B ）AC AC /2,/2ττσ==；（C ）AC AC /2,/2ττσ==；（D ）AC AC /2,/2ττσ=-=。

4、矩形截⾯简⽀梁受⼒如图（a ）所⽰，横截⾯上各点的应⼒状态如图（b ）所⽰。

关于它们的正确性，现有四种答案，正确答案是（ D ）。

(b)(a)（A）点1、2的应⼒状态是正确的；（B）点2、3的应⼒状态是正确的；（C）点3、4的应⼒状态是正确的；（D）点1、5的应⼒状态是正确的。

5、对于图⽰三种应⼒状态（a）、（b）、（c）之间的关系，有下列四种答案，正确答案是（ D ）。

τ(a) (b)(c)（A）三种应⼒状态均相同；（B）三种应⼒状态均不同；（C）（b）和（c）相同；（D）（a）和（c）相同；6、关于图⽰主应⼒单元体的最⼤切应⼒作⽤⾯有下列四种答案，正确答案是（ B ）。

(A) (B) (D)(C)解答：maxτ发⽣在1σ成45o的斜截⾯上7、⼴义胡克定律适⽤范围，有下列四种答案，正确答案是（ C ）。

（A）脆性材料；（B）塑性材料；（C）材料为各向同性，且处于线弹性范围内；（D）任何材料；8、三个弹性常数之间的关系：/[2(1)]G E v =+ 适⽤于（ C ）。

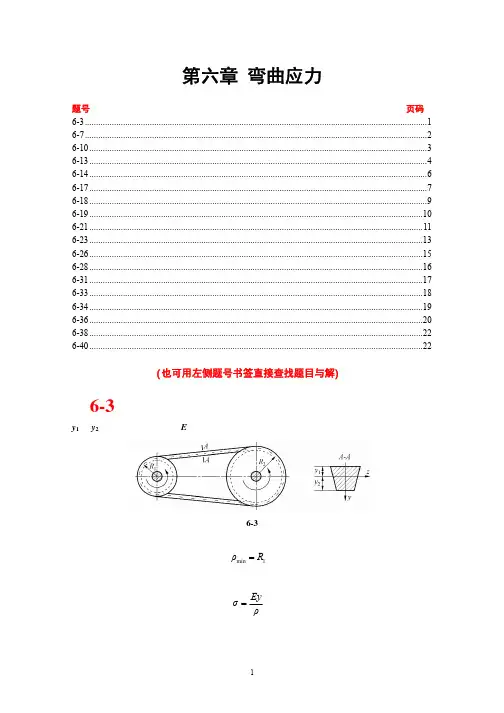
材料力学(金忠谋)第六版答案第06章(总27页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2弯曲应力6-1 求图示各梁在m －m 截面上A 点的正应力和危险截面上最大正应力。

题 6-1图解：（a ）m KN M m m ⋅=-5.2 m KN M ⋅=75.3max 48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ （压）3 MPa 2.38108.4901051075.3823max =⨯⨯⨯⨯=--σ （b ）m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ （压） MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ （c ）m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ （压） MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D ＝6 cm 的圆轴，其外伸段为空心，内径d ＝4cm ，求轴内最大正应力。

4解：)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。

材料力学习题册答案第六章材料力学习题册答案第六章材料力学作为工程力学的一个重要分支，研究材料在受力作用下的力学性能和变形行为。

在学习过程中，习题册是一个很好的辅助工具，能够帮助我们巩固所学的知识。

本文将为大家提供材料力学习题册第六章的答案，希望能够对大家的学习有所帮助。

第六章主要涉及材料的应变和应力分析，包括平面应变和平面应力的分析方法。

在这一章中，我们将学习如何计算材料在受力作用下的应变和应力分布，以及如何通过应变和应力分布来判断材料的强度和稳定性。

在第六章的习题中，我们会遇到一些典型的问题，例如平面应变和平面应力的计算，应变和应力的变换关系，以及应力的主方向和主应力的计算等。

以下是一些典型问题的答案，供大家参考：1. 一个长方形钢板的尺寸为20cm×30cm，厚度为5mm。

当该钢板受到拉伸力为5000N时，求钢板上的应力分布。

答案：首先计算钢板的截面积，即20cm×30cm=600cm²=0.06m²。

然后应力等于受力除以截面积，即5000N/0.06m²=83333.33Pa。

因此钢板上的应力分布为83333.33Pa。

2. 一个正方形钢材的尺寸为10cm×10cm，厚度为2mm。

当该钢材受到压力为2000N/m²时，求钢材上的应变分布。

答案：首先计算钢材的截面积，即10cm×10cm=100cm²=0.01m²。

然后应变等于受力除以截面积，即2000N/m²/0.01m²=200000。

因此钢材上的应变分布为200000。

3. 一个矩形钢板的尺寸为30cm×40cm，厚度为5mm。

当该钢板受到拉伸力为10000N时，求钢板上的最大应力和最小应力。

答案：首先计算钢板的截面积，即30cm×40cm=1200cm²=0.12m²。

然后最大应力等于受力除以截面积，即10000N/0.12m²=83333.33Pa。

第六章 结构位移计算§6-1 概述1. 位移种类图6.1(1) 线位移，∆C 、∆D 、∆K ；(2) 角位移，ϕA 、ϕB 、ϕK ；(3) 相对线位移，∆C =∆D =∆CD ； (4) 相对角位移，B A B A ϕϕϕ=+。

2. 计算位移的目的(1) 校核结构刚度，尤其是大型结构与高层建筑；(2) 施工控制与定位；(3) 解超静定结构的需要。

3. 产生位移的原因荷载，支座移动，温度变化，材料收缩，制造误差等。

对于静定结构，只有荷载产生内力，但产生位移的原因有多种。

超静定结构，多种原因均产生内力与位移。

4. 位移计算原理 变形体虚功原理。

§6-2 变形体的虚功原理1. 实功与虚功实功：，W =F ⋅S 。

，W ≠F ⋅∆，**∆d F dW⋅=，∆∆∆⋅=⋅=⎰F d F W 210**。

虚功：，121∆F W =(实功，恒为正)；2*∆F W =，外力虚功，内力有M 与F S ，也作功，称为内力虚功，虚功可正可负。

虚功就是作功的力与位移没有关系。

2. 质点系虚功原理(虚位移原理)虚位移：一个体系发生约束条件许可的任何微小位移。

即(1) 是可能的位移状态；(2) 微小性。

质点系虚位移原理：具有理想约束的质点系，在某一位置处于平衡的必要且充分条件是，对于任何虚位移，作用于质点系上的主动力所作虚总和为0.(1) 理想约束：约束反力在虚位移上的虚功恒为0称为理想约束。

(2) 主动力即作用荷载，不包括约束反力。

(3) 虚位移即可能的位移状态，即有可能。

刚体：任两点距离保持不变，可认为任两点之间有刚性链杆相连(理想约束)，即刚体是具有理想约束的质点系。

刚体体系：若干个刚体用理想约束连接起来的体系。

刚体虚位移原理：刚体体系处于平衡状态的必要且充分条件是，对于任意虚位移，所有主动力所作虚功总和为0. (注意，此处包括所有外力，即荷载与约束反力) 3. 变形体虚功原理变形体处于平衡状态的必要且充分条件是，对于任何虚位移，外力所作虚功总和等于内力在其虚变形上所作的虚功总和。