下载文档原格式
连接体专题复习1. 连接体：多个相互关联的物体连接(叠放、并排或由弹簧、绳子、细杆联系)在一起构成的物体系统称为连接体。
连接体一般具有相同的运动情况(速度、加速度)。
2. 解决连接体问题的两种方法3. 整体法、隔离法应注意的问题(1)不涉及系统内力时，优先考虑应用整体法，即“能整体、不隔离”。
(2)同样应用“隔离法”，也要先隔离“简单”的物体，如待求量少、或受力少、或处于边缘处的物体。
(3)将“整体法”与“隔离法”有机结合、灵活应用。
(4)各“隔离体”间的关联力，表现为作用力与反作用力，对整体系统则是内力特别提醒 当系统内各物体的加速度不同时，一般不直接用整体法，要采用隔离法解题。
例1 如图所示，在建筑工地，民工兄弟用两手对称水平施力将两长方体水泥制品夹紧并以加速度a 竖直向上匀加速搬起，其中A 的质量为m ，B 的质量为2m ，水平作用力为F ，A 、B 之间的动摩擦因数为μ，在此过程中，A 、B 间的摩擦力为( ) A.μF B.12m (g ＋a )C.m (g ＋a )D.32m (g ＋a )例2 质量为2 kg 的木板B 静止在水平面上，可视为质点的物块A 从木板的左侧沿木板上表面水平冲上木板，如图甲所示。
A 和B 经过1 s 达到同一速度，之后共同减速直至静止，A 和B 的v －t 图象如图乙所示，重力加速度g ＝10 m/s 2，求：(1)A 与B 上表面之间的动摩擦因数μ1； (2)B 与水平面间的动摩擦因数μ2； (3)A 的质量。
例3如图所示，质量为m1和m2的两物块放在光滑的水平地面上。
用轻质弹簧将两物块连接在一起。
当用水平力F作用在m1上时，两物块均以加速度a做匀加速运动，此时，弹簧伸长量为x；若用水平力F′作用在m1上时，两物块均以加速度a′＝2a做匀加速运动，此时弹簧伸长量为x′。
则下列关系正确的是() A.F′＝2F B.x′>2xC.F′>2FD.x′<2x例4如图所示，质量分别为m、M的两物体P、Q保持相对静止，一起沿倾角为θ的固定光滑斜面下滑，Q的上表面水平，P、Q之间的动摩擦因数为μ，则下列说法正确的是()A. P处于超重状态B. P受到的摩擦力大小为μmg，方向水平向右C. P受到的摩擦力大小为mg sin θcos θ，方向水平向左D. P受到的支持力大小为mg sin 2θ例5（多选）如图所示，质量分别为m A、m B的A、B两物块用轻质弹簧连接放在倾角为θ的斜面上，用始终平行于斜面向上的拉力F拉B物块，使它们沿斜面匀加速上升，A、B与斜面间的动摩擦因数均为μ，为了减小弹簧的形变量，可行的办法是()A.减小A物块的质量B.增大B物块的质量C.增大倾角θD.增大动摩擦因数μ针对训练1．如图所示，在倾角为30°的光滑斜面上放置质量分别为m和2m的四个木块，其中两个质量为m的木块间用一不可伸长的轻绳相连，木块间的最大静摩擦力是f m。
常见连接体问题(一)“死结”“活结”1．如图甲所示，轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为10 kg 的物体，∠ACB＝30°；图乙中轻杆HG一端用铰链固定在竖直墙上，另一端G通过细绳EG拉住，EG与水平方向也成30°，轻杆的G点用细绳GF拉住一个质量也为10 kg 的物体．g取10 m/s2，求(1)细绳AC段的张力FAC与细绳EG的张力FEG之比；(2)轻杆BC对C端的支持力；(3)轻杆HG对G端的支持力．(二)突变问题2。
在动摩擦因数μ=0.2的水平质量为m=1kg的小球，小球与水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳一端相连，如图所示，此时小球处于静止平衡状态，且水平面对小球的弹力恰好为零，当剪断轻绳的瞬间，取g=10m/s2，求：（1）此时轻弹簧的弹力大小（2）小球的加速度大小和方向．(三)力的合成与分解3．如图所示，用一根细线系住重力为、半径为的球，其与倾角为的光滑斜面劈接触，处于静止状态，球与斜面的接触面非常小，当细线悬点固定不动，斜面劈缓慢水平向左移动直至绳子与斜面平行的过程中，下述正确的是()．A．细绳对球的拉力先减小后增大B．细绳对球的拉力先增大后减小C．细绳对球的拉力一直减小D．细绳对球的拉力最小值等于G(四)整体法4.如图所示，质量分别为m1、m2的两个物体通过轻弹簧连接。
在力F的作用下一起沿水平方向做匀速直线运动（m1在地面，m2在空中），力F与水平方向成θ角，则m1所受支持力N和摩擦力f正确的是（）A．N=m1g+m2g－FsinθB．N=m1g+m2g－FcosθC．f=FcosθD．f=Fsinθ(五)隔离法5．如图所示，水平放置的木板上面放置木块，木板与木块、木板与地面间的摩擦因数分别为μ1和μ2。
已知木块质量为m，木板的质量为Ｍ，用定滑轮连接如图所示，现用力Ｆ匀速拉动木块在木板上向右滑行，求力Ｆ的大小？6．跨过定滑轮的绳的一端挂一吊板，另一端被吊板上的人拉住，已知人的质量为70 kg，吊板的质量为10 kg，绳及定滑轮的质量，滑轮的摩擦均可不计，取重力加速度g=10 m/s2，当人以440 N的力拉绳时，人与吊板的加速度a和人对吊板的压力F分别为（）A．a=1 m/s2，FN=260 NB．a=1 m/s2，FN=330 NC．a=3 m/s2，FN=110 ND．a=3 m/s2，FN=50 N7．如图所示，静止在水平面上的三角架的质量为M，它中间用两根质量不计的轻质弹簧连着一质量为m的小球，当小球上下振动，三角架对水平面的压力为零的时刻，小球加速度的方向与大小是（）A．向下，mMgB．向上，gC．向下，gD．向下，m gmM)(+(六)综合8. 如图所示，一夹子夹住木块，在力F作用下向上提升，夹子和木块的质量分别为m、M，夹子与木块两侧间的最大静摩擦均为f，若木块不滑动，力F的最大值是（）答案1。
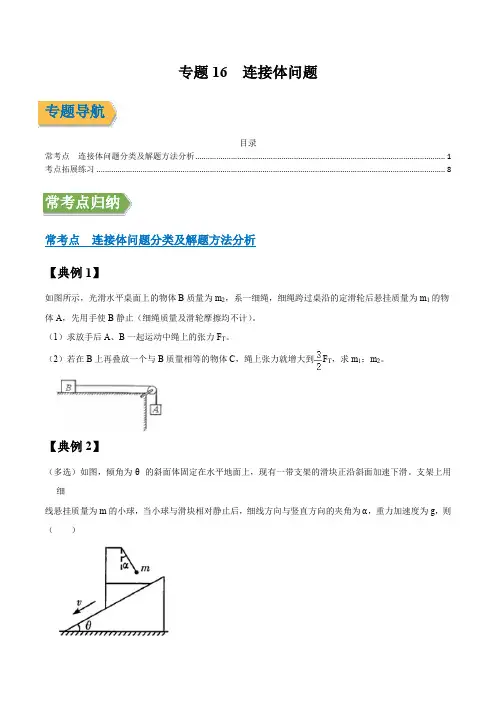
如图1-15所示：把质量为M的的物体放在光滑的水平高台上，用一条可以忽略质量而且不变形的细绳绕过定滑轮把它与质量为m的物体连接起来，求：物体M和物体m的运动加速度各是多大？⒈“整体法”解题采用此法解题时，把物体M和m看作一个整体，它们的总质量为(M+m)。
把通过细绳连接着的M与m之间的相互作用力看作是内力，既然水平高台是光滑无阻力的，那么这个整体所受的外力就只有mg了。
又因细绳不发生形变，所以M与m应具有共同的加速度a。
现将牛顿第二定律用于本题，则可写出下列关系式：mg=(M+m)a所以，物体M和物体m所共有的加速度为：⒉“隔离法”解题采用此法解题时，要把物体M和m作为两个物体隔离开分别进行受力分析，因此通过细绳连接着的M与m之间的相互作用力T必须标出，而且对M和m单独来看都是外力（如图1-16所示）。
根据牛顿第二定律对物体M可列出下式：T=Ma ①根据牛顿第二定律对物体m可列出下式：mg-T=ma ②将①式代入②式：mg-Ma=ma mg=(M+m)a所以物体M和物体m所共有的加速度为：最后我们还有一个建议：请教师给学生讲完上述的例题后，让学生自己独立推导如图1-17所示的另一个例题：用细绳连接绕过定滑轮的物体M和m，已知M>m，可忽略阻力，求物体M和m的共同加速度a。
：【思路整理】⒈既然采用“整体法”求连接体运动的加速度比较简便？为什么还要学习“隔离法”解题呢？这有两方面的原因：①采用“整体法”解题只能求加速度a，而不能直接求出物体M与m之间的相互作用力T。
采用“隔离法”解联立方程，可以同时解出a与T。
因此在解答比较复杂的连接体运动问题时，还是采用“隔离法”比较全面。
②通过“隔离法”的受力分析，可以复习巩固作用力和反作用力的性质，能够使学生加深对“牛顿第三定律”的理解。
⒉在“连接体运动”的问题中，比较常见的连接方式有哪几种？比较常见的连接方式有三种：①用细绳将两个物体连接，物体间的相互作用是通过细绳的“张力”体现的。
牛顿第二定律——连接体问题（整体法与隔离法）一、连接体：当两个或两个以上的物体通过绳、杆、弹簧相连，或多个物体直接叠放在一起的系统 二、处理方法——整体法与隔离法系统运动状态相同整体法问题不涉及物体间的内力 使用原则隔离法三、连接体题型：1【例1】A 、B 平力N F A 6=推A ，用水平力N F B 3=拉B ，A 、B【练1】如图所示，质量为M 的斜面A 在水平向左的推力F 作用下，A 与B 物体B 的质量为m ，则它们的加速度a A. ()(,sin μθ++==g m M F g a B. θθcos )(,cos g m M F g a +==C. ()(,tan μθ++==g m M F g a D. g m M F g a )(,cot +==μθ【练2】如图所示，质量为2m 的物体2滑定滑轮连接质量为1m 的物体，与物体1A. 车厢的加速度为θsin gB. 绳对物体1的拉力为θcos 1gmC. 底板对物体2的支持力为g m m )(12-D. 物体2所受底板的摩擦力为θtan 2g m2、连接体整体内部各部分有不同的加速度：【例2有一个环，箱和杆的总质量为M ，环的质量为m 加速度大小为a 时（a ＜g A. Mg + mg B. Mg —【练3】如图所示，一只质量为m 杆下降的加速度为（ ）A. gB. g M mC. g M m M +【练4个重4 N 的读数是（A.4 NB.23 NC.0 N【练5】如图所示，A 、B 的质量分别为m A =0.2kg ，m B =0.4kg ，盘C 的质量m C =0.6kg ，现悬挂于天花板O 处，处于静止状态。
当用火柴烧断O 处的细线瞬间，木块A 的加速度a A 多大？木块B 对盘C 的压力F BC 多大？（g 取10m/s 2）连接体作业1、如图所示，小车质量均为M ，光滑小球P 的质量为m ，绳的质量不计，水平地面光滑。
要使小球P 随车一起匀加速运动（相对位置如图所示），则施于小车的水平拉力F 各是多少？（θ已知）A BO球刚好离开斜面 球刚好离开槽底F= F= F= F=2、如图所示，A 、B 质量分别为m1，m2，它们在水平力F 的作用下均一起加速运动，甲、乙中水平面光滑，两物体间动摩擦因数为μ，丙中水平面光滑，丁中两物体与水平面间的动摩擦因数均为μ，求A 、B 间的摩擦力和弹力。
专题：连接体问题一、考情链接：“连接体”问题一直是高中物理学习的一大难题，也是高考考察的重点内容。
二、知识对接：对接点一、牛顿运动定律牛顿第一定律（惯性定律）：任何一个物体在不受外力或受平衡力的作用时，总是保持静止状态或匀速直线运动状态。
注意：各种状态的受力分析是解决连接体问题的前提。
牛顿第二定律：物体的加速度跟物体所受的合外力成正比，跟物体的质量成反比，加速度的方向跟合外力的方向相同。
注意：①物体受力及加速度一定要一一对应，即相应的力除以相应的质量得到相应的加速度，切不可张冠李戴！②分析运动过程时要区分对地位移和相对位移。
》牛顿第三定律：两个物体之间的作用力和反作用力，在同一直线上，大小相等，方向相反。
注意：不要忽视牛顿第三定律的应用，尤其是在求“小球对轨道压力”时经常用到牛顿第三定律，且均在评分标准中占1-2分，一定不要忘记。
对接点二、功能关系与能量守恒（什么力做功改变什么能）1、合力做功量度了物体的动能变化W合=ΔE K2、重力做功量度了物体的重力势能的变化：W G=ΔE PG3、弹簧的弹力做功量度了弹性势能的变化：W弹=ΔE P弹4、除重力和弹簧的弹力以外的其他力做功量度了系统的机械能的变化：W其他=ΔE机5、系统内相互作用的摩擦力做功：A、系统内的一对静摩擦力做功：一对静摩擦力对系统做功的代数和为零，其作用是在系统内各物体间传递机械能。
)B、系统内的一对滑动摩擦力做功：其作用是使系统部分机械能转化为系统的内能，Q= fs相对。
6、电场力做功量度了电势能的变化：W E=ΔE PE7、安培力做功量度了电能的变化：安培力做正功，电能转化为其他形式能；克服安培力做功，其他形式能转化为电能。
三、规律方法突破突破点一、整体法与隔离法的运用①解答问题时，不能把整体法和隔离法对立起来，而应该把这两种方法结合起来，从具体问题的实际出发，灵活选取研究对象，恰当使用隔离法和整体法。
②在选用整体法和隔离法时，要根据所求的力进行选择，若所求为外力，则应用整体法；若所求为内力，则用隔离法。
2020年高考物理专题复习：连接体问题的解题技巧考点精讲1. 连接体的分类根据两物体之间相互连接的媒介不同，常见的连接体可以分为三大类。
（1）绳（杆）连接：两个物体通过轻绳或轻杆的作用连接在一起；（2）弹簧连接：两个物体通过弹簧的作用连接在一起；（3）接触连接：两个物体通过接触面的弹力或摩擦力的作用连接在一起。
2. 连接体的运动特点轻绳——轻绳在伸直状态下，两端的连接体沿绳方向的速度总是相等。
轻杆——轻杆平动时，连接体具有相同的平动速度；轻杆转动时，连接体具有相同的角速度，而线速度与转动半径成正比。
轻弹簧——在弹簧发生形变的过程中，两端连接体的速率不一定相等；在弹簧形变最大时，两端连接体的速率相等。
特别提醒：（1）“轻”——质量和重力均不计。
（2）在任何情况下，绳中张力的大小相等，绳、杆和弹簧两端受到的弹力大小也相等。
3. 连接体问题的分析方法（1）分析方法：整体法和隔离法。
（2）选用整体法和隔离法的策略：①当各物体的运动状态相同时，宜选用整体法；当各物体的运动状态不同时，宜选用隔离法；②对较复杂的问题，通常需要多次选取研究对象，交替应用整体法与隔离法才能求解。
典例精析例题1 质量为M、长为3L的杆水平放置，杆两端A、B系着长为3L的不可伸长且光滑的柔软轻绳，绳上套着一质量为m的小铁环。
已知重力加速度为g，不计空气影响。
（1）现让杆和环均静止悬挂在空中，如图甲，求绳中拉力的大小；（2）若杆与环保持相对静止，在空中沿AB方向水平向右做匀加速直线运动，此时环恰好悬于A端的正下方，如图乙所示。
①求此状态下杆的加速度大小a；②为保持这种状态需在杆上施加一个多大的外力，方向如何？【考点】牛顿第二定律、共点力平衡【思路分析】（1）如图甲，设平衡时，绳中拉力为T，有2T cos θ－mg ＝0 ① 由图中几何关系可知cos θ＝36② 联立①②式解得T ＝46mg ③ （2）①此时，对小铁环的受力分析如图乙， 有T ′sin θ′＝ma ④ T ′＋T ′cos θ′－mg ＝0 ⑤ 由图中几何关系可知θ′＝60°，代入④⑤式解得 a ＝33g ⑥②如图丙，设外力F 与水平方向成α角，将杆和小铁环当成一个整体，有丙F cos α＝（M ＋m ）a ⑦ F sin α－（M ＋m ）g ＝0 ⑧联立⑥⑦⑧式，解得F ＝332 （M ＋m ）g tan α＝3（或α＝60°） 【答案】（1）46mg （2）①33g ②外力大小为332 （M ＋m ）g ，方向与水平方向成60°角斜向右上方【技巧点拨】如图所示，一夹子夹住木块，在力F 作用下向上提升。
如图1-15所示：把质量为M的的物体放在光滑的水平高台上，用一条可以忽略质量而且不变形的细绳绕过定滑轮把它与质量为m的物体连接起来，求：物体M和物体m的运动加速度各是多大？⒈“整体法”解题采用此法解题时，把物体M和m看作一个整体，它们的总质量为(M+m)。
把通过细绳连接着的M与m之间的相互作用力看作是内力，既然水平高台是光滑无阻力的，那么这个整体所受的外力就只有mg了。
又因细绳不发生形变，所以M与m应具有共同的加速度a。
现将牛顿第二定律用于本题，则可写出下列关系式：mg=(M+m)a所以，物体M和物体m所共有的加速度为：⒉“隔离法”解题采用此法解题时，要把物体M和m作为两个物体隔离开分别进行受力分析，因此通过细绳连接着的M与m之间的相互作用力T必须标出，而且对M和m单独来看都是外力（如图1-16所示）。
根据牛顿第二定律对物体M可列出下式：T=Ma ①根据牛顿第二定律对物体m可列出下式：mg-T=ma ②将①式代入②式：mg-Ma=ma mg=(M+m)a所以物体M和物体m所共有的加速度为：最后我们还有一个建议：请教师给学生讲完上述的例题后，让学生自己独立推导如图1-17所示的另一个例题：用细绳连接绕过定滑轮的物体M和m，已知M>m，可忽略阻力，求物体M和m的共同加速度a。
：【思路整理】⒈既然采用“整体法”求连接体运动的加速度比较简便？为什么还要学习“隔离法”解题呢？这有两方面的原因：①采用“整体法”解题只能求加速度a，而不能直接求出物体M与m之间的相互作用力T。
采用“隔离法”解联立方程，可以同时解出a与T。
因此在解答比较复杂的连接体运动问题时，还是采用“隔离法”比较全面。
②通过“隔离法”的受力分析，可以复习巩固作用力和反作用力的性质，能够使学生加深对“牛顿第三定律”的理解。
⒉在“连接体运动”的问题中，比较常见的连接方式有哪几种？比较常见的连接方式有三种：①用细绳将两个物体连接，物体间的相互作用是通过细绳的“张力”体现的。
在“抛砖引玉”中所举的两个例题就属于这种连接方式。
②两个物体通过“摩擦力”连接在一起。
③两个物体通互相接触推压连接在一起，它们间的相互作用力是“弹力”。
⒊“连接体运动”问题是否只限于两个物体的连接？不是。
可以是三个或更多物体的连接。
在生活中我所见的一个火车牵引着十几节车厢就是实际的例子。
但是在中学物理解题中，我们比较常见的例题、习题和试题大多是两个物体构成的连接体。
只要学会解答两个物体构成的连接体运动问题，那么解答多个物体的连接体运动问题也不会感到困难，只不过列出的联立方程多一些，解题的过程麻烦一些。
二、解题范例例题1：如图1-18所示：在光滑的水平桌面上放一物体A，在A上再放一物体B，物体A和B间有摩擦。
施加一水平力F于物体B，使它相对于桌面向右运动。
这时物体A相对于桌面A. 向左运B. 向右运C. 不动D. 运动，但运动方向不能判断。
【思维基础】解答本题重要掌握“隔离法”，进行受力分析。
分析思路：物体A、B在竖直方向是受力平衡的，与本题所要判断的内容无直接关系，可不考虑。
物体B在水平方向受两个力：向右的拉力F，向左的A施于B的摩擦力f，在此二力作用下物体B相对于桌面向右运动。
物体A在水平方向只受一个力：B施于A的向右的摩擦力f，因此物体A应当向右运动。
注1、水平桌面是光滑的，所以对物体A没有作用力。
注2、物体A与物体B间的相互摩擦力是作用力和反作用力，应当大小相等、方向相反、同生同灭，分别作用于A和B两个物体上。
答案：（B）例题2：如图1-19所示：两个质量相同的物体1和2紧靠在一起，放在光滑水平桌面上，如果它们分别受到水平推力F1和F2，且F1>F2，则物体1施于物体2的作用力的大小为：A. F1B. F2C. (F1+F2)D. (F1-F2)【思维基础】：解答本题不应猜选答案（这是目前在一些中学生里的不良倾向），而应列出联立方程解出答案，才能作出正确选择。
因此掌握“隔离法”解题是十分重要的。
分析思路：已知物体1和2的质量相同，设它们的质量都为m；设物体1和2之间相互作用着的弹力为N；设物体1和2运动的共同加速度为a。
则运用“隔离法”可以列出下列两个方程：F1-N=ma ①N-F2=ma ②∵①、②两式右端相同∴F1-N=N-F2 2N=F1+F2 得出：N=(F1+F2) 答案：（C）【模仿学习】为了提高学生的解题能力，我们还需要讲述综合性例题进行指导。
例题3：一条细绳（忽略质量）跨过定滑轮在绳子的两端各挂有物体A和B（如图1-20所示），它们的质量分别是mA=0.50kg，mB=0.10kg。
开始运动时，物体A距地面高度hA=0.75m，物体B距地面高度hB=0.25m，求：物体A 落地后物体B上升的最大高度距地面多少米？启发性问题：⒈在本题中细绳连接着物体A和B一块运动，这是一种什么类型的动力学问题？⒉在运动过程中物体A和B的加速度大小相同吗？求它们的加速度有几种方法？⒊当物体A落到地面时物体B开始作什么性质的运动？⒋有人说物体B上升的最大高度H=hA+hB，你认为是否正确？为什么？⒌在求解过程中本题需要运用哪些关系式？（请你先把所需的关系式写在纸上，然后通过解题和对照后面答案看看是否写完全了。
）分析与说明：⒈本题属于“连接体运动问题”。
⒉物体A和B的加速度大小是相同的。
求它们的加速度有两种方法──“整体法”和“隔离法”。
由于本题不需要求出细绳的张力，所以采用“整体法”求加速度比较简便。
⒊当物体A落到地面时，因为物体B有向上运动的速度，所以物体B不会立即停止运动，而是开始作竖直上抛运动直至升到最大高度。
物体A落地时的末速度VAt与物体B作竖直上抛运动的初速度VB0是大小相等的（但方向相反）。
⒋认为物体B上升的最大高度H=hA+hB是不正确的。
这种错误是由于没有考虑到物体B作竖直上抛运动继续上升的高度h上。
所以物体B距地面的最大高度H=hA+hB+h上才是正确的。
从下列“求解过程”中可以看到解答本题所需用的关系式。
求解过程：先用整体法求出物体A和B共同的加速度。
)/(5.68.910.050.010.050.0)(2S m gm m m m a am m g m g m BA BA B A B A =⨯+-=+-=+=-再求物体A 落到地面时的末速度： （可暂不求出数值）因为物体A 和B 是连接体运动，所以物体A 落地时的末速度与物体B 作竖直上抛运动的初速度大小相等。
根据高一学过的匀变速运动规律Vt2-V02=2aS ，当Vt=0, V0=VB0, a=g, S=h 上可导出下式：综上所述可知物体B 距地面的最大高度是由下列三部分合成的：物体B 原来距地面的高度hB=0.25m 物体B 被物体A 通绳拉上的高度hA=0.75m 物体作竖直上抛运动继续上升的高度h 上=0.50m所以物体B 距地面的最大高度为：H=hB+hA+h 上=0.25m+0.75m+0.50m=1.5m解题后的思考：物体B 所达到的最大高度是保持不住的，因为上抛至最高处时就会按自由落体的方式下落，因此物体B 停止运动后，最终的距地面高度h=hA+hB=0.75m+0.25m=1m ，但这不是物体B 在运动过程中曾经达到的最大高度。
补充说明：“竖直上抛运动”是一种匀减速运动，它的初速度V0是竖直向上的；它的加速度是重力加速度g ，方向是竖直向下的；当物体的运动速度减为零时也就达到了最大高度。
有关这类问题我们还将在下章中进行深入的讨论。
【举一反三】上面所讲的例题虽然具有典型性和综合性，但是灵活性还不够。
为了进一步提高分析问题的能力，我们讲授下列例题，加强学生的思维锻炼。
例题4：如图1-21之(a),(b)所示：将m1=4kg 的木块放在m2=5kg 的木块上，m2放在光滑的水平面上。
若用F1=12N 的水平力拉m1时，正好使m1相对于m2开始发生滑动；则需用多少牛顿的水平力（F2）拉m2时，正好使m1相对于m2开始滑动？“准备运动”（解题所需的知识与技能）：解答本题的关键在于──“受力分析”和“运动分析”。
根据题意可分析出物体m1和m2之间必有相互作用着的摩擦力f 。
因此图1-22之(c),(d)所示的就是(a),(b)两种状态的受力分析图。
又因m2是置于光滑水平面上的，所以由m1和m2所构成的连接体在受到外力作用时一定会产生加速度。
由于(c),(d)图示的受力形式不同，所产生的加速度a'和a“也不同。
（还请读者注意题文中的“正好”二字，因此二物体相对滑动的瞬间仍可当作具有共同的加速度。
）解题的过程：根据前面的图(c)用隔离法可以列出下面两个方程：F1-f=m1a'①f=m2a'②由①、②两式相加可得：F1=(m1+m2)a'③根据前面图(d)用隔离法可以列出下面两个方程：F2-f=m2a“④f=m1a“⑤由④、⑤两式相加可得：F2=(m1+m2)a“⑥由③、⑥两式相除可得：⑦由②、⑤两式相除可得：即：⑧根据：⑦、⑧两式可以写出：⑨将已知量m1=4kg，m2=5kg，F1=12N代入⑨式：解出答案：F2=15N“整理运动”（解题后的思考）：⒈你想到了物体m1和m2之间必存在着摩擦力吗？⒉你想到了在(a),(b)两种情况下物体m1和m2都作加速运动吗？为什么在(a),(b)两种情况下运动的加速度不相等？在解题过程中你有什么体会？你还能想出其它的解法吗？三、解题步骤⒈若连结体内（即系统内）各物体具有相同的加速度时，首先应该把这个连接体当成一个整体（可看作一个质点），分析它受到的外力和运动情况，再根据牛顿第二定律求出加速度；若要求连接体内各物体相互作用的内力，这时可把某个物体隔离出来，对它单独进行受力和运动情况的分析，再根据牛顿第二定律列式求解。
若连接体内各物体的加速度大小或方向不相同时，一般采用隔离法。
如果不要求系统内物体间的相互作用力，也可采用整体法，步骤如下：(1)分析系统受到的外力；(2)分析系统内各物体加速度的大小和方向；(3)建立直角坐标系；(4)列方程求解。
【练习与检测】选择题1. 如图1-23所示，质量分别为m1=2kg，m2=3kg的二个物体置于光滑的水平面上，中间用一轻弹簧秤连接。
水平力F1=30N和F2=20N分别作用在m1和m2上。
以下叙述正确的是：A. 弹簧秤的示数是10N。
B. 弹簧秤的示数是50N。
C. 在同时撤出水平力F1、F2的瞬时，m1加速度的大小13m/S2。
D. 若在只撤去水平力F1的瞬间，m1加速度的大小为13m/S2。
2. 如图1-24所示的装置中，物体A在斜面上保持静止，由此可知：A. 物体A所受摩擦力的方向可能沿斜面向上。
B. 物体A所受摩擦力的方向可能沿斜面向下。
