下载文档原格式
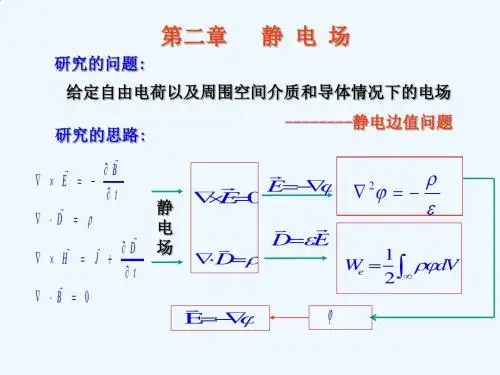
第二章 静电场带电体系：电荷静止，所激发的电场不随时间变化；给定自由电荷的分布以及周围空间介质或者导体的分布，运用电磁场理论求解这样的带电体系的电场。
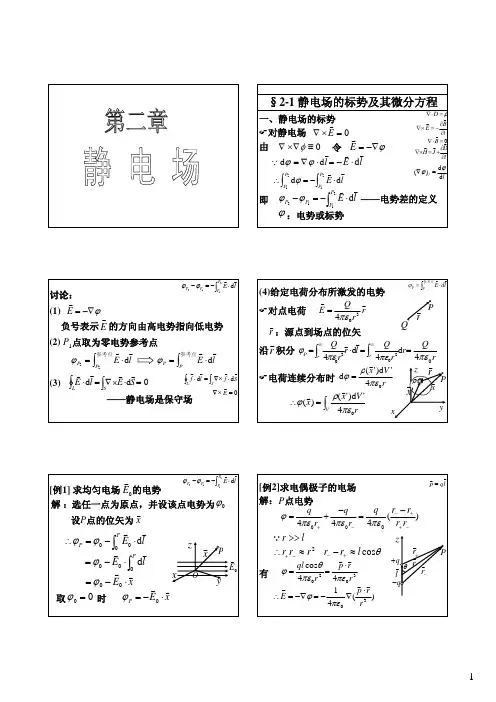
§1 静电场的标势及其微分方程 1、 静电场的标势——静电势 麦克斯韦方程0 , ,=⋅∇∂∂+=⨯∇∂∂-=⨯∇=⋅∇B tD J H tB E Dρ静电条件：()00==∂∂J t 物理量 将静电条件代入麦克斯韦方程得到00=⋅∇=⨯∇=⋅∇=⨯∇B H D Eρ✧ 在静电条件下，电场和磁场相互独立，可以分开求解；✧ 静电场是无旋场；自由电荷分布是D的源。
解决静电问题的基本方程： 微分方程0 =⨯∇=⋅∇E D ρ +边界条件f D D n σ=-⋅1221+介质的电磁性质方程静电势的定义：静电场的无旋性是静电场的一个重要的特征，其积分形式为0d =⋅⎰l E L——（1.3）“电场沿任一闭合回路的线积分等于零。
”将单位电荷从1P 点移至2P 点时电场对它所做的功⎰⋅21d P P l E将单位电荷从1P 点移至2P 点时电场对它所做的功与具体的路径无关，只与起点和终点有关。
0d =⋅⎰l E L0d d 21=⋅+⋅⎰⎰-C C l E l E0d d 21=⋅-⋅⎰⎰C C l E l E⎰⎰⋅=⋅21d d C C l E l E利用这一特点，引入电势的概念，是空间位置的标量函数（标势）； 定义两点间的电势差为⎰⋅-=-21d )()(12P P l E P Pϕϕ ——（1.4）推论：如果电场对（单位）正电荷做正功，则电势降低；只有两点的电势差才具有物理意义； 如果知道空间的电场的分布，则可以计算空间任意两点间的电势差；实际的计算中为了方便，常选取某个参考点，规定该点的电势为零，这样整个空间里的电势就有一个确定的值。
如果电荷分布在有限的空间里，则可以取无穷远处的电势为零，即()0=∞ϕ这样空间P 点的电势为()⎰∞⋅=Pl E P d ϕ相距为ld 的两点的电势的增量为l E dd ⋅-=ϕ式中()lz y x z y x zzy y x x z y x y y xd de d e d e e e e d d d d ⋅∇=++⋅⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂=∂∂+∂∂+∂∂=ϕϕϕϕϕϕϕϕ从而得到，ϕ-∇=E——（1.5）如果知道了空间电势的分布情况，则可采用上式计算电场强度的分布。
目录•课程介绍与基础知识•静电场•稳恒电流场•恒定磁场•时变电磁场•电磁辐射与散射课程介绍与基础知识0102 03电动力学的定义和研究范围电动力学是物理学的一个重要分支，主要研究电磁场的基本性质、相互作用和变化规律。
电动力学的发展历史从库仑定律、安培定律到麦克斯韦方程组的建立，电动力学经历了漫长的发展历程。
电动力学在物理学中的地位电动力学是经典物理学的基础之一，对于理解物质的微观结构和相互作用具有重要意义。
电动力学概述03电磁场与物质的相互作用洛伦兹力、电磁辐射等。
01静电场和静磁场的基本性质电荷守恒定律、库仑定律、高斯定理等。
02电磁感应和电磁波的基本性质法拉第电磁感应定律、麦克斯韦方程组等。
电磁现象与基本规律数学物理方法简介向量分析和场论基础向量运算、微分和积分运算、场论的基本概念等。
微分方程和偏微分方程基础常微分方程、偏微分方程、分离变量法等。
复变函数和积分变换基础复数运算、复变函数、傅里叶变换和拉普拉斯变换等。
特殊函数和数学物理方程简介勒让德多项式、贝塞尔函数、超几何函数等，以及波动方程、热传导方程、泊松方程等数学物理方程的基本概念和求解方法。
静电场库仑定律与电场强度库仑定律描述两个点电荷之间的相互作用力，其大小与电荷量的乘积成正比，与它们之间的距离的平方成反比。
电场强度表示电场中某点的电场力作用效果的物理量，其方向与正电荷在该点所受的电场力方向相同。
电场强度的计算通过库仑定律和叠加原理，可以计算多个点电荷在某点产生的电场强度。
电势与电势差电势描述电场中某点电势能的物理量，其大小等于将单位正电荷从该点移动到参考点时电场力所做的功。
电势差表示电场中两点间电势的差值，等于将单位正电荷从一点移动到另一点时电场力所做的功。
电势的计算通过电势的定义和叠加原理，可以计算多个点电荷在某点产生的电势。
1 2 3在静电场中，导体内部电场强度为零，电荷分布在导体的外表面。
导体的这种性质使得它可以用来屏蔽电场。
