(完整版)鲁教版六年级数学第一单元丰富的图形世界
- 格式:doc
- 大小:1.22 MB
- 文档页数:12





第一章丰富的图形世界
1.1生活中的立体图形
1 能正确识别简单的立体图形
2 会对几何体进行分类
3 会算N棱柱(锥)的面数、(侧)棱数、顶点数,并会逆向确定是几棱柱(锥)
4 会用点、线、面之间的关系来解释一些现象
5 简单图形与旋转体的连线问题
1.2展开与折叠
1 会判断简单几何体的展开(折叠)图形是否正确
2 会用找对面(邻面)的方法确定正方体某些面的位置
1.3截一个几何体
1 根据图形能说出一些截面的名称
2 知道简单几何体的截面是什么图形
1.4从三个方向看物体的形状
1 会画三视图
2 通过视图求几何体的面积、体积
3 通过俯视图的数字可以画出主视图、左视图
4 通过主视图、左视图能算出最少、最多需要几个正方体。

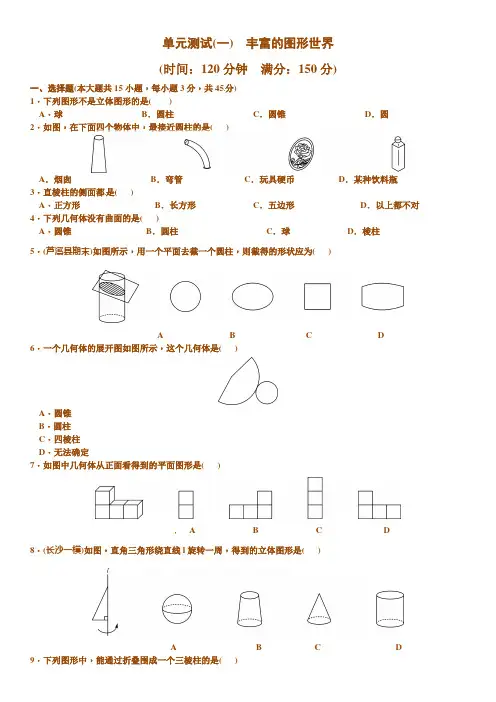
单元测试(一)丰富的图形世界(时间:120分钟满分:150分)一、选择题(本大题共15小题,每小题3分,共45分)1.下列图形不是立体图形的是( )A.球B.圆柱C.圆锥D.圆2.如图,在下面四个物体中,最接近圆柱的是( )A.烟囱B.弯管C.玩具硬币D.某种饮料瓶3.直棱柱的侧面都是( )A.正方形B.长方形C.五边形D.以上都不对4.下列几何体没有曲面的是( )A.圆锥B.圆柱C.球D.棱柱5.(芦溪县期末)如图所示,用一个平面去截一个圆柱,则截得的形状应为( )A B C D6.一个几何体的展开图如图所示,这个几何体是( )A.圆锥B.圆柱C.四棱柱D.无法确定7.如图中几何体从正面看得到的平面图形是( )A B C D 8.(长沙一模)如图,直角三角形绕直线l旋转一周,得到的立体图形是( )A B C D10.如图的四个几何体,它们各自从正面,上面看得到的形状图不相同的几何体的个数是( )A.1 B.2 C.3 D.411.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )12.下列说法不正确的是( )A.球的截面一定是圆B.组成长方体的各个面中不可能有正方形C.从三个不同的方向看正方体,得到的平面图形都是正方形D.圆锥的截面可能是圆13.将四个棱长为1的正方体如图摆放,则这个几何体的表面积是( )A.3 B.9 C.12 D.1814.(深圳期末)用平面去截如图所示的三棱柱,截面形状不可能是( )A.三角形B.四边形C.五边形D.六边形15.明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其他空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )A B C D二、填空题(本大题共5小题,每小题5分,共25分)16.飞机表演的“飞机拉线”用数学知识解释为:________________.17.下列图形中,是柱体的有________ .(填序号)19.一个棱柱有12个顶点,所有侧棱长的和是48 cm,则每条侧棱长是________cm.20.一个正方体盒子的展开图如图所示,如果要把它粘成一个正方体,那么与点A重合的点是________.三、解答题(本大题共7小题,共80分)21.(12分)将下列几何体与它的名称连接起来.22.(6分)如图,求这个棱柱共有多少个面?多少个顶点?有多少条棱?23.(10分)若要使图中平面图形折叠成正方体后,相对面上的数字相等,求x+y+z的值.24.(10分)如图是一个由若干个小正方体搭成的几何体从上面看到的形状图,其中小正方形内的数字是该位置小正方体的个数,请你画出它从正面和从左面看到的形状图.25.(12分)如图所示的正方体被竖直截去了一部分,求被截去的那一部分的体积.(棱柱的体积等于底面积乘以高)26.(14分)如图所示,长方形ABCD的长AB为10 cm,宽AD为6 cm,把长方形ABCD绕AB边所在的直线旋转一周,然后用平面沿AB方向去截所得的几何体,求截面的最大面积.27.(16分)根据如图所给出的几何体从三个方向看得到的形状图,试确定几何体中小正方体的数目的范围.参考答案1.D 2.C 3.B 4.D 5.B 6.A7.D8.C9.C10.C11.C12.B13.D14.D15.B16.点动成线17.②③⑥18.答案不唯一,如:球、正方体等19.820.C、E 21.略.22.这个棱柱共有7个面,10个顶点,15条棱.23.“2”与“y”相对,“3”与“z”相对,“1”与“x”相对.则x+y+z=1+2+3=6.24.从正面和从左面看到的形状图如图所示.25.V=12×(5-4)×(5-3)×5=5(cm3).答:被截去的那一部分体积为5 cm3.26.由题意得:把长方形ABCD绕AB边所在的直线旋转一周,得到的几何体为圆柱,且圆柱的底面半径为6 cm,高为10 cm.所以截面的最大面积为:6×2×10=120(cm2).27.根据题意,从上面看,构成几何体所需小正方体最多情况如图1所示,所需小正方体最少情况如图2所示:所以最多需要11个小正方体,最少需要9个小正方体.。

六年級數學個性化輔導講義授課題目:豐富の圖形世界任課教師:數學學科輔導講義[5]圖形是由點、線、面構成の。
點構成線,線構成面,面構成體。
1、圓柱可以看成是長方形繞著一邊旋轉一周所成の幾何體2、圓錐可以看成是由直角三角形繞著一條直角邊旋轉一周所成の幾何體3、球體可以看成是由半圓繞著直徑旋轉一周所成の幾何體舉例:下雨看起來是一根線說明——,電扇轉起來像一個整體の圓盤說明——,把一張紙繞一根軸旋轉一周成為一個圓柱說明——2、展開與折疊定義:1、在棱柱中,任何相鄰兩個面得交線都叫做棱2、相鄰兩個側面の交線叫做側棱3、棱柱得所有側棱長都相等4、棱柱の上、下底面の形狀相同,側面の形狀都是長方形5、通常根據底面圖形の邊數將棱柱分為三棱柱、四棱柱、五棱柱…它們底面圖形の形狀分別為三角形、四邊形、五邊形…歸納:1、棱柱展開後n棱柱就有n個長方形,以及2個n邊形。
2、圓錐展開是一個扇形和一個圓。
3、圓柱の展開圖是長方形和2個圓。
正方體の平面展開圖小結(共11種):由於正方體中上與下,左與右,前與後都是相對の面,上與前,上與後,上與左,上與右等都是相鄰の面,按不同の方法剪開,可得到不同の展開圖形。
の正方形作側面,兩邊各一個正方形作上下底面,如圖の六種圖像,簡記為“一四一型”2.中間一行三個相連の正方形作側面,上(或下)邊の兩個正方形一個做底面一個作側面,單獨相連の一個正方形作底面,如圖の三種情形,簡記為“二三一型”3每行有兩個相連の正方形且成階梯狀分佈,如圖簡記為“二二二型”4.兩行中只能有一個正方形相連,如圖,簡記為“三三型”典型例題例1.下列是正方體の展開圖の是()變式訓練(1)の展開圖の有()A、2個B、3個C、4個D、5個變式訓練(2)明明用紙(如下圖左)折成了一個正方體の盒子,裏面裝了一瓶墨水,混放在下麵の盒子裏,只憑觀察,選出墨水在哪個盒子中()變式訓練(3)將正方體沿粗線剪開得到の展開圖是()3、截一個幾何體定義:用一個平面去截一個幾何體,截出の面叫做截面體。
自信是成功的起点,坚持是成功的终点!
六年级数学
个性化辅导讲义
授课题目:丰富的图形世界
任课教师:
数学学科辅导讲义
[5]图形是由点、线、面构成的。
点构成线,线构成面,面构成体。
1、圆柱可以看成是长方形绕着一边旋转一周所成的几何体
2、圆锥可以看成是由直角三角形绕着一条直角边旋转一周所成的几何体
3、球体可以看成是由半圆绕着直径旋转一周所成的几何体
举例:下雨看起来是一根线说明——,电扇转起来像一个整体的圆盘说明——,把一张纸绕一根轴旋转一周成为一个圆柱说明——
2、展开与折叠
定义:
1、在棱柱中,任何相邻两个面得交线都叫做棱
2、相邻两个侧面的交线叫做侧棱
3、棱柱得所有侧棱长都相等
4、棱柱的上、下底面的形状相同,侧面的形状都是长方形
5、通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱…它们底面图形的形状分别为三角形、四边形、五边形…
归纳:
1、棱柱展开后n棱柱就有n个长方形,以及2个n边形。
2、圆锥展开是一个扇形和一个圆。
3、圆柱的展开图是长方形和2个圆。
正方体的平面展开图小结(共11种):
由于正方体中上与下,左与右,前与后都是相对的面,上与前,上与后,上与左,上与右等都是相邻的面,按不同的方法剪开,可得到不同的展开图形。
1.中间一行四个相连的正方形作侧面,两边各一个正方形作上下底面,如图的六种图像,简记为“一四一型”
2.中间一行三个相连的正方形作侧面,上(或下)边的两个正方形一个做底面一个作侧面,单独相连的一个正方形作底面,如图的三种情形,简记为“二三一型”
3每行有两个相连的正方形且成阶梯状分布,如图简记为“二二二型”
4.两行中只能有一个正方形相连,如图,简记为“三三型”
典型例题
例1.下列是正方体的展开图的是()
变式训练(1)
例1.如图是正方体的展开图的有()
A、2个
B、3个
C、4个
D、5个
变式训练(2)
明明用纸(如下图左)折成了一个正方体的盒子,里面装了一瓶墨水,混放在下面的盒子里,只凭观察,选出墨水在哪个盒子中()
变式训练(3)
将正方体沿粗线剪开得到的展开图是()
3、截一个几何体
定义:用一个平面去截一个几何体,截出的面叫做截面体。
归纳:
1、一个平面截一个正方体,截面可以是正方形、长方形、三角形、五边形、
六边形。
不可能是七边形,因为正方体一共六个面。
( ) ( ) ( ) ( ) ( )
15. 判断下列叙述是否正确(概念变式)
[1].柱体上下两个面一样大。
()
[2].圆柱、圆锥的底面都是圆。
()
[3].棱柱的底面是三角形。
()
[4].棱锥的侧面是三角形。
()
[5].球体不是多面体。
()
[6].圆锥是多面体。
()
[7].柱体都是多面体。
()
[8].棱锥、棱柱是多面体。
()
16.下面的几何体是棱柱的是()
17.下面几种几何图形中,含有曲面的是()
18. 观察图形,问:圆锥的三视图是()
A. 主视图和俯视图是三角形,侧视图是圆。
B. 主视图和侧视图是三角形,俯视图是圆。
C. 主视图和侧视图是三角形,俯视图是圆和圆心。
D. 主视图和俯视图是三角形,侧视图是圆和圆心。
19.看图思考
点动成_______,线动成_______,面动成_______.
A B C D
20.用平面截下列几何体,找出相应的截面形状.
三、我准确——疯狂操练
1.矩形绕其一边旋转一周形成的几何体叫__________。
2.主视图、俯视图和左视图都是正方形的几何体是__________。
3.你看这位“”可爱吧!表面能展开平面图形“”的是()
A.圆柱 B.圆台 C.圆锥 D.球
4.侧面展开图是一个长方形的几何体是()
A、圆锥
B、圆柱
C、四棱锥
D、球
5.物体的形状如图所示,则此物体的俯视图是()
6.如图所示,用四个不同的平面去截一个正方体,请根据截面的形状填空:
(1)(2)(3)(4)(1)截面是;(2)截面是;
(3)截面是;(4)截面是。
四、我提升——综合题解
1.如图,用简单的平面图形画出三位携手同行的的小人物,请你仔细观察,图中共有三角形____个,圆_____个.
2.如图,桌子上放着一个圆锥和一个圆柱,请写出下面三副图中从哪具方向看到的?
(1) (2) (3)
4.甲、乙、丙、丁四人分别面对面坐在一个四边形桌子旁边,桌上一张纸上写着数字“9”,甲说他看到的是“6”,乙说他看到的是“”,丙说他看到的是“”,丁说他看到的是“9”,则下列说法正确的是( )
A.甲在丁的对面,乙在甲的左边,丙在丁的右边
B.丙在乙的对面,丙的左边是甲,右边是乙
C.甲在乙的对面,甲的右边是丙,左边是丁
D.甲在丁的对面,乙在甲的右边,丙在丁的右边
5.正方体的截面不可能是( )
A.四边形
B.五边形
C.六边形
D.七边形
6.在第一行中找出第二行对应的几何体的表面展开图,并划线把它们连起来。
7.水平放置的正方体的六个面分别用“前面、后面、上面、
下面、左面、右面”表示.如右图,是一个正方体的平面
展开图,若图中的“似”表示正方体的前面, “锦”
表示右面, “程”表示下面.则“祝”、“你”、
“前”分别表示正方体的______________________.
程
前
你
祝
似锦
五、我疯了——挑战极限
1.如图所示的积木是由16块棱长为1cm的正方体堆积而成的,请求出它们的表面积.
2.现有4枚相同的骰子,骰子的展开图如图1-14所示,这4枚骰子摞在一起后,如图1-15,相互接触的两个面点数之和都是8,这4个骰子每个骰子都有一个面被遮住了,你能说出每个被遮住的面各是几个点吗?
3.如图,已知一个正方体的六个面上分别写着
六个连续的整数,且每两个相对面上的两个数的
和都相等,图中所能看到的数是16,19和20,
求这6个整数的和.
六、我不忘——巩固练习
例2.由正方体搭成的几何体的俯视图如图,小正方体中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图和左视图.
总结
俯视图的列和主视图的列相对应,俯视图的行和左视图的列相对应。
变式训练(1)
如图,已知一个由小正方体组成的几何体的左视图和俯视图
(1)该几何体需要小正方体的块数最多是
(2)画出该几何体的主视图
1 3
1
2
1
例3.如图,一只蜘蛛在A处,它饶圆柱侧面一周到达B处,试确定蜘蛛爬行的最短距离。
变式训练
在下列几何体的侧面上确定点A到点B的最短路线。
例4.用小立方块搭成的几何体,主视图和俯视图如下,问这样的几何体有多少可能?它最多需要小立方块,最少需要小立方块,请画出最少和最多时的左视图;
最多时的左视图最少时的左视图
变式训练
用小立方体搭一个几何体,使它的主视图和俯视图如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的左视图。
(6分)
主视图俯视
主视图俯视图
【名书·名校·竞赛·中考在线】
1.如图所示,是一个由小立方体搭成的几何体的俯视图,小正方形中数字表示该位置的小立方块的个数,则它的主视图为()
2.将下图中左边的图形折叠起来围成一个正方体,应该得到右图中的( )
3.如图是由一些相同的小正方体构成几何体的三种视图,那么构成这几何体的小正方体有()
A、4个
B、5个
C、6个
D、无法确定
4.左图是正方体的表面展开图,如果将其合成原来的正方体(右图)时,与点P 重合的两点应该是( )
A.S和Z B.T和Y
C.U和Y D.T和V
5.如图所示,用1、2、3、4标出的四块正方形,以及由字母标出的八块正方形中任意一块,一共要用5块连在一起的正方形折成一个无盖方盒,共有几种不同的方法?请选择合适的方法。
(1、2、3、4、A);(1、2、3、4、B);
(1、2、3、4、C );(1、2、3、4、D);
(1、2、3、4、E);(1、2、3、4、G)。
6.一个几何体的主视图和俯视图如图所示,这样的几何体最少要个立方块,最多要个立方块。
1 2
1
2
4
3
A B C D
俯视图
左视图
主视图
A B C
E
F
G
H
D 1 2 3
4。