基于matlab数字均衡器设计

摘要本文的数字均衡器以MA TLAB为设计平台，有.wav文件的获取、滤波、保存和播放功能。

在对声音文件进行基本波形分析和频率分析的基础上，增加了高通、低通、带通和带阻滤波的功能，并有8段均衡器可对声音信号进行调节后保存播放。

关键词：滤波器、数字均衡器、傅立叶反变换第一章概述1.1 均衡器简介均衡器是一种用来对频响曲线进行调节的音频设备，换名话说，均衡器能对不同频率的声音信号中过多的频率成分。

因此，它能补偿由于各种原因造成的信号欠缺的频率成分，也能抑制信号中过多的频率成分。

例如，均衡器可以抑制频率为60~250Hz的低频交流声，也可以抑制频率为6~12kHz的高频噪声；利用均衡器还可以进行音调调节和音色加工。

均衡器的原意是将传输系统中不平衡的频率特性用相反的特性曲线进行频率均衡，在此基础上增加了音色加工和美化的功能。

均衡器的作用主要如下。

①校正各种音频设备产生的频率失真，以获得平坦响应。

②改善室内声场，改善由于房间共振特性或吸声特性不均匀而造成的传输增益（频率）失真，确保其频率特性平直。

③抑制声反馈，提高系统传声增益，改善扩声音质。

④提高语言清晰度和自然度。

⑤在音响艺术创作中，用于刻画乐器和演员的音色个性，提高音响艺术的表现效果。

均衡器的种类很多，但基本上工作原理都是相同的。

它们都是将音频信号的全频带（20Hz~20kHz）或全频带的主要部分，按一定的规律分成几个甚至几十个频点（也称频段），再利用LC串联谐振的选频特性，分别进行提升或衰减，从而获得所希望的频率校正曲线。

运用数字滤波器组成的均衡器称为数字均衡器，数字均衡器即可作成图示EQ，有可做成参量EQ，还可以做成两者兼有的EQ，它不仅各项性能指标优异，操作方便，而且还可同时储存多种用途的频响均衡特性，供不同节目要求选用，可多至储存99种频响特性曲线。

SONY的SRP-E300是一款多功能2通道的数字均衡器具有10段参量均衡和29段图示均衡，可同时或独立工作，带有限制器和噪声门功能，高精度的48kHz取样，20比特线性模数/数模转换；带有模拟和数字输入/输出；RS-232C C接口，可用于外部遥控，它的出现会逐步淘汰普通的模拟均衡器，是一款专业音频扩声领域具有极高性价比的产品。

Matlab中的均匀设计与优化实验方法介绍引言在科学研究和工程实践中，实验设计和优化方法是不可或缺的工具。

Matlab作为一种强大的数值计算和可视化软件，是科学家和工程师常用的工具之一。

在Matlab中，有许多方法可以用于设计均匀实验和进行优化。

本文将介绍Matlab中的一些常见的均匀设计和优化实验方法。

一、均匀设计实验方法1.1 背景均匀设计实验是一种将样本分布在整个实验空间中的方法，以确保样本之间的差异性最小化。

在科学研究中，均匀设计实验常用于确定因素对响应变量的影响，并评估其主效应和交互作用。

在Matlab中，有几种方法可以实现均匀设计实验。

1.2 完全随机设计完全随机设计是最简单的均匀设计实验方法之一。

在Matlab中，可以使用rand函数生成随机数，然后将其映射到实验空间的范围。

例如，rand(100,2)将生成一个100行2列的随机矩阵，其中每个元素均匀地分布在0到1之间。

为了将这些随机数映射到实验空间的范围，可以使用线性变换。

1.3 拉丁超立方设计拉丁超立方设计是一种常用的均匀设计实验方法。

在Matlab中，可以使用lhsdesign函数生成拉丁超立方设计。

该函数的输入参数包括实验空间的维数和样本点的个数。

例如，X = lhsdesign(10,2)将生成一个10行2列的拉丁超立方设计矩阵，其中每个元素均匀地分布在0到1之间。

二、优化实验方法2.1 背景优化实验是一种通过系统地变化实验条件来最大化或最小化某个目标函数的方法。

在Matlab中，有几种方法可以用于优化实验。

2.2 泛化回归神经网络泛化回归神经网络是一种基于人工神经网络的优化实验方法。

在Matlab中，可以使用fitnet函数创建一个泛化回归神经网络模型，并使用该模型进行优化实验。

该函数的输入参数包括输入数据和目标数据。

例如，net = fitnet(10)将创建一个包含10个隐藏层节点的泛化回归神经网络模型。

2.3 粒子群优化算法粒子群优化算法是一种基于群体智能的优化实验方法。

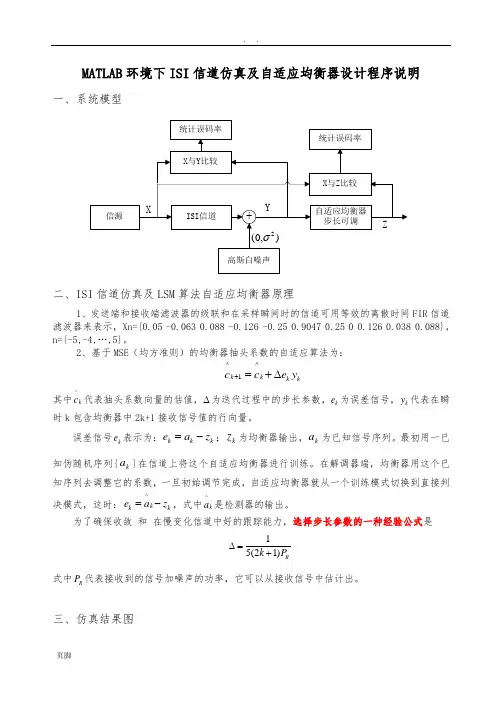
MATLAB 环境下ISI 信道仿真及自适应均衡器设计程序说明一、系统模型二、ISI 信道仿真及LSM 算法自适应均衡器原理1、发送端和接收端滤波器的级联和在采样瞬间时的信道可用等效的离散时间FIR 信道滤波器来表示，Xn={0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088}，n={-5,-4,…,5}。

2、基于MSE （均方准则）的均衡器抽头系数的自适应算法为：^^1k k k k c c e y +=+∆其中^k c 代表抽头系数向量的估值，∆为迭代过程中的步长参数，k e 为误差信号，k y 代表在瞬时k 包含均衡器中2k+1接收信号值的行向量。

误差信号k e 表示为：k k k e a z =-；k z 为均衡器输出，k a 为已知信号序列。

最初用一已知伪随机序列{k a }在信道上将这个自适应均衡器进行训练。

在解调器端，均衡器用这个已知序列去调整它的系数，一旦初始调节完成，自适应均衡器就从一个训练模式切换到直接判决模式，这时：^k k k e a z =-，式中^k a 是检测器的输出。

为了确保收敛 和 在慢变化信道中好的跟踪能力，选择步长参数的一种经验公式是15(21)R k P ∆=+ 式中R P 代表接收到的信号加噪声的功率，它可以从接收信号中估计出。

三、仿真结果图四、结论分析从结果图中我们可以看出，在信噪比逐渐增大的过程中，未经均衡器均衡的差错率没有明显改善，可知系统中始终存在码间干扰造成的误码；经均衡器均衡后的差错率则有明显改善。

但我们同时也可以看到在信噪比较低情况下，均衡器均衡之后的误码率并没有明显改善，甚至没有未均衡的差错率低，这主要是因为噪声为随机信号，功率大时对源信号影响较大，而且均衡器不易跟踪；当我们把均衡器的步长调低后，跟踪能力增强，差错率降低。

附源程序代码：main_plot.mclear;clc;echo off;close all;N=10000; %指定信号序列长度info=random_binary(N); %产生二进制信号序列SNR_ in _dB=8:1:18; %AWGN信道信噪比for j=1:length(SNR _in_ dB)[y, len ]=channel(info, SNR _in _dB(j)); %通过既有码间干扰又有白噪声信道numoferr=0; %初始误码统计数for i=len+1:N+len, %从第len个码元开始为真实信元if (y(i)<0), %判决译码decis=-1;elsedecis=1;end;if (decis~=info(i-5)), %判断是否误码，统计误码码元个数numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 未经均衡器均衡，得到的误码率end;semilogy(SNR_in_dB,Pe,'red*-'); %未经均衡器，误码率结果图hold on;delta_1=0.11; %指定自适应均衡器的步长delta_2=0.09; %指定自适应均衡器的步长for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_1); %通过自适应均衡器，并设置步长为0.11 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;if (decis~=info(i)),numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后，得到的误码率end;semilogy(SNR _in _ dB, Pe ,'blacko-'); %自适应均衡器均衡之后，误码率结果图 hold on;for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_2); %通过自适应均衡器，并设置步长为0.09 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;if (decis~=info(i)),numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后，得到的误码率end;semilogy(SNR_in_dB,Pe,'blue.-'); %自适应均衡器均衡之后，误码率结果图hold on;xlabel('SNR in dB');ylabel('Pe');title('ISI信道自适应均衡系统仿真');legend('未经均衡器均衡','经自适应均衡器均衡，步长detla=0.11',...'经自适应均衡器均衡，步长detla=0.09');random_binary.m%产生二进制信源随机序列function [info]=random_binary(N)if nargin == 0, %如果没有输入参数，则指定信息序列为10000个码元N=10000;end;for i=1:N,temp=rand;if (temp<0.5),info(i)=-1; % 1/2的概率输出为-1elseinfo(i)=1; % 1/2的概率输出为1endend;channel.m%模拟既有码间干扰又有高斯白噪声的信道function [y,len]=channel(x,snr_in_dB)SNR=exp(snr_in_dB*log(10)/10); %信噪比真值转换sigma=1/sqrt(2*SNR); %高斯白噪声的标准差%指定信道的ISI参数，可以看出此信道质量还是比较差的actual_isi=[0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088];len_ actual _isi=(length(actual_isi)-1)/2;len=len_actual_isi;y=conv(actual_isi,x); %信号通过信道，相当于信号序列与信道模型序列作卷积%需要指出，此时码元序列长度变为N+len-1，译码时我们从第len个码元开始到N+len个结束for i=1:2:size(y,2),[noise(i) noise(i+1)]=gngauss(sigma); %产生噪声end;y=y+noise; %叠加噪声gngauss . m%产生高斯白噪声function [gsrv1,gsrv2]=gngauss(m,sgma)if nargin == 0, %如果没有输入实参，则均方为0，标准差为1m=0; sgma=1;elseif nargin == 1, %如果输入实参为1个参数，则标准差为输入实参，均值为0 sgma=m; m=0;end;u=rand;z=sgma*(sqrt(2*log(1/(1-u))));u=rand;gsrv1=m+z*cos(2*pi*u);gsrv2=m+z*sin(2*pi*u);lm _equalizer .m%LSM算法自适应滤波器实现function [z]=lms_equalizer(y,info,delta)estimated_c=[0 0 0 0 0 1 0 0 0 0 0]; %初始抽头系数K=5;for k=1:size(y,2)-2*K,y_k=y(k:k+2*K); %获取码元，一次11个z_k=estimated_c*y_k'; %各抽头系数与码元相乘后求和e_k=info(k)-z_k; %误差估计estimated_c=estimated_c+delta*e_k*y_k; %计算校正抽头系数z(k)=z_k; %均衡后输出的码元序列end;。

DFE均衡器1.基本原理均衡器用来消除码间干扰，DFE即判决均衡器的主要思路是：一旦一个信息符号被检测并被判定后，就可在检测后续符号之前预测并消除由这个信息符号带来的码间干扰。

其基本功能是消除当前估计中的符号间干扰，这个干扰是由前面检测的符号流引起的。

2．仿真程序（1）DFE主程序如下：clear allclose allclcglobal cir_matrix_tglobal Nglobal flagflag = 1;snr = [6:16];iter_num = 10;N = 1000;ber = [];for snr_index=1:length(snr)err = 0;lambda = power(10,-snr(snr_index)/20);for iter =1:iter_numequal_bit = [];bit_signal = randint(1,N)；% bit_signal为1000列的随机矩阵，矩阵的元素为0和1modul_signal = mod_4PSK(bit_signal);rx_sym = Through_channel(modul_signal,N/2);rx_signal = awgn(rx_sym,snr(snr_index));% rx_signal = rx_symequal_signal = equalizer(rx_signal,lambda);for k=1:N/2if real(equal_signal(1,k))>0.5equal_bit = [equal_bit 0 0];elseif real(equal_signal(1,k)<-0.5)equal_bit = [equal_bit 1 1];elseif imag(equal_signal(1,k))>0.5equal_bit = [equal_bit 1 0];else equal_bit = [equal_bit 0 1 ];endenderrr = sum(abs(equal_bit-bit_signal));err = err+ errr;enderr/(N*iter_num);snr_index;ber = [ber err/(N*iter_num)];endbersemilogy(snr,ber,'*-')hold ongrid on（2）equalizer子程序如下：function equal_out = equalizer(in_signal,lambda)global cir_matrix_tglobal Nglobal flagNf = 16;Nb = 8;len = length(in_signal);b_signal = zeros(1,Nb);for k = 1:N/2cir = cir_matrix_t(:,k).';cir_len = length(cir);Hff = convmtx(cir,Nf);Hfb = Hff(:,end-cir_len+2:end);Hfb = [Hfb,zeros(16,Nb-cir_len+1)];Vff = eye(Nf+cir_len-1);Vff(Nf+1:end,Nf+1:end) = zeros(cir_len-1);Sff = Hff(:,Nf);Fffn = inv(Hff*Vff*Hff'+(lambda^2)*eye(Nf))*Sff;Ffb = -Hfb'*Fffn;f_signal = [zeros(1,max(0,k+Nf-1-len)) in_signal(min(len,k+Nf-1):-1:k) ].';out_sym = Fffn'*f_signal+Ffb'*b_signal.';equal_out(1,k) = hard_4QAM_demodul(out_sym);b_signal = [equal_out(1,k) b_signal(1:end-1)];end（3）hard_4QAM_demodul子程序如下：function symb_hard =hard_4QAM_demodul(in_signal)in_signal = in_signal*exp(j*pi/4);if real(in_signal)>0if imag(in_signal)>0symb_hard = 1;else symb_hard = -1*i;endelseif imag(in_signal)>0symb_hard = i;else symb_hard = -1;endend（4）Through_channel子程序如下：function rx_signal = Through_channel(tx_signal,signal_len)global cir_matrix_tglobal flagcir_matrix = [];if flag == 0C2=[-0.59175538208125-0.26921505269338i; 0 ; 0 ; 0 ; 0 ;0 ;-0.75903722101890-0.034804026909066i];elseC2=[0.2 1 0.3162 -0.2 0.1 -0.05 0.02].';C2= C2/norm(C2)';endc_end = [0.2 1 0.3162 -0.2 0.1 -0.05 0.02].';%[-0.3920 0.0152 0.8320 0.0152 -0.3920 0.0178 0.163].';c_end = c_end/norm(c_end);% cir_cir = C2 ;cir_len = length(c_end);cir_matrix = [cir_matrix C2];for k=1:signal_len+cir_len-1cir_matrix = [cir_matrix C2+(c_end-C2)/(2*(signal_len+cir_len-1))];endcir_matrix_t = cir_matrix;[ cir_len , conv_len] = size(cir_matrix) ;tx_temp=zeros(1,cir_len);for k=1:conv_lenif k<signal_len+1tx_temp = [tx_signal(1,k) tx_temp(1,1:end-1)];else tx_temp = [0 tx_temp(1,1:end-1)];endcir = cir_matrix(:,k);cir = cir/norm(cir)';rx_signal(1,k) = tx_temp * cir;end（5）mod_4PSK子程序如下：function y=mod_4PSK(x)% 4PSK Modulator% x -- binary input bits. The length of x must be multiples of 4.% y -- complex output. vectorcons =exp(j*([ 8 2 6 4]*pi/4));% cons =exp(j*([ 1 8 2 3 7 6 5 4]*pi/4));temp = reshape(x,2,length(x)/2);y = cons(bi2de(temp')+1);3．运行结果如下ber = 0.0486 0.0338 0.0203 0.0069 0.0057 0.0021 0.0005 0 0 0 0678910111210101010。

基于Matlab的数字滤波器设计及均衡器设计1数字滤波器设计背景及目的数字滤波器是一个离散时间系统，是一种按预定的算法，将输入离散时间信号转换为所要求的输出离散时间信号的特定功能装置。

数字滤波器具有高精度、高可靠性、可程控改变特性或复用、便于集成等优点。

数字滤波器在语言信号处理、图像信号处理、医学生物信号处理以及其他应用领域都得到了广泛应用。

数字滤波器有低通、高通、带通、带阻和全通等类型。

它可以是时不变的或时变的、因果的或非因果的、线性的或非线性的。

应用最广的是线性、时不变数字滤波器，以及FIR滤波器。

本次设计的目的是在Matlab R2007a的软件平台上，应用所学知识，设计一款FIR数字滤波器，要求有便于用户操作的用户界面，能完成低通、高通、带通及带阻等常用滤波功能。

2数字滤波器设计原理数字滤波器可以按所处理信号的维数分为一维、二维或多维数字滤波器。

一维数字滤波器处理的信号为单变量函数序列，例如时间函数的抽样值。

二维或多维数字滤波器处理的信号为两个或多个变量函数序列。

例如，二维图像离散信号是平面坐标上的抽样值。

本次设计的滤波器属于一维数字滤波器。

数字滤波器的优点是利用差分方程可求离散系统的瞬态解，如下图2所示。

FIR滤波器又称为有限脉冲响应滤波器，FIR就来源于名词“有限脉冲响应”的英文单词首字符缩写。

FIR传递函数：脉冲响应函数：由于h(k)是一个有限长度的序列，故FIR滤波器称为有限脉冲响应滤波器。

FIR滤波器的滤波公式：y(k)=h(0)x(k-m/2)+h(1)x(k-m/2+1) +...+h(m) x(k+m/2)FIR滤波器系数脉冲响应函数设计方法如下其中低通、高通、带通及带阻的设计原理如下图所示。

3设计内容7.3 搭建GUI界面Matlab环境下的图形用户界面（GUI）是由窗口、光标、按键、菜单、文字说明等对象（Objects）构成的一个用户界面。

用户通过一定的方法（如鼠标或键盘）选择、激活这些图形对象，使计算机产生某种动作或变化，比如实现计算、绘图等。

目录1.引言 (2)2.同类产品的比较 (2)3.设计原理 (3)3.1滤波器的设计 (3)3.2均衡器的设计 (4)4.具体设计步骤 (5)4.1界面设计 (5)4.2.程序设计 (7)4.2.1滤波函数 (7)4.2.2均衡器 (8)5.误差分析 (11)6.总结 (11)7.心得与建议 (11)8.参考文献： (12)1.引言均衡器（Equalizer、EQ，港台地区叫做等化器），是一种可以分别调节各种频率成分电信号放大量的电子设备，通过对各种不同频率的电信号的调节来补偿扬声器和声场的缺陷，补偿和修饰各种声源及其它特殊作用，一般调音台上的均衡器仅能对高频、中频、低频三段频率电信号分别进行调节。

均衡器分为三类：图示均衡器，参量均衡器和房间均衡器。

]1[运用数字滤波器组成的均衡器称为数字均衡器，数字均衡器即可作成图示EQ，有可做成参量EQ，还可以做成两者兼有的EQ，它不仅各项性能指标优异，操作方便，而且还可同时储存多种用途的频响均衡特性，供不同节目要求选用，可多至储存99种频响特性曲线。

]2[现在市面上的数字均衡器种类繁多，根据所要使用的场合不同，均衡器的参数设置和具体功能也不尽相同。

本项目的均衡器的设计主要基于MATLAB的图形用户界面和后台程序开发。

所设计出来的仪器功能非常简单，操作也比较容易。

2.同类产品的比较几乎每个人的电脑上都有千千静听这个软件，在其播放界面上就附有十段数字均衡器，可供用户调节。

界面如图所示：图2.1 千千静听均衡器界面3.项目综述按照老师的要求，本文需要完成八段数字均衡器的设计，以达到对声音信号的处理效果。

具体实施中，我利用的是MATLAB这个软件来实现的。

MATLAB 是一个数据分析和处理功能十分强大的工程实用软件，他的滤波器设计工具箱为实现声音信号的数字滤波提供了十分方便的函数和命令。

但它也有明显的缺点，就是运算速度比较慢。

当所要处理的声音信号比较复杂时，其滤波过程往往要耗一小段时间，有事甚至会达到一秒多。

一：应用背景利用所学习的数字信号处理知识，自己动手制作一个有趣的音效处理系统，看看能不能完成声音的逐渐放大和逐渐衰减、看看能不能让自己的声音发生一些改变（变得尖声尖气或粗声粗气）、看看改变声音播放速度有什么方法等等，你还可以自己想想还有什么有趣的变化，可以通过我们已有的知识让它实现。

作为课程设计，以下要求分为基本必做部分和提高必做部分，在提高部分你可以选择全部内容和部分内容，当然分数值是不一样。

二、基于MATLAB数字音效处理器2.1：实现步骤基本要求描述（40分）1）语音信号的采集（2分）要求利用Windows下的录音机,录制一段自己的话音,时间在5s内，存为*.WA V的文件。

然后在Matlab软件平台下,利用函数wavread对语音信号进行采样,记住采样频率和采样点数。

2）语音信号的频谱分析（10分）要求首先画出语音信号的时域波形;然后对语音号进行快速傅里叶变换,得到信号的频谱特性，分析基频。

3）设计数字滤波器和画出其频率响应（10分）给出各滤波器的性能指标：(1)低通滤波器性能指标fb＝1 000 Hz,fc＝1 200 Hz,As＝100 dB,Ap＝1 dB。

(2)高通滤波器性能指标fc＝4 800 Hz,fb＝5 000 Hz As＝100 dB,Ap＝1 dB。

(3)带通滤波器性能指标fb1＝1 200 Hz,fb2＝3 000 Hz,fc1＝1 000 Hz,fc2＝3 200 Hz,As ＝100 dB,Ap＝1 dB。

4）用滤波器对信号进行滤波（5分）要求学生用自己设计的各滤波器分别对采集的信号进行滤波,在Matlab中,FIR滤波器利用函数fftfilt对信号进行滤波,IIR滤波器利用函数filter对信号进行滤波。

5）比较滤波前后语音信号的波形及频谱（10分）要求在一个窗口同时画出滤波前后的波形及频谱，做出分析。

6）回放语音信号（1分）在Matlab中,函数sound可以对声音进行回放。

摘要毕业设计（论文）原创性声明和使用授权说明原创性声明本人郑重承诺：所呈交的毕业设计（论文），是我个人在指导教师的指导下进行的研究工作及取得的成果。

尽我所知，除文中特别加以标注和致谢的地方外，不包含其他人或组织已经发表或公布过的研究成果，也不包含我为获得及其它教育机构的学位或学历而使用过的材料。

对本研究提供过帮助和做出过贡献的个人或集体，均已在文中作了明确的说明并表示了谢意。

作者签名：日期：指导教师签名：日期：使用授权说明本人完全了解大学关于收集、保存、使用毕业设计（论文）的规定，即：按照学校要求提交毕业设计（论文）的印刷本和电子版本；学校有权保存毕业设计（论文）的印刷本和电子版，并提供目录检索与阅览服务；学校可以采用影印、缩印、数字化或其它复制手段保存论文；在不以赢利为目的前提下，学校可以公布论文的部分或全部内容。

作者签名：日期：学位论文原创性声明本人郑重声明：所呈交的论文是本人在导师的指导下独立进行研究所取得的研究成果。

除了文中特别加以标注引用的内容外，本论文不包含任何其他个人或集体已经发表或撰写的成果作品。

对本文的研究做出重要贡献的个人和集体，均已在文中以明确方式标明。

本人完全意识到本声明的法律后果由本人承担。

作者签名：日期：年月日学位论文版权使用授权书本学位论文作者完全了解学校有关保留、使用学位论文的规定，同意学校保留并向国家有关部门或机构送交论文的复印件和电子版，允许论文被查阅和借阅。

本人授权大学可以将本学位论文的全部或部分内容编入有关数据库进行检索，可以采用影印、缩印或扫描等复制手段保存和汇编本学位论文。

涉密论文按学校规定处理。

作者签名：日期：年月日导师签名：日期：年月日注意事项1.设计（论文）的内容包括：1）封面（按教务处制定的标准封面格式制作）2）原创性声明3）中文摘要（300字左右）、关键词4）外文摘要、关键词5）目次页（附件不统一编入）6）论文主体部分：引言（或绪论）、正文、结论7）参考文献8）致谢9）附录（对论文支持必要时）2.论文字数要求：理工类设计（论文）正文字数不少于1万字（不包括图纸、程序清单等），文科类论文正文字数不少于1.2万字。

文章主题：深入理解mmse均衡的matlab代码一、引言在通信系统中，信道均衡是非常重要的环节，它可以帮助系统在传输过程中减小信号受到的衰减和失真。

而在数字通信领域中，mmse （最小均方误差）均衡是一种常见且有效的均衡方法。

本文将围绕着mmse均衡的matlab代码展开深入讨论，旨在帮助读者更全面地理解这一主题。

二、mmse均衡的原理和过程在通信系统中，信道的衰减和失真会导致信号的受损，从而影响接收端对信号的正确解析。

而mmse均衡正是为了解决这一问题而提出的一种均衡方法。

其原理是通过最小化接收信号与发送信号之间的均方误差，从而实现信道均衡。

matlab代码实现mmse均衡的过程主要包括以下几个步骤：1. 接收到信号的采样和量化2. 估计信道的冲激响应3. 生成mmse均衡器4. 对接收信号进行mmse均衡处理5. 输出均衡后的信号三、mmse均衡的matlab代码实现在matlab中，可以使用一系列函数和工具箱来实现mmse均衡。

我们可以先利用matlab中的函数对接收信号进行采样和量化，并利用信道估计工具箱来估计信道的冲激响应。

可以借助matlab中的滤波器设计工具箱来生成mmse均衡器，并将接收信号输入均衡器进行处理。

我们可以得到经过mmse均衡处理后的输出信号。

四、个人观点和理解在对mmse均衡的matlab代码进行深入研究后，我对其有了更深刻的理解。

我认为，mmse均衡作为一种经典的均衡方法，不仅在理论上具有很强的可行性，在实际应用中也展现出了良好的性能。

而通过编写和理解mmse均衡的matlab代码，我对其实现原理和过程有了更清晰的认识，从而可以更好地应用于实际工程项目中。

五、总结通过上述讨论，我们对mmse均衡的matlab代码有了全面的了解。

从理论原理到实际代码实现，我们对这一主题有了更为深刻的认识。

采用mmse均衡处理的通信系统可以更好地抵抗信道的衰减和失真，从而提高系统的性能和可靠性。

Graphic Equalizer Project——project2Xun Wang10112746101.introductionWith the rapidly development of digital technology,people have higher and higher requirement on the graphics,waves and sounds produced by electronics.In the process of real-time processing digital signals,Thereconstruction of analog signal which relates to D/A and A/D transform is the most important in deciding the quality of the output signal of digitalsystem.In the processes of reading sound signal and transfer it through audio devices,the amplitude responses to frequency are not consistent,that leads to the output sound to be not perfect.So we use equalizer to promote the performance of these devices by control the amplitudes of signals in different frequencies in order to make our sense of hearing comfortable.2.2.FilterFilter design Step1：calculate the ideal impulse responseIn order to design a FIR digital band-pass filter,the first thing we should to is to set the frequency properties of ideal band-pass filter which can be used to approach to.The frequency properties of a ideal band-pass filter can be expressed as:()⎪⎩⎪⎨⎧ω≤ω≤ω=ωothers e H j d 0121(2-1)In order to explain the problem clearly,we set ()2210ω+ω=ω,()212ω−ω=ωd .0ωis the center frequency of pass-band,d ωis half of the width of pass-band.Taking Fourier transform of ()ωj d e H :[]()∫ππ−ωωωπ=d e e H n h j j d d 21()()⎟⎠⎞⎜⎝⎛ω+ωπ=∫∫ω+ωω−ωωω−ω−ω+ω−ωd d d d d e d e n j n j 000021()()⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛+⎟⎟⎠⎞⎜⎜⎝⎛π=ω+ωω−ωωω−ω−ω+ω−ωd d d d n j n j e jn e jn 00001121()()()()()()()n j n j n j n j d d d d e e e e jn ω−ωω+ωω+ω−ω−ω−−+−π=000021()()()()()n j n j jn d d ω−ω−ω+ωπ=00sin 2sin 221()()+∞<<∞−ωωπ=n n n n d 0cos sin 2(2-2)Step2:Select the type of windowIn this project,I choose rectangle window and bartlett window.Their impulse response areFig.1rectangle windowFig.2bartlett windowStep3:calculate the real impulse responseBecause []n h d is equation (2-2)and it is infinite,we must change it to afinite one.So we take a window to multiply it to get [][]][*n w n h n h d =,which is finite.Taking the middle band as an example,the figure of ][n h is:Fig.3real impulse response after passed thorough rectangle windowFig.4real impulse response after passed thorough bartlett windowStep4:take fourier transform on real impulse response signal After we get ][n h ,we just need to take fft transform on it,then we can get a band-pass filter in frequency domain.This is the output we need.This is the frequency response of the middle band.Fig.5Amplitude of the middle band filterFrom this figure we can find that the filter made with rectangle window has the biggest passband ripple and steepest transition band,and the filter made with bartlett window has a smooth passband,but it is a little lower than the ideal filter in passband,and the transition band of it is not as steep as filter made with rectangle window.Step5:compose the five filtersIn the main program,I call the function five times and sum them up to get a filter produced with rectangle window method which can be expressed as54321323132h h h h h h ++++=.The situation is the same as filter produced by bartlett window.So we get two filters,their magnitude frequency response curves are:Fig.6the composed filter with rectangle windowFig.7the composed filter with rectangle window3.Experimental ResultsThe filtering process can be explained in the block diagram below:Fig.8block diagram of the systemThe original sound is stored in a.wav document.We can use wavread() function to load the sound into a matrix.The spectrum of the original signalis:Fig.9spectrum of the original sound signalWe can find that there are two different colors in the spectrum.This means there are two channels in the signal.In order to explain this problem clearly,I seperate the signal into two channels and stored them in differentmatrix,xxx1and xxx2.The spectrum of the two tracks are:Fig.10spectrum of the signals of two tracksThe spectrogram of the input signal is:Fig.11spectrogram of the input signalThen we pass the original signal through the filter.Because the length of signal is262128,and the length of filter is1024,they are different.So we should use convolution on the two channels of signals and filter to get the response.We can pass the signal through the five signals and then compose them,but because of the properties of convolution,we can also compose the five filters together and then pass the signal through.It means:s_out=h1*s+h2*s+h3*s+h4*s+h5*s=(h1+h2+h3+h4+h5)*s(2-3) Then we recompose the signal of to two channels to get the intact signal.The wave of the signal filtered in time domain are:Fig.12spectrum of filtered signals in time domainFig.13spectrum of signal in frequencydomain(rectangle window and bartlett window)Fig.14spectrogram of the signal filtered by rectangle filter Fig.15spectrogram of the signal filtered by bartlett filterCompare Fig.14and Fig.15to Fig.11,we can find that the signal in middle frequency band is badly weakened,and the signal in second and forth band is also weakened,but not as badly as in middle band.4.ConclusionIn design this filter I have acquired many knowledge in this field and thoroughly know the windowing method.I think there are many things we can do to improve this project,such as design a interactive controllable window to change the magnitude of every filter.Then we can give this product to users.We can also beautify this controllable window. Appendix:Function matlab code(to get filters):function[HHreturn,h]=getfilter(a,b,c,kind)%This function is used to acquire a filter,HHreturn is the filter in%frequency domain,h is the filter in time domain.a is the normalized low%cutoff frequency,b is the normalized high cutoff frequency.c is the%normalized bandwidth of the filter.kind is used to decide the window we use in design the filter.wpl=a;wph=b;%assign the low and high cutoff frequencies to wpl and wph%[bbb,fs]=wavread('gorka.wav');%read the sound to get fsN1=c;%Set the number of point of sampling the ideal impulse response function belowN=1025;%length(bbb(:,1));wd=(b-a)/2;w0=wpl+wd;M=(N1-1)/2;nn=-M:M;n=nn+eps;%wd is half of the passband width,w0is center frequency,nn is the scope of%sampling on hd,n is a integer.hd=2*sin(wd*n).*cos(w0*n)./(pi*n);%ideal impulse responseswitch kindcase'bartlett'w=window(@bartlett,N1);case'barthannwin'w=window(@barthannwin,N1);case'blackman'w=window(@blackman,N1);case'blackmanharris'w=window(@blackmanharris,N1);case'bohmanwin'w=window(@bohmanwin,N1);case'chebwin'w=window(@chebwin,N1);case'flattopwin'w=window(@flattopwin,N1);case'gausswin'w=window(@gausswin,N1);case'hamming'w=window(@hamming,N1);case'hann'w=window(@hann,N1);case'kaiser'w=window(@kaiser,N1);case'nuttallwin'w=window(@nuttallwin,N1);case'parzenwin'w=window(@parzenwin,N1);case'rectwin'w=window(@rectwin,N1);case'taylorwin'w=window(@taylorwin,N1);case'tukeywin'w=window(@tukeywin,N1);case'triang'w=window(@triang,N1);end%select the kind of windowh=hd.*w';%get filter in time domainHreturn=fft(h,1025);HHreturn=fftshift(Hreturn);%get filter in frequency domainH=20*log10(abs(fft(h,1025)));HH=fftshift(H);figure;subplot(221),stem(nn,hd,'k');xlabel('n');ylabel('hd');title('ideal impulse response');axis([-M M-0.41.0]);subplot(222),stem(nn,w,'k');axis([-M M-0.11.2]);title('window');xlabel('n');subplot(223),stem(nn,h,'k');axis([-M M-0.41.0]);xlabel('n');ylabel('h');title('real impulse response');w=(-(N/2):(N/2-1))/(N/2-1);subplot(224),plot(w,HH,'k');axis([-11-10010]);xlabel('\omega/\pi');ylabel('|H(w)|(dB)')title('amplitude of filter');set(gcf,'color','w');%plot ideal impulse response,window,real impulse response and filterMain program:clear all;clc;close all;lenth=ceil(11*pi/((400/22050)*pi));%set the number of sample[Y1_rec,h1_rec]=getfilter(0,(400/22050)*pi,lenth,'rectwin');[Y1_bar,h1_bar]=getfilter(0,(400/22050)*pi,lenth,'bartlett');[Y2_rec,h2_rec]=getfilter((400/22050)*pi,(2500/22050)*pi,lenth,'rectwin'); [Y2_bar,h2_bar]=getfilter((400/22050)*pi,(2500/22050)*pi,lenth,'bartlett'); [Y3_rec,h3_rec]=getfilter((2500/22050)*pi,(6000/22050)*pi,lenth,'rectwin'); [Y3_bar,h3_bar]=getfilter((2500/22050)*pi,(6000/22050)*pi,lenth,'bartlett'); [Y4_rec,h4_rec]=getfilter((6000/22050)*pi,(11000/22050)*pi,lenth,'rectwin'); [Y4_bar,h4_bar]=getfilter((6000/22050)*pi,(11000/22050)*pi,lenth,'bartlett'); [Y5_rec,h5_rec]=getfilter((11000/22050)*pi,1*pi,lenth,'rectwin');[Y5_bar,h5_bar]=getfilter((11000/22050)*pi,1*pi,lenth,'bartlett');%call filter for ten times to get two sets of filters with different%windowsYY1_rec=Y1_rec;hh1_rec=h1_rec;YY1_bar=Y1_bar;hh1_bar=h1_bar;YY2_rec=(2/3)*Y2_rec;hh2_rec=(2/3)*h2_rec;YY2_bar=(2/3)*Y2_bar;hh2_bar=(2/3)*h2_bar;YY3_rec=(1/3)*Y3_rec;hh3_rec=(1/3)*h3_rec;YY3_bar=(1/3)*Y3_bar;hh3_bar=(1/3)*h3_bar;figure;cc2=linspace(-22050,22050,length(YY3_rec));plot(cc2,abs(YY3_rec),'c');hold on;cc3=linspace(-22050,22050,length(YY3_bar));plot(cc3,abs(YY3_bar),'--r');hold on;ideal_Y=zeros(1,1025);ideal_Y(1,374:455)=1/3;ideal_Y(1,571:652)=1/3;cc1=linspace(-22050,22050,1025);plot(cc1,abs(ideal_Y),'k');axis([-220502205000.41]);xlabel('f');ylabel('|H(w)|');title('amplitude of the middle filter');legend('rectangle window filter','bartlett window filter','ideal filter'); set(gcf,'color','w');%plot the frequency response of two middle filters with different %windows and ideal filter.YY4_rec=(2/3)*Y4_rec;hh4_rec=(2/3)*h4_rec;YY4_bar=(2/3)*Y4_bar;hh4_bar=(2/3)*h4_bar;YY5_rec=Y5_rec;hh5_rec=h5_rec;YY5_bar=Y5_bar;hh5_bar=h5_bar;YY_rec=YY1_rec+YY2_rec+YY3_rec+YY4_rec+YY5_rec;YY_bar=YY1_bar+YY2_bar+YY3_bar+YY4_bar+YY5_bar;h_rec=hh1_rec+hh2_rec+hh3_rec+hh4_rec+hh5_rec;h_bar=hh1_bar+hh2_bar+hh3_bar+hh4_bar+hh5_bar;%sum five filters up to get the intact filterfigure;[x,fs]=wavread('gorka.wav');vv=linspace(-(fs/2),(fs/2),length(x));plot(vv,fftshift(abs(fft(x))));axis([-(fs/2)(fs/2)-501600]);xlabel('f');ylabel('amplitude of original sound');set(gcf,'color','w');%plot the frequency response of signalfigure;N=1025;w=linspace(-22050,22050,length(YY_rec));plot(w,abs(YY_rec),'k');axis([-(fs/2)(fs/2)01.2]);xlabel('f');ylabel('H(w)');title('amplitude of the sum of rectangle filter');set(gcf,'color','w');figure;%plot frequency response of filter with rectangle windowww=(1:(N/2))/(N/2);semilogx(((10^4)*ww),abs(YY_rec(((N/2)+1):N)),'k');xlabel('\omega/\pi');ylabel('H(w)');title('amplitude of the sum of rec_filter(log)');set(gcf,'color','w');figure;%plot filter when x is expressed in logw=linspace(-22050,22050,length(YY_bar));plot(w,abs(YY_bar),'k');axis([-(fs/2)(fs/2)01.2]);xlabel('f');title('amplitude of the sum of bartlett filter');set(gcf,'color','w');figure;%plot frequency response of filter with bartlett windowww=(1:(N/2))/(N/2);semilogx(((10^4)*ww),abs(YY_bar(((N/2)+1):N)),'k');xlabel('\omega/\pi');title('amplitude of the sum of bar_filter(log)'); set(gcf,'color','w');figure;%plot filter when x is expressed in logsubplot(221);plot(x(:,1),'b');axis([0length(x(:,1))-0.350.35]);title('wave of track1sound');xxx1=x(:,1)';subplot(222);plot(x(:,2),'r');axis([0length(x(:,2))-0.350.35]);title('wave of track2sound');xxx2=x(:,2)';%seperate signal into two tracksyyy11=fft(xxx1);yyy1=fftshift(yyy11);Nsignal=length(x(:,1));w=(-(Nsignal/2):((Nsignal/2)-1))/((Nsignal/2)-1);subplot(223);plot(w,abs(yyy1),'b');axis([-1.11.1-21300]);xlabel('\omega/\pi');title('spectrum of track1sound');yyy22=fft(xxx2);yyy2=fftshift(yyy22);w=(-(Nsignal/2):((Nsignal/2)-1))/((Nsignal/2)-1);subplot(224);plot(w,abs(yyy2),'r');axis([-1.11.1-21300]);xlabel('\omega/\pi');title('spectrum of track2sound');set(gcf,'color','w');%plot the signals of two tracks in time and frequency domainfigure;ww=(1:(Nsignal/2))/(Nsignal/2);semilogx(((10^4)*ww),abs(yyy1((Nsignal/2+1):Nsignal)),'k');xlabel('\omega/\pi');title('spectrum of the track1sound(log)');set(gcf,'color','w');figure;ww=(1:(Nsignal/2))/(Nsignal/2);semilogx(((10^4)*ww),abs(yyy2((Nsignal/2+1):Nsignal)),'k');xlabel('\omega/\pi');title('spectrum of the track2sound(log)');set(gcf,'color','w');figure;%plot the signals of two tracks in time and frequency domain when x is log signaloutrec1=conv(h_rec,xxx1);signaloutrec2=conv(h_rec,xxx2);signaloutrec(:,1)=signaloutrec1';signaloutrec(:,2)=signaloutrec2';%filtering signal of two tracks with reatangle window filter signaloutbar1=conv(h_bar,xxx1);signaloutbar2=conv(h_bar,xxx2);signaloutbar(:,1)=signaloutbar1';signaloutbar(:,2)=signaloutbar2';%filtering signal of two tracks with bar window filterplot(real(signaloutrec));axis([0length(signaloutrec)-0.350.35]);title('spectrum of sound pass rectangle window');set(gcf,'color','w');figure;%plot the signal filtered by rectangle window filter in time domainplot(real(signaloutbar));axis([0length(signaloutbar)-0.350.35]);title('spectrum of sound pass bartlett window');set(gcf,'color','w');figure;%plot the signal filtered by bartlett window filter in time domain soundy1recfft=abs(fftshift(fft(signaloutrec)));Nplot1=linspace(-(fs/2),(fs/2),length(signaloutrec1));plot(Nplot1,soundy1recfft);axis([-(fs/2)(fs/2)-501200]);xlabel('f');ylabel('amplitude of sound');title('wave filtered by rectangle filter');set(gcf,'color','w');%plot the signal filtered by rectangle window filter in frequency domain figure;soundy1barfft=abs(fftshift(fft(signaloutbar)));Nplot2=linspace(-(fs/2),(fs/2),length(signaloutbar1));plot(Nplot2,soundy1barfft);axis([-(fs/2)(fs/2)-501200]);xlabel('f');ylabel('amplitude of sound');title('wave filtered by bartlett filter');set(gcf,'color','w');%plot the signal filtered by bartlett window filter in frequency domain figure;specgram(x(:,1),1025,fs);title('spectrogram of input signal');set(gcf,'color','w');figure;specgram(signaloutrec(:,1),1025,fs);title('spectrogram of output signal(rectangle window)');set(gcf,'color','w');figure;specgram(signaloutbar(:,1),1025,fs);title('spectrogram of output signal(bartlett window)');set(gcf,'color','w');%plot the spectrogram of input and output signals。

DFE均衡器1.基本原理均衡器用来消除码间干扰，DFE即判决均衡器的主要思路是：一旦一个信息符号被检测并被判定后，就可在检测后续符号之前预测并消除由这个信息符号带来的码间干扰。

其基本功能是消除当前估计中的符号间干扰，这个干扰是由前面检测的符号流引起的。

2．仿真程序（1）DFE主程序如下：clear allclose allclcglobal cir_matrix_tglobal Nglobal flagflag = 1;snr = [6:16];iter_num = 10;N = 1000;ber = [];for snr_index=1:length(snr)err = 0;lambda = power(10,-snr(snr_index)/20);for iter =1:iter_numequal_bit = [];bit_signal = randint(1,N)；% bit_signal为1000列的随机矩阵，矩阵的元素为0和1modul_signal = mod_4PSK(bit_signal);rx_sym = Through_channel(modul_signal,N/2);rx_signal = awgn(rx_sym,snr(snr_index));% rx_signal = rx_symequal_signal = equalizer(rx_signal,lambda);for k=1:N/2if real(equal_signal(1,k))>0.5equal_bit = [equal_bit 0 0];elseif real(equal_signal(1,k)<-0.5)equal_bit = [equal_bit 1 1];elseif imag(equal_signal(1,k))>0.5equal_bit = [equal_bit 1 0];else equal_bit = [equal_bit 0 1 ];endenderrr = sum(abs(equal_bit-bit_signal));err = err+ errr;enderr/(N*iter_num);snr_index;ber = [ber err/(N*iter_num)];endbersemilogy(snr,ber,'*-')hold ongrid on（2）equalizer子程序如下：function equal_out = equalizer(in_signal,lambda)global cir_matrix_tglobal Nglobal flagNf = 16;Nb = 8;len = length(in_signal);b_signal = zeros(1,Nb);for k = 1:N/2cir = cir_matrix_t(:,k).';cir_len = length(cir);Hff = convmtx(cir,Nf);Hfb = Hff(:,end-cir_len+2:end);Hfb = [Hfb,zeros(16,Nb-cir_len+1)];Vff = eye(Nf+cir_len-1);Vff(Nf+1:end,Nf+1:end) = zeros(cir_len-1);Sff = Hff(:,Nf);Fffn = inv(Hff*Vff*Hff'+(lambda^2)*eye(Nf))*Sff;Ffb = -Hfb'*Fffn;f_signal = [zeros(1,max(0,k+Nf-1-len)) in_signal(min(len,k+Nf-1):-1:k) ].';out_sym = Fffn'*f_signal+Ffb'*b_signal.';equal_out(1,k) = hard_4QAM_demodul(out_sym);b_signal = [equal_out(1,k) b_signal(1:end-1)];end（3）hard_4QAM_demodul子程序如下：function symb_hard =hard_4QAM_demodul(in_signal)in_signal = in_signal*exp(j*pi/4);if real(in_signal)>0if imag(in_signal)>0symb_hard = 1;else symb_hard = -1*i;endelseif imag(in_signal)>0symb_hard = i;else symb_hard = -1;endend（4）Through_channel子程序如下：function rx_signal = Through_channel(tx_signal,signal_len)global cir_matrix_tglobal flagcir_matrix = [];if flag == 0C2=[-0.59175538208125-0.26921505269338i; 0 ; 0 ; 0 ; 0 ;0 ;-0.75903722101890-0.034804026909066i];elseC2=[0.2 1 0.3162 -0.2 0.1 -0.05 0.02].';C2= C2/norm(C2)';endc_end = [0.2 1 0.3162 -0.2 0.1 -0.05 0.02].';%[-0.3920 0.0152 0.83200.0152 -0.3920 0.0178 0.163].';c_end = c_end/norm(c_end);% cir_cir = C2 ;cir_len = length(c_end);cir_matrix = [cir_matrix C2];for k=1:signal_len+cir_len-1cir_matrix = [cir_matrix C2+(c_end-C2)/(2*(signal_len+cir_len-1))];endcir_matrix_t = cir_matrix;[ cir_len , conv_len] = size(cir_matrix) ;tx_temp=zeros(1,cir_len);for k=1:conv_lenif k<signal_len+1tx_temp = [tx_signal(1,k) tx_temp(1,1:end-1)];else tx_temp = [0 tx_temp(1,1:end-1)];endcir = cir_matrix(:,k);cir = cir/norm(cir)';rx_signal(1,k) = tx_temp * cir;end（5）mod_4PSK子程序如下：function y=mod_4PSK(x)% 4PSK Modulator% x -- binary input bits. The length of x must be multiples of 4.% y -- complex output. vectorcons =exp(j*([ 8 2 6 4]*pi/4));% cons =exp(j*([ 1 8 2 3 7 6 5 4]*pi/4));temp = reshape(x,2,length(x)/2);y = cons(bi2de(temp')+1);3．运行结果如下ber = 0.0486 0.0338 0.0203 0.0069 0.0057 0.0021 0.0005 0 0 0 0678910111210101010。

2．设计原理2.1数字滤波器数字滤波器的原理简介数字滤波器的功能是把输入序列通过一定的运算，变换成输出序列。

数字滤波器一般可用两种方法实现：一种是根据描述数字滤波器的数学模型或信号流程图，用数字硬件构成专用的数字信号处理机，即硬件方式；另一种是编写滤波器运算程序，在计算机上运行，即软件方式。

考虑到软件的灵活性及易于实现，本文采用软件方式实现数字滤波器。

数字滤波器有无限冲激响应(IIR)和有限冲激响应(FIR)两种。

下面分别介绍：(1) IIR滤波器IIR滤波器的特点是：单位冲激响应h(n)是无限长的；系统函数H(z)在有限长Z平面（0<|Z|<∞)有极点存在；结构上存在输出到输入的反馈，也即结构上是递归型的；因果稳定的IIR滤波器其全部极点一定在单位圆内。

其系统函数为(1)计算机上实现时则需要用到差分方程的形式，如下(2)IIR滤波器有四种基本的网络结构(具体参看文献[3])，直接I型、直接II型、级联型与并联型。

其中直接I型需要2N个延迟单元，而直接II型只需要N个延迟单元。

因此，用软件实现时，直接II型少占用存储单元。

级联型则是将N阶IIR系统函数分解成二阶因式连乘积，并联型则是将系统函数化成部分分式之和，则可得到IIR数字滤波器的并联结构。

(2) FIR滤波器IIR滤波器的特点是：系统的单位冲激响应h(n)是个有限长序列；系统函数|H(z)|在|z|>0处收敛，极点全部在z=0处(即FIR一定为稳定系统)；结构上主要是非递归结构，没有输出到输入反馈。

但有些结构中（例如频率抽样结构）也包含有反馈的递归部分。

其系统函数的一般形式为(3)对应的差分方程为(4)FIR系统的基本结构有直接型、级联型、快速卷积型、频率取样型等。

FIR与IIR滤波器的比较与选择IIR滤波器可以用比FIR滤波器少的阶数来满足相同的技术指标，这样，IIR滤波器所用的存储单元和所用的运算次数都比FIR滤波器少。

电子信息系综合课程设计基于Matlab的自适应均衡器设计专业名称通信工程班级学号学生姓名指导教师设计时间2010.12.20~2011.1.7课程设计任务书专业：学号：学生姓名（签名）：设计题目：基于Matlab的自适应均衡器设计一、设计实验条件实验室，Matlab软件二、设计任务及要求1. 课题要求系统学习时域均衡原理，掌握理论知识；2. 首先进行时域均衡原理和算法设计，再在所用的仿真软件Matlab上对设计进行仿真分析，最后写实验报告；3. 对整个系统设计进行回顾，总结心得。

三、设计报告的内容1.设计题目与设计任务（设计任务书）2.前言（绪论）(设计的目的、意义等)3.设计主体（各部分设计内容、分析、结论等）4.结束语（设计的收获、体会等）5.参考资料四、设计时间与安排1、设计时间：3周2、设计时间安排：熟悉实验设备、收集资料: 4天设计图纸、实验、计算、程序编写调试: 7天编写课程设计报告: 3天答辩: 1天基于Matlab的自适应均衡器设计一、设计目的及意义：通过本学期通信原理课程的学习，主要对数字信号系统的通信原理、传输机制等有了系统深入的了解。

而实践性的课程设计能够起到提高综合运用能力，加强理论知识的学习，提高实验技术，启发创造新思想的效果。

此次课程设计是自适应均衡器设计。

我们按照查找资料、软件选择、系统设计、仿真实现、结果优化这一流程进行。

不仅使我们进一步巩固了课程知识，也提高了我们分析问题、解决问题的能力。

二、设计主体：1 、设计原理数字信号经过这样的信道传输以后，由于受到了信道的非理想特性的影响，在接收端就会产生码间干扰(ISI)，使系统误码率上升，严重情况下使系统无法继续正常工作。

理论和实践证明，在接收系统中插入一种滤波器，可以校正和补偿系统特性，减少码间干扰的影响。

这种起补偿作用的滤波器称为均衡器。

时域均衡是利用均衡器产生的时间波形去直接校正已畸变的波形，使包括均衡器在内的整个系统的冲击响应满无码间串扰条件。

基于MATLAB的自适应均衡器的研究【摘要】:随着科技的发展，如何实现工作高效发展已经成为各个领域的首要因素，在通信领域亦是如此。

ISI（码间串扰）是干扰时变通信质量和传输速度的主要因素。

由于基带传输的通信系统不可能满足实际波形不失真的实时传输系统中，所以串扰是必然会发生的。

通常把消除串扰的滤波器称为均衡器，它其实就是一个逆滤波器通道。

信道失真在高速通信，无线通信中会更加严重，从而信道均衡技术是成为了通信传输中不可缺少的。

在通信系统中，优良的信道均衡器可以弥补信道不理想特性，降低信号传输错误率，从而达到降低信号失真的一种重要技术手段。

本文介绍了自适应均衡器的设计原则，结合递归最小二乘算法和最小均方算法。

最后运用MATLAB进一步分析仿真实现这些算法的自适应线性滤波器并分析其性能。

【关键词】：LMS算法；自适应；线性均衡器；RLS算法Research on Adaptive Equalizer Based on MATLABAbstract：With the development of technology，how to efficiently achieve development has become a primary factor in various field，is also true in the field of communication. ISI is one of the important reasons for varying interference communication quality and transmission speed. Baseband transmission of the communication system can not meet the real-time actual waveform of undistorted transmission system，crosstalk is bound to arise. Crosstalk elimination circuit usually called equalizer came from the principle that it is an inverse filter channel. In communication systems，good channel equalizer to compensate for non-ideal characteristics of the channel in order to minimize signal distortion，an important technology to reduce the transmission error rate of the signal. Channel distortion in a high speed communication，wireless communication is more severe，so that channel equalization techniques become indispensable communication transmission.The article describes the design principles of the adaptive equalizer，combined with recursive least squares algorithm and the minimum mean square algorithm. Finally，further analysis of simulation using MATLAB adaptive linear filter these algorithms and analyze their performance.Key words：LMS algorithm；Adaptive；Linear equalizer；RLS algorithm目录第一章绪论 (1)1.1 均衡器研究背景及意义 (1)1.2 国内外研究现状 (2)1.3 本文研究内容和主要工作 (3)第二章自适应均衡器原理及其分类 (4)2.1 信道 (4)2.2 自适应均衡的原理和特点 (5)2.3自适应滤波器的分类和基本构成 (6)2.4自适应过程 (7)2.5 横向滤波器的实现结构 (8)第三章基于LMS算法的自适应均衡原理 (10)3.1 最小均方(LMS)算法基本原理 (10)3.2 LMS算法 (13)3.3 LMS 算法的应用 (20)第四章基于RLS算法的自适应均衡原理 (21)4.1 RLS算法 (21)4.2 RLS算法的应用 (24)4.3 RLS算法与LMS算法的比较 (24)第五章 LMS与RLS算法的性能仿真及分析 (26)第六章总结 (33)致谢....................................................................................................... 错误！未定义书签。

基于MATLAB的数字滤波器设计摘要：通过Matlab 强大的信号处理功能，分析数字均衡器的设计要求，对各种数字音频信号进行滤波处理，设计出一种比较合理的数字滤波器，并在此基础上设计一种均衡器，最后对该数字滤波器和均衡器进行综合测试并改进，使其达到要求的指标。

关键词： MATLAB；数字滤波器；均衡器一、概述随着数字化技术的快速、深入发展，人们对数字化电子产品所产生的图像、图形以及声音等质量的要求越来越高。

在实时数字处理过程中，与D/A 和A/D 转换相关的模拟信号重构过程是决定数字系统输出质量的关键。

在声音的拾取过程及通过音响设备的传送过程中，由于设备或器件的原因，其幅度对频率的响应往往不一致，这样就达不到原来的效果，往往需要对目标信号进行滤波处理，以满足用户对信号的要求。

MATLAB 是一个数据分析和处理功能十分强大的工程实用软件，它的滤波器设计工具箱为实现声音信号的数字滤波提供了十分方便的函数和命令。

本文将介绍基于MATLAB设计出的一种实用的数字滤波器，并对其功能进行扩展，设计出一种均衡器。

滤波器的种类很多，按所通过信号的频段分为低通、高通、带通和带阻滤波器四种。

低通滤波器：它允许信号中的低频或直流分量通过，抑制高频分量或干扰和噪声。

高通滤波器：它允许信号中的高频分量通过，抑制低频或直流分量。

带通滤波器：它允许一定频段的信号通过，抑制低于或高于该频段的信号、干扰和噪声。

带阻滤波器：它抑制一定频段内的信号，允许该频段以外的信号通过。

上述每种滤波器又可以分为模拟滤波器和数字滤波器。

如果滤波器的输入输出都是数字信号，则这样的滤波器称之为数字滤波器，它通常通过一定的运算关系改变输入信号所含频率成分的相对比例或者滤除某些频率成分来实现滤波。

根据数字滤波器冲激响应的时域特性，可将数字滤波器分为两种，即无限长冲激响应（IIR）滤波器和有限长冲激响应（FIR）滤波器。

根据数字信号处理的一般理论，IIR滤波器的特征是具有无限持续时间的冲激响应，而FIR滤波器使冲激响应只能持续一定的时间。